Сложение и вычитание квадратных корней примеры. Как складывать квадратные корни
Содержимое:
Складывать и вычитать квадратные корни можно только при условии, что у них одинаковое подкоренное выражение, то есть вы можете сложить или вычесть 2√3 и 4√3, но не 2√3 и 2√5. Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).
Шаги
Часть 1 Постигаем основы
- 1 (выражение под знаком корня). Для этого разложите подкоренное число на два множителя, один из которых является квадратным числом (число, из которого можно извлечь целый корень, например, 25 или 9). После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения).
 Вот как решать данную задачу:
Вот как решать данную задачу:- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Здесь вы раскладываете 50 на множители 25 и 2; затем из 25 извлекаете корень, равный 5, и 5 выносите из-под корня. Затем 5 умножаете на 6 (множитель у корня) и получаете 30√2.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Здесь вы раскладываете 12 на множители 4 и 3; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 5 (множитель у корня) и получаете 10√3.
- 2 Подчеркните корни, подкоренные выражения которых одинаковы. В нашем примере упрощенное выражение имеет вид: 30√2 — 4√2 + 10√3. В нем вы должны подчеркнуть первый и второй члены (30√2 и 4√2 ), так как у них одинаковое подкоренное число 2. Только такие корни вы можете складывать и вычитать.

- 3 Если вам дано выражение с большим количеством членов, многие из которых имеют одинаковые подкоренные выражения, используйте одинарное, двойное, тройное подчеркивание для обозначения таких членов, чтобы облегчить решение этого выражения.
- 4
У корней, подкоренные выражения которых одинаковы, сложите или вычтите множители, стоящие перед знаком корня, а подкоренное выражение оставьте прежним (не складывайте и не вычитайте подкоренные числа!
). Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
- 30√2 — 4√2 + 10√3 =
- (30 — 4)√2 + 10√3 =
- 26√2 + 10√3
Часть 2 Практикуемся на примерах
- 1 Пример 1: √(45) + 4√5.
- Упростите √(45). Разложите 45 на множители: √(45) = √(9 x 5).
- Вынесите 3 из-под корня (√9 = 3): √(45) = 3√5.
- Теперь сложите множители у корней: 3√5 + 4√5 = 7√5
- 2 Пример 2: 6√(40) — 3√(10) + √5.

- Упростите 6√(40). Разложите 40 на множители: 6√(40) = 6√(4 x 10).
- Вынесите 2 из-под корня (√4 = 2): 6√(40) = 6√(4 x 10) = (6 x 2)√10.
- Перемножьте множители перед корнем и получите 12√10.
- Теперь выражение можно записать в виде 12√10 — 3√(10) + √5. Так как у первых двух членов одинаковые подкоренные числа, вы можете вычесть второй член из первого, а первый оставить без изменений.
- Вы получите: (12-3)√10 + √5 = 9√10 + √5.
- 3 Пример 3. 9√5 -2√3 — 4√5. Здесь ни одно из подкоренных выражений нельзя разложить на множители, поэтому упростить это выражение не получится. Вы можете вычесть третий член из первого (так как у них одинаковые подкоренные числа), а второй член оставить без изменений. Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
- 4 Пример 4. √9 + √4 — 3√2.
- √9 = √(3 х 3) = 3.
- √4 = √(2 х 2) = 2.
- Теперь вы можете просто сложить 3 + 2, чтобы получить 5.
- Окончательный ответ: 5 — 3√2.

- 5 Пример 5. Решите выражение, содержащее корни и дроби. Вы можете складывать и вычислять только те дроби, у которых общий (одинаковый) знаменатель. Дано выражение (√2)/4 + (√2)/2.
- Найдите наименьший общий знаменатель этих дробей. Это число, которое делится нацело на каждый знаменатель. В нашем примере на 4 и на 2 делится число 4.
- Теперь вторую дробь умножьте на 2/2 (чтобы привести ее к общему знаменателю; первая дробь уже приведена к нему): (√2)/2 х 2/2 = (2√2)/4.
- Сложите числители дробей, а знаменатель оставьте прежним: (√2)/4 + (2√2)/4 = (3√2)/4 .
- Перед суммированием или вычитанием корней обязательно упростите (если возможно) подкоренные выражения.
Предупреждения
- Никогда не суммируйте и не вычитайте корни с разными подкоренными выражениями.
- Никогда не суммируйте и не вычитайте целое число и корень, например,
- Примечание: «х» в одной второй степени и квадратный корень из «х» – это одно и то же (то есть x 1/2 = √х).

- Примечание: «х» в одной второй степени и квадратный корень из «х» – это одно и то же (то есть x 1/2 = √х).
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. 2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.
2 = x, √x = a. Как и над любыми числами, над квадратными корнями можно выполнять арифметические операции сложения и вычитания.
Инструкция
- Во-первых, при сложении квадратных корней попробуйте извлечь эти корни. Это будет возможно, если числа под знаком корня являются полными квадратами. Например, пусть задано выражение √4 + √9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: √4 + √9 = 2 + 3 = 5.
- Если под знаком корня нет полных квадратов, то попробуйте вынести из под знака корня множитель числа. Например, пусть дано выражение √24 + √54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, который можно вынести из под знака квадратного корня. В числе 54 — множитель 9. Таким образом, получается что: √24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6. В данном примере в результате выноса множителя из под знака корня получилось упростить заданное выражение.

- Пусть сумма двух квадратных корней является знаменателем дроби, например, A / (√a + √b). И пусть перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда можно воспользоваться следующим способом. Умножьте числитель и знаменатель дроби на выражение √a — √b. Таким образом в знаменателе получится формула сокращенного умножения: (√a + √b) * (√a — √b) = a – b. По аналогии, если в знаменателе дана разность корней: √a — √b, то числитель и знаменатель дроби необходимо умножить на выражение √a + √b. Для примера, пусть дана дробь 4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3).
- Рассмотрите более сложный пример избавления от иррациональности в знаменателе. Пусть дана дробь 12 / (√2 + √3 + √5). Необходимо умножить числитель и знаменатель дроби на выражение √2 + √3 — √5:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / ((√2 + √3 + √5) * (√2 + √3 — √5)) = 12 * (√2 + √3 — √5) / (2 * √6) = √6 * (√2 + √3 — √5) = 2 * √3 + 3 * √2 — √30.
- И наконец, если вам необходимо только приблизительное значение, то можно посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для каждого числа и запишите с необходимой точностью (например, два знака после запятой). А затем совершите требуемые арифметические операции, как с обычными числами. Например, пусть необходимо узнать приблизительное значение выражения √7 + √5 ≈ 2,65 + 2,24 = 4,89.
Свойства квадратных корней
До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение , деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т. д.
В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.
Доказательство. Введем следующие обозначения:https://pandia. ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»> Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное.
ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»> Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное.
Завершая параграф, отметим еще одно достаточно простое и в то же время важное свойство:
если a > 0 и n — натуральное число , то
Преобразование выражений, содержащих операцию извлечения квадратного корня
До сих пор мы с вами выполняли преобразования толькорациональных выражений , используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т. д. В этой главе мы ввели новую операцию — операцию извлечения квадратного корня; мы установили, что
где, напомним, a, b — неотрицательные числа.
Используя эти формулы , можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения.
Пример 3. Внести множитель под знак квадратного корня:
Пример 6 . Упростить выражение Решение. Выполним последовательные преобразования:
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Как складывать корни с разными показателями.
 Правила вычитания корней
Правила вычитания корнейКвадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .
Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.
Шаг 1. Извлечение квадратных корней
Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.
Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .
В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .
Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .
Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .
Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .
Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .
Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .
Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .
Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально. 2=400\\
\hline \end{array}\]
2=400\\
\hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\]
Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\)
, то первоначально вы должны найти значения \(\sqrt{25}\)
и \(\sqrt{49}\)
, а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\)
или \(\sqrt b\)
при сложении \(\sqrt
a+\sqrt b\)
найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt
2+ \sqrt {49}\)
мы можем найти \(\sqrt{49}\)
– это \(7\)
, а вот \(\sqrt
2\)
никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt
2+7\)
. Дальше это выражение, к сожалению, упростить никак нельзя \(\bullet\)
Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad
\sqrt a:\sqrt b=\sqrt{a:b}\]
(при условии, что обе части равенств имеют смысл )
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot
2}=\sqrt{64}=8\)
;
\(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\)
;
\(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}=
5\cdot 8=40\)
. \(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
\(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\)
. Так как \(44100:100=441\)
, то \(44100=100\cdot 441\)
. По признаку делимости число \(441\)
делится на \(9\)
(так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\)
, то есть \(441=9\cdot 49\)
.
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}=
\sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\]
Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}=
\sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{
\dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot
\sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\)
Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\)
(сокращенная запись от выражения \(5\cdot
\sqrt2\)
). Так как \(5=\sqrt{25}\)
, то \
Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\)
,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\)
. 2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\)
и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\)
(число “пи”, приблизительно равное \(3,14\)
), \(e\)
(это число называют числом Эйлера, приблизительно оно равно \(2,7\)
) и т.д.
\(\bullet\)
Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\)
.
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\)
Модуль вещественного числа \(a\)
– это неотрицательное число \(|a|\)
, равное расстоянию от точки \(a\)
до \(0\)
на вещественной прямой. 2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3
\(\bullet\)
Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\
&\sqrt 3\approx 1,7 \end{aligned}\]
Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\)
Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. 2=168\cdot 168=28224\)
.
2=168\cdot 168=28224\)
.
Следовательно, \(\sqrt{28224}=168\)
. Вуаля!
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор
. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.

- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
Тема про квадратные корни является обязательной в школьной программе курса математики. Без них не обойтись при решении квадратных уравнений. А позже появляется необходимость не только извлекать корни, но и выполнять с ними другие действия. Среди них достаточно сложные: возведение в степень, умножение и деление. Но есть и достаточно простые: вычитание и сложение корней. Кстати, они только на первый взгляд кажутся такими. Выполнить их без ошибок не всегда оказывается просто для того, кто только начинает с ними знакомиться.
Что такое математический корень?
Это действие возникло в противовес возведению в степень. Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Если в степени стоит двойка, то и корень будет квадратным. Он является самым распространенным в школьной математике. У него даже нет указания, что он квадратный, то есть возле него не приписывается цифра 2. Математическая запись этого оператора (радикала) представлена на рисунке.
Из описанного действия плавно вытекает его определение. Чтобы извлечь квадратный корень из некоторого числа, нужно выяснить, какое даст при умножении на себя подкоренное выражение. Это число и будет квадратным корнем. Если записать это математически, то получится следующее: х*х=х 2 =у, значит √у=х.
Какие действия с ними можно выполнять?
По своей сути корень — это дробная степень, у которой в числителе стоит единица. А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
И требования к этим действиям у них одинаковые. Если умножение, деление и возведение в степень не встречают затруднений у учеников, то сложение корней, как и их вычитание, иногда приводит в замешательство. А все потому что хочется выполнить эти операции без оглядки на знак корня. И здесь начинаются ошибки.
По каким правилам выполняется их сложение и вычитание?
Сначала нужно запомнить два категорических «нельзя»:
- нельзя выполнять сложение и вычитание корней, как у простых чисел, то есть невозможно записать подкоренные выражения суммы под один знак и выполнять с ними математические операции;
- нельзя складывать и вычитать корни с разными показателями, например квадратный и кубический.
Наглядный пример первого запрета: √6 + √10 ≠ √16, но √(6 + 10) = √16 .
Во втором случае лучше ограничиться упрощением самих корней. А в ответе оставить их сумму.
Теперь к правилам
- Найти и сгруппировать подобные корни. То есть те, у которых не только стоят одинаковые числа под радикалом, но и они сами с одним показателем.

- Выполнить сложение корней, объединенных в одну группу первым действием. Оно легко осуществимо, потому что нужно только сложить значения, которые стоят перед радикалами.
- Извлечь корни в тех слагаемых, в которых подкоренное выражение образует целый квадрат. Другими словами, не оставлять ничего под знаком радикала.
- Упростить подкоренные выражения. Для этого нужно разложить их на простые множители и посмотреть, не дадут ли они квадрата какого-либо числа. Понятно, что это справедливо, если речь идет о квадратном корне. Когда показатель степени три или четыре, то и простые множители должны давать куб или четвертую степень числа.
- Вынести из-под знака радикала множитель, который дает целую степень.
- Посмотреть, не появилось ли опять подобных слагаемых. Если да, то снова выполнить второе действие.
В ситуации, когда задача не требует точного значения корня, его можно вычислить на калькуляторе. Бесконечную десятичную дробь, которая высветится в его окошке, округлить. Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Это вся информация о том, как выполняется сложение корней. Примеры, расположенные ниже, проиллюстрируют вышесказанное.
Первое задание
Вычислить значение выражений:
а) √2 + 3√32 + ½ √128 — 6√18;
б) √75 — √147 + √48 — 1/5 √300;
в) √275 — 10√11 + 2√99 + √396.
а) Если следовать приведенному выше алгоритму, то видно, что для первых двух действий в этом примере ничего нет. Зато можно упростить некоторые подкоренные выражения.
Например, 32 разложить на два множителя 2 и 16; 18 будет равно произведению 9 и 2; 128 — это 2 на 64. Учитывая это, выражение будет записано так:
√2 + 3√(2 * 16) + ½ √(2 * 64) — 6 √(2 * 9).
Теперь нужно вынести из-под знака радикала те множители, которые дают квадрат числа. Это 16=4 2 , 9=3 2 , 64=8 2 . Выражение примет вид:
√2 + 3 * 4√2 + ½ * 8 √2 — 6 * 3√2.
Нужно немного упростить запись. Для этого производится умножение коэффициентов перед знаками корня:
√2 + 12√2 + 4 √2 — 12√2.
В этом выражении все слагаемые оказались подобными. Поэтому их нужно просто сложить. В ответе получится: 5√2.
б) Подобно предыдущему примеру, сложение корней начинается с их упрощения. Подкоренные выражения 75, 147, 48 и 300 будут представлены такими парами: 5 и 25, 3 и 49, 3 и 16, 3 и 100. В каждой из них имеется число, которое можно вынести из-под знака корня:
5√5 — 7√3 + 4√3 — 1/5 * 10√3.
После упрощения получается ответ: 5√5 — 5√3. Его можно оставить в таком виде, но лучше вынести общий множитель 5 за скобку: 5 (√5 — √3).
в) И снова разложение на множители: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. После вынесения множителей из-под знака корня имеем:
5√11 — 10√11 + 2 * 3√11 + 6√11. После приведения подобных слагаемых получим результат: 7√11.
Пример с дробными выражениями
√(45/4) — √20 — 5√(1/18) — 1/6 √245 + √(49/2).
На множители нужно будет разложить такие числа: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
3/2 √5 — 2√5 — 5/ 3 √(½) — 7/6 √5 + 7 √(½) = (3/2 — 2 — 7/6) √5 — (5/3 — 7) √(½) = — 5/3 √5 + 16/3 √(½).
Это выражение требует того, чтобы избавиться от иррациональности в знаменателе. Для этого нужно умножить на √2/√2 второе слагаемое:
5/3 √5 + 16/3 √(½) * √2/√2 = — 5/3 √5 + 8/3 √2.
Для полноты действий нужно выделить целую часть у множителей перед корнями. У первого она равна 1, у второго — 2.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения. 2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.
Инструкция
1. Во-первых, при сложении квадратных корней испробуйте извлечь эти корни. Это будет допустимо, если числа под знаком корня являются полными квадратами. Скажем, пускай задано выражение?4 + ?9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: ?4 + ?9 = 2 + 3 = 5.
2. Если под знаком корня нет полных квадратов, то испробуйте перенести из под знака корня множитель числа. Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 – множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.
3. Пускай сумма 2-х квадратных корней является знаменателем дроби, скажем, A / (?a + ?b). И пускай перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда дозволено воспользоваться дальнейшим методом. Умножьте числитель и знаменатель дроби на выражение?a – ?b. Таким образом в знаменателе получится формула сокращенного умножения: (?a + ?b) * (?a – ?b) = a – b. По аналогии, если в знаменателе дана разность корней: ?a – ?b, то числитель и знаменатель дроби нужно умножить на выражение?a + ?b. Для примера, пускай дана дробь 4 / (?3 + ?5) = 4 * (?3 – ?5) / ((?3 + ?5) * (?3 – ?5)) = 4 * (?3 – ?5) / (-2) = 2 * (?5 – ?3).
4. Разглядите больше непростой пример избавления от иррациональности в знаменателе. Пускай дана дробь 12 / (?2 + ?3 + ?5). Нужно умножить числитель и знаменатель дроби на выражение?2 + ?3 – ?5:12 / (?2 + ?3 + ?5) = 12 * (?2 + ?3 – ?5) / ((?2 + ?3 + ?5) * (?2 + ?3 – ?5)) = 12 * (?2 + ?3 – ?5) / (2 * ?6) = ?6 * (?2 + ?3 – ?5) = 2 * ?3 + 3 * ?2 – ?30.
5. И наконец, если вам нужно только примерное значение, то дозволено посчитать значения квадратных корней на калькуляторе. Вычислите значения отдельно для всего числа и запишите с нужной точностью (скажем, два знака позже запятой). А после этого совершите требуемые арифметические операции, как с обыкновенными числами. Скажем, пускай нужно узнать примерное значение выражения?7 + ?5 ? 2,65 + 2,24 = 4,89.
Видео по теме
Обратите внимание!
Квадратные корни ни в коем случае невозможно складывать как примитивные числа, т.е. ?3 + ?2 ? ?5!!!
Полезный совет
Если вы раскладываете число на множители, дабы перенести квадрат из под знака корня, то совершите обратную проверку – перемножьте все получившиеся множители и получите изначальное число.
Сложение и вычитание квадратных корней
Что такое квадратные корни? Квадратный корень числа — это часть числа, которую можно умножить само на себя, чтобы получить исходное значение. Например, если мы решим 2 x 2, то получим 4. Таким образом, мы можем сказать, что 4 — это квадрат 2, а 2 — это квадратный корень из 4.
Например, если мы решим 2 x 2, то получим 4. Таким образом, мы можем сказать, что 4 — это квадрат 2, а 2 — это квадратный корень из 4.
Некоторые квадратные корни можно легко идентифицировать, например 2 и 4, в то время как другие могут быть более сложными. Например, если мы попытаемся найти квадратный корень из 2, мы получим «иррациональное» число. Это означает, что нет простого способа записать его, кроме его радикальной формы, которой является $\sqrt2$.
Как упростить квадратный корень?Точно так же, как при упрощении других математических выражений, мы можем упростить квадратные корни в радикальных формах, комбинируя «подобные члены» или «подобные радикалы» посредством сложения или вычитания.
Одним из важных ключей при объединении радикалов путем сложения или вычитания является просмотр подкоренного числа. Если данные квадратные корни имеют одинаковые подкоренные, они подобны радикалам, и их объединение возможно. Если нет, то вы не можете объединить два квадратных корня. Это похоже на объединение одинаковых терминов в алгебраическом выражении. Вы можете обращаться с квадратными корнями в радикальной форме как с переменными и комбинировать одинаковые члены, добавляя или вычитая их числовые коэффициенты и присоединяя их общую переменную. Например, чтобы объединить $\sqrt{x}$ и 2$\sqrt{x}$, у нас может быть $\sqrt{x}$+ 2$\sqrt{xy}$ . Радикал $\sqrt{x}$ имеет числовой коэффициент 1 , поэтому мы можем визуализировать его как 1$\sqrt{xy}$, тогда как радикал 2$\sqrt{x}$ имеет числовой коэффициент 2. Чтобы объединить, просто сложите их числовые коэффициенты. Итак, $\sqrt{x}+ 2\sqrt{x}=(1+2)\sqrt{x}=3\sqrt{x}$.
Это похоже на объединение одинаковых терминов в алгебраическом выражении. Вы можете обращаться с квадратными корнями в радикальной форме как с переменными и комбинировать одинаковые члены, добавляя или вычитая их числовые коэффициенты и присоединяя их общую переменную. Например, чтобы объединить $\sqrt{x}$ и 2$\sqrt{x}$, у нас может быть $\sqrt{x}$+ 2$\sqrt{xy}$ . Радикал $\sqrt{x}$ имеет числовой коэффициент 1 , поэтому мы можем визуализировать его как 1$\sqrt{xy}$, тогда как радикал 2$\sqrt{x}$ имеет числовой коэффициент 2. Чтобы объединить, просто сложите их числовые коэффициенты. Итак, $\sqrt{x}+ 2\sqrt{x}=(1+2)\sqrt{x}=3\sqrt{x}$.
Упрощение квадратных корней — это процесс их записи в наиболее эффективной и компактной возможной структуре с сохранением значения исходного выражения. Это полезный математический навык, потому что он преобразует сложные или трудночитаемые радикальные выражения в более простые. Ниже приведены некоторые правила и шаги по упрощению выражения квадратного корня.
Упрощение квадратных корней без переменных
- По возможности факторизовать подкоренное число . Найдите любые делители подкоренного числа, являющегося полным квадратом. Например, в выражении $\sqrt{50}$ мы можем разложить 50 так, чтобы один множитель был полным квадратом, то есть $\sqrt{50} = \sqrt{25 x 2}$. Полный квадрат здесь равен 25, потому что 25 = 5 5.
- Выведите квадратный корень из множителя полного квадрата . Извлеките квадратный корень из полного квадрата и поставьте его перед знаком радикала. Оставьте оставшийся множитель внутри радикала. Итак, в приведенном выше примере $\sqrt{50} = \sqrt{25 x 2}=5\sqrt{2}$ .
Упрощение квадратных корней с помощью переменных
Предположим, что все переменные представляют неотрицательные действительные числа, чтобы упростить правила упрощения.
Упрощение квадратных корней с переменными похоже на упрощение квадратных корней без переменных. 8}$ показатель степени переменной четен, что равно 8. Следовательно, чтобы найти квадратный корень из b 9{3}\sqrt{(5)(x)}$
8}$ показатель степени переменной четен, что равно 8. Следовательно, чтобы найти квадратный корень из b 9{3}\sqrt{(5)(x)}$
При сложении квадратных корней мы объединяем одинаковые радикалы, а разноименные радикалы записываются как есть. Итак, если мы добавим 4$\sqrt{2}$ и 2$\sqrt{2}$, это возможно, потому что они похожи на радикалы. Мы можем думать об этом следующим образом: «Если у нас есть четыре квадратных корня из 2, и мы добавим их к двум квадратным корням из 2, то сколько всего у нас будет квадратных корней из 2?» Ну, четыре из них плюс два из них — в общей сложности шесть из них. Итак, мы получаем 6$\sqrt{2}$. Другими словами, мы просто добавили их коэффициент и присоединили к их общему радикалу.
Если подкоренные квадратные корни не совпадают, то они не похожи на подкоренные, и мы не можем их объединить. Итак, если у нас есть $\sqrt{2}$ и $\sqrt{3}$, мы не можем прибавить или вычесть одно из них из другого. Подкоренные разные (один 2, другой 3), поэтому они не похожи на подкоренные и не могут быть объединены.
Подкоренные разные (один 2, другой 3), поэтому они не похожи на подкоренные и не могут быть объединены.
Не всегда можно складывать и вычитать квадратные корни с разными подкоренными. Иногда нам нужно упростить радикалы, чтобы получить похожие радикалы. Например, кажется, что $\sqrt{3}+\sqrt{27}$ нельзя упростить, поскольку подкоренные члены терминов различны. Но $\sqrt{27}$ можно упростить до 3$\sqrt{3}$. Теперь $\sqrt{3}$ и 3$\sqrt{3}$ похожи на радикалы и поэтому могут быть объединены в 4$\sqrt{3}$.
Даже подкоренные числа разные; иногда один или несколько радикалов в выражении можно переписать так, чтобы радикалы были одинаковыми. Таким образом, важно искать возможности переписать радикалы, прежде чем сделать вывод, что они не похожи на радикалы и не могут быть объединены.
Пример #1
Какова сумма 2$\sqrt{5}$ и 5$\sqrt{5}$?
Решение
| Процесс сложения квадратных корней | Пошаговое объяснение |
| 2$\sqrt{5}+ 5\sqrt{5}$ | Настройте дополнение. |
| 7$\sqrt{5}$ | Объедините одинаковые радикалы в один член, сложив их коэффициенты. |
| Следовательно, сумма 2$\sqrt{5}$ и 5$\sqrt{5}$ равна 7$\sqrt{5}$. |
Пример #2
Найдите сумму 2$\sqrt{x}$ и 2$\sqrt{y}$?
Решение
| Процесс добавления квадратных корней | Пошаговый объяснение |
| 2 $ \ SQRT {x}+ 2 \ SQRT {y} $ | 9 3 SQRT {x}+ 2 \ SQRT {y} $ 3. |
| 2$\sqrt{x}+ 2\sqrt{y}$ | Обратите внимание, что эти два термина не являются радикалами, поэтому мы не можем объединить их в один термин. |
| Следовательно, сумма $2\sqrt{x}\:and\:2\sqrt{y}$ равна 2$\sqrt{x}+ 2\sqrt{y}$ . |
Пример #3
Добавить $x\sqrt{3}\:and\:2\sqrt{12}$?
Solution
| Square Roots Addition Process | Step-by-step Explanation |
| $x\sqrt{3} + 2\sqrt{12}$ | Set up the добавление. |
| $x\sqrt{3} + 2\sqrt{4×3}$ | По возможности разложите подкоренные числа так, чтобы хотя бы один множитель был полным квадратом. В этом случае подкоренное число 12 можно разложить как 4 х 3, где 4 — полный квадрат. |
| $x\sqrt{3} + (2×2)\sqrt{3}$ | Получите квадратный корень из 4 и поставьте его перед знаком радикала. |
| $x\sqrt{3} + 4\sqrt{3}$ | Упростите любую задачу на умножение в выражении. |
| $(x+4)\sqrt{3}$ | Объедините одинаковые радикалы в один член, сложив их коэффициенты. |
| Следовательно, сумма $x\sqrt{3}\:and\:2\sqrt{12}\:is\:(x + 4)\sqrt{3}$. |
Процесс вычитания квадратных корней такой же, как и процесс их сложения. Единственное отличие состоит в том, что при вычитании одного члена квадратного корня из другого вы должны менять знаки каждого члена в вычитаемом выражении, а затем объединять подобные радикалы.
Но почему мы должны менять знаки математического выражения при вычитании? Возьмем в качестве примера два числа, 2 и −1. Предположим, что если нам нужно вычесть -1 из 2, мы запишем это как 2-(-1). Мы знаем, что произведение двух положительных знаков или двух отрицательных знаков положительно, а произведение двух разных знаков отрицательно. В примере: 2−(−1) = 2 + 1 = 3. Если мы не поменяем знак, то получим 2 – 1 = 1, что является совершенно другим результатом. Итак, изменение знаков вычитаемого при вычитании выражений необходимо. Другими словами, символ вычитания (-) должен быть распределен по каждому члену вычитаемого перед объединением математических терминов.
Пример #1
Вычтите -$\sqrt{3}$ из $3\sqrt{3}$.
Решение
| Процесс вычитания квадратных корней | . вычитание вверх. |
| $3\sqrt{3} + \sqrt{3}$ | Распределить знак минус перед членом в вычитаемом. Таким образом, -$\sqrt{3}$ станет $\sqrt{3}$. Затем действуйте, как в процессе сложения. Таким образом, -$\sqrt{3}$ станет $\sqrt{3}$. Затем действуйте, как в процессе сложения. |
| $4\sqrt{3}$ | Объедините одинаковые радикалы в один член, сложив их коэффициенты. Обратите внимание, что если у радикала нет записанного коэффициента, подразумевается, что он имеет 1 в качестве своего коэффициента. |
| Таким образом, вычитание -$\sqrt{3}$ из $3\sqrt{3}$ даст $4\sqrt{3}$. |
Пример #2
Каков результат вычитания $\sqrt{2y}$ из $\sqrt{2x}$?
Решение
| Процесс вычитания квадратных корней | Пошаговый объяснение | |
| $ \ sqrt {2x}-(\ sqrt {2y}) $ | . | |
| $\sqrt{2x}-\sqrt{2y}$ | Распределить знак минус перед членом в вычитаемом. Таким образом, $\sqrt{2y}$ станет -$\sqrt{2y}$. Затем действуйте, как в процессе сложения. | |
| $\sqrt{2x}-\sqrt{2y}$ | Обратите внимание, что эти два термина не являются радикалами, поэтому мы не можем объединить их в один термин. 92} – ( 3x \sqrt{16(2)})$ 92} – ( 3x \sqrt{16(2)})$ | По возможности разложите подкоренные числа так, чтобы в качестве множителей были полные квадраты. |
| $2(2)(x)\sqrt{2} -( 3x (4)\sqrt{2})$ | Получите квадратные корни из правильных квадратов и поместите их перед подкоренным знаком | |
| $4x\sqrt{2} – (12x\sqrt{2})$ | Упростите любую задачу на умножение в выражении. | |
| $4x\sqrt{2} – 12x\sqrt{2}$ | Распределить знак минус перед членом в вычитаемом. Таким образом, $12x\sqrt{2}$ станет -$12x\sqrt{2}$. Затем действуйте, как в процессе сложения. 9{4}$ |
Задача №1
У Марка и Джона квадратный сад. Площадь сада Маркса составляет 18x + 9 квадратных футов, а площадь сада Джона — 8x + 4 квадратных фута. Чем отличается длина сторон их сада?
Решение
| Процесс | Пошаговое объяснение | ||||||||||
| $T= \sqrt{M} – \sqrt{J}$ | Установите рабочую формулу. Чтобы получить длину стороны квадрата, мы должны получить квадратный корень из его площади. Пусть T — разность длин сторон террариумов, M — площадь сада Марка, J — площадь сада Джона. Чтобы получить длину стороны квадрата, мы должны получить квадратный корень из его площади. Пусть T — разность длин сторон террариумов, M — площадь сада Марка, J — площадь сада Джона. | ||||||||||
| $T= \sqrt{18x + 9} – \sqrt{8x + 4}$ | Подставьте значения в рабочую формулу. | ||||||||||
| $T= \sqrt{9(2x + 1)} – \sqrt{4(2x + 1)}$ | Умножьте подкоренные, если возможно. В этом случае мы можем разложить 18x + 9 как 9 (2x + 1) и 8x + 4 как 4 (2x + 1) | ||||||||||
| $T= 3\sqrt{(2x + 1)} – \sqrt{2 (2x + 1)}$ | Извлеките квадратный корень из 9 и 4, чтобы он мог выйти из подкоренного знака. Итак, $\sqrt{9 (2x + 1)} – \sqrt{4 (2x + 1)} = 3\sqrt{(2x + 1)} – 2\sqrt{(2x + 1)}$ | ||||||||||
| $T= \sqrt{(2x + 1)}$ | Объедините одинаковые радикалы в один член, добавив их числовые коэффициенты. 9{3}b}$ дюймов. Решение
Понимание иррациональных чисел Рабочие листы по математике для 8-го класса Мы тратим много времени на изучение и компиляцию информация на этом сайте. Как складывать квадратные корни вместе примеры, формулы и практические задачиПодкоренное число относится к числу под знаком корня. В приведенном ниже радикале подкоренной является число «5». Видео в Как складывать квадратные корниКак складывать упрощенные квадратные корни?Давайте рассмотрим следующий пример. Вы можете добавлять только квадратные корни (или радикалы), которые имеют одинаковые подкоренные числа . То же правило действует и для вычитания. Рассмотрим следующий пример: Вы можете вычитать квадратные корни с одним и тем же подкоренным числом, которое является первым и последним членами. Практика ПроблемыНаправления: Добавьте квадратные корни ниже. Проблема 1 Только первый и последний квадратный корень имеют одинаковые подкоренные числа, поэтому вы можете сложить эти два члена. Проблема 2Помните — то же правило применяется и к вычитанию квадратных корней — подкоренные должны быть одинаковыми. Как складывать квадратные корни, не являющиеся упрощеннымиДавайте рассмотрим следующий пример. Здесь вы можете сразу увидеть проблему: подкоренные числа не совпадают. Поэтому мы можем , а не добавить их в данный момент. Однако, если мы сначала упростим квадратные корни, мы сможем их добавить. Давайте используем этот пример задачи, чтобы проиллюстрировать общие шаги для добавления квадратных корней. Упростите каждый квадратный корень. Шаг 1Добавьте квадратные корни с теми же подкоренными. Проблема 3Шаг 1 Упростите каждый квадратный корень. Шаг 2 Добавьте квадратные корни с теми же подкоренными. Проблема 4Шаг 1 Упростите каждый квадратный корень. Шаг 2 Сложение квадратных корней с одинаковыми подкоренными. Проблема 5Шаг 1 Упростите каждый квадратный корень. Шаг 2 Сложение квадратных корней с одинаковыми подкоренными. Проблема 6Шаг 1 Упростите каждый квадратный корень. Шаг 2 Помните: то же правило применяется и к вычитанию квадратных корней с одними и теми же подкоренными. Как складывать квадратные корни с коэффициентами?Давайте рассмотрим следующий пример. Вы видите, что отличает это выражение от нескольких последних задач? Каждый квадратный корень имеет коэффициент . Правила сложения квадратных корней с коэффициентами очень похожи на те, что мы только что практиковали в последних нескольких задачах — с 1 дополнительным шагом — который заключается в умножении коэффициентов на упрощенный квадратный корень. Не обращайте внимания на коэффициенты (2 и 5) и упрощайте каждый квадратный корень. Шаг 1Умножьте коэффициенты (2 и 5) на любые числа, которые «вылезли» из квадратного корня (3 и 2 соответственно). Шаг 1Добавьте любые радикалы с тем же корнем и Проблема 7Шаг 1 Не обращайте внимания на коэффициенты (4 и 5) и упрощайте каждый квадратный корень. Шаг 2 Умножьте коэффициенты (4 и 5) на любые числа, которые «вылезли» из квадратного корня (3 и 2 соответственно). |







 д.
д.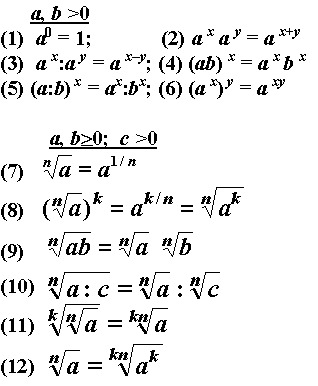 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.


 Периметр равнобедренного треугольника можно определить, добавив длину двух его равных сторон и длину его основания. Пусть P — периметр, L — мера катетов, а B — мера основания.
Периметр равнобедренного треугольника можно определить, добавив длину двух его равных сторон и длину его основания. Пусть P — периметр, L — мера катетов, а B — мера основания.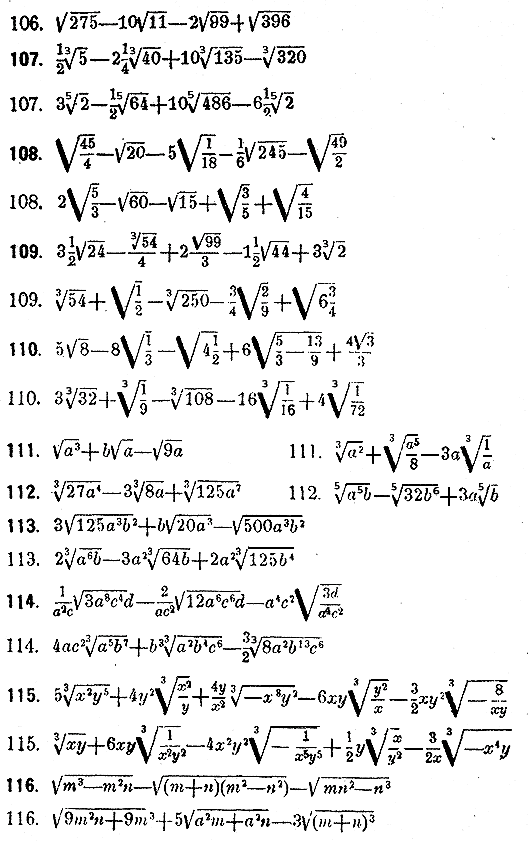 Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку! Итак, в приведенном выше примере вы можете добавить первый и последний термины:
Итак, в приведенном выше примере вы можете добавить первый и последний термины:




