Логарифмическая функция, ее свойства и график – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Логарифмической функцией называют функцию
,
где – любое положительное число, отличное от 1.
Основные свойства логарифмической функции:
- Область определения логарифмической функции – множество всех положительных чисел: .
- Множество значений логарифмической функции – множество R всех действительных чисел: .
- Логарифмическая функция на всей области определения возрастает при или убывает при \(0.
- Логарифмическая функция не является ни четной, ни нечетной.
- График логарифмической функции всегда проходит через точку .
- Функция не имеет точек максимума и минимума.
- Функция не ограничена сверху, не ограничена снизу.
- Функция непрерывна.
График логарифмической функции называют логарифмической кривой.
Ось для графика логарифмической функции является вертикальной асимптотой (то есть, при стремлении к нулю график приближается к оси ).
Графики функций симметричны относительно оси .
Графики функций симметричны относительно прямой . Эти функции являются взаимно обратными.
Вопросы
Найдите область определения функции.
\(y=\lg(3x-2)\)
Найдите область определения функции.
\(y=2\ln(1+x)-3\lg(3x-1)\)
Найдите область определения функции.
2)\)
Сообщить об ошибке
«Логарифмическая функция, её свойства и график»
МОУ лицей №10
города Советска
Калининградской области
учитель математики
Разыграева Татьяна Николаевна
Функция y = log a x ,
её свойства и график.
Работа устно:
№
a
1
b
2
3
c
4
d
Е
Е
Н
Р
П
Джон Непер
John Napier
Дата рождения:
1550 год
Место рождения:
замок Мерчистон, в те годы предместье Эдинбурга
Дата смерти:
4 апреля 1617
Место смерти:
Эдинбург
Научная сфера:
математика
Альма-матер:
Сент-Эндрюсский университет
Известен как:
изобретатель логарифмов
Прочитайте и назовите график функции,
изображённый на рисунке.
y
План
Какими свойствами
обладает эта
функция
при 0
1
1
0
x
План прочтения графика:
1) D(f) – область определения функции .2) Чётность или нечётность функции .
3) Промежутки возрастания, убывания функции .
4) Ограниченность функции .
5) Наибольшие, наименьшие значения функции .
6) Непрерывность функции.
7) E(f) – область значений функции.
8) Выпуклость функции.
Леонард Эйлер
нем. Leonhard Euler
Дата рождения:
4 (15) апреля 1707
Место рождения:
Базель, Швейцария
Дата смерти:
7 (18) сентября 1783 (76 лет)
Место смерти:
Санкт-Петербург, Российская империя
Научная сфера:
Математика, механика, физика, астрономия
Современное определение показательной,
y = x
Показательная функция
Логарифмическая функция
y
Если точка (с;b)
принадлежит
показательной
функции, то
(c ; b)
b
Или, на «языке
логарифмов»
(b ; c)
c
Что можно сказать
о точке (b;c)?
0
x
c
b
Вывод:
y = x
График функции симметричен графикуфункции относительно прямой y = x.
y
a
1
a
0
x
1
y = x
График функции симметричен графику
функции относительно прямой y = x.
y
1
0
1
x
Постройте графики функций:
2 вариант
1 вариант
x
¼
y = log 2 x
-2
½
1
-1
2
0
4
1
2
8
3
x
y = log 1/2 x
¼
½
2
1
1
0
2
-1
4
8
-2
-3
Проверка:
y
График
логарифмической
функции
называют
логарифмической
кривой.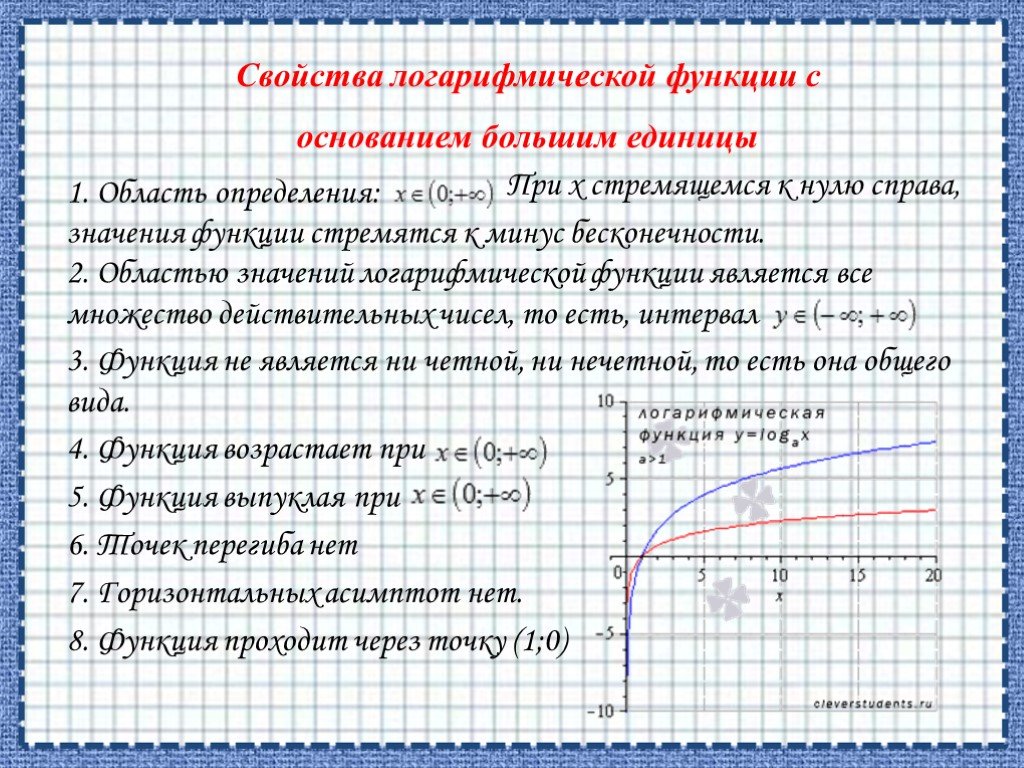
3
2
1
x
0
1
4
2
8
— 1
— 2
— 3
График функции y = log a x.
y
Опишите свойства
логарифмической
функции.
3
2
1 вариант:
при a 1
1
0
x
2
1
4
2 вариант:
при 0
— 1
— 2
8
Свойства функции у = log a x, a 1.
у
1) D(f) = (0, + ∞) ;
2) не является ни чётной,
ни нечётной;
х
0
3) возрастает на (0, + ∞) ;
4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞ , + ∞) ;
8) выпукла вверх.
13
Свойства функции у = log a x, 0
у
1) D(f) = (0, + ∞) ;
2) не является ни чётной,
ни нечётной;
х
0
3) убывает на (0, + ∞) ;
4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞ , + ∞) ;
8) выпукла вниз.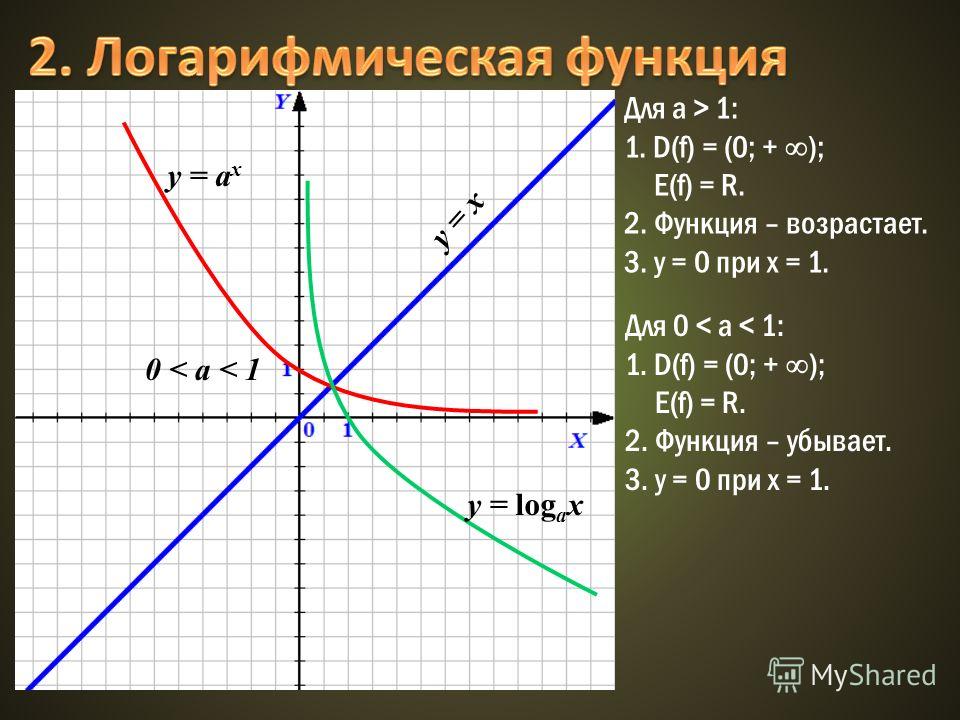
14
Основные свойства логарифмической
функции
№
a 1
1
0
D(f) = (0, + ∞)
2
не является ни чётной, ни нечётной;
3
возрастает на (0, + ∞)
4
не ограничена сверху, не ограничена снизу
убывает на (0, + ∞)
5
не имеет ни наибольшего, ни наименьшего значений
6
непрерывна
7
E(f) = (- ∞ , + ∞)
8
выпукла вверх
выпукла вниз
Задание №1
Найдите наибольшее и наименьшее значения
функции на промежутке:
у
у
х
х
Функция возрастает,
значит: y наим.
= lg1 = 0
y наиб. = lg1000 = lg10 ³ = 3
Функция убывает,
значит: y наим. = -3
y наиб. = 2
16
Задание №2
Решите уравнение и неравенства:
y
Ответ: х = 1
1
Ответ: х 1
0
x
1
— 1
Ответ: 0
Самостоятельно:
Решите уравнение и неравенства:
Ответ: 0
Ответ: х 1
Ответ: х = 1
у
у
у
х
х
х
18
x = — 2
Задание №3
Постройте графики функций:
y
Самостоятельно.
Проверить!
1
x
0
1
Проверить!
y = — 3
19
Проверка:
y
1
0
x
1
Проверка:
y
3
1
0
x
1
4
2
-3
Установите для предложенных
графиков значение параметра a (a 1, 0
у
у
у
х
х
х
у
Не является графиком логарифмической функции
х
22
Блиц — опрос.
Отвечать только «да» или «нет»
- Ось у является вертикальной асимптотой графика
логарифмической функции.
- Графики показательной и логарифмической функций
симметричны относительно прямой у = х.
- Область определения логарифмической функции – вся
числовая прямая, а область значений этой функции –
промежуток (0, + ∞).
- Монотонность логарифмической функции зависит от
основания логарифма.
- Не каждый график функции проходит
через точку с координатами (1;0).
23
Блиц — опрос.
Отвечать только «да» или «нет»
- Логарифмическая кривая это та же экспонента, только
по — другому расположенная в координатной плоскости.
- Выпуклость логарифмической функции не зависит от
основания логарифма.
- Логарифмическая функция не является ни чётной, ни
нечётной.
- Логарифмическая функция имеет наибольшее значение
и не имеет наименьшего значения при a 1 и наоборот
при 0
Проверка:
Да, да, нет, да, нет, да, нет, да, нет
24
Домашнее задание
Удачи!!!!!
§ 49
№ 1463, 1467,1480,1460
1 вариант – а,б;
2 вариант – в,г.
25
Используемые ресурсы
и литература
Мордкович А.Г. Алгебра и начала анализа. 10 – 11 кл.:
Учебн. для общеобразоват. учреждений. – 3-е изд.
– М.:Мнемозина, 2007.
Алгебра и начала анализа. 10 – 11 кл.: Задачник для общеобразоват. учреждений/А.Г.Мордкович, Л.О. Денищева, Т.А. Корешкова, Т.Н. Мишустина, Е.Е. Тульчинская. – 3-е изд., испр. – М.:Мнемозина, 2007.
Л.А. Александрова Алгебра и начала анализа. 11 класс. Самостоятельные работы:Учеб. пособие для общеобразоват. учреждений/ Под ред. А.Г. Мордковича. – 2-е изд. – М.: Мнемозина, 2006. – 96 с.
http://ru.wikipedia.org
http://nayrok.ru
26
Экспоненциальные и логарифмические функции: Логарифмические функции
Логарифмические функции являются обратными
экспоненциальные функции. Обратная экспоненциальная функция y = a x равна x = a y . Логарифмическая функция y = log a x определяется как эквивалентная
к экспоненциальному уравнению x = a y . г = журнал a x только при следующих
условия: x = a y , a > 0 и a ≠1.
Он называется логарифмическим
функция с базой и .
Рассмотрим, что означает обратная экспоненциальная функция: x = a y . Данный число x и основание a , в какую степень y нужно возвести a , чтобы получить x ? Этот неизвестный показатель, y , равно log a x . Итак, вы видите логарифм есть не что иное, как экспонента. По определению, a log a x = x для каждого реальные x > 0.
Ниже изображены графики вида y = log a x , когда a > 1 и когда 0 < a < 1. Обратите внимание, что домен состоит только из положительных действительных чисел, и
что функция всегда возрастает как x увеличивается. Рисунок %: два графика y = log a x . Слева y = log 10 x , а справа
справа, y = логарифм x .
Область определения логарифмической функции — это действительные числа больше нуля, и
диапазон — действительные числа. График y = log a x симметричен
график y = a x относительно линии г = х . Это отношение
верно для любой функции и ее обратной.
Вот некоторые полезные свойства логарифмов, которые следуют из тождеств включая показатели степени и определение логарифма. Помните a > 0, и х > 0.
логарифм
| журнал a 1 = 0. |
| бревно а а = 1. |
log a ( a x ) = x . |
| a журнал a x = x . |
log a ( bc ) = log a b + log a 84 c. | . |
| бревно a ( x d ) = d бревно a x 3 |
Натуральная логарифмическая функция — это логарифмическая функция с основанием e .
ф ( x ) = log e x = ln x , где x > 0. ln x — это просто новая форма
запись логарифмов с основанием e . Большинство калькуляторов имеют кнопки, помеченные
«журнал» и «лн». Кнопка «журнал» предполагает, что основание равно десяти, а кнопка «ln»,
конечно, пусть база равна e . Логарифмическая функция с основанием 10:
иногда называется десятичной логарифмической функцией. Он широко используется, потому что
наша система счисления имеет основание десять. Натуральные логарифмы чаще встречаются в
исчисление.
Существуют две формулы, позволяющие изменить основание логарифмической функции.
В первом говорится следующее: log a b = . Чем более известен и
Полезная формула для смены основания обычно называется изменением основания.
Формула. Он позволяет изменить основание логарифмической функции на любое
положительное действительное число ≠1. В нем указано, что журнал a x = .
В этом случае a , b и x — все положительные действительные числа.
и a , b ≠1.
В следующем разделе мы обсудить некоторые приложения экспоненциальных и логарифмических функций.
логарифмов — Сомнение по поводу домена в логарифмических функциях.
спросил
Изменено 7 лет, 5 месяцев назад
Просмотрено 1к раз
$\begingroup$
Согласно моей книге, логарифмическая функция $$\log_{a}x=y$$ определена, если и $x$, и $a$ положительны и $x\neq 0$ и $a\neq 1$.
Значит, это не так? $$\log_{-3}9=2$$ $$\log_{-2}-8=3$$
- функции
- логарифмы
$\endgroup$
5
$\begingroup$
Самый простой аргумент состоит в том, что эти два уравнения неверны, потому что они нарушают определение.
Логарифмическая функция допускает строго положительное основание, не равное единице, и строго положительный домен. 9p\right) = p\log_a(x)$. Но мы не можем иметь и то, и другое. Аналогичное противоречие можно вывести и со вторым уравнением. В конечном счете, гораздо выгоднее сохранить $a$ положительным и не равным единице, чем потерять эти прекрасные свойства логарифмирования. То же самое можно сказать и о разрешении отрицательных аргументов в логарифме. Это все с точки зрения того, что вы работаете с действительными числами, так как с комплексными числами нужно обращаться иначе.
$\endgroup$ 9{1/2}$, где $x=1/2$ не является действительным числом. Как правило, ограничения, которые они дают, гарантируют, что для реальных входных данных (домена) вы получите реальные выходные данные (диапазон) — и цель состоит в том, чтобы домен был как можно больше. Кроме того, как указал @graydad, обычные правила логарифмирования не работают, если $a<0$.
Короче говоря, вы можете определять логарифмы с отрицательным основанием, но вы действительно не хотите (потому что ничто не работает так, как вы хотите/ожидаете).