Дифференциальные уравнения вольфрам альфа: Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha

Новое в Wolfram Language | Аналитическое решение уравнений в частных производных / Хабр

Перевод поста Devendra Kapadia «New in the Wolfram Language: Symbolic PDEs».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации.

---

Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3.

История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось.

И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами.

Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t:

Затем мы задаём граничные условия, указав тем самым, что концы струны при колебаниях сохраняют свои положения.

Зададим теперь начальные условия для движения струны, указав смещения и скорости различных точек струны в момент времени t=0:

Теперь мы можем использовать DSolve для решения волнового уравнения с начальными и краевыми условиями:

Как указано выше, решение есть бесконечная сумма тригонометрических функций. Сумма возвращается в невычисленной форме (

Inactive), поскольку каждый отдельный член разложения имеет физическую интерпретацию, и зачастую даже небольшое количество членов может являться хорошим приближением. К примеру, мы можем взять первые четыре члена для получения приближенного решения asol(x,t)

Каждый член в сумме представляет собой стоячую волну, которые могут быть представлены следующим образом:

И все эти стоячие волны складываются воедино, образуя гладкую кривую, как показано на анимации ниже:

Волновое уравнение относится к классу линейных гиперболических уравнений в частных производных, описывающих распространение сигналов с конечными скоростями. Это УрЧП представляет собой удобный способ для моделирования колебаний в струне или в каком-то другом деформирумом теле, однако ещё более важную роль оно играет в современной физике и инженерных приложениях, т.к. оно описывает распространение света и электромагнитных волн.

Давайте теперь смоделируем поток тепла в стержне единичной длины, изолированном с обоих концов, с помощью представленного ниже уравнения теплопроводности:

Поскольку стержень изолирован с обоих концов, то через них проходит нулевой поток тепла, что можно выразить как граничные условия вида х = 0 и х = 1:

Теперь нужно указать начальное температурное распределение в стержне. В этом примере мы будем использовать приведённую ниже линейную функцию. В левом конце (х = 0) начальная температура — 20 градусов, в правом (х = 1) — 100:

И теперь мы можем решить уравнение теплопроводности с заданными условиями:

Как и в приведённом выше примере с волновым уравнением, мы можем извлечь несколько членов суммы и получить приближенное решение:

Первый член приближенного решения — 60 — среднее от температур на границах стержня, и она является стационарной температурой для этого стержня. Как показано на графике функции температуры от длины, представленном ниже, температура стержня быстро достигает стационарного значения в 60 градусов:

Уравнение теплопроводности относится к классу линейных параболических уравнений в частных производных, которые описывают процессы диффузии. Это простое на вид уравнение часто можно встретить в самых различных, а иногда и весьма неожиданных областях. Далее в статье мы рассмотрим два примера этого явления.

Рассмотрим теперь уравнение Лапласа, которое используется для моделирования стационарного состояния систем, т. е. поведения после некоторых зависящих от времени уже законченных переходных процессов. В двумерном случае это уравнение можно представить следующим образом:

Ограничим координаты х и у прямоугольной областью Ω, как показано ниже:

Классическая задача Дирихле — найти функцию u(x,y), удовлетворяющую уравнению Лапласа внутри области Ω с заданным условием Дирихле (DirichletCondition), которое определяет значения на границах области Ω, как показано ниже:

Задачу Дирихле можно решить с помощью функции DSolve, весьма изящно задав при этом область:

Как и в примерах ранее, мы можем извлечь некоторое количество членов (скажем, 100) из суммы и визуализировать решение:

Следует заметить, что решение u(x,y) задачи Дирихле представляется гладким в Ω, несмотря на то, что граничные условия имеют резкие черты. Помимо этого, u(x,y) достигает экстремальных значений на границах, в то время как в центре прямоугольника находится седловая точка. Эти черты характерны для линейных эллиптических уравнений — класса уравнений в частных производных, к которым и принадлежит уравнение Лапласа.

Волновое уравнение, уравнение теплопроводности, уравнение Лапласа — самые известные примеры классических УрЧП. Теперь мы рассмотрим три примера типичных современных УрЧП, первым среди которых будет уравнение Бюргерса для вязкой жидкости, которое может быть представлено следующим образом:

Это нелинейное УрЧП было введено Иоханнесом Бюргерсом в сороковых годах в качестве простой модели для турбулентных потоков (параметр ϵ в уравнении представляет собой вязкость жидкости). Однако, десять лет спустя, Э. Хопф и Д. Коул показали, что уравнение Бюргерса сводится к уравнению теплопроводности, а это значит, что данное уравнение не может проявлять хаотического поведения. Преобразование Коула-Хопфа позволяет решать уравнения Бюргерса в замкнутой форме для начального условия, заданного, к примеру, так:

В этом примере мы будем использовать функцию DSolveValue, которая возвращает только выражение для решения. Члены с функцией ошибок (Erf) в формуле ниже возникают из решения соответствующей граничной задачи теплового уравнения:

Представленный ниже график демонстрирует изменение во времени гипотетического одномерного поля скоростей потока. Решение представляется гладким для положительного ϵ, при том что начальное условие есть кусочно заданная функция:

Как можно заметить на нижепреведённых графиках, решение стремится к разрывному при сремлении вязкости ϵ к нулю. Подобные решения с резким переходом (shock solutions) — известная особенность уравнений Бюргерса для невязкой (ϵ = 0) среды.

В качестве второго примера современных УрЧП рассмотрим уравнение Блэка-Шоулза, используемое в финансовых расчётах. Это уравнение впервые представили Фишер Блэк и Майрон Шоулз в 1973 году в качестве модели для определения теоретической цены на европейские опционы, и формулируется оно следующим образом:

где:
c — цена опциона как функция от стоимости акций s и времени t,
r — процентная ставка без риска,
σ — волатильность акций.

В их эпохальной статье (которая была процитирована более 28000 раз), Блэк и Шоулз отметили, что их уравнения с помощью преобразования переменных могут быть сведены к уравнению теплопроводности. Это резкое упрощение приводит к знаменитой формуле Блэка-Шоулза для европейских опционов с конечными условиями, основанными на цене исполнения (strike price) k актива в момент времени t=Т:

Вооружившись этой формулой, мы можем вычислить значения финансовых опционов для типичных значений параметров:

Ответ согласуется со значением, полученным с помощью встроенной функции FinancialDerivative:

В качестве третьего примера современных УрЧП рассмотрим уравнение Шредингера для электрона в одномерной потенциальной яме с глубиной d и соответствующим начальным условием. Уравнение и условия можно сформулировать следующим образом:

Этот пример имеет элементарное решение, которое принимает мнимые значения из-за наличия I в уравнении Шредингера:

Функция плотности вероятности для электрона ρ = Ψ^⊹ Ψ, с использованием подходящих значений параметров в задаче, может быть вычислена следующим образом:

Мы можем создать анимацию изменения плотности вероятности во времени, которая показывает, что «центр» электрона в яме движется из стороны в сторону:

Собственные значения и собственные функции играют важную роль как в решении уравнения Шрёдингера, так и в других УрЧП.

В частности, они предоставляют «строительные блоки» для решений волновых уравнений и уравнений теплопроводности в виде бесконечных сумм, которые приводились ранее в статье. Поэтому, в качестве нашего последнего примера рассмотрим задачу о нахождении девяти наименьших собственных значений и собственных функций для оператора Лапласа с однородным (нулевым) условием Дирихле для трехмерной сферической области. Найдем девять наименьших значений λ и соответствующих им функций ϕ, удовлетворяющих Λϕ = λ ϕ, которые определяются следующим образом:

Новая функция DEigensystem в версии 10.3 позволяет вычислить требуемые собственные значения и функции следующим образом:

Собственные значения в этой задаче выражаются через BesselJZero. Вот пример:

Собственные значения можно визуализировать с помощью функции

DensityPlot3D, которая возвращает красивые графики, как показано ниже:

УрЧП являются важным инструментом во многих отраслях науки и техники, в статистике и финансах. На более фундаментальном уровне они предоставляют точные математические формулировки некоторых самых глубоких и тонких вопросов о нашей Вселенной, скажем, о возможности существования голых сингулярностей. По моему опыту, изучение УрЧП награждает редким сочетанием из практических идей и интеллектуального удовлетворения.

Рекомендую изучить документацию по DSolve, NDSolve, DEigensystem, NDEigensystem и методу конечных элементов, чтобы узнать больше о различных подходах к решению УрЧП в Wolfram Language.

УрЧП в символьной форме поддерживаются в Wolfram Mathematica и Wolfram Language с версии 10.3, а в ближайшее время будут представлены и во всех остальных программных продуктах Wolfram.

Использование Wolfram Alpha для решения задач курса высшей математики технического вуза

Байбисенова Асия Армановна,студентка 2 курса факультeта «Нефтегазовая и строительная техника», ФГБОУ ВО «Сибирский государственный автомобильнодорожный университет (СибАДИ)», г. Омск[email protected]

Гамалий Дмитрий Алексеевич,студент 2 курса факультeта «Нефтегазовая и строительная техника», ФГБОУ ВО «Сибирский государственный автомобильнодорожный университет (СибАДИ)», г.Омск[email protected]

Рождественская Елена Александровна,кандидат педагогических наук, доцент кафедры «Высшая математика» ФГБОУ ВО «Сибирский государственный автомобильнодорожный университет (СибАДИ)», г.Омск[email protected]

Использование Wolfram Alpha для решения задач курса высшей математики технического вуза

Аннотация.В статье описаны возможности программы Wolfram Alpha для поиска информации и решения математических задач применительно к различным разделам высшей математики технического вуза.Ключевые слова:Высшая математика, решение задач, графики функций и поверхностей, дифференцирование, интегрирование, численные методы, дифференциальные уравнения, технический вуз.

Wolfram Alpha –онлайнпрограмма, которую можно использовать для решения различных математических, инженерных и научных задач. Автором Wolfram Alpha является английский математик и программист Стивен Вольфрам.Впервые программа была представлена в мае 2009 года. Вскоре было выпущено мобильное приложение для Android.Поддержку сервиса Wolfram Alpha для мобильных устройств осуществляет виртуальный ассистент Siri, использующий технологии обработки речи;виртуальная клавиатура программы адаптирована для ввода математических формул.Wolfram Alpha представляет собой вычислительную машину знаний. Кроме вычислительных возможностей, в программе заложен поиск информации с последующей обработкой математическими методами, способность выдавать выкладки в виде готового результата, а не ссылок, этим программа отличается от поисковиков, подобныхGoogle. Программа существует в виде интегрируемых модулей применительно к разным областям знаний: математике, химии, физике, инженерии, медицине, истории и т.п.Wolfram Alpha написана на языке «Mathematica». Поисковый запрос вводится на естественном языке (доступна только англоязычная версия), а система Wolfram Alphaиспользует базу вложенных в нее данных, знаний, методов и алгоритмов, чтобы сгенерировать ответ. 2), или график функции и график производной этой функции. Систему Wolfram Alpha можно спросить о том, кто такой «Эйлер» («Euler»), или вывести сведения и формулировку великой теоремы Ферма, или, например, перевести число из одной системы счисления в другую, перечислить проблемы современной математики и т.п.Начать работу с программой предельно просто, для этого необходимо зайти на сайт разработчиков и в поисковое окно ввести вопрос или задание на английском языке [1]. Системаприветствуетвасподсказкой«Enter what you want to calculate or know about». При наборе первых символов появляются похожие запросы, и можно выбрать уже готовый шаблон, который можно изменить с помощью своих данных. Даже непродвинутого пользователя заинтересует возможность построить объемные геометрические тела и графики поверхностей. На рисунке1 по нашему запросу «plot violet icosahedron» программа построила икосаэдр фиолетового цвета.

Рис. 1 ИкосаэдрвWolfram Alpha

Для построения графиков функций и поверхностей в Wolfram Alphaможно использовать функцию «рlot», можно также добавить параметры построения, указав границы по оси Ох; даже если вы не укажете функцию «рlot»,система распознает и построит функцию, автоматически подобрав масштабирование. Многие возможности программы представлены бесплатно, пошаговое решение и более подробные выкладки держатели программы предлагают оплатить покупкой доступа на определенный период, причем доступны приложения для студентов, так и разработки продвинутого уровня для инженеров и научных работников. На рисунке2 показан результат запроса на построение двуполостного гиперболоида по его уравнению. Заменяя некоторые знаки сложения и вычитания, мы мгновенно получим другую поверхность. Варьируя знаки и числовые параметры в данном примере, можно получить представление о различных поверхностях второго порядка, выполнив небольшое исследование «онлайн» даже в бесплатной версии. Например, читателя статьи может заинтересовать поверхность, называемая «сердце Тобина», для этого в браузер программы необходимо ввести запрос «Red Taubin’s heart surface»).

Рис.2 Построение двуполостного гиперболоида вWolfram Alpha

Эти возможности графической визуализации можно использовать в процессе обучения, например, при создании презентаций, а лучше, если есть доступ в интернет, интересно выполнять построения в режиме «онлайн». Возможности программы быстро генерировать ответ можно также использовать для быстрой самопроверки решения.Студентам, знакомым с математическим анализом, будет интересно узнать, что система позволяет дифференцировать и интегрировать, решать дифференциальные уравнения и многое другое, то есть охватывает курс высшей математики технического вуза вместе с различными специальными разделами, многие из которых не изучаются в стандартном курсе. Вопрос, каким образом это делается системой, представляет отдельный интерес. Знакомить студентов с возможностями программы целесообразно в конце изучения курса «Высшая математика».На рисунке3 представлено решение обыкновенного дифференциального уравнения, которое ранее «вручную» решалось в курсе математического анализа, система решила его, определила тип –линейное дифференциальное уравнение первого порядка, а также было построено семейство решений. Полноценное пошаговое решение («steр bystepsolution») недоступно, но доступ к данному функционалу можно купить, что для студента необязательно.

Рис. 3 Решение дифференциального уравнения в Wolfram Alpha

Таким образом, огромные математические возможности программы заключены в наборе функционала, с помощью которого можно получать решения алгебраических, дифференциальных, рекуррентных и функциональных уравнений и неравенств, использовать различные численные методы для нахождения корней уравнений и систем уравнений; возможность решать задачи дифференциального и интегрального исчислений, проводить анализ рядов и анализ Фурье, кластерный анализ и многое другое, то есть решать любые задачи курса математики технического вуза. Фактически, это та же математическая среда, но, в отличии от программных пакетов Maple, Mathcad, Matlab и других специализированных математических программ, адаптированная для использования среднестатистическим пользователем сети Интернет, не требующая предварительной установки. Применительно к курсу математики технического вуза, система Wolfram Alpha может работать с заданиями из линейной алгебры: совершать действия над матрицами, вычислять определители и решать системы линейных алгебраических уравнений. Применительно к аналитической геометрии и векторной алгебре, программа позволяет строить уравнения прямых, плоскостей, кривых и поверхностей второго и высших порядков, решать задачи на нахождение скалярного, векторного и смешанного произведений и т.п. Wolfram Alpha также может работать с доказательствами теорем, с логическими функциями и операторами. Wolfram Alpha может работать с кривыми Безье, Bсплайнами, кривыми и поверхностями, проводить интерполяцию и аппроксимацию данных. Особенно важна возможность получать численные решения задач, которые не имеют аналитических решений вообще или аналитически простых решений. Широкий набор основных операций и алгоритмов на графах. Доступны математические константы любой точности, например,πили e.Встроена математическая статистика, включая автоматическую оценку параметров и проверку гипотез, анализ и построение статистических моделей с возможностью экспорта и импорта данных. Применительно к разделу математического анализа Wolfram Alpha позволяет находить производные, неопределенные и определенные интегралы, криволинейные интегралы, решать прикладные задачи. Программа поддерживает различные форматы для импорта и экспорта, включая электронные таблицы, двумерные и трехмерные графические форматы,мультимедиафайлы, документы, архивные файлы и т.п. Встроены функции для вывода графиков из точек, линий и поверхностей, гистограмм, двумерных и трехмерных диаграмм разного вида.В продвинутых версиях программы многими параметрами математической задачи можно управлять интерактивно, изменяя их с помощью кнопок«ползунков», либо с помощью калькулятора с окнами для ввода различных параметров, что представляет огромные возможности для математического исследования. Проиллюстрируем применение методов численного интегрирования для вычисления «неберущихся» интегралов. На рисунке 4 показано решение интеграла Гаусса в Wolfram Alpha.

Рис.4 Вычисление «неберущегося» интеграла вWolfram Alpha

Некоторые операции из курса математики представлены в таблице 1. Отметим, что сам запрос может быть оформлен различными способами, и система отлично распознает его.Таблица 1Операторы для решения задач курса высшей математики

Название операцииОператорНахождение производной (дифференцирование)d/dxНахождение пределаlimitРешение различных уравненийsolveПостроение графиков и поверхностейplotНахождение неопределенного интегралаintegrateВычисление длины дугиarc lengthПолиномиальная интерполяция interpolating polynomial

Пользователь Wolfram Alphaможет обратиться к сайту русскоязычной поддержки программы[2], на котором представлены примеры из различных разделов курса математики,также к сайтам, содержащим синтаксис программы [3], либо к учебникам по Wolfram Alpha. Можно воспользоваться сайтами поддержки с готовыми примерами.Галерея встроенных примеров доступна на сайте разработчиков во вкладке «Visual Gallery of Examples». Многие приложенияWolfram Alpha весьма интересны. В своем докладе Стивен Вольфрам [4] показывает пример работы одного из приложений программы: с помощью теории графов, позволяет анализировать связи между вашими друзьями в фейсбуке и проводить различные операции, например, визуализировать кластеры сообществ. По нашему мнению, решение стандартных и прикладных математических задач, которые можно осуществлять с помощью программы совместно с традиционным решением вручную, обогащает методику обучения математике, позволяет поддерживать интерес студентов к изучению математики и исследованиям, которые позволяют осуществить понимание математики и использование современных программных средств [5, 6]. Отметим важную мысль о том, что умение работать с программой не может заменять фундаментальных знаний, получаемых студентами технического вуза из курса высшей математики и специальных дисциплин. Знакомство сразличными программными средствами и интернетсервисами гармонично дополняет курс математики, делая инженерное образование отвечающим современным научным реалиям, способствует формированию информационнокомпьютерной компетентности преподавателя и математической компетентности студента [7, 8]. Особое внимание при преподавании математики должно быть уделено задаче выработки у студентов навыков математического исследования прикладных вопросов и умений перевести профессиональную задачу на математический язык [9], работа в программе Wolfram Alphaпоказывает студенту необходимость освоения данной компетенции, а также предоставляет огромные возможности для исследования и анализа решений прикладной задачи.Таким образом, Wolfram Alpha представляет собой мощную вычислительную и информационную среду, которая, несомненно, обладает тем преимуществом, что использовать ее может даже школьник и студент и доступ к ней осуществляется через интернет, посредством запроса на естественном языке. Для студентов же программа полезна и интересна даже в бесплатном ее варианте. Wolfram Alpha отлично справляется с заданиями курса математики технического вуза, в том числе с прикладными и с нестандартными, является прекрасным дополнением к изучению курса. Wolfram Alpha не требует глубоких знаний от начинающего пользователя. В то же время, чем лучше ваши математические познания, тем эффективнее вы сможете ее использовать, ведь система не ограничивается простой демонстрацией решения и визуализацией, она выдает описание множество свойств вызываемых математических объектов и относящихся к решению задач, не ограничиваясь ответом. Отметим, что преимуществом перед другими программами является ее простота использования и получение ответа и решения за счет действий с окном браузера в «в один клик».Прикладные возможности и исследовательские инструменты, предоставляемые ею, огромны как для студента, так и для инженера и ученого. Wolfram Alpha – это действительно современный и удобный инструмент для науки нового типа. Учитывая факт, что система совместима с различными устройствами, работает с облачными сервисами и различными технологиями, а также темпы расширения ее функционала и применения своих разработок все к большему числу областей, можно заключить, что возможности данной системы безграничны.

Ссылки на источники1.1.Wolfram Alpha/ Сайт разработчиков Wolfram Alpha. –URL:http://www.wolframalpha.com/.2.Синтаксис Wolfram Alpha // Викиучебник.–URL:https://ru.wikibooks.org/wiki/Синтаксис_Wolfram_Alpha.3.Вольфрам Альфа порусски / Сайт. –URL: wolframalpharu.com.4.ВольфрамС. Внедряя вычисления повсюду.–URL: https://habrahabr.ru/company/wolfram/blog/221487/.5.Рождественская Е. А., Болдовская Т. Е. Реализация прикладной направленности обучения высшей математике посредством рассмотрения алгоритмов решениязадач в интернетсервисах // Научнометодический электронный журнал «Концепт». –2015. –Т. 13. –С. 366–370. –URL: http://ekoncept.ru/2015/85074.htm.6.Болдовская Т. Е., Полякова Т. А., Рождественская Е. А. Реализация прикладной направленности обучения математике в учебных пособиях и задачниках по математике // Научнометодический электронный журнал «Концепт». –2016. –№ 10 (октябрь). –С. 120–126. –URL: http://ekoncept.ru/2016/16220.htm.7.Рождественская Е. А., Болдовская Т. Е. Информационнокомпьютерная компетентность преподавателя математики в высшей школе // Научнометодический электронный журнал «Концепт».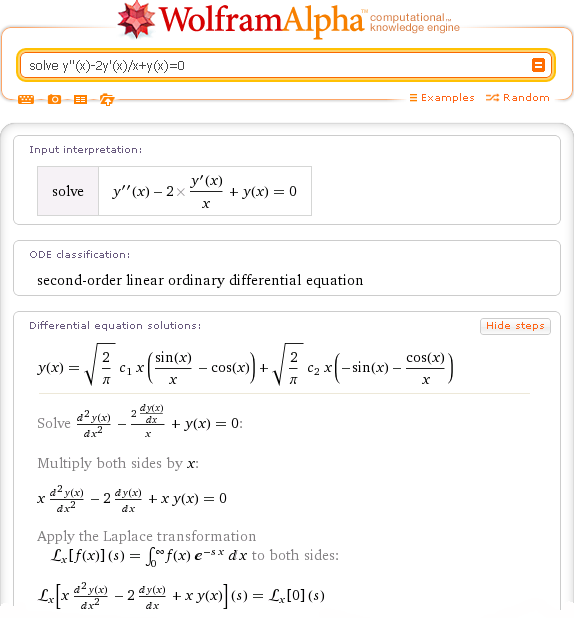 –2016. –№ 4 (апрель). –С. 23–28. –URL:http://ekoncept.ru/2016/16064.htm.8.Болдовская Т. Е., Полякова Т. А., Рождественская Е. А. Методика формирования математической компетентности студента инженерного вуза: цели и перспективы // Научнометодический электронный журнал «Концепт». –2016. –№ 3 (март). –С. 76–80. –URL: http://ekoncept.ru/2016/16054.htm.9.Иванова О. В. Использование крупномодульных опор при изучении математических разделов в вузе // Научнометодический электронный журнал «Концепт». –2016. –№ 8 (август). –С. 79–85. –URL: http://ekoncept.ru/2016/16167.htm.

ядерная физика — Почему все изотопы вольфрама считаются (теоретически) нестабильными?

Задавать вопрос

спросил 3 года, 3 месяца назад

Изменено 6 месяцев назад

Просмотрено 312 раз

9{21}$ лет. {180}\mathrm W$)

• ядерная физика
• атомная физика
• радиоактивность

$\endgroup$

0

$\begingroup$

Можно рассчитать Q-значение (которое является максимальной альфа-кинетической энергией) по разности масс. Когда это положительно, распад теоретически может произойти.

Альфа-распад происходит путем туннелирования через барьер вокруг ядра. Я думаю, что это Гамов сделал вывод, что связь между кинетической энергией и скоростью распада является экспоненциальной.

Уран-238 имеет Q-значение 4,27 МэВ, и его период полураспада все еще довольно велик.

В таблице 1 в Danevich et al. показаны значения Q для W-180, равные 2,5 МэВ. Другие изотопы вольфрама имеют Qs ниже 2 МэВ.

$\endgroup$

5

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

сопротивление и удельное сопротивление | Физика

Цели обучения

К концу этого раздела вы сможете:

• Объяснять понятие удельного сопротивления.
• Используйте удельное сопротивление для расчета сопротивления заданных конфигураций материала.
• Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.

Зависимость сопротивления от материала и формы

Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор на рисунке 1 легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорциональна его длине L , подобно сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет. Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же аналогично потоку жидкости по трубе). На самом деле R обратно пропорционально площади поперечного сечения цилиндра A .

Рис. 1. Однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А, тем меньше его сопротивление.

Для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы оказывают различное сопротивление потоку заряда. Определим удельное сопротивление ρ вещества так, что сопротивление R объекта прямо пропорционально ρ . Удельное сопротивление ρ является внутренним свойством материала, не зависящим от его формы или размера. Сопротивление R однородного цилиндра длиной L , площадью поперечного сечения A , изготовленного из материала с удельным сопротивлением ρ , равно

[латекс] R = \ frac{\rho L}{A }\\[/латекс].

В таблице 1 приведены репрезентативные значения ρ . Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления. Проводники имеют наименьшее удельное сопротивление, а изоляторы — наибольшее; полупроводники имеют промежуточное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться. Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что будет рассмотрено в последующих главах.

Таблица 1. Удельные сопротивления ρ различных материалов при 20ºC

Материал	Удельное сопротивление ρ ( Ом ⋅ м )
Проводники
Серебро	1. 59 × 10 −8
Медь	1. 72 × 10 −8
Золото	2. 44 × 10 −8
Алюминий	2. 65 × 10 −8
Вольфрам	5. 6 × 10 −8
Железо	9. 71 × 10 −8
Платина	10. 6 × 10 −8
Сталь	20 × 10 −8
Свинец	22 × 10 −8
Манганин (сплав меди, марганца, никеля)	44 × 10 −8
Константан (сплав Cu, Ni)	49 × 10 −8
Меркурий	96 × 10 −8
Нихром (сплав Ni, Fe, Cr)	100 × 10 −8
Полупроводники [1]
Углерод (чистый)	3,5 × 10 5
Углерод	(3,5 − 60) × 10 5
Германий (чистый)	600 × 10 −3
Германий	(1−600) × 10 −3
Кремний (чистый)	2300
Кремний	0,1–2300
Изоляторы
Янтарный	5 × 10 14
Стекло	10 9 − 10 14
Люцит	>10 13
Слюда	10 11 − 10 15
Кварц (плавленый)	75 × 10 16
Резина (твердая)	10 13 − 10 16
Сера	10 15
Тефлон	>10 13
Дерево	10 8 − 10 11

Пример 1.

{-9{-5}\text{m}\end{массив}\\[/latex].

Обсуждение

Диаметр чуть меньше десятой доли миллиметра. Он приводится только с двумя цифрами, потому что ρ известен только с двумя цифрами.

Изменение сопротивления в зависимости от температуры

Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. рис. 2.)

Рис. 2. Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры его сопротивление делает резкий скачок, а затем возрастает почти до линейно с температурой.

И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы вибрируют быстрее и преодолевают большие расстояния при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, что фактически увеличивает удельное сопротивление.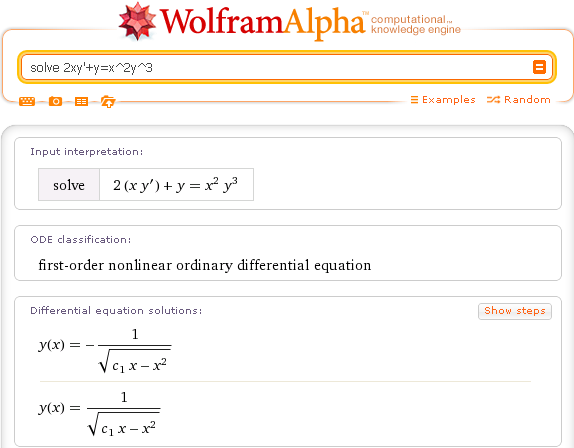 При относительно небольших изменениях температуры (около 100ºC или меньше) удельное сопротивление ρ изменяется с изменением температуры Δ T , как выражается в следующем уравнении

ρ = ρ ₀  (1 + α Δ T ),

, где ρ ₀ – исходное удельное сопротивление, а α – температурный коэффициент 0 50 . (См. значения α в Таблице 2 ниже.) Для больших изменений температуры α может варьироваться, или может потребоваться нелинейное уравнение для нахождения ρ . Обратите внимание, что α положительно для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Манганин (состоящий из меди, марганца и никеля), например, имеет α близок к нулю (до трех знаков по шкале в табл. 2), поэтому его удельное сопротивление мало изменяется с температурой. Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.

Таблица 2. Температурные коэффициенты сопротивления α

Материал	Коэффициент (1/°C) [2]
Проводники
Серебро	3,8 × 10 −3
Медь	3,9 × 10 −3
Золото	3,4 × 10 −3
Алюминий	3,9 × 10 −3
Вольфрам	4,5 × 10 −3
Железо	5,0 × 10 −3
Платина	3,93 × 10 −3
Свинец	3,9 × 10 −3
Манганин (сплав Cu, Mn, Ni)	0,000 × 10 −3
Константан (сплав Cu, Ni)	0,002 × 10 −3
Меркурий	0,89 × 10 −3
Нихром (сплав Ni, Fe, Cr)	0,4 × 10 −3
Полупроводники
Углерод (чистый)	−0,5 × 10 −3
Германий (чистый)	−50 × 10 −3
Кремний (чистый)	−70 × 10 −3

Обратите внимание, что α является отрицательным для полупроводников, перечисленных в таблице 2, что означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. Сопротивление объекта также зависит от температуры, так как R ₀ прямо пропорционально ρ . Для цилиндра мы знаем, что R = ρL / A , и поэтому, если L и A не сильно меняются с температурой, то R будет иметь такую ​​же зависимость от температуры, как ρ . (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L и A составляет примерно два порядка меньше, чем на ρ .) Таким образом,

R = R ₀ (1 + α Δ T )

IS The The Δ T )

IS IS The The Δ T )

IS. температурная зависимость сопротивления объекта, где R ₀ — исходное сопротивление, R — сопротивление после изменения температуры Δ T . Многие термометры основаны на влиянии температуры на сопротивление. (См. рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.

Рисунок 3. Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры. (кредит: Biol, Wikimedia Commons)

Пример 2. Расчет сопротивления: сопротивление горячей нити

Хотя следует соблюдать осторожность при применении ρ = ρ ₀ (1 + α Δ

) и R = R ₀ (1 + α Δ T ) для изменений температуры более 100ºC, для вольфрама уравнения работают достаточно хорошо для очень больших изменений температуры. {-3}/º\text{C }\right)\left(2830º\text{C}\right)\right]\\ & =& {4.8\Omega}\end{массив}\\[/latex].

Обсуждение

Это значение согласуется с примером сопротивления фары в Законе Ома: сопротивление и простые схемы.

Исследования PhET: сопротивление в проводе

Узнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.

Нажмите, чтобы запустить симуляцию.

Резюме сечения

• Сопротивление R цилиндра длиной L и площадью поперечного сечения A равно [латекс]R=\frac{\rho L}{A}\\[/latex], где ρ — удельное сопротивление материала.
• Значения ρ в таблице 1 показывают, что материалы делятся на три группы: проводники, полупроводники и изоляторы .
• Температура влияет на удельное сопротивление; для относительно небольших изменений температуры Δ T , удельное сопротивление равно [латекс]\rho ={\rho }_{0}\left(\text{1}+\alpha \Delta T\right)\\[/latex] , где ρ ₀  исходное удельное сопротивление, а [латекс]\текст{\альфа}[/латекс] — температурный коэффициент удельного сопротивления.
• В таблице 2 приведены значения для α , температурного коэффициента удельного сопротивления.
• Сопротивление R объекта также зависит от температуры: [латекс]R={R}_{0}\left(\text{1}+\alpha \Delta T\right)\\[/latex], где R ₀ — исходное сопротивление, а R — сопротивление после изменения температуры.

Концептуальные вопросы

1. В каком из трех полупроводниковых материалов, перечисленных в таблице 1, примеси создают свободные заряды? (Подсказка: изучите диапазон удельного сопротивления для каждого из них и определите, имеет ли чистый полупроводник более высокую или более низкую проводимость. )

2. Зависит ли сопротивление объекта от пути прохождения тока через него? Рассмотрим, например, прямоугольный стержень — одинаково ли его сопротивление по длине и по ширине? (См. рис. 5.)

Рис. 5. Встречает ли ток, проходящий двумя разными путями через один и тот же объект, разное сопротивление?

3. Если алюминиевый и медный провода одинаковой длины имеют одинаковое сопротивление, какой из них имеет больший диаметр? Почему?

4. Объясните, почему [латекс]R={R}_{0}\left(1+\alpha\Delta T\right)\\[/latex] для температурного изменения сопротивления R  объекта не так точен, как [латекс]\rho ={\rho }_{0}\left({1}+\alpha \Delta T\right)\\[/latex], что дает температурное изменение удельного сопротивления р .

Задачи и упражнения

1. Каково сопротивление 20,0-метрового отрезка медной проволоки 12-го калибра и диаметром 2,053 мм?

2. Диаметр медной проволоки нулевого калибра 8,252 мм. Найти сопротивление такого провода длиной 1,00 км, по которому осуществляется передача электроэнергии.

3. Если вольфрамовая нить диаметром 0,100 мм в электрической лампочке должна иметь сопротивление 0,200 Ом при 20ºC, то какой длины она должна быть?

4. Найти отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление на единицу длины (как в бытовой электропроводке).

5. Какой ток протекает через стержень из чистого кремния диаметром 2,54 см и длиной 20,0 см, если к нему приложено напряжение 1,00 × 10 ³ В? (Такой стержень можно использовать, например, для изготовления детекторов ядерных частиц). ? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?

7. Резистор из нихромовой проволоки используется в приложениях, где его сопротивление не может измениться более чем на 1,00% от его значения при 20,0ºC. В каком диапазоне температур его можно использовать?

8. Из какого материала изготовлен резистор, если его сопротивление при 100°С на 40,0% больше, чем при 20,0°С?

9. Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0ºC до 55,0ºC, содержит резисторы из чистого углерода. Во сколько раз увеличивается их сопротивление в этом диапазоне?

10. (a) Из какого материала сделана проволока, если она имеет длину 25,0 м, диаметр 0,100 мм и сопротивление 77,7 Ом при 20,0ºC? б) Каково его сопротивление при 150°С?

11. При постоянном температурном коэффициенте удельного сопротивления, каково максимальное уменьшение сопротивления константановой проволоки в процентах, начиная с 20,0ºC?

12. Проволоку протягивают через матрицу, растягивая ее в четыре раза по сравнению с первоначальной длиной. Во сколько раз увеличивается его сопротивление?

13. Медный провод имеет сопротивление 0,500 Ом при 20,0°С, а железный провод имеет сопротивление 0,525 Ом при той же температуре. При какой температуре их сопротивления равны?

14. (a) Цифровые медицинские термометры определяют температуру путем измерения сопротивления полупроводникового устройства, называемого термистором (которое имеет α  = –0,0600/ºC), когда оно имеет ту же температуру, что и пациент. Какова температура тела пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0°С (нормальная температура тела)? (b) Отрицательное значение для α может не поддерживаться при очень низких температурах. Обсудите, почему и так ли это, здесь. (Подсказка: сопротивление не может стать отрицательным.)

15. Комплексные концепции  (a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити. Вы можете принять коэффициент теплового расширения равным 12 × 10 ⁻⁶ /ºC. б) На сколько процентов ваш ответ отличается от ответа в примере?

16. Необоснованные результаты  (a) До какой температуры нужно нагреть резистор из константана, чтобы удвоить его сопротивление при постоянном температурном коэффициенте удельного сопротивления? б) Разрезать пополам? в) Что неразумного в этих результатах? (d) Какие предположения неразумны, а какие предпосылки противоречивы?

Сноски

1. 1 Значения сильно зависят от количества и типов примесей
2. 2 Значения при 20°C.

   No related posts.