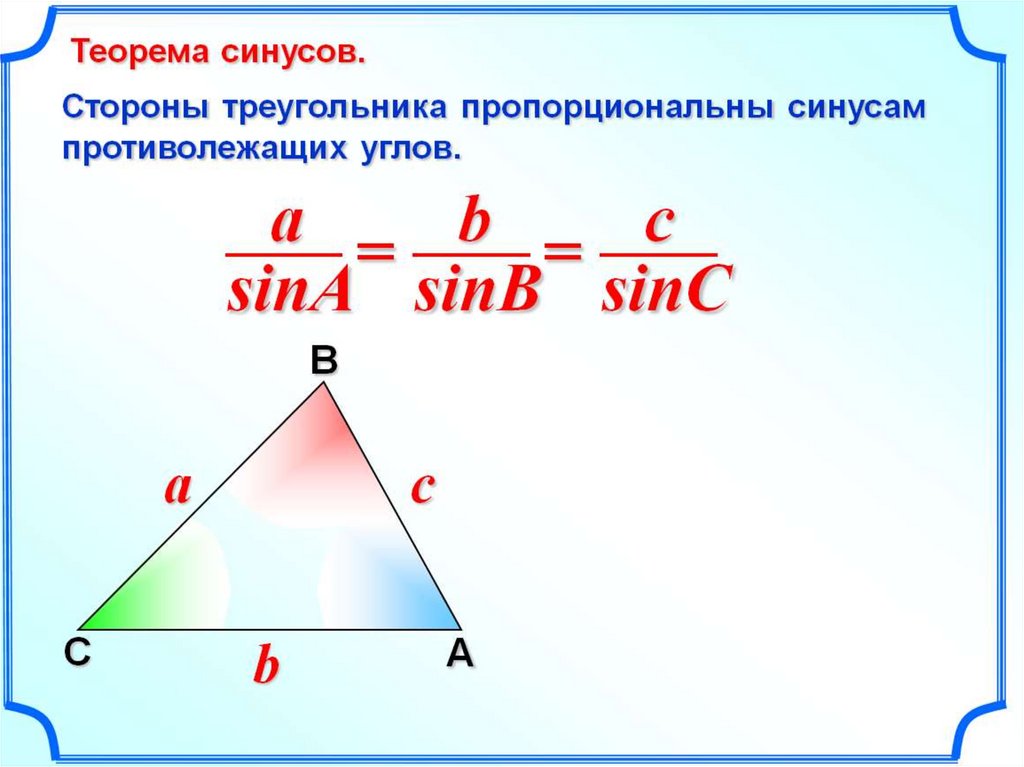
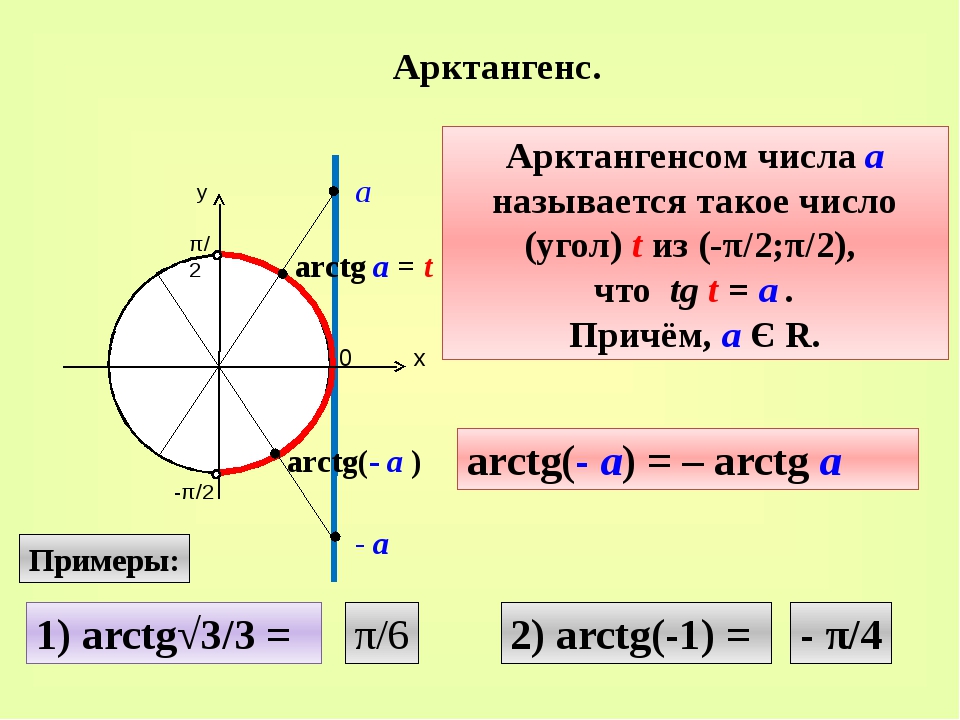
Так Называется Синус, Деленный На Тангенс
Решение этого кроссворда состоит из 7 букв длиной и начинается с буквы К
Ниже вы найдете правильный ответ на Так называется синус, деленный на тангенс, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
Понедельник, 4 Января 2021 Г.
CodyCross Дикий Запад Rруппа 421
КОСИНУС
предыдущий следующий
ты знаешь ответ ?
ответ:
CODYCROSS Дикий Запад Группа 421 ГОЛОВОЛОМКА 4
- Победительница фабрики звёзд 5 виктория
- Появление у особи признаков далёких предков
- Итальянский сыр из молока аостских коров
- Безвластие, вседозволенность
- » радость», созвучная с детёнышем собаки
- Модельер, создавший бодисьют
- Название вида легкой пехоты в средневековой японии
- Главный персонаж произведения «муму»
- Гребное судно в венеции
- Ежедневное информирование о происходящем в мире
- Самая крупная птица из совиных
связанные кроссворды
- Косинус
- В геометрии синус, __ и тангенс
- Отношение прилежащего катета к гипотенузе
- Косинус
- Математическая тригонометрическая функция
- Хорошее отношение катета к гипотенузе
- Косинус
- Тригонометр функция 7 букв
- Собрат тангенса 7 букв
похожие кроссворды
- Синдром синус-бронхиальный
- Одна из тригонометрических функций, синус дополнительного угла 7 букв
- В геометрии синус, __ и тангенс
- Синус, косинус, секанс, 8 букв
- Единица, делённая на синус 8 букв
- Его можно найти, если синус поделить на косинус
- Как сейчас называется центральная фабрика союзкино?
- Как называется народный сказитель у кумыков?
Сборник ответов к кроссвордам и сканвордам: ‘Синус, косинус, секанс, .
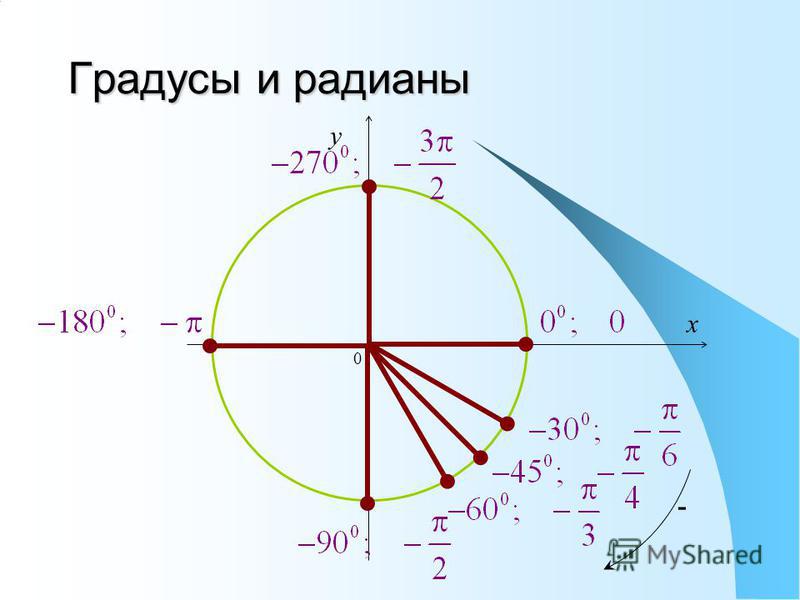..’КОСЕКАНС
Первая буква К
Вторая буква О
Третья буква С
В середине буква Е
В середине буква К
В середине
буква А
Предпоследняя буква Н
Последняя буква С
В этот день все верующие отмечают праздник Воскрешения Иисуса Христа
-А-Х-
Смотреть ответ
Еще вопросы к слову‘КОСЕКАНС’ |
|---|
• Функция y=cosec(x) |
• Функция cosec(x) |
• Единица, деленная на синус |
• Функция в тригонометрии |
• Геометрическая функция |
• Коллега котангенса |
• Коллега тангенса и котангенса |
• М. мтм. секанс дополнения дуги и угла к |
• Обратен синусу |
• Одна из тригонометрических функций |
• Отношение длины гипотенузы к неприлегающему углу катета |
• Собрат синуса и косинуса |
• Тригонометрическая функция |
Похожие вопросы в кроссвордах |
|---|
Косинус-И-У- |
Нос — . .., глаза — косинус-И-У- |
Синус, деленный на косинус-А-Г-Н- |
Единица, деленная на косинус-Е—Н- |
Косинус, деленный на синус.-О-А—Н- |
Тангенс, умноженный на косинус-И-У- |
Косинус, умноженный на тангенс-И-У- |
Косинус, деленный на котангенс-И-У- |
Секанс в пангинги (карточный термин)-Е-Е—К- |
М. мтм. секанс дополнения дуги и угла к-О-Е—Н- |
Рука из карт одной масти; козырной секанс в пинокле. (карточный термин)-Л-Ш- |
Синдром синус-бронхиальный-И-О——И- |
Синус вверх тормашками-О-И-У- |
Синус, умноженный на котангенс-О-И-У- |
Единица, деленная на синус-О-Е—Н- |
Синус, деленный на тангенс-О-И-У- |
Синус по отношению к косинусу-А-Г-Н- |
Название этой тригонометрической функции в переводе на русский означает «дополняющий синус»-О-И-У- |
Широкая перевязь из плотной ткани, заменившая синус тоги, обязательная часть костюма консула-О-Т——И- |
Хирургическая операция рассечения сращений в области радужно-роговичного угла глаза (угла передней камеры) с целью улучшения оттока водянистой влаги через венозный синус склеры-О-И—-И- |
√ Тригонометрические тождества (определение, правила, примеры) | Σ
by Sigma
Содержание
Прямоугольный треугольник
Тригонометрические тождества — это уравнения, которые верны для прямоугольных треугольников.
Каждая сторона прямоугольного треугольника имеет имя:
- Смежная всегда находится рядом с углом
- Противоположная сторона находится напротив угла
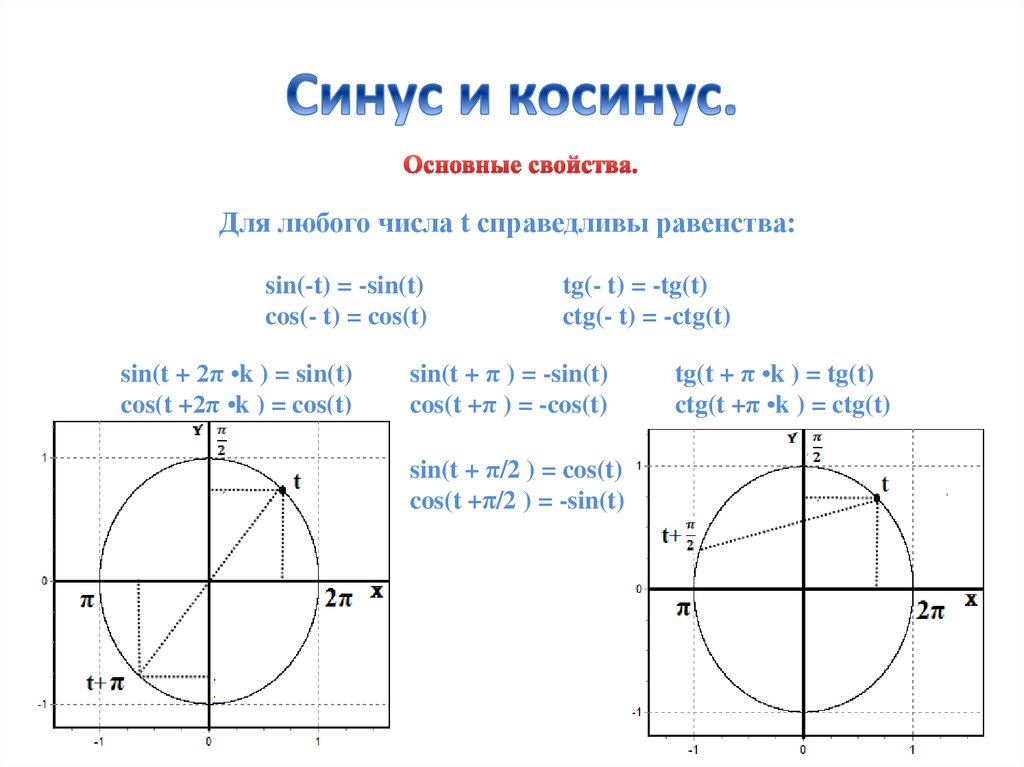
Синус, косинус и тангенс
3 основные функции в тригонометрии: синус, косинус и тангенс . Это просто длина одной стороны, деленная на другую
для правого треугольника с углом θ:
| Синусоидальная функция | SIN (θ) = противоположный / гипотенусный | tan(θ) = Противоположный / Смежный |
Для заданного угла θ каждое отношение остается одним и тем же независимо от того, насколько большим или маленьким является треугольник.
Когда мы делим синус на косинус, мы получаем:
Итак, мы можем сказать:
Косеканс, секанс и котангенс
Мы также можем разделить «наоборот» (например, смежный/противоположный вместо противоположного/примыкающего):
| функция косеканса | csc(θ) = гипотенуза 90/противоположный |
| Сексуальная функция | с (θ) = гипотенуза / смежная кроватка |
| Котангентная функция | Cot (θ) = соседний / противоположный |
Пример
, когда на противоположность = 1 и гипт = 2
.
0005
sin(θ) = 1/2 и
csc(θ) = 2/1
Из всего, что мы можем сказать:
sin(θ) = 1/csc(θ)
cos(θ) ) = 1/сек(θ)
tan(θ) = 1/cot(θ)
И наоборот:
csc(θ) = 1/sin(θ)
сек(θ) = 1 /cos(θ)
cot(θ) = 1/tan(θ)
Теорема Пифагора
Следующие тригонометрические тождества начнем с теоремы Пифагора:
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат a плюс квадрат b равен квадрату c:
A 2 + B 2 = C 2
Дирация на C 2 дает
, что может быть упрощено на:
- A / C. C. / C. C. C. / C. C. is sin(θ)
- b/c — смежная / гипотенуза, которая равна cos(θ)
Итак, (a/c) 2 + (b/c) 2 = 1 также можно записать:
sin 2 θ + cos 2 θ = 1
Примечание:
SIN 2 θ означает найти синус θ, затем квадрат, и
SIN θ 2 sine function
Related identities
Related identities include
sin 2 θ = 1 − cos 2 θ
cos 2 θ = 1 − sin 2 θ
tan 2 θ + 1 = сек 2 θ
tan 2 θ = sec 2 θ − 1
cot 2 θ + 1 = csc 2 θ
cot 2 θ = csc 2 θ − 1
Opposite Angle Identities
sin(−θ) = −sin(θ)
cos(−θ) = cos(θ)
tan(−θ) = −tan(θ)
Тождества с двойным углом
Тождества с половинным углом
Обратите внимание, что «±» означает, что это может быть любой из них, в зависимости от значения θ/2
Сумма углов и разности Тождества
| Синус | sin (A+B) = sin A cos B + cos A sin B sin (A-B) = sin A cos B – cos A sin B |
| Косинус | cos (A+B) B) = cos a cos b-sin a sin b cos (a-b) = cos a cos b + sin a sin b |
| Tangent | |
| Cotangent |
Learn
99930.
Решение треугольников SSS
Sohcahtoa
Solving SSA Triangles
Finding an Angle in a Right Angled Triangle
Categories AlgebraAlgebra Index
Trigonometric Functions — Тригонометрические тождества
Во-первых, позвольте нам представить вам сумму синуса и тождество разности .
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
и
sin(α – β) = sin(α)cos(β) – cos(α)sin(β)
Довольно дико, правда? Докажем, что они действительно работают.
Посмотрите на рисунок ниже, на котором показаны два угла α и β.
Представьте, что линия OB качается вокруг O и заметает угол α, а затем заметает угол β.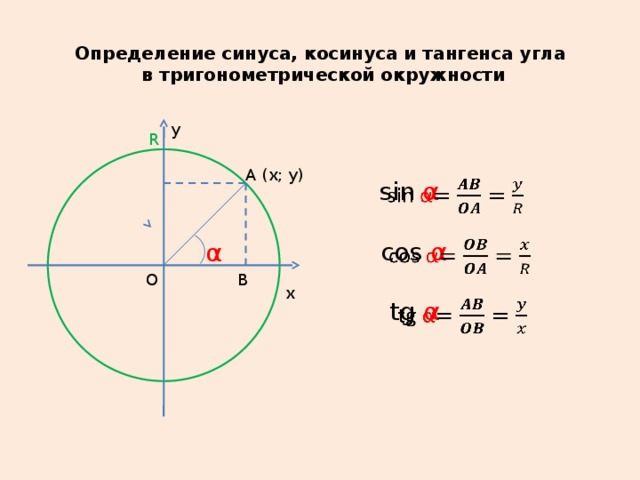
(Вещи определенно движутся здесь, в тригонометрической стране.)
Посмотрите внимательно, и вы увидите, что перпендикулярные линии были добавлены, чтобы сформировать несколько прямоугольных треугольников.
Во-первых, обратите внимание, что ∠ BOE = α + β.
Это означает, что sin(∠ BOE ) = sin(α + β).
Теперь посмотрите на Δ OAE и выделите коэффициент запуска для синуса.
Поскольку BD = AC , мы можем переписать это как .
Оставайтесь с нами сейчас… пришло время сделать некоторые изменения.
Перетасуем знаменатели. (Покер, кто-нибудь?)
Задержитесь на этом уравнении на секунду, пока мы совершим быстрое боковое путешествие. Нам нужно показать, что ∠ CED совпадает с углом α для остальной части доказательства.
Хорошо, посмотрите, как линия OD пересекает обе параллельные линии CD и OB ? Это означает, что ∠ ODC имеет ту же меру, что и угол α, из-за теоремы об альтернативных внутренних углах из геометрии.
Из рисунка также видно, что ∠ ODC и ∠ CDE образуют прямой угол, поэтому m∠ CDE = 90° – m∠ ODC . А с ∠ ODC = α, мы можем переписать это как m∠ CDE = 90° – α. Верно? Верно.
Поскольку три угла в треугольнике CDE в сумме составляют 180° (как и в любом треугольнике), это означает:
m∠ DCE + m∠ CDE + m∠ CED = 1800°
90° + (90° – α) + м∠ КЭД = 180°
180° – α + м∠ КЭД = 180° CED = α
Фух. Хорошая сделка; этот угол в верхней части рисунка имеет ту же меру, что и угол α. Поверьте нам, это важно.
Теперь вернемся к диаграмме в последний раз и запишем ряд триггерных соотношений для углов α и β.
(Это работает, потому что мы только что проделали всю работу, чтобы показать, что m∠ CED = α.)
Как эти ребята нам помогают? Ура, теперь мы можем подставить все те корявые отношения, которые мы придумали ранее:
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
Победа! это наша сумма синуса тождество .
Теперь мы можем найти тождество разности, подставив -β вместо β следующим образом:
sin(α – β) = sin[α + (-β)] = sin(α)cos(-β) + cos (α)sin(-β)
Из наших тождеств с отрицательными углами мы знаем, что:
cos(-β) = cos(β)
и
sin(-β) = -sin(β)
Это означает, что у нас есть тождество разности синусов :
sin(α – β) = sin(α)cos(β) – cos(α)sin(β)
Косинус получает поворот
Теперь перейдем к тождеству суммы косинусов .
cos(α + β) = cos(α)cos(β) – sin(α)sin(β)
Мы можем доказать тождество суммы косинусов, применив наше тождество кофункции:
cos(α + β) = sin[90° – (α + β)]
Удалите эти надоедливые скобки:
cos(α + β) = sin(90° – α – β) = sin[(90° – α) – β]
Затем подставьте это в наше тождество разности синусов:0° – α)sin(β)
Снова используя тождества кофункций, мы можем заменить sin(90° – α) на cos(α) и заменить cos(90° – α) на sin(α) на заканчивать.
cos(α + β) = cos(α)cos(β) – sin(α)sin(β)
Бам. Успешно справился.
Чтобы найти идентичность разности косинусов, подставьте -β вместо β, точно так же, как вы делали это для идентичности разности синусоид.
cos(α – β) = cos[α + (-β)] = cos(α)cos(-β) – sin(α)sin(-β)
Подставьте эти отрицательные угловые тождества, чтобы получить косинусная разность тождество :
cos(α – β) = cos(α)cos(β) + sin(α)sin(β)
Теперь давайте возьмем наши с трудом заработанные тождества суммы и разности и используем их для решения задач .
Пример задачи
Используйте тождество суммы или разности, чтобы найти точное значение cos(75°) без калькулятора.
Для этого мы смотрим на угол 75°, чтобы увидеть, является ли он суммой или разностью каких-либо углов из наших эталонных треугольников.
Мы видим, что 75° = 30° + 45°.
Итак:
cos(75°) = cos(30° + 45°)
Мы можем использовать тождество суммы косинусов.
cos(α + β) = cos(α)cos(β) – sin(α)sin(β)
cos(30° + 45°) = cos(30°)cos(45°) – sin( 30°)sin(45°)
Теперь подставьте значения из ваших эталонных треугольников. (О, это снова они.)
И ответ:
Пример задачи
Используйте тождество суммы или разности, чтобы найти точное значение sin(165°).
В каком квадранте находится 165°?
Он больше 90°, но меньше 180°, значит, находится в квадранте II.
Для этого мы смотрим на 165°, чтобы увидеть, является ли это суммой или разностью наших углов от наших эталонных треугольников.
165° = 120° + 45°
Итак:
Пример задачи
Используйте тождество суммы или разности, чтобы найти точное значение cos(255°).
В каком квадранте находится 255°?
Да, это в квадранте III. Давайте посмотрим на 255°, чтобы увидеть, является ли это суммой или разностью каких-либо специальных углов.
255° = 300° – 45°
Итак:
Переход по быстрой касательной
Тождества суммы и разности тангенса можно найти из тождеств суммы и разности синусов и косинусов.
К счастью для нас, тангенс угла — это то же самое, что синус над косинусом.
Подставьте суммы тождеств для синуса и косинуса.
Далее небольшое деление поможет нам в пути (дроби никогда не помешают).
Разделить числитель и знаменатель на cos(α)cos(β).
Теперь разделите термины.
Замените каждый термин на «1» или «загар», где это уместно. Помните, что тангенс больше синуса, чем косинуса.
Теперь, еще немного упростив, мы получим тождество суммы тангенса :
Затем таким же образом мы можем найти тангенс(α – β).
Еще раз, с небольшой помощью нашего знакомого деления, разделите числитель и знаменатель на cos(α)cos(β).
Теперь разделите термины и замените каждый термин на «1» или «тан», где это уместно.
Мы почти у цели — там есть а там, мы обещаем. Если немного упростить, то получится. Вот наше тождество разности тангенсов :
Пример задачи
Используйте тождество суммы или разности, чтобы найти tan(255°).