Граф построение онлайн: Граф Онлайн: Примеры графов

Graphviz — рисуем графы — Ещегодник

Достаточно часто встречается задача, когда надо нарисовать нечто, представляющее из себя граф. Это может быть иерархическая сструктура работ проекта, иерархическая структура рисков, организационная структура, топология сети и т.п. Если же количество вершин и ребер достаточно велико, то нарисовать это красиво становится нетривиальной задачей. К счастью, существует программа Graphviz, которая использует язык описания графов dot и имеет графический интерфейс под Windows.

Сама программа бесплатна и может быть скачена по ссылке.  После установки в Windows в меню «Пуск» появится приложение gvedit, которое является графическим интерфесом к установленному пакету программ. В Mac OS X такого не произойдет и обходное решение описано ниже (если, конечно, вы не готовы работать в терминале).

Рассмотрим направленный граф, описывающий все возможные коммуникации между четырьмя участниками проекта. Листинг, описывающий граф привожу ниже:

digraph test{
   1->2;
   1->3;
   1->4;
   2->1;
   2->3;
   2->4;
   3->1;
   3->2;
   3->4;
   4->1;
   4->2;
   4->3;
}

В приложении это будет выглядеть следующим образом:

 

В данном случае, был использован параметр по умолчанию и для построения графа использована утилита dot.

Для примера, тот же граф, построенный с помощью:

circo	fdp	twopi

Подробнее это описано в документации на сайте. Если кратко, то dot, а далее в статье используется только он, рисует граф в заданном в порядке ветвления; twopi — использует радиальное построение, когда вершины располагаются на концентрических окружностях, circo — связанные вершины располагаются по кругу.

В данном случае, у нас был изображен орграф. Если граф не ориентирован, иными словами «стрелочки» на рисунке нам не важны, то граф описывается следующим образом (обратите внимание на первой слово «graph» вместо «digraph», как задаются связи («—» вместо «->»), а также на команду node [shape = box] — задающую прямоугольники в качестве вершин). Несомненно, формат стрелок можно определить и в самом графе на языке dot, но алгоритмы построения для ориентированных и неориентированных графов имеют небольшое отличие.

graph test{
   node [shape = box];
   "Проект А"--"Фаза 1";
   "Проект А"--"Фаза 2";
   "Проект А"--"Фаза 3";
   "Фаза 1"--"Задача 1";
   "Фаза 1"--"Задача 2";
   "Фаза 2"--"Задача 3";
   "Фаза 2"--"Задача 4";
}

Результат выглядит так:

Пример из заметки по динамическому программированию: меняем ориентацию графа (строится справа налево), добавляем подписи и стили линий и задаем размер листа.

digraph ex01 {
    rankdir=LR;
    size="8,5"
    node [shape = box];
    "1" -> "2" [ label = "3",style=bold,color=red ];
    "1" -> "3" [ label = "7",style=dotted];
    "1" -> "4" [ label = "2",style=dotted ];
    "2" -> "5" [ label = "9",style=dotted ];
    "2" -> "6" [ label = "11",style=bold,color=red ];
    "3" -> "5" [ label = "5",style=dotted ];
    "3" -> "6" [ label = "10",style=dotted ];
    "3" -> "7" [ label = "7",style=dotted ];
    "4" -> "6" [ label = "15",style=dotted ];
    "4" -> "7" [ label = "13",style=dotted ];
    "5" -> "8" [ label = "7",style=dotted ];
    "5" -> "9" [ label = "5",style=dotted ];
    "6" -> "8" [ label = "3",style=bold,color=red ];
    "6" -> "9" [ label = "4",style=dotted ];
    "7" -> "8" [ label = "7",style=dotted ];
    "7" -> "9" [ label = "1",style=dotted ];
    "8" -> "10" [ label = "1",style=bold,color=red ];
    "9" -> "10" [ label = "4",style=dotted ];
}

 

Более сложные пример приведен в заметке по методу анализа иерархии.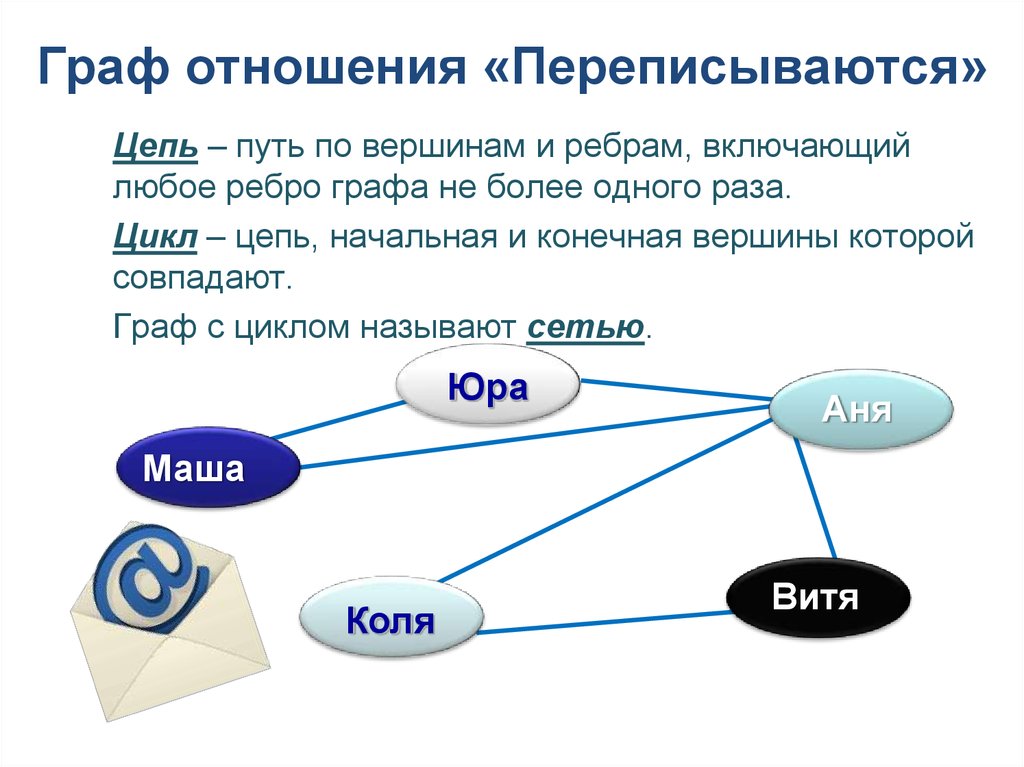

При выборе формата записи результирующего графа, определенный интерес представляет формат svg в поле Output File Type. Формат svg — векторный формат, файлы в этом  формате можно редактировать, например, с помощью Inkscape.  Также обратите внимание на векторный формат emf, позволяющий внедрять и масштабировать рисунки в Word без потери качества. Для этого сайта был использован растровый формат png.

И последний пример, использование структуры в качестве вершины графа.

digraph structs { 
    node [shape=record,];
    struct1 [label="<f0> Инициация|<f1> Планирование|<f2> Исполнение|<f3> Завершение",
             fillcolor=yellow];
    struct2 [label="<f0> Мониторинг|<f1> Контроль"]; 
    struct1:f0-> struct2:f0;
    struct1:f1-> struct2:f0;
    struct1:f2-> struct2:f0;
    struct1:f3-> struct2:f0;
    struct2:f1 -> struct1:f0 [color="red"];
    struct2:f1 ->struct1:f1 [color="red"];
    struct2:f1 ->struct1:f2 [color="red"];
    struct2:f1 ->struct1:f3 [color="red"];
}

 

Самый простой вариант создать диаграмму — это запустить в консоли соответсвующую команду (на рисунке показано окно Терминала под Mac OS X), например, dot.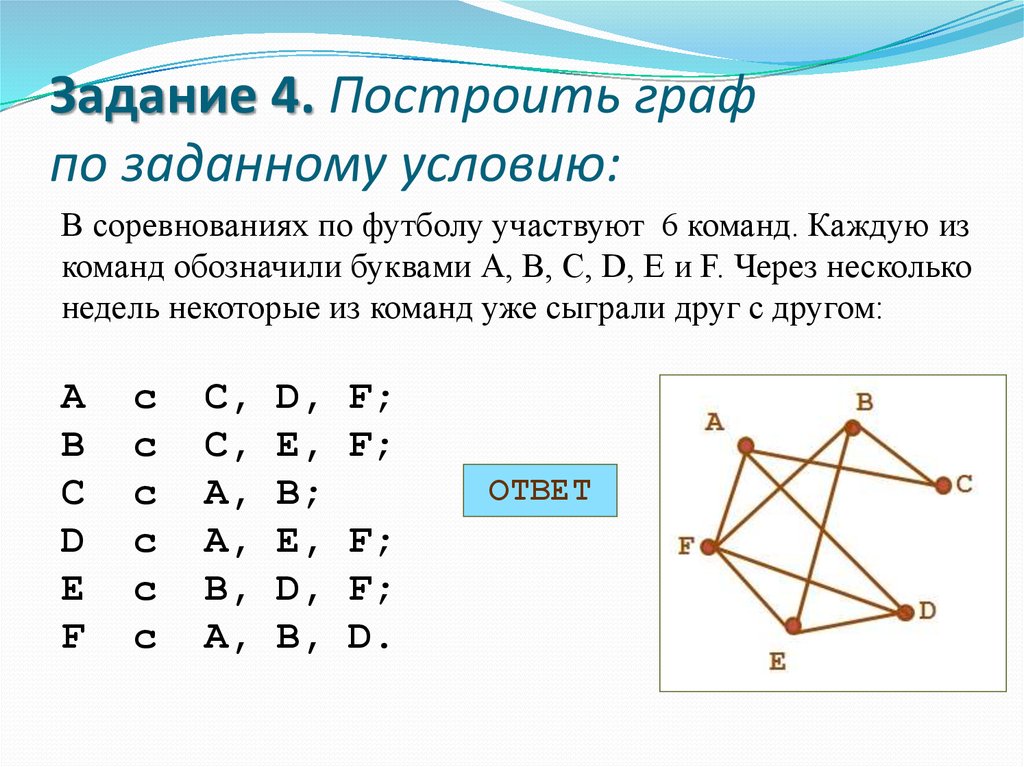 Если файл называется test.gv, а на выходе мы хотим получить png, то команда будет такая, как это показано ниже (а также выше на рисунке). Решение универсально и работает в любой операционной системе.

dot -Tpng -O test.gv

Следует отметить, что в Mac OS X при установке graphviz такой удобной графической оболочки как в Windows, вы не получите. Если вариант собрать его из исходников из портов (если вы хоть что-то поняли из написанных слов, значит инструкции не нужны), можно использовать консоль, как это показано выше, но также имеется возможноть использовать средства языка R и RStudio. Возможно, что кому-то это будет проще.

Для корректной работы вам понадобится пакет DiagrammeR. Установите его из меню или командой

install.packages("DiagrammeR")

После установки создайте файл, скопируйте туда код, сохраните его с расширением .gv, поставьте галочку «Preview on Save». Обратите внимание, если вы работаете в Windows, то файл необходимо сохранять в кодировке cp1251, иначе вместо русского языка вы получите кракозябры.

Дальше, используя кнопку Export, можно сохранить получившуюся диаграмму в формате png или jpeg.

Следует отметить, что DiagrammeR позволяет работать и с диаграммами в формате mermaid. В таком случае, файлы надо сохранять с расширением .mmd. Помимо простых графов, этот формат позволяет описать диаграмму последовательности, как это показано на рисунке ниже.

Код:

sequenceDiagram
  Покупатель->>Кассир: запрос билетов
  Кассир->>База данных: наличие мест
  alt билеты имеются
    База данных->>Кассир: Имеются
    Кассир->>Покупатель: Подтверждение
    Покупатель->>Кассир: Согласие
    Кассир->>База данных: Бронирование мест
    Кассир->>Принтер: Печать билета
  else билеты проданы
    База данных->>Кассир: Свободных мест нет
    Кассир->>Покупатель: Извините
  end

Диаграмма (обратите внимание, что пропали стрелки и непонятно, как идут сообщения.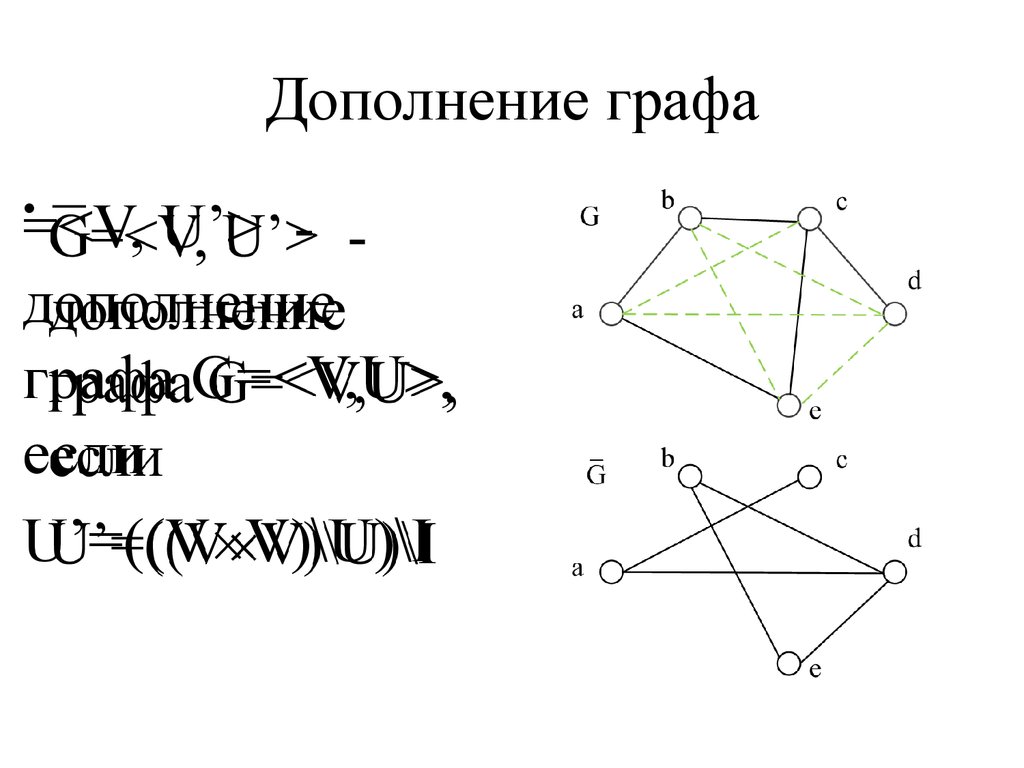

 Это давно известная ошибка, которую так и не исправили):

К счастью, в формате mermaid можно редактировать online с сохранением результата в формате SVG, где результат будет выглядеть больше похожим на то, что ожидалось.

Дополнительные материалы

1. Примеры на сайте graphviz. При кликании мышкой по графу показывается его код.
2. Документация: различные типы узлов
3. Документация: различные типы стрелок
4. Документация: цветовая палитра

Инцидентность и смежность в графах, матрицы смежности, матрицы инцидентности

• Инцидентность и смежность в графах
• Матрицы смежности
• Матрицы инцидентности
• Списки инцидентности
• Преимущества и недостатки каждого способа

Инцидентность — это когда вершина a является либо началом либо концом ребра e. Две вершины называются инцидентными, если у них есть общее ребро.

Для того, чтобы задать граф аналитически, множества V вершин графа и множества U рёбер графа, которые фигурировали в определении графа, будет недостаточно.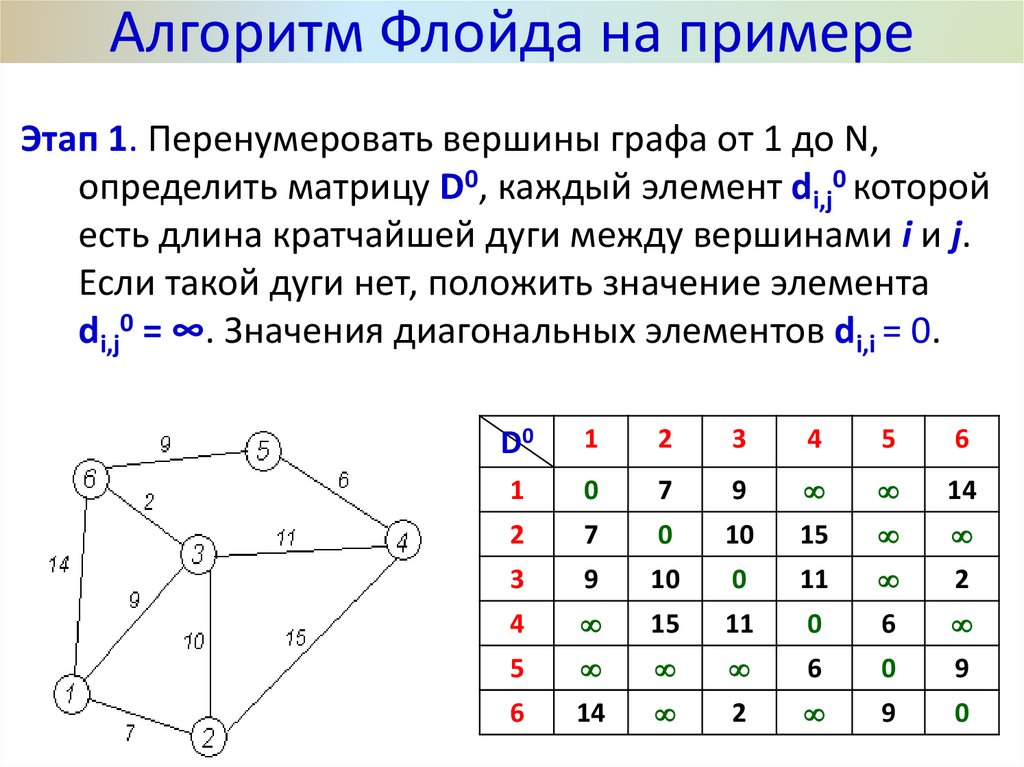 Потребуется ещё и множество P троек вида (a, u, b), указывающих какую пару a, b элементов множества вершин V соединяет тот или иной элемент u множества рёбер U графа. Элементы множества P называются инциденциями графа. Вот мы и подошли к одному из первых понятий теории графов — инцидентности.

Понятие инцидентности — одно из главных при создании структур данных для представления графов в памяти ЭВМ, к которым мы перейдём после примера 1.

Пример 1. Задать аналитически граф, представленный на рисунке ниже. (рис. А)

Решение. Распространённые ошибки — не заметить вершины графа, которые не соединены ни с одной другой вершиной, в том числе с самой собой, и не включить их во множество вершин графа, а также указать не все рёбра графа, соединяющие две вершины. Поэтому вершину f данного графа обязательно включаем во множество вершин графа V, а, рёбра 6 и 7, хотя они соединяют одну и ту же вершину саму с собой и обе не имеют направления, включаем во множество рёбер U.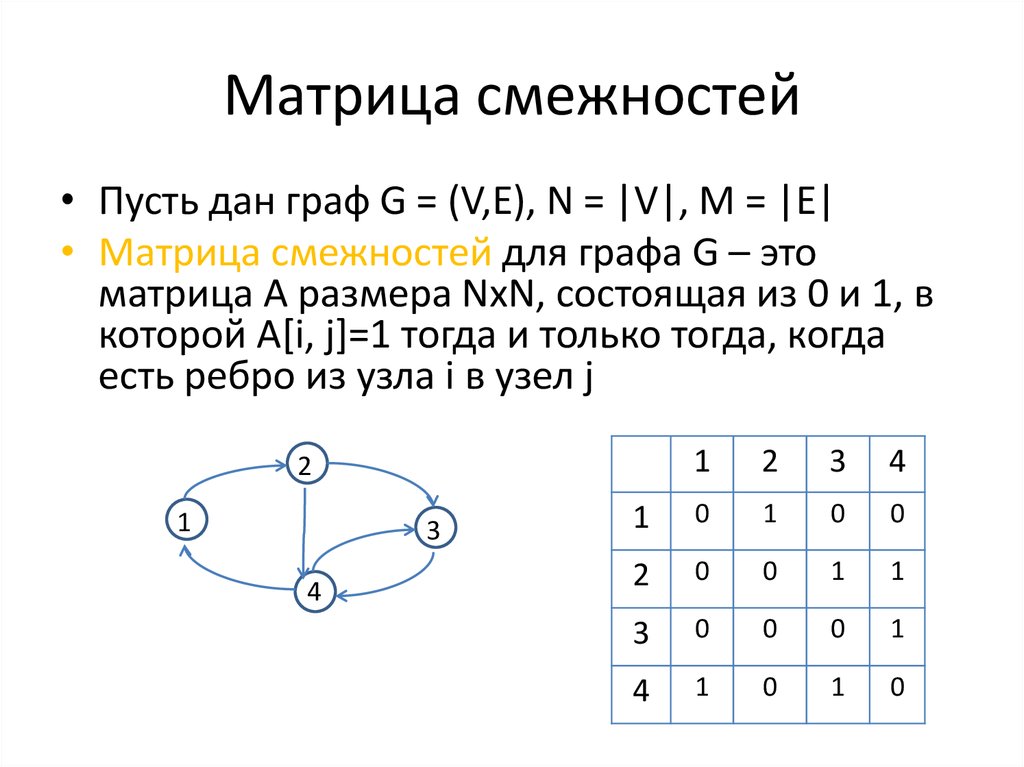

Итак, задаём граф следующими множествами:

множество вершин: V = {a, b, c, d, e, f}

множество рёбер: U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}

множество инциденций: P = {(b, 1, a), (b, 2, a), (a, 3, b), (b, 4, b), (b, 5, b), (c, 6, c), (c, 7, c), (b, 8, d), (d, 8, b), (b, 9, d), (b, 10, e), (b, 11, e), (e, 11, b)}

Смежность вершин графа — это когда две вершины графа соединены ребром.

Зададимся вопросом: можно ли поместить слона в компьютер? Ответ: можно, если слона смоделировать в виде графа, в котором вершинами являются части его тела, а рёбра соединяют те части тела, которые соединены в слоне как биологическом объекте.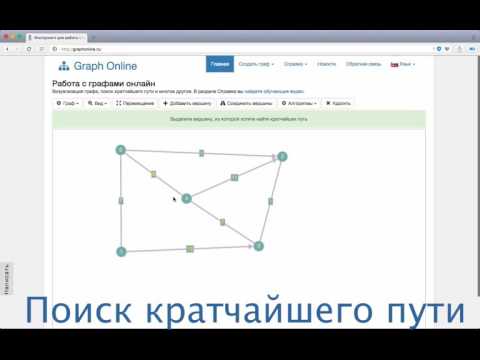 При этом получившийся граф должен быть представлен в памяти компьютера в понятном компьютеру виде.

В связи с широким применением графов в программировании и информационных технологиях вообще возникает вопрос о представлении графа в виде структуры данных. Различные способы представления графов в памяти компьютера отличаются объёмом занимаемой памяти и скоростью выполнения операций над графами.

Наиболее часто используются три такие структуры данных — матрица смежности, матрица инцидентности и список инцидентности.

Матрица смежности, как и матрица инцидентности, позволяет установить множество вершин, соседних с заданной (то есть рассматриваемой в конкретной задаче), не прибегая к полному просмотру всей матрицы. Матрицы смежности обычно представляются двумерным массивом размера n x n, где n — число вершин графа.

Матрица смежности S — это квадратная матрица, в которой и число строк, и число столбцов равно n — числу вершин графа. В ячейки матрицы смежности записываются некоторые числа в зависимости от того, соединены соответствующие вершины рёбрами или нет, и от типа графа.

Матрица смежности для неориентированного графа

Элемент матрицы смежности sij неориентированного графа определяется следующим образом:

— равен единице, если вершины vi и vj смежны;

— равен нулю, если вершины vi и vj не смежны.

Если для элемента матрицы vij имеет место i = j, то есть элемент находится на диагонали, то этот элемент равен единице, если этот элемент имеет петлю, и нулю, если элемент не имеет петли.

Пример 2. Составить матрицу смежности для графа, представленного на рисунке ниже.

Ответ.

V	1	2	3	4	5
1	0	1	1	0	0
2	1	0	0	1	1
3	1	0	0	0	1
4	0	1	0	0	0
5	0	1	1	0	0

Таким образом, матрица смежности неориентированного графа симметрична относительно главной диагонали.

Матрица смежности для ориентированного графа

Элемент матрицы смежности sij ориентированного графа определяется следующим образом:

— равен единице, если из вершины vi в вершину vj входит дуга;

— равен нулю, если из вершины vi в вершину vj дуга не входит.

Как и для неориентированных графов, так и для ориентированных, если для элемента матрицы vij имеет место i = j, то есть элемент находится на диагонали, то этот элемент равен единице, если этот элемент имеет петлю, и нулю, если элемент не имеет петли.

Пример 3. Составить матрицу смежности для графа, представленного на рисунке ниже.

Ответ.

V	1	2	3	4	5
1	0	1	0	0	0
2	0	1	0	0	0
3	1	0	0	0	0
4	0	1	0	0	0
5	0	1	1	0	0

Таким образом, матрица смежности ориентированного графа не симметрична.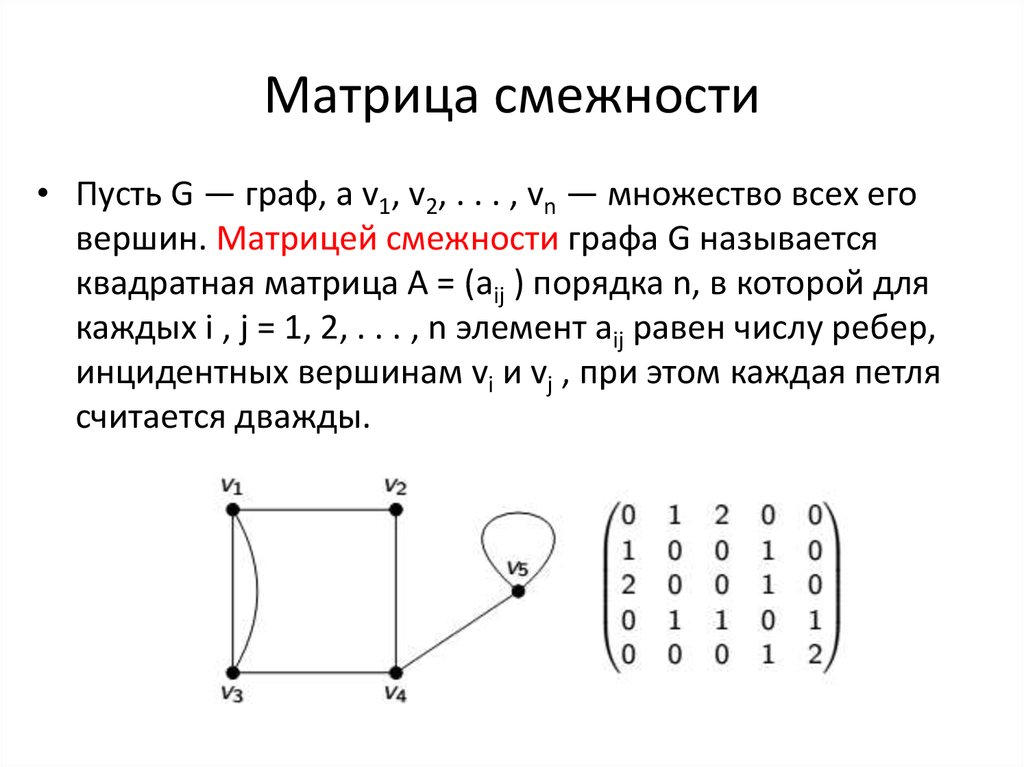

Матрица смежности для графа с кратными рёбрами

Если в графе есть вершины, соединённые между собой несколькими рёбрами, то элемент матрицы смежности sij равен числу рёбер, соединяющих вершины vi и vj. Из этого следует, что если вершины vi и vj не соединены рёбрами, то элемент матрицы смежности sij равен нулю.

Пример 4. Составить матрицу смежности для графа, представленного на рисунке ниже.

Ответ.

V	1	2	3	4	5
1	0	3	2	0	0
2	3	0	0	1	1
3	2	0	0	0	1
4	0	1	0	0	0
5	0	1	1	0	0

Нет времени вникать в решение? Можно заказать работу!

Матрица смежности для взвешенного графа

В случае взвешенного графа элемент матрицы смежности sij равен числу w, если существует ребро между вершинами vi и vj с весом w. Элемент sij равен нулю, если рёбер между вершинами vi и vj не существует.

Пример 5. Составить матрицу смежности для графа, представленного на рисунке ниже.

Ответ.

V	1	2	3	4	5
1	0	11	9	0	0
2	11	0	0	5	8
3	9	0	0	0	2
4	0	5	0	0	0
5	0	8	2	0	0

Матрица инцидентности H — это матрица размера n x m, где n — число вершин графа, m — число рёбер графа.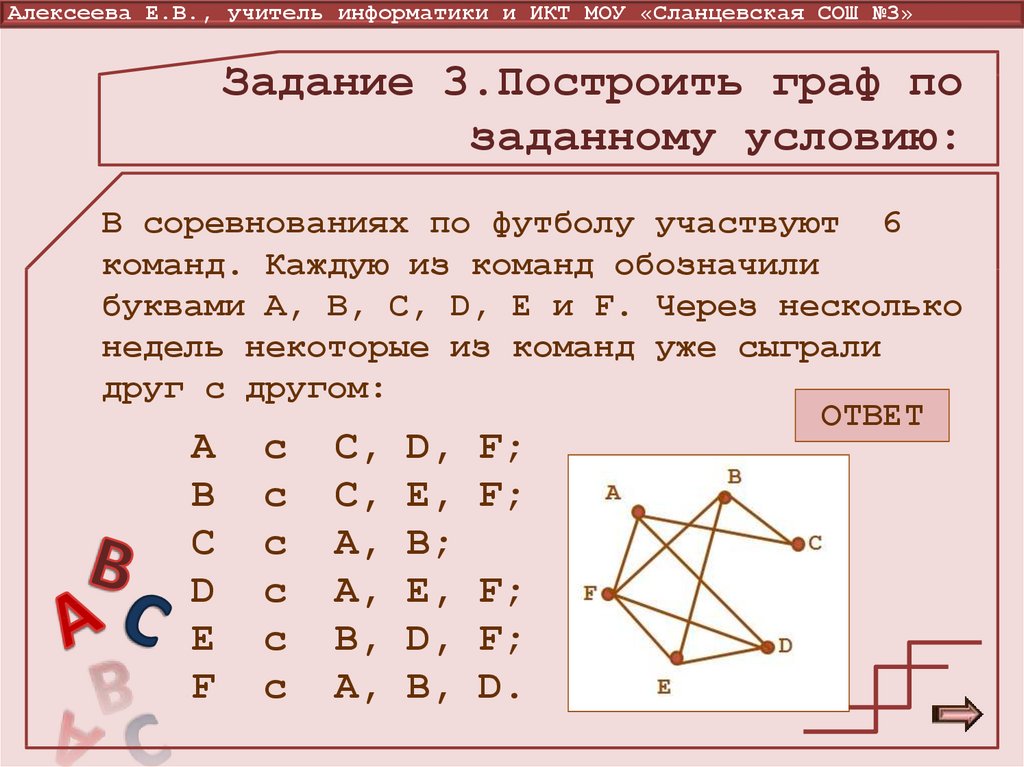 Обычно в матрице инцидентности строки соответствуют вершинам графа, а столбцы — рёбрам графа.

Матрица инцидентности для неориентированного графа

Элемент матрицы инцидентности для неориентированного графа hij определяется следующим образом:

— равен единице, если вершина vi инцидентна ребру ej;

— равен нулю, если вершина vi не инцидентна ребру ej.

Пример 6. Составить матрицу инцидентности для графа, представленного на рисунке ниже.

Ответ.

V	1-2	1-3	2-4	2-5	3-5
1	1	1	0	0	0
2	1	0	1	1	0
3	0	1	0	0	1
4	0	0	1	0	0
5	0	0	0	1	1

Матрица инцидентности для ориентированного графа

Элемент матрицы инцидентности для ориентированного графа hij определяется следующим образом:

— равен минус единице, если вершина vi является началом ребра ej;

— равен единице, если вершина vi является концом ребра ej;

— равен нулю, если вершина vi не инцидентна ребру ej.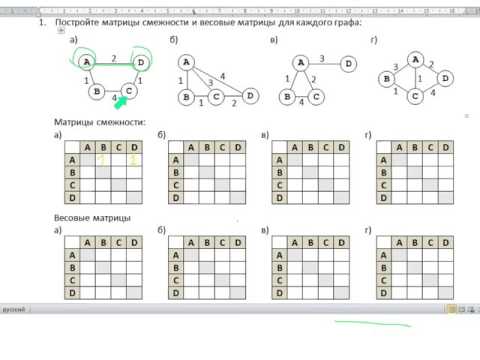

Пример 7. Составить матрицу инцидентности для графа, представленного на рисунке ниже.

Ответ.

V	1-2	1-3	2-4	2-5	3-5
1	1	-1	0	0	0
2	-1	0	-1	-1	0
3	0	1	0	0	-1
4	0	0	1	0	0
5	0	0	0	1	1

На сайте есть пример реализации на языке программирования С++ алгоритма обхода в глубину графа, представленного матрицей инцидентности.

Графы значительного объёма целесообразно хранить в памяти компьютера в форме списков инцидентности.

Список инцидентности одной вершины графа включает номера вершин, смежных с ней.

Ссылки на начало этих списков образуют одномерный массив, индексами которого служат номера вершин графа.

Пример 8. Составить списки инцидентности для графа, представленного на рисунке ниже.

Ответ.

1:2→3
2:1→4→5
3:1→5
4:2
5:2→3

Матрицы смежности и инцидентности целесообразнее использовать когда:

• число вершин графа невелико;
• число рёбер графа относительно большое;
• в алгоритме часто требуется проверять, соединены ли между собой две вершины;
• в алгоритме используются фундаментальные понятия теории графов, например, связность графа.

Из-за последнего обстоятельства матрицы чаще используются в теоретических исследованиях графов.

Списки инцидентности целесообразнее использовать когда:

• число вершин графа велико;
• число рёбер графа относительно невелико;
• граф формируется по какой-либо модели;
• во время действия алгоритма часто требуется модифицировать граф;
• в алгоритме часто используются локальные свойства вершин, например, например, окрестности вершин.

На практике списки чаще используются в прикладных целях.

Назад

Листать

Вперёд>>>

Весь блок «Теория графов»

Теория графов: основные понятия и задачи

Основные виды графов

Математические модели в виде графов. Дерево решений. Дерево игры

Виды вершин и рёбер графа. Маршруты, цепи, циклы в графах

К началу страницы

Бесплатная миллиметровка в Интернете / Асимметричная и специальная сетчатая бумага в формате PDF

Сгенерированные здесь документы считаются общественным достоянием.
Их можно использовать, распространять и переиздавать без разрешения.

Если вам нравится то, что я делаю, поддержите меня на Patreon!

Cross Grid

Стильный и минималистичный

Треугольные точки

Равносторонние треугольники

Коробки

Отдельно стоящие квадраты

Точки сетки

Классический

Шестигранная точка

Светлые вертикали

С подкладкой

Line Dots

Пояс и подтяжки

Iso-Dots

Четные ряды смещены

Сгенерированные здесь документы считаются общественным достоянием.
Их можно использовать, распространять и переиздавать без разрешения.

Если вам нравится то, что я делаю, поддержите меня на Patreon!

Простые коробки

X by Y коробки
определенного размера

Плоская сетка

X линий/см

Круговая сетка

Круг, наложенный на квадратную сетку

Акцентированная сетка

Жирный шрифт через каждые X строк

Аксонометрический

Дополнительные X и Y
Биссектрисы

Перевернутая сетка

Белые линии на цвете

Multi-Weight

1 цвет
3 толщины линий

Многоцветный

3 цвета
3 толщины линий

Сгенерированные здесь документы считаются общественным достоянием.
Их можно использовать, распространять и переиздавать без разрешения.

Если вам нравится то, что я делаю, поддержите меня на Patreon!

Сетка для вязания

X» в ширину и Y» в высоту

Асимметричный

X линий/см на
Y линий/см

Восьмиугольный

8-сторонний

Треугольник

Равносторонний

Переменный треугольник

Что вам нужно?

Шестигранник

6-сторонний

Макет кирпичей

Кирпичи и изделия из бисера

Кельтский узел

Жирные линии 1 дюйм

Алмаз

Трапеция
Ромб

Кувыркающийся блок

Классический квилтинг

Круги — Hex

Круги — Сетка

Мавританский узор

Переменная форма
Мавританская плитка

Сгенерированные здесь документы считаются общественным достоянием.
Их можно использовать, распространять и переиздавать без разрешения.

Если вам нравится то, что я делаю, поддержите меня на Patreon!

174 Бумага

Правительство Великобритании
Вдохновленный

Бумага инженера

Сбор данных
Наполнитель для блокнота

Полярная

X окружности Y спицы
Градусы или радианы

Бухгалтерская книга

Бухгалтерский учет
Финансовый

Лог/полулогарифм

Полный или полулогарифмический
До 6 циклов

Spider Graph

Многоугольники X
Спицы Y

Сгенерированные здесь документы считаются общественным достоянием.
Их можно использовать, распространять и переиздавать без разрешения.

Если вам нравится то, что я делаю, поддержите меня на Patreon!

Блокнот

Бумага для наполнителя
Широкая и узкая линейка

строк

Чистописание

Сплошные направляющие с пунктирной средней линией

Двойной почерк

2 сплошные средние линии

Cornell Lined

Конспектирование

Cornell Grid

Ведение заметок

Шестигранник с накоплением

Китайская каллиграфия
Детское письмо

Stacked Hash

Китайские иероглифы
Руководство — стиль Hash

Stacked X

Китайские иероглифы
Направляющая — стиль X

Каллиграфия

Стандартное соотношение сторон 3/2/5/5

Сложенные блоки

Гэнкоёси

Сложенные четвертинки

Дважды разделенные пополам

Сгенерированные здесь документы считаются общественным достоянием.
Их можно использовать, распространять и переиздавать без разрешения.

Если вам нравится то, что я делаю, поддержите меня на Patreon!

Раскадровки

Переменные соотношения сторон

Музыкальные нотоносцы

X строк на нотоносец

Номер Строка

От X до Y
Увеличение на Z

Диаграммы грифа

X Струны
Y Лады

Перспектива

Одна точка
Исчезающая перспектива

Музыкальная сетка

Направляющие гроссбуха
Вертикальные направляющие

Cornell Music

Создание заметок
Создание заметок

Схема подключения

Схемы трубопроводов и

Теперь установите: 8 1/2 x 11 Бумага. Правило в дюймах.

Print ColorPrint Серый

Print ColorPrint Серый

Печать ColorPrint Серый

Печать ColorPrint Серый

Печать ColorPrint Серый

Печать ColorPrint Серый

Patreon!

Если вы уже зарегистрированы на Patreon, подумайте о пожертвовании в размере 2 долларов США! Если вы еще не на Patreon, я не могу объяснить, насколько это весело. Когда попадете на Патреон, вернитесь и поддержите миллиметровку, музыку и все другие замечательные вещи!!

KgBase — графы знаний без кода

KgBase — графы знаний без кода

Наш простой в использовании пользовательский интерфейс позволяет перемещаться по графику, отображать результаты в виде таблиц и диаграмм и многое другое

Основные моменты

Посмотрите, что происходит. Оставайтесь с нами в курсе.

• Предыдущий
• Следующий

Данел Даян

Battery Ventures

«Мы использовали KgBase, чтобы определить две многообещающие молодые компании для отслеживания»

Марта Лопата (директор по развитию @KgBase) выступила на конференции The Knowledge Graph 2020

https://www. knowledgegraph.tech

Продукт дня №3

09 апреля 2020 г.

Подробнее на producthunt.com

Мэйси Вайншенк

Директор по работе с клиентами

Cello Health

KgBase стал для нас отличным инструментом! Это позволяет пользователю отображать большие и сложные разговоры и приступать к осмыслению данных четким, визуально привлекательным способом.

Мы не только полагались на KgBase для составления карт сети влиятельных лиц, но также использовали их функцию анализа текста, чтобы понять, как более крупные темы обсуждаются в Интернете.

Построитель обхода

Поиграйте с данными графика. Создайте свой запрос и смотрите, как обновляются результаты в режиме реального времени.

Это похоже на написание кода запроса в Cypher или Gremlin, только проще. И быстро.

Функция белой метки

Усильте свой бренд , настроив платформу KgBase под своим брендом. Интегрируйте его на свой веб-сайт, чтобы он выглядел как ваш собственный продукт.

Добавляйте фирменные графы знаний в статьи, сообщения блога или на свой веб-сайт.

Подходит для любого варианта использования

KgBase отлично работает как с большими графами (миллионы узлов), так и с простыми проектами.

• Начните с шаблона

  Внедрите графики в свою организацию, создав график из шаблона.

• Нарисуй что-нибудь

  Результаты любого запроса можно легко превратить в визуализацию диаграммы.

• Импорт/экспорт

  Вы можете импортировать/экспортировать свои данные в более чем 20 стандартных форматов графических данных.

• Совместная работа в команде

  Настройте правила доступа для каждого члена команды.

  No related posts.