Синус и косинус что это такое: Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.

Синус — что это такое, значения синусов для разных углов

Обновлено 2 марта 2023 Просмотров: 56 511 Автор: Дмитрий Петров

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о том, что такие СИНУС.

Наверняка многие знают, что это понятие относится к математике. Все мы учились в школе и проходили тригонометрию.

С понятиями СИНУС, КОСИНУС, ТАНГЕНС и КОТАНГЕНС школьники знакомятся в 8 классе.

И сейчас без этих знаний не обойтись на ЕГЭ. И задачки по тригонометрии обязательно входят в программу тестов единого государственного экзамена.

Так что эта статья будет в первую очередь полезна старшеклассникам. А читателям более старшего возраста будет полезно лишний раз освежить давно забытые знания.

Что такое тригонометрия

Но давайте начнем совсем с азов. Раз уж мы сказали, что СИНУС – это некая тригонометрическая функция, давайте расскажем и что такое тригонометрия.

Тригонометрия – это раздел математики, который был основан еще в Древней Греции. Само слово состоит из двух половин «τρίγωνον» и «μετρέω», что можно дословно перевести как «изучение треугольников».

Впервые нечто похожее на тригонометрические функции появилось в Древней Греции. Во всяком случае, их можно отследить по трудам Евклида и Архимеда, то есть в III веке до нашей эры.

Хотя ученые не исключают, что похожими вычислениями пользовались и при строительстве Египетских пирамид. А это уже 2-2,5 тысячи лет до нашей эры.

И опять же, пирамиды ведь имеют треугольную форму (в плоскости). И тригонометрия связана напрямую с треугольниками. Возможно совпадение, а возможно и нет.

Правда, в тригонометрии рассматривают конкретные треугольники – прямоугольные. Напомним, это такие фигуры, у которых две стороны из трех пересекаются друг с другом под углом 90 градусов.

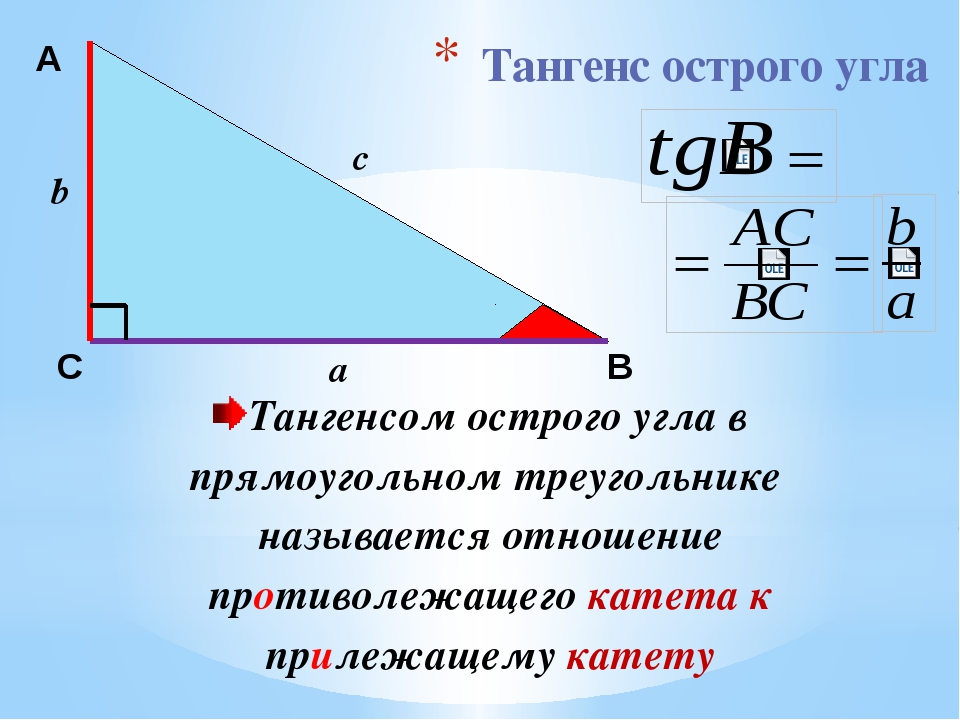
Выглядит такой треугольник вот так:

У такого треугольника стороны имеют определенные названия:

1. КАТЕТЫ – это стороны, которые пересекаются под прямым углом.

   В нашем случае это стороны АВ и ВС. Это название также имеет древнегреческие корни. Так, слово «káthetos» переводится как «перпендикуляр, опущенный, ответственный».

2. ГИПОТЕНУЗА – сторона, которая идет под наклоном и соединяет между собой два катета.

   В нашем случае это отрезок АС. Слово также родом из Древней Греции, «ὑποτείνουσα» означает «натянутая». И это очень хорошо характеризует этот отрезок, ведь он действительно выглядит как натянутая струна между двух опор. И даже если перевернуть треугольник, это ощущение не изменится.

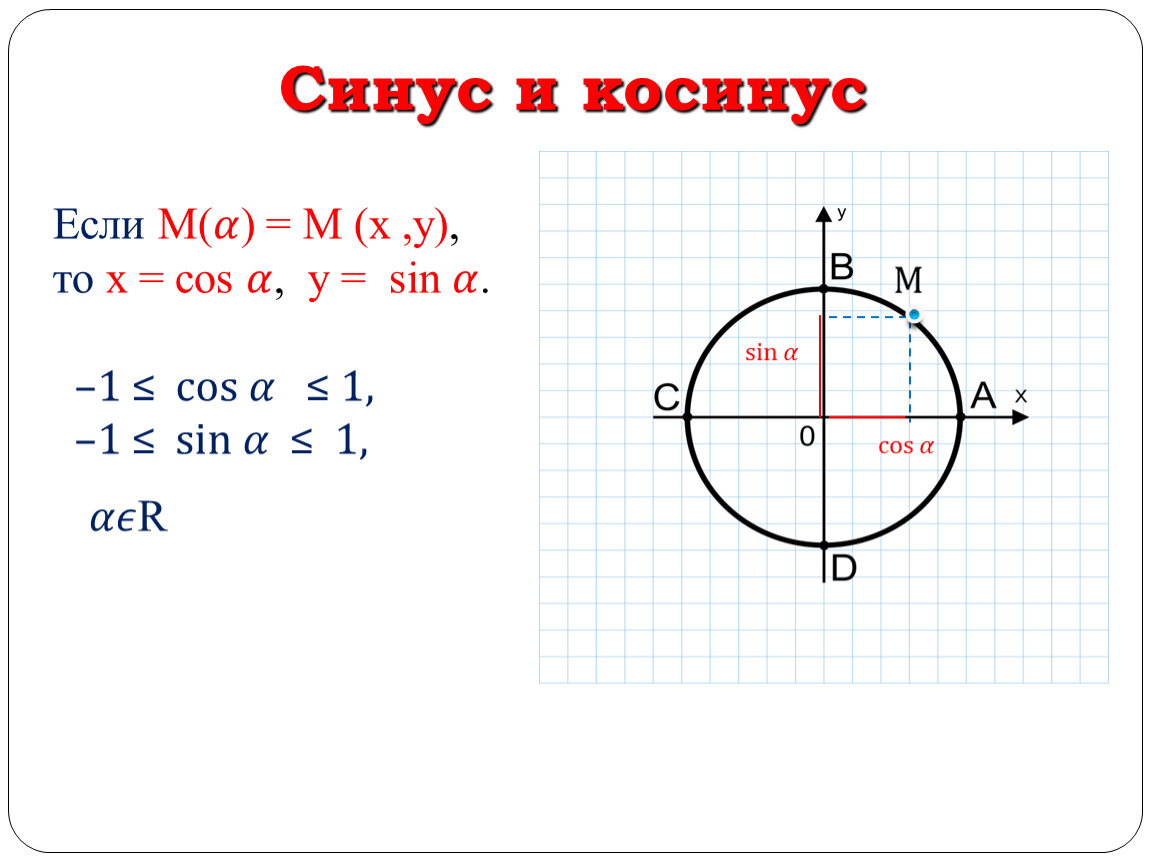
Синус — это …

А вот теперь мы подобрались к самому главному, определению СИНУСА. Это величина не существует сама по себе. Она имеет отношение к какому-то углу треугольника. А конкретно к углам α (альфа) и β (бета), которые наглядно показаны на следующем рисунке.

А вот теперь долгожданное определение:

СИНУС угла – это отношение противолежащего катета к гипотенузе.

Чтобы было понятно, о чем речь, взгляните еще раз на наш рисунок прямоугольного треугольника. В данном случае, противолежащим катетом к углу α будет сторона ВС. А противолежащим катетом к углу β будет сторона АС.

Соответственно, катет ВС для угла α будет прилежащим. И точно таким же будет катет ВС для угла β.

Конкретные формулы синусов будут такими:

Значения синусов

Чаще всего школьники имеют дело с определенными углами. Например, 30, 45, 60, 90 градусов и так далее. И чтобы не высчитывать каждый раз значение тригонометрических функций через стороны треугольника, есть уже готовые таблицы:

1. 0 градусов — SIN = 0;
2. 30 градусов — SIN = ½;
3. 45 градусов — SIN = √2/2;
4. 60 градусов – SIN = √3/2;
5. 90 градусов – SIN = 1;
6. 180 градусов – SIN = 0;
7. 270 градусов – SIN = -1;
8. 360 градусов – SIN = 0.

Вместо заключения

СИНУС – это не единственная тригонометрическая функция, которую проходят в школе. Есть еще и другие, и все они также связаны с прямоугольным треугольником.

А называются они вот так:

1. КОСИНУС – это обратная синусу величина (даже в переводе с латыни это слово означает «перевернутый синус»). Косинус равен отношению прилежащего катета к гипотенузе.
2. ТАНГЕНС – это отношение противолежащего катета к прилежащему. Или отношение синуса к косинусу.
3. КОТАНГЕНС – это отношение прилежащего катета к противолежащему. Или отношение косинуса к синусу.

Вот и все, что мы хотели рассказать о тригонометрической функции СИНУС.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

• Математика

Поделиться в соцсетях

Зачем нужны синусы и косинусы?

Давно известная проблема о бесполезности тригонометрии в нашей жизни недавно стала предметом спора между мной и моим товарищем. Решили мы тут вспомнить, для чего же мы все изучали все эти синусы и косинусы. И в итоге разговор свелся к тому, что «где-то они все-таки нужны, наверное. Зачем-то их изучают».

Давайте будем называть вещи своими именами. Подавляющему большинству из вас они никогда не пригодятся. Разве что, когда ваши дети пойдут в школу и начнут изучать тригонометрические функции, они вам тоже зададут вопрос «Зачем нужны синусы и косинусы?» и, в добавок, попросят объяснить, что это такое.

Деньгами мы пользуемся каждый день уже не одну тысячу лет и прекрасно обходимся без всяких синусов, косинусов и прочих изящных математических штучек. Уверяю вас, и через миллионы лет в подсчете денег ничего не изменится. Не потому, что мы такие тупые, а потому, что таковы математические свойства денег: нельзя рубли умножить на рубли и с деньгами во второй степени бежать в автосалон покупать «Ламбарджини».

Так зачем же нужны синусы и косинусы? По сравнению с Древней Грецией, у нас сегодня имеется очень много разных штучек, о которых древние греки даже мечтать не могли. Даже их Боги не ездили на машинах, не пользовались мобильной связью, не общались по Интернету. Зато всё это есть у нас и мы постоянно этим пользуемся. Откуда же всё это невиданное богатство взялось? Его создали мы сами. Сперва ученые делали научные открытия. Потом инженеры, на основании сделанных учеными открытий, создавали всякие полезные штуки. Мы сегодня этими штуками пользуемся, не имея ни малейшего понятия о том, что находится внутри этих штук и какие научные законы положены в основу их работы. Так вот, если бы не было синусов и косинусов, не было бы и всех этих клевых штук.

Наиболее эффективно синусы и косинусы применяются учеными и инженерами. Я не скажу, что они непрерывно только тригонометрическими функциями пользуются. Нет, они используют их редко, но метко. Синусы и косинусы часто присутствуют в формулах разных расчетов, инженерных или научных.

Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности.

Преподаватели математики по роду своих обязанностей постоянно имеют дело с тригонометрическими функциями. В этом году они рассказывали о синусах и косинусах вам, на следующий год учителя математики будут рассказывать то же самое другим ученикам. Такая у них работа — учить.

Всё! Остальным синусы и косинусы не нужны вообще! В повседневной жизни большинство людей почти никогда их не используют. Если я ошибаюсь, поправьте меня.

Так зачем тогда вообще учить эти синусы и косинусы? Ну, во-первых, такова школьная программа. Во-вторых, если вам в жизни понадобится применить синус или косинус, вы уже знаете, что это такое и где нужно искать информацию о них. Полученных в школе знаний вам вполне хватит, что бы самостоятельно во всем разобраться.

Так что же такое синусы, косинусы и другие тригонометрические функции? Это математический инструмент, которым нужно уметь пользоваться. То, что мы этим инструментом почти никогда не пользуемся, говорит не о том, что изучать их не надо, а о том, что эффективность применения полученных нами знаний практически равна нулю. Но это уже совсем другая тема.

Источник

Tags: Интересное, Математика

синусоидальных и косинусоидальных графиков | Brilliant Math & Science Wiki

Пи Хан Го, Мэй Ли, Рагхав Вайдьянатан, и

способствовал

Содержимое

• Графики синуса и косинуса
• Характеристики
• Связь между графиками синусов и косинусов
• Растяжка и движение
• Решение проблем

На графике функции синуса ось \(x\) представляет значения \(\theta\), а ось \(y\) представляет значения \(\sin \theta\).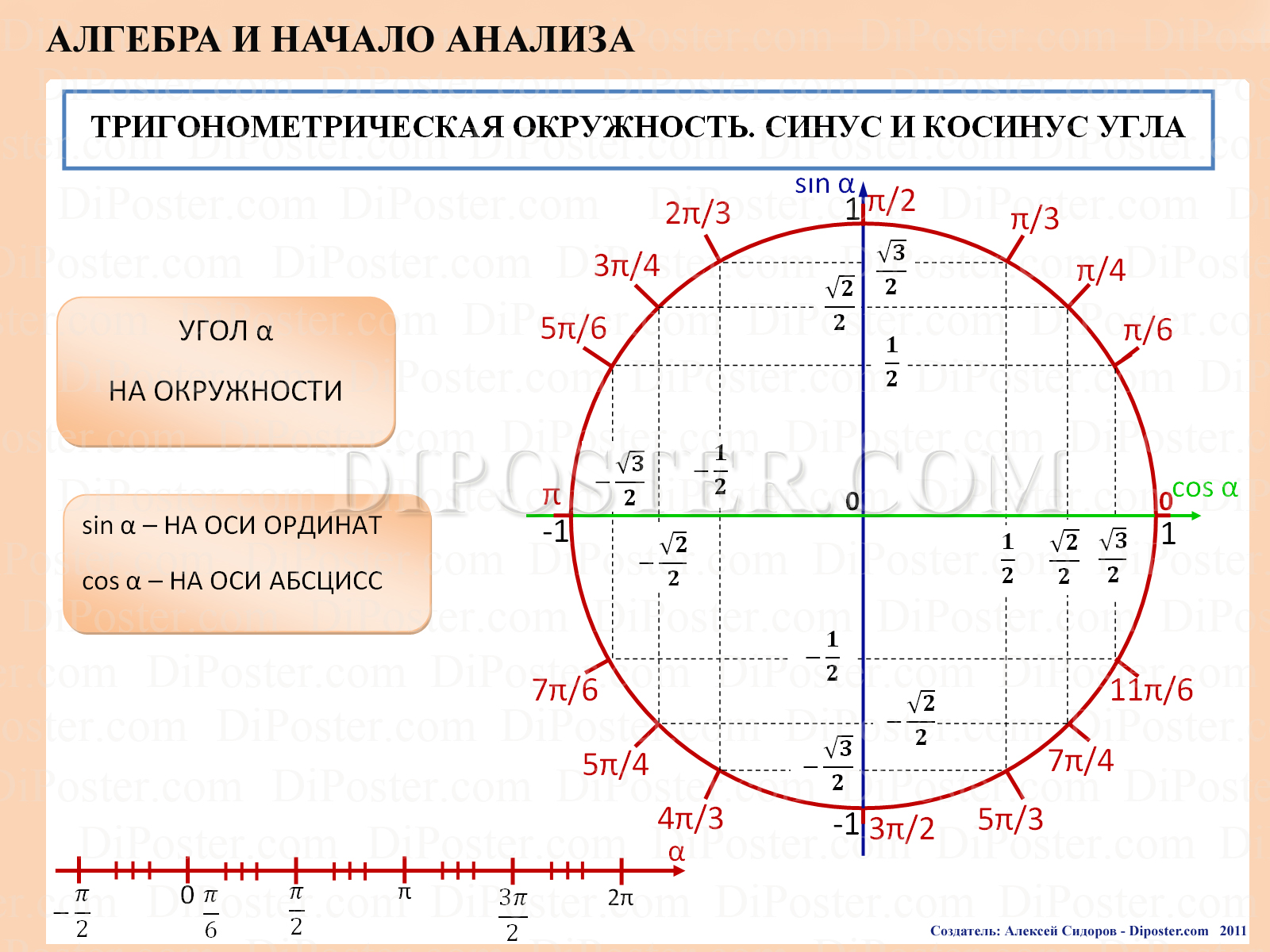

Например, \(\sin 0=0,\) означает, что точка \((0,0)\) является точкой на синусоидальном графике. Если мы нанесем значения функции синуса для большого числа углов \(\theta\), мы увидим, что точки образуют кривую, называемую синусоида :

Аналогичным образом, построение значений функции косинуса для большого числа углов образует кривую, называемую кривой косинуса :

Мы можем визуализировать взаимосвязь между этими графиками и определением косинуса и синуса из единичного круга следующим образом:

Анимация предоставлена ​​commons.wikimedia.org

Сколько точек пересечения есть между графиками \(\sin x\) и \(\cos x\) в интервале \([0, 2\pi]\)?

---

Из графиков синуса и косинуса видно, что количество точек пересечения в заданном диапазоне равно \(2\).

\(_\квадрат\)

Диаграммы синуса и косинуса имеют диапазон \([-1,1]\) и повторяются значения каждые \(2\pi\) (называемые амплитудой и периодом). Однако графики различаются по другим параметрам, например, по интервалам возрастания и убывания. Ниже описаны свойства каждого графа:\[\]

Свойства синуса:

• \(y\)-отрезок: \(0\)
• \(x\)-intercept: \( n \pi,\) где \(n\) здесь целое число на
• возрастание на интервалах \(\left[\frac{(4n-1)\pi}{2},\frac{(4n+1)\pi}{2} \right]\)
• убывающее на интервалах \(\left[\frac{(4n+1)\pi}{2},\frac{(4n+3)\pi}{2} \right]\)
• Симметрия: функция симметрична относительно начала координат.
• Максимум \(\sin \theta\) достигается для \(\theta=\frac{(4n+1)\pi}{2}\).\[\]

Свойства косинуса:

• \(y\)-отрезок: 1
• \(x\)-intercept: \(\left(n + \frac{1}{2} \right) \pi, \) где \(n\) здесь целое число на
• возрастание на интервалах \(\left[(2n-1)\pi,2n\pi\right]\)
• убывает по интервалам \(\left[2n\pi,(2n+1)\pi \right]\)
• Симметрия: функция симметрична относительно оси \(y\).
• Максимум \(\cos \theta\) достигается для \(\theta=2n\pi\).\[\]

Найдите все \(x\)-отрезки для \(f(x) = 2\cos 3x +2 \) в интервале \(0\leq x\leq 2\pi \).

---

Когда кривая \(f(x)\) пересекает ось \(x\), \(f(x) = 0 \). Итак, \(2\cos 3x + 2 = 0 \стрелка вправо \cos 3x = -1 \).
Так как \(0 \leq x \leq 2\pi \Rightarrow 0\leq 3x \leq 6\pi \) и функция косинуса имеет период \(2\pi\), мы имеем \[3x = \pi, ~\pi+2\pi, ~\pi+4\pi \Rightarrow x=\frac{\pi}{3}, ~\pi, ~\frac{5\pi}{3 },\] которые являются тремя \(x\)-перехватами, которые мы ищем. \(_\квадрат\)

Каково число точек пересечения между двумя кривыми \(f(x) = 5\cos x + 7 \) и \(g(x) = -6\sin x — 10 \) в интервале \(0 \ leq x \leq 2\pi\)?

---

Поскольку и \(f(x)\), и \(g(x)\) являются растяжками и имеют сдвиг по вертикали, мы сначала попытаемся найти, есть ли общее пересечение между этими двумя кривыми.

Поскольку \(-1 \leq \cos x \leq 1 \Rightarrow -5 \leq 5\cos x \leq 5 \Rightarrow 2 \leq 5\cos x + 7 \leq 12 \), диапазон \(f (х) \) есть \([2, 12]\).

Аналогично, поскольку \(-1 \leq -\sin x \leq 1 \Rightarrow -6\leq -6\sin x \leq 6 \Rightarrow -16 \leq -6\sin x -10 \leq -4 \) , диапазон \(g(x)\) равен \([-16, -4]\).

Поскольку \(f(x)\) строго положительна, а \(g(x)\) строго отрицательна, между этими двумя кривыми нет точки пересечения. В частности, у этих кривых нет точки пересечения в интервале \( 0 \leq x \leq 2\pi. \ _\square \)

График синуса имеет ту же форму, что и график косинуса. Действительно, график синуса можно получить, сдвинув график косинуса на \(\frac{(4n+1)\pi}{2}\) единиц вдоль положительной оси \(x\) (\(n\ ) является целым числом). Также график косинуса можно получить, сдвинув график синуса на \(\frac{(4n+1)\pi}{2}\) единиц вдоль отрицательной оси \(x\). Другими словами:

\[\cos{\theta}=\sin{\left(\frac{(4n+1)\pi}{2}-\theta\right)}, ~\sin{\theta}=\cos{ \left(\frac{(4n+1)\pi}{2}-\theta\right)}.\]

Упростить \( \sin \left( \frac{9 \pi }{ 2} — \theta \right) \).

---

Поскольку функция \( \sin \theta \) имеет период \(2\pi\), \(\sin(-\theta) \) также имеет период \(2\pi\), так

\[ \sin\left(\frac{9\pi}2 -\theta\right) = \sin\left(\frac{9\pi}2 -\theta — 2\pi — 2\pi \right) = \sin\left(\frac{\pi}2 -\theta\right) = \cos \theta. \]

В качестве альтернативы мы распознаем это как форму \( \sin \left( \frac{(4n+1)\pi}{2} — \theta \right) \) с \( n = 2 \). Следовательно, он равен \(\cos\theta\). \(_\квадрат\)

Упростить \( \cos \left ( \theta + \frac{\pi}{2} \right) \).

---

Существует несколько подходов к использованию:

1. Используя перечисленные выше свойства, мы имеем
   \[ \cos \left ( \theta + \frac{\pi}{2} \right) = \sin ( — \theta ) = — \sin \theta. \]

2. Нарисуйте график и сравните его с тем, что мы уже знаем.
   Нарисовав график, мы можем визуально увидеть, что он равен \( — \sin \theta \).

3. Расширьте, используя косинус — формулы суммы и разности, что дает нам
   \[ \cos \left ( \theta + \frac{\pi}{2} \right) = \cos \theta \cos \frac{\pi {2} — \sin \theta \sin \frac{\pi}{2} = — \sin \theta.

   \ _\квадрат \]

Полную информацию см. в разделе Преобразование графика.

Мы можем манипулировать основным тригонометрическим графом, добавляя константы следующим образом:

\[y = a \sin (b x — c) + d.\] \[y = a \cos (b x — c) + d.\]

Рассмотрим, как каждая из этих констант изменяет график:

• Значение \(a\) растягивает график по вертикали.
• Значение \(b\) стягивает график по горизонтали
• Значение \(c\) сдвигает график по горизонтали
• Значение \(d\) переводит график вертикально.

Найдите амплитуду, период, сдвиг по горизонтали и сдвиг по вертикали функции

.

\[ y = 2 \cos \left( \frac{\pi}{2} x — \pi \right) + 4.\]

---

Итак, мы хотим найти значения \(a,b,c\) и \(d\), когда сравниваем их с формой \(a \cos(bx-c) + d \).

Легко видеть, что \(a = 2, b = \frac\pi2, c =\pi, d = 4 \). Интерпретация значений показывает следующее:

• Период этой функции \(y = 2 \cos \left( \frac{\pi}{2} x — \pi \right) + 4 \) равен \( 2\pi \div \frac{\pi }2 = 4 \).
• Амплитуда равна максимальному абсолютному значению скалярного кратного тригонометрической функции. В данном случае это \( \left | 2 \cos \left( \frac{\pi}{2} x — \pi \right) \right | \leq 2 \).
• Так как \(c = \pi\), функция сдвинута по горизонтали на \(\pi\) единиц вправо.
• Аналогично, поскольку \(d = 4\), функция была смещена по вертикали на \(4\) единиц вверх. \(_\квадрат \)

Учитывая функцию \[y = a \sin (b x — c) + d\] для констант \(a,b,c,\) и \(d\), каковы максимальное и минимальное возможные значения \(y?\)

---

Так как \( -1 \leq \sin \theta \leq 1 \), то \( -|a| \leq a \sin (bx -c) \leq |a| \). Таким образом, наибольшее возможное значение равно \( |a| + d \), а наименьшее возможное значение равно \( — |a| + d \). \(_\квадрат\)

Положение пружины как функция времени представляется уравнением вида \(p(t) = a \cos bt\). Если пружина начинается на 3 единицы выше точки покоя, отскакивает на 3 единицы ниже точки покоя, а затем возвращается на 3 единицы выше точки покоя всего за 2 секунды, найдите уравнение, описывающее это движение.

---

Из контекста «пружина начинается на 3 единицы выше точки покоя» мы можем интерпретировать это как \(p(0) = 3 \), что подразумевает \(3 = a\cos(b\times0) \Rightarrow а = 3\).

Из контекста «а затем обратно на 3 единицы выше точки покоя всего за 2 секунды» мы можем интерпретировать это как основной период \(p(t)\) равный \(2\). Итак, \(2 \pi \div b = 2 \rightarrow b = \pi \).

Следовательно, уравнение, описывающее это движение, имеет вид \(p(t) = 3 \cos \pi t.\ _\square \)

Процитировать как: Графики синуса и косинуса. Brilliant.org . Извлекаются из https://brilliant.org/wiki/sine-and-cosine-graphs/

Геометрия для старших классов – специальные прямоугольные треугольники

Овладейте семью столпами успеха в школе

Улучшите свои оценки и снизьте стресс

Общий базовый стандарт G. SRT.6 Геометрия для старших классов

Перейдите по этой ссылке, чтобы найти калькулятор триггерной функции, чтобы проверить свою работу

Простые расчеты — калькулятор углов прямоугольного треугольника

* Синус = Противоположный/Гипотенуза

   Косинус = Смежная/Гипотенуза

   Касательная = Противоположная/ Смежные

* Тригонометрия существует с 1500 г. н.э. и происходит от греческих слов «тригонон», что означает треугольник, и «метрон», что означает мера.

* Прямоугольные треугольники имеют число 9угол 0 градусов и два дополнительных угла.

* Самая длинная сторона треугольника, расположенная напротив символа прямоугольного треугольника, называется гипотенузой. Сторона, которая находится напротив угла, на который вы смотрите, является «противоположной» стороной, а оставшийся угол — «прилегающей» стороной.

* Тангенс — единственная триггерная функция, не включающая гипотенузу.

* Популярным сокращением для запоминания триггерных функций является SOH CAH TOA, но есть и другие сокращения: 

• У Оскара была куча яблок
  

• О, черт возьми, еще час алгебры
  

• У некоторых ее детей проблемы с алгеброй
  9 0010

• Какой-то старый хиппи пробежался по нашей квартире
  

* Синус угла равен косинусу дополнительного угла.

Например, sin 40 = cos 50 и sin 10 = cos 80 Перейдите по этой ссылке, чтобы узнать, как использовать калькулятор синуса, косинуса и тангенса.

* Косинус, синус, тангенс полезны в реальном мире, когда используются треугольники. Например, рамы велосипедов, мотоциклов, самолетов, крыш, каркасов зданий, автомобилей, лодок — все они используют треугольники в своей конструкции.

* Синус, деленный на косинус, равен тангенсу, Sin/Cos = Tan

Нахождение угла

Учитывая BC = 6 и AB = 10, найдите m

1. На основе предоставленной информации выберите триггерную функцию. В этом примере используйте sin, потому что заданы противоположность и гипотенуза.

      sin θ  = противолежащее/гипотенуза

2. При нахождении угла используйте обратную функцию калькулятора. Чтобы вычислить Sin-1:

      В большинстве калькуляторов нажмите «inv»

      На калькуляторе TI нажмите секунду, затем Sin

​     Sin-1 (6/10) = 36,86  9008 8

     следовательно, угол A = 36,86 градуса

3. Найдите угол B.

    Острые углы прямоугольного треугольника     дополнительны, поэтому используйте

    90 — ∠A

    90-36,86 = 53,14 ◦ угол B

Нахождение стороны

9 0020 На основе предоставленной информации решите, какую функцию запуска использовать.

Дано: BC = 6, AC = 8 и θ=36,86 градуса

Найдите AB.

1.  Вы можете использовать Sin, потому что дано обратное, а гипотенуза отсутствует.

2. Установите соотношение: sin 36,86 = 6/x

3. Используйте калькулятор, чтобы получить

      sin 36,86 = 0,599 

4. Подставьте 0,599 в пропорцию.

      0,599/1 = 6/x

  x =6/0,599 

    x =10 единиц длина гипотенузы

Использование тригонометрических функций для нахождения недостающих углов прямоугольных треугольников

Нахождение длины стороны прямоугольного треугольника с помощью тригонометрических соотношений

Предварительная алгебра/Выражения, Уравнения, Целые числа

Предварительная алгебра/Дроби, Проценты

Al gebra/Exponents,Equations,Radicals

Math Calculators

Geometry/Shapes

Геометрия/SAT

Геометрия/Плоскость

Хорошие навыки обучения

Геометрия/Основы

Противоположное равно 6 единицам
90 003

Смежный = 8 единиц

Гипотенуза неизвестна

​θ =36,86◦ 

Противоположная = 6 единиц

Соседняя неизвестна

Гипотенуза = 10 единиц

Стенограмма

Добро пожаловать в MooMooMath. Сегодня мы собираемся установить, как найти грех и косинус. Давайте рассмотрим, Sin острого угла равен противоположному по гипотенузе. Косинус острого угла равен прилежащему к гипотенузе. Как мы определяем, какая сторона какая? Сначала давайте посмотрим на угол A из угла a, мы должны посмотреть на наши исходные стороны. Если мы пойдем на нашу противоположную сторону, это будет наша противоположная сторона, и я обозначу ее как противоположную. Гипотенуза (обозначенная h) всегда находится напротив угла схватки, поэтому она примыкает к углу А или находится рядом с ним. (обозначенная а) Теперь давайте добавим некоторые измерения. Предположим, что противоположная сторона равна 6, а гипотенуза равна 10, чтобы найти мой грех, он будет противоположен гипотенузе, поэтому грех угла А будет равен 6/10, что является моей противоположностью гипотенузе. Косинус примыкает к гипотенузе. Длина а неизвестна, поэтому я могу использовать теорему Пифагора, чтобы найти эту сторону. Итак, я возьму в квадрате плюс b в квадрате, что равно 6, плюс с, что равно 10 в квадрате, поэтому, чтобы записать это, я получаю a^2+6^2 = 10^2, что становится a^2+36=100, поэтому a^2 равно 64, поэтому длина A должна быть равна 8 (возьмите квадратный корень из 64). Теперь я могу решить для A. Cos of A будет 8 на 10, потому что он смежн по гипотенузе, и именно так я бы решил. Вы также можете посмотреть из угла B, противоположная сторона будет здесь нижним углом, примыкающая здесь, а гипотенуза всегда находится напротив прямого угла. Таким образом, противоположное и соседнее будут переворачиваться в зависимости от того, под каким углом. Надеюсь, это было полезно.

Тангенс, Синус, Косинус

Именование сторон прямоугольного треугольника

Одним из ключей к правильному использованию триггерных функций является правильное определение сторон прямоугольного треугольника.

Гипотенуза всегда находится напротив угла в 90 градусов

Вам также может понравиться ….

Таблица тангенсов

Типы треугольников

Что такое косинус, синус и тангенс?

Косинус, синус, тангенс объяснение

Стр. 1 Стр. 2 Стр. 3

Синус косинус тангенс для начинающих

Стр.