Синусы каких углов выражаются формулами?
В 8 классе ученики заучивают таблицу синусов и других тригонометрических функций. Она выглядит так:
угол $\alpha$, o | 30 | 45 | 60 | 90 | |
sin$\alpha$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | 1 | |
cos$\alpha$ | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | |
tg$\alpha$ | $\frac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | — | |
ctg$\alpha$ | — | $\sqrt{3}$ | 1 | $\frac{1}{\sqrt{3}}$ |
Есть очень хороший мнемонический приём, позволяющий запомнить значения тригонометрических функций табличных углов.
o = \frac{\sqrt{5}+1}{4}\frac{\phi}{2}$
Можно выражать с помощью форул с корнями синусы сумм и разностей углов, тригонометрические функции которых тоже выражаются формулами с корнями. Поскольку все исходные углы делятся на 3, то и точные формулы тригонометрических функций можно получить для углов, кратных тём градусам. Приведём значения значения синусов. Значения остальных фнукций углов можно получить, воспользовавшись формулами приведения и соотношениями между тригонометрическими функциями.
sin 0o = 0
sin 3o
sin 6o = $\frac{\sqrt{30-\sqrt{180}}-\sqrt5-1}{8}$ — это центральный угол правильного 30-угольника
sin 9o = $\tfrac{1}{8} \left[\sqrt{10}+\sqrt2-2\sqrt{5-\sqrt5}\right]$ — это центральный угол правильного 20-угольника
sin 12o = $\tfrac{1}{8} \left[\sqrt{2(5+\sqrt5)}+\sqrt3-\sqrt{15}\right]$ — это центральный угол правильного 15-угольника
sin 15o = $\tfrac{1}{4}(\sqrt6-\sqrt2)$
sin 18o = $\tfrac{1}{4}\left(\sqrt5-1\right)$ — это центральный угол правильного 10-угольника
sin 21o = $\tfrac{1}{16}\left[2(\sqrt3+1)\sqrt{5-\sqrt5}-(\sqrt6-\sqrt2)(1+\sqrt5)\right]$
sin 24o = $\tfrac{1}{8}\left[\sqrt{15}+\sqrt3-\sqrt{2(5-\sqrt5)}\right]$
sin 27o = $\tfrac{1}{8}\left[2\sqrt{5+\sqrt5}-\sqrt2\;(\sqrt5-1)\right]$
sin 33o = $\tfrac{1}{16}\left[2(\sqrt3-1)\sqrt{5+\sqrt5}+\sqrt2(1+\sqrt3)(\sqrt5-1)\right]$
sin 36o = $\frac{\sqrt{10-\sqrt{20}}}{4}$ — это центральный угол правильного 5-угольника
sin 39o = $\tfrac1{16}[2(1-\sqrt3)\sqrt{5-\sqrt5}+\sqrt2(\sqrt3+1)(\sqrt5+1)]$
sin 42o = $\frac{\sqrt{30+\sqrt{180}}-\sqrt5+1}{8}$
sin 45o = $\frac{1}{\sqrt2}$ — это центральный угол правильного 4-угольника
sin 48o = $\frac{\sqrt{15}-\sqrt3+\sqrt{10+\sqrt{20}}}{8}$
sin 51o = $\tfrac1{16}[2(1+\sqrt3)\sqrt{5-\sqrt5}+\sqrt2(\sqrt3-1)(\sqrt5+1)]$
sin 54o = $\frac{\sqrt5+1}{4}$
sin 57o = $\tfrac{1}{16}\left[2(\sqrt3+1)\sqrt{5+\sqrt5}+\sqrt2(1-\sqrt3)(\sqrt5-1)\right]$
sin 60o = $\frac{sqrt{3}}{2}$
sin 63o = $\tfrac{1}{8}\left[2\sqrt{5+\sqrt5}+\sqrt2\;(\sqrt5-1)\right]$
sin 66o = $\tfrac{1}{8}\left(\sqrt{6(5-\sqrt5)}+\sqrt5+1\right)$
sin 69o = $\tfrac{1}{16}\left[2(\sqrt3-1)\sqrt{5-\sqrt5}+(\sqrt6+\sqrt2)(1+\sqrt5)\right]$
sin 72o = $\tfrac{1}{4}\sqrt{2(5+\sqrt5)}$
sin 75o = $\tfrac{1}{4}(\sqrt6+\sqrt2)$
sin 78o = $\tfrac{1}{8} \left[\sqrt{6(5+\sqrt5)}+\sqrt5-1\right]$
sin 81o = $\tfrac{1}{8} \left[\sqrt{10}+\sqrt2+2\sqrt{5-\sqrt5}\right]$
sin 84o = $\frac{\sqrt{10-\sqrt{20}}+\sqrt3+\sqrt{15}}{8}$
sin 87o = $\frac{(2+\sqrt{12})\sqrt{5+\sqrt5}+(\sqrt{10}-\sqrt2)(\sqrt3-1)}{16}$
sin 90o = 1
Итак, только для этих целых углов первой четверти синусы, косинусы и им подобные функции можно выразить точно.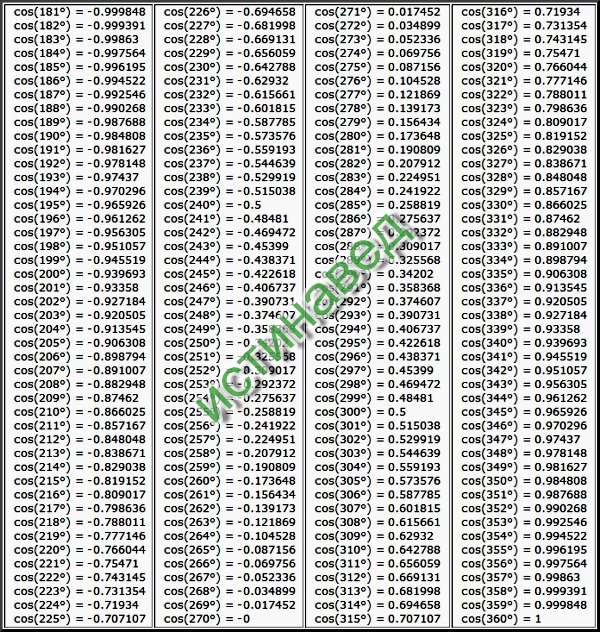
Также существуют методы построения для правильного 257- и 65537 угольников. Они дают точные формулы для бесконечного количества синусов рациональных углов.
Тригонометрия на пальцах — IntoMath
Как вы, возможно, уже знаете, тригонометрия — это раздел математики, изучающий отношения между длинами сторон и углами треугольников. В тригонометрии используются три основные функции: синус, косинус, тангенс, обычно обозначаются как sin, cos, tan соответственно.
Давайте рассмотрим, что делает каждая из вышеперечисленных функций. Давайте также научимся делать тригонометрию на пальцах.
В непрямоугольных треугольниках мы используем законы синусов и законы косинусов для определения длин сторон и углов.
Тригонометрия широко используется во многих сферах нашей жизни, особенно в строительстве, астрономии, физике, электронной музыке, бортовой технике, морской технике, навигации, медицине, картографии, электричестве и т.
д.
Рассмотрим один из практических Использование тригонометрии в нашей жизни.
Задача :
Крыша вашего дома образует треугольник, как показано ниже.
Вам необходимо рассчитать длину скатов крыши AB и ВС , когда заданы углы места А и С . Мера угла B = 180 o – (A + B) = 180 o – (35 o + 41 o ) = 104 o .
Теперь давайте рассмотрим еще одну задачу по тригонометрии, с которой мы обычно сталкиваемся в школе.
Нам часто приходится вычислять значения тригонометрических функций, таких как sin 41 , cos 30 , tan 90 , sin 45 , …. sin X , cos X , tan X и так далее .
Оценить значения этих функций для любого угла не так уж и просто, но есть некоторые из них, которые очень распространены и часто используются.
Наиболее распространенными углами являются: 0, 30, 45, 60 и 90 , и для этих углов нам обычно приходится запоминать таблицу «Тригонометрических соотношений стандартных углов», которая может быть ошеломляющей и казаться «ракетной наукой». .
Хорошей новостью является то, что вы можете использовать пальцы левой руки, чтобы легко найти соотношение функций синуса и косинуса.
Ниже приведена хорошая иллюстрация того, что мы только что обнаружили.
Попробуйте сами и проверьте свой результат в таблице «Тригонометрические соотношения стандартных углов», приведенной выше.
Как насчет косинуса?
Попробуйте найти отношения косинусов для стандартных углов, используя пальцы левой руки, и проверьте результаты в таблице выше.
Что насчет касательной????
Подсказка???
Вот вы здесь:
Тригонометрия — это весело, и теперь вы знаете, как быстро выполнить тригонометрию специальных углов на пальцах.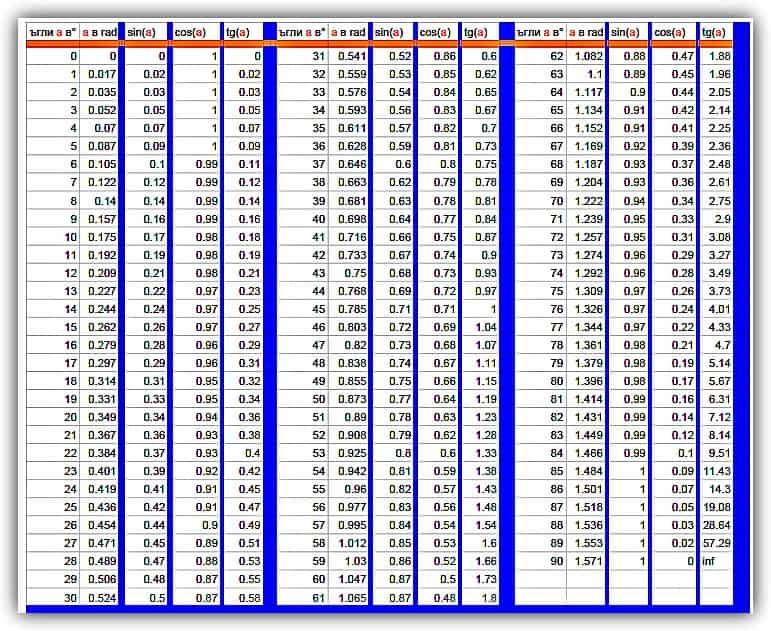
Чтобы получить эффективную математическую помощь и попрактиковаться, ознакомьтесь с IntoMath
Опубликовано