Синусы и косинусы тригонометрия: Синус и косинус. Тангенс и котангенс — урок. Алгебра, 10 класс.

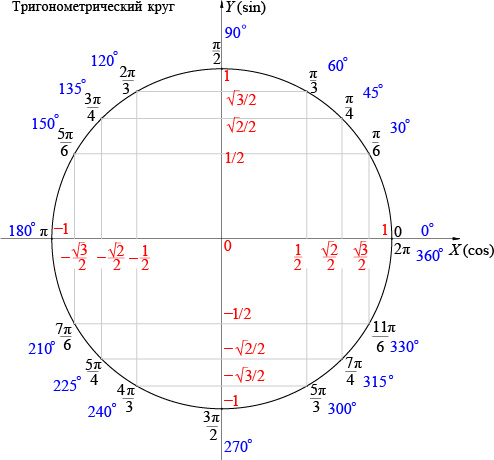
Произведение синусов и косинусов

Все ресурсы по тригонометрии

6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept

Помощь по тригонометрии » Сумма, разница и идентичность продукта » Произведение синусов и косинусов

Какой из следующих вариантов дополняет тождество 

Возможные ответы:

Правильный ответ:

Пояснение:

Эту формулу можно вывести непосредственно из тождеств суммы и разности косинусов .

---

Сообщение о ошибке

Выведите продукт синуса от идентификаторов для суммы и различий тригонометрических функций.

Возможные ответы:

Правильный ответ:

 

---

 

4  

4 Пояснение:

Во-первых, мы должны знать формулу произведения синусов, чтобы знать, что мы ищем. Формула этого тождества такова. Используя известные тождества суммы/разности косинусов, мы можем таким образом вывести произведение синусов. Иногда бывает полезно представить произведение тригонометрических функций в виде суммы. Это может либо упростить проблему, либо позволить вам визуализировать функцию по-другому.

Сообщить об ошибке

Использовать произведение косинусов для оценки Объяснение:

Мы используем идентификатор . Мы позволим  и .

Отчет о ошибке

Используйте продукт сини. 0012

Правильный ответ:

Пояснение:

Формула произведения синусов . Мы позволим  и .

Отчет о ошибке

или ложь: все идентификаторы продукта могут быть приобретены. -идентификаторы продуктов

Возможные ответы:

Верно

Неверно

Правильный ответ:

Верно

Объяснение:

Все эти тождества могут быть получены с помощью тождеств суммы к произведению путем сложения или вычитания двух тождеств суммы и сокращения членов. Путем некоторой алгебры и манипуляций вы можете получить идентичность каждого продукта.

Сообщить об ошибке

Используйте произведение синуса и косинуса для оценки .

Возможные ответы:

Правильный ответ:

Объяснение:

Идентификатор, который нам нужно будет использовать для решения этой проблемы: . Мы позволим  и  .

Отчет о ошибке

Используйте продукт косинелей для оценки. Держите свой ответ в терминах .

Возможные ответы:

Правильный ответ:

Объяснение:

Мы будем использовать идентификатор . Мы позволим  и .

Сообщить об ошибке

Используйте произведение синусов для оценки .

Возможные ответы:

Правильный ответ:

Объяснение:

Нам нужно будет использовать идентификатор . Мы позволим  и .

 

Отчет о ошибке

Уведомление об авторском праве

Все тригономерные ресурсы

6. 155 практических тестов Вопрос дня Карточки Learn by Concept

Закон синусов и косинусов – x-engineer.org

В большинстве практических приложений, связанных с тригонометрией, нам нужно вычислить углы и стороны разносторонний треугольник а не прямоугольный треугольник. Разносторонний треугольник — это треугольник, у которого три неравные стороны, каждая из которых имеет разную длину. Это означает, что также все углы треугольника не равны друг другу.

Наиболее важными законами, связанными с разносторонними треугольниками, являются закон синусов и закон косинусов .

Закон синусов

Изображение: Закон синусов для разностороннего треугольника

Разносторонний треугольник выше имеет:

• the sides a , b and c
• the angles  α ,  β and  γ
• the angle  α is opposite to side a ,  β to b и γ по c
• все углы острые

описанная окружность имеет радиус r .

Закон синусов утверждает, что в разностороннем треугольнике отношение одной стороны к синусу противоположного угла равно диаметру описанной окружности .

\[\ bbox[#FFFF9D]{\ frac {a} {\ text {sin} (\ alpha)} = \ frac {b} {\ text {sin} (\ beta)} = \ frac {c} {\text{sin}(\gamma)}=d} \tag{1}\]

, где d — диаметр описанной окружности :

\[d = 2 \cdot r \tag{ 2}\]

Закон синусов можно также интерпретировать так: в разностороннем треугольнике отношение двух сторон равно отношению синусов противоположных углов.

\[ \begin{split}
\frac{a}{b}=\frac{\text{sin}(\alpha)}{\text{sin}(\beta)}\\
\frac{a }{c}=\frac{\text{sin}(\alpha)}{\text{sin}(\gamma)}\\
\frac{b}{c}=\frac{\text{sin}( \beta)}{\text{sin}(\gamma)}
\end{split} \]

Из уравнений (1) и (2) мы также можем извлечь выражения каждой стороны, функции радиуса описанной окружности и синус противоположного угла:

\[ \begin{split}
a = 2 \cdot r \cdot \text{sin}(\alpha)\\
b = 2 \cdot r \cdot \text{sin }(\бета)\\
c = 2 \cdot r \cdot \text{sin}(\gamma)
\end{split} \]

Закон синусов можно использовать для вычисления остальных сторон треугольника, когда одна сторона и известны два угла. Этот метод также известен как триангуляция .

Закон косинусов

Изображение: Закон косинусов для разностороннего треугольника

Теорема Пифагора является частным случаем закона косинусов .

Закон косинусов гласит, что в разностороннем треугольнике 92}{2 \cdot b \cdot a} \right )
\end{split} \]

Курсовой угол самолета для компенсации ветра

Закон синусов и косинусов применим в авиационной навигации. Вычисление необходимого угла курса самолета для компенсации скорости ветра и движения в нужном направлении до пункта назначения является классической задачей авиационной навигации.

Изображение: угол курса самолета для компенсации ветра

Самолет движется со скоростью (самолет против ветра)  v _aw  = 150 м/с . Учитывая скорость ветра относительно земли v _wg = 17 м/с и угол ветра γ = 15° , вычислите угол курса α [°] и скорость самолета относительно земли v _ag [ м/с] ?

Три вектора скорости образуют разносторонний треугольник. Чтобы найти угол курса α , мы можем использовать закон синусов

:

\[\frac{v_{wg}}{\text{sin}(\alpha)}=\frac{v_{aw}} {\ текст {грех} (\ гамма)} \]

, из которого мы можем извлечь выражение угла курса  α :

\[\alpha = \text{arcsin} \left (\frac{v_{wg}}{v_{aw}} \cdot \text {sin}(\gamma) \right )\]

Перед заменой числовых значений имейте в виду, что аргументы тригонометрических функций необходимо преобразовать из градусов в радианы.

No related posts.