Тригонометрические уравнения решение: Решение тригонометрических уравнений — 39 примеров!

Учебное пособие «Решение тригонометрических уравнений»

Учебное пособие

по теме «Решение тригонометрических уравнений»

https://infourok.ru/site/upload

Аннотация

Настоящее пособие предназначено для обучающихся 10 – 11 классов, которые хотят научиться решать тригонометрические уравнения. Оно может служить пособием при подготовке к урокам, самостоятельным и контрольным работам, для самостоятельной подготовки к ЕГЭ.

Как правило, обучающиеся испытывают большие затруднения при решении тригонометрических уравнений. Основное содержание данного пособия составляют методы решения тригонометрических   уравнений. Изложение материала построено на решении типовых уравнений от простых до сложных и сопровождается всеми необходимыми для этого теоретическими сведениями. Поэтому работу с пособием лучше начинать с повторения теоретического материала, последовательно разбирая пример за примером и закрепляя затем рассмотренные методы решения тригонометрических уравнений, решая уравнения, предложенные для самостоятельной работы.

Большинство задач представлено с решениями, что способствует более углублённому освоению материала.

Предложенная форма подачи материала позволяет систематизировать теоретический материал по данной теме, способствует формированию навыка решения различных типов тригонометрических уравнений.

СОДЕРЖАНИЕ

ИСТОРИЧЕСКИЕ СВЕДЕНИЯ О РАЗВИТИИ ТРИГОНОМЕТРИИ 3 стр. МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

1 ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 5 стр.

2 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

РАЗЛОЖЕНИЕМ НА МНОЖИТЕЛИ 6 стр.

3 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ,

СВОДЯЩИХСЯ К КВАДРАТНЫМ 9 стр.

4 РЕШЕНИЕ ОДНОРОДНЫХ УРАВНЕНИЙ 10 стр.

5 РЕШЕНИЕ УРАВНЕНИЙ С ПОМОЩЬЮ ВВЕДЕНИЯ

ВСПОМОГАТЕЛЬНОГО АРГУМЕНТА 11 стр.

6 РЕШЕНИЕ УРАВНЕНИЙ С ПРИМЕНЕНИЕМ ФОРМУЛ

ПОНИЖЕНИЯ СТЕПЕНИ 13 стр.

7 РЕШЕНИЕ УРАВНЕНИЙ С ПРИМЕНЕНИЕМ ФОРМУЛ

ТРОЙНОГО АРГУМЕНТА 15 стр.

8 РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ УНИВЕРСАЛЬНОЙ

ПОДСТАНОВКИ 16 стр.

9 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ,

СОДЕРЖАЩИХ ЗНАК МОДУЛЯ ИЛИ ЗНАК КОРНЯ 17 стр.

10 ИСПОЛЬЗОВАНИЕ ОГРАНИЧЕННОСТИ ФУНКЦИЙ ПРИ

РЕШЕНИИ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ 18 стр.

11 ФУНКЦИОНАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ

И КОМБИНИРОВАННЫХ УРАВНЕНИЙ 19 стр.

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 20 стр.

СПРАВОЧНЫЙ МАТЕРИАЛ 21 стр.

ЗАКЛЮЧЕНИЕ 22 стр.

ИСТОРИЧЕСКИЕ СВЕДЕНИЯ О РАЗВИТИИ ТРИГОНОМЕТРИИ

Слово «тригонометрия» составлено из двух греческих слов: «тригонон» — треугольник и «метрео» — измеряю. Основной задачей тригонометрии является нахождение неизвестных параметров треугольника по данным значениям других его параметров. Например, по данным сторонам треугольника можно вычислить его углы, по известным значениям площади и двух углов вычислить его стороны и т. д.

Первые методы нахождения неизвестных параметров данного треугольника были развиты учеными Древней Греции за несколько веков до нашей эры. Греческие астрономы не знали синусов, косинусов и тангенсов. Вместо таблиц этих величин они употребляли таблицы, позволявшие отыскивать хорду окружности по стягиваемой ею дуге. Дуги измерялись в градусах и минутах.

Все древние цивилизации вносили свой вклад в дело накопления тригонометрических знаний. На одной из глиняных табличек Древнего Вавилова, возраст которой определяется вторым тысячелетием до нашей эры, решается тригонометрическая задача.

Значительно развили тригонометрию индийские средневековые астрономы и арабские ученые. В X веке багдадский ученый Абу-ль-Вефа присоединил к понятиям синусов и косинусов понятия тангенсов, котангенсов, секансов и косекансов. Абу-ль-Вефа установил также основные соотношения между ними. Благодаря работам знаменитого арабского ученого Насир эд-Дина (1201—1274) тригонометрия становится самостоятельной научной дисциплиной. Насир эд-Дин рассмотрел все случаи решения плоских и сферических треугольников. В XII веке с арабского языка на латинский был переведен ряд астрономических работ, по которым европейцы познакомились с тригонометрией, не многие работы Насир эд-Дина остались им неизвестны.

Выдающийся немецкий астроном XV века Региомонтан (1436—1476) заново сформулировал теоремы Насир эд-Дина. Региомонтан составил таблицы синусов плоских углов с точностью до седьмой значащей цифры. В середине XVIII века, благодаря русскому академику Леонарду Эйлеру (1707—1783), тригонометрия приняла современный вид. Он разработал её как науку о тригонометрических функциях, ввел записи sinx, tgx, обозначил а, в, с для сторон и А,В,С  для противоположных углов Δ АВС.

Эйлер рассматривал тригонометрические функции аргумента х — радианной меры соответствующего угла, давая этому аргументу различные значения: положительные, отрицательные и даже комплексные. Он же ввел и обратные тригонометрические функции.

МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решения полученного простейшего тригонометрического уравнения. 

1 ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ

Формулы для решения простейших тригонометрических уравнений:

Особо отметим некоторые частные случаи простейших тригонометрических уравнений, когда решение может быть записано без применения общих формул:

Каждая из функций y = arcsin  и y = arccos определена на отрезке [-1; 1] и

.

Функция  y = arcsin является нечетной, то есть arcsin = – arcsin .

Функция y = arccos   не является ни четной, ни нечетной:

arccos = – arccos .
Функции y = arctg  и  y = arcctg определены на всей числовой прямой и

.

Функция  является нечетной, то есть = – .

Функция  не является ни четной, ни нечетной:

.

При решении тригонометрического уравнения, не являющегося простейшим, его сводят тем или иным способом к одному или нескольким простейшим. 

Пример 1. Решите уравнение tg²x = 3. (1)

Решение.
Исходное уравнение равносильно совокупности

Решением первого уравнения этой совокупности является семейство  , а второго – семейство   . Объединение этих двух множеств и есть решение уравнения (1).

Эти решения можно для краткости записать в виде  .
Ответ:  .

Пример 2. Решите уравнение . (2)

Решение.
Грубая ошибка, которую допускают при решении этого уравнения, состоит в следующем: обучающиеся записывают решение  , однако они не учитывают, что  , следовательно, уравнение (2) решений не имеет.
Ответ: решений нет.

Пример 3. Решите уравнение (3)

Решение.
Применив формулу решения простейшего тригонометрического уравнения, получим

(4)

По определению арифметического квадратного корня перейдём к равносильной системе уравнений, так как .

⇔ .

Ответ. .

2 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

РАЗЛОЖЕНИЕМ НА МНОЖИТЕЛИ

Метод разложения на множители заключается в следующем: если

f(x)=f₁(x)· f₂(x)· ··· ·f_n(x),

То всякое решение уравнения f(x) = 0 (1)

является решением совокупности уравнений (2)

Обратное утверждение, неверно: не всякое решение совокупности уравнений (2) является решением уравнения (1). Это объясняется тем, что решения отдельных уравнений (2) могут не входить в область определения функции f(x).
Поэтому, если при решении тригонометрического уравнения методом разложения на множители, функции, входящие в уравнение, определены не для всех значений аргумента, после нахождения решения должна быть сделана проверка, чтобы исключить лишние корни. Можно поступать другим способом: находить область допустимых значений исходного уравнения и выбирать только те корни, которые входят в найденную область допустимых значений.

Пример 1. Решить уравнение (2 (3)

Решение.
Используя основное тригонометрическое тождество, представим уравнение в виде

(4)

Грубой ошибкой, которую часто допускают при решении, является сокращение левой и правой части уравнения (4) на (1+cosx), так как при этом теряются корни. При правильном подходе к решению данного уравнения следует перенести все слагаемые в правую часть и вынести общий множитель за скобки, получая равносильное уравнение

(1 + cosx)(2sinx – cosx – 1 + cosx) = 0;

(1 + cosx)(2sinx – 1) = 0;

Ответ.

Пример 2. Решить уравнение (5)

Решение.
Преобразуем правую часть уравнения (5) следующим образом:

.

Затем перенесем все слагаемые в левую часть и получим

(6)

ОДЗ уравнения (6) являются все  , за исключенем  . На данной ОДЗ уравнение (6) равносильно совокупности двух уравнений

Первое уравнение имеет решение  ,

а второе .

Однако ОДЗ принадлежат лишь , которые и являются решением исходного уравнения (5).

Ответ: .

Пример 3. Решить уравнение

Решение. 

   Перенесём все члены уравнения влево: sin x + cos x – 1 = 0 .

Преобразуем и разложим на множители выражение в левой части уравнения:

Данное уравнение равносильно совокупности двух уравнений:

Ответ.                

              

Пример 4 . Решить уравнение  cos ² x + sin x · cos x = 1.

 

Решение .   Перенесём все члены уравнения влево:

cos ² x + sin x · cos x  – 1 = 0.

 Заменив 1 выражением sin ² x + cos ² x , получим

cos ² x + sin x · cos x – sin ² x – cos ² x = 0.

Разложим на множители выражение в левой части уравнения:

                                               sin x · cos x – sin ² x = 0,

                                              sin x · ( cos x – sin x ) = 0.

 Данное уравнение равносильно совокупности двух уравнений:

     Ответ.                              

    П р и м е р   5.   Решить уравнение: cos 2x – cos 8x + cos 6x = 1. 

  

  Решение.  Выполним ряд преобразований

cos 2x + cos 6x = 1 + cos 8x ;

2 cos 4x cos 2x = 2 cos ² 4x ;

cos 4x · ( cos 2x –  cos 4x ) = 0 ;

cos 4x · 2 sin 3x · sin x = 0 .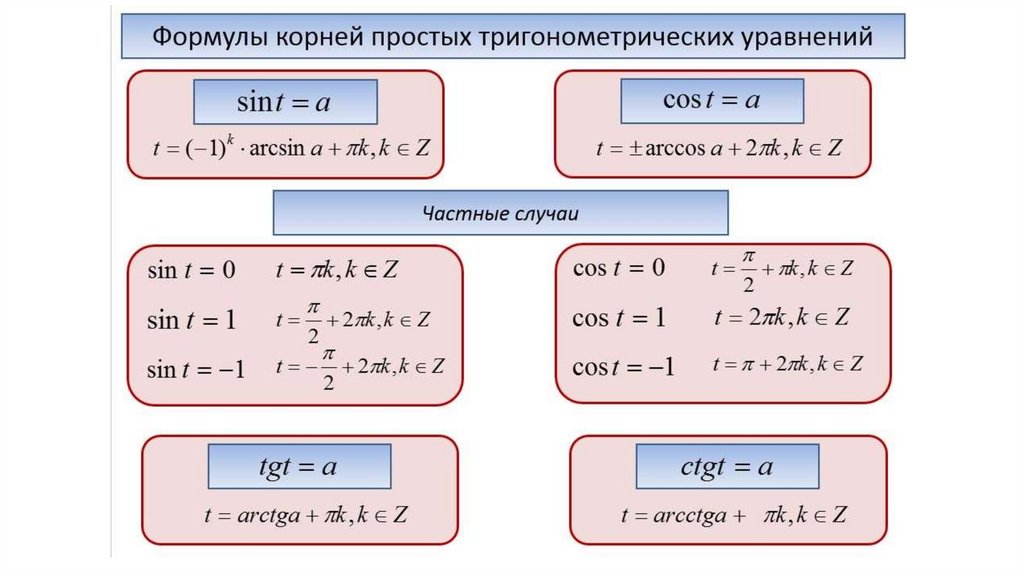

 Данное уравнение равносильно совокупности трёх уравнений

                                            

Ответ.

3 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ,

СВОДЯЩИХСЯ К КВАДРАТНЫМ

При решении уравнений указанного типа в основном применяются следующие тригонометрические тождества:

Пример 1. Решить уравнение 6cos²x +5sinx – 7 = 0 (1)

Решение.
Используя основное тригонометрическое тождество, осуществим замену cos²x = 1 – sin²x , тогда уравнение (1) примет вид 6sin²x – 5sinx +1 = 0.

Введем подстановку y = sinx, тогда получим квадратное уравнение 6y² – 5y +1 = 0.

Решая его, находим корни  y₁ = , y₂ =  . Затем осуществляя обратную подстановку   или  , получаем решение исходного уравнения:

Ответ:   

Пример 2. Решить уравнение (2)

Решение.
Введем подстановку , тогда уравнение (2) примет вид y² – 3y – 4 = 0.

Решив его, получим следующие корни уравнения: у₁ = 1, у₂ = – 4.

Так как  , то при у₁ = 1 уравнение корней не имеет.

Следовательно, при у₂ = – 4 имеем

.

Ответ:  .

4 РЕШЕНИЕ ОДНОРОДНЫХ УРАВНЕНИЙ

Однородное уравнение – это уравнение, в котором каждое слагаемое имеет одну и ту же степень.

₀sinⁿx + ₁sin^n-1xcosx + ₂sin^n-2xcos²x + ….+ _n-1sinxcos^n-1x + _ncosⁿx = 0,

где – действительные числа, n – показатель однородности.

Алгоритм решения однородных уравнений:

   а) перенести все его члены в левую часть;

   б) вынести все общие множители за скобки;

   в) приравнять все множители и скобки нулю;

   г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на  cosх ( или sinх ) в старшей степени; 

   д) решить полученное алгебраическое уравнение относительно tgx.  

Пример 1. Решить уравнение sinx – cosx =0. (1)

Решение.
Уравнение (1) является однородным уравнением первой степени. Разделив обе части на cosx, получим равносильное уравнение tgx – 2 = 0, откуда tgx = 2. Откуда находим семейство x = arctg2 +  , представляющее собой решение исходного уравнения (1). 
Ответ:  x = arctg2 +  

Пример 2. Решите уравнение 3sinx + 4cosx = 5. (2)

Решение. Уравнение (2) не является однородным, однако его можно преобразовать к однородному c помощью формул тригонометрии.

3sin 2 + 4cos 2 = 5·1;

.

Если , тогда и (и наоборот), что противоречит основному тригонометрическому тождеству, значит . Разделив обе части уравнения на , получим следующее уравнение:

;

Ответ.

Примечание. Данное уравнение можно решить другим способом – с помощью введения вспомогательного аргумента (решение в следующем пункте).

 

Пример 3. Решите уравнение

sin⁴x + sin³x·cosx + sin²x ·cos²x + sinx ·cos³x + cos⁴x = 1. (3)

Решение.
Уравнение (3) не является однородным, однако его можно преобразовать к однородному, если представить единицу следующим образом:

1 = (sin²x + cos²x)² = sin⁴x + 2 sin²x ·cos²x + cos⁴x.

Тогда уравнение (3) примет вид sin³x·cosx – sin²x·cos²x + sinx·cos³x = 0, которое равносильно совокупности трех уравнений

Решая их, найдем  
Ответ:  .

Пример 4. Решите уравнение 3sin ² x + 4 sin x · cos x + 5 cos ² x = 2.

Решение.  3sin ² x + 4 sin x · cos x + 5 cos ² x = 2sin ² x + 2cos ² x ,

                               sin ² x + 4 sin x · cos x + 3 cos ² x = 0 ,

                              tg ² x + 4 tg x + 3 = 0 .  

Введём новую переменную y = tgx и получим следующее уравнение y ² + 4y +3 = 0.

Корни этого уравнения y₁ =  – 1,  y₂ =  – 3. Вернёмся к исходной переменной. Получили совокупность двух уравнений

Ответ.

 

5 РЕШЕНИЕ УРАВНЕНИЙ С ПОМОЩЬЮ ВВЕДЕНИЯ

ВСПОМОГАТЕЛЬНОГО АРГУМЕНТА

Рассмотрим уравнение (1)

1 Если с = 0, то уравнение однородное.

2 Если (то есть хотя бы одно из чисел и не равно нулю).

Разделим левую и правую часть уравнения (1) на  :

Так как то существует угол φ такой, что

при этом

Тогда уравнение (1) примет вид

Если , то корней нет.

Если , тогда

Отметим, что к выбору угла φ в задачах с параметрами нужно относиться внимательно: выбор и выбор будут не всегда равносильны.

Пример 1. Решить уравнение

Решение. Так как 3² + 4² < 6² , то корней нет.

Ответ. корней нет.

 
Пример 2. Решить уравнение (2)

Решение.
Разделим левую и правую часть уравнения на  . Тогда получим

Ответ можно записать в другом виде. Для этого, положив k = 2n, n и k = 2n + 1, n получим x = 2

 
Ответ:  x = 2

Пример 3. Решить уравнение (3)

Решение.
Разделим левую часть на 2 и положим  . Тогда уравнение (3) примет вид

Применив формулу  , получим

Откуда

Следовательно,

Ответ:   .

Пример 4. Решить уравнение 3sin x + 4 cos x = 5.

Решение. Так как 3² + 4² 5² , то уравнение имеет корни. Разделим обе части уравнения на . Получим следующее уравнение

Так как , то существует такой угол .

Тогда получим ;

Ответ.

6 РЕШЕНИЕ УРАВНЕНИЙ С ПРИМЕНЕНИЕМ

ФОРМУЛ ПОНИЖЕНИЯ СТЕПЕНИ

При решении широкого круга тригонометрических уравнений ключевую роль играют формулы понижения степени

Пример 1. Решить уравнение

Решение.
Применив формулу понижения степени, получим

Последнее уравнение равносильно совокупности трех уравнений

которые имеют соответственно следующие множества решений:

Решения из множества   при k = 2l, l  содержаться в множестве (n=5l) , а при k = 2l + 1  в множестве (m = l)   

Ответ: 

Пример 2. Решить уравнение

Решение. Применив формулы  и  , приведем уравнение к виду

 

Далее осуществим ряд простых преобразований:

Последнее уравнение равносильно совокупности трех уравнений:

Решение первого из них есть  второго – 

третьего – 
Решением исходного уравнения является объединение полученных множеств.

Ответ:  

7 РЕШЕНИЕ УРАВНЕНИЙ С ПРИМЕНЕНИЕМ

ФОРМУЛ ТРОЙНОГО АРГУМЕНТА

При решении ряда уравнений наряду с другими существенную роль играют формулы

(1)

(2)

Пример 1. Решить уравнение

 Решение.
Применив формулу (2), получим

Последнее уравнение равносильно совокупности двух уравнений 

 Откуда

  
Ответ: 

Пример 2. Решить уравнение

Решение.
Применив формулы понижения степени, приведем уравнение к виду:

В соответствие с формулой (2), получаем равносильное уравнение

откуда имеем совокупность трех уравнений

Следовательно, 

Объединив два последних множества решений, получим

Ответ: ,

8 РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ

УНИВЕРСАЛЬНОЙ ПОДСТАНОВКИ

Тригонометрическое уравнение вида

где R – рациональная функция, k, l, m, n , с помощью тригонометрических формул двойного и тройного аргумента, а также формул сложения можно свести к рациональному уравнению относительно аргументов   после чего уравнение (1) может быть сведено к рациональному уравнению относительно  с помощью формул универсальной тригонометрической подстановки:

(2)

Следует отметить, что применение формул может приводить к сужению ОДЗ исходного уравнения, поскольку   не определен в точках  поэтому в таких случаях нужно проверять, являются ли углы x  корнями исходного уравнения.  

Пример 1. Решить уравнение

Решение.
По условию задачи Применив формулы (2) и сделав замену  , получим откуда t=0 и, следовательно, x=2  

Ответ:  x=2

Пример 2. Решить уравнение

Решение.
По условию задачи  . Используем формулы (2) и заменим  , тогда получим

Уравнение корней не имеет.

Следовательно Значит,  .
Заметим, что в данном случае применение подстановки  не сужает ОДЗ исходного уравнения. 
Ответ: 

9 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ,

СОДЕРЖАЩИХ ЗНАК МОДУЛЯ ИЛИ ЗНАК КОРНЯ

Специфика тригонометрических уравнений, содержащих знак модуля или знак корня, состоит в том, что они сводятся к смешанным системам, где кроме уравнений нужно решать тригонометрические неравенства и из решений уравнений выбирать лишь те, которые удовлетворяют неравенствам.

Пример 1. Решить уравнение (1)

Решение.
Уравнение (1) равносильно совокупности двух систем

Уравнение  равносильно совокупности двух уравнений 

откуда  x = – 3  и x = .

Промежутку [-3;+∞) принадлежат x = – 3  и x =  .
Уравнение   равносильно совокупности двух уравнений 

откуда  x = – 3  и  x = .

Множеству ( – ∞; – 3) принадлежат и x =

 

 Ответ: x = – 3  и x =

x =

Пример 2. Решить уравнение (3)

Решение.
Преобразуем уравнение (3) к виду

Так как , то уравнение (4) на ОДЗ равносильно совокупности двух систем

Уравнение из первой системы равносильно совокупности двух уравнений

   , а решением неравенства является множество

. Из решений  указанному множеству принадлежат .
Во второй системе совокупности (5) уравнение имеет решения 

 ,

множеству   (решению неравенства принадлежат .
Ответ:  

.

10 ИСПОЛЬЗОВАНИЕ ОГРАНИЧЕННОСТИ ФУНКЦИЙ ПРИ РЕШЕНИИ

ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

При решении некоторых тригонометрических уравнений часто используется свойство ограниченности функций sinx  и cosx , то есть следующие неравенства:

 .

Пример 1. Решить уравнение (1)

Решение.
Проведем равносильные преобразования:

(2)

Так как а  , то   ,
так как  а , то .
Сумма двух неположительных слагаемых в (2) равна нулю тогда и только тогда, когда каждое из слагаемых равно нулю. Значит, уравнение (2) равносильно системе

(3)

Решением первой совокупности системы (3) являются углы  , а решением второй – .

Общими являются углы. 

Ответ: . 

 

Пример 2. Решить уравнение (4)

Решение.
Используя прием, изложенный в примере 1, сведем уравнение (4) к равносильной системе:

(5)

Находя решение каждой совокупности системы (5), нетрудно установить, что общими будут углы   

Ответ: 

11 ФУНКЦИОНАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ

И КОМБИНИРОВАННЫХ УРАВНЕНИЙ

Не всякое уравнение f(x)=g(x) в результате преобразований может быть сведено к уравнению того или иного стандартного вида, для которого существует определенный метод решения. В таких случаях оказывается полезным использовать такие свойства функций f(x) и g(x), как монотонность, ограниченность, четность, периодичность и др. Так, если одна из функций убывает, а вторая возрастает на промежутке X, то при наличии у уравнения f(x)=g(x) корня на этом промежутке, этот корень единственный, и тогда его, например, можно найти подбором.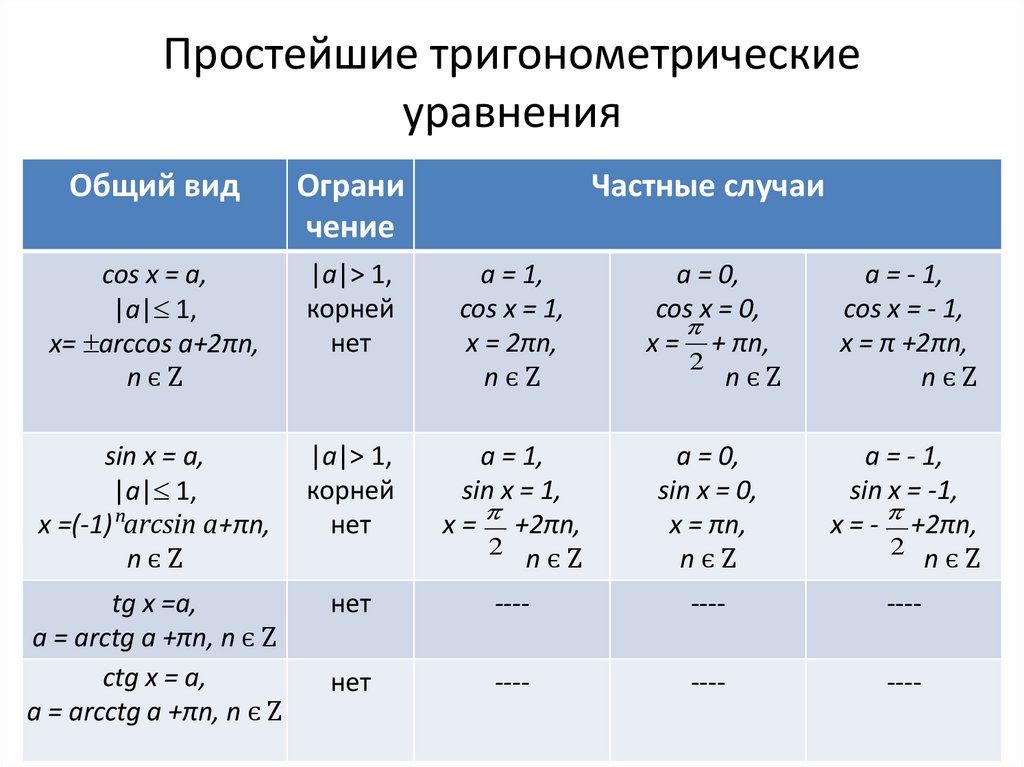 Если, далее, функция f(x) на промежутке X ограничена сверху, причем  , а функция g(x) ограничена снизу, причем  , то уравнение f(x)=g(x) равносильно системе уравнении Иногда для решения уравнения f(x)=g(x) можно построить графики функции y = f(x), y = g(x) и определить абсциссы точек пересечения. В этом параграфе также рассматривается применение производной для исследования тригонометрических уравнений.

Пример 1. Решить уравнение cos

Решение. Преобразуем уравнение (1) к виду

cos

Так как , а , то последнее уравнение равносильно системе

Второе уравнение системы (2) имеет единственный корень х=2, подставляя его в первое уравнение, убеждаемся, что он удовлетворяет ему. Следовательно, х = 2 — корень системы (2), а значит, и уравнения (1).

Ответ: х=2.

Пример 2. Решить уравнение

Решение. Воспользовавшись основным тригонометрическим тождеством, запишем исходное уравнение в равносильном виде

Последнее уравнение равносильно системе

решением которой является x = 1,5.  

Ответ: x = 1,5. 

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. . (Ответ. х = )

2. tg²3x = cos2x – 1 (. (Ответ. х = )

3. 1 + cos2xcos3x = 0.5sin²3x . (Ответ. х = )

4. (Ответ. х =

5. cosx = |sin(2x – 1| (Ответ. х = .

6. 2sin²(x ) = 2sin²x – tgx (Ответ. х =

7. (Ответ. х = 2arctg(2 )

8. (Ответ. х =

9. (Ответ. х = )

10. sin²x – cos²x = cos (Ответ.

11. sin³x +4cos³x = 0 (Ответ. х =

12. Найдите все значения параметра при которых уравнение f ‘(x) = 0, где

f(x)=1 – cosx + имеет не более одного корня. (Ответ.

13. При каких значениях параметра уравнение

cos² имеет единственное решение. (Ответ.

14. 2tg²x + 3 = (Ответ.

15. (Ответ.

16. tg²x = cos2x – 1 (Ответ.

СПРАВОЧНЫЙ МАТЕРИАЛ

Числовая окружность

Таблица значений тригонометрических функций некоторых углов

Знаки тригонометрических функций

Основные тригонометрические формулы

Формулы сложения и вычитания тригонометрических функций

Формулы двойного угла

Формулы понижения степени

 

ЗАКЛЮЧЕНИЕ

В данном учебном пособии рассмотрены основные методы решения тригонометрических уравнений, приведены примеры решения разных типов задач. Данное пособие может оказать помощь обучающимся как при подготовке к занятиям при изучении данной темы, так и при подготовке к итоговой аттестации в форме ЕГЭ. Выполняя задания для самостоятельного решения, обучащиеся могут самостоятельно оценить свои знания, умения и навыки по данной теме. Материал может быть полезен преподавателям при подготовке к проведению факультативных занятий.

19

Тригонометрические уравнения — презентация онлайн

1. Методика решения тригонометрических уравнений

L/O/G/O

2. Слово «тригонометрия» греческого происхождения. В пере-воде на русский язык оно означает «измерение треугольников». Как и все

Слово «тригонометрия»
греческого происхождения. В переводе на русский язык оно означает
«измерение треугольников». Как и
все разделы математики, зародившиеся в глубокой древности, тригонометрия возникла в результате
попыток решить те задачи, с
которыми человеку приходилось
сталкиваться на практике.
Основы тригонометрии, как и основы
алгебры и начал анализа закладываются в
школе. Тригонометрические функции
начинают изучать в 8 классе на уроках
геометрии и продолжают в 10-11 классах.
Тригонометрические уравнения слишком
разнообразны для того, чтобы попытаться
дать их общую классификацию или общий
метод решения. Мы можем указать лишь
способы решения некоторых типов таких
уравнений.
Решение тригонометрических
уравнений
Для тригонометрических
уравнений применимы общие методы
решения (разложение на множители,
замена переменной, функциональнографические) и равносильные
преобразования общего характера.

5. Методы решения тригонометрических уравнений

Основные методы:
• замена переменной,
• разложение на множители,
•однородные уравнения,
прикладные методы:
• по формулам преобразования суммы в произведение
и произведения в сумму,
• по формулам понижения степени,
• универсальная тригонометрическая подстановка
• введение вспомогательного угла,
• умножение на некоторую тригонометрическую функцию.
Проблемы ,возникающие при решении
тригонометрических уравнений
1.Потеря корней:
делим на g(х).
опасные формулы (универсальная подстановка).
Этими операциями мы сужаем область определения.
2. Лишние корни:
возводим в четную степень.
умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область
определения.

7. Наша задача: свести любое тригонометрическое уравнение к простейшему виду.

Наша задача:
свести любое
тригон ометрическое
урав н ен и е
к п ростей шему вид у.
Решение простейших
тригонометрических
уравнений

9. Формулы корней простых тригонометрических уравнений

1.cost = а , где |а| ≤ 1
2.sint = а, где | а |≤ 1
3. tgt = а, аЄR
t = arctg а + πk‚ kЄZ
или
или
4. ctgt = а, аЄR
Частные случаи
Частные случаи
1)cost=0
t = π/2+πk‚ kЄZ
1)sint=0
t = 0+πk‚ kЄZ
2)cost=1
t = 0+2πk‚ kЄZ
2)sint=1
t = π/2+2πk‚ kЄZ
3)cost = -1
t = π+2πk‚ kЄZ
3)sint = — 1
t = — π/2+2πk‚ kЄZ
t = arcctg а + πk‚ kЄZ
• При повторении формул решения уравнений
следует обратить внимание на то, что формулы
задают множества чисел, которые образованы по
закону арифметической прогрессии с разностью
2π или π.
• С другой стороны использование общей
формулы серий решений не всегда является
удобной при отборе корней, в частности, на
числовой окружности. В этом случае как раз
удобнее не объединять серии решений
тригонометрических уравнений, а представлять
их совокупностью, выделяя разность 2π
соответствующих прогрессий.

13. tg x и ctg x

14. Решение простейших уравнений

2) cos(x+π/3) = ½
1) tg2x = -1
2x = arctg (-1) + πk, kЄZ
2x = -π/4 + πk, kЄZ
x = -π/8 + πk/2, kЄZ
Ответ: -π/8 + πk/2, kЄZ.
x+π/3 = ±arccos1/2 + 2πk, kЄZ
x+π/3 = ±π/3 + 2πk, kЄZ
x = -π/3 ± π/3 + 2πk, kЄZ
Ответ: -π/3 ± π/3 + 2πk, kЄZ
3) sin(π – x/3) = 0
упростим по формулам
приведения
sin(x/3) = 0
частный случай
x/3 = πk, kЄZ
x = 3πk, kЄZ.
Ответ: 3πk, kЄZ.
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РАЗЛОЖЕНИЕМ НА МНОЖИТЕЛИ.
Метод разложения на множители заключается в следующем: если
То всякое решение уравнения
Является решением совокупности уравнений
Обратное утверждение, неверно: не всякое решение совокупности уравнений (2)
является решением уравнения (1). Это объясняется тем, что решения отдельных
уравнений (2) могут не входить в область определения функции
.Поэтому,
если при решении тригонометрического уравнения методом разложения
на множители, функции,
входящие в уравнение, определены не для всех значений аргумента, после
нахождения решения должна быть сделана проверка,
чтобы исключить лишние корни. Можно поступать другим способом: находить
область допустимых значений исходного уравнения и выбирать только те корни,
которые входят в найденную область допустимых значений
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РАЗЛОЖЕНИЕМ НА МНОЖИТЕЛИ.
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ,
СВОДЯЩИХСЯ К КВАДРАТНЫМ.
Уравнения сводимые к квадратным
a∙sin²x + b∙sinx + c=0
Пусть sinx = p, где |p| ≤1, тогда
a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и решить простые уравнения.
При решении уравнений указанного типа в основном применяются следующие
тригонометрические тождества:
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ,
СВОДЯЩИХСЯ К КВАДРАТНЫМ.
Пример 1. Решить уравнение
Решение.
2 sin2x + sinx — 1 = 0.
Введём новую переменную t = sinx. Тогда данное
уравнение примет вид
2t2 + t — 1 = 0.
Решим его: D = 1 + 8 = 9,
1 3 1
t1
,
4
2
1 3
t2
1 .
4
Cледовательно,
sinx = 1/2
или
sinx = -1.
1) sinx = 1/2,
1
х ( 1) arcsin k , k Z ,
2
k
x ( 1)
k
6
k, k Z.
2) sinx = -1,
х
2
2 n, n Z .
Ответ : ( 1)
k
6
k, k Z ,
2
2 n, n Z .

20. Решение уравнений, однородных относительно синуса и косинуса

в которых сумма показателей степеней у sinx и cosx (степень уравнения) во
всех членах уравнения одинакова. Например,

22. Однородные тригонометрические уравнения

ОДНОРОДНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
2.Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно не равны нулю, то разделим обе
части уравнения на cosx. Получим: простое уравнение
a∙tgx + b = 0 или tgx = m
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x. Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.
В частности, уравнения вида
приводятся к однородным путем представления правой части в виде:

23. Решение уравнений с помощью введения вспомогательного аргумента.

:
РЕШЕНИЕ УРАВНЕНИЙ С ПОМОЩЬЮ ВВЕДЕНИЯ
ВСПОМОГАТЕЛЬНОГО АРГУМЕНТА.
Рассмотрим уравнение
Разделим левую и правую часть уравнения на
Так как
то существует угол φ такой, что
при этом
Тогда уравнение примет вид
будут не всегда равносильны.
Отметим, что к выбору угла φ в задачах с параметрами нужно относиться внимательно:
выбор
и выбор
Решите уравнения:
Уравнения, линейные относительно
sin x и cos x
а sin x + в cos x = с.
Если а=в=0, а с не равно 0, то уравнение теряет смысл;
Если а=в=с=0, то х – любое действительное число, то есть уравнение
обращается в тождество.
Рассмотрим случаи, когда а,в,с не равны 0.
Примеры:
3 sin 5x — 4 cos 5x = 2
2 sin x cos x 2
2 sin 3x + 5 cos 3x = 8.
Последнее уравнение не имеет решений, так как левая часть его не
превосходит 7. Уравнения, этого вида можно решить многими способами:
с помощью универсальной подстановки, выразив sin x и cos x через tgх ;
сведением уравнения к однородному; введением вспомогательного
аргумента и другими.
2
2
2
Решение этих уравнений существует при a b c

27. Решение уравнений с применением формул понижения степени.

:
Решение уравнений с применением
формул понижения степени.
При решении широкого круга тригонометрических уравнений ключевую роль играют
формулы понижения степени
Решение уравнений с применением
формул тройного аргумента.
(1)
(2)
При решении ряда уравнений наряду с другими существенную роль играют формулы

28. Решение уравнений методом универсальной подстановки.

Тригонометрическое уравнение вида
где R – рациональная функция,
с помощью тригонометрических формул двойного и тройного аргумента, а также
формул сложения можно свести к рациональному уравнению относительно аргументов
после чего уравнение может быть сведено к рациональному уравнению относительно
с помощью формул универсальной тригонометрической подстановки
Следует отметить, что применение формул может приводить к сужению ОДЗ исходного
уравнения, поскольку
не определен в точках
поэтому в таких случаях нужно проверять, являются ли углы
корнями исходного уравнения.

29. тригонометрические уравнения, содержащие знак модуля или знак корня.

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, СОДЕРЖАЩИЕ
ЗНАК МОДУЛЯ ИЛИ ЗНАК КОРНЯ.
Специфика тригонометрических уравнений, содержащих знак модуля или
знак корня, состоит в том, что они сводятся к смешанным системам, где
кроме уравнений нужно решать тригонометрические неравенства и из
решений уравнений выбирать лишь те, которые удовлетворяют
неравенствам.
Решите уравнения:

30. Использование ограниченности функций при решении тригонометрических уравнений.

ИСПОЛЬЗОВАНИЕ ОГРАНИЧЕННОСТИ ФУНКЦИЙ ПРИ
РЕШЕНИИ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ.
При решении некоторых тригонометрических уравнений часто используется свойство
ограниченности функций
, то есть следующие неравенства:
и

31. Функциональные методы решения тригонометрических и комбинированных уравнений.

ФУНКЦИОНАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ
ТРИГОНОМЕТРИЧЕСКИХ И КОМБИНИРОВАННЫХ
УРАВНЕНИЙ.
Не всякое уравнение f(x)=g(x) в результате преобразований может быть сведено к
уравнению того или иного стандартного вида, для которого существует определенный
метод решения. В таких случаях оказывается полезным использовать такие свойства
функций f(x) и g(x), как монотонность, ограниченность, четность, периодичность и др. Так,
если одна из функций убывает, а вторая возрастает на промежутке X, то при наличии у
уравнения f(x)=g(x) корня на этом промежутке, этот корень единственный, и тогда его,
например, можно найти подбором. Если, далее, функция f(x) на промежутке X ограничена
сверху, причем
, а функция g(x) ограничена снизу, причем
то уравнение f(x)=g(x) равносильно системе уравнении
Иногда для решения уравнения f(x)=g(x) можно построить графики функции y=f(x),
y=g(x) и определить абсциссы точек пересечения. Также рассматривается
применение производной для исследования тригонометрических уравнений.

32. Способы отбора корней тригонометрических уравнений на заданном промежутке

• Арифметический способ
Перебор значений целочисленного параметра n и
вычисление корней
• Алгебраический способ
Перебор значений целочисленного параметра n и
вычисление корней
• Геометрический способ
Изображение корней на тригонометрической
окружности с последующим отбором с учетом
имеющихся ограничений

33.

Арифметический способ Перебор значений целочисленного параметра n и вычисление корнейcos x a, a 1
x arccos a 2 k , k Z
x arccos a 2 k , k Z
Решить уравнение
Записать корни уравнения
Разделить виды решения для
x
косинуса; подсчитать значения x
k
-2
-1 0
2 …
arccos a 2 k
arccos a 2 k
при целых n до тех пор, пока
значения x не выйдут за пределы
sin x a, a 1
данного отрезка.
x ( 1) k arcsin a k , k Z
Записать ответ.
1
x
k
( 1) k arcsin a k
-2 -1 0 1 2 …

34. Алгебраический способ Решение неравенства относительно неизвестного параметра n и вычисление корней

cos x a, a 1, c; d
Записать двойное неравенство
для неизвестного (x),
соответственное данному отрезку
или условию; решить уравнение.
2. Для синуса и косинуса разбить
решения на два.
3. Подставить в неравенство
вместо неизвестного (x)
найденные решения и решить его
относительно n.
4. Учитывая, что n принадлежит
Z, найти соответствующие
неравенству значения n.
5. Подставить полученные
значения n в формулу корней.
1.
x arccos a 2 k , k Z
x arccos a 2 k , k Z
с arccos a 2 k d
с arccos a 2 k d
Т.к. k Z ,
то k1 …; x1 …
k2 …; x2 …
sin x a, a 1, c; d
x arcsin a 2 k , k Z
x arcsin a 2 k , k Z
с arcsin a 2 k d
с arcsin a 2 k d
Т.к. k Z ,
то k1 …; x1 …
k2 …; x2 …

35. Геометрический способ Изображение корней на тригонометрической окружности с последующим отбором с учетом имеющихся ограничений

cos x a, a 1, c; d
На окружности
1. Решить уравнение.
2. Обвести дугу,
соответствующую данному
отрезку на окружности.
3. Разделить виды решений для
синуса и косинуса.
4. Нанести решения уравнения
на окружность.
5. Выбрать решения, попавшие
на обведенную дугу.
x arccos a 2 k , k Z
x arccos a 2 k , k Z
y
arccos a
d
а
0
-arccos a
c
x

36. Геометрический способ Изображение корней на графике с последующим отбором с учетом имеющихся ограничений

На графике
1. Решить уравнение.
2. Построить график
данной функции, прямую у
= а, на оси х отметить
данный отрезок.
3. Найти точки
пересечения графиков.
4. Выбрать решения,
принадлежащие данному
отрезку.
sin x a, a 1, c; d
x arcsin a 2 k , k Z
x arcsin a 2 k , k Z
y
y=a
a
с
arcsin a
П-arcsin a
d
y = sin x
x
Пример: Найти все корни уравнения
10 cos 2 (
2
которые удовлетворяют условию x [
Решение.
10sin2 x = – cos 2x + 3;
10sin2 x = 2sin2 x – 1 + 3,
8sin2 x = 2;
1
sin 2 x ;
4
1
sin x ;
2
k
x
(
1
)
k , k Z ,
6
x ( 1) m ( ) m, m Z ;
6
6
n, n Z ;
7
2 x) 3,
2
2 19
;
].
3 12
y
2
5
6
6
0
7
6
С помощью числовой окружности получим:
x
x) sin(
x
3
2
6
Выберем корни, удовлетворяющие условию задачи.
Из первой серии: 2 n 19 , n Z ;
3
6
12
8 2 12 n 19 , n Z ;
10 12n 17, n Z .
Следовательно n=0 или n=1, то есть x ,
6
x 7 .
6
2
19
n
,n Z;
3
6
12
8 2 12 n 19 , n Z ;
Из второй серии:
6 12n 21, n Z .
Следовательно n=0 или n=1, то есть
x 6 ,
x 5 .
6
Ответ : {
5 7
;
6 6
;
6
}.

39. Спасибо за внимание!

L/O/G/O

Однородные тригонометрические уравнения

Тригонометрическое уравнение называется однородным относительно sin x и cos x , если степени всех членов в уравнении одинаковы. Эта степень называется степенью однородного уравнения.

Например, уравнение вида

\[а\sin x + b\cos x = 0\]

— однородное уравнение первого порядка. Обратите внимание, что в однородном уравнении справа от знака равенства стоит нуль. 92}x = 0.\]

Пример 6

Найдите общее решение уравнения

\[\sin x + \cos x = \frac{1}{{\cos x}}.\]

Пример 1.

Решить уравнение

\[\sin x + \cos x = 0. \]

Раствор.

Разделим обе части уравнения на \(\cos x.\) Это можно сделать, потому что \(\cos x \ne 0.\) Действительно, косинус и синус в левой части не могут быть одновременно равны нулю , поэтому \(\cos x = 0\) не является решением уравнения. 92} — 4 \cdot 5 \cdot \left( { — 3} \right) = 64, \Rightarrow {t_{1,2}} = \frac{{ — 2 \pm \sqrt {64} }}{{ 10}} = — 1,\frac{2}{5}.\]

Получаем два семейства растворов:

\[\tan x = {t_1} = — 1, \Rightarrow {x_1} = \arctan \left( { — 1} \right) + \pi n = — \frac{\pi }{4} + \pi n,\,n \in \mathbb{Z};\]

\[\tan x = {t_2} = \frac{2}{5}, \Rightarrow {x_2} = \arctan \frac{2}{5} + \pi k,\,k \in \mathbb{Z }.\]

Ответ:

\[{x_1} = — \frac{\pi }{4} + \pi n,{x_2} = \arctan \frac{2}{5} + \pi k,\;n,k \in \mathbb {Z}.\] 92}x = {t_2} = \frac{1}{3}, \Rightarrow \tan x = \pm \frac{1}{{\sqrt 3 }}, \Rightarrow x = \arctan \left( { \pm \frac{1}{{\sqrt 3 }}} \right) + \pi n = \pm \frac{\pi }{6} + \pi n,\,n \in \mathbb{Z}. \]

Пример 6.

Найдите общее решение уравнения

\[\sin x + \cos x = \frac{1}{{\cos x}}.\]

Раствор.

Заметим, что область определения уравнения определяется условием \(\cos x \ne 0.\) Перепишем правую часть уравнения: 92}х = 0.\]

Фактор левой стороны:

\[\sin x\left( {\cos x — \sin x} \right) = 0.\]

Первый набор решений дается

\[\sin x = 0, \Rightarrow {x_1} = \pi n,\,n \in \mathbb{Z}.\]

Другой набор решений следует из однородного уравнения первого порядка:

\[\cos x — \sin x = 0, \Rightarrow 1 — \tan x = 0, \Rightarrow \tan x = 1, \Rightarrow {x_2} = \frac{\pi }{4} + \pi k ,\,k \in \mathbb{Z}.\]

Следовательно, общее решение дается выражением

\[{x_1} = \pi n,\;{x_2} = \frac{\pi }{4} + \pi k,\;n,k \in \mathbb{Z}.\]

Решение тригонометрических уравнений (градусы) — IntoMath

Тригонометрическое уравнение s — это уравнения, которые позволяют нам определить взаимосвязь между входом и выходом тригонометрических функций, а также решить для определенного значения или значений входа, которые дают желаемый результат.

Триггерные уравнения могут быть линейными и квадратичными. Иногда нам также может понадобиться использовать тригонометрические тождества для решения тригонометрических уравнений.

Когда мы изменяем период функции, это влияет на то, сколько решений уравнение имеет на определенном интервале и какие типы решений.

Если периодическая функция не представляет конкретную ситуацию, связанную с величинами, отличными от углов и тригонометрических отношений, мы решаем тригонометрические уравнения для определения мер всех возможных углов, которые дают определенное тригонометрическое отношение.

Некоторые тригонометрические уравнения можно решить, рассматривая специальные треугольники, поскольку тригонометрические отношения в этих уравнениях задаются как точные тригонометрические отношения углов в 30, 60 или 45 градусов, а также углов, которые падают на оси.

Также полезно хорошо понимать и работать с единичным кругом при решении тригонометрических уравнений, а также знать принцип, лежащий в основе правила CAST, которое определяет знак определенного коэффициента триггера внутри единичного круга. Диаграмма ниже поясняет этот процесс.

1. Определите, является ли заданное тригонометрическое уравнение линейным или квадратным
2. Проверьте, выражается ли уравнение в виде одного тригонометрического отношения, в противном случае используйте тригонометрические тождества, чтобы выразить его в терминах одного тригонометрического отношения
3. Если уравнение представляет собой линейное тригонометрическое уравнение, определите, задано ли отношение в точной форме и соответствует ли оно тригонометрическим отношениям одного из специальных углов или углов на осях. Если это так, используйте специальный треугольник и правило CAST для определения решений.
4. Если уравнение представляет собой линейное тригонометрическое уравнение, а тригонометрическое отношение не соответствует ни одному из специальных углов, используйте калькулятор, чтобы определить обратное отношение. Определите обратную сторону положительного отношения, чтобы получить связанный острый угол, если данное отношение отрицательно, а затем используйте правило CAST для поиска решений.

   No related posts.