Sinx cosx формула: Такой страницы нет на нашем сайте.

alexxlab / / Разное

Содержание

Курс высшей математики, Т.1

Курс высшей математики, Т.1
  

В.И.Смирнов Курс высшей математики, Т.1.: Изд-во «Наука». 1974. — 479 с.

Фундаментальный учебник по высшей математике, выдержавший более двадцати изданий, переведенный на множество языков мира, отличается, с одной стороны, систематичностью и строгостью изложения, а с другой – простым языком, подробными пояснениями и многочисленными примерами. Книга состоит из пяти томов. Тома третий и четвертый – каждый из двух частей.

Для студентов университетов и технических вузов.



Оглавление

ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
1. Величина и ее измерение.
2. Число.

3. Величины постоянные и переменные.
4. Промежуток.
5. Понятие о функции.
6. Аналитический способ задания функциональной зависимости.
7. Неявные функции.
8. Табличный способ.
9. Графический способ изображения чисел.
10. Координаты.
11. График и уравнение кривой.
12. Линейная функция.
13. Приращение. Основное свойство линейной функции.
14. График равномерного движения.
15. Эмпирические формулы.
16. Парабола второй степени.
17. Парабола третьей степени.
18. Закон обратной пропорциональности.
19. Степенная функция.
20. Обратные функции.
21. Многозначность функции.
22. Показательная и логарифмическая функции.
23. Тригонометрические функции.
24. Обратные тригонометрические, или круговые, функции.
§ 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
25. Упорядоченное переменное.
26. Величины бесконечно малые.
27. Предел переменной величины.
28. Основные теоремы.
29. Величины бесконечно большие.

30. Монотонные переменные.
31. Признак Коши существования предела.
32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
33. Примеры.
34. Непрерывность функции.
35. Свойства непрерывных функций.
36. Сравнение бесконечно малых и бесконечно больших величин.
37. Примеры.
38. Число е.
39. Недоказанные предложения.
40. Вещественные числа.
41. Действия над вещественными числами.
42. Точные границы числовых множеств. Признаки существования предела.
43. Свойства непрерывных функций.
44. Непрерывность элементарных функций.
ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
45. Понятие о производной.
46. Геометрическое значение производной.
47. Производные простейших функций.
48. Производные сложных и обратных функций.
49. Таблица производных и примеры.
50. Понятие о дифференциале.
51. Некоторые дифференциальные уравнения.
52. Оценка погрешностей.
§ 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
53. Производные высших порядков.
54. Механическое значение второй производной.
55. Дифференциалы высших порядков.
56. Разности функций.
§ 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
57. Признаки возрастания и убывания функций.
58. Максимумы и минимумы функций.
59. Построение графиков.
60. Наибольшее и наименьшее значения функций.
61. Теорема Ферма.
62. Теорема Ролля.
63. Формула Лагранжа.
64. Формула Коши.
65. Раскрытие неопределенностей.
66. Различные виды неопределенностей.
§ 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
68. Частные производные и полный дифференциал функции двух независимых переменных.
69. Производные сложных и неявных функций.
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
70. Дифференциал дуги.
71. Выпуклость, вогнутость и кривизна.
72. Асимптоты.
73. Построение графиков.
74. Параметрическое задание кривой.
75. Уравнение Ван-дер-Ваальса.
76. Особые точки кривых.
77. Элементы кривой.
78. Цепная линия.
79. Циклоида.
80. Эпициклоиды и гипоциклоиды.
81. Развертка круга.
82. Кривые в полярных координатах.
83. Спирали.
85. Овалы Кассини и лемниската.
ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
86. Понятие о неопределенном интеграле.
87. Определенный интеграл как предел суммы.
88. Связь определенного и неопределенного интегралов.
89. Свойства неопределенного интеграла.
90. Таблица простейших интегралов.
91. Правило интегрирования по частям.
92. Правило замены переменных. Примеры.
93. Примеры дифференциальных уравнений первого порядка.
§ 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
94. Основные свойства определенного интеграла.
95. Теорема о среднем.
96. Существование первообразной функции.
97. Разрыв подынтегральной функции.
98. Бесконечные пределы.
99. Замена переменной под знаком определенного интеграла.
100. Интегрирование по частям.
§ 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
101. Вычисление площадей.
102. Площадь сектора.
103. Длина дуги.
104. Вычисление объемов тел по их поперечным сечениям.
105. Объем тела вращения.
106. Поверхность тела вращения.
107. Определение центров тяжести. Теоремы Гульдина.
108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
109. Формула касательных и формула Понселе.
110. Формула Симпсона.
111. Вычисление определенного интеграла с переменным верхним пределом.
112. Графические способы.
113. Площади быстро колеблющихся кривых.
§ 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
115. Разбиение промежутка на части и образование различных сумм.
116. Интегрируемые функции.
117. Свойства интегрируемых функций.
ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
118. Понятие о бесконечном ряде.
119. Основные свойства бесконечных рядов.
120. Ряды с положительными членами. Признаки сходимости.
121. Признаки Коши и Даламбера.
122. Интегральный признак сходимости Коши.
123. Знакопеременные ряды.
124. Абсолютно сходящиеся ряды.
125. Общий признак сходимости.
§ 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
126. Формула Тейлора.
127. Различные виды формулы Тейлора.
128. Ряды Тейлора и Маклорена.
129. Разложение exp(x).
130. Разложение sin x и cos x.
131. Бином Ньютона.
132. Разложение log(1+x).
133. Разложение arctg x.
134. Приближенные формулы.
135. Максимумы, минимумы и точки перегиба.
136. Раскрытие неопределенностей.
§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
137. Свойства абсолютно сходящихся рядов.
138. Умножение абсолютно сходящихся рядов.
139. Признак Куммера.
140. Признак Гаусса.
141. Гипергеометрический ряд.
142. Двойные ряды.
143. Ряды с переменными членами. Равномерно сходящиеся ряды.
144. Равномерно сходящиеся последовательности функций.
145. Свойства равномерно сходящихся последовательностей.
146. Свойства равномерно сходящихся рядов.
147. Признаки равномерной сходимости.
148. Степенные ряды. Радиус сходимости.
149. Вторая теорема Абеля.
150. Дифференцирование и интегрирование степенного ряда.
ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
152. О предельном переходе.
153. Частные производные и полный дифференциал первого порядка.
154. Однородные функции.
155. Частные производные высших порядков.
156. Дифференциалы высших порядков.
157. Неявные функции.
158. Пример.
159. Существование неявных функций.
160. Кривые в пространстве и поверхности.
§ 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
162. Необходимые условия максимума и минимума функции.
163. Исследование максимума и минимума функции двух независимых переменных.
164. Примеры.
165. Дополнительные замечания о нахождении максимумов и минимумов функции.

166. Наибольшее и наименьшее значения функции.
167. Относительные максимумы и минимумы.
168. Дополнительные замечания.
169. Примеры.
ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
170. Комплексные числа.
171. Сложение и вычитание комплексных чисел.
172. Умножение комплексных чисел.
173. Деление комплексных чисел.
174. Возвышение в степень.
175. Извлечение корня.
176. Показательная функция.
177. Тригонометрические и гиперболические функции.
178. Цепная линия.
179. Логарифмирование.
180. Синусоидальные величины и векторные диаграммы.
181. Примеры.
182. Кривые в комплексной форме.
183. Представление гармонического колебания в комплексной форме.
§ 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
185. Разложение многочлена на множители.
186. Кратные корни.
187. Правило Горнера.
188. Общий наибольший делитель.
189. Вещественные многочлены.
190. Зависимость между корнями уравнения и его коэффициентами.
191. Уравнение третьей степени.
192. Решение кубического уравнения в тригонометрической форме.
193. Способ итерации.
194. Способ Ньютона.
195. Способ простого интерполирования.
§ 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
196. Разложение рациональной дроби на простейшие.
197. Интегрирование рациональной дроби.
198. Интеграл от выражений, содержащих радикалы.
199. Интегралы вида…
200. Интегралы вида…
201. Интегралы вида…

Вывод производной sin(x) и cos(x) — Лисья нора

Главная » Математика » Вывод производной sin(x) и cos(x)

§

Производная sin(x)

По формуле нахождения производной:

sin'(x) = \lim_{\Delta x \to 0} \frac{sin(x + \Delta x) — sin(x)}{\Delta x}

На самом деле, здесь используется формула разности синусов:

sin(a) — sin(b) = 2sin\frac{a-b}{2}cos\frac{a+b}{2}

В данном случае,

a = x + \Delta x

и

b = x

, необходимо подставить выражение:

  • Первое \frac{a-b}{2} = \frac{x + \Delta x — x}{2} = \frac{\Delta x}{2}
  • Второе \frac{a+b}{2} = \frac{x + \Delta x + x}{2} = \frac{2x + \Delta x}{2} = x + \frac{\Delta x}{2}

Если подставить эти вычисленные выражения, то получится так:

sin(x + \Delta x) — sin(x) = 2sin\frac{\Delta x}{2}cos(x+\frac{\Delta x}{2})

Теперь надо перенести в формулу для поиска производной

\lim_{\Delta x \to 0} \frac{2sin\frac{\Delta x}{2}cos(x+\frac{\Delta x}{2})}{\Delta x}

Есть один нюанс. Дело в том, что можно сделать так, чтобы верхняя 2 перенеслась под

{\Delta x}

внизу и получится следующее:

\lim_{\Delta x \to 0} \frac{sin\frac{\Delta x}{2}}{\frac{\Delta x}{2}}cos(x+\frac{\Delta x}{2})

Можно заметить первый замечательный предел с синусом, который будет равен 1, а значит, остается только лишь один косинус:

sin'(x) = \lim_{\Delta x \to 0} cos(x+\frac{\Delta x}{2}) = cos(x)

Поскольку лимит здесь стремится к 0, потому дельта x обнуляется. Вот, собственно и всё.

§

Производная косинуса

Как и в предыдущем параграфе, необходимо найти решение лимита для получения производной:

cos'(x) = \lim_{\Delta x \to 0} \frac{cos(x + \Delta x) — cos(x)}{\Delta x}

Но вместо разности синусов нужно подставить разность косинусов:

cos(a) — cos(b) = -2sin\frac{a+b}{2}sin\frac{a-b}{2}

Добавим вычисленные ранее суммы углов в эту формулу и получим следующее:

cos(a) — cos(b) = -2sin (x + \frac{\Delta x}{2}) sin (\frac{\Delta x}{2})

Теперь впишем, как и ранее, в формулу с лимитом, и, как в прошлый раз, перенесем 2 под

\Delta x

.

cos'(x) = \lim_{\Delta x \to 0} -2sin (x + \frac{\Delta x}{2}) \frac{ sin (\frac{\Delta x}{2})}{\Delta x} = \lim_{\Delta x \to 0} -sin (x + \frac{\Delta x}{2}) \frac{ sin (\frac{\Delta x}{2})}{\frac{\Delta x}{2}}

Здесь отлично видно первый замечательный предел с синусом, который стремится к 1, то есть, его можно убрать из формулы, а дельту заменить на ноль:

cos'(x) = \lim_{\Delta x \to 0} -sin (x + \frac{\Delta x}{2}) = -sin(x)

Таким образом, доказано, что производная от косинуса равна минус синус от икс.

Мяу.

30 янв, 2022

© 2007-2023 Правда в том, что мышь кусает конем

Тригонометрические тождества и формулы

Ниже приведены некоторые из наиболее важных определений, тождеств и формул в тригонометрии.

  1. Тригонометрические функции острых углов

    sin X = opp / hyp = a / c , csc X = hyp / opp = c / a
    tan X = opp/adj = a/b, cot X = adj/opp = b/a
    cos X = прил / hyp = b / c , сек X = hyp / прил = c / b ,

  2. Тригонометрические функции произвольных углов

    грех X = b / r , csc X = r / b
    загар X = b/a, раскладушка X = a/b
    cos X = a/r, сек X = r/a

  3. Специальные треугольники

    С помощью специальных треугольников можно найти тригонометрические функции особых углов: 30, 45 и 60 градусов.

  4. Законы синусов и косинусов в треугольниках

    В любом треугольнике имеем:
    1 — Закон синусов
    грех А / а = грех В / б = грех С / с
    2 — Законы косинусов
    а 2 = b 2 + c 2 — 2 b c cos A
    b 2 = a 2 + c 2 — 2 a c cos B
    c 2 = a 2 + b 2 — 2 a b cos C

  5. Отношения между тригонометрическими функциями

    cscX = 1/sinX
    sinX = 1/cscX
    секХ = 1/cosX
    cosX = 1/секX
    tanX = 1 / cotX
    cotX = 1 / tanX
    tanX = sinX / cosX
    cotX = cosX / sinX

  6. Пифагорейские тождества

    sin 2 X + cos 2 X = 1
    1 + тангенс 2 X = сек 2 X
    1 + детская кроватка 2 X = csc 2 X

  7. Тождества с отрицательным углом

    sin(-X) = — sinX , нечетная функция
    csc(-X) = — cscX , нечетная функция
    cos(-X) = cosX , четная функция
    sec(-X) = secX , четная функция
    tan(-X) = — tanX , нечетная функция
    cot(-X) = — cotX , нечетная функция

  8. Кофункции Идентичности

    грех (π/2 — X) = cosX
    cos(π/2 — X) = sinX
    тангенс(π/2 — X) = cotX
    раскладушка(π/2 — X) = tanX
    сек(π/2 — X) = cscX
    csc(π/2 — X) = secX

  9. Формулы сложения

    cos(X + Y) = cosX уютный — sinX sinY
    cos(X — Y) = cosX cosy + sinX sinY
    sin(X + Y) = sinX cosy + cosX sinY
    sin(X — Y) = sinX уютный — cosX sinY
    tan(X + Y) = [ tanX + tanY ] / [ 1 — tanX tanY]
    tan(X — Y) = [ tanX — tanY ] / [ 1 + tanX tanY]
    раскладушка (X + Y) = [ раскладушка X раскладушка Y — 1 ] / [ раскладушка X + раскладушка Y]
    раскладушка(X — Y) = [ раскладушкаX раскладушка Y + 1 ] / [раскладушкаY — раскладушкаX]

  10. Суммировать формулы произведения

    cosX + уют = 2cos[ (X + Y) / 2 ] cos[ (X — Y) / 2 ]
    sinX + sinY = 2sin[ (X + Y) / 2 ] cos[ (X — Y) / 2 ]

  11. Отличие от формул продукта

    cosX — уютный = — 2sin[ (X + Y) / 2 ] sin[ (X — Y) / 2 ]
    sinX — sinY = 2cos[ (X + Y) / 2 ] sin[ (X — Y) / 2 ]

  12. Формулы произведения для суммы/разности

    cosX уютный = (1/2) [ cos (X — Y) + cos (X + Y) ]
    sinX cosy = (1/2) [ sin (X + Y) + sin (X — Y) ]
    cosX sinY = (1/2) [ sin (X + Y) — sin [ (X — Y) ]
    sinX sinY = (1/2) [ cos (X — Y) — cos (X + Y) ]

  13. Формулы разности квадратов

    sin 2 X — sin 2 Y = sin(X + Y)sin(X — Y)
    cos 2 X — cos 2 Y = — sin(X + Y)sin(X — Y)
    cos 2 X — sin 2 Y = cos(X + Y)cos(X — Y)

  14. Формулы двойного угла

    sin(2X) = 2 sinX cosX
    cos(2X) = 1 — 2sin 2 X = 2cos 2 X — 1
    загар(2X) = 2загарX / [ 1 — загар 2 X ]

  15. Формулы множественных углов

    sin(3X) = 3sinX — 4sin 3 X
    cos(3X) = 4cos 3 X — 3cosX
    sin(4X) = 4sinXcosX — 8sin 3 XcosX
    cos(4X) = 8cos 4 X — 8cos 2 X + 1

  16. Формулы половинного угла

    sin (X/2) = + или — √ ((1 — cosX) / 2)
    cos (X/2) = + или — √ ((1 + cosX) / 2)
    тангенс (X/2) = + или — √ ((1 — cosX) / (1 + cosX))
    = sinX / (1 + cosX) = (1 — cosX) / sinX

  17. Формулы для снижения мощности

    sin 2 X = 1/2 — (1/2)cos(2X))
    cos 2 X = 1/2 + (1/2) cos(2X))
    sin 3 X = (3/4)sinX — (1/4)sin(3X)
    cos 3 X = (3/4)cosX + (1/4)cos(3X)
    sin 4 X = (3/8) — (1/2)cos(2X) + (1/8)cos(4X)
    cos 4 X = (3/8) + (1/2) cos(2X) + (1/8)cos(4X)
    sin 5 X = (5/8)sinX — (5/16)sin(3X) + (1/16)sin(5X)
    cos 5 X = (5/8)cosX + (5/16)cos(3X) + (1/16)cos(5X)
    sin 6 X = 5/16 — (15/32)cos(2X) + (6/32)cos(4X) — (1/32)cos(6X)
    cos 6 X = 5/16 + (15/32) cos(2X) + (6/32)cos(4X) + (1/32)cos(6X)

  18. Периодичность тригонометрических функций

    sin (X + 2π) = sin X , период 2π
    cos (X + 2π) = cos X , период 2π
    сек (X + 2π) = сек X , период 2π
    csc (X + 2π) = csc X , период 2π
    тангенс (X + π) = тангенс X , период π
    раскладушка (X + π) = раскладушка X , период π
  19. Тригонометрические таблицы.
  20. Свойства шести тригонометрических функций. График, домен, диапазон, асимптоты (если есть), симметрия, точки пересечения x и y, а также точки максимума и минимума каждой из 6 тригонометрических функций.

Дополнительные ссылки по тригонометрии

Тригонометрия.
Решение задач по тригонометрии .
Бесплатные вопросы по тригонометрии с ответами.

сообщите об этом объявлении

Sin 2x — Формула, вывод, тождества, примеры

Формула Sin2x является одной из очень немногих важных формул тригонометрии, используемых для решения различных математических задач. Это одна из различных формул двойного угла, используемых в тригонометрии. Эта формула используется для нахождения синуса угла с двойным значением. Грех входит в число основных тригонометрических соотношений, которые определяются отношением перпендикуляра к гипотенузе в прямоугольном треугольнике. Диапазон sin2x равен [-1, 1].

Коэффициент синуса рассчитывается путем вычисления отношения длины противоположной стороны угла к длине гипотенузы. Обозначается аббревиатурой sin .

 

Если θ — угол между основанием и гипотенузой прямоугольного треугольника, то

sin θ = Перпендикуляр/Гипотенуза

Что такое Sin 2 раза?

Sin2x — это формула, используемая в тригонометрии для решения различных математических и других задач. Это помогает упростить различные тригонометрические выражения, включающие двойные углы. Sin2x выражается в различных формах с использованием различных тригонометрических функций. Самая распространенная формула sin2x: sin2x = 2 sinx cosx .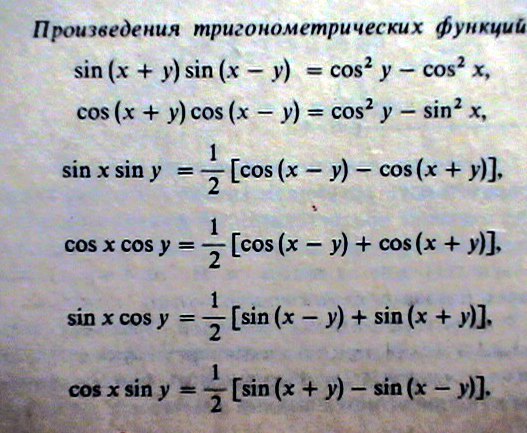 Его также можно выразить через функцию тангенса.

Sin2x Формула

Sin 2x — тождество двойного угла в тригонометрии. Поскольку функция sin является обратной величиной функции косеканса, в качестве альтернативы ее можно записать как sin2x = 1/cosec 2x. Это важное тригонометрическое тождество, которое можно использовать для решения широкого круга задач тригонометрии и интегрирования. Значение sin 2x повторяется через каждые π радиан, то есть sin 2x = sin (2x + π). Он имеет гораздо более узкий график, чем sin x. Это тригонометрическая функция, которая вычисляет функцию греха двойного угла. Наряду с этим для решения математических задач используются различные другие тригонометрические соотношения.

sin 2x = 2 sin x cos x

Sin 2x Формула вывода

Формулу для sin 2x можно получить, используя формулу суммы углов для функции синуса.

Используя тригонометрические тождества, sin (x + y) = sin x cos y + cos x sin y

Чтобы найти синус двойного угла, мы должны положить x = y

Полагая x = y, мы получаем,

sin (x + x) = sin x cos x + cos x sin x

sin 2x = sin x cos x + sin x cos x

sin 2x = 2 sin x cos x

Отсюда выводится формула для двойного угла отношения синуса.

Формула Sin2x в терминах тангенса

sin 2x также может быть выражена в терминах функции тангенса. Давайте посмотрим, как Sin 2x выражается через тангенс x

sin 2x = 2 sin x cos x

Умножив и разделив его на cos x.

sin 2x = (2 sin x cos 2 x)/(cos x)

         = 2 (sin x/cosx ) × (cos 2 x)               {sin x/cos x = тангенс х и соз х = 1/(сек х)}

sin 2x = 2 tan x × (1/сек 2 x)                       {sec 2 x = 1 + tan 2 x}

sin 2x = (2tan x)​/(1 + tan 2 x)

Таким образом, формула sin  2x для тангенса такова: sin 2x = (2tan x)​/(1 + tan 2 x).

Формула Sin2x в терминах функции cos

sin 2x также может быть выражена в терминах функции cos. Давайте посмотрим, как Sin 2x выражается через cos x

sin 2x = 2 sin x cos x …(1)

мы знаем, что sin x = √(1 – cos 2 x), используя это в уравнении (1)

sin 2x = 2 √(1 – cos 2 x) × cos x 9000 4

Это необходимая формула для Sin 2x через Cos x.

Sin2x Формула в терминах Sin

sin 2x также может быть выражена в терминах функции sin. Давайте посмотрим, как Sin 2x выражается через sin x

sin 2x = 2 sin x cos x …(1)

мы знаем, что cos x = √(1 – sin 2 x), используя это в уравнении (1). .

Sin

2 x

Sin 2 x формулы используются для решения сложных математических задач, они также используются для упрощения тригонометрических тождеств. Две формулы для sin 2 x можно вывести, используя теорему Пифагора и формулы двойного угла функции косинуса.

Sin

2 x Формула

Для вывода формулы sin 2 x мы используем тригонометрические тождества sin 2 x + cos 2 x = 1 и формулу двойного угла функции косинуса потому что 2x = 1 – 2 sin 2 х. Используя эти тождества, sin 2 x можно выразить через cos 2 x и cos2x. Выведем формулы:

Sin

2 x Формула в терминах Cos x

Мы знаем, что, используя тригонометрические тождества,

sin 2 x + cos 2 x = 1 используя уравнение и переводя cos 2 x в левую часть, которая меняет знак, мы получаем,

sin 2 х = 1 – cos 2 x

Sin

2 x Формула в терминах Cos 2x

Мы знаем, что, используя формулу двойного угла,

cos 2x = 1 – 2sin 2 x с помощью уравнения и разделения sin 2 х в одну сторону получаем,

sin 2 x = (1 – cos 2x) / 2

Следовательно, две основные формулы sin 2 x таковы:

sin 2 x = 1 – cos 2 x

sin 2 x = (1 – cos 2x) / 2

Важные формулы sin 2x = (2tan x)​/(1 + tan 2 x)

Другие формулы

sin 2 x = 1 – cos 2 x 
sin 2 x = (1 – cos2x)/2

Решенные примеры для Sin 2 x Формула

Пример 1. Если sin x = 3/5, найдите значение sin 2x по формуле.

Решение:

Итак, sin x = 3/5.

Ясно, что cos x = 4/5.

Используя полученную формулу,

sin 2x = 2 sin x cos x

= 2 (3/5) (4/5)

= 24/25

Пример 2. Если cos x = 12/13, найдите значение sin 2x по формуле.

Решение:

Имеем cos x = 12/13.

Очевидно, sin x = 5/13.

Используя полученную формулу,

sin 2x = 2 sin x cos x

= 2 (5/13) (12/13)

= 120/169

Пример 3. Если tan х = 12 /5, найдите значение sin 2x по формуле.

Решение:

Имеем тангенс х = 12/5.

Используя полученную формулу,

sin2x = (2tan x)​/(1 + tan 2 x). Пример 4. Если cosec x = 17/8, найдите значение sin 2x используя формулу.

Решение:

Имеем cosec x = 17/8.

Очевидно, что sin x = 8/17 и cos x = 15/17.

Используя формулу получаем,

sin 2x = 2 sin x cos x

= 2 (8/17) (15/17)

= 240/289

Пример 5. Если cot x = 15/8, найти значение sin 2x по формуле.

Решение:

Имеем, cot x = 15/8

tan x = 1 / cot x = 1 / (15/8) 

        = 8 / 15

Используя полученную формулу,

sin2x = (2tan x)​/(1 + tan 2 x).

         = 2 × (18/15) / {1 + (18/15) 2 }

        = 240/289

Пример 6. Если cosec x = 13/12, найдите значение sin 2x по формуле.

Решение:

Имеем cosec x = 13/12.

Очевидно, sin x = 12/13 и cos x = 5/13 (используя теорему Пифагора)

Используя формулу, получаем /13)

         = 120/169

Пример 7. Если sec x = 5/3, найдите значение sin 2x по формуле.

Решение:

Имеем, сек х = 5/3.

Ясно, что cos x = 3/5 и sin x = 4/5 (используя теорему Пифагора)

Используя формулу, получаем /5)

          = 24/25

Часто задаваемые вопросы

по формуле Sin 2x

Вопрос 1: В чем отличие Sin 2x?

Ответ:

Дифференциация sin 2x равна 2cos 2x

Вопрос 2: Что такое интеграция Sin2x?

Ответ: 

Интегрирование sin 2x равно (-cos 2x)/2

Вопрос 3. Что представляет собой формула Sin 2x с точки зрения функции тангенса?

Ответ:

Формула Sin 2x с точки зрения функции тангенса: sin2x = (2tan x)​/(1 + tan 2 x).

Вопрос 4: Напишите формулу для тангенса 2x.

Ответ:

Формулы, используемые для tan 2x:

  • tan2x = sin 2x/cos 2x

    • Вопрос 5: Напишите формулу для cos 2x.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *