Sinx cosx решить уравнение: Решите уравнение cos(x)=sin(x) (косинус от (х) равно синус от (х))

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28 Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

решить уравнение корень из 3 умножить на sinx — cosx=1 — Учеба и наука

Ответы

Михаил Александров
15. 09.15

Ответ понравился автору вопроса

✔Олеся / Математика

от 100 p.
Читать ответы

Elena

от 50 p.
Читать ответы

Андрей Андреевич

от 70 p.
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Нужно решить ребус: КА 3,048 дм бол

начерти отрезок длиной 10 см и разделите его штрихами на 5 равных частей . Напишите над одним концом отрезка число 0 , а над другим число 10 . Напишите числа над каждым штрихом шкалы.

1.Периметр прямоугольника 24 см. Одна сторона этого прямоугольника на 2 см больше, чем другая. Найти длину сторон прямоугольника.

На экскурсию поехало детей 4 раза больше чем взрослых. Сколько детей поехало на экскурсию если взрослых на 6 человек меньше чем детей //…

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.

Пользуйтесь нашим приложением

Методы решения тригонометрических уравнений — презентация онлайн

МЕТОДЫ РЕШЕНИЯ
ТРИГОНОМЕТРИЧЕСКИХ
УРАВНЕНИЙ
1. Какие методы решения тригонометрических уравнений вы знаете?
2. Определите и ответьте, какими методами нужно решать данные
тригонометрические уравнения?
а) sin 2x – cos x = 0
б) 2sin²x — 5sinx = -3
в) cos²x – sin²x = sinx – cosx
г) sin2 x – 3sinx cosx + 2cos²x = 0
3. Решите простейшие тригонометрические уравнения:
Некоторые типы тригонометрических уравнений.
1. Уравнения, сводящиеся к квадратным,
относительно
cos х = t, sin х = t.
A sin2 x + B cosx + C = 0
A cos2 x + В sinx + C = 0
Решаются методом введения новой переменной.
2.Однородные уравнения первой и второй степени.
I степени.
II степени.
A sinx + B cosx = 0
: cosx
A tg x + B = 0
A sin2 x + B sinx cosx + A cos2 x = 0
A tg2 x + B tgx + C = 0
: cos2x
Решаются методом разложения на множители и методом
введения новой переменной.
3. Уравнение вида:
А sinx + B cosx = C.
А, В, С 0
Применимы все методы.
4. Понижение степени.
2
А cos2x + В cos x = C.
A cos2x + B sin 2 x = C.
Решаются методом разложения на множители.
A sin2x + B sin 2 x = C.
2
A sin2x + B cos x = C.
2
2
sin
x
cos
x).
Сводятся к однородным уравнениям С = С(
Формулы.
Универсальная подстановка.
x
2tg
2 ;
sinx
x
1 tg 2
2
x
1 — tg
2;
cosx
x
1 tg 2
2
2
x
2 ;
tgx
x
1 tg 2
2
2tg
х + 2 n;
Проверка
обязательна!
Понижение степени.
cos 2 x = (1 + cos2x ) : 2
sin 2 x = (1 – cos 2x) : 2
Метод вспомогательного аргумента.
a cosx +b sinx заменим на C sin(x+ ), где С a 2 b 2 ;
b
а
cos = ; — вспомогательный аргумент.
sin = ;
С
С
Сведение к однородному.
Уравнения вида
Пример. 5 sin2 x +
A sin2x + B sin2 x = C,
Asin2x + Bcos2 x = C.
3 sinx cosx + 6 cos2 x = 5.
Разложение на множители.
Пример.
cos 2 x
— 2 cosx = 4 sinx — sin2x
Проблемы ,возникающие при решении
тригонометрических уравнений
1.Потеря корней:
делим на g(х).
опасные формулы (универсальная подстановка).
Этими операциями мы сужаем область определения.
2. Лишние корни:
возводим в четную степень.
умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область определения.
Уравнение 2 sin x 3 cos x 0 .
Уравнение 2 sin x 3 cos x 0 .
Поделив уравнение на cos x , получим
2tgx 3 0 , tgx
3
3
x
arctg
n, n .
2 ,
2
При решении этой задачи обе части уравнения 2 sin x 3 cos x 0 были
поделены на cos x .
Напомним, что при делении уравнения на выражение, содержащее неизвестное,
могут быть потеряны корни. Поэтому нужно проверить, не являются ли корни
уравнения cos x 0 корнями данного уравнения. Если cos x 0 , то из
уравнения 2 sin x 3 cos x 0 следует, что sin x 0 . Однако sin x и
cos x не могут одновременно равняться нулю, так как они связаны
равенством sin 2 x cos 2 x 1 . Следовательно, при делении
a sin x b cos x 0, где a 0 , b 0 , на cos x (или sin x )
уравнения
получаем уравнение, равносильное данному.
Решить уравнение cos²x + sinx cosx = 0
1) Делить на cosx нельзя, так как в условии не указано , что cosx не
равен нулю. Но можно утверждать, что sinx не равен нулю, так как
в противном случае cosx равен 0, что невозможно , так как sin²xcos²x =1. Значит можно разделить на sin²x.
2) Решим уравнение разложением на множители:
cos²x + sinx cosx = 0,
сosx(cosx + sinx ) = 0,
сosx = 0
x
2
или
n, n ;
cosx + sinx = 0,
tg x=-1,
x
4
k , k ;
Уравнения, линейные относительно sin x и cos x
а sin x + в cos x = с.
Если а=в=0, а с не равно 0, то уравнение теряет смысл;
Если а=в=с=0, то х – любое действительное число, то есть уравнение обращается
в тождество.
Рассмотрим случаи, когда а,в,с не равны 0.
Примеры:
2 sin x cos x 2
3 sin 5x — 4 cos 5x = 2
2 sin 3x + 5 cos 3x = 8.
Последнее уравнение не имеет решений, так как левая часть его не превосходит 7.
Уравнения, этого вида можно решить многими способами: с помощью
универсальной подстановки, выразив sin x и cos x через tgх ; сведением уравнения
к однородному; введением вспомогательного аргумента и другими.
Решение этих уравнений существует при a 2 b 2 c 2
2 sin x cos x 2
Данное уравнение является уравнением
вида a sin x b cos x c ,
(1)
где a 0 , b 0 , c 0 , которое можно решить другим способом.
Разделим обе части этого уравнения на a 2 b 2 :
a
a2 b
sin x
2
a
a2 b
Введем вспомогательный аргумент
cos
a
a2 b
c
cos x
2
a 2 b 2.
, такой, что
(2)
b
, sin
2
a 2 b 2.
Такое число существует, так как
2
2
a
b
2
1.
2
2
2
a b a b
Таким образом, уравнение можно записать в виде
sin x cos cos x sin
sin( x )
c
a b
c
2
a2 b2
2
,
.
Последнее уравнение является простейшим тригонометрическим уравнением.
Уравнение
2 sin
x
cos
x
2
.
x
x
x — sin2 x и
2
2
2
2
x
x
2
правую часть уравнения в виде 2 2 1 2(sin
cos 2 ,)
2
2
Используя формулы sin x = 2 sin
записывая
cos
, cos x = cos2
x
x
x
x
x
x
cos cos 2 sin 2 2 sin 2 2 cos 2 ,
2
2
2
2
2
2
x
x
x
x
x
3 sin2 4 sin cos cos2 0. Поделив это уравнение на cos 2 ,
2
2
2
2
2
x
2 x
4tg 1 0.
получим равносильное уравнение 3tg
2
2
x
1 .
Обозначая tg y , получаем 3 y 2 4 y 1 0 , откуда y1 1, y2
2
3
x 1 x
1
1
tg , arctg n, x 2arctg 2 n, n .
1)
2 3 2
3
3
x
x
2)
tg 1, n, x 2 n, n ;
2
2 4
2
получаем 4 sin
Ответ:
x
2
2 n, n ; x 2arctg 1 2 n, n .
3

13. Решить уравнение

4sin²x – 4sinx – 3 = 0
2cos²x – sinx – 1 = 0

14. Ответы.

4sin²x — 4 sinx – 3 = 0
( -1)n+1 П/6 +Пn, n
Z.
2 сos²x – sin x – 1 = 0
±П/6 +Пn; -П/2+2Пn, n
Z.

15. Решить уравнение

4 sin x 3 cos x 5.
Решить уравнение 4 sin x 3 cos x 5.
Здесь a 4, b 3, c 5, a 2 b2 5
Поделим обе части уравнения на 5:
4
3
sin x cos x 1.
5
5
4
Введем вспомогательный аргумент , такой, что cos ,
Исходное уравнение можно записать в виде
5
3
sin .
5
sin x cos cos x sin
, 1
sin( x ) , 1
4
4
откуда x 2 n, где arccos , x arccos 2 n, n Z
2
5
2
5
Ответ:
x
4
arccos 2 n, n .
2
5
6
=30°
sin x
1
2
cos x
3
2
3
3
tg x
ctg x
3
4
=45°
2
2
2
2
3
= 60°
3
2
1
2
1
3
1
3
3
А
0°
2
= 90°
=180°
3
2
=270°
2
=360°
sin x
0
1
0
-1
0
cos x
1
0
-1
0
1
tg x
0
—
0
—
0
ctg x
—
0
—
0
—

3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт. 92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 92+n-72)=1/(n+9)

тригонометрия — Когда $\sin(x) = \cos(x)$?

Спросил

Изменено 6 лет, 1 месяц назад

Просмотрено 4k раз

$\begingroup$

Как решить следующее уравнение?

$$\cos(x) — \sin(x) = 0$$

Мне нужно найти минимум и максимум этой функции: 92}$$

Я продифференцировал его, и чтобы найти стационарные точки, мне нужно положить числитель равным нулю. Но я не могу найти способ решить это тригонометрическое уравнение.

  • тригонометрия

$\endgroup$

2

$\begingroup$

Вот альтернативная подсказка с более геометрическим привкусом: каковы углы в равнобедренном прямоугольном треугольнике?

$\endgroup$

909\круг) $$

$\endgroup$

7

$\begingroup$

Прямой подход: используйте определение синуса и косинуса в виде единичной окружности.

Рассмотрим единичную окружность вокруг начала декартовой плоскости. Поскольку в этой задаче $x$ уже используется как угол, мы не можем пометить две оси $x$ и $y$ как обычно, поэтому давайте пометим их Вместо этого $u$ (по горизонтальной оси) и $v$ (по вертикальной оси). Тогда определение единичного круга говорит, что если мы возьмем точку под углом $x$ радиан против часовой стрелки по единичной окружности, координаты в этот момент будет \начать{выравнивать} и &= \cos х, \\ v &= \sin х. \end{выравнивание}

Уравнение $\cos x = \sin x$ тогда говорит нам, что $u = v$, которое представляет собой уравнение линии при $\frac\pi4$ радианах ($45$ градусах) через происхождение. Но мы получили эти координаты в первую очередь как координаты точки на единичной окружности, поэтому решение должно находиться в точке, где прямая $u = v$ пересекает единичную окружность. Нарисуйте график, как на рисунке ниже: таких точек две.

Координаты этих точек оказались $ \ влево (\ гидроразрыва {\ sqrt2} {2}, \ гидроразрыва {\ sqrt2} {2} \ вправо) $ и $\left(-\frac{\sqrt2}{2},-\frac{\sqrt2}{2}\right)$, но даже не разбираясь в этом, так как ты знаешь угол линии $u=v$ вы можете легко увидеть два возможных значения $x$ в диапазоне от $0$ до $2\pi$ радиан (от $0$ до $360$ градусов). 92 x = 1$

Итак, $\cos x = \sin x = \pm \sqrt{\frac 12}$

2) $\sin x$ — прилежащая сторона прямоугольного треугольника. $\cos x $ — обратная сторона. $\sin x = \cos x$ означает, что треугольник равнобедренный. Значит, углы при основании равны. Таким образом, $x + x + 90 = 180 $.

3) $\sin x = \cos (\frac {\pi}2 -x)$

поэтому $\cos x = \sin x = \cos (\frac {\pi}2-x)$

Теперь ты можешь это понять?

Есть некоторые проблемы с квадрантами, которые нужно решить, но они несложные.

$\endgroup$

0

$\begingroup$

Если у вас есть уравнение вида $$ \cos f(x)=\sin g(x) $$ вы можете переписать его как $$ \ cos f (x) = \ cos \ left (\ frac {\ pi} {2} -g (x) \ right) $$ так что $$ f(x)=\frac{\pi}{2}-g(x)+2k\pi \qquad\text{или}\qquad f(x)=-\frac{\pi}{2}+g(x)+2k\pi $$

В вашем конкретном случае $f(x)=g(x)=x$, так что у вас есть $$ х = \ гидроразрыва {\ пи} {2} — х + 2k \ пи \qquad\text{или}\qquad х = — \ гидроразрыва {\ пи} {2} + х + 2k \ пи $$ Конечно, вторая возможность не дает решения; первый случай дает $$ х = \ гидроразрыва {\ пи} {4} + к \ пи $$ 9{2it}=\frac{1+i}{1-i}=i$$ $$\cos2t+i\sin2t=i$$ $$\подразумевает\cos 2t=0 \text{ }\cap \sin2t=1$$ $$x=\frac{\pi}4+n\pi,n\in\Bbb{N}$$

$\endgroup$

$\begingroup$

$cos(x)=sin(x) \подразумевает x = \pi n-\frac{3\pi}{4}$, где n — целое число.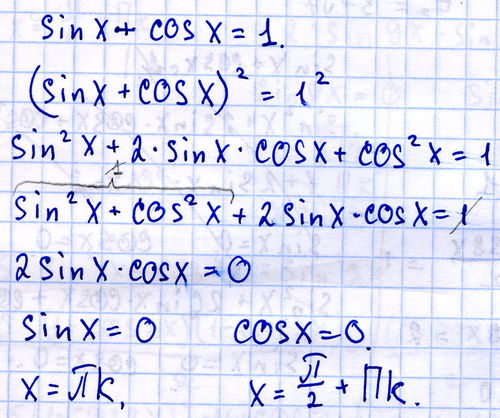

$\endgroup$

1

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

алгебраическое предварительное исчисление — Решение следующего тригонометрического уравнения: $\sin x + \cos x = \frac{1}{3} $

Задавать вопрос

Спросил

Изменено 6 лет, 6 месяцев назад 92 x -\dfrac{1}{3}\cos x -\dfrac{4}{9} = 0}$$

Могу ли я просто заменить $\cos x$ на $z$ и решить, как если бы это было простое уравнение второй степени, а затем получить $x$, взяв арккосинус? Я пытался сделать это, но я не могу получить правильный результат. Если я это сделаю, то получу следующие результаты:

$$ z_1 = -0,520517 \longrightarrow x_1 = 121,4º\\ z_2= 0,8538509 \longrightarrow x_2 = 31,37º$$

Я получаю $x$ из $z$, взяв арккосинус.

Правильный результат должен быть около 329º что соответствует 4,165 рад. Мой вопрос заключается в том, неправильно ли то, что я делаю, потому что я пытался несколько раз и получаю один и тот же результат (или, в худшем случае, я совершал одну и ту же ошибку несколько раз).

  • алгебра-предварительное исчисление
  • тригонометрия
  • квадратика

$\endgroup$

12

$\begingroup$

Подсказка: я думаю, что подход @JanEerland поучителен. Вот некоторые мысли, как мы могли бы найти такую ​​​​замену.

При взгляде на \начать{выравнивать*} \sin x+\cos x=\frac{1}{3} \конец{выравнивание*} и мы думаем о тригонометрических формулах сложения мы знаем, что \начать{выравнивать*} \sin(x+a)=\sin x \cos a+\cos x\sin a \конец{выравнивание*} Было бы удобно, если бы $\cos a=\sin a$, чтобы можно было их разделить. Это так, если $a=\frac{\pi}{4}$ и мы получаем \начать{выравнивать*} \sin\left(x+\frac{\pi}{4}\right) &=\sin x\sin \frac{\pi}{4}+\cos x\cos \frac{\pi}{4}\\ &=\frac{\sqrt{2}}{2}\left(\sin x+\cos x\right) \конец{выравнивание*} Следует \начать{выравнивать*} \sin x+\cos x&=\frac{1}{3}\\ \ sin \ left (x + \ frac {\ pi} {4} \ right) & = \ frac {1} {3 \ sqrt {2}} \end{выравнивание*}

$\endgroup$

0

$\begingroup$

$$\cos(x)+\sin(x)=\frac{1}{3}\Longleftrightarrow$$

Использование:

$$\cos(x)+\sin(x)=\ sqrt {2} \ left [\ frac {\ cos (x)} {\ sqrt {2}} + \ frac {\ sin (x)} {\ sqrt {2}} \ right] = $ $ $$\sqrt{2}\left(\sin\left(\frac{\pi}{4}\right)\cos(x)+\cos\left(\frac{\pi}{4}\right) \sin(x)\right)=\sqrt{2}\sin\left(\frac{\pi}{4}+x\right)$$

$$\sqrt{2}\sin\left( \ frac {\ pi} {4} + x \ right) = \ frac {1} {3} \ Longleftrightarrow $ $ $$\sin\left(\frac{\pi}{4}+x\right)=\frac{1}{3\sqrt{2}}$$

Теперь, когда мы возьмем арксинус обеих сторон, мы получим два варианта: $n_1\space\wedge\space n_2\in\mathbb{Z}$:

  • $$\frac{\pi}{ 4}+x=\pi-\arcsin\left(\frac{1}{3\sqrt{2}}\right)+2\pi n_1\Longleftrightarrow x=\frac{3\pi}{4}-\ arcsin\left(\frac{1}{3\sqrt{2}}\right)+2\pi n_1$$
  • $$\frac{\pi}{4}+x=\arcsin\left(\frac{1}{3\sqrt{2}}\right)+2\pi n_1\Longleftrightarrow x=\arcsin\left( \frac{1}{3\sqrt{2}}\right)+2\pi n_2-\frac{\pi}{4}$$

$\endgroup$ 9{-1}\left(\frac{1}{10} \left(9+\sqrt{161}\right)\right)\right)$$

$\endgroup$

2

$\begingroup$

Другие предложили другие правильные методы решения уравнения.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *