Сколькими способами можно рассадить 7 мужчин и 7 женщин за круглым столом: 9.Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие…

Содержание

Kat&Pop — Склад — ВМШ — 2 семестр

Kat&Pop — Склад — ВМШ — 2 семестр — Занятие 4.

Kat&Pop — Рефераты — Программа ВМШ — семестр 2, занятие 4.

Занятие четвертое
. (8.10.2000г.)
Комбинаторика
(
правило произведения) Пусть имеется два множества предметов, в одном из них А предметов, а в другом В предметов. Образуем пары предметов: один из них берем из первого множества, а второй — из второго. Тогда число таких пар равно А´ В.

Из города Лисса в город Гель-Гью можно проехать только через Зурбаган. Из Лисса в Зурбаган ведет 5 дорог, из Зурбагана в Гель-Гью 3 дороги. Сколько путей ведет из Лисса в Гель-Гью?
Вася собрал 15 васильков и 10 маргариток и решил подарить их двум девочкам — Марго и Рите. Сколькими способами он может разделить свои цветы на два букета, если хочет, чтобы у каждой девочки было хотя бы по одному васильку и не менее двух маргариток?

Осел, Козел, Мартышка и Косолапый Мишка затеяли играть квартет. Дело не пошло, и звери решили усесться на тех же четырех местах по-другому. Сколькими способами можно это сделать? А если каждый из зверей не хочет сидеть на том месте, на котором уже сидел? Сколькими способами можно расположить на 5 пеньках 5 зверей? А на шести пеньках 6? А на семи пеньках 6 зверей

Семь девушек водят хоровод. Сколькими способами они могут встать вкруг?

если способы, отличающиеся поворотом на одну, две, три… девушек не различаются? если важно только то, какие у девушки соседки?

В классе 25 учеников. Учитель решил назначить двух дежурных. Сколькими способами он может это сделать? А трех дежурных?

Сколькими способами можно рассадить 5 животных на 7

местах? n животных на (n+2) местах? 7 животных на 11 местах?

Имеется 5 одинаковых с виду замков и 5 похожих ключей

. Сколько попыток надо сделать, чтобы установить, какой замок открывается каким ключом.

Та же задача,

но замков 7, а ключей 10.

Та же задача, но среди замков два абсолютно одинаковые (и ключи к ним одинаковые).

В городе Лиссе автобусные номера записывают четырьмя цифрами: от 0000 до

9999. Автобус называется счастливым, если сумма первых двух цифр его номера равна сумме последних двух цифр его номера. Сколько в городе Лиссе счастливых автобусов с суммой первых двух цифр 7? Сколько всего в Лиссе счастливых автобусов?

Сколькими способами можно прочитать слово АВРАКАДАБРА по таблице:

Сколькими способами можно разбить 10 человек на пары? А 2
n человек? Домашняя работа по теме Комбинаторика (все задачи по 12 баллов):

Штирлиц хочет послать телеграмму из
n слов. Всего в секретном языке m слов. Сколько вариантов телеграмм он может составить?
В оркестре
«Незадачливых зверей» n участников. Вначале они сидели на m пеньках (некоторые пеньки были пустые), теперь они хотят пересесть по-другому, потому что считают, что так станут лучше играть. Сколькими способами они могут пересесть?
В классе
n человек. Надо выбрать для дежурства m человек. Сколькими способами это можно сделать?
(20
баллов) В большой коробке лежат шарики цветов (шарики ничем не отличаются). Для игры Коля хочет взять n шариков и положить их в m коробок. Сколькими способами он может это сделать?
В классе
n учеников. Надо отправить делегацию покупать подарок учителю. Сколькими способами это можно сделать?

Дополнительные задачи по комбинаторике.

Сколькими способами можно посадить 7 мужчин и 7 женщин за круглый стол так, чтобы никакие две женщины не сидели рядом?

Сколько существует перестановок чисел 1, 2, 3,
…n, в которых 1 и 2 не стоят на своих местах?
Сколькими способами можно составить трехцветный флаг, если имеется материал
5 различных цветов? Тот же вопрос, но одна из полос должна быть красная.
На школьном вечере присутствуют 12 юношей и 15 девушек. Сколькими способами можно выбрать из них 4 пары для танца?

Сколько существует счастливых билетов? (Счастливый билет — это такой билет с шестизначным номером, у которого сумма первых трех цифр равна сумме последних трех цифр.
)
Сайт создан в системе uCoz

Ошибка
Перейти к основному содержанию
Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+
)
Извините, не удалось найти запрашиваемый Вами файл
Подробнее об этой ошибке
Перейти на… Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ). Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра. Линейные операции над векторами»Лекционный материал по теме «Скалярное, векторное и смешанное произведения векторов»Примеры решения задач по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Скалярное, векторное и смешанное произведения векторов»ВЕКТОРНАЯ АЛГЕБРАВекторная алгебра и аналитическая геометрияПрезентация по теме «Векторная алгебра»Векторная алгебра.
Аналитическая геометрияТеоретический материал по теме «Метод координат на плоскости и в пространстве»Лекционный материал по теме «Прямая на плоскости»Лекционный материал по теме «Кривые второго порядка»Лекционный материал по теме «Прямая в пространстве»Лекционный материал по теме «Плоскость в пространстве»Лекционный материал по теме «Поверхности второго порядка»Примеры решения задач по теме «Прямая на плоскости»Примеры решения задач по теме «Кривые второго порядка»Примеры решения задач по темам «Прямая и плоскость в пространстве»АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВекторная алгебра и аналитическая геометрияСправочный материал «Прямая на плоскости»Справочный материал «Кривые второго порядка»Справочный материал «Прямая и плоскость в пространстве»Линейная алгебра для экономистовПрезентация по теме «Прямая на плоскости»Презентация по теме «Уравнения плоскости и прямой в пространстве»▶ Виртуальный тренажер «Прямая на плоскости» 👨‍🎓Введение в анализНачала анализаЛекционный материал по теме «Множества, функции, основные характеристики функций.

Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨‍🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления.
Правила Лопиталя»Лекционный материал по теме «Формулы Тейлора и Маклорена»Лекционный материал по теме «Приложения дифференциального исчисления»Примеры решения задач по теме «Дифференциальное исчисление функций одной переменной»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙТест «Основные правила и формулы дифференцирования»Тест «Дифференциальное исчисление функций одной переменной»Основы дифференцирования. Часть 1Основы дифференцирования. Часть 2Основы дифференцирования. Часть 3Приложения производной Исследование функций, Примеры решения задачПрименение производных при решении экономических задачИнтегральное исчисление функции одной переменнойЛекционный материал по теме «Неопределенный интеграл»Лекционный материал по теме «Определенный интеграл»Практическое занятие 1. Непосредственное интегрирование (неопределённый интеграл)Практическое занятие 2. Интегрирование заменой переменной (неопределённый интеграл)Практическое занятие 3. Интегрирование по частям. Интегрирование выражений, содержащих квадратный многочлен (неопределённый интеграл)Практическое занятие 4.
Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1. Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий. Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности.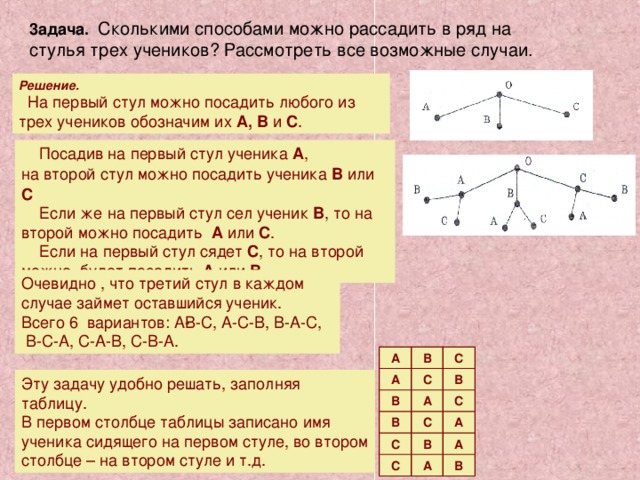 Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика». Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа. Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)
5.3. Перестановки — математика для специалистов в области общественного здравоохранения и гигиены труда
В предыдущем примере нас попросили найти последовательности слов, образованные с использованием букв { A , B , C }, если ни одна буква не должна повторяться. Древовидная диаграмма дала нам следующие шесть расположений:
ABC , ACB , BAC , BCA , CAB и CBA
Подобные расположения, в которых важен порядок и ни один элемент не повторяется, называются перестановками.

Перестановки : Перестановка набора элементов представляет собой упорядоченное расположение, в котором каждый элемент используется один раз.

Сколько последовательностей слов из трех букв можно составить, используя буквы { A , B , C , D }?
Решение
Есть четыре варианта первой буквы слова, три варианта второй буквы и два варианта третьей.
Применяя аксиому умножения, мы получаем 4 · 3 · 2 = 24 различных расположения.

Сколько перестановок букв слова СТАТЬЯ имеют согласные на первой и последней позициях?
Решение
В слове СТАТЬЯ 4 согласных. Так как первая буква должна быть согласной, у нас есть четыре варианта для первой позиции, и как только мы используем согласную, остается только три согласных для последней позиции. Мы показываем следующим образом:
Поскольку ограничений больше нет, мы можем продолжить и сделать выбор для остальных позиций. Пока мы израсходовали 2 буквы, поэтому осталось пять. Таким образом, для следующей позиции есть пять вариантов, для позиции после нее — четыре варианта и так далее. Получаем:
4 5 4 3 2 1 3
Таким образом, общее количество перестановок равно 4 · 5 · 4 · 3 · 2 · 1 · 3 = 1440.

Даны пять букв { A , B , C , D , E }. Найдите следующее:
а. Количество последовательностей слов из четырех букв.
б. Количество последовательностей слов из трех букв.
в. Количество последовательностей двухбуквенных слов.
Решение
Задача легко решается с помощью аксиомы умножения, и ответы следующие:
а. Число последовательностей слов из четырех букв равно 5 · 4 · 3 · 2 = 120.
b. Число последовательностей слов из трех букв равно 5 · 4 · 3 = 60.
c. Количество двухбуквенных последовательностей слов равно 5 · 4 = 20.
Мы часто сталкиваемся с ситуациями, когда у нас есть набор из n объектов, и мы выбираем r объектов для формирования перестановок. Мы называем это перестановками n объектов взяты r за раз , и мы записываем это как n Pr .
Следовательно, на этот пример также можно ответить, как указано ниже:
a. Количество последовательностей слов из четырех букв равно 5 P 4 = 120.
b. Количество последовательностей слов из трех букв равно 5 P 3 = 60.
c. Количество двухбуквенных последовательностей слов равно 5 P 2 = 20.

Прежде чем мы дадим формулу для n P r , мы хотели бы ввести символ, который мы будем часто использовать в этой, а также в следующей главе.

Факториал : n ! = n ( n − 1)( n − 2)( n − 3)··· 3 · 2 · 1.
Где n — натуральное число.
0! = 1

Теперь определим n P r .

Количество перестановки N объектов, взятых R за время :
N P R = N ( N — 1) ( N –2) ( N — 1) ( N –2) ( N — 1) − 3)···( n − r +1), или
n P r =
Где n и r — натуральные числа 90,004.

Читатель должен ознакомиться с обеими формулами и чувствовать себя комфортно при их применении.

Вычислите следующее, используя обе формулы.
а. 6П3
б. 7P2
Решение
Мы идентифицируем n и r в каждом случае и решим, используя предоставленные формулы.
а. 6 P 3 = 6 · 5 · 4 = 120, попеременно 6 P 3 = = = = 120
б. 7 P 2 = 7 · 6 = 42 или 7 P 2 = = = 42

Далее мы рассмотрим еще несколько задач перестановки, чтобы лучше понять эти концепции.

Сколькими способами можно рассадить четырех человек по прямой линии, если двое из них настаивают на том, чтобы сидеть рядом друг с другом?
Решение
Предположим, у нас есть четыре человека A , B , C и D . Далее предположим, что A и B хотят сесть вместе. Ради аргумента мы связываем A и B вместе и относимся к ним как к одному человеку. Четыре человека CD . Поскольку рассматривается как одно лицо, у нас есть следующие возможные схемы:
CD , DC , CD , DC , CD , DC
Обратите внимание, что существует еще шесть таких перестановок, потому что A и B также могут быть связаны в заказ ВА . И они таковы:
CD , DC , CD D , DC C , CD , DC
Итак, всего существует 12 различных перестановок.
Давайте теперь решим задачу, используя аксиому умножения.
После того, как мы свяжем двух людей вместе и будем обращаться с ними как с одним человеком, мы можем сказать, что у нас есть только три человека. Аксиома умножения говорит нам, что три человека могут сидеть на 3! способы. Так как два человека могут быть связаны вместе 2! способов, есть 3!2! = 12 различных аранжировок.

У вас есть 4 книги по математике и 5 книг по истории, которые нужно поставить на полку с 5 ячейками. Сколькими способами можно расставить книги по полкам, если первые три ячейки заняты учебниками по математике, а следующие две — учебниками по истории?
Решение
Сначала решим задачу, используя аксиому умножения.
Так как учебники по математике помещаются в первые три слота, есть 4 варианта для первого слота, 3 для второго и 2 для третьего. Четвертый слот требует книги по истории и имеет пять вариантов. Как только этот выбор сделан, остается 4 книги по истории и, следовательно, 4 варианта для последнего слота. Возможные варианты показаны ниже:
4 3 2 5 4
Таким образом, количество перестановок равно 4 · 3 · 2 · 5 · 4 = 480. С другой стороны, мы можем видеть, что 4 · 3 · 2 действительно то же самое, что и 4 P 3, а 5 · 4 равно 5 P 2. Таким образом, ответ можно записать как (4 P 3) (5 P 2) = 480.

Очевидно, в этом есть смысл. Для каждой перестановки трех учебников по математике, размещенных в первых трех слотах, есть 5 P 2 перестановок учебников по истории, которые можно поместить в два последних слота. Следовательно, применима аксиома умножения, и мы имеем ответ (4 P 3) (5 P 2). Подводим итоги.
Перестановки : Перестановка набора элементов представляет собой упорядоченное расположение, в котором каждый элемент используется один раз.
Факториал : n ! = n ( n − 1)( n − 2)( n − 3)···3 · 2 · 1. Где n – натуральное число. 0! = 1
Перестановки n Объектов, взятых r одновременно 9или n P r = . Где n и r — натуральные числа.

В этом разделе мы рассмотрим следующие две проблемы.
Сколькими способами можно рассадить пять человек в круг?
Сколькими способами можно расставить буквы в слове МИССИСИППИ?
Первая задача относится к категории Циклические перестановки , а вторая — к Перестановки с похожими элементами .

Круговые перестановки
Предположим, у нас есть три человека с именами A , B и C . Мы уже определили, что их можно рассадить по прямой за 3! или 6 способов. Наша следующая задача — посмотреть, сколькими способами этих людей можно рассадить в круг. Рисуем схему:
Получается, что есть только два способа посадить троих в круг. Такая перестановка называется круговой перестановкой. В таких случаях, где бы ни сидел первый человек, перестановка не затрагивается. Каждый человек может перемещаться сколько угодно мест, и перестановка не изменится. Представьте себе людей на карусели; вращение перестановки не порождает новую перестановку. Таким образом, в круговых перестановках первый человек считается заполнителем, и где он сидит, не имеет значения.

Круговые перестановки : Количество перестановок n элементов в круге равно ( n − 1)!

Сколькими способами можно рассадить пять человек за круглым столом?
Решение
Мы уже определили, что первое лицо является просто заполнителем. Таким образом, есть только один выбор для первого места. У нас есть:
1 4 3 2 1
Итак, ответ 24.

Сколькими способами можно рассадить четыре пары за круглым столом, если мужчины и женщины хотят сесть попеременно?
Решение
Еще раз подчеркнем, что первый человек может сидеть где угодно, не влияя на перестановку. Таким образом, есть только один выбор для первого места. Предположим, первым сел мужчина. Стул рядом с ним должен принадлежать женщине, и есть 4 варианта. Следующий стул принадлежит мужчине, так что есть три варианта и так далее. Мы перечисляем варианты ниже.
1 4 3 3 2 2 1 1
Итак, ответ 144.

Теперь решаем вторую проблему.

Перестановки с аналогичными элементами
Определим количество различимых перестановок букв ЭЛЕМЕНТ.
Предположим, мы сделали все буквы разными, пометив их следующим образом.
E ₁ LE ₂ ME ₃ NT
Поскольку все буквы теперь другие, их 7! разные перестановки.
Давайте теперь посмотрим на одну такую перестановку, скажем:
LE ₁ ME ₂ NE ₃ T
Предположим, мы формируем новые перестановки из этого расположения, перемещая только буквы Е. Ясно, что их 3! или 6 таких аранжировок. Мы перечисляем их ниже:
LE ₁ ME ₂ NE ₃ T
LE ₁ ME ₃ NE ₂ T
LE ₂ ME ₁ NE ₃ T
LE ₃ ME ₃ NE ₁ T
LE ₃ ME ₂ NE ₁ T
LE ₃ ME ₁ NE ₂ T
Поскольку буквы Е не отличаются друг от друга, существует только одна аранжировка LEMENET, а не шесть. Это справедливо для любой перестановки.
Допустим, имеется n различных перестановок букв ЭЛЕМЕНТ. Тогда есть п · 3! перестановки букв E ₁ LE ₂ ME ₃ NT. Но мы знаем, что их 7! перестановки букв E ₁ LE ₂ ME ₃ NT. Следовательно: n · 3! = 7!
или n = .
Это дает нам метод, который мы ищем.

Перестановки с подобными элементами :
Количество перестановок n элементов n за один раз, с r ₁ элементов одного вида, r ₂ элементов другого вида и т. д. составляет

Найдите количество различных перестановок букв в слове МИССИСИППИ.
Решение
В слове МИССИСИППИ 11 букв. Если бы все буквы были другими, их было бы 11! разные перестановки. Но в МИССИССИПИ есть 4 одинаковых S, 4 I и 2 P.
Итак, ответ
Что равно 34 650.

Если монету подбросить шесть раз, сколько будет различных исходов, состоящих из 4 орлов и 2 решек?
Решение
Опять же, у нас есть перестановки с похожими элементами. Ищем перестановки для букв HHHHTT.
Ответ .

Сколькими способами можно расположить в ряд 4 пятицентовика, 3 десятицентовика и 2 четвертака?
Решение
Предполагая, что все пятицентовые монеты одинаковы, все десятицентовики аналогичны и все четвертак аналогичны, мы имеем перестановки с одинаковыми элементами. Следовательно, ответ:
.

Биржевой маклер хочет назначить 20 новых клиентов поровну 4 своим продавцам. Сколькими различными способами это можно сделать?
Решение
Это означает, что каждый продавец получает 5 клиентов. Эту проблему можно рассматривать как проблему упорядоченных разделов. В этом случае по формуле получаем:

Подводим итоги:
Круговые перестановки : Количество перестановок n элементов в круге равно ( n − 1)!
Перестановки с подобными элементами : Количество перестановок n элементов, взятых n одновременно, с r ₁ элементами одного вида, r _{8 элементами другого вида, таким образом, 2 _{8 элементов другого вида на, что n = r ₁ + r ₂ +···+ r _k is}}
Также называется упорядоченными разделами .

1. Группа из 15 человек, состоящих в волонтерском клубе, желает выбрать стул и секретаря. Сколькими различными способами это можно сделать?
2. Сколько перестановок букв слова БЕЗОПАСНОСТЬ оканчивается на согласную?
3. Сколькими способами можно рассадить пять человек в ряд, если двое из них настаивают на том, чтобы сидеть рядом друг с другом?
4. Сколькими способами можно поставить на полку 3 книги по английскому языку, 3 книги по истории и 2 книги по математике, если книги по английскому языку стоят слева, по истории посередине, а по математике справа?
5. Найдите количество различных перестановок букв в слове MASSACHUSETTS.
6. Если команда сыграет 10 игр, сколько различных исходов из 6 побед и 4 поражений возможно?
7. Вы и шесть других одноклассников решили сделать групповое селфи:
а. Сколько различных вариантов возможно?
б. Сколько различных аранжировок возможно, если вы настаиваете на том, чтобы быть в центре фотографии?
г. Сколько различных вариантов расположения возможно, если один из ваших друзей настаивает на том, чтобы быть справа от фотографии, а два других друга настаивают на том, чтобы стоять рядом друг с другом?

Количество способов, которыми 7 человек могут сесть за круглый стол так, чтобы у каждого человека не было одних и тех же соседей в любых двух расстановках, равно: A. 360Б. 720С. 700Д. 300
Last updated date: 03rd Feb 2023
•
Total views: 241.2k
•
Views today: 7.33k
Answer
Verified
241.2k+ views
Hint : The above question требует понимания круговых перестановок, это количество способов рассадить n человек за круглым столом, т. е. по кругу. Круговую перестановку можно выполнить двумя способами: по часовой стрелке и против часовой стрелки.
Полный пошаговый ответ :
Так как в этом вопросе мы должны расположить людей в круг, а 7 человек должны быть расположены в кругу, чтобы у каждого человека не было одного и того же соседа.
Мы знаем, что места за круглым столом не нумеруются и нет различия между первым и последним местом, требуется только изменение взаимных позиций. Поэтому мы фиксируем одного человека из семи на одну позицию, а затем расставляем оставшиеся (n-1) лиц в $ (n — 1)! $, где значение n равно 7:
$
   \Стрелка вправо (7 — 1)! = 6! \\
   \Стрелка вправо 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720 \;
$
В приведенной выше круговой перестановке мы различали вращение по часовой стрелке и против часовой стрелки, где у каждого человека один и тот же сосед, но нам это не нужно, нас попросили организовать так, чтобы ни у одного человека не было одного и того же соседа, что можно сделать как:
$
  \dfrac{{(n — 1)!}}{2} = \dfrac{{6!}}{2} \\
   \Стрелка вправо \dfrac{{720}}{2} = 360 \ ;
$
Таким образом, существует 360 $ способов сделать вышеописанное, и, следовательно, правильный вариант — A.
No related posts.