Решительно уравнение:
( x( в степени 4))(в степени 32): x( в степени 43): ( x( в степени 5))(в степени 17)(дробь )* x=201
Прошу решите(умоляю(
…
Математика
Литература
Алгебра
Русский язык
Геометрия
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мирГеография
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Сколько будет «а» умножить на «а»?
? Previous Entry | Next EntryУ одной моей знакомой, руководителя среднего звена на технологически сложном предприятии, есть тест, который она использует при приеме на работу, в том числе ИТР.
Она спрашивает у соискателя рабочего места: «Сколько будет «а» умножить на «а»?» Как вы думаете, что чаще всего отвечают соискатели?
Самый распространенный ответ: а × а = 2а (два «а»).
Попадаются и экзотические ответы, вроде: а × а = а (корень квадратный из «а»).
Конечно, иногда дают и правильный ответ: а × а = а² («а» в квадрате). Но это совсем не массовое явление. Примечательно, что ответ «2а» дают не только двоечники после средней школы, но и люди, имеющие на руках диплом о высшем экономическом, педагогическом и даже техническом образовании.
Общим местом уже стали «перлы» школьников, вроде того что
В чем причина такого положения дел? На мой взгляд, главная причина состоит в том, что, когда в стремлении утвердить в нашей стране западные ценности отечественная правящая элита и поддерживавшая ее часть населения прилагали все усилия, чтобы поскорее разрушить советскую систему ценностей, одной из первых была уничтожена ценность хорошего образования.
В среде так называемых «новых русских» и у стремившихся им подражать обывателей твердо возобладала точка зрения известной госпожи Простаковой из фонвизинского «Недоросля», что при наличии извозчика географию учить совсем необязательно. Кино, телевидение, глянцевые журналы активно тиражировали для подражания такие образы, в которых образованности и уму места совсем не оставалось. Эта ценностная катастрофа усугубилась широким распространением в отечественном образовании различных «платных услуг», а также заимствованием на Западе далеко не самых передовых образцов педагогической науки, «Болонской системы» для высшего образования и системы ЕГЭ для средней школы.
В результате кризис отечественного образования сегодня достиг такой глубины, что похохатывать и ерничать уже не время – пора принимать решительные меры. Слова о чрезвычайной остроте этой проблемы звучали и на последнем заседании Совета по науке и образованию при президенте РФ.
Но прежде чем предпринимать какие-либо шаги, необходимо получить исчерпывающее представление о том, что думает наше общество о проблемах образования, какой оно желает видеть эту сферу.
В последнем выпуске программы «Смысл игры», который представлен в начале этого поста, подробно рассказывается о целях данного социологического исследования. На сайте http://eot.su/node/18939 есть инструкция и анкета для опроса. Прошу каждого, кому не безразлично будущее нашей страны и наших детей, принять участие в опросе. Это наша страна и наши дети. Кроме нас самих, позаботиться о них некому…
| April 2021 | ||||||
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | |
- takoe_nebo : (no subject) [+7]
- livejournal : (no subject) [+0]
- olom1980 : (no subject) [+0]
- livejournal : What is Love? Ночной расчувственности пост [+0]
Powered by LiveJournal.
com
Функции умножения — Криста Кинг Математика
Как умножить две функции вместе
Вы можете перемножить функции, чтобы получить произведение функций. Есть два способа умножения функций.
Вы можете либо ввести значение для ???x??? в каждую функцию, а затем перемножить выходные данные вместе, или вы можете перемножить функции вместе, а затем ввести значение для ???x??? и упростить. Запишем произведение двух функций ???f(x)??? и ???г(х)??? как
???(f\cdot g)(x)=f(x)\cdot g(x)???
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Пример умножения функций и вычисления произведения в определенной точке
Пример
Найти ???fg(-4)??? если ???f(x)=x+2??? и ???g(x)=x-5???.
Нам нужно найти ???(fg)(-4)???, которое можно переписать как ???(f)(-4)\cdot g(-4)???.
Итак, мы можем подключить ???x=-4??? в каждую функцию, а затем умножить результаты вместе.
Сначала найдем ???f(-4)???.
???f(-4)=-4+2???
???f(-4)=-2???
Теперь найдем ???g(-4)???.
???г(-4)=-4-5???
???г(-4)=-9???
Затем произведение ???(fg)(-4)???
???(fg)(-4)=f(-4)\cdot g(-4)???
???(fg)(-4)=-2\cdot-9???
???(fg)(-4)=18???
Мы также могли бы перемножить функции вместе, а затем подставить ???x=-4??? найти ответ.
???(fg)(x)=(x+2)(x-5)??? 92-3(-4)-10???
???(fg)(-4)=16+12-10???
???(fg)(-4)=16+2???
???(fg)(-4)=18???
Видео пример нахождения произведения функций
Пройти курс
Хотите узнать больше об Алгебре 1? У меня есть пошаговый курс для этого. 🙂
Учить больше
Давайте рассмотрим еще один пример, где мы находим произведение функций 92-2х-48???
Если у вас есть несколько функций, вы можете использовать несколько простых правил, чтобы найти их сумму, разность, произведение или частное.
Как вы могли догадаться, найти произведение функций так же просто, как перемножить функции вместе. Когда вы перемножаете две функции вместе, в результате вы получите третью функцию, и эта третья функция будет произведением двух исходных функций.
Например, если вы умножите f(x) и g(x), их произведение будет равно h(x)=fg(x) или h(x)=f(x)g(x). Вы также можете оценить продукт в определенной точке. Итак, если вы хотите узнать значение продукта при x = 2, вы можете подставить x = 2 в функцию произведения h (x), чтобы найти h (2) = fg (2) = f (2) g (2) .
В качестве альтернативы вместо того, чтобы сначала находить функцию произведения, а затем вычислять ее при x=2, можно сначала вычислить f(x) и g(x) при x=2, а затем перемножить эти результаты, чтобы получить произведение h (2).
Получить доступ к полному курсу Алгебра 1
Начать
Учим математикуКриста Кинг Функции умножения, умножение
0 лайковалгебраическое предварительное исчисление. Если возведение числа в квадрат означает умножение этого числа на себя, то не должно ли взятие квадратного корня из числа означать деление числа на себя?
Задавать вопрос
спросил
Изменено 2 года, 6 месяцев назад
Просмотрено 34к раз 92=2 \cdot 2=4 $ .
Но квадратный корень из $2$ не равен $\frac{2}{2}=1$ .
- алгебра-предварительное исчисление
$\endgroup$
22
$\begingroup$
извлечение квадратного корня означает обращение эффекта возведения в квадрат .
Деление числа само по себе этого не делает (а всегда возвращает 1, как вы заметили).
Сравните свой вопрос со следующим: если удвоение числа означает прибавление его к самому себе, то разве деление числа пополам не должно означать его вычитание из самого себя? Ответ: очевидно нет.
$\endgroup$
6
$\begingroup$
Квадрат при объяснении на простом английском языке использует слово «себя». Вот попытка определить обратный процесс, нахождение квадратного корня, используя слово «себя»:
Квадратный корень числа $N$ — это такое число $x$, что при делении $N$ на $x$ оно дает само себя (у меня плохая грамматика, подлежащее и дополнение в этом предложении. Но я надеюсь, вы уловили суть)
Изменить: эта идея, переведенная в уравнение, даст следующее: если $N = 9$, то $x = 3$ и $N/x = 9$?? Я предполагаю, что сам в этом контексте относится к $x$, а не к $N$
$\endgroup$
4
$\begingroup$
Поскольку этот вопрос напрямую связан с некоторыми фундаментальными идеями математики, этот ответ пытается объяснить эти идеи таким же фундаментальным образом.
Возведение числа в квадрат можно рассматривать как процедуру. Конкретная процедура возведения числа в квадрат может использовать шаблон, подобный следующему:
$$ \Box \longrightarrow \Box\times\Box \longrightarrow \Box $$
Мы помещаем «входное» значение, например, $2$, в крайнее левое поле, например:
$$ 2 \longrightarrow \Box\times\Box \longrightarrow \Box $$
Далее делаем копии самого левого блока и помещаем их в два коробки посередине:
$$ 2 \longrightarrow 2 \times 2 \longrightarrow \Box $$
Обратите внимание, что эти два поля должны содержать одинаковое число. Наконец, выполняем указанное умножение и записываем результат в последнем поле справа:
$$ 2 \longrightarrow 2 \times 2 \longrightarrow 4 $$
Чтобы извлечь квадратный корень, мы хотим обратить процедуру, то есть работайте в обратном направлении. Итак, берем «входное» число, например, $9$, и поместите его в поле справа:
$$ \Box \longrightarrow \Box\times\Box \longrightarrow 9$$
Теперь нам нужно решить, что положить в два ящика посередине.
Мы знаем, что нам нужно, чтобы содержимое двух ящиков было одинаковым, и мы знаем, что
что когда мы делаем умножение, результат должен быть $9$.
Предположим, мы предположили, что число в каждой ячейке должно быть $3$. Тогда мы имеем:
$$ \Box \longrightarrow 3\times3 \longrightarrow 9 $$
Мы можем подтвердить, что $3\times3$ действительно дает результат $9$, так что все пока хорошо. Теперь нам просто нужно вывести, какое число было в крайний левый ящик. Мы знаем, что средние поля были заполнены копированием этого поля, поэтому он также должен был содержать $3$. Итак, у нас есть
$$ 3 \longrightarrow 3\times3 \longrightarrow 9 $$
Вот почему квадратный корень из $9$ равен $3$, а не $9/9$. (Ну, это и тот факт, что мы отказываемся класть $-3$ в два ящика в посередине, потому что жизнь становится лучше, когда мы последовательно следуем правилу где говорится, что «квадратный корень» никогда не должен быть отрицательным числом.)
Позже мы можем научиться находить квадратные корни способом,
полагаться так много на удачную догадку.
Но это вопрос
алгоритм для 9{\ гидроразрыва {2} {2}} $.
Даже если ваша задача безразмерна, считайте, что она имеет $d$-единиц» на измерение, умножьте и разделите степени.
Другой вопрос: можно ли представить квадрат с отрицательными сторонами? Потому что его площадь такая же, как у с положительными сторонами. Из $9$ есть два квадратных корня: $-3$ и $3$.
$\endgroup$
4
$\begingroup$
Имя 92-А=0$ .
В этой форме не имеет ничего общего с разделением. На самом деле нам даже не нужно знать, что такое деление, чтобы его сформулировать.
Дополнение: Итак, чтобы явно ответить на вопрос — нет, мы не должны иметь в виду делить число само по себе при извлечении квадратного корня, потому что оно не будет удовлетворять (решать) это уравнение. (за исключением A=1, чтобы быть полностью точным)
$\endgroup$
1
$\begingroup$
Это бесполезная функция, потому что она всегда равна 1 (кроме 0/0).
Кроме того, $2\to4$ противоположно $4\to2$, где вы делите на число, с которого вы начали, а не на 4.
$\endgroup$
1
$\begingroup$
Рассмотрим следующий вопрос, который принадлежит только вам с заменой более простых операций. Тогда вы, надеюсь, поймете.
Если удвоение числа означает прибавление этого числа к самому себе, то разве деление числа пополам не должно означать вычитание числа из самого себя?
И если у вас есть это, вот еще кое-что для размышления. Предположим, ваш начальник предлагает поднять вам жалованье на любой процент, который вам нравится, с единственным условием, что в конце года оно будет снова снижено на тот же процент; какой процент вы бы выбрали? Выделенный вопрос относится к выбору «100%».
$\endgroup$
9n=a.
$
$\endgroup$
$\begingroup$
В вашем вопросе много аналогий:
«Если прибавление числа к самому себе означает умножение его на 2, то почему вычитание числа из самого себя не означает деление его на 2?» и так далее
Проблема, которую вы заметили, вовсе не редкость . Это проблема определения логики, которая выглядит правдоподобной для одного конкретного случая, но не может быть обобщена. Попробуйте:
«Если взять третью степень числа означает умножить это число на себя два раза, то не должен ли корень третьей степени означать (что делать) число само по себе?»
Хотя ваш вопрос кажется логичным, вы не можете распространить его на какую-либо высшую степень.
Вы согласны с тем, что, возведя в квадрат квадратный корень, вам нужно вернуться к исходному числу. Очевидно, что если мы определим это по-вашему, вы этого не сделаете.
Умножение и деление не являются противоположными операциями.
2$ 91$ или $\sqrt[1]{x}$ не являются действительными примерами степенной или корневой функции, поскольку они не содержат их характеристик в каком-либо конкретном смысле.
$\endgroup$
1
$\begingroup$
Вы должны различать обычный язык и технический язык. Для удобства обычный язык смешивается с техническим языком, но вы должны остерегаться того, чтобы обычный язык не вводил вас в заблуждение. В частности, термин «противоположный» в обыденном языке не имеет четкого определения. Например, является ли путешествие по суше противоположным путешествию по морю? или авиаперевозок? Так и в отношении вашего вопроса: деление — не единственная «противоположность» умножению. Рассмотрим распределительное свойство:
а(б + с) = аб + ас. Распределительное свойство, применяемое слева направо, называется умножением, а применяемое справа налево — факторингом.
Таким образом, разложение на множители также является «противоположным» умножению и, как оказалось, тем, что применимо в данном случае, то есть нахождение квадратного корня числа означает нахождение «двух равных множителей» для числа.
Худший (или лучший) пример несоответствия между обычным языком и математическим языком касается делителей 0. Согласно определению делителя, 23 является делителем 0, как и 37. Следовательно, исходя из обычного языка, действительная система счисления имеет делители 0, но, согласно математическому языку, действительная система счисления НЕ имеет делителей 0.
Еще один хороший (плохой) пример несоответствия между обычным языком и техническим языком — разница в значении между формулой для простых процентов и формула для сложных процентов: формула для простых процентов дает вам именно то, что она говорит, но формула для сложных процентов дает вам общую сумму роста (поэтому, чтобы получить сумму сложных процентов, вы должны вычесть главное из него).
Преимущество этого примера разрыва между обычным языком и техническим языком состоит в том, что он не требует знакомства с соображениями теории колец.
Еще одним хорошим (плохим) примером разрыва между обычным языком и техническим языком является тот факт, что наивная реакция на фразу «ошибка, связанная с использованием правила трапеций» такова: «Ну, если ошибка связана с используя правило трапеций, то совершенно очевидно, что мы не должны его использовать».
Еще одним хорошим (плохим) примером разрыва между обычным языком и техническим языком является определение понятия «наибольшего» общего делителя, даже если не определено (или, по крайней мере, не обязательно какое-либо) отношение порядка ( т. е. для области целостности).
$\endgroup$
2
$\begingroup$
Другое объяснение, которого я не вижу в других ответах:
Квадратный корень из числа $N$ ($\mathrm{4}$ в вашем примере) — это число, которое, если возвести в квадрат ($\mathrm{2}$) , получится $N$ ( $\mathrm{4}$) .
Другой способ представления «обратной операции» (как уже отмечали другие) — это операция «что, если». Что касается квадратного корня в вашем примере, вы спрашиваете: «Что, если бы у меня было число, которое при возведении в квадрат равно $\mathrm{4}$? Какой у меня будет номер?» 92$ — это сама квадратная операция. Запросить квадратный корень — это вопрос «какой корень ($R$), если его возвести в квадрат, получится из нашего числа ($N$)?»
$\endgroup$
$\begingroup$
Более конкретный перевод с прозаических языков на математический помогает.
Мне очень нравится этот вопрос, потому что для меня он суммирует общие проблемы преподавания математики.
$\endgroup$
$\begingroup$
Когда вы «возводите в квадрат» число, вы умножаете число само на себя. Но когда вы извлекаете «квадратный корень» из числа, вы, по сути, находите число, которое при «возведении в квадрат» дает число, из которого мы извлекаем «квадратный корень».
Я думаю, что геометрическая аналогия может помочь вам осмыслить. Думайте о «возведении в квадрат» как о нахождении площади квадрата с определенной длиной сторон, в то время как «извлечение квадратного корня» будет относиться к нахождению длины сторон квадрата с определенной площадью.
$\endgroup$
$\begingroup$
Давайте посмотрим, у нас есть:
- квадрат ? хорошо, тогда умножить
- квадратный корень ? хорошо, тогда делим на
Пока все хорошо. Теперь кажется, что умножение происходит на само число. У нас есть:
- квадрат ? хорошо, тогда используйте сам номер
- квадратный корень ? хорошо, тогда используйте …?
Кажется, что в целом операции (например, умножение) и обратные операции (например, деление) являются действительными инверсиями друг друга только при работе с данным повторяющимся значением.
Одно и то же значение должно быть заданным операндом для обеих операций. Следовательно, в этом контексте, где нет такого повторяющегося операнда, обратная связь более недействительна.
$\endgroup$
$\begingroup$
Здесь я использую немного другой подход и скажу просто потому что:
Квадратные корни не так определялись.
Математика полностью построена на определениях. Это не квадратный корень, потому что он по определению не является квадратным корнем.
$\endgroup$
1
$\begingroup$
TL:DR? «Корень» имеет особое значение в математике. Извлечение квадратного корня из числа означает получение «корня» уравнения, в котором число находится с одной стороны от знака «=», а операция возведения в квадрат — с другой.
Во-первых, немного терминологии:
Говоря простым языком, математическое выражение представляет собой оператор, который может представлять одно число. например. (5+6)x2 или (3+n)/(4+n) (где n представляет другое число) и т. д.
В последнем примере выражение содержит переменную n. Мы говорим, что это выражение является « функцией от n», которую мы можем записать как f(n) (или g(n), или h(n), или myfunction(n) и т. д.). В этом примере мы можем написать: f(n) := (3+n)/(4+n) (Обратите внимание, что := означает «определяется как быть».)
Уравнение — это утверждение о равенстве между двумя разными математическими выражениями. например. (5+6)x2 = 22, или (3+n)/(4+n) = 100, или 15-8=n.
Если уравнение содержит одно неизвестное, как в последних двух примерах выше, то должно существовать одно или несколько значений, которые может принимать это неизвестное, чтобы уравнение удовлетворялось (т.
2.
Если мы знаем ответ на это, например. 64, то мы можем написать уравнение: 92 = 64.
«Корнями» этого уравнения являются подходящие значения n. В данном случае 8 и -8.
Итак: КВАДРАТНЫЙ КОРЕНЬ числа X является одним и единственным положительным КОРЕНЬ , n, уравнения, где X равен функции квадрата , примененной к n:
квадрат(n) = X .
(Мы берем положительный корень по соглашению.)
$\endgroup$
$\begingroup$
Рассмотрим эти две функции: 9{-1}$ принимает в качестве входных данных продукты и забирает то, что лежит сверху.
Это очень похоже на инвертирование умножения † на постоянный множитель: вы внесли некоторую модификацию и знаете, что результат имеет некоторую структуру (например, лимон, сидящий сверху), поэтому вы можете легко отменить умножение, а именно путем деления.
Во втором примере все иначе. Здесь лимонный сок уже смешался с напитком к тому времени, когда вы пытаетесь его отнять. Выбрасывать ложку с поверхности напитка явно нехорошо. С квадратным корнем у вас аналогичная проблема: умножая на себя переменное число, вы забываете информацию о том, где именно что-то было умножено. Вы не можете распознать заданную форму ломтика лимона, которую можно было бы снять/разделить.
† Возможно, это больше похоже на сложение и вычитание, чем на умножение и деление. Но эти две пары ведут себя одинаково, несмотря на все, что имеет значение для этого вопроса (математически говоря: они обе образуют группы).
$\endgroup$
2
$\begingroup$
Когда ты квадрат число это цветы …
Как вы знаете, когда вы возводите число в квадрат, оно становится действительно большим, а затем все больше и больше — вы можете думать об этом как о , разветвляющемся на .
И наоборот, когда вы идете «вниз» к корню числа, вы идете вниз «внутрь» его. Он становится все меньше и меньше.
Как вы знаете, умножение и деление на самом деле просто сложение и вычитание. Там нет этой разветвленной силы.
Отбросив мнемонику, кстати, фактический ответ прост:
вот и все.
В данном случае это «решение» «квадрата».
Итак, x 2 = 9, каков «корень» или «решение» этого уравнения.
(Невероятно, что только один ответчик выше указал на это!)
$\endgroup$
2
$\begingroup$
Это то же самое, что сказать, что если умножение числа на 2 означает прибавление его к самому себе, то не должно ли деление числа на 2 означать его вычитание из самого себя? То же самое здесь. 92$, а не при $x = z$. $y = \sqrt{x}$ пересекается с $y = x \div \sqrt{z}$ в точке $x = z$.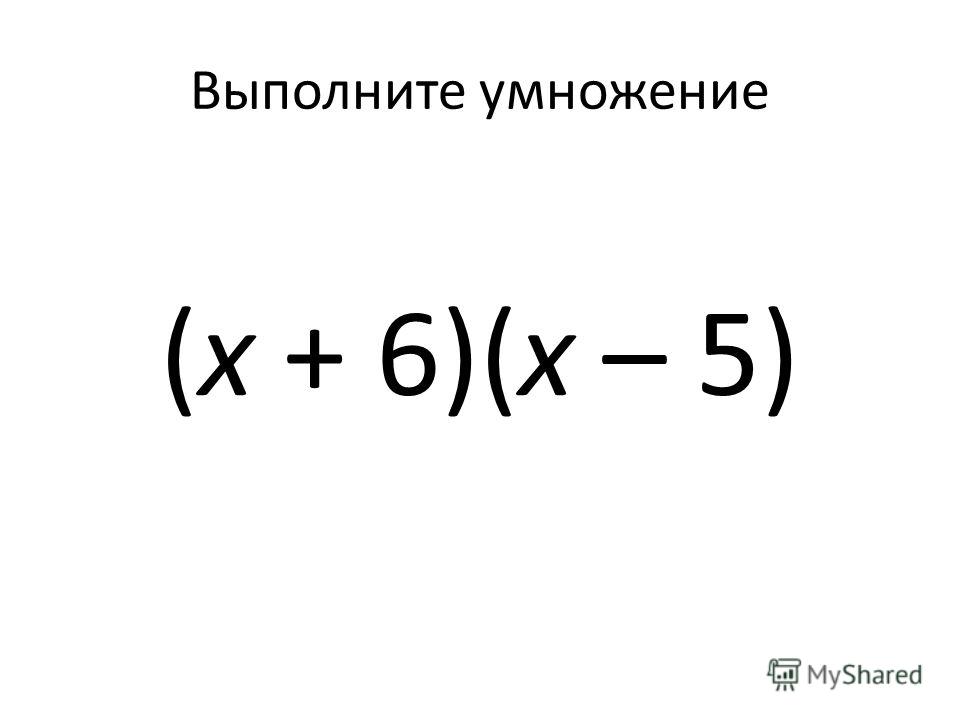
Вопрос возникает из-за очень тонкой логической ошибки смешения функции $\lambda x \space \space x \cdot x$ с функцией $\lambda a \space \space a \cdot x$. Приведенный выше график обращает внимание на разницу между этими функциями.
Если бы возведение числа в квадрат означало умножение этого числа на $z$, а квадратный корень определялся как величина, обратная квадрату, тогда да, извлечение квадратного корня из числа означало бы деление его на $z$.
$\endgroup$
$\begingroup$
Если возведение числа в квадрат означает его умножение само на себя, то извлечение квадратного корня из числа означает деление числа на его квадратный корень.
Теперь, как определение, это немного циклично. Разведение этого круга в квадрате не может быть выражено с помощью основных арифметических операций.
$\endgroup$
2
$\begingroup$
Какая польза от термина для деления числа на себя? Результат всегда $1$.