Сложение чисел с одинаковой степенью: Свойства степеней, действия со степенями

Сложение и вычитание одночленов 7 класс онлайн-подготовка на Ростелеком Лицей

Напоминание определений и правила приведения к стандартному виду уроков

 

Вспомним, что называется одночленом, и какие операции можно делать с одночленами. Одночлен – это произведение чисел и степеней. Рассмотрим два примера:

 

;

;

Оба выражения являются одночленами и перед тем, как приступить к сложению или вычитанию, необходимо привести их к стандартному виду:

;

;

Напомним, что для приведения одночлена к стандартному виду необходимо вначале получить численный коэффициент, перемножив все численные множители, а после этого перемножить соответствующие степени.

Выясним, можно ли складывать наши два одночлена – нет, нельзя, потому что можно складывать лишь те одночлены, которые имеют одинаковую буквенную часть, то есть только подобные одночлены. То есть, мы должны научиться различать подобные и не подобные одночлены.

 

Определение подобия одночленов, примеры

 

 

Рассмотрим примеры подобных одночленов:

 

Одночлены  и  являются подобными, так как имеют одинаковую буквенную часть —

Еще один пример. Запишем одночлен  и одночлен . Мы можем приписать второму одночлену абсолютно любой численный коэффициент и получим одночлен, подобный первому. Выберем, например, коэффициент  и получим два подобных одночлена:  и

Рассмотрим следующий пример. Первый одночлен , его коэффициент равен единице. Запишем теперь его буквенную часть  и добавим к ней произвольный численный коэффициент, например, . Имеем два подобных одночлена:   и .

Сделаем вывод: подобные одночлены имеют одинаковую буквенную часть, и такие одночлены можно складывать и вычитать.

 

Сложение подобных одночленов, примеры и правило

 

 

Теперь приведем примеры не подобных одночленов:

 

 и ; данные одночлены имеют разную буквенную часть, переменная а в них представлена в разных степенях, поэтому одночлены не являются подобными

Еще один пример: одночлены  и  также не являются подобными, их буквенные части отличаются степенями переменной а.

Рассмотрим третью пару одночленов:  и  также не являются подобными.

Теперь разберем сложение подобных одночленов, для этого выполним пример:

Сложить два одночлена:

Очевидно, что данные одночлены подобны, так как легко заметить, что буквенные части их одинаковы, однако математически подобие одночленов можно доказать заменив буквенную часть другой буквой, и если для обоих одночленов эта буква окажется одинаковой, то одночлены подобны. Переходя к примеру, заменим в первом одночлене  на ? Тогда и во втором одночлене ту же самую буквенную часть заменим на  

Получим:

Сложив два эти выражения, получим . Теперь вернемся к исходным переменным – заменим в ответе переменную t на , получаем окончательный ответ:

Теперь сформулируем правило сложения одночленов:

Для того чтобы получить сумму подобных одночленов необходимо сложить их коэффициенты, а буквенную часть дописать такую же, как у исходных слагаемых.

Рассмотрим примеры:

1)

2)

Комментарий к примеру №1: сначала мы записываем в результат сумму коэффициентов одночленов, то есть , затем переписываем буквенную часть без изменений, то есть

Комментарий к примеру №2: аналогично первому примеру сначала записываем сумму коэффициентов, то есть , затем переписываем буквенную часть без изменений — .

 

Формулировка правила вычитания подобных одночленов, примеры

 

 

Перейдем к правилу вычитания одночленов. Рассмотри примеры:

 

1) 

Правило вычитания подобных одночленов аналогично правилу сложения: буквенную часть переписываем без изменений, а коэффициенты вычесть, при чем вычесть в правильном порядке. Для нашего примера:

2) 

3) 

 

Выводы относительно сложения и вычитания подобных одночленов

 

 

Сделаем вывод: складывать и вычитать можно любые, но только подобные одночлены, для этого нужно складывать или вычитать их коэффициенты, буквенную часть переписывая в исходном виде. Не подобные одночлены ни складывать, ни вычитать нельзя.

 

 

Решение задачи на упрощение выражения – прямая задача

 

 

Теперь, зная алгоритм сложения и вычитания подобных одночленов, мы можем решать некоторые типовые задачи.

 

Задачи на упрощение:

Упростить выражение:

Первый одночлен записан в стандартном виде, его больше упростить нельзя, второй и третий не в стандартном виде, значит, первым действием при упрощении выражений с одночленами выполняем приведение к стандартному виду одночленов, которые можно к нему привести.

Итак, приведем к стандартному виду вначале второй, а потом и третий одночлены:

Перепишем исходное выражение с учетом выполненных преобразований:

Мы видим одинаковую буквенную часть у всех трех одночленов, а, значит, они подобны, то есть мы имеем право складывать их и вычитать. Согласно правилу, мы выполним необходимые действия с коэффициентами, а буквенную часть перепишем без изменений:

 

Решение обратной задачи – разложение одночлена на слагаемые

 

 

Существует обратная задача. Задан одночлен . Представить одночлен в виде суммы одночленов.

 

У всех одночленов, в виде суммы которых мы представим заданный, будет одинаковая буквенная часть, одинаковая также и с заданным одночленом — . Представим наш одночлен, например, в виде суммы двух слагаемых. Для этого представим коэффициент как сумму:

А теперь запишем полученное представление: сначала пишем первое слагаемое, умноженное на буквенную часть, а затем второе также умноженное на буквенную часть:

Данная задача имеет бесконечное количество решений, так как число 30 можно представить по-разному, например:

Тогда:

 

Решение задачи на определение подобных одночленов и их сложение

 

 

Рассмотрим еще один вид типовых задач: среди данных одночленов найти подобные и сложить их:

 

; ; ;

Очевидно, что одинаковую буквенную часть имеют первый, второй и последний одночлены. Теперь выполним сложение:

;

 

Список рекомендованной литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ 

3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы интернет

1. Школьный помощник (Источник).

2. Сайт учителя математики и информатики (Источник).

 

Рекомендованное домашнее задание

Задание 1: упростить выражения.

а) ;

б) ;

в) ;

г) ;

Задание 2: разложить одночлен на сумму или разность четырьмя различными способами:

;

Задание 3: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7,  №263, стр.58. Для каждой пары подобных одночленов выполнить сложение и вычитание, а для не подобных указать, какие действия необходимо выполнить, чтобы они стали подобными.

 

Математики обнаружили идеальный способ перемножения чисел / Хабр

Разбивая крупные числа на мелкие, исследователи превысили фундаментальное математическое ограничение скорости

Четыре тысячи лет назад жители Вавилонии изобрели умножение. А в марте этого года математики усовершенствовали его.

18 марта 2019 два исследователя описали самый быстрый из известных методов перемножения двух очень больших чисел. Работа отмечает кульминацию давнишнего поиска наиболее эффективной процедуры выполнения одной из базовых операций математики.

«Все думают, что метод умножения, который они учили в школе, наилучший, но на самом деле в этой области идут активные исследования», — говорит Йорис ван дер Хувен, математик из Французского национального центра научных исследований, один из соавторов работы.

Сложность множества вычислительных задач, от подсчёта новых цифр числа π до обнаружения крупных простых чисел сводится к скорости перемножения. Ван дер Хувен описывает их результат как назначение своего рода математического ограничения скорости решения множества других задач.

«В физике есть важные константы типа скорости света, позволяющие вам описывать всякие явления, — сказал ван дер Хувен. – Если вы хотите знать, насколько быстро компьютеры могут решать определённые математические задачи, тогда перемножение целых чисел возникает в виде некоего базового строительного блока, по отношению к которому можно выразить такую скорость».

Почти все учатся перемножать числа одинаково. Записываем числа в столбик, перемножаем верхнее число на каждую цифру нижнего (с учётом разрядов) и складываем результат. При перемножении двух двузначных чисел приходится проделать четыре более мелких перемножения для получения итогового результата.

Школьный метод «переноса» требует выполнения n² шагов, где n – количество цифр в каждом из перемножаемых чисел. Вычисления с трёхзначными числами требуют девяти перемножений, а со стозначными – 10 000.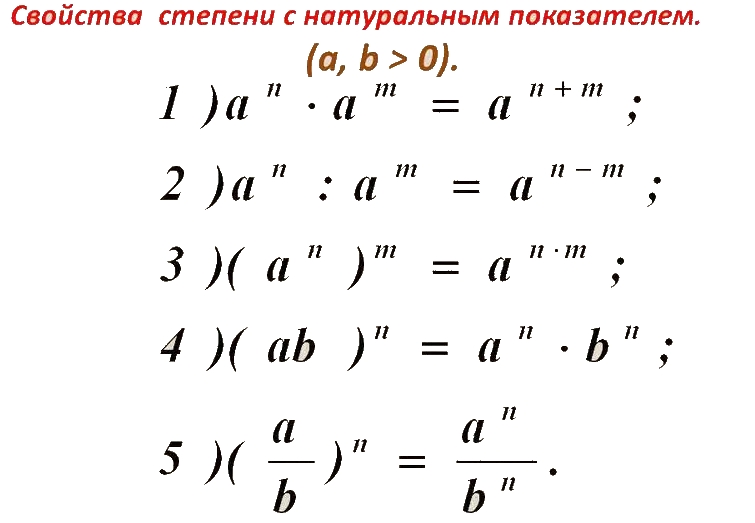

Метод переноса нормально работает с числами, состоящими из нескольких цифр, однако начинает буксовать при перемножении чисел, состоящих из миллионов или миллиардов цифр (чем и занимаются компьютеры при точном подсчёте π или при всемирном поиске больших простых чисел). Чтобы перемножить два числа с миллиардом цифр, нужно будет произвести миллиард в квадрате, или 10¹⁸, умножений, – на это у современного компьютера уйдёт порядка 30 лет.

Несколько тысячелетий считалось, что быстрее перемножать числа нельзя. Затем в 1960 году 23-летний советский и российский математик Анатолий Алексеевич Карацуба посетил семинар, который вёл Андрей Николаевич Колмогоров, советский математик, один из крупнейших математиков XX века. Колмогоров заявил, что не существует обобщённого способа умножения, требующего меньше, чем n² операций. Карацуба решил, что такой способ есть – и после недели поисков он его обнаружил.

Анатолий Алексеевич Карацуба

Умножение Карацубы заключается в разбиении цифр числа и повторной их комбинации новым способом, который позволяет вместо большого количества умножений провести меньшее количество сложений и вычитаний. Метод экономит время, поскольку на сложения уходит всего 2n шагов вместо n².

Традиционный метод умножения 25х63 требует четыре умножения на однозначное число и несколько сложений

Умножение Карацубы 25х63 требует трёх умножений на однозначное число и несколько сложений и вычитаний.
a) разбиваем числа
b) перемножаем десятки
c) перемножаем единицы
d) складываем цифры
e) перемножаем эти суммы
f) считаем e – b – c
g) собираем итоговую сумму из b, c и f

При росте количества знаков в числах метод Карацубы можно использовать рекурсивно.

Традиционный метод умножения 2531х1467 требует 16 умножений на однозначное число.

Умножение Карацубы 2531х1467 требует 9 умножений.

«Сложение в школе проходят на год раньше, потому что это гораздо проще, оно выполняется за линейное время, со скоростью чтения цифр слева направо», — сказал Мартин Фюрер, математик из Пенсильванского государственного университета, создавший в 2007 быстрейший на то время алгоритм умножения.

Имея дело с крупными числами, умножение Карацубы можно повторять рекурсивно, разбивая изначальные числа почти на столько частей, сколько в них знаков. И с каждым разбиением вы меняете умножение, требующее выполнения многих шагов, на сложение и вычитание, требующие куда как меньше шагов.

«Несколько умножений можно превратить в сложения, учитывая, что с этим компьютеры будут справляться быстрее», — сказал Дэвид Харви, математик из Университета Нового Южного Уэльса и соавтор новой работы.

Метод Карацубы сделал возможным умножать числа с использованием лишь n^1,58 умножений на однозначное число. Затем в 1971 году Арнольд Шёнхаге и Фолькер Штрассен опубликовали метод, позволяющий умножать большие числа за n × log n × log(log n) небольших умножений. Для умножения двух чисел из миллиарда знаков каждое метод Карацубы потребует 165 трлн шагов.

Йорис ван дер Хувен, математик из Французского национального центра научных исследований

Метод Шёнхаге-Штрассена используется компьютерами для умножения больших чисел, и привёл к двум другим важным последствиям. Во-первых, он ввёл в использование технику из области обработки сигналов под названием быстрое преобразование Фурье. С тех пор эта техника была основой всех быстрых алгоритмов умножения.

Во-вторых, в той же работе Шёнхаге и Штрассен предположили возможность существования ещё более быстрого алгоритма – метода, требующего всего n × log n умножений на один знак – и что такой алгоритм будет наибыстрейшим из возможных. Это предположение было основано на ощущении, что у такой фундаментальной операции, как умножение, ограничение операций должно записываться как-то более элегантно, чем n × log n × log(log n).

«Большинство в общем-то сошлось на том, что умножение – это такая важная базовая операция, что с чисто эстетической точки зрения ей требуется красивое ограничение по сложности, — сказал Фюрер. – По опыту мы знаем, что математика базовых вещей в итоге всегда оказывается элегантной».

Нескладное ограничение Шёнхаге и Штрассена, n × log n × log(log n), держалось 36 лет. В 2007 году Фюрер побил этот рекорд, и всё завертелось. За последнее десятилетие математики находили всё более быстрые алгоритмы умножения, каждый из которых постепенно подползал к отметке в n × log n, не совсем достигая её. Затем в марте этого года Харви и ван дер Хувен достигли её.

Их метод является улучшением большой работы, проделанной до них. Он разбивает числа на знаки, использует улучшенную версию быстрого преобразования Фурье и пользуется другими прорывами, сделанными за последние 40 лет. «Мы используем быстрое преобразование Фурье гораздо более грубо, используем его несколько раз, а не один, и заменяем ещё больше умножений сложением и вычитанием», — сказал ван дер Хувен.

Алгоритм Харви и ван дер Хувена доказывает, что умножение можно провести за n × log n шагов. Однако он не доказывает отсутствия более быстрого метода. Гораздо сложнее будет установить, что их подход максимально быстрый. В конце февраля команда специалистов по информатике из Орхусского университета опубликовала работу, где утверждает, что если одна из недоказанных теорем окажется верной, то этот метод и вправду будет скорейшим из способов умножения.

И хотя в теории этот новый алгоритм весьма важен, на практике он мало что поменяет, поскольку лишь немного выигрывает у уже используемых алгоритмов. «Всё, на что мы можем надеяться, это на трёхкратное ускорение, — сказал ван дер Хувен. – Ничего запредельного».

Кроме того, поменялись схемы компьютерного оборудования. Двадцать лет назад компьютеры выполняли сложение гораздо быстрее умножения. Разрыв в скоростях умножения и сложения с тех пор серьёзно уменьшился, в результате чего на некоторых чипах умножение может даже обгонять сложение. Используя определённые виды оборудования, «можно ускорить сложение, заставляя компьютер умножать числа, и это какое-то безумие», — сказал Харви.

Оборудование меняется со временем, но лучшие алгоритмы своего класса вечны. Вне зависимости от того, как компьютеры будут выглядеть в будущем, алгоритм Харви и ван дер Хувена всё ещё будет самым эффективным способом умножать числа.

{-2}$$

не являются таковыми, поскольку эти числа не соответствуют всем критериям.

Степень монома равна сумме показателей всех включенных переменных. Константы имеют мономиальную степень 0.

Если мы посмотрим на наши примеры выше, мы увидим, что

Мономиальная	Градус
42	0
5x	0 + 1 = 1
14х 12	0 + 12 = 12
2 шт.	0 + 1 + 1 = 2

Многочлен в отличие от монома представляет собой сумму мономов, где каждый моном называется членом. Степень полинома – это наибольшая степень его членов. Многочлен обычно записывается так, чтобы член с наивысшим показателем переменной сначала а затем уменьшался слева направо. Первый член многочлена называется старшим коэффициентом. 9{2}+x$$

4, 2 и 1 , наивысшая степень равна 4, что означает, что степень многочлена равна 4.

---

Мы можем складывать и вычитать многочлены. Мы просто добавляем или вычитаем одинаковые члены, чтобы объединить два многочлена в один.

---

Пример

Сложите полиномы.

$$({\color{зеленый} {4x+8}})+({\color{синий} {3x+2}})$$

Убираем скобки и группируем все подобные термины.

$${\color{зеленый} {4x+8}}+{\color{синий} {3x+2}}$$

$${\color{green} {4x}}+{\color{blue}{3x}}+{\color{green}{2}}+{\color{blue} {8}}$$

Складываем все одинаковые члены, чтобы получить сумму многочленов.

$$7x+10$$

---

Пример

Вычесть многочлены.

$$({\color{green}{4x+8}})-({\color{blue} {3x+2}})$$

Удаляем круглые скобки, и так как мы получили отрицательный знак перед вторая скобка нам нужно изменить знаки.

$${\color{green} {4x+8}}-{\color{blue}{3x-2}}$$ 9{2}-2x+4)$$

9.

2.1: Добавление целых чисел — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

64039

• Проект NROC

Цели обучения

• Сложите два или более целых числа с одинаковым знаком.
• Сложите два или более целых числа с разными знаками.

Введение

В очень холодный день температура может быть -10. Если температура поднимется на 8 градусов, как вы найдете новую температуру? Знание того, как складывать целые числа, важно здесь и в большей части алгебры.

Сложение целых чисел с одинаковым знаком

Начиная с положительных целых чисел — это то же самое, что и натуральные числа, сложение двух положительных целых чисел — это то же самое, что сложение двух натуральных чисел. Чтобы сложить положительные целые числа на числовой прямой, вы двигаетесь вправо (в положительном направлении).

Дополнительное интерактивное занятие

Попробуйте интерактивную числовую строку ниже. Выберите несколько пар положительных целых чисел для сложения. Нажмите и перетащите синюю и красную точки и посмотрите, как работает добавление.

Чтобы добавить отрицательные целые числа в числовую строку, вы перемещаетесь влево (в отрицательном направлении).

Дополнительное интерактивное занятие

Попробуйте интерактивную числовую строку ниже. Выберите несколько пар отрицательных целых чисел для сложения. Нажмите и перетащите синюю и красную точки и посмотрите, как работает вычитание.

В обоих случаях общее количество перемещенных единиц равно общему пройденному расстоянию. Так как расстояние числа от 0 является абсолютным значением этого числа, то абсолютное значение суммы целых чисел является суммой абсолютных значений слагаемых .

Когда оба числа отрицательные, вы двигаетесь влево в отрицательном направлении, и сумма будет отрицательной. Когда оба числа положительны, вы двигаетесь вправо в положительном направлении, и сумма положительна.

Чтобы сложить два числа с одинаковым знаком (оба положительные или оба отрицательные):

• Сложите их абсолютные значения и присвойте сумме одинаковый знак.

Пример

Найти -23+(-16).

Решение

Оба слагаемых имеют одинаковый знак (отрицательный).

Итак, сложите их абсолютные значения:

|-23|=23 и |-16|=16

Сумма этих чисел равна 23+16=39.

Поскольку оба слагаемых отрицательны, сумма отрицательна.

-23+(-16)=-39

При наличии более двух слагаемых с одинаковым знаком используйте один и тот же процесс для всех слагаемых.

Пример

Найти -27+(-138)+(-55).

Решение

Все слагаемые имеют одинаковый знак (отрицательный).

Итак, складываем их абсолютные значения:

|-27|=27, |-138|=138 и |-55|=55

Сумма этих чисел равна 27+138+55=220.

Поскольку все слагаемые отрицательны, сумма отрицательна.

-27+(-138)+(-55)=-220

Упражнение

Найдите -32+(-14).

1. 46
2. 18
3. -18
4. -46

Ответить

1. Неверно. Вы нашли сумму абсолютных значений, но сумма должна быть отрицательной, так как вы добавляете два отрицательных числа. Правильный ответ -46
2. Неверно. Вы вычли 14 из 32. Сумма находится путем сложения абсолютных значений слагаемых: |-32|+|-14|=32+14=46. Затем вы должны поставить сумму того же знака, что и два слагаемых. Правильный ответ -46.
3. Неверно. Сумма находится путем сложения абсолютных значений слагаемых: |-32|+|-14|=32+14=46. Затем вы должны поставить сумму того же знака, что и два слагаемых. Правильный ответ -46.
4. Правильно. Сумма находится путем сложения абсолютных значений слагаемых: |-32|+|-14|=32+14=46. Тогда вы должны поставить сумму того же знака, что и два слагаемых, поэтому ответ равен -46.

Сложение целых чисел с разными знаками

Что происходит, когда слагаемые имеют разные знаки, как в задаче о температуре во введении? Если будет -10 градусов, а потом температура поднимется на 8 градусов, новая температура будет -10+8. Как рассчитать новую температуру?

При сложении положительного и отрицательного целых чисел вы перемещаетесь в положительном (вправо) направлении к первому числу, а затем в отрицательном (влево) направлении добавляете отрицательное целое число.

Поскольку расстояния перекрываются, абсолютное значение суммы равно разности их расстояний. Таким образом, чтобы добавить положительное число и отрицательное число, вы вычитаете их абсолютные значения (их расстояния от 0).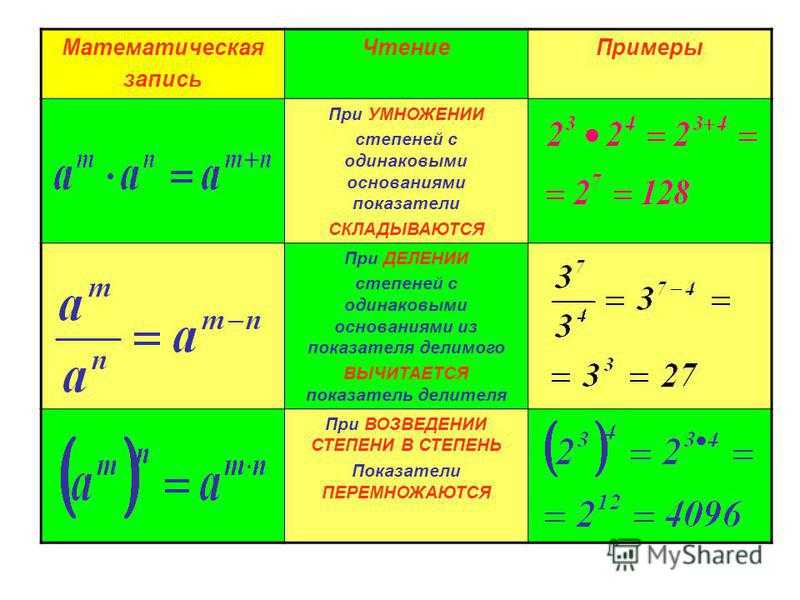

Дополнительное интерактивное задание

Попробуйте сложить целые числа с разными знаками с помощью этой интерактивной числовой строки. Двигайтесь в положительном направлении (вправо), чтобы добавить положительное число, и двигайтесь в отрицательном направлении (влево), чтобы добавить отрицательное число. Посмотрите, сможете ли вы найти правило сложения чисел без использования числовой строки.

Какой знак у суммы положительного и отрицательного целых чисел? Это довольно легко понять. Если вы сдвинулись дальше вправо, чем влево, вы оказались справа от 0, и ответ положительный; а если двигаться дальше влево, ответ будет отрицательным.

Если у вас не было числовой прямой, на которую можно было бы сослаться, вы могли бы найти сумму -1+4 на

• , вычитая расстояния из нуля (абсолютные значения) 4-1=3 и затем
• , применяя знак самого дальнего от нуля (наибольшего абсолютного значения). В этом случае 4 дальше от 0, чем -1, поэтому ответ положительный: -1+4=3

Посмотрите на рисунок ниже.

Если у вас нет числовой строки, на которую нужно ссылаться, вы можете найти сумму -3+2 на

• , вычитая расстояния из нуля (абсолютные значения) 3-2=1, а затем
• , применяя знак самого дальнего от нуля (наибольшего абсолютного значения). В этом случае |-3|>|2|, поэтому ответ отрицательный: -3+2=-1

Чтобы сложить два числа с разными знаками (одно положительное и одно отрицательное):

• Найдите разность их абсолютных значений.
• Присвойте сумме тот же знак, что и у числа с большим абсолютным значением.

Обратите внимание: когда вы находите разницу абсолютных значений, вы всегда вычитаете меньшее абсолютное значение из большего. В приведенном ниже примере показано, как решить вопрос о температуре, который вы рассматривали ранее.

Пример

Найти 8+(-10).

Решение

Слагаемые имеют разные знаки.

Итак, найдите разницу их абсолютных значений.

|-10|=10 и |8|=8

Разница абсолютных значений 10-8=2.

Поскольку 10>8, сумма имеет тот же знак, что и -10.

8+(-10)=-2

Пример

Вычислить \(\ x+37\), когда \(\ x=-22\).

Решение

\(\ х+37\) \(\ -22+37\)	Замените \(\ -22\) на \(\ x\) в выражении.
\(\ |-22|=22 \текст { и }|37|=37\) \(\ 37-22=15\)	Слагаемые имеют разные знаки. Итак, найдите разницу их абсолютных значений. Поскольку |37|>|-22|, сумма имеет тот же знак, что и 37.

-22+37=15

Имея более двух слагаемых, вы можете добавить первые два, затем следующее и так далее.

Пример

Найти -27+(-138)+55.

Решение

	Прибавляйте по два за раз, начиная с -27+(-138).
\(\ \begin{array}{c} |-27|=27 \text { и }|-138|=138 \\ 27+138=165 \\ -27+-138=-165 \end{массив}\)	Поскольку у них одинаковые знаки, вы складываете их абсолютные значения и используете один и тот же знак, чтобы получить -165.
\(\ \begin{array}{c} -165+55 \\ |-165|=165 \text { и }|55|=55 \\ 165-55=110 \end{ массив}\)	Теперь добавьте -165+55. Так как -165 и 55 имеют разные знаки, вы сложите их на 90 318, вычитая 90 319 их абсолютных значений.
\(\ -165+55=-110\)	Поскольку 165>55, знак конечной суммы такой же, как и знак -165.

\(\ -27+(-138)+55=-110\)

Упражнение

Найдите 32+(-14).

1. 46
2. 18
3. -18
4. -46

Ответить

1. Неверно. Вы нашли сумму абсолютных значений. Поскольку слагаемые имеют разные знаки, необходимо найти разность абсолютных значений. |32|=32 и |-14|=14. Разница 32-14=18. Знак суммы такой же, как у слагаемого с большей абсолютной величиной. Поскольку |32|>|-14|, сумма положительна, тот же знак, что и у 32. Правильный ответ: 18.
2. Правильно. Поскольку слагаемые имеют разные знаки, необходимо найти разность абсолютных значений. |32|=32 и |-14|=14. Разница 32-14=18. Знак суммы такой же, как у слагаемого с большей абсолютной величиной. Поскольку |32|>|-14|, сумма положительна.
3. Неверно. Вы нашли разницу абсолютных значений слагаемых. Однако, поскольку |32|>|-14|, знак суммы должен быть таким же, как у 32. Правильный ответ — 18.
4. Неверно. Вы сложили абсолютные значения слагаемых и дали сумме неверный знак. Поскольку слагаемые имеют разные знаки, необходимо найти разность абсолютных значений. |32|=32 и |-14|=14. Разница 32-14=18. Знак суммы такой же, как у слагаемого с большей абсолютной величиной. Поскольку |32|>|-14|, сумма положительна, тот же знак, что и у 32. Правильный ответ: 18.

Сводка

При сложении целых чисел следует учитывать два случая. Когда знаки совпадают, вы добавляете абсолютные значения слагаемых и используете тот же знак. Когда знаки разные, вы находите разницу абсолютных значений и используете тот же знак в качестве слагаемого с большим абсолютным значением.

---

Эта страница под названием 9.2.1: Добавление целых чисел предоставляется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована проектом NROC посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.