Длина окружности овала: Длина эллипсаФормулы по геометрии

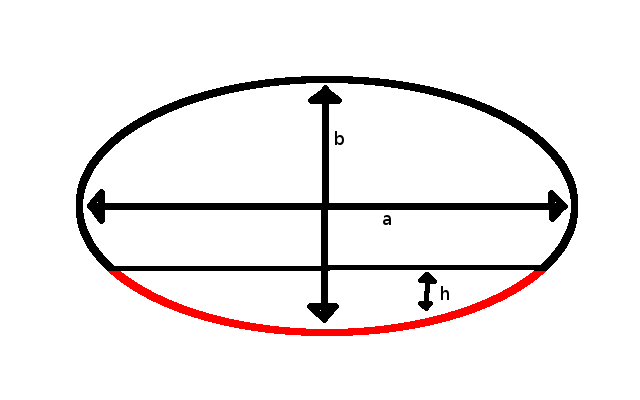
Как найти радиус овала? – Обзоры Вики

Например, квадратный корень из 39 равен 6.245, округленному до ближайшей тысячной. Следовательно, малая полуось или кратчайший диаметр составляет 6.245 см. Разделите измерение малой полуоси пополам вычислить его радиус. Например, 6.245 см разделить на два равно 3.122 см.

Отсюда, есть ли формула для овала? Площадь такого эллипса равна Площадь = Пи * А * В , очень естественное обобщение формулы для окружности!

Дополнительно Какова площадь овала калькулятора? Калькулятор площади овала

1. Формула. А=пи*а/2*b/2.
2. Большая ось.
3. Малая ось.

Как найти радиус фигуры? Радиус равен половине диаметра, поэтому используйте формула r = D / 2. Это идентично методу, используемому для вычисления радиуса круга по его диаметру. Если у вас есть сфера диаметром 16 см, найдите радиус, разделив 16/2, чтобы получить 8 см. Если диаметр 42, то радиус 21.

Как измерить овальную форму?

Радиус равен половине диаметра? Радиус половина длины диаметра.

Как измерить длину овальной дорожки?

Также как изменить диаметр на радиус? Просто разделите на два; половина диаметра — это радиус. Например, если у вас диаметр 6 см, просто разделите на 2. Вы получите половину значения, которое составляет 3 см; это радиус.

Что такое радиусы в окружности?

В классической геометрии радиус круга или сферы равен любой из отрезков от центра до периметра, а в более современном использовании это также их длина. Название происходит от латинского радиуса, означающего луч, но также и спицы колеса колесницы.

Диаметр это радиус? Диаметр равно удвоенному радиусу.

Как найти радиус изгиба?

Как найти радиус криволинейной стены?

Если дуга стены составляет 180 градусов или больше, измерьте расстояние поперек стены в ее самом широком месте. Разделите это расстояние на 2 для расчета радиуса.

Как вычислить радиус изгиба? Если вы натянули лук с внутренней стороны изгиба, добавить 1/2 наружного диаметра трубки чтобы получить истинный радиус центральной линии. Если вы нарисовали дугу с внешней стороны (вверху) изгиба, вычтите 1/2 внешнего диаметра трубы, чтобы получить истинный радиус центральной линии.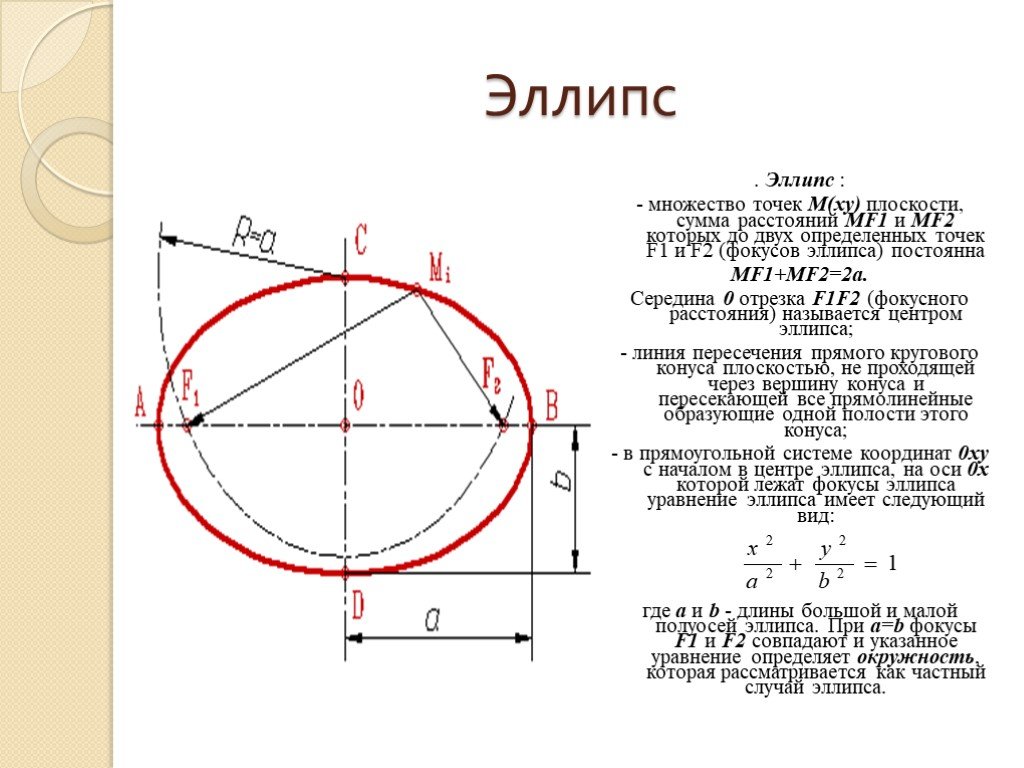

Как найти периметр овала? Следовательно, для нахождения периметра эллипса можно использовать формулу приближения:

1. Периметр эллипса = 2π√a2+b22.
2. Периметр эллипса = 2π√a2+b22.
3. Следовательно, периметр эллипса = 2×3.14√102+522=49.64.

Как найти диаметр и радиус окружности?

Возьмите длину окружности и разделите ее на число Пи. Например, если длина окружности 12.56, вы должны разделить 12.56 на 3.14159, чтобы получить 4, что является диаметром круга. Использовать диаметр, чтобы найти радиус, разделив диаметр на 2. Например, если диаметр равен 4, радиус будет равен 2.

Что такое диаметр и радиус окружности? Диаметр круга — это отрезок линии от одного конца круга до другого конца круга, проходящий через центр круга. При этом радиус a круг — это длина отрезка от центра круга до точки на окружности круга..

Как найти радиус, когда у вас есть площадь?

Чтобы найти радиус, разделите площадь на пи, затем извлеките квадратный корень.

Какова длина радиуса? Радиус является своего рода базовой единицей окружности: его длина равна расстояние от центра круга до любой точки на его окружности и это формирует основу для радиана. Вы можете использовать длину радиуса круга, чтобы найти его длину окружности (C=2πr), площадь (A=πr2) и диаметр (d=2r).

Радиус и радиус одинаковы?

Радиусы множественное число слова радиус.

Что такое радиусы в математике? прямая линия, идущая от центра круга или сферы к окружности или поверхности: Радиус круга равен половина диаметра. длина такой строчки.

Как найти диаметр?

Формула для определения диаметра устанавливает соотношение между диаметром и радиусом. Диаметр состоит из двух сегментов, каждый из которых имеет радиус. Следовательно, формула такова: Диаметр = 2 * измерение радиуса. Вы можете сократить эту формулу как d = 2r.

Как измерить радиус локтя?

Какова формула припуска на изгиб?

Формула (см. Формулы изгиба): Допуск на изгиб = Угол * (π / 180) * (Радиус + К-фактор * Толщина).

Эллипс. Полуоси эллипса. Фокус эллипса.

• Альфашкола
• Статьи
• Эллипс

Эллипс- замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость.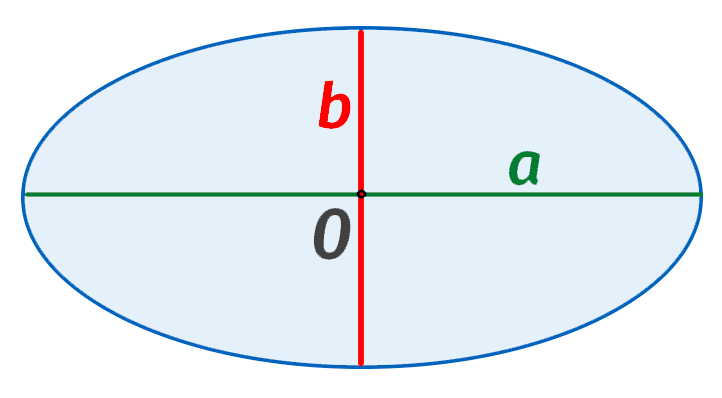 На рисунке ниже показано несколько примеров.

 

Круг-это частный случай эллипса, который получается, когда сечение через конус или цилиндр ортогонально оси конуса или цилиндра.

Эллипс-это фигура, в результате сечения конуса и прямого кругового цилиндра

Эллипс симметричен относительно горизонтальной и вертикальной осей, как показано на рисунке выше. Максимальное расстояние между двумя  точками происходит вдоль горизонтальной оси (называемой главной осью или поперечным диаметром), а минимальное расстояние между двумя  точками-вдоль вертикальной оси (называемой малой осью или сопряженным диаметром). Антиподальные точки — это любые две точки по периметру эллипса, так что соединяющий их отрезок линии должен проходить через центр с эллипса (что происходит на пересечении горизонтальной и вертикальной осей). Эллипс симметричен относительно его большой и малой осей.

 

Полуось — это та часть оси, которая лежит между центром \(C\) и периметром эллипса — называется полуосью.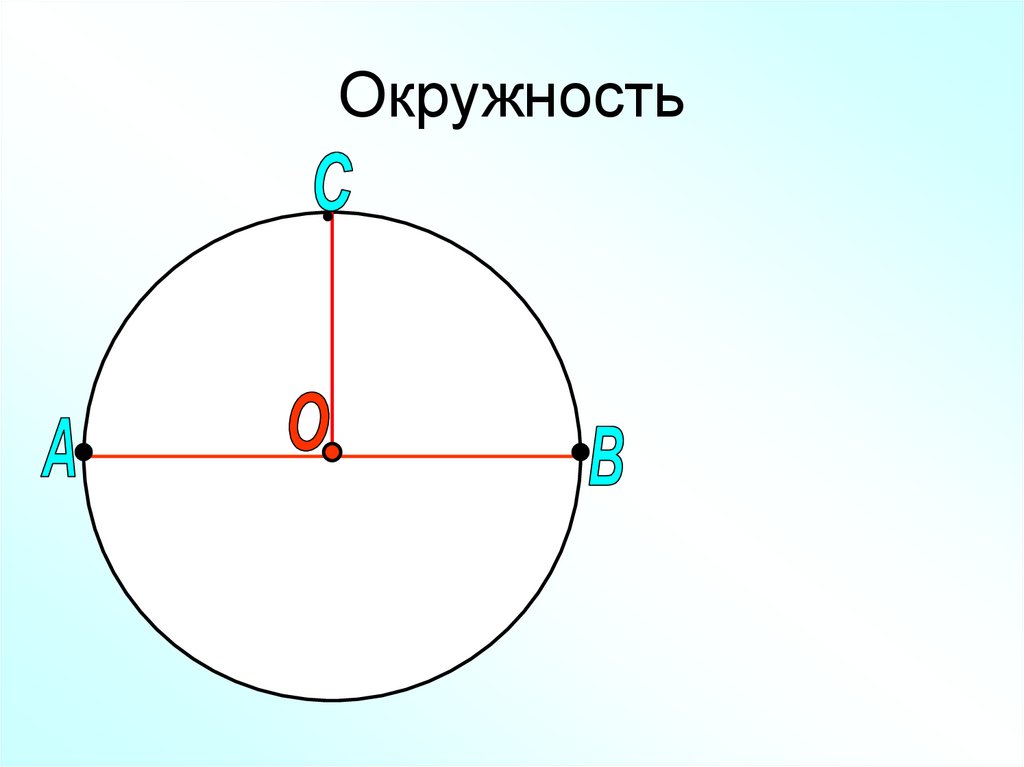 Полуоси, принадлежащие к главной оси —  большая полуось, а полуось, принадлежащих к малой оси —  малая полуось. На приведенной выше рисунке мы обозначили каждую из двух полуосей \(a\) и каждую из двух полуосей \(b\). Точки, показанные красным цветом по периметру эллипса, являются точками, где большая и малая оси пересекают периметр эллипса. Это вершины эллипса. Вершины — это точки, в которых кривизна эллипса максимальна (т. е. где главная ось пересекает периметр эллипса). 

 

Есть две специальные точки, которые лежат на главной оси эллипса, равноудаленной от его центра C, каждая из которых является фокусом эллипса. Эти две точки (совместно называемые фокусами эллипса) обычно обозначаются как \(F1\) и \(F2\). Расположение фокусов таково, что для любой точки \(p\) по периметру эллипса сумма расстояний от \(F1\) до \(P\) и от \(F2\) до \(P\) остается постоянной и будет равна длине главной оси. Фактически, принимая любую произвольную пару точек в качестве фокусов и любое значение длины главной оси, которое больше расстояния между этими двумя точками, соответствующий эллипс определяется как набор точек, для которых сумма расстояний между точкой и каждым из фокусов равна длине главной оси.

2} \)

 

где \(a\) и \(b\)-длины главной и малой осей соответственно. Обратите внимание, что чем дальше фокусы от центра эллипса, тем меньше сходство между эллипсом и окружностью. Кривизна в вершинах эллипса будет увеличиваться, в то время как кривизна в \(cо\)-вершинах будет уменьшаться. Другими словами, эллипс станет более плоским по мере увеличения значения \(c\).

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Ирина Владимировна Никитина

Репетитор по математике

Стаж (лет)

Образование:

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Елена Александровна Гинько

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный педагогический университет имени Максима Танка

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Райхан Талгатовна Иманбаева

Репетитор по математике

Стаж (лет)

Образование:

Санкт-Петербургский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Подготовка к ЕГЭ по математике (профильный уровень)
• Репетитор по химии для подготовки к ОГЭ
• Репетитор для подготовки к ЕГЭ по физике
• Подготовка к ОГЭ по английскому языку
• Английский язык для начинающих
• Репетитор по английскому для взрослых
• Репетитор для подготовки к ВПР по русскому языку
• Подготовка к ОГЭ по биологии
• Подготовка к ЕГЭ по географии
• Подготовка к ЕГЭ по информатике

Похожие статьи

• Правила вычитания векторов
• МГУ ВМК: вступительные испытания
• Как решать иррациональные уравнения?
• Степенные ряды
• ЕГЭ по математике, базовый уровень. Задачи на исследование функций (вариант 1)
• Материальное поощрение детей: за и против
• Первая школьная любовь и как помочь подростку пережить ее?
• Нескучный русский: интересные факты о родном языке

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Калькулятор окружности эллипса

Калькулятор окружности эллипса поможет вам найти общий периметр вокруг эллипса, который также называется окружностью эллипса. Длина окружности эллипса зависит от длин большой и малой полуосей. Читайте дальше, чтобы узнать больше о том, как найти длину окружности эллипса и формулу для ее расчета.

Что такое длина окружности эллипса?

длина окружности эллипса это общая длина граница эллиптической формы . Другими словами, мы также называем периметр эллипса его окружностью .

Какова формула длины окружности эллипса?

Чтобы вычислить длину окружности эллипса, нам нужно знать длины большой и малой полуосей . Получив их, мы найдем длину окружности эллипса по следующей формуле:

p≈π(a+b)(1+3h20+4−3h)\small p \ приблизительно \pi (a+b) \left ( 1 + \frac {3h}{10 + \sqrt{4-3h}} \right )p≈π(a+b)(1+10+4−3h 92}h=(a+b)2(a−b)2​

Таким образом, используя приведенные выше уравнения для длины окружности эллипса, мы можем найти ее приблизительное значение.

Как пользоваться калькулятором длины окружности эллипса?

Чтобы найти длину окружности эллипса с помощью нашего калькулятора, необходимо сделать следующее:

1. Введите значение большой полуоси (а) .
2. Введите значение малой полуоси (b)
   .
3. Вуаля! Инструмент выполнит все тяжелые вычисления для расчета окружность эллипса и отобразит его как результат!

Окружности и эллипсы
Знаете ли вы, что эллипс с равными большой и малой осями — это окружность. Узнайте больше о кругах, используя наши специальные инструменты для расчета уравнения круга, калькулятора единичного круга и калькулятора площади круга.

Другие калькуляторы эллипса

Если вы нашли этот инструмент полезным, вы также можете проверить наш широкий выбор калькуляторов, связанных с эллипсом:

• Калькулятор эллипса;
• Калькулятор площади эллипса;
• Вычислитель центра эллипса;
• Калькулятор периметра Эллипса; и
• Вычислитель фокусов эллипса.

Часто задаваемые вопросы

Как найти длину окружности эллипса?

Чтобы найти длину окружности эллипса, нам нужно использовать уравнение длины окружности эллипса, которое состоит из следующих шагов:

1. Найдите значения большой полуоси (a) и малой полуоси (б) .
2. Вычислить значение переменной h по формуле h = (a - b)²/(a + b)² .
3. Подставьте значения a, b и h в формулу длины окружности, полученную с помощью следующего уравнения:
   Длина окружности = π × (a + b)[1 + (3 × h/(10 + √(4) - 3ч)))] .
4. Тада! Теперь у вас есть приблизительное значение длины окружности эллипса !

Есть ли у эллипса длина окружности?

Да! Мы иногда называем границу эллипса окружностью эллипса ! Хотя термин окружность обычно ассоциируется с окружностью, мы также используем его для обозначения периметра эллипса.

Калькулятор эллипса — Институт монолитных куполов

Калькуляторы Обновлено 13 июня 2022 г. По Дэйв Саут

Большой радиус

Малый радиус

Единицы

Расчет эллипсаСсылка на калькулятор эллипса

Калькулятор эллипса Института монолитных куполов — это простой калькулятор для обманчиво сложной формы. Он будет рисовать и вычислять площадь, окружность и фокусы для эллипса любого размера. Его легко использовать и легко делиться результатами.

Введите главный радиус, малый радиус и предпочтительные единицы измерения и нажмите «Перейти». Он нарисует эллипс и выведет вычисления. URL-адрес страницы сохранит значения, и его можно добавить в закладки или поделиться с другими. Используйте «Копировать в буфер обмена», чтобы быстро копировать и вставлять результаты в электронные письма, сообщения или исследовательские заметки.

На этот калькулятор распространяются наши Условия предоставления услуг.

Диаграмма результатов калькулятора эллипса по умолчанию с большим радиусом (a) и малым радиусом (b) плюс одна фокусная точка (фокусы).

Большой радиус. Большой радиус, большая полуось или «а» эллипса — это расстояние от центра координат до самой дальней точки эллипса. Это половина большого диаметра, большой оси или «А» эллипса.

Малый радиус.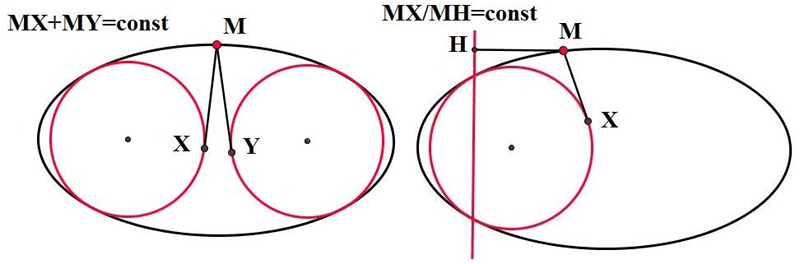 Малый радиус, малая полуось или «b» эллипса — это расстояние от центра координат до ближайшей возможной точки эллипса. Это половина меньшего диаметра, малой оси или «В» эллипса. Малая ось всегда перпендикулярна большой оси.

Окружность. Окружность — это периметр вокруг эллипса. Существует множество формул, разработанных для аппроксимации длины окружности с разным уровнем точности. В этом калькуляторе используется «Infinite Series 2», которую можно найти на веб-сайте Math is Fun. Он использует 20 биномиальных коэффициентов для аппроксимации и достаточно точен для больших эллиптических следов.

Искривление. Радиус кривизны является мерой самой кривой в малой (b) вершине. Расстояние от кривой до воображаемой точки отсчета, которая описывает окружность той же кривизны.

Район. Площадь эллипса по формуле A = πab.

Очаги. Расстояние от центра координат на большой оси — в обоих направлениях — до эллиптических фокусных точек. Используйте фокусное расстояние плюс метод булавки и веревки, чтобы нарисовать эллипс на бумаге или на рабочей площадке.

Единицы. Выбор единиц измерения предназначен только для форматирования вывода.

На этот калькулятор распространяются наши Условия предоставления услуг.

Эскиз понятий в эллипсе. Фокальные точки (фокусы) — это большой радиус (а) расстояния от вершины (б) до точки пересечения на большой оси. Расстояние от фокусов до эллипса и фокусов всегда равно полной длине большой оси. Вот почему мы рисуем эллипс, используя нить и две булавки в фокусах (см. видео ниже).

Дэйв Саут

Четкое объяснение того, почему нет уравнения для периметра эллипса, а также другие факты из математики эллипса. Он также включает демонстрацию строкового метода для рисования эллипса. Это стоит посмотреть!

Математика стоя

Идти в ногу с куполами

Подпишитесь на ежемесячную электронную рассылку новостей Monolith Dome Roundup, чтобы получать последние новости и ссылки об инновационной архитектуре, тонкостенных конструкциях и индустрии монолитных куполов.