Что такое научная нотация? Определение и важность • BUOM
17 марта 2021 г.
Многие математики, статистики и другие специалисты, которые регулярно работают с большими числами, используют экспоненциальную запись, чтобы разбить числа на более удобные суммы и упростить вычисления. Научное уведомление позволяет людям легче понять число и упростить арифметические операции. В этой статье мы исследуем определение научной нотации, почему это важно, как она работает и как вы можете писать в научной нотации.
Что такое научная нотация?
Научная нотация — это способ выражения чисел, которые слишком велики или малы для записи в основной десятичной форме. В некоторых случаях научная нотация также называется стандартной формой, научной формой или стандартной индексной формой. Наиболее часто используемые учеными, математиками и инженерами, научные обозначения позволяют профессионалам и другим людям записывать очень длинные числа в более понятной форме. При использовании инженерного калькулятора научную запись можно реализовать, выбрав режим отображения «SCI». 8 нельзя, потому что восемь не кратно трем.
8 нельзя, потому что восемь не кратно трем.
Преимущества научной нотации
Ниже приведены основные преимущества записи в экспоненциальном представлении:
Научная запись значительно упрощает работу с большими числами при решении арифметических задач.
Научное обозначение делает каждое число в уравнении более управляемым и легким для отслеживания.
Научное представление обеспечивает точность и снижает вероятность ошибки при использовании очень маленьких или очень больших чисел.
Научная нотация упрощает интерпретацию больших чисел, особенно для тех, кто не привык работать с такими большими числами.
Научное обозначение позволяет легче читать числа, не отвлекаясь на несущественные значения.
виды, как решать с разными основаниями, формулы с примерами
Показательные уравнения — определение
Определение 1Показательными в алгебре называют уравнения с неизвестным, которое записано в показателе степени.
Простейшее показательное уравнение в теории имеет вид:
ax=b
Здесь a>0,a≠1.
Пример формулы простейшего показательного уравнения:
1000x=100
При решении показательных уравнений многие математики советуют привести их к следующему виду:
Cfx=Cgx
После преобразования необходимо решить уравнение:
f(x)=g(x).
Виды показательных уравнений
Существуют разные типы показательных уравнений, как и неравенств. К примеру, самым простым из них является:
ax=b
Знак перед b определяет количество корней показательного уравнения:
- приb≤0 решения отсутствуют x∈∅;
- когда b>0,x=logab.
Показательным является уравнение в кратком виде:
afx=b
В этом случае, неизвестная определяется таким образом:
- При b≤0⇒x∈∅.
- При b>0⇒fx=logab.
Показательное уравнение может быть записано таким способом:
afx=agx
Данное уравнение является равносильным следующему уравнению:
fx=gx
Другой вариант записи показательного уравнения:
φxfx=φxgx
В этом случае возможны следующие решения:
- при φx=1 все части данного уравнения являются равными для каких-либо fx,gx;
- при φx>0,φx≠1 такое уравнение равносильно уравнению fx=gx;
- при φx=0 уравнение равносильно fx>0,gx>0.

Записанное показательное уравнение является равносильным совокупности систем:
φx=1,x∈R,φx>0,φx≠1,fx=gx,φx=0,fx>0,gx>0.
Существуют показательные уравнения, которые допускается привести к квадратным. Как пример:
A·a2x+B·ax+C=0
В этом случае A отлично от нуля, B и C являются какими-либо числами, a>0 и не равно единице.
В процессе решения подобных показательных уравнений требуется выполнить замену:
ax=t
При этом t должно быть больше нуля. Получим:
A·afx+B·a-fx+C=0
Здесь A, B, a являются какими-либо числами, отличными от нуля. При этом а отлично от единицы, C определяется, как произвольное действительное число. Умножим все части уравнения на afx>0, чтобы свести его к квадратному уравнению:
A·afx2+B+C·afx=0
Выполним обратную замену afx=t,t>0 и запишем квадратное уравнение:
At2+Ct+B=0
Следующим видом показательных уравнений являются однородные.
Определение 2Однородные показательные уравнения первой степени являются такими уравнениями, которые записаны в виде:
afx=bfx
Свести подобное уравнение к показательному afx=bнесложно. Достаточно обе части равенства разделить на afx>0 (или bfx>0):
Достаточно обе части равенства разделить на afx>0 (или bfx>0):
afxbfx=1⇒abfx=1⇒fx=0
Определение 3Однородным показательным уравнением второй степени называют уравнение в виде:
A·a2fx+B·afx·bfx+C·b2fx=0
Подобные уравнения решают, согласно стандартному алгоритму. В первую очередь следует сократить обе части уравнения на a2fx>0, либо на b2fx>0. Таким образом, выражение примет следующий вид:
A·a2fx+B·afx·bfx+C·b2fx=0,:b2fx>0
A·a2fxb2fx+B·afx·bfxb2fx+C=0
или
A·ab2fx+B·abfx+C=0
Если заменить abfx=t, где t больше нуля, то получится квадратное уравнение:
At2+Bt+C=0
Метод решения показательных уравнений через приведение к одинаковому основанию
В процессе решения показательных уравнений ax=b обычно b заменяют какой-то степенью числа а. В результате уравниваются основания. Важно правильно определить общий множитель, и решение значительно упроститься.
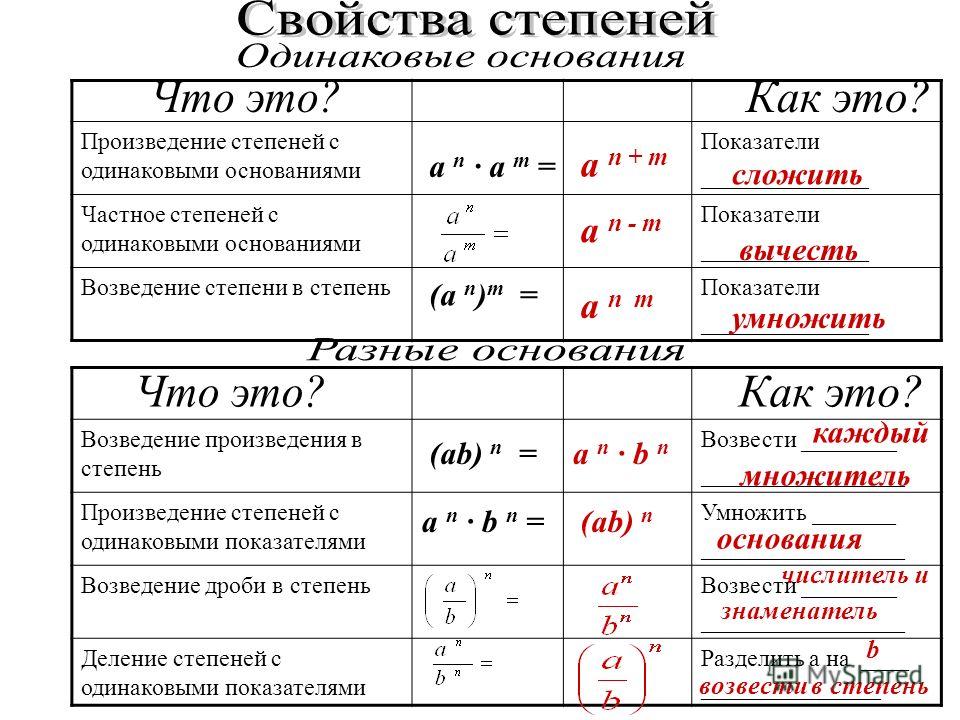
Правило 1При идентичных основаниях, но отличающихся показателях степени, умножение чисел предполагает сложение степеней, а в процессе деления степени вычитаются.
Рассмотрим правило на примере решения показательного уравнения, содержащего корень:
1642-x=18
Заметим, что для чисел 64 и 8 общим множителем является число 2. Запишем степени:
642=212
8=23
Подставим полученные значения и преобразуем уравнение:
(1212)-x=123
12-12x=1223
(12)-12x=(12)23
-12x=32
x=-18
В результате получилась дробь.
Попробуем решить следующее показательное уравнение. Здесь будет преобразована каждая часть выражения:
(0,5)x2×4x+1=64-1
Вычислим, каким должно быть общее основание:
0,5=12=2-1
4=22
64=26
В результате получим:
(2-1)x2×(22)x+1=(26)-1
2-x2×22x+2=2-6
2-x22x+2=2-6
-x2+2x+2=-6
x2-2x-8=0
Заметим, что для данного показательного уравнения имеется пара решений: -2 и 4
Метод решения показательных уравнений через приведение к одинаковой степени
Не всегда при решении показательных уравнений получается использовать предыдущий метод. В некоторых случаях можно упростить задачу с помощью преобразования показателей степени. Данная методика имеет место лишь в том случае, когда в выражении используются операции умножения или деления.
В некоторых случаях можно упростить задачу с помощью преобразования показателей степени. Данная методика имеет место лишь в том случае, когда в выражении используются операции умножения или деления.
Умножить числа, которые отличаются основаниями, но имеют идентичные степенные показатели, можно путем умножения лишь оснований. Степень при этом не меняется:
axbx=(ab)x
Потренируемся использовать записанное правило. Решим пример:
52x-4=492-x
В этом случае можно заметить отсутствие общих множителей в обеих частях выражения. Это не позволит найти общее основание и преобразовать уравнение. Тогда поработаем с показателями:
52x-4=492-x
52x-4=74-2x
52x-4=172x-4
352x-4=1
2x-4 = 0
х = 2
Закрепить принцип решения показательных уравнений с помощью приведения к одинаковой степени можно на следующем примере:
2x-2=52-x
Приведем части уравнения слева и справа к одному показателю степени. С помощью свойства степенных функций преобразуем правую часть:
2x-2=15x-2
Затем следует умножить полученное выражение на 5x-2:
2x-2×5x-2=1
10x-2=1
10x-2=100
х – 2 = 0
х = 2
Примеры решения показательных уравнений
Задача 1Найти корни уравнения:
5x=25
Решение
Заметим, что здесь b=25>0.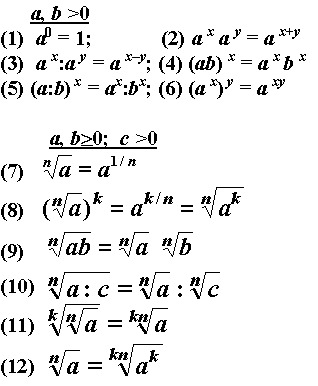 Таким образом:
Таким образом:
x=log525
Руководствуясь свойствами логарифма, преобразуем выражение:
x=log552=2·log55=2·1=2
Ответ: x=2
Задача 2Решить уравнение:
x2x+1=x3x-4
Решение
Заметим, что данное уравнение равносильно системе:
x=1,x∈R,x>0,x≠1,2x+1=3x-4,x=0,2x+1>0,3x-4>0
⇒x=1x∈0; 1∪1; +∞,-x=-5,x=0,x>-12,x>43 ⇒
⇒x=1x∈0; 1∪1; +∞,x=5,x=0,x>43,
⇒x=1,x=5,x∈∅
⇒x=1,x=5.
Ответ: x1=1,x2=5
Задача 3Требуется найти решения уравнения:
2x-3·4x=216x
Решение
В первую очередь преобразуем все части равенства так, чтобы основанием было число 2:
Решим приведенное уравнение:
3x-3=12-4x⇒7x=72⇒x=12 .
Ответ: x=12
Задача 4Найти корни уравнения:
5x-2·5x-2=23
Решение
Здесь требуется вынести число 5 в самой маленькой степени, то есть в степени (х-2). В процессе разделим каждое из слагаемых на этот множитель:
5x-2·5x-x-2-2=23⇒5x-2·5x-x+2-2=23⇒5x-2·25-2=23⇒
⇒5x-2·23=23⇒5x-2=1
Таким образом:
x-2=log51⇒x-2=0⇒x=2
С учетом, что 1=a0, уравнение 5x-2=1 допустимо записать таким образом:
5x-2=1⇒5x-2=50⇒x-2=0⇒x=2
Ответ: x=2
Задача 5Необходимо решить уравнение:
4x+1-3·2x=10
Решение
Здесь необходимо привести выражение к единому основанию:
4x·4-3·2x-10=0⇒4·22x-3·2x-10=0⇒4·2×2-3·2x-10=0
Заменим 2x=t, при этом t больше нуля. Получим:
Получим:
4t2-3t-10=0
Получилось квадратное уравнение, которое можно решить:
D=-32-4·4·-10=9+160=169=132
t1=3+132·4=168=2
Если выполнить обратную замену, то получится простейшее показательное уравнение 2x=2:
2x=21⇒x=1Ответ: x=1
Задача 6Найти корни уравнения:
3x+32-x=10
Решение
Преобразуем уравнение:
3x+32·3-x=10.
Умножим уравнение на 3x>0. Получим:
3×2+9=10·3x⇒3×2-10·3x+9=0
Заменим 3x=t, при этом t больше нуля. Получится квадратное уравнение:
t2-10t+9=0
Согласно теореме Виета, решениями такого уравнения являются:
t1=9
t2=1
Выполним обратную замену:
3x=9,3x=1⇒3x=32,3x=30
x=2
x=0.
Ответ: x1=2,x2=0
Задача 7Вычислить корни уравнения:
2x+1=3x+1
Решение
В этом случае целесообразно разделить уравнение, то есть все его части, на 3x+1>0:
23x+1=1
В результате:
x+1=log231⇒x+1=0⇒x=-1
Ответ: x=-1
Задача 8Требуется решить уравнение:
4x+6x=2·9x
Решение
В этом случае следует перенести все слагаемые в левую часть.
22x+2·3x-2·32x=0
2×2+2x·3x-2·3×2=0,:32x>0
23×2+23x-2=0
Выполним замену 23x=t, где t не равно нулю. В итоге получится квадратное уравнение:
t2+t-2=0
Решения данного уравнения:
t1=-2<0∉, t2=1
Обратная замена даст нам показательное уравнение в простейшем виде:
23x=1⇒23x=230⇒x=0
Ответ: x=0
{0}\).Приведенное выше выражение также называется полиномиальным в стандартной форме, где \(a_0, a_1, a_2………a_n\) – константы, а n – целое число. Например, x 2 + 2x + 3, 5x 4 — 4x 2 + 3x +1 и 7x — √3 являются многочленами.
| 1. | Как складывать многочлены? |
| 2. | Вычитание многочленов |
| 3. | Шаги для сложения и вычитания многочленов |
| 4. | Часто задаваемые вопросы о сложении и вычитании многочленов |
Как складывать многочлены?
Сложение многочленов простое. Добавляя многочлены, мы просто добавляем похожие члены. Мы можем использовать столбцы, чтобы сопоставлять правильные термины вместе в сложной сумме. При сложении полиномов помните о двух правилах.
Добавляя многочлены, мы просто добавляем похожие члены. Мы можем использовать столбцы, чтобы сопоставлять правильные термины вместе в сложной сумме. При сложении полиномов помните о двух правилах.
- Правило 1: Всегда берите одинаковые термины вместе при выполнении сложения.
- Правило 2: Знаки всех многочленов остаются прежними.
Например, добавьте 2x 2 + 3x +2 и 3x 2 — 5x -1
- Шаг 1: Приведение полинома к стандартной форме. В этом случае они уже в своих стандартных формах.
- Шаг 2: Аналогичные члены в двух приведенных выше многочленах:
2x 2 - Шаг 3: Вычисления с одинаковыми знаками:
Похожие термины
Подобные термины — это термины, переменные которых, а также их показатели степени, совпадают. Например, 2x, 7x, -2x и т. д. — все они похожи на переменные.
Например, 2x, 7x, -2x и т. д. — все они похожи на переменные.
Непохожие термины
Непохожие термины — это термины, у которых переменные, показатели степени или обе переменные и показатели не совпадают. Например, 2, 7x 2 , -2y 2 и т. д. — все это разные переменные.
Вычитание многочленов
Вычитание многочленов так же просто, как сложение многочленов. Использование столбцов поможет нам сопоставить правильные термины вместе в сложном вычитании. При вычитании многочленов отделяйте одинаковые члены и просто вычитайте их. При выполнении вычитания многочленов помните о двух правилах.
- Правило 1: При выполнении вычитания всегда берите одинаковые члены вместе.
- Правило 2: Знаки всех членов полинома вычитания изменятся, + изменится на — и — изменится на +.
Например, нам нужно вычесть 2x 2 + 3x +2 из 3x 2 — 5x -1
- Шаг 1: Приведение многочлена в стандартную форму.
 В этом случае они уже в своих стандартных формах.
В этом случае они уже в своих стандартных формах. - Шаг 2: Подобные члены в двух приведенных выше многочленах: 2x 2 и 3x 2 ;3x и -5x;2 и -1
- Шаг 3: Заключите часть многочлена, которую нужно вычесть, в круглые скобки с префиксом минус (-). Затем удалите скобки, изменив знак каждого члена полиномиального выражения.
- Шаг 4: Вычисления после изменения знаков полиномов вычитания:
Шаги для сложения и вычитания многочленов
Сложение или вычитание полиномов очень просто выполнить, все, что нам нужно сделать, это помнить о некоторых шагах. Для выполнения операции сложения и вычитания многочленов полиномы могут располагаться вертикально для сложных выражений. Для более простых расчетов мы можем выполнить операцию, используя горизонтальное расположение.
Сложение и вычитание многочленов по горизонтали
Многочлены можно складывать и вычитать по горизонтали, используя шаги, указанные ниже,
- Шаг 1: Расположите многочлены в их стандартной форме.

- Шаг 2: Разместите многочлены рядом друг с другом по горизонтали.
- Шаг 3: Сначала разделите похожие термины.
- Шаг 4: Расположите одинаковые термины вместе.
- Шаг 5: Кроме того, знаки всех многочленов остаются прежними. В режиме вычитания знаки членов полинома вычитания меняются.
- Шаг 6: Выполните вычисления.
Сложение и вычитание многочленов по вертикали
Многочлены можно складывать и вычитать по вертикали, используя шаги, указанные ниже,
- Шаг 1: Расположите многочлены в их стандартной форме
- Шаг 2: Расположите многочлены вертикально, с одинаковыми членами, расположенными друг над другом в обоих многочленах.
- Шаг 3: Мы можем представить отсутствующий член мощности в стандартной форме с «0» в качестве коэффициента, чтобы избежать путаницы при упорядочении членов.

- Шаг 4: Кроме того, знаки всех многочленов остаются прежними. В режиме вычитания знаки членов полинома вычитания меняются.
- Шаг 5: Выполните вычисления
Следуя этим шагам, мы можем решить сложение и вычитание многочленов.
Пример: (3x 3 + x 2 — 2x -1) + (x 3 + 6x + 3).
Данные многочлены расположены в их стандартных формах.
Сложение выполняется по горизонтали:
- Шаг 1: Разделите одинаковые члены: 3x 3 и x 3 ; х 2 ; -2х и 6х; -1 и 3
- Шаг 2: Расположите одинаковые члены вместе: 3x 3 + x 3 + x 2 + (-2x + 6x) + (-1 + 3)
- Шаг 3: Выполните вычисления: (3 + 1)x 3 + x 2 + (-2 + 6)x + (-1 + 3)= 4x 3 + x 2 + 4x + 2
Сложение выполнено по вертикали:
- Шаг 1: Расположите оба полинома один над другим, чтобы одинаковые члены расположили один над другим.
 Мы можем представить отсутствующий член мощности в стандартной форме с «0» в качестве коэффициента, чтобы избежать путаницы при расположении членов. 92 + 4x + 2 \\ \hline \end{align}\]
Мы можем представить отсутствующий член мощности в стандартной форме с «0» в качестве коэффициента, чтобы избежать путаницы при расположении членов. 92 + 4x + 2 \\ \hline \end{align}\]Важные примечания:
- Высшая степень переменной в полиноме называется степенью полинома.
- Алгебраические выражения, имеющие отрицательную или иррациональную степень переменной, не являются полиномами.
- Сложение и вычитание в многочленах могут выполняться только на одинаковых условиях.
Сложный вопрос о сложении и вычитании многочленов
Найдите значение a, если сложить полиномы (a-2)x 3 + 3x 2 + 4x -1 и (2a + 1)x 3 + 2x 2 — — 3 — квадратичный многочлен.
Часто задаваемые вопросы о сложении и вычитании многочленов
Как складывать и вычитать многочлены?
 При сложении или вычитании полиномов нам нужно помнить о правилах сложения и вычитания полиномов. Правила можно объяснить так:
При сложении или вычитании полиномов нам нужно помнить о правилах сложения и вычитания полиномов. Правила можно объяснить так:- Правило 1: Всегда берите одинаковые члены вместе при выполнении сложения или вычитания.
- Правило 2: Кроме того, знаки всех многочленов остаются прежними. В режиме вычитания знаки вычитающих многочленов меняются.
Что такое биномы?
Биномы — это многочлены, содержащие только два члена. Например, x 2 + y 2 и 3x + 2y являются биномами. Например, x + y + z не является биномом.
Что главное помнить при сложении и вычитании многочленов?
Главное, что нужно помнить при выполнении сложения и вычитания полиномов:
- помнить о концепции подобных членов
- при умножении многочлена с отрицательным знаком все знаки будут изменены. т. е. + к — и — к +
Как вы комбинируете похожие термины?
В то время как комбинирует подобные термины , такие как 2x и 7x, мы просто добавляем их коэффициенты.
 Например, 2x + 7x = (2+7)x = 9Икс.
Например, 2x + 7x = (2+7)x = 9Икс.Что такое похожие термины?
Подобные термины — это термины, переменные которых, а также их показатели степени, совпадают. Например, 2x, 7x, -2x и т. д. — все они похожи на переменные.
Можете ли вы комбинировать термины с разными показателями степени?
Нет, вы можете комбинировать члены только с одной и той же переменной и одним и тем же показателем степени. Это означает , что вы можете комбинировать только квадраты переменных с квадратами переменных, кубы переменных с кубами переменных и т. д.
Видео с вопросами: Определение степени алгебраического выражения
Стенограмма видео
Какое из приведенных ниже выражений имеет ту же степень, что и три 𝑥 в восьмой степени плюс три 𝑥 в четвертой степени умноженные на 𝑦 в квадрате плюс четыре 𝑦 в квадрате? Это вариант (А) два 𝑥 в четвертой степени плюс два 𝑥 в восьмой степени, умноженные на 𝑦 в кубе плюс три 𝑦 в четвертой степени? Это вариант (B) три 𝑎 в седьмой степени плюс три 𝑎 в кубе, умноженные на 𝑏 в четвертой степени, плюс два 𝑏 в квадрате? Это вариант (C) три 𝑥 в квадрате плюс два 𝑥 в четвертой степени, умноженные на 𝑦 в четвертой степени, плюс три 𝑦 в седьмой степени? Или это вариант (D) три 𝑏 в девятой степени плюс три 𝑎 в кубе, умноженные на 𝑏, плюс два 𝑎 в шестой степени?
В этом вопросе нам даны четыре выражения.
 И нам нужно определить, какое из этих четырех выражений имеет ту же степень, что и заданный многочлен. Чтобы ответить на этот вопрос, начнем с того, что вспомним, что мы понимаем под степенью полиномиального выражения. Это наибольшая сумма показателей переменных в любом отдельном термине. А мы знаем, что можем найти только степень полиномиального выражения. Это означает, что нам нужно проверить две вещи. Во-первых, нам нужно проверить, являются ли четыре заданных параметра полиномиальными выражениями. Затем нам также нужно проверить их степени.
И нам нужно определить, какое из этих четырех выражений имеет ту же степень, что и заданный многочлен. Чтобы ответить на этот вопрос, начнем с того, что вспомним, что мы понимаем под степенью полиномиального выражения. Это наибольшая сумма показателей переменных в любом отдельном термине. А мы знаем, что можем найти только степень полиномиального выражения. Это означает, что нам нужно проверить две вещи. Во-первых, нам нужно проверить, являются ли четыре заданных параметра полиномиальными выражениями. Затем нам также нужно проверить их степени.Итак, давайте начнем с проверки того, являются ли четыре заданных параметра полиномами. Для этого нам сначала нужно вспомнить, что мы подразумеваем под полиномиальным выражением. Мы помним, что полиномиальное выражение — это выражение, в котором каждый член является произведением констант и переменных, где наши переменные должны быть возведены в неотрицательные целые степени. И мы видим, что это верно для четырех заданных вариантов. Все члены являются произведениями констант и переменных, и все переменные возводятся в неотрицательные целые степени.
 Следовательно, все четыре приведенных варианта являются многочленами, и мы можем вычислить их степени.
Следовательно, все четыре приведенных варианта являются многочленами, и мы можем вычислить их степени.Чтобы сравнить степени, нам нужно сначала найти степень многочлена, данного нам в вопросе. И мы собираемся сделать это, найдя степень каждого члена в отдельности. Начнем с первого термина. Мы хотим найти степень трех 𝑥 в восьмой степени. И мы можем сделать это из определения степени. Это наибольшая сумма показателей переменных в одном термине. Однако нас интересует только один термин. Поэтому нам просто нужно найти сумму показателей степени переменных в этом термине. И этот термин имеет только одну переменную 𝑥. Таким образом, сумма показателей переменных в этом члене будет равна одному члену, восьми. Это означает, что степень этого первого члена как раз равна восьми.
Точно так же мы можем найти степень второго члена. Еще раз, степень этого термина является суммой показателей переменных. На этот раз этот термин имеет две переменные, 𝑥 и 𝑦. Поэтому нам нужно сложить их показатели вместе.
 Четыре плюс два равно шести. Следовательно, второй член в этом выражении имеет шестую степень. Нам нужно применить этот процесс еще раз, чтобы определить степень третьего члена, четыре 𝑦 в квадрате. Еще раз, этот термин имеет только одну переменную, 𝑦. Так что, как и в случае с первым членом, степень этого многочлена будет показателем степени этой переменной. Поскольку показатель степени равен двум, его степень равна двум.
Четыре плюс два равно шести. Следовательно, второй член в этом выражении имеет шестую степень. Нам нужно применить этот процесс еще раз, чтобы определить степень третьего члена, четыре 𝑦 в квадрате. Еще раз, этот термин имеет только одну переменную, 𝑦. Так что, как и в случае с первым членом, степень этого многочлена будет показателем степени этой переменной. Поскольку показатель степени равен двум, его степень равна двум.Наконец, помните, что степень всего выражения равна наибольшей сумме показателей степени переменных в любом отдельном члене. И это еще один способ сказать, что степень многочлена — это наибольшая степень любого из его отдельных членов. И мы показали, что наибольшая из этих трех степеней равна восьми. Это означает, что мы показали, что полиномиальное выражение, данное в вопросе, имеет восьмую степень. И нам нужно определить, какой из четырех заданных вариантов имеет восьмую степень. Мы можем сделать это, выполнив один и тот же процесс для всех четырех заданных вариантов, чтобы определить их степень и посмотреть, какой из них имеет степень восемь.

Однако есть несколько сокращений, которые можно использовать для облегчения этого процесса. Например, в варианте (D) мы можем заметить, что переменная возведена в девятую степень. А это значит, что степень этого отдельного термина должна быть больше или равна девяти. Конечно, мы не можем просто вычислить степень этого термина. Поскольку есть только одна переменная 𝑏, степень этого члена будет просто степенью 𝑏. Будет девять. Но тогда мы можем заметить кое-что интересное. Степень полинома — это наибольшая степень любого из его отдельных членов. Итак, поскольку мы показали, что степень одного из членов равна девяти, мы можем заключить, что степень этого полиномиального выражения должна быть больше или равна девяти. Это нижняя граница степени. Следовательно, степень варианта (D) больше или равна девяти. Оно не может быть равно восьми. Так что вариант (Г) неверен.
Ну, конечно, стоит отметить, что мы можем просто вычислить степень этого многочлена. Степень второго члена равна сумме показателей переменных: три плюс один равно четырем.
 А третий и последний член имеет только одну переменную. Таким образом, его степень — это просто показатель степени этой переменной, шесть. Тогда наибольшая из этих трех степеней равна девяти. Значит, этот многочлен имеет девятую степень. Если мы проверим все остальные параметры, то увидим, что ни одна из переменных не возводится в степень, большую или равную девяти. Поэтому мы не можем использовать это, чтобы исключить другие варианты. Однако мы можем просто найти степень всех трех оставшихся вариантов.
А третий и последний член имеет только одну переменную. Таким образом, его степень — это просто показатель степени этой переменной, шесть. Тогда наибольшая из этих трех степеней равна девяти. Значит, этот многочлен имеет девятую степень. Если мы проверим все остальные параметры, то увидим, что ни одна из переменных не возводится в степень, большую или равную девяти. Поэтому мы не можем использовать это, чтобы исключить другие варианты. Однако мы можем просто найти степень всех трех оставшихся вариантов.Начнем с варианта (А). Первый и последний термин являются только терминами с одной переменной. Таким образом, степень каждого из этих двух членов будет просто показателем степени переменной. Оба они будут четвертой степени. Давайте теперь определим степень второго члена, два 𝑥 в восьмой степени, умноженные на 𝑦 в кубе. Этот термин имеет две переменные, поэтому нам нужно сложить показатели переменных вместе. Восемь плюс три равно 11. Тогда мы можем видеть, что наибольшая из степеней любого отдельного члена равна 11.
 Таким образом, мы показали, что многочлен в варианте (А) имеет степень 11. Это не та же степень, что и у полиномиальное выражение, данное в вопросе.
Таким образом, мы показали, что многочлен в варианте (А) имеет степень 11. Это не та же степень, что и у полиномиальное выражение, данное в вопросе.Точно такой же процесс можно применить для нахождения степеней вариантов (B) и (C). Во-первых, в вариантах (B) и (C) и первый, и последний термин имеют по одной переменной. Таким образом, степени этих членов будут показателями этих переменных, семь и два, соответственно. Далее, второй член имеет две переменные. Итак, нам нужно сложить показатели переменных вместе. Три плюс четыре равно семи. Теперь нам нужно найти наибольшую из этих степеней. И первый, и второй члены имеют степень семь, которая является наибольшей из величин. Значит, этот многочлен имеет седьмую степень. Это не та же степень, что и полином, указанный в вопросе. Так что вариант (Б) неверен.
Теперь давайте проделаем то же самое с вариантом (C). Опять же, первый и последний члены являются одиночными переменными. Таким образом, мы можем найти их степень, просто взглянув на показатель степени переменных.



 В этом случае они уже в своих стандартных формах.
В этом случае они уже в своих стандартных формах.

 Мы можем представить отсутствующий член мощности в стандартной форме с «0» в качестве коэффициента, чтобы избежать путаницы при расположении членов. 92 + 4x + 2 \\ \hline \end{align}\]
Мы можем представить отсутствующий член мощности в стандартной форме с «0» в качестве коэффициента, чтобы избежать путаницы при расположении членов. 92 + 4x + 2 \\ \hline \end{align}\]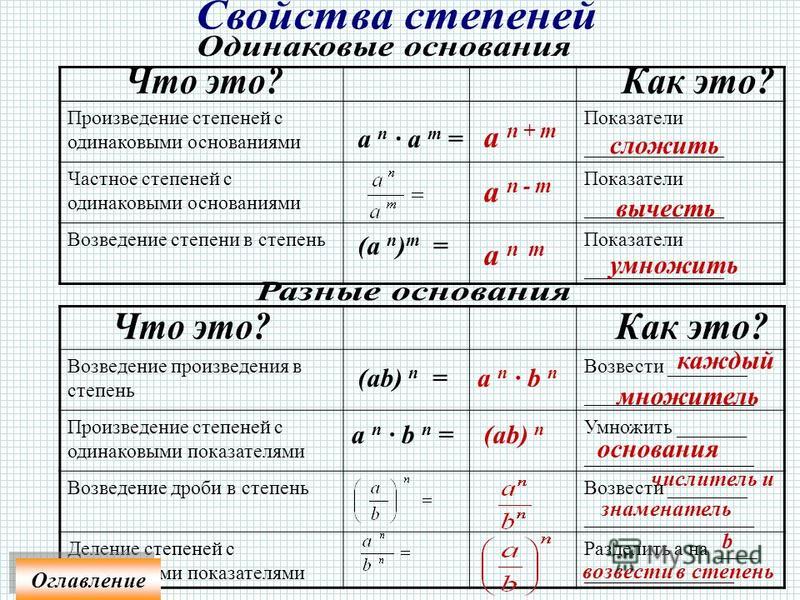 При сложении или вычитании полиномов нам нужно помнить о правилах сложения и вычитания полиномов. Правила можно объяснить так:
При сложении или вычитании полиномов нам нужно помнить о правилах сложения и вычитания полиномов. Правила можно объяснить так: Например, 2x + 7x = (2+7)x = 9Икс.
Например, 2x + 7x = (2+7)x = 9Икс. И нам нужно определить, какое из этих четырех выражений имеет ту же степень, что и заданный многочлен. Чтобы ответить на этот вопрос, начнем с того, что вспомним, что мы понимаем под степенью полиномиального выражения. Это наибольшая сумма показателей переменных в любом отдельном термине. А мы знаем, что можем найти только степень полиномиального выражения. Это означает, что нам нужно проверить две вещи. Во-первых, нам нужно проверить, являются ли четыре заданных параметра полиномиальными выражениями. Затем нам также нужно проверить их степени.
И нам нужно определить, какое из этих четырех выражений имеет ту же степень, что и заданный многочлен. Чтобы ответить на этот вопрос, начнем с того, что вспомним, что мы понимаем под степенью полиномиального выражения. Это наибольшая сумма показателей переменных в любом отдельном термине. А мы знаем, что можем найти только степень полиномиального выражения. Это означает, что нам нужно проверить две вещи. Во-первых, нам нужно проверить, являются ли четыре заданных параметра полиномиальными выражениями. Затем нам также нужно проверить их степени. Следовательно, все четыре приведенных варианта являются многочленами, и мы можем вычислить их степени.
Следовательно, все четыре приведенных варианта являются многочленами, и мы можем вычислить их степени. Четыре плюс два равно шести. Следовательно, второй член в этом выражении имеет шестую степень. Нам нужно применить этот процесс еще раз, чтобы определить степень третьего члена, четыре 𝑦 в квадрате. Еще раз, этот термин имеет только одну переменную, 𝑦. Так что, как и в случае с первым членом, степень этого многочлена будет показателем степени этой переменной. Поскольку показатель степени равен двум, его степень равна двум.
Четыре плюс два равно шести. Следовательно, второй член в этом выражении имеет шестую степень. Нам нужно применить этот процесс еще раз, чтобы определить степень третьего члена, четыре 𝑦 в квадрате. Еще раз, этот термин имеет только одну переменную, 𝑦. Так что, как и в случае с первым членом, степень этого многочлена будет показателем степени этой переменной. Поскольку показатель степени равен двум, его степень равна двум.
 А третий и последний член имеет только одну переменную. Таким образом, его степень — это просто показатель степени этой переменной, шесть. Тогда наибольшая из этих трех степеней равна девяти. Значит, этот многочлен имеет девятую степень. Если мы проверим все остальные параметры, то увидим, что ни одна из переменных не возводится в степень, большую или равную девяти. Поэтому мы не можем использовать это, чтобы исключить другие варианты. Однако мы можем просто найти степень всех трех оставшихся вариантов.
А третий и последний член имеет только одну переменную. Таким образом, его степень — это просто показатель степени этой переменной, шесть. Тогда наибольшая из этих трех степеней равна девяти. Значит, этот многочлен имеет девятую степень. Если мы проверим все остальные параметры, то увидим, что ни одна из переменных не возводится в степень, большую или равную девяти. Поэтому мы не можем использовать это, чтобы исключить другие варианты. Однако мы можем просто найти степень всех трех оставшихся вариантов. Таким образом, мы показали, что многочлен в варианте (А) имеет степень 11. Это не та же степень, что и у полиномиальное выражение, данное в вопросе.
Таким образом, мы показали, что многочлен в варианте (А) имеет степень 11. Это не та же степень, что и у полиномиальное выражение, данное в вопросе.