Сложение и вычитание векторов
На уроках геометрии вы уже познакомились с простейшими операциями над векторами: нахождением их суммы и разности. Напомним это.
Сложение векторов. Чтобы найти сумму двух векторов, необходимо: а) параллельным переносом совместить начала векторов; б) дополнить чертёж двумя отрезками так, чтобы получился параллелограмм; в) провести вектор суммы из точки начал векторов в точку соединения дополняющих отрезков (по диагонали параллелограмма).
Проиллюстрируем это правило на примере из § 12-в, когда автомобиль перемещается сначала по вектору AВ1 и затем по вектору В1В2 до поворота на мост (см. чертёж слева). Другими словами, мы ищем вектор суммы или, что то же самое, сумму векторов AВ1 и В1В2.
Сделаем новые чертежи обсуждаемых векторов (см. ниже). На чертеже «а» применим параллельный перенос и переместим вектор В1В2 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним двумя отрезками СВ2 и В1В2 до образования параллелограмма. На чертеже «в» проведём вектор суммы из точки А начал векторов в точку В2 соединения дополняющих отрезков (по диагонали параллелограмма).
На чертеже «в» проведём вектор суммы из точки А начал векторов в точку В2 соединения дополняющих отрезков (по диагонали параллелограмма).
Итак, мы нашли вектор суммы или сумму векторов:
Проверим правильность результата: автомобиль, переместившись из точки А в точку В1, затем переместился из точки В1 в точку В2. Иначе говоря, он совершил перемещение «по» вектору АВ2, который мы только что построили, применив правило паралеллограмма.
Вычитание векторов. Чтобы найти разность двух векторов, нужно: а) параллельным переносом совместить начала векторов; б) дополнить чертёж отрезком так, чтобы получился треугольник; в) придать отрезку направление от вычитаемого к уменьшаемому, создав вектор разности.
Проиллюстрируем это правило на том же примере из § 12-в, когда автомобиль подъезжает к середине моста. Для этого из вектора полного перемещения АВ3 вычтем перемещение на третьем этапе, вектор B2В3.
Другими словами, сейчас мы ищем вектор разности:
На чертеже «а» применим параллельный перенос и переместим вектор В2В3 началом в точку А (то есть совместим начала векторов).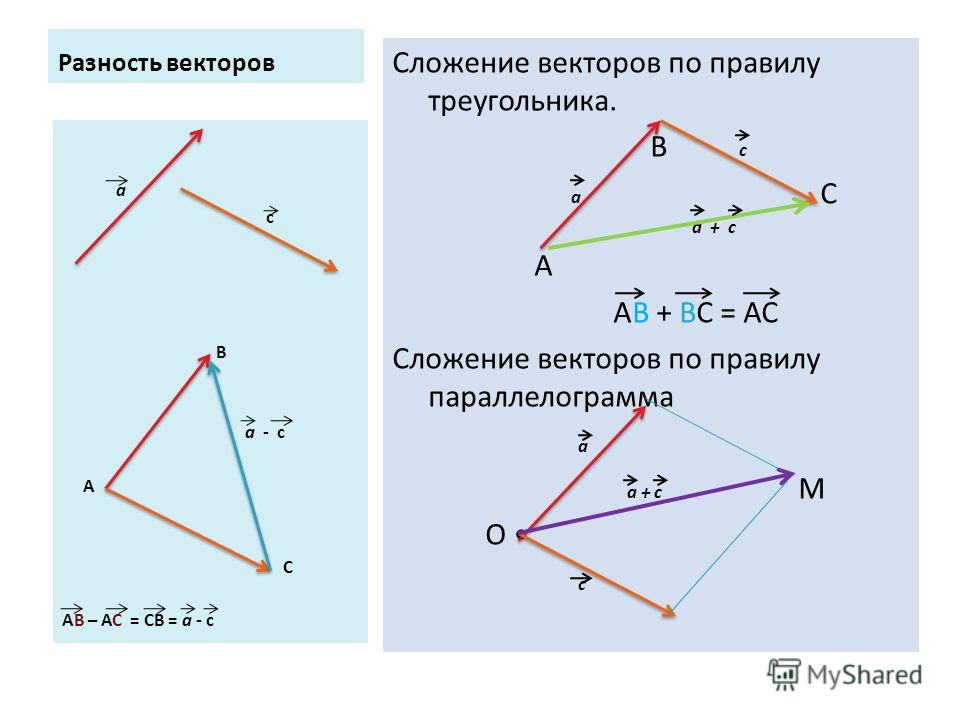 Чертёж «б» дополним отрезком DВ3 до образования треугольника. На чертеже «в» придадим отрезку направление от вычитаемого (синего вектора) к уменьшаемому (красному вектору), создав вектор разности DВ3.
Чертёж «б» дополним отрезком DВ3 до образования треугольника. На чертеже «в» придадим отрезку направление от вычитаемого (синего вектора) к уменьшаемому (красному вектору), создав вектор разности DВ3.
Контурной стрелкой показан параллельный перенос найденного вектора разности в точку А. Важно: построенный вектор DВ3 равен искомому вектору разности АВ2. Это, по сути, проверка правильности результата, поскольку этот вектор мы уже находили по правилу параллелограмма.
Заметим, что векторы можно складывать и «треугольником», а вычитать «параллелограммом». Но мы рекомендуем запомнить именно правило параллелограмма для суммы векторов и правило треугольника для разности векторов, поскольку в дальнейшем эти правила понадобятся нам именно в таком виде.
Опубликовано в разделах: 9 класс, Введение в кинематикув чем оно состоит, примеры решения задач
Основные понятия
Определение 1Направленный вектор — это отрезок, для которого указано, какая из его граничных точек является началом, а какая концом.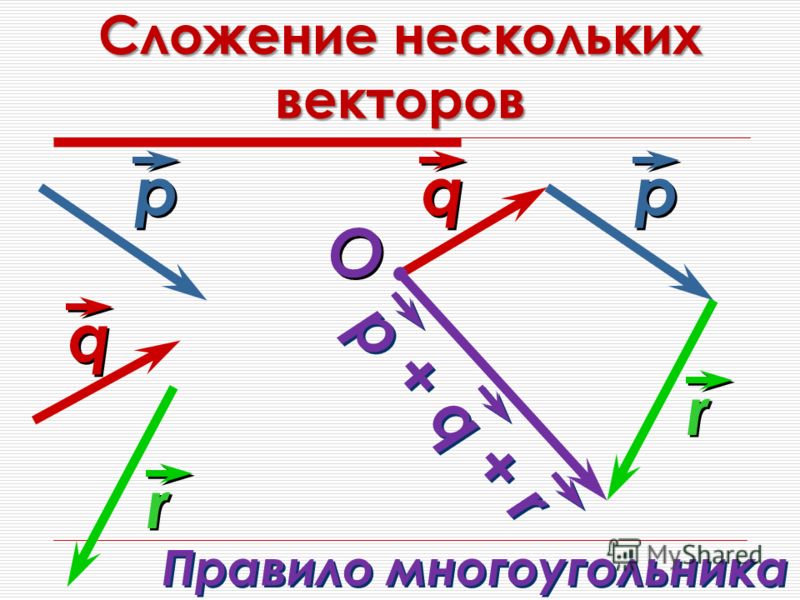
Обозначается следующим образом:
Коллинеарность векторов означает: ненулевые векторы, которые лежат на одной прямой или на параллельных прямых. Нулевой вектор (вектор нулевой длины) является коллинеарным любому вектору.
Определение 2Сонаправленные векторы — векторы, направленные в одну сторону.
Определение 3Противонаправленные векторы — векторы, направленные в разные стороны.
Определение 4
Равные векторы — векторы, которые коллинеарны, сонаправлены и имеют одинаковую длину.
Формулировка компланарности векторов: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Три вектора, среди которых имеются два коллинеарных, также компланарны.
Некомпланарный вектор не имеет равный ему вектор, лежащий в одной плоскости.
Складывать векторы можно несколькими способами. Мы рассмотрим сложение векторов методом параллелограмма.
Сложение векторов по правилу параллелограмма
Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти векторы и построить на них параллелограмм. Диагональ параллелограмма, исходящая из этой точки, и будет суммой векторов.
Диагональ параллелограмма, исходящая из этой точки, и будет суммой векторов.
На рисунке все наглядно проиллюстрировано.
сочетательный закон:
Из произвольной точки А отложим вектор , прибавим к нему вектор , получим их сумму . К этой сумме прибавим вектор , получим результат:
В правой части выражения мы сначала получили сумму векторов , после прибавили ее к вектору и получили результат:
Таким образом, мы провели доказательство сочетательного закона сложения векторов.
Когда векторы расположены в пространстве и они не компланарны, для их сложения применяется правило параллелепипеда.
Для начала проводят построение:
- Векторы приводят к общему началу А.
2. На этих трех ребрах строиться параллелепипед.
3. Диагональ параллелепипеда, которая выходит из этой же точки, изображает суммы векторов АВ, AD, AA1.
Примеры решения задач
Пример 1Определить вид четырехугольника ABCD, если:
Решение:
Данный четырехугольник — ромб. Обоснуем это.
Обоснуем это.
Мы знаем, что векторы и равны, отсюда следует, что равны их модули — то есть длины отрезков.
Векторы по условию сонаправлены и коллинеарны, то есть принадлежат параллельным прямым. Таким образом, заданный четырехугольник — параллелограмм.
Данный факт обоснован признаком параллелограмма: если две стороны четырехугольника принадлежат параллельным прямым и длины их равны, то данный четырехугольник — параллелограмм.
Согласно второму условию: , соседние стороны параллелограмма равны друг другу, а такой параллелограмм является ромбом.
Пример 2Дан параллелепипед ABCDА1B1С1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: AB+AD+AА1.
Решение:
AB+AD=AC, AC+AA1=AC1
Ответ: AC1.
Задания для самостоятельной работы
Задание 1Дан параллелограмм ABCD. Найдите сумму векторов CD+DB+BA.
Задание 2Дан параллелепипед ABCDА1B1С1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: DA+DC+DD1.
Математика и наука были изобретены людьми для описания и понимать окружающий мир. Заметим, что существуют некоторые величины и процессы в наш мир, которые зависят от направления , в котором они происходят, и есть некоторые величины, которые не зависят по направлению. Математики и ученые называют количество который зависит от направления a количество векторов . Количество которая не зависит от направления, называется скалярной величиной . А векторное количество имеет две характеристики: величина и направление . Когда сравнение две векторные величины одного и того же типа, вы должны сравнить обе величина и направление. На этом слайде мы описываем метод сложения двух векторов.
Сложение векторов — это один из аспектов большой векторной алгебры, которую мы изучаем. , а не будет представлен на этом сайте. Добавление вектора представлено
здесь потому, что встречается довольно часто при изучении ракет
и потому что он демонстрирует некоторые фундаментальные различия между
векторы и скаляры. Векторы обычно обозначаются на рисунках стрелкой. Длина стрелки указывает величину и кончик стрелки указывает направление. Вектор помечены буквой в алфавитном порядке буква с линией сверху, чтобы отличить ее от скаляра. Величину вектора будем обозначать символом |а| . Направление будет измеряться углом фи относительно координаты ось х . Ось координат y перпендикулярна х . Примечание: Оси координат x и y сами по себе векторы! Они имеют величину и направление. Ты первый столкнуться с осями координат, когда вы учитесь строить графики. Так что у тебя есть использовал векторы в течение некоторого времени, даже не подозревая об этом! Если мы построим пунктирную линию от кончика вектора a идущий параллельно оси х, он пересекает ось у в том месте, где мы
этикетка или . Точно так же линия от кончика вектора
параллельно оси y пересекает ось x в точке x . Чтобы добавить два вектора, а и б , мы сначала разбиваем каждый вектор на его компоненты, x и a , и bx и по , как показано на рисунке. Из правил, регулирующих равенство векторов, синий вектор b равен черному вектору b потому что он имеет одинаковую равную длину и одинаковое направление. Теперь, поскольку компоненты вектора и вектор b скаляры, мы можем добавить x-компоненты для генерации x-компонент нового вектора c : сх = топор + Ьх Точно так же мы можем добавить y-компонентов : су = ау + по Новые компоненты cx и cy полностью определяют
новый вектор c , указав как величину, так и направление.
Внимательно взглянув на диаграмму, мы видим, что сложение двух векторов дает
новый вектор, равный , а не в направлении любого из
исходные векторы, величина которых равна , а не и равна сумме
величин исходных векторов. Примечание: На этом слайде для простоты мы разработали компоненты только в двух измерениях; имеются две оси координат. В действительности существуют три пространственных измерения и три компонента мира. все силы. Это важно для нашего вывода общие уравнения с движением для траекторий полета и для Навье-Стокса и уравнения Эйлера, которые описать силы и результирующее движение жидкостей в двигателе. Мы можем разбить очень сложные трехмерные векторные задачи на всего три скалярных уравнения. Экскурсии с гидом
Деятельность: Связанные сайты: |
геометрия — Причина закона сложения векторов
спросил
Изменено 3 года, 4 месяца назад
Просмотрено 201 раз
$\begingroup$
В чем причина треугольного закона сложения векторов, другими словами, как это действительно оправдано?
- векторы
- геометрия
- математика
$\endgroup$
4
$\begingroup$
Наивный ответ.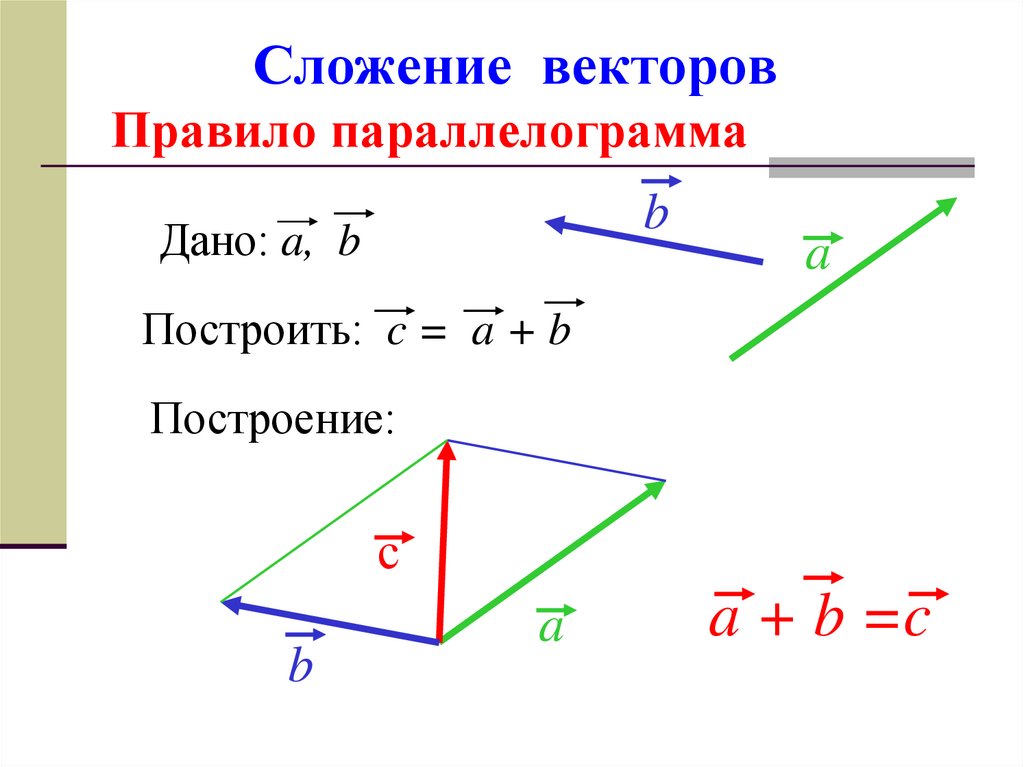 ..
..
Если вы идете из A в B, а затем из B в C, вы можете представить свое перемещение из A в B в виде стрелки, а из B в C — в другую стрелку. Ясно, что ваше смещение от А к С может быть представлено стрелкой, идущей от А к С, или двумя уже упомянутыми стрелками, помещенными так, чтобы хвост второй касался головы первой. Это правило добавления смещений, и, возможно, оно самоочевидно. Правило можно распространить на любое количество перемещений.
Скорость — это перемещение в единицу времени, поэтому скорости должны складываться как смещения.
Импульс и ускорение определяются через скорость, поэтому импульсы и ускорения должны складываться как смещения.
Аргумент можно распространить с помощью второго закона Ньютона на силы и напряженности поля.
$\endgroup$
3
$\begingroup$
При сложении двух векторов результирующий вектор формируется путем сложения компонентов двух отдельных векторов.


 Величины x и ay называются
составные части
вектора, и оба являются скалярными квантитами.
Величины x и ay называются
составные части
вектора, и оба являются скалярными квантитами.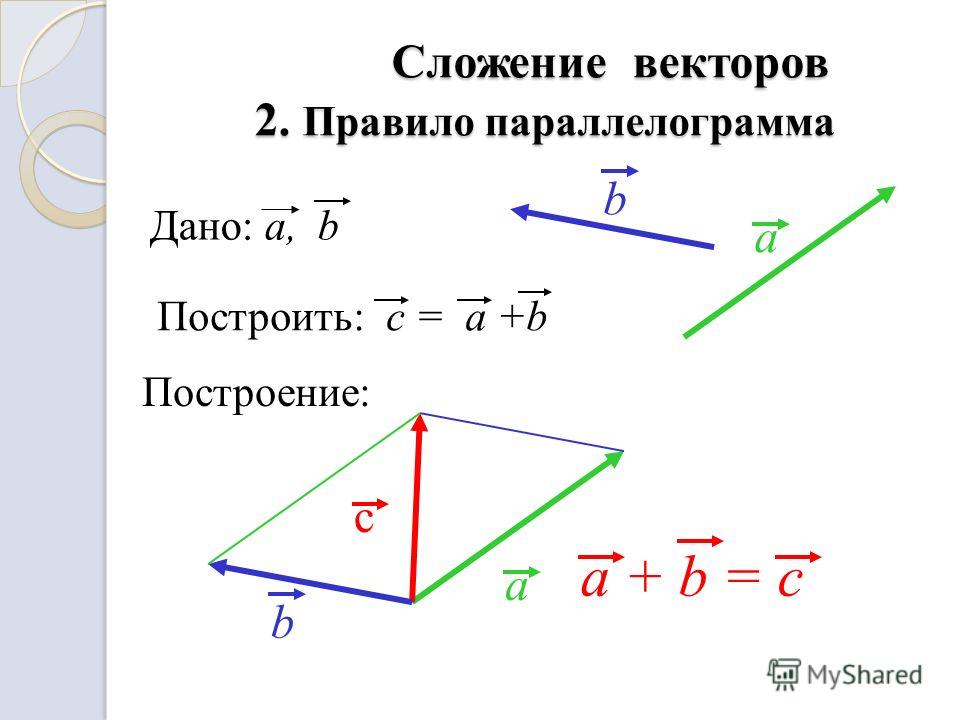 Векторная алгебра сильно отличается от скалярной алгебры, потому что она должна
учитывать как величину, так и направление.
Векторная алгебра сильно отличается от скалярной алгебры, потому что она должна
учитывать как величину, так и направление.