Калькулятор площадь треугольника прямоугольного: Площадь прямоугольного треугольника | Онлайн калькулятор

Найти площадь прямоугольного треугольника — онлайн калькулятор

Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• длины катетов a и b
• длину гипотенузы с и длину любого из катетов (a или b)
• длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
• длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• длину гипотенузы с и один из острых углов (α или β)

Найти площадь прямоугольного треугольника по двум катетам

Катет a =
Катет b =
S =

Просто введите длины двух катетов, и получите ответ.

Теория

Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?

Формула

S = ½ ⋅ a ⋅ b

Пример

К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:

S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²

Найти площадь прямоугольного треугольника по катету и гипотенузе

Гипотенуза c =
Катет (a или b) =
S =

Введите длины гипотенузы и одного из катетов, и получите ответ.

Теория

Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?

Формула

S = ½ ⋅ a ⋅ √c² — a² = ½ ⋅ b ⋅ √c² — b²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:

S = 2 ⋅ √5² — 2² / 2 = √25 — 4 ≈ 4.58 см²

Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу

Катет (a или b) =
Прилежащий угол (β или α) = °
S =

Введите длину одного из катетов и прилежащий к нему острый угол в градусах.

То есть к катету a прилежащий ∠β, а к катету

b — ∠α

Теория

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:

S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²

Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу

Катет (a или b) =
Противолежащий угол (α или β) = °
S =

Введите длину одного из катетов и противолежащий к нему острый угол в градусах.

То есть к катету a противолежащий ∠α, а к катету b — ∠β

Теория

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:

S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²

Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов

Гипотенуза c =
Угол (α или β) = °
S =

Введите длину гипотенузы и один из острых угол в градусах.

Теория

Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?

Формула

S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:

S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.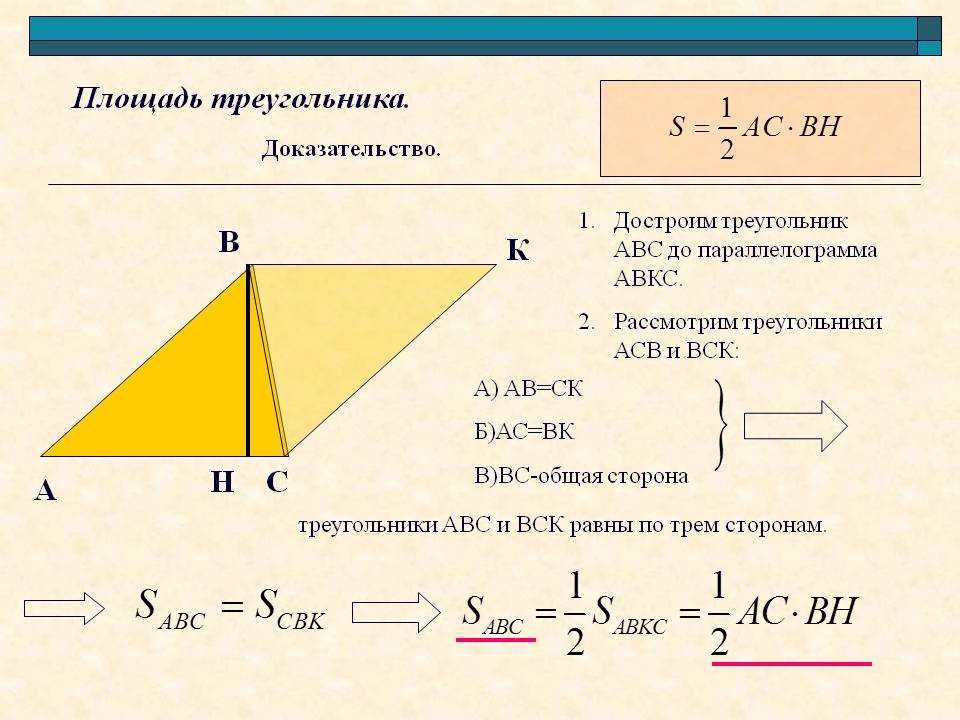 7071067812 ⋅ 0.7071067812 ≈ 16 см²

Площадь прямоугольного треугольника онлайн

С помощю этого онлайн калькулятора можно найти площадь прямоугольного треугольника. Для нахождения площади прямоугольного треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Содержание

• Площадь прямоугольного треугольника по двум катетам
• Площадь прямоугольного треугольника по катету и гипотенузе
• Площадь прямоугольного треугольника по гипотенузе и углу
• Площадь прямоугольного треугольника по катету и прилежащему углу
• Площадь прямоугольного треугольника по катету и противолежащему углу
• Площадь прямоугольного треугольника по гипотенузе и вписанной окружности
• Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность

Площадь прямоугольного треугольника по двум катетам

Как известно, площадь треугольника равна половине произведения его основания на высоту (см. страницу Площадь треугольника онлайн).В прямоугольном треугольнике катеты перпендикулярны друг другу. Поэтому можно один из них считать как основание, а другой − как высоту.

На рисунке 1 можем считать a как основание, а b − как высоту. Тогда площадь прямоугольного треугольника равна:

Пример 1. Известны катеты прямоугольного треугольника: Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (1). Подставляя значения в (1), получим:

Ответ:

Площадь прямоугольного треугольника по катету и гипотенузе

Пусть в прямоугольном треугольнике известны катет a и гипотенуза c (Рис.2):

Найдем площадь треугольника. Из формулы Пифагора имеем:

Подставляя (2) в (1), получим формулу вычисления площади прямоугольного треугольника по катету и гипотенузе:

Пример 2. Известны катет и гипотенуза прямоугольного треугольника: Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (3).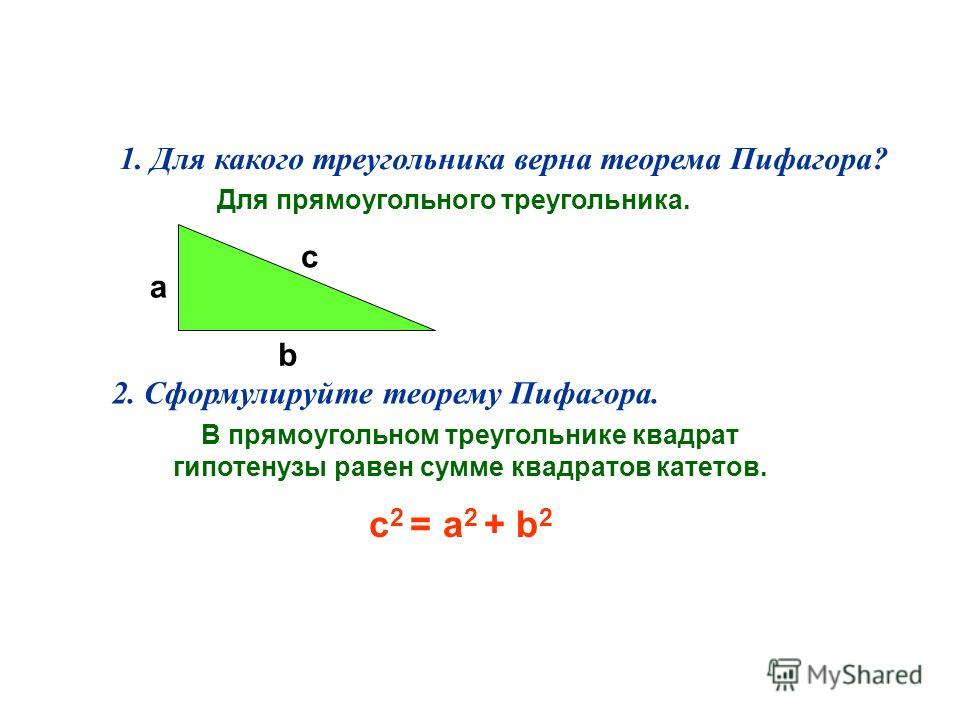 Подставляя значения в (3), получим:

Ответ:

Площадь прямоугольного треугольника по гипотенузе и углу

Пусть в прямоугольном треугольнике известны гипотенуза с и угол α (Рис.3):

Найдем площадь прямоугольного треугольника. Из теоремы синусов имеем:

или

Подставим (4) в (1):

Из формулы произведения тригонометрических функций имеем:

Подставим в (6) \( \small \beta=\alpha \):

Применяя (7) относительно формулы (5), получим:

Пример 3. Известны гипотенуза и прилегающий угол прямоугольного треугольника: . Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (8). Подставляя значения в (8), получим:

Ответ:

Площадь прямоугольного треугольника по катету и прилежащему углу

Пусть в прямоугольном треугольнике известны катет a и прилежащий угол α (Рис.4):

Найдем площадь прямоугольного треугольника. Тангенс угла α прямоугольного треугольника равна:

Откуда

Подставляя (9) в (1), получим формулу площади прямоугольного треугольника по катету и прилежащему углу:

Пример 4. Известны катет и прилегающий угол прямоугольного треугольника: . Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (10). Подставляя значения в (10), получим:

Ответ:

Площадь прямоугольного треугольника по катету и противолежащему углу

Пусть в прямоугольном треугольнике известны катет a и противолежащий угол α (Рис.5):

Найдем площадь прямоугольного треугольника. Коангенс угла α прямоугольного треугольника равна:

Откуда

Подставляя (12) в (1), получим формулу площади прямоугольного треугольника по катету и противожащему углу:

Пример 5. Известны катет и противолежащий угол прямоугольного треугольника: . Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (13). Подставляя значения в (13), получим:

Ответ:

Площадь прямоугольного треугольника по гипотенузе и вписанной окружности

Пусть в прямоугольном треугольнике известны гипотенуза с и радиус вписанной окружности r (Рис. 6):

Найдем площадь прямоугольного треугольника. Соединим центр окружности O c вершинами A, B и с точками D, E, F.

Треугольники AOD, AOF, BOD, BOE прямоугольные, поскольку Прямоугольные треугольники AOD и AOF равны по гипотенузе и катету (сторона AO общая, OD=OF):

Прямоугольные треугольники BOD и BOE равны по гипотенузе и катету (сторона BO общая, OD=OE):

Запишем формулы площадей прямоугольных треугольников AOD и BOD и квадрата OECF:

Тогда, учитывая (14) и (15), площадь прямоугольного треугольника ABC равна:

Подставляя (16), (17) в (18), получим:

или

Пример 6. Известны гипотенуза и радиус вписанной окружности прямоугольного треугольника: Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (19). Подставляя значения в (19), получим:

Ответ:

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность

Пусть в прямоугольном треугольнике известны отрезки AD и DB (Рис. 6). Найдем площадь прямоугольного треугольника выраженные через эти отрезки. Площадь прямоугольного треугольника через катеты имеет вид:

Учитывая, что , (20) примет вид:

То есть

Сравнивая формулы (19) и (21) можем записать:

Таким образом формула площади прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность имеет следующий вид:

Пример 7. Известны отрезки гипотенузы разделенные вписанной окружностью прямоугольного треугольника (Рис.6) Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (22). Подставляя значения в (22), получим:

Ответ:

Смотрите также:

• Площадь треугольника онлайн
• Площадь равностороннего треугольника онлайн
• Площадь равнобедренного треугольника онлайн

Калькулятор прямоугольного треугольника

| PI Day

C (Hypotenuse)

---

Периметр

Угол 1

Угол 2

Угол 3

Вернитесь в калькуляторы. прямоугольный треугольник в верхние поля. Затем калькулятор определит длину оставшейся стороны, площадь и периметр треугольника, а также все углы треугольника.

Как найти площадь и стороны прямоугольного треугольника

Сделай сам

Если мы знаем только две стороны прямоугольного треугольника, мы можем использовать эту информацию, чтобы найти третью сторону, площадь и периметр треугольника, и все углы треугольника. Удивительно, правда? Давайте рассмотрим, как мы найдем каждую из этих частей.

Как найти недостающую сторону прямоугольного треугольника

Чтобы найти недостающую сторону прямоугольного треугольника, мы используем знаменитую теорему Пифагора.

Нам нужно быть немного осторожными, чтобы знать, какую сторону мы находим. Прямоугольные треугольники имеют два катета и гипотенузу, которая является самой длинной стороной и всегда находится напротив прямого угла. Когда мы пытаемся найти гипотенузу, мы заменяем две наши известные стороны на и b на . Неважно, какая ножка a , а какая b . Затем мы находим c , складывая квадраты значений a и b и извлечь квадратный корень из обеих частей.

Когда мы пытаемся найти один из катетов, мы вводим известный катет для a и известную гипотенузу для c . Затем мы находим b с помощью простой алгебры (вычитаем значение a в квадрате с обеих сторон, затем извлекаем квадратный корень из обеих сторон).

Как найти площадь прямоугольного треугольника

Чтобы найти площадь прямоугольного треугольника, нам нужно знать только длину двух катетов. Нам вообще не нужна гипотенуза. Это потому, что катеты определяют основание и высоту треугольника в каждом прямоугольном треугольнике. Поэтому мы используем общую формулу площади треугольника (A = основание • высота/2) и подставляем a и b для основание и высота . Итак, наша новая формула для площади прямоугольного треугольника: A = ab/2.

Как найти периметр прямоугольного треугольника

Чтобы найти периметр или расстояние вокруг нашего треугольника, нам просто нужно сложить все три стороны вместе. Если мы знаем только две стороны, нам нужно сначала использовать теорему Пифагора, чтобы найти третью сторону.

Как найти углы прямоугольного треугольника

Чтобы найти углов прямоугольного треугольника, мы используем тригонометрию. Это не так сложно, как кажется. Нам просто нужно найти одну специальную кнопку на наших карманных калькуляторах. Для начала нам нужно знать все длины сторон, поэтому, если мы их еще не знаем, мы сначала воспользуемся теоремой Пифагора, чтобы найти их.

Когда у нас есть все стороны, мы определяем, какой угол мы собираемся найти.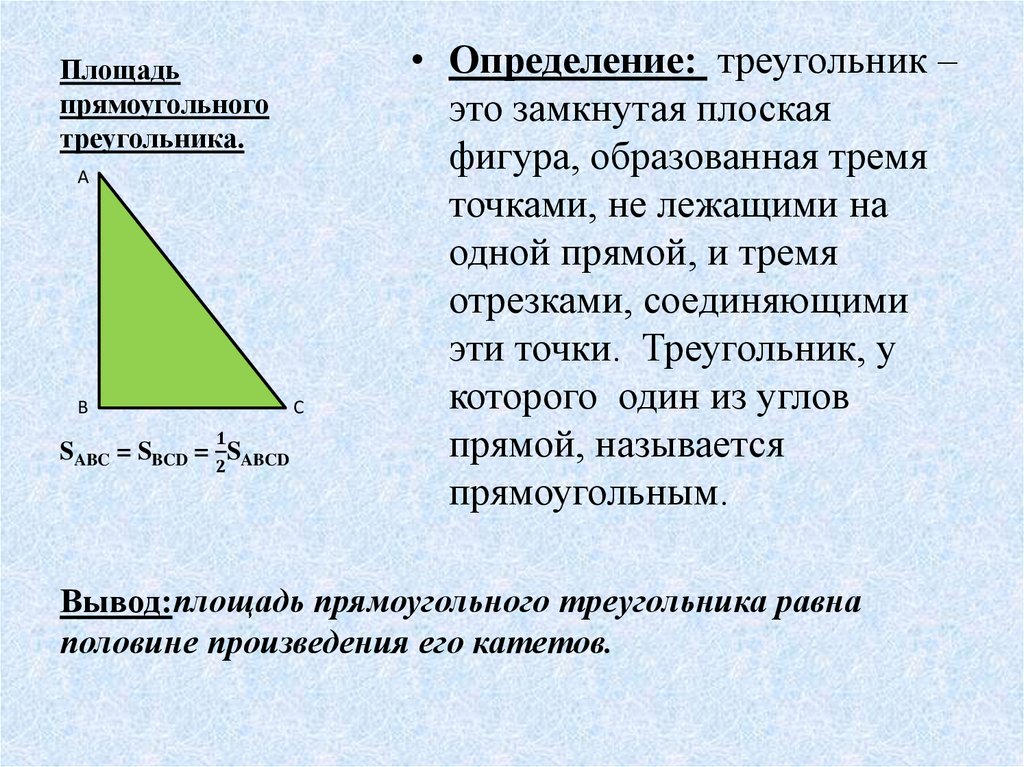 Затем мы берем сторону, противоположную этому углу, и делим ее на длину гипотенузы, которая равна стороне 9.0016 с . Это даст нам значение от 0 до 1. Теперь нам просто нужно найти кнопку ARCSIN на нашем калькуляторе, которая часто помечается как SIN ^-1 . Нахождение ARCSIN нашего десятичного значения дает нам угол. Убедитесь, что калькулятор настроен на угловой режим, а не на радианный.

Мы можем повторить этот процесс, чтобы найти другой неизвестный угол в треугольнике, еще раз разделив его противоположную сторону на гипотенузу, а затем взяв ARCSIN.

Или мы могли бы продемонстрировать еще больше знаний о треугольниках, используя вычитание, чтобы найти его, поскольку мы знаем, что сумма внутренних углов треугольника должна составлять 180°. Вычитание угла, который мы только что нашли, из 180°, а затем вычитание нашего известного прямого угла (90°) также даст нам третий угол.

Этот калькулятор отлично подходит для получения всей этой информации только с двух сторон прямоугольного треугольника, но это забавная задача, чтобы попытаться найти стороны, углы, площадь и периметр самостоятельно без него.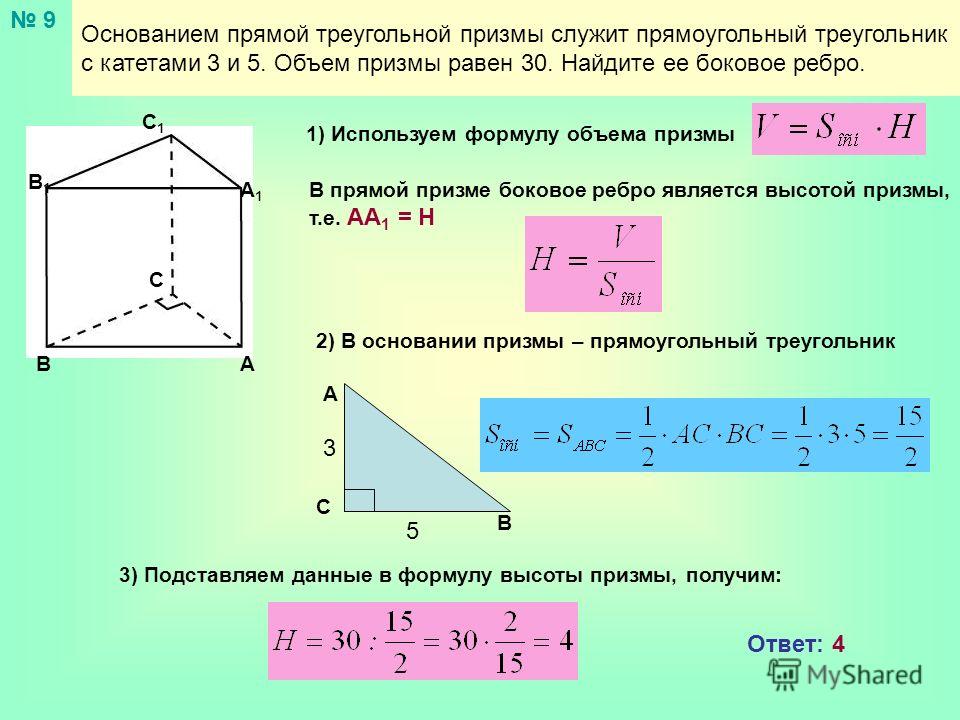 Затем вы можете использовать его, чтобы проверить наши ответы.

Равнобедренный, прямоугольный треугольник — Калькулятор геометрии

Геометрия | Формы | Контакты и конфиденциальность	Геометрические калькуляторы	Немецкий: Geometriechner, Formen
1DЛиния, дуга окружности, парабола, спираль, кривая Коха 2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, многоугольник, десятиугольник, десятиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: Треугольник, прямоугольный треугольник, равнобедренный треугольник, ИК-треугольник, четырехугольник, прямоугольник, золотой прямоугольник, ромб, параллелограмм, полуквадрат, прямой змей, воздушный змей, правильная трапеция, равнобедренная трапеция, трехравносторонняя трапеция, трапеция, тупая трапеция, циклическая Четырехугольник, Касательный четырехугольник, Стрелка, Вогнутый четырехугольник, Перекрещенный прямоугольник, Антипараллелограмм, Форма дома, Симметричный пятиугольник, Диагонально разделенный восьмиугольник, Вырезанный прямоугольник, Вогнутый пятиугольник, Вогнутый правильный пятиугольник, Вытянутый пятиугольник, Прямой восьмиугольник, разделенный пополам, Вытянутый шестиугольник, Симметричный шестиугольник, Параллелогон , Вогнутый шестиугольник, Стреловидный шестиугольник, Прямоугольный шестиугольник, Г-образная форма, Острый изгиб, Т-образная форма, Усеченный квадрат, Вытянутый восьмиугольник, Рамка, Открытая рамка, Сетка, Крест, Х-образная форма, Н-образная форма, Три звезды, Четыре звезды, Пентаграмма , Гексаграмма, Уникурсальная гексаграмма, Октаграмма, Звезда Лакшми, Многоугольник двойной звезды, Полиграмма, Многоугольник Круглые формы: Круг, Полукруг, Круглый сектор, Круглый сегмент, Круглый слой, Круглый центральный сегмент, Круглый угол, Круглый угол, Круговая касательная стрелка, Форма капли, Полумесяц, Заостренный овал, Два круга, Стрельчатая арка, Холм , Кольцо, Сектор кольца, Изогнутый прямоугольник, Скругленный многоугольник, Скругленный прямоугольник, Эллипс, Полуэллипс, Эллиптический сегмент, Эллиптический сектор, Эллиптическое кольцо, Стадион, Спираль, Бревно. Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник 3Д Platonic Solids: Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron Archimedean Solids: Truncated Tetrahedron, Cuboctahedron, Truncated Cube, Truncated Octahedron, Rhombicuboctahedron, Truncated Cuboctahedron, Icosidodecahedron, Truncated Dodecahedron, Truncated Icosahedron, Snub Cube, Rhombicosidodecahedron , Truncated Icosidodecahedron, Snub Dodecahedron Catalan Solids: Triakis Tetrahedron, Rhombic Dodecahedron, Triakis Octahedron, Tetrakis Hexahedron, Deltoidal Icositetrahedron, Hexakis Octahedron, Rhombic Triacontahedron, Triakis Icosahedron, Pentakis Dodecahedron, Pentagonal Icositetrahedron, Deltoidal Hexecontahedron, Hexakis Icosahedron, Пятиугольный шестигранник Johnson Solids: Pyramids, Cupolae, Rotunda, Elongated Pyramids, Gyroelongated Pyramids, Bipyramids, Elongated Bipyramids, Gyroelongated Square Dipyramid, Gyrobifastigium, Disheptahedron, Snub Disphenoid, Sphenocorona, Disphenocingulum Other Polyhedrons: Cuboid, Square Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр Круглые формы: Сфера, полусфера, сферический угол, цилиндр, срезанный цилиндр, косой цилиндр, изогнутый цилиндр, эллиптический цилиндр, обобщенный цилиндр, конус, усеченный конус, наклонный круговой конус, эллиптический конус, усеченный эллиптический конус, общий конус , Общий усеченный конус, двояконус, усеченный двояконус, заостренный столб, закругленный конус, капля, сфероид, эллипсоид, полуэллипсоид, сферический сектор, сферическая крышка, сферический сегмент, сферический центральный сегмент, двойной калот, сферический клин, полуцилиндр, диагонально разделенный пополам Цилиндр, Цилиндрический клин, Цилиндрический сектор, Цилиндрический сегмент, Цилиндр с плоским концом, Полуконус, Конический сектор, Конический клин, Сферическая оболочка, Полусферическая оболочка, Цилиндрическая оболочка, Вырезанная цилиндрическая оболочка, Наклонная цилиндрическая оболочка, Полый конус, Усеченный полый конус, Сферический Кольцо, тор, тор веретена, тороид, сектор тора, сектор тора, арка, тетраэдр Рело, капсула, сегмент капсулы, двойная точка, антиконус, усеченный антиконус, Sphe повторный цилиндр, линза, вогнутая линза, бочонок, форма яйца, параболоид, гиперболоид, олоид, тела Штейнмеца, тело вращения 4Д Тессеракт, Гиперсфера	Anzeige Расчеты при равнобедренном и прямоугольном треугольнике (45-45-90-треугольник). Введите одно значение и выберите количество знаков после запятой. Затем нажмите Рассчитать. Формулы: C = √2 * a H C = M C = √2 * A / 2 H A = H B 44444444444444444444444444444444444444444. = √5 * a / 2 p = ( 2 + √2 ) * a A = a² / 2 r c = a / √2 r i = a / (2 + √2 ) Углы гипотенузы: 45° например, метр), площадь имеет эту единицу измерения в квадрате (например, квадратный метр). Anzeige Стороны a и b, катеты (ножки), имеют одинаковую длину. Треугольник осесимметричен относительно высоты h c , это идентично средней линии s c . Высота h a и h b идентичны сторонам b и a. Центроид находится на пересечении срединных линий. периметр р, площадь А стороны и углы высота срединные линии и центр тяжести перпендикулярные биссектрисы и описанная окружность биссектрисы и вписанная окружность Поделиться: © Jumk. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт