4.10. Как производятся арифметические операции в позиционных системах счисления? (Сложение, Вычитание, Умножение, Деление)
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
Сложение
Таблицы сложения легко составить, используя Правило Счета.
| Сложение в двоичной системе | Сложение в восьмеричной системе |
Сложение в шестнадцатиричной системе
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 1. Сложим числа 15 и 6 в различных системах счисления.
| Шестнадцатеричная: F16+616
|
Ответ: 15+6 = 2110 = 101012 = 258 = 1516.
Проверка. Преобразуем полученные суммы к десятичному виду: |
Пример 2. Сложим числа 15, 7 и 3.
| Шестнадцатеричная: F16+716+316
|
Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916.
Проверка:
|
Пример 3. Сложим числа 141,5 и 59,75.
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416
Проверка. Преобразуем полученные суммы к десятичному виду:
311,28 = 3*82 + 1
- 81 + 1*80 + 2*8-1 = 201,25
C9,416 = 12*161 + 9*160 + 4*16-1 = 201,25 Вычитание
Пример 4.
Вычтем единицу из чисел 102, 108 и 1016
Пример 5. Вычтем единицу из чисел 1002, 1008 и 10016.
Пример 6. Вычтем число 59,75 из числа 201,25.
Ответ: 201,2510 — 59,7510 = 141,510 = 10001101,12
= 215,48 = 8D,816.Проверка. Преобразуем полученные разности к десятичному виду:
10001101,12 = 27 + 23 + 22 + 20 + 2-1 = 141,5;
215,48 = 2*82 + 1*81 + 5*80 + 4*8-1 = 141,5;
8D,816 = 8*161 + D*160 + 8*16-1 = 141,5.
Умножение
Выполняя умножение многозначных чисел в различных
позиционных системах счисления, можно использовать обычный алгоритм
перемножения чисел в столбик, но при этом результаты перемножения и
сложения однозначных чисел необходимо заимствовать из соответствующих
рассматриваемой системе таблиц умножения и сложения.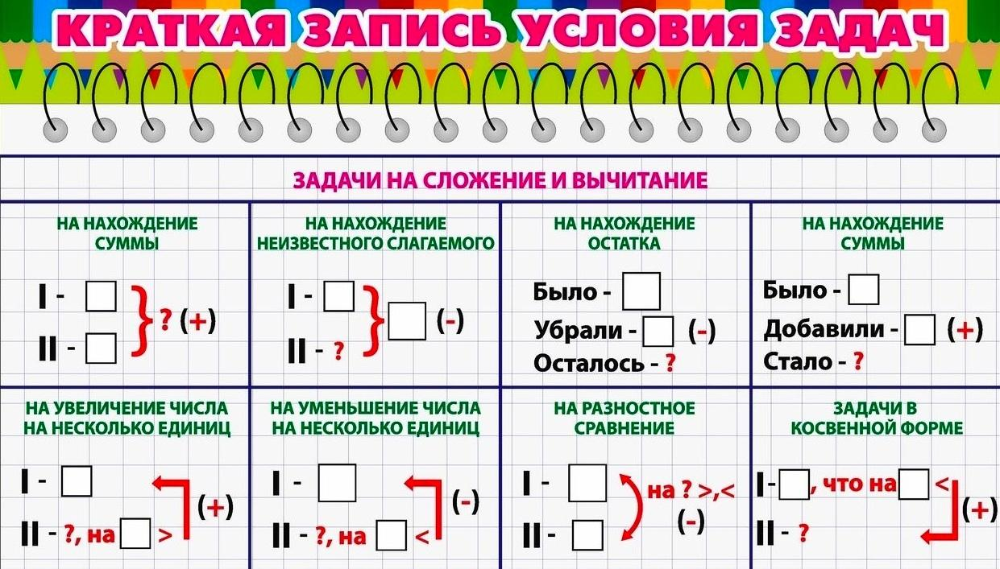
| Умножение в двоичной системе | Умножение в восьмеричной системе |
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.
Пример 7. Перемножим числа 5 и 6.
Ответ: 5*6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные произведения к десятичному виду:
111102 = 24 + 23 + 22 + 21 = 30;
368 = 3•81 + 6•80 = 30.
Пример 8. Перемножим числа 115 и 51.
Ответ: 115*51 = 586510 = 10110111010012 = 133518.
Проверка. Преобразуем полученные произведения к десятичному виду:
10110111010012 = 212 + 210 + 29 + 27 + 26 + 25 + 23 + 20 = 5865;
133518 = 1*84 + 3*83 + 3*82 + 5*81 + 1*80 = 5865.
Деление
Деление в любой позиционной системе счисления
производится по тем же правилам, как и деление углом в десятичной
системе. В двоичной системе деление выполняется особенно просто, ведь
очередная цифра частного может быть только нулем или единицей.
Пример 9. Разделим число 30 на число 6.
Ответ: 30 : 6 = 510 = 1012 = 58
Пример 10. Разделим число 5865 на число 115.
Восьмеричная: 133518 :1638
Ответ: 5865 : 115 = 5110 = 1100112 = 638.
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 + 21 + 20 = 51; 638 = 6*81 + 3*80 = 51.
Пример 11. Разделим число 35 на число 14.
Восьмеричная: 438 : 168
Ответ: 35 : 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду:
10,1 2 = 21 + 2 -1 = 2,5;
2,48 = 2*80 + 4*8-1 = 2,5.
Примеры на сложение, вычитание и умножение чисел
Выполним сложение в двоичной системе счисления 11112+1012 .
Имеем
1+1=2, но в двоичной системе цифры 2 нет,
поэтому мы её не можем записать: два уже
есть единица более высокого разряда (в
данном случае десятков).
Значит, в сумме
нет единиц, пишем 0, а единицу следующего
разряда удерживаем в уме.
Выполняем сложение десятков: 1+0=1, да ещё один десяток в уме всего 2. В десятки пишем 0 и одну единицу следующего разряда удерживаем в уме. Складываем сотни: 1+1=2, да ещё 1 сотня, удерживается в уме, всего 3 единицы третьего разряда: 3 мы записать не можем, поэтому записываем 1 сотню, а две сотни двоичной системы составляют одну тысячу, одну тысячу удерживаем в уме. Одна тысяча да ещё одна, удерживаемая в уме, нуль пишем, а одна единица высшего разряда записывается в десятки тысяч. Сложение закончено.
Выполним
вычитание в троичной системе счисления
11003 – 1123 . Имеем, от 0 отнять не можем, занимаем
единицу более высокого разряда (в данном
случае десятков). От 3 отнимаем 2, получаем
1. В разряде десятков мы занимали, поэтому
от 2 отнимаем 1. в разряде сотен остался
0. так как от 0 мы отнять не можем, занимаем
единицу более высокого разряда (в данном
случае тысяч).
От 3 отнимаем 1, получаем
2. Ответ: 2113.
Выполним умножение в пятеричной системе 415 × 325. Имеем, 1 умножаем на 2, получаем 2. 4 умножаем на 2, получаем 8, но числа 8 в пятеричной системе нет, заменяем его числом 13. Умножим 3 на 1, получаем 3 и подписываем, смещая на один знак влево, как и при умножении в десятичной системе счисления. Умножим 3 на 4, получаем 12, но числа 12 в пятеричной системе нет, заменяем его числом 22. Складываем результаты. Число 2 сносим. Складываем 3 и 3, получаем 6, но числа 6 нет в данной системе, заменяем числом 11, 1 пишем, 1 запоминаем. Складываем 1 и 2, да 1 запоминали, получаем 4 и сносим цифру 2. получили число 2412 5.
Проверим законы сложения, вычитания и умножения.
Переместительный закон сложения. 45326 + 13456 = 13456 + 45326.
45326 + 13456 = 103216 и 13456 + 45326 = 103216 .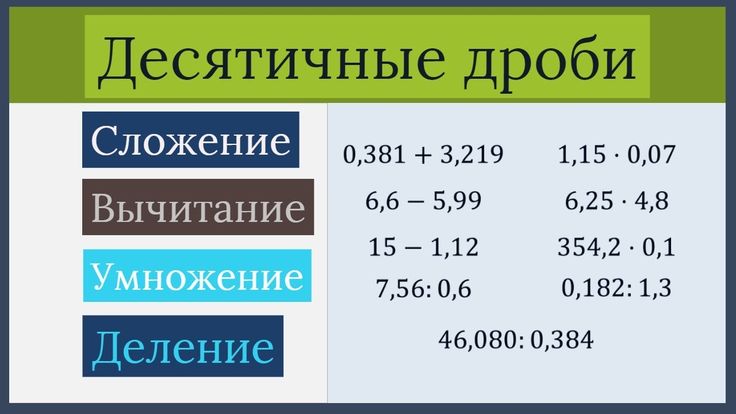
Закон выполняется.
Переместительный закон умножения. 436
Сочетательный закон сложения. (45326 + 13456) + 32446 = 45326 + (13456 + 32446 ). 45326 + 13456 = 103216 и 103216 + 32446 = 140056 ; 13456 + 32446 = 50336 и 50336 + 45326 = 140056. Закон выполняется.
Сочетательный закон умножения. (436× 236)×126 = 436×(236×126).
436×
236 =
15136 и
15136×126 = 230006;
236×126=3206 и 3206×436=230006.
Закон выполняется.
Перевод числа из десятичной системы счисления в систему с другим основанием
Метод поэтапного деления на основание системы счисления заключается в последовательном выполнении действий:
1. Исходное число делим на основание системы счисления с остатком в десятичной системе счисления.
2. Если частное от деления не равно 0, выполняем п.1.
3. Полученные остатки записываем последовательно от последнего к первому.
4. Полученная запись — искомое число.
Методом поэтапного деления можно перевести целое десятичное число в любую позиционную систему счисления.
Например: переведем число 105 в двоичную систему счисления методом поэтапного деления на основание системы счисления
10510 = 11010012
Перевод
целых чисел из системы счисления с
основанием, отличным от 10, в десятичную
систему счисления.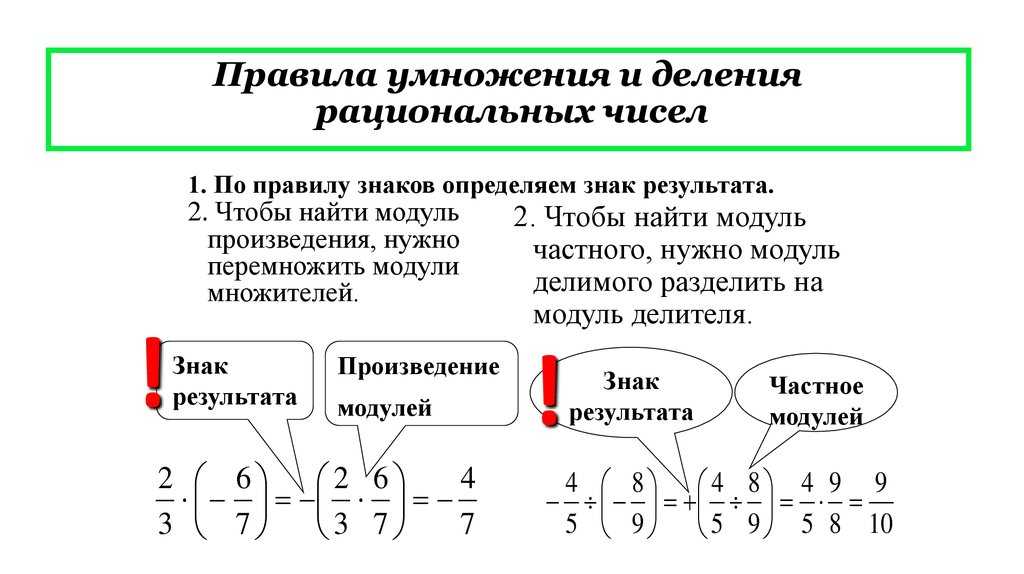
Например, для того, чтобы перевести двоичное число в десятичную систему счисления необходимо выполнить алгоритм.
Алгоритм перевода А2® А10
1. Записать число в развернутой форме записи.
2. Вычислить полученное значение суммы.
3. Результат — искомое десятичное число.
Например: Переведем двоичное число 1000111012 в десятичную систему счисления.
1000111012 = 1 × 28 + 0× 27 + 0× 26 + 0× 25 + 1 × 24 + 1× 23 + 1× 22 + 0× 21 + 1×20 = 1 × 256 + 0× 128 + 0× 64 + 0× 32 + 1× 16 + 1× 8 + 1× 4 + 0× 2 + 1× 1 = 256 + 16 + 8 + 4 + 1 = 28510
Аналогично переводятся числа из любой позиционной системы счисления в десятичную систему счисления.
Математика: сложение, вычитание, умножение, деление | СЕ
Тип ресурса:
Дома,
Учебная программа,
Учебный ресурс,
Интерактив,
Педагогика,
Явления,
Видео,
Визуализация/Моделирование
Источник:
СК-12
Опубликовано:
2021
Последнее обновление:
2021
Предполагаемый уровень обучения:
ПреК-2,
3-5,
МС,
ГС
Ссылки на ресурсы:
Сообщить о неработающей ссылке
Описание:
cK-12 — это некоммерческая бесплатная база данных учебных ресурсов по всем предметам, которая включает в себя полный контент, интерактивные материалы и симуляции, тесты, видео и многое другое.
Содержание энергии включает в себя содержание, относящееся к базовому содержанию, требуемому в NGSS.
Место нахождения:
Национальный
Содержание энергии:
Электроэнергетика,
Электричество и магнетизм,
Производство электроэнергии,
Электроны,
Основы энергетики,
Свет (видимый),
Потенциальная и кинетическая энергия,
Звук,
Источники энергии
Основная дисциплинарная идея NGSS:
ESS1.B: Солнечная система,
ESS1.C: История Земли,
ESS2.A: Земляные материалы и системы,
ESS2.C: Вода на Земле,
ESS2.D: Погода и климат,
ESS3.A: Природные ресурсы,
ESS3..jpg)
C: Влияние человека,
ESS3.D: Изменение климата,
LS2.B: Циклы материи и энергии,
LS2.C: Динамика экосистем,
LS4.D: Биоразнообразие и люди,
PS1.A: Материя: структура и свойства,
PS1.B: Химические реакции,
PS1.C: Ядерные процессы,
PS2.A: Силы и движение,
PS2.B: Взаимодействие между силами,
PS3.A: Определения энергии,
PS3.B: Энергосбережение и передача,
PS3.C: Энергия и силы,
PS3.D: Энергия в химических процессах,
PS4.A: Свойства волны,
PS4.B: Электромагнитное излучение,
PS4.C: Информационные технологии
Педагогика и практика:
Создание культуры науки,
Многоязычные стратегии,
Несколько стилей обучения
Другие затронутые темы:
ELA: информационный текст,
ELA: Чтение: литература,
ELA: Чтение: научное и техническое,
ELA: говорить и слушать,
ELA: письмо,
ELA: Развитие словарного запаса,
Математика: сложение, вычитание, умножение, деление,
Математика: Алгебра,
Математика: Функции,
Математика: Геометрия,
Математика: графика и представление,
Математика: измерение,
Математика: статистика и вероятность,
Математика: соотношения и пропорции,
Математика: тригонометрия/исчисление,
Общественные науки: анализ,
Общественные науки: обществоведение,
Общественные науки: экономика,
Общественные науки: география,
Общественные науки: история,
Социальные науки: мультикультурные исследования
Математика для детей (основы сложения, вычитания, умножения, деления) — триггерные тождества
Что такое базовая математика?
Базовая математика определяется как «наука о количестве», она дает вам основные концепции математики.
Каждый учащийся должен знать эти понятия и практиковать их в повседневной жизни, решая текстовые задачи.
Базовая математика — это простые понятия, которые подготавливают учащихся к изучению дробей, НОК и НОД. Обычно основная математика — это счет, сложение, вычитание, умножение и деление. Все математические понятия основаны на этих четырех операциях (сложение, вычитание, умножение и деление). С этими операциями учащийся также должен понимать различные свойства и связь с этими операциями.
Вот основные понятия математики, а также примеры для учащихся, которые хотят изучать основы математики. Сегодня мы собираемся обсудить математику для детей , что очень важно для начала изучения математики.
Их также называют натуральными числами, потому что они, естественно, являются первыми числами, которые мы изучаем (1, 2, 3, 4 и т. д.). Иногда их также называют положительными числами.
Эти арифметические операции используются для подсчета физических объектов в мире.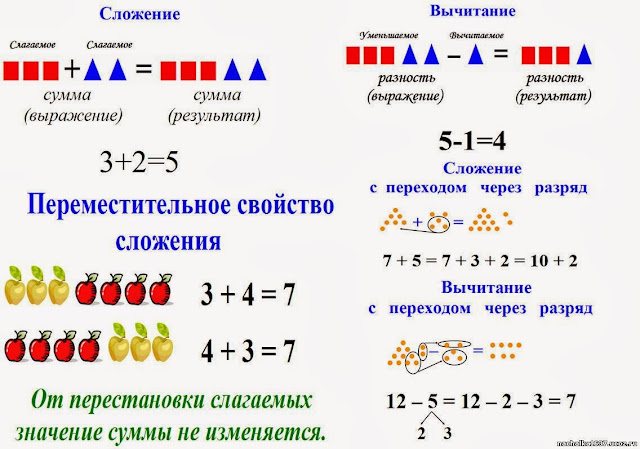
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10…
повседневные примеры
Ответ : . .
Ответ: есть 20 номеров.
- Сосчитайте носки, чтобы убедиться, что у вас есть совпадающие пары (2).
Ответ: Если у вас есть 6 носков, то у вас есть 12 одинаковых пар.
- Подсчитайте, сколько людей в вашем доме.
- Подсчитайте учеников в вашем классе.
- Подсчитайте, сколько дней осталось до ваших бумаг.
- Подсчитайте все алфавиты. (А, В, С… и так далее).
- Расположите все эти числа в правильном порядке (98, 23, 67, 12, 45, 56 и 10).
Ваш ребенок умеет считать, если правильно ответит на все вопросы. Хотя ему/ей нужно немного практики ежедневно.
Сложение Сложение — одна из основных математических операций. Простыми словами сложение означает соединение двух вещей вместе или добавление двух вещей.
Его также можно определить как набор объектов или их сложение вместе. Он представлен
Знак «+».
Примеры
Допустим, у вас есть 2 синих мяча, а у вашего друга Джона 3 красных мяча. Вы и Джон думаете, что можете подсчитать количество мячей, чтобы у вас обоих было больше мячей для игры, но сначала вы находите общее количество мячей у каждого из них.
Вместо того, чтобы считать каждый мяч отдельно, вы можете использовать базовую математическую операцию (Сложение), чтобы быстрее найти общее количество мячей. Сложение — это когда мы складываем два числа вместе, чтобы найти сумму чисел.
У вас 2 мяча, а у Джона 3 мяча, поэтому сумма мячей равна 5.
2 синих шара + 3 красных шара = 5 мячей
Пример 2 4 печенья. Они хотят испечь кекс, но для этого им нужно подсчитать, сколько у них печенья.
Вместо того, чтобы подсчитывать отдельные файлы cookie, они просто используют базовую арифметическую операцию (всего) для сложения чисел.
4 куки + 4 куки = 8 куки
Пример
Решайте вопросы по добавлению
5 12 34 56 47
+19 +34 +14 +34 +23 +19 +34 +14 +34 +23 +19 +34 +14 +34333 +19 +34 +14 +34333 +1. : 24 46 48 90 70 Это основная арифметическая операция, используемая для нахождения разницы между двумя числами. Когда у вас много денег и вы вычитаете из них половину, то денег становится меньше. В вычитании есть три части, начальное число — уменьшаемое. Вычитаемое число является вычитаемым, а число, оставшееся после вычитания, известно как разность. Методы вычитания Существуют различные методы вычитания. Первый метод заключается в простом вычитании двух чисел, как указано ниже. 5 яиц – 2 яйца = 3 яйца. А Б Знаете вы это или нет, но иногда вы делаете умножение, просто складывая их. Существует два метода умножения. Метод 1: Пример: На приведенном выше рисунке есть три группы, и каждая из этих групп имеет 6 файлов cookie. Таким образом, общее количество файлов cookie в трех группах равно 5 + 5 + 5 = 15 файлов cookie. Пример 2: Допустим, у вас есть три группы, и в каждой группе по 6 маркеров, поэтому вы подсчитываете общее количество маркеров. Итак, 6 маркеров + 6 маркеров + 6 маркеров = 18 маркеров. Метод 2: Примеры А Б Example: 11 13 2 4 9 7 6 * 2 * 4 * 5 * 3 * 2 *7 * 2 __________________________________________________________ Answers 22 52 10 12 18 49 12 Деление — это просто процесс деления числа на две равные части. Дивиденд 10/ делитель 2= частное 5 Для представления деления у нас есть два оператора Чтобы разделить любые числа, вам всегда нужны следующие шаги: Повторяйте эти шаги, пока проблема не будет решена. Дела: При делении двух чисел учитываются некоторые случаи. 20 / 1 = 20 5 / 1 = 5 20/0= не определено 40/0=не определено. Если делимое равно делителю, то ответ всегда равен единице. 20/20 = 1 2) 5/5 = 1 Пример: А Б Вы можете узнать больше о математике на trigidentities.
? Вычесть 12 34 23 13 7 3 67 _ 2 32 12 10 903:50 3 1 34 А-Б 10 2 11 3 4 2 33 
Умножение 12 6 5 9 4 3 4 * 2 5 3 10 3 1 8 А * В 24 12 15 90 12 3 32 
Когда вы делите число, вы начинаете с большого числа, а после деления оно делится на свою половину. Делимым является первое число; делитель — это число, которое вы хотите разделить, а частное — это ответ числа.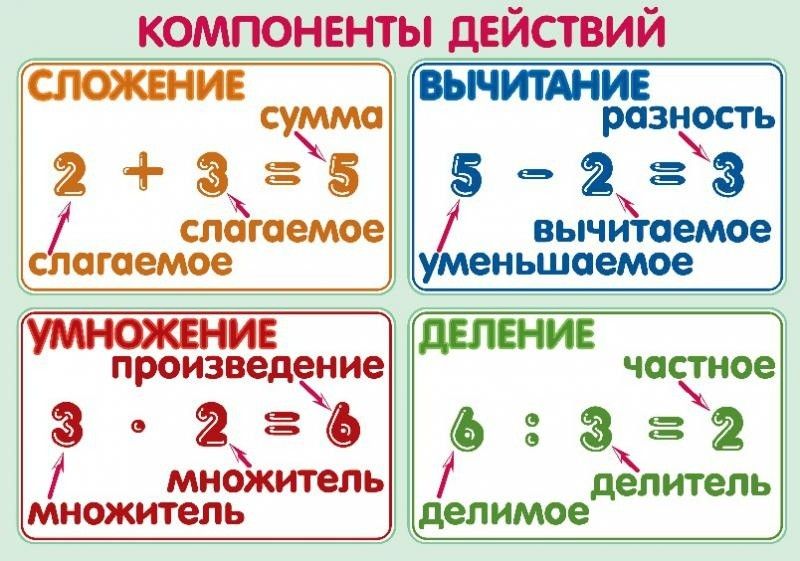
Отдел 12 6 12 10 20 3 8 / 2 3 3 2 5 1 4 А/Б 6 2 4 5 4 3 2 