Смежные и вертикальные углы | Презентация к уроку по геометрии (7 класс):
Слайд 1
Тема урока: Смежные и вертикальные углы.
Слайд 2
Цели урока: Ознакомить учащихся с понятиями смежных и вертикальных углов, рассмотреть их свойства; Научить строить угол, смежный с данным углом, изображать вертикальные углы, находить на рисунке вертикальные и смежные углы.
Слайд 3
Давай вспомним! Что такое угол?
Слайд 4
АОВ О В ВОА А О Луч ОА Луч ОВ Как обозначаются углы?
Слайд 5
Для измерения углов используют транспортир . Какой инструмент можно использовать для измерения углов? 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Слайд 6
10 20 50 60 70 80 90 100 110 120 130 140 150 160 170 180 180 170 160 150 140 130 120 110 100 80 0 10 20 30 40 50 60 70 0 40 30 А Б и с с е к т р и с а I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 А OB = 70 0 Что называется биссектрисой угла ? B O
Слайд 7
Виды углов ОСТРЫЙ УГОЛ Название угла Рисунок Градусная мера ПРЯМОЙ УГОЛ ТУПОЙ УГОЛ РАЗВЕРНУТЫЙ менее 90 ˚ 90 ˚ >90 ˚, но
Слайд 8
Какой угол образует клюв вороны, когда: «Ворона сыр во рту держала?» А когда «Ворона каркнула во все воронье горло?»
Слайд 9
Острый Тупой
Слайд 10
К вашим знаниям об углах сегодня добавится еще два вида: Смежные и вертикальные углы.
Слайд 11
1 2 A B C O Начертите развернутый угол АОС. Начертите произвольный луч О B , лежащий между сторонами развернутого угла.
Слайд 12
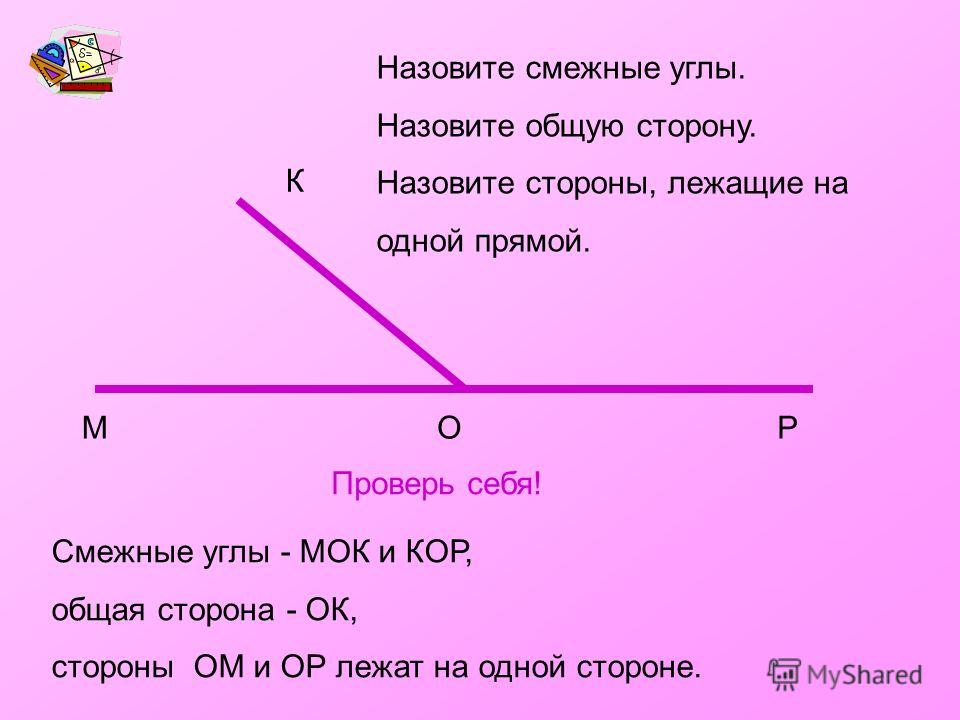
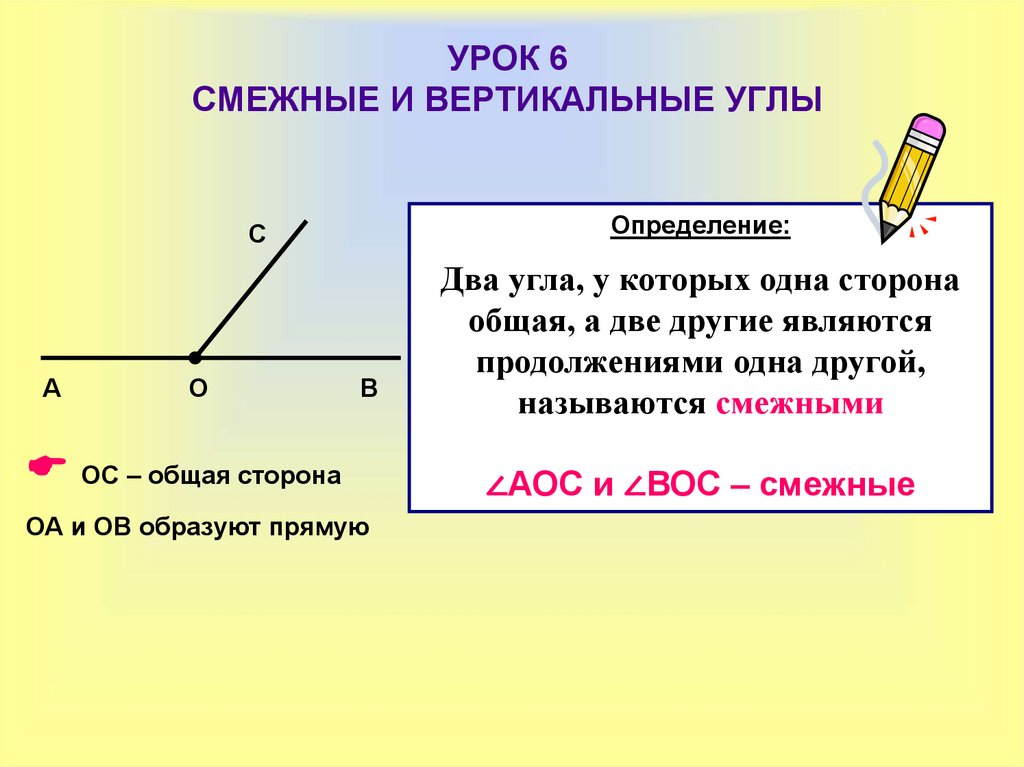
Определение смежных углов Определение. Два угла называются смежными , если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. А О В С ВОА и ВОС смежные А О В С А О В С А О В С А О В С А О В С А О В С А О В С
Слайд 13
Являются ли смежными углы AOD и BOD AO С и DO С AO С и DO В AO С и BO С ?
Слайд 14
Построение смежных углов
Слайд 15
А О В С Угол смежный для острого угла является тупым . 1.Одну из сторон угла продолжить за его вершину. 2.Получившийся угол АОС является смежным с углом АОВ. I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Слайд 16
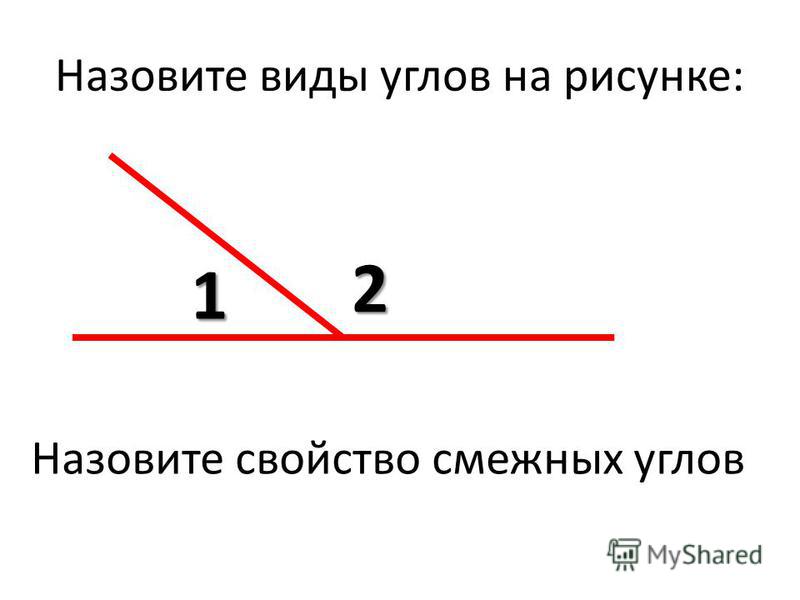
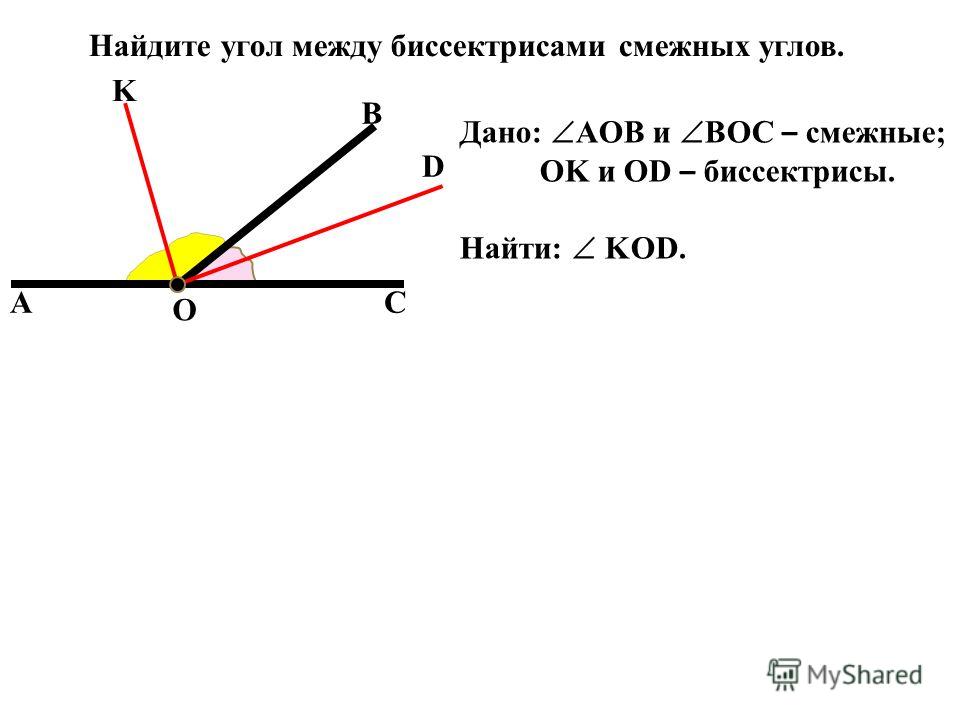
Теорема.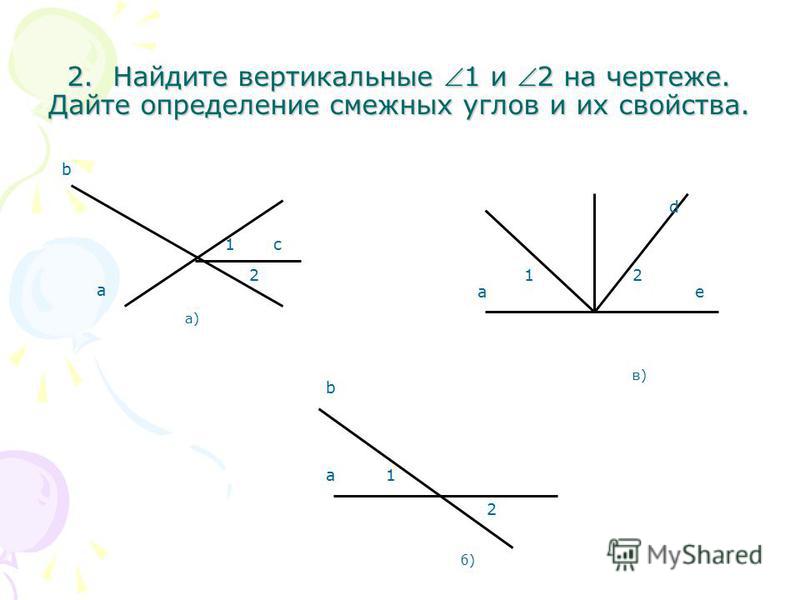 Сумма смежных углов равна 180 0 Дано : AOC и BOC – смежные. Доказать : AOC + BOC = 180 . Доказательство . 1) Так как AOC и BOC – смежные, то лучи ОА и ОВ – противоположные, то есть, AOB – развернутый, следовательно, AOB = 180 . 2) Луч OC проходит между сторонами AOB , значит, AOC + BOC = AOB = 180 С О A B C войство смежных углов 1. Сколько углов изображено на рисунке? Какие это углы? 2. Существует ли какая-нибудь взаимосвязь между этими углами?
Сумма смежных углов равна 180 0 Дано : AOC и BOC – смежные. Доказать : AOC + BOC = 180 . Доказательство . 1) Так как AOC и BOC – смежные, то лучи ОА и ОВ – противоположные, то есть, AOB – развернутый, следовательно, AOB = 180 . 2) Луч OC проходит между сторонами AOB , значит, AOC + BOC = AOB = 180 С О A B C войство смежных углов 1. Сколько углов изображено на рисунке? Какие это углы? 2. Существует ли какая-нибудь взаимосвязь между этими углами?
Слайд 17
130 0 ? Решение:
Слайд 18
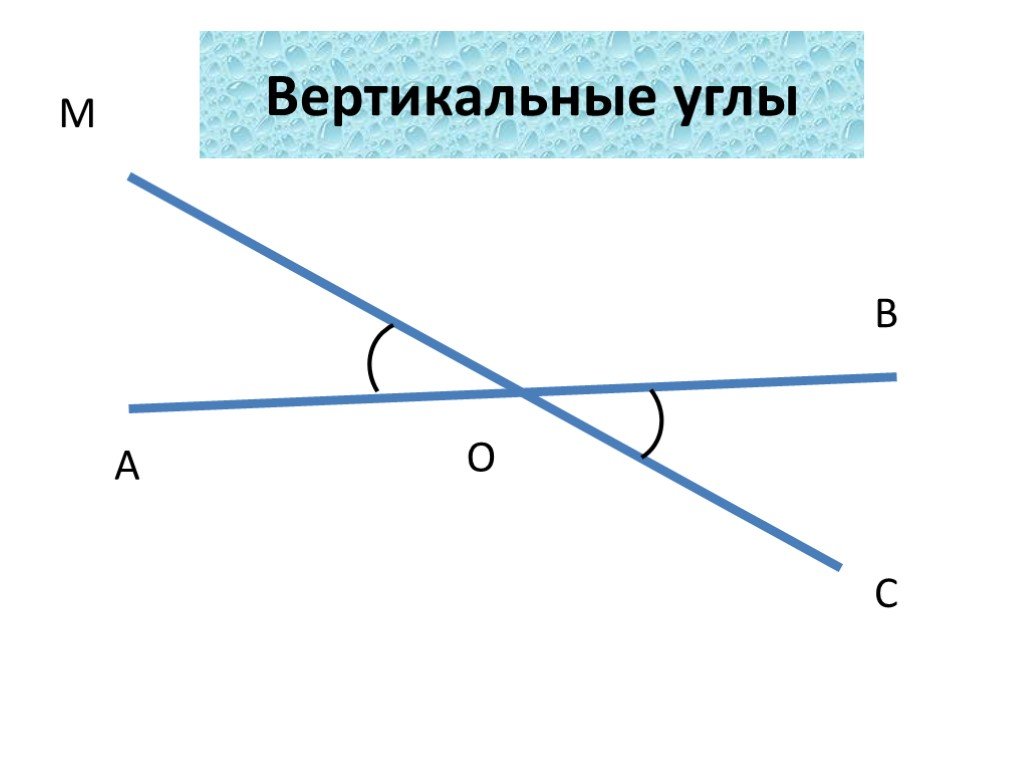
Начертите произвольный AOB . Постройте лучи OC и OD , противоположные к его сторонам. Определение. Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными. В С А О D
Слайд 19
А D B C O Найдите вертикальные углы. N B А С D O B А С D
Слайд 20
А О В I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 C D Построить угол. 2.Продлить каждую сторону угла за его вершину.
2.Продлить каждую сторону угла за его вершину.
Слайд 21
Свойство вертикальных углов A O D B C Теорема. Вертикальные углы равны. Дано : AOD и COB – вертикальные. Доказать : AOD= COB Доказательство . Каждый из углов AOD и COB является смежным с углом AOB . По свойству смежных углов: AOD + AOB = 180 и CO В + AOB = 180 . Имеем: AOD = 180 – AOB и COB = 180 – AOB , значит, AOD = COB
Слайд 22
Решите задачу по чертежу Решение:
Слайд 23
Закончи предложение Если один из смежных углов равен 50°, то другой равен… Угол, смежный с прямым, … Если один из вертикальных углов прямой, то второй… Угол смежный с острым… Если один из вертикальных углов равен 25°, то второй угол равен… 130 ° прямой прямой тупой 25 °
Слайд 24
Образец оформления решения задачи При пересечении двух прямых образовалось четыре угла. Один из них равен 43 0 . Найдите величины остальных углов . M O F P K 43 0 Дано: Найти: Решение: Ответ: 137 0 , 43 0 , 137 0 МК PF = О МО F = 43 ° FOK, KOP, POM.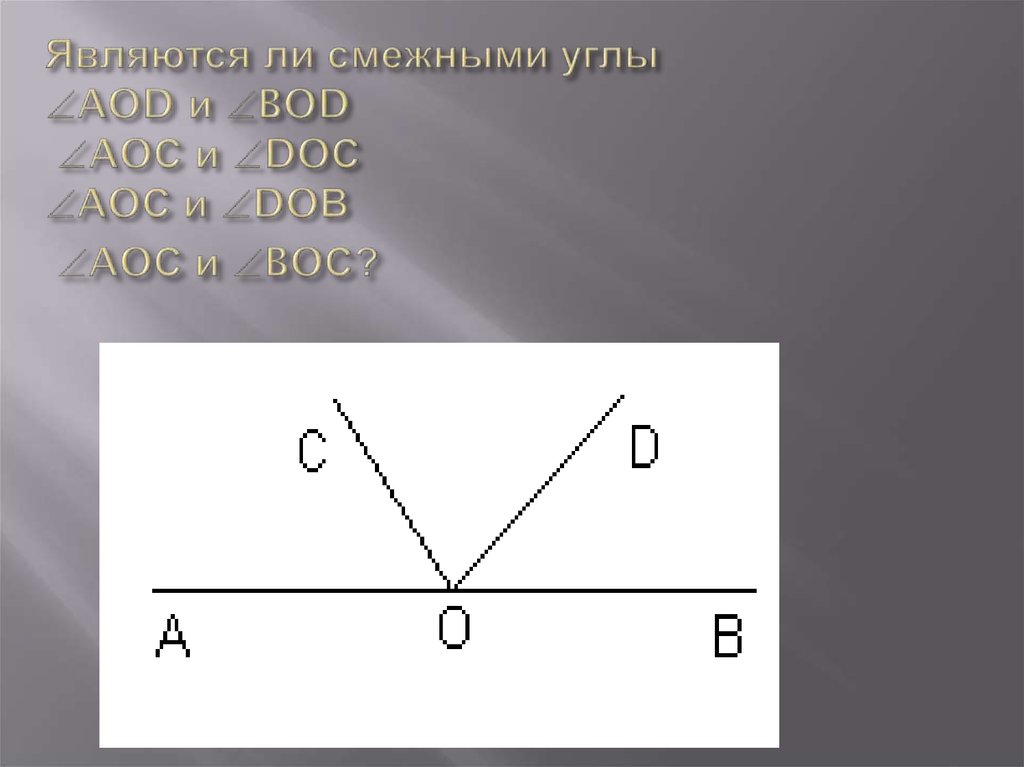 МО F и KOP вертикальные, значит, по свойству вертикальных углов, МО F = KOP , KOP = 43 ° МО F + FOK = 180 ° , так как они смежные. Отсюда FOK = 180 ° — 43 ° =137 ° FOK и POM вертикальные, значит FOK = POM , POM =137 °
МО F и KOP вертикальные, значит, по свойству вертикальных углов, МО F = KOP , KOP = 43 ° МО F + FOK = 180 ° , так как они смежные. Отсюда FOK = 180 ° — 43 ° =137 ° FOK и POM вертикальные, значит FOK = POM , POM =137 °
Слайд 25
Домашнее задание п.6 (стр.22-24), №58,62,66
Слайд 26
Т Е С Т по теме «Вертикальные и смежные углы»
Слайд 27
1. Сумма смежных углов равна…. 360 0 90 0 180 0 A B C
Слайд 28
2. Как называется угол меньше 180 0 , но больше 90 0 острый тупой прямой A B C
Слайд 29
3. Чему равен угол, если смежный с ним равен 47 0 ? 133 0 47 0 43 0 C B A
Слайд 30
4. Какой угол образуют часовая и минутная стрелки часов, когда они показывают 6 часов? тупой развернутый прямой C B A
Слайд 31
5. Найдите
Слайд 32
6. Найдите
Слайд 33
7. Найдите смежные углы, если один из них в два раза больше другого. 60 0 и 120 0 90 0 и 100 0 40 0 и 80 0 C B A
Слайд 34
8. Угол равен 72 0 .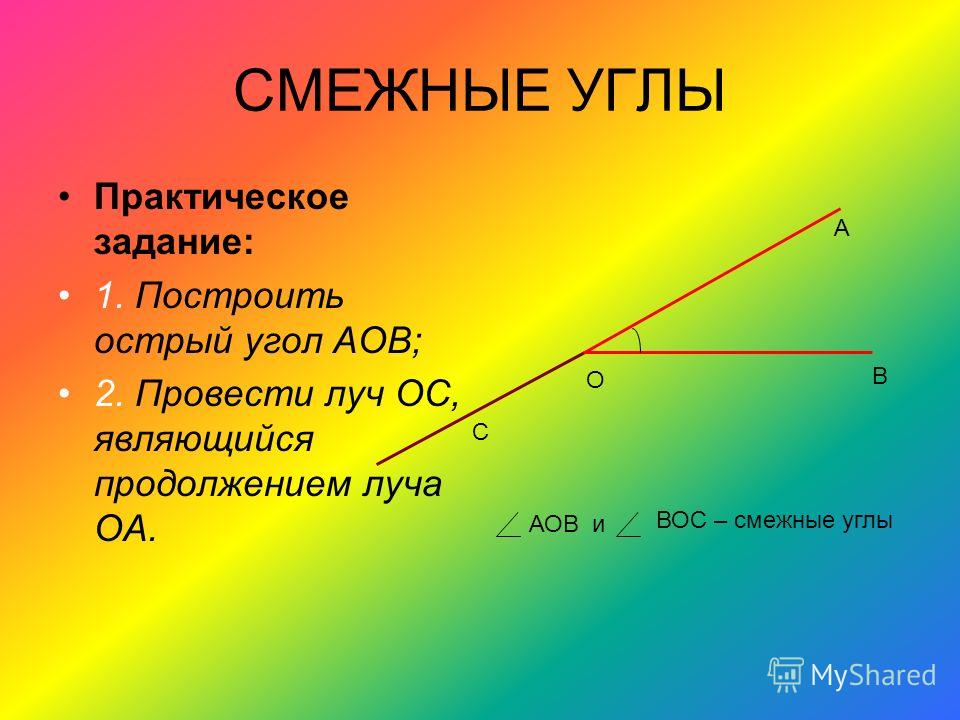 Чему равен вертикальный ему угол? 72 0 108 0 18 0 C B A
Чему равен вертикальный ему угол? 72 0 108 0 18 0 C B A
Слайд 35
9. Какой угол образуют часовая и минутная стрелки часов, когда они показывают три часа? острый тупой прямой C B A
Слайд 36
Проверь себя. 1. C 2. B 3. A 4. B 5. B 6. B 7. B 8. C 9. C
7 класс. Геометрия. Атанасян. Учебник. Ответы к стр. 24
Начальные геометрические сведения
Перпендикулярные прямые
Смежные и вертикальные углы. Перпендикулярные прямые. Построение прямых углов на местности
Ответы к стр. 24
Практические задания
54. Начертите острый угол АОВ и на продолжении луча ОВ отметьте точку D. Сравните углы АОВ и AOD.
Углы АОВ и АОD — смежные, ∠АОВ — острый, ∠АОD — тупой ⇒ ∠АОВ < ∠АОD.
55. Начертите три угла: острый, прямой и тупой. Для каждого из них начертите смежный угол.
∠АОВ — острый, смежный угол ВОС (тупой).
∠DOE — прямой, смежный угол EOF (прямой).
∠KОL — тупой, смежный угол LOM (острый).
56. Начертите неразвернутый угол hk. Постройте угол h1k1 так, чтобы углы hk и h1k1 были вертикальными.
Углы hk и h1k1 — вертикальные (∠hk = ∠h1k1).
57. Начертите неразвернутый угол MON и отметьте точку Р внутри угла и точку Q — вне его. С помощью чертежного угольника и линейки через точки Р и Q проведите прямые, перпендикулярные к прямым ОМ и ON.
α ⊥ ОN, b ⊥ OM, c ⊥ ON, d ⊥ OM.
Задачи
58. Найдите угол, смежный с углом ABC, если: a) ∠ABC = 111°; б) ∠ABC = 90°; в) ∠ABC = 15°.
Р е ш е н и е
Сумма смежных углов равна 180°.
а) 180° — 111° = 69°;
б) 180° — 90° = 90°;
в) 180° — 15° = 165°.
О т в е т. а) 69°, б) 90°, в) 165°.
59. Один из смежных углов прямой. Каким (острым, прямым, тупым) является другой угол?
Р е ш е н и е
Сумма смежных углов равна 180°.
180° — 90° = 90° — прямой смежный угол.
О т в е т. Прямой.
60. Верно ли утверждение: если смежные углы равны, то они прямые?
Р е ш е н и е
Сумма смежных углов равна 180°.
180° : 2 = 90° — два смежных угла по 90° каждый.
О т в е т. Верно.
61. Найдите смежные углы hk и kl, если:
a) ∠hk меньше ∠kl на 40°;
б) ∠hk больше ∠kl на 120°;
в) ∠hk больше ∠kl на 47°18′;
г) ∠hk = 3∠kl;
д) ∠hk : ∠kl = 5 : 4.
Р е ш е н и е
Сумма смежных углов равна 180°.
а) ∠hk + ∠kl = 180°, ∠hk = ∠kl — 40°, тогда:
(∠kl — 40°) + ∠kl = 180°,
2∠kl = 180° + 40°,
∠kl = 220° : 2,
∠kl = 110°
∠hk = ∠kl — 40° = 110° — 40° = 70°
б) ∠hk + ∠kl = 180°, ∠hk = ∠kl + 120°, тогда:
(∠kl + 120°) + ∠kl = 180°,
2∠kl = 180° — 120°,
∠kl = 60° : 2,
∠kl = 30°
∠hk = ∠kl + 120° = 30° + 120° = 150°
в) ∠hk + ∠kl = 180°, ∠hk = ∠kl + 47°18′, тогда:
(∠kl + 47°18′) + ∠kl = 180°,
2∠kl = 180° — 47°18′,
∠kl = 132°42′ : 2,
∠kl = 66°21′
∠hk = ∠kl + 47°18′ = 66°21′ + 47°18′ = 113°39′
г) ∠hk + ∠kl = 180°, ∠hk = 3∠kl, тогда:
3∠kl + ∠kl = 180°,
4∠kl = 180°,
∠kl = 180° : 4,
∠kl = 45°
∠hk = 3∠kl = 3 • 45° = 135°
д) ∠hk + ∠kl = 180°, ∠hk : ∠kl = 5 : 4 или ∠hk : ∠kl = 5/4 ⇒ ∠hk = 5/4 • ∠kl, тогда:
5/4 ∠kl + ∠kl = 180°,
9/4 ∠kl = 180°,
∠kl = 180° : 9/4,
∠kl = 180° • 4/9,
∠kl = 80°
∠hk = 5/4 ∠kl = 5/4 • 80° = 100°
О т в е т. а) ∠kl = 110°, ∠hk = 70°;
а) ∠kl = 110°, ∠hk = 70°;
б) ∠kl = 30°, ∠hk = 150°;
в) ∠kl = 66°21′, ∠hk = 113°39′;
г) ∠kl = 45°, ∠hk = 135°;
д) ∠kl = 80°, ∠hk = 100°.
62. На рисунке 46 углы BOD и COD равны. Найдите угол AOD, если ∠COB = 148°.
Р е ш е н и е
∠AOD = ∠AOC + ∠COD
Углы AOC и COB — смежные, тогда:
∠AOC + ∠COB = 180° ⇒ ∠АОС = 180° — ∠СОВ = 180° — 148° = 32°.
∠СОВ = ∠СОD + ∠DOB = 148°, ∠СОD = ∠DOB ⇒ ∠СОD = 148° : 2 = 74°.
∠AOD = 32° + 74° = 106°.
О т в е т. ∠AOD = 106°.
63. Даны два равных угла. Равны ли смежные с ними углы?
Р е ш е н и е
∠1 = ∠2
∠1 + ∠3 = 180° ⇒ ∠3 = 180° — ∠1
∠2 + ∠4 = 180° ⇒ ∠4 = 180° — ∠2
Так как ∠1 = ∠2, то ∠3 = 180° — ∠1 = 180° — ∠2 = ∠4 или
∠4 = 180° — ∠2 = 180° — ∠1 = ∠3
О т в е т. Равны.
Равны.
64. Найдите изображенные на рисунке 41 углы:
а) 1, 3, 4, если ∠2 = 117°;
б) 1, 2, 4, если ∠3 = 43°27′.
Р е ш е н и е
а) Углы 2 и 4 — вертикальные, тогда ∠2 = ∠4 = 117°
Углы 1 и 2 — смежные, тогда ∠1 + ∠2 = 180° ⇒ ∠1 = 180° — ∠2 = 180° — 117° = 63°
Углы 1 и 3 — вертикальные, тогда ∠1 = ∠3 = 63°
б) Углы 1 и 3 — вертикальные, тогда ∠1 = ∠3 = 43°27′
Углы 1 и 2 — смежные, тогда ∠1 + ∠2 = 180° ⇒ ∠2 = 180° — ∠1 = 180° — 43°27′ = 136°33′
Углы 2 и 4 — вертикальные, тогда ∠2 = ∠4 = 136°33′
О т в е т. а) ∠1 = ∠3 = 63°, ∠4 = 117°; б) ∠1 = 43°27′, ∠2 = ∠4 = 136°33′.
ГДЗ. Ответы по геометрии. 7 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Геометрия. 7 класс
Сборка кубика Рубика: верхняя часть
Сборка первой стороны кубика
Существует множество способов собрать первую сторону кубика, и на этой странице показаны некоторые из них. Первый шаг — выбрать цвет для первой стороны (синий на следующих рисунках). Затем переместите четыре угловых элемента с синей стороной на место, убедившись, что соседние угловые элементы имеют тот же цвет стороны, а не только синий. Ходы и фигуры из шага 1 помогут вам в этом. Наконец, заполните промежутки между угловыми частями соответствующими краевыми частями; Шаг 2 помогает проиллюстрировать это.
Первый шаг — выбрать цвет для первой стороны (синий на следующих рисунках). Затем переместите четыре угловых элемента с синей стороной на место, убедившись, что соседние угловые элементы имеют тот же цвет стороны, а не только синий. Ходы и фигуры из шага 1 помогут вам в этом. Наконец, заполните промежутки между угловыми частями соответствующими краевыми частями; Шаг 2 помогает проиллюстрировать это.
Легенда
- U обозначает верхнюю (верхнюю) сторону,
- D обозначает нижнюю (нижнюю) сторону,
- L обозначает левую сторону,
- R обозначает правую сторону,
- F обозначает лицевую сторону,
- H обозначает средний горизонтальный срез между верхней и нижней сторонами. На следующих рисунках он всегда содержит красные, зеленые, розовые и желтые центральные части.
Цифры, следующие за каждым движением, указывают, в каком направлении поворачивать сторону: 1 для одной четверти оборота по часовой стрелке, -1 для одной четверти оборота против часовой стрелки и 2 для двух четвертей оборота (половина оборота).
Для горизонтального среза H посмотрите на куб через вершину (сторона 1), чтобы определить направление по часовой стрелке.
Шаг 1. Разместите верхние угловые детали
Первый шаг — выбрать цвет для первой стороны. Расположите куб так, чтобы центральная часть этого цвета была сверху. Затем расположите четыре соответствующих угловых элемента вокруг верхней части, убедившись, что соседние угловые элементы имеют тот же цвет стороны, как показано на рисунке слева. Чтобы помочь вам в этом, на следующих рисунках показаны различные ситуации, с которыми вы можете столкнуться при размещении угловых элементов, а также ходы для размещения нужного элемента. |
На рис. 1 показан угловой элемент нижнего слоя, который необходимо вставить в верхний слой. Установите куб, как показано на рисунке 1, и используйте Move 1, чтобы вставить его. | |
Ход 1: Л-1 Ф-1 Л
| |
На рис. 2 также показан угловой элемент вдоль нижнего слоя, который необходимо вставить в верхний слой. Однако на этот раз синий цвет обращен вперед. Установите куб, как показано на рисунке 2, и используйте Move 2, чтобы вставить его. | |
Ход 2: D-1 R-1 D R | |
На рис. 3 также показан угловой элемент вдоль нижнего слоя, который необходимо вставить в верхний слой. Однако на этот раз синий цвет обращен вниз. | |
Ход 3: R-1 D R F D2 F-1 | |
Если нужная вам угловая деталь уже установлена, но неправильно ориентирована (как показано на рис. 4), выдвиньте ее с помощью «Перемещения 4». Теперь используйте «Перемещение 1», «2» или «3», чтобы снова вставить ее. | |
Ход 4: R-1 D-1 R D | |
Если нужный угловой элемент расположен не в том месте на верхнем слое (как показано на рис. 5), переместите его с помощью Перемещения 5. Теперь используйте Перемещение 1, 2 или 3, чтобы вставить его. | |
Ход 5: Л Д Л-1 | |
Шаг 2. Расположите кромки между верхними углами
Теперь, когда верхние углы на месте, можно расположить краевые части, которые находятся между углами. Чтобы помочь вам в этом, на следующих рисунках показаны различные ситуации, с которыми вы можете столкнуться при размещении краевых фигур, а также ходы для размещения нужной фигуры. |
На рис. 6 показана крайняя часть со стороны, которую необходимо разместить в верхнем слое между красно-синими угловыми частями. Установите куб, как показано на рисунке 6, и используйте Move 6, чтобы вставить его. | |
Движение 6: H-1 F H F-1
| |
На рис. 7 также показан краевой элемент со стороны, который необходимо разместить в верхнем слое между красно-синими угловыми элементами. На этот раз синяя сторона кромки обращена вперед. Установите куб, как показано на рисунке 7, и используйте Move 7, чтобы вставить его. | |
Ход 7: h3 F-1 H-1 F | |
На рис. 8 нужная деталь находится внизу, синей стороной вперед. Установите куб, как показано на рисунке 8, и используйте Move 8, чтобы вставить его. | |
Движение 8: F-1 H F | |
На рисунке 9 нужная часть находится внизу, но синяя сторона обращена вниз. Установите куб, как показано на рисунке 9, и используйте Move 9, чтобы вставить его. | |
Движение 9: F-1 H-1 F2 H F-1 | |
Если нужная вам крайняя часть уже находится на своем месте, но неправильно ориентирована, или если она расположена где-то еще в верхнем слое, то установите куб, как показано на рисунке 10, и используйте Перемещение 10, чтобы удалить эту часть. Теперь вернитесь и используйте Move 6 или 7, чтобы вставить кусок. | |
Движение 10: F H-1 F-1 H | |
Назад к обзору шага 1
Что такое Пентагон? Определение, типы, свойства, примеры
Что такое Пентагон?
Двухмерный многоугольник с пятью сторонами и пятью углами называется пятиугольником.
«Пента» означает «пять», а «гон» переводится как «углы» на греческом языке, и, следовательно, если мы объединим оба слова «пента + угольник», мы получим слово «пятиугольник».
Родственные игры
Как выглядит Пентагон?
Вот как выглядит пятисторонняя фигура:
Связанные рабочие листы
Части пятиугольника
- Сторона: Это один из пяти отрезков, образующих эту форму.
 Всего у этой фигуры пять сторон. На изображении отрезок «а» показывает одну из 5 сторон пятиугольника.
Всего у этой фигуры пять сторон. На изображении отрезок «а» показывает одну из 5 сторон пятиугольника. - Вершина: Это точка, где встречаются две стороны фигуры. Проще говоря, он также известен как угол. Например, когда вы посмотрите на страницу своей записной книжки, вы обнаружите, что она имеет четыре угла или четыре вершины, образующие угол 90°. На изображении выше A, B, C D и E — пять вершин этой формы.
- Диагональ: Это линия, соединяющая две несмежные вершины. Когда вы соединяете любые два несмежных угла или вершины 2D-фигуры с помощью прямой линии, эта прямая линия называется диагональю. Диагональ представлена буквой «d» на изображении для справки.
- Внутренний угол : Угол, образованный двумя смежными сторонами фигуры внутри. Когда две прямые линии встречаются или пересекаются, они образуют два типа углов в замкнутой двумерной фигуре. Угол, лежащий внутри фигуры, называется внутренним углом. Углы, отмеченные зеленым цветом на изображении ниже, показывают внутренние углы.

- Внешний угол
Типы пятиугольников
Пятиугольники можно разделить на четыре типа в зависимости от их сторон, углов и вершин.
- Обычный
- Нестандартный
- Выпуклая
- Подбарабанье
Правильные и неправильные пятиугольники
Если все пять сторон равны по длине и все пять углов имеют одинаковую меру, то форма называется правильной. Когда сторона и углы не равны, он называется неправильным. Чтобы лучше понять это, если вы посмотрите на правильный пятиугольник с любой стороны, он всегда будет выглядеть одинаково, поскольку он симметричен. Но неправильный может выглядеть по-разному со всех сторон или углов, поскольку у него разные длины сторон и углы.
Выпуклые и вогнутые пятиугольники
Выпуклый пятиугольник — это пятиугольник, у которого все вершины направлены наружу. Вогнутая форма относится к фигуре, у которой хотя бы одна вершина направлена внутрь.
Вогнутая форма относится к фигуре, у которой хотя бы одна вершина направлена внутрь.
Другими словами, вогнутый пятиугольник будет иметь чашеобразную форму между некоторыми сторонами, а выпуклый не будет иметь такой формы, так как все его вершины направлены наружу.
Свойства пятиугольника
- Эта фигура должна иметь пять сторон, образующих замкнутую двумерную фигуру. (Замкнутая фигура — это фигура, у которой все стороны встречаются друг с другом, образуя вершины.)
- Пятиугольник имеет пять диагоналей, соединяющих пять вершин с противоположными вершинами.
- В правильном пятиугольнике каждый внутренний угол равен 108°, а каждый внешний угол равен 72°.
- Сумма всех пяти внутренних углов любого пятиугольника равна 540°.
Пентагон Примеры из жизни
- Футбол : Футбол состоит из нескольких черно-белых пятен пятиугольной формы.
- Бамия : В следующий раз, когда будете есть бамию, внимательно посмотрите на внутреннее поперечное сечение, так как оно имеет пятиугольную форму.

- Пентагон здание : Штаб-квартира Министерства обороны США в Вашингтоне, округ Колумбия, представляет собой пятиугольное здание под названием Пентагон.
Площадь пятиугольника
Площадь этой фигуры равна общему пространству внутри ее пяти сторон. Чтобы найти область, мы должны сначала определить ее тип и информацию, которую мы имеем о ней.
Площадь правильного пятиугольника:
Правильный пятиугольник образует пять подобных треугольников.
Площадь обычного Пентагона = 5 × площадь треугольника или
= 1/2 × Периметр × Apothem SQ UNITS
Apothem является перпендикулярной линией от центра полигона до одного его SIDS. Он также известен как радиус формы.
Площадь неправильного пятиугольника
Чтобы найти площадь неправильного пятиугольника, разделите его на меньшие многоугольники. Сумма всех площадей меньших многоугольников дает общую площадь фигуры.
Периметр пятиугольника
Суммарная длина пяти сторон правильного или неправильного многоугольника называется его периметром.
Периметр пятиугольника = (сторона 1 + сторона 2 + сторона 3 + сторона 4 + сторона 5) единиц
Периметр правильной пятиугольной фигуры равен (5 x сторона) единицам, если все стороны измерение.
Забавные факты
Знаете ли вы, что можно создать простой пятиугольник из полоски бумаги?
Шаг 01 : Возьмите длинную полоску бумаги. Вы можете выбрать свой любимый цвет.
Шаг 02: Теперь сделайте из бумаги узелок, похожий на крендель. Посмотрите на изображение и следуйте инструкциям.
Шаг 03: Удерживая бумагу плоской, затяните узел мягкими руками. Будьте осторожны, чтобы не порвать его.
Шаг 04: Теперь, если есть лишняя бумага, отогните ее или обрежьте.
Шаг 05: Вуаля! Теперь он готов.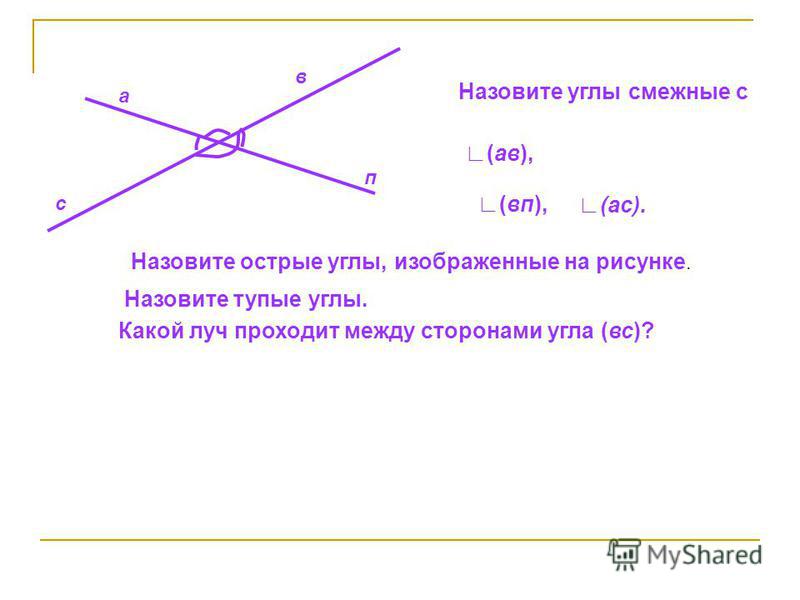 Вы можете проверить, все ли стороны имеют одинаковую длину и все углы имеют одинаковую меру.
Вы можете проверить, все ли стороны имеют одинаковую длину и все углы имеют одинаковую меру.
Заключение
Пятиугольники широко используются архитекторами и встречаются повсюду в мире природы. Они также очень часто используются в фундаментальной геометрии. Чтобы изучать принципы геометрии в увлекательной игровой форме, ознакомьтесь с обучающими играми, курсами и рабочими листами SplashLearn для детей.
Решенные примеры
- Нил измеряет правильный пятиугольник и находит, что его сторона равна 8 футам, а длина апофемы 6 футов . Как он найдет его площадь?
Solution:
Given in question,
Apothem = 6 feet
Side = 8 feet
Area of Regular Pentagon = ½ × perimeter × apothem
= ½ × 5 × 8 × 6
= ½ × 240
= 120 квадратных футов
Следовательно, площадь = 120 футов 2
- Если у правильного пятиугольника длина стороны 10 см, а апофема 5 см, найдите его площадь.

Решение: Дано,
Длина стороны = 10 см
Длина апофемы = 5 см
Площадь правильного пятиугольника = ½ × периметр × апофема
= 1/2 × 5 x = 10 × 5
Площадь 125 см 2
- Если периметр правильного пятиугольника равен 200 см, какова длина каждой стороны?
Решение :
Периметр правильного пятиугольника = 200 см
5 × сторона = 200
Сторона = 200/5
Сторона = 40 см
Длина каждой стороны 40 см.
Практические задачи
1
Сколько параллельных сторон может быть в правильном пятиугольнике?
1
5
3
Правильный ответ: 0
Правильный пятиугольник не имеет параллельных сторон. Неправильный может иметь две (одна пара) или четыре (две пары) параллельных сторон.
2
Длина стороны периметра 6 см.
 Чему равен периметр пятиугольника?
Чему равен периметр пятиугольника?30 см
33 см
36 см
40 см
Правильный ответ: 30 см
Периметр пятиугольника = длина стороны пятиугольника x 5
Данная длина стороны равна 6 см.
3
Если периметр правильного пятиугольника равен 250 см, какова будет длина каждой стороны?
50 см
60 см
30 см
90 см
Правильный ответ: 50 см
Периметр правильного пятиугольника = 250 см0460 Сторона = 50 см
4
На сколько треугольников можно разделить пятиугольник?
5
3
4
6
Правильный ответ: 3
Пятиугольник можно разделить на 3 треугольника.
5
Если мера четырех внутренних углов неправильного пятиугольника равна 135, 78, 119 и 117°, то какова мера его пятого внутреннего угла?
90
91
60
45
Правильный ответ: 91
Сумма всех внутренних углов пятиугольника равна 540°.
Следовательно, $135 + 78 + 119 + 117 + X$ = $540$ (X — неизвестный угол)
$X$ = $540$ – $449$ = $91°$
6
Какова площадь пятиугольника, сторона которого 9 см, а апофема 10 см?
340 см²
225 см²
235 см²
210 см²
Правильный ответ: 225 см²
Периметр Пентагона = Длина боковой длины x 5
Периметр = 9 x 5 = 45 см
. 2 × п × а
Площадь = ½ x 45 x 10
Площадь = 225 см²
Часто задаваемые вопросы
Является ли пятиугольник также параллелограммом?
Нет, пятиугольник — это пятиугольник, а у параллелограмма только четыре стороны.
Чем похожи четырехугольник и пятиугольник?
A. Четырехугольник и пятиугольник являются замкнутыми многоугольниками, сумма внешних углов которых равна 360°.
Какие три атрибута правильного пятиугольника?
- Все пять сторон должны быть конгруэнтными (одинаковой длины).


 Установите куб, как показано на рисунке 3, и используйте Move 3, чтобы вставить его.
Установите куб, как показано на рисунке 3, и используйте Move 3, чтобы вставить его.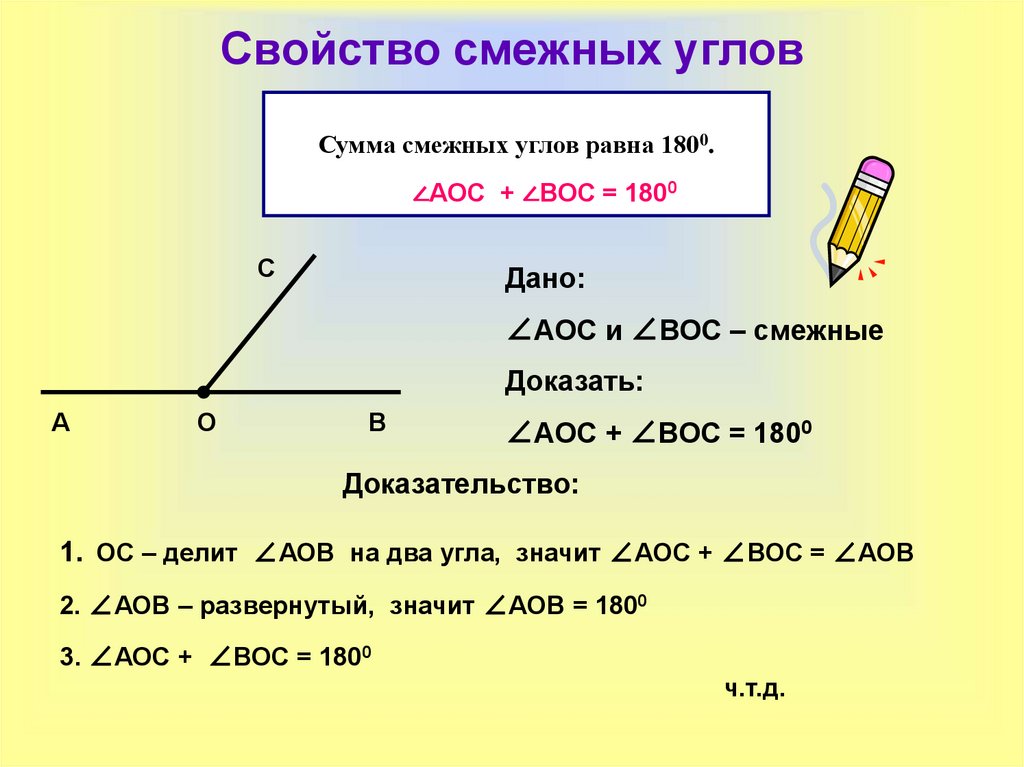 Вы найдете краевые части верхней стороны, разбросанные по кубу. Для каждой части определите, куда она идет, и поместите ее туда, не нарушая верхнюю часть.
Вы найдете краевые части верхней стороны, разбросанные по кубу. Для каждой части определите, куда она идет, и поместите ее туда, не нарушая верхнюю часть.

 Всего у этой фигуры пять сторон. На изображении отрезок «а» показывает одну из 5 сторон пятиугольника.
Всего у этой фигуры пять сторон. На изображении отрезок «а» показывает одну из 5 сторон пятиугольника.