Содержание
ВЫСШАЯ МАТЕМАТИКА.
Раздел «Линейная алгебра»
Электронное учебно-методическое пособие
для студентов 1 курса экономического факультета
Федеральное агентство по образованию
ГОУ ВПО «Кемеровский государственный университет»
Кафедра высшей математики
ВЫСШАЯ МАТЕМАТИКА.
Раздел «Линейная алгебра»
Электронное учебно-методическое пособие
для студентов 1 курса экономического факультета
Кемерово 2009
Составитель: старший преподаватель Айнетдинова Л.Н.
Высшая математика.
Раздел «Линейная алгебра». Электронное
учебно-методическое пособие для студентов
1 курса экономического факультета./
сост. Л.Н. Айнетдинова; ГОУ ВПО «Кемеровский
государственный университет».
Электронное учебно-методическое пособие написано по курсу Высшая математика. Раздел «Линейная алгебра» для студентов 1 курса экономического факультета в соответствии с Государственным образовательным стандартом высшего профессионального образования.
Учебно-методическое пособие содержит вопросы, которые необходимо знать для изучения предложенной темы практического занятия, разработаны примеры задач, приведены задачи для работы в аудитории и для самостоятельной работы.
Рекомендовано методической комиссией математического факультета «____» ________________ 2009 г. Председатель методической комиссии факультета _______________ В.А. Шалаумов | Рекомендовано к утверждению на заседании кафедры высшей математики «____» ________________
2009 г. Заведующий кафедрой _____________ С.П. Брабандер |
Содержание 4
Введение 5
Тема 1 6
Матрицы 6
Примеры решения задач 6
Тема 2 10
Свойства определителей 10
Примеры решения задач 10
Тема 3 14
Обратная матрица. Матричные уравнения. 14
Примеры решения задач 14
Тема 4 17
Система линейных алгебраических уравнений (СЛАУ) 17
Примеры решения задач 17
Тема 5 21
Ранг матрицы СЛАУ. 21
Примеры решения задач 21
Тема 6 25
Однородная система линейных уравнений. ФСР. 25
Примеры решения задач 25
Тема 7 28
Линейная зависимость векторов. 28
Базис и размерность линейного пространства. 28
Примеры решения задач 29
Тема 8 35
Линейные операторы. 35
Тема 9 37
Квадратичные формы. 37
Тема 10 39
Аналитическая
геометрия на плоскости.
Простейшие
задачи. 39
Тема 11 41
Кривые второго порядка. 41
Тема 12 44
Прямая и плоскость в пространстве. 44
Тема 13 46
Векторная алгебра. 46
Справочные материалы 48
ГЛОССАРИЙ 50
ПЕРЕЧЕНЬ УМЕНИЙ 54
Литература 58
Введение
Учебно-методическое пособие по курсу «Высшая математика» разработано в соответствии с типовой учебной программой и преследует собой – устранить недостаточность и разрозненность задачников по данному курсу.
Данное пособие предназначено для изучения следующих разделов курса: «Линейная алгебра», «Векторная алгебра», «Аналитическая геометрия».
К каждой теме
приведены вопросы, которые необходимо
знать для изучения предложенной темы.
Представлены примеры для решения
студентами, как на практических занятиях,
так и для выполнения домашних заданий.
В конце пособия приведен глоссарий к
разделу «Линейная алгебра» и справочный
материал по теме «Векторная алгебра».
Тема 1 Матрицы
Контрольные вопросы.
Что называется матрицей?
Что понимается под операцией транспонирования матрицы? Существует ли транспонированная матрица для матрицы ?
Свойства операции транспонирования матриц
Можно ли сложить две матрицы с размерами
Как перемножаются матрицы? Можно ли умножить матрицу с размерами на матрицу с такими же размерами.
Как связаны между собой минор и алгебраическое дополнение элемента ? Запишите минор и алгебраическое дополнение элемента .
Примеры решения задач
Пример 1. Вычислить произведение матриц .
Решение.
Перемножим матрицы, умножая элементы
каждой строки на соответствующие
элементы каждого столбца.
Пример 2. Доказать, что матрица удовлетворяет уравнению
Решение. Подставим матрицу в исходное уравнение
Следовательно, матрица является корнем матричного уравнения .Задания
Даны матрицы . Вычислите
Найти значение многочлена от матрицы :
Как изменится произведение матриц , если:
а) переставить —ю и —ю строки ;
б) к -й строке матрицы прибавить -ую строку, умноженную на число ;
в) переставить -й и -й столбцы матрицы ;
г) к
-му
столбцу матрицы
прибавить
-й
столбец, умноженный на число
.
Найдите те из произведений матриц , которые существуют:
Вычислить , где
Какие из следующих операций можно провести с матрицами А, В?
Является ли матрица корнем уравнения
Собственные числа и вектора матриц. Методы их нахождения
- Подробности
- Просмотров: 269212
Рейтинг: 4 / 5
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Квадратная таблица $$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$$ составленная из четырех действительных или комплексных чисел называется квадратной матрицей 2-го порядка.
Аналогично если $$A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$$
— квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число
$$\det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=$$ $$a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}.$$
Эту формулу называют «правило треугольника»: одно из трех слагаемых, входящих в правую часть со знаком «+», есть произведение элементов главной диагонали матрицы, каждое из двух других — произведение элементов лежащих на параллели к этой диагонали и элемента из противоположного угла матрицы, а слагаемые, входящие в со знаком минус, строятся таким же образом, но относительно второй (побочной) диагонали.
$D=25-16=9$
$x_1=\frac{-5-3}{2}=-4;\qquad x_2=\frac{-5+3}{2}=-1.$
Ответ: $x_1=-4;\,\,\, x_2=-1.$
{jumi[*4]}
3.13. $\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}.$
Решение.
$\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}=3\cdot 7\cdot8+(-5)\cdot 8\cdot(-1)+4\cdot(-2)\cdot2-(-5)\cdot7\cdot2-$
$-4\cdot8\cdot8-3\cdot(-2)\cdot(-1)=168+40-16+70-256-6=0.$
Ответ: $0.$
3.16. $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}.$
Решение.
$\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}=\sin\alpha\cos\beta+\sin\beta\cos\gamma+\cos\alpha\sin\gamma-$
$-\cos\beta\sin\gamma-\sin\alpha\cos\gamma-\cos\alpha\sin\beta=$
$=\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha).
T=\det A.$
2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.
3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.
4) Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.
5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.
6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).
Примеры:
3.24. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}.
$
Доказательство.
$\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$\begin{vmatrix}a_1&a_1-b_1x&c_1\\a_2&a_2-b_2x&c_2\\a_3&a_3-b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1-b_1x&c_1\\b_2x&a_2-b_2x&c_2\\b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$=\begin{vmatrix}a_1&a_1&c_1\\a_2&a_2&c_2\\a_3&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}b_1x&b_1x&c_1\\b_2x&b_2x&c_2\\b_3x&b_3x&c_3\end{vmatrix}=$
$-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}=$ $-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$
$-2\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}.
{3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$
$=a(-27-8-8+3+24+24)-b(18+16+24-9-16-48)+$
$+c(-12-4-18+6+4+36)-d(-16-16-27+24+6+48)=$
$=8a+15b+12c-19d.$
Ответ: $8a+15b+12c-19d.$
{jumi[*4]}
3.61. Вычислить определитель: $\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}.$
Решение.
Вычислим этот определитель с помощью приведения определителя к треугольному виду:
$\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}=$ от каждой из первых четырех строк отнимем пятую $=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\1&1&1&1&6\end{vmatrix}=$ от пятой строки отнимем первую, затем пятую строку умножим на два
$=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&1&1&1&11\end{vmatrix}=$ $\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&2&2&2&22\end{vmatrix}=$ Далее от пятой строки отнимем вторую, после чего пятую строку умножим на $\frac{3}{2}:$ $=\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&2&2&27\end{vmatrix}=$ $\frac{1}{2}\frac{2}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&3&3&40,5\end{vmatrix}=$ Теперь от пятой строки отнимем третью, после чего пятую строку умножим на $\frac{4}{3}:$ $=\frac{1}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&3&45,5\end{vmatrix}=$ $\frac{1}{3}\frac{3}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&4&\frac{182}{3}\end{vmatrix}=$ Отнимем от пятой строки четвертую и перемножив диагональные элементы получаем ответ: $=\frac{1}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&0&\frac{197}{3}\end{vmatrix}=$ $=\frac{1}{4}\cdot2\cdot3\cdot4\cdot\frac{197}{3}=394.
2.$
Вычислить определители, используя подходящее разложение по строке или столбцу.
3.51. $\begin{vmatrix}-1&5&2\\0&7&0\\1&2&0\end{vmatrix}.$
Ответ: $-14.$
3.52. $\begin{vmatrix}2&1&0\\1&2&1\\0&1&2\end{vmatrix}.$
Ответ: $4.$
3.54. (б) $\begin{vmatrix}5&a&2&-1\\4&b&4&-3\\2&c&3&-2\\4&d&5&-4\end{vmatrix}.$
Ответ: $2a-8b+c+5d.$
3.62. Вычислить определитель: $\begin{vmatrix}5&6&0&0&0\\1&5&6&0&0\\0&1&5&6&0\\0&0&1&5&6\\0&0&0&1&5\end{vmatrix}.$
Ответ: $665.$
{jumi[*4]}
матриц с примерами и вопросами с решениями
матрицы с примерами и вопросами с решениями Приведены примеры и вопросы по матрицам вместе с их решениями.
Определение матрицы
Ниже приведены примеры матриц (множественное число от матрицы ).Нулевая матрица имеет все элементы, равные нулю.
Пример 1
Следующая матрица имеет 3 строки и 6 столбцов.
Запись матрицы (или элемент)
Элемент (или элемент) в строке i и столбце j матрицы A (заглавная буква A) обозначается символом \((A)_{ij} \) или \( a_{ij} \ ) (строчная буква а).Пример 2
В матрице A, показанной ниже, \(a_{11} = 5 \), \(a_{12} = 2 \) и т. д. .
.. или \( (A)_{11} = 5 \ ), \( (A)_{12} = 2 \) и т. д. …
\[
\textbf{А} =
\begin{bматрица}
5 и 2 и 7 и -3 \\
-9 и -2 и -7 и 11\\
\end{bmatrix}
= \begin{bmatrix}
а_{11} и а_{12} и а_{13} и а_{14} \\
а_{21} и а_{22} и а_{23} и а_{24} \\
\end{bmatrix}
\]Квадратная матрица
Квадратная матрица имеет количество строк, равное количеству столбцов.Пример 3
Для каждой приведенной ниже матрицы определите порядок и укажите, является ли она квадратной матрицей.
\[ а) \begin{bmatrix} -1 и 1 и 0 и 3 \\ 4 и -3 и -7 и -9\\ \end{bmatrix} \;\;\;\; б) \begin{bmatrix} -6 & 2 & 0 \\ 3&-3&4\ -5 и -11 и 9 \end{bmatrix} \;\;\;\; \\ в) \begin{bmatrix} 1 и -2 и 5 и -2 \end{bmatrix} \;\;\;\; г) \begin{bmatrix} -2 и 0 \\ 0 и -3 \end{bmatrix} \;\;\;\; д) \begin{bmatrix} 3 \end{bmatrix} \]
Решения
а) порядок: 2 × 4. Количество строк и столбцов не равно, поэтому матрица не квадратная.
б) порядок: 3 × 3. Количество строк и столбцов одинаковое, поэтому эта матрица является квадратной матрицей.
c) порядок: 1 × 4. Количество строк и столбцов не равно, поэтому матрица не квадратная. Матрица с одной строкой называется матрицей-строкой (или вектором-строкой).
г) порядок: 2 × 2. Количество строк и столбцов одинаково, поэтому это квадратная матрица.
e) порядок: 1 × 1. Количество строк и столбцов одинаково, поэтому эта матрица является квадратной матрицей.
Матрица идентичности
Единичная матрица I n представляет собой квадратную матрицу размера n × n, в которой все ее элементы по диагонали равны 1, а все остальные элементы равны нулю.Пример 4
Ниже приведены все матрицы идентичности. \[I_1= \begin{bmatrix} 1\\ \end{bmatrix} \четверка, \четверка I_2= \begin{bmatrix} 1 и 0\\ 0 и 1 \end{bmatrix} \quad , \quad I_3= \begin{bmatrix} 1 и 0 и 0\\ 0 и 1 и 0 \\ 0 и 0 и 1 \end{bmatrix} \]
Диагональная матрица
Диагональная матрица — это квадратная матрица, все элементы которой (элементы) равны нулю, за исключением элементов главной диагонали сверху слева направо снизу.
\[A = \begin{bmatrix}
6 и 0 и 0 \\
0 и -2 и 0 \\
0 и 0 и 2
\end{bmatrix} \]Треугольная матрица
Верхняя треугольная матрица — это квадратная матрица, у которой все элементы ниже главной диагонали равны нулю. Матрица U, показанная ниже, является примером верхней треугольной матрицы. Нижняя треугольная матрица — это квадратная матрица, все элементы которой выше главной диагонали равны нулю. Показанная ниже матрица L является примером нижней треугольной матрицы.\(U = \begin{bmatrix} 6 и 2 и -5 \\ 0 и -2 и 7 \\ 0 и 0 и 2 \end{bmatrix} \qquad L = \begin{bmatrix} 6 и 0 и 0 \\ -2 и -2 и 0 \\ 10 и 9Т\).
Пример 6
Симметричные матрицы \[ \begin{bmatrix} 4&-2&1\ -2&5&7\ 1 и 7 и 8 \end{bmatrix} \]
Вопросы по матрицам: часть A
Учитывая матрицы: \[ А = \begin{bmatrix} -1 и 23 и 10\ 0&-2&-11\ \end{bmatrix} ,\четверка B = \begin{bmatrix} -6&2&10\ 3&-3&4\ -5&-11&9\ 1 и -1 и 9 \end{bmatrix} ,\четверка С = \begin{bmatrix} -3 и 2 и 9 и -5 и 7 \end{bматрица} \\ D = \begin{bmatrix} -2 и 6\ -5 и 2\\ \end{bmatrix} ,\четверка Е = \begin{bmatrix} 3 \end{bmatrix} ,\четверка F = \begin{bmatrix} 3\\ 5\\ -11\ 7 \end{bmatrix} ,\четверка G = \begin{bmatrix} -6&-4&23\ -4 и -3 и 4 \\ 23 и 4 и 9Т\).
Вопросы по матрицам: часть B
1) Учитывая матрицы: \[ А = \begin{bmatrix} 23 и 10\ 0 & -11 \\ \end{bmatrix} ,\четверка B = \begin{bmatrix} -6 & 0 & 0 \\ -1 и -3 и 0 \\ -5 и 3 и -9 \\ \end{bmatrix} ,\четверка С = \begin{bmatrix} -3 и 0\\ 0 и 2 \end{bматрица} \\ ,\четверка D = \begin{bmatrix} -7 и 3 и 2 \ 0 и 2 и 4 \\ 0 и 0 и 9 \\ \end{bmatrix} ,\четверка Е = \begin{bmatrix} 12 & 0 & 0 \\ 0 и 23 и 0 \\ 0 и 0 и -19Т = \begin{bmatrix} -6 и -4 и 23\\ -4 и -3 и 4\\ 23 и 4 и 9 \end{bmatrix} \]Ответы на вопросы в части B
а) С и Еб) Б
в) А и Г
Больше Справок и ссылок
- Сложение, вычитание и скалярное умножение матриц
- Умножение и мощность матриц
- Линейная алгебра
- Операции со строками и элементарные матрицы
- Матрица (математика)
- Матрицы, применяемые к электрическим цепям
- Обратная квадратная матрица
Матрицы и линейная алгебра (математика)
Матрицы и линейная алгебра (математика)| Математика |
Вопросы вычислений
Одной из наиболее важных задач технических вычислений является решение одновременных линейных уравнений.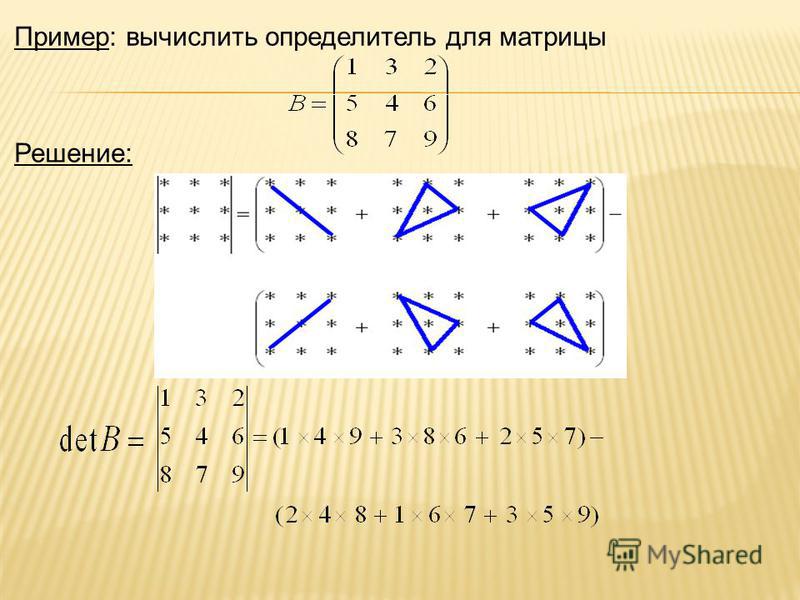
В матричной записи эту задачу можно сформулировать следующим образом.
Для заданных двух матриц A и B существует уникальная матрица X , такая что AX = B или XA = B ?
Поучительно рассмотреть пример 1 на 1.
Уравнение
есть уникальное решение?
Конечно, да. Уравнение имеет единственное решение x = 3. Решение легко получается делением на .
Решение , а не обычно получается путем вычисления обратного 7, то есть 7 -1 = 0,142857…, а затем умножения 7 -1 на 21. , если 7 -1 представлено конечным числом цифр, менее точно. Аналогичные соображения применимы к системам линейных уравнений с более чем одним неизвестным;
MATLAB решает такие уравнения без вычисления обратной матрицы.
Хотя это не стандартная математическая запись, MATLAB использует терминологию деления, известную в скалярном случае, для описания решения общей системы одновременных уравнений.
Два символа деления, косая черта , / и обратная косая черта , \ используются для двух ситуаций, когда неизвестная матрица появляется слева или справа от матрицы коэффициентов.
| Обозначает решение матричного уравнения AX = B . |
| Обозначает решение матричного уравнения XA = В . |
Вы можете думать о «делении» обеих частей уравнения AX = B или XA = B на A . Матрица коэффициентов A всегда находится в «знаменателе».
Условия совместимости размеров для X = A\B требуют, чтобы две матрицы A и B имели одинаковое количество строк.
Решение X имеет то же количество столбцов, что и B , а размерность его строки равна размерности столбца A . Для X = B/A роли строк и столбцов меняются местами.
На практике линейные уравнения вида AX = B встречаются чаще, чем уравнения вида XA = B . Следовательно, обратная косая черта используется гораздо чаще, чем косая черта. Оставшаяся часть этого раздела посвящена оператору обратной косой черты; соответствующие свойства оператора косой черты можно вывести из тождества
(В/А)' = (А'\В')
Матрица коэффициентов A не обязательно должна быть квадратной. Если A равно м на n , возможны три случая.
| м = п | Квадратная система. Ищите точное решение. |
| м > п | Переопределенная система. |
