Метод главных компонент: аналитическое решение / Хабр
В этой статье мы залезем под капот одному из линейных способов понижения размерности признакового пространства данных, а именно, подробно ознакомимся с математической стороной метода главных компонент (Principal Components Analysis, PCA).
Содержание статьи:
Примечания автора
Вместо введения
1) Значение принципа максимизации дисперсии в методе главных компонент
1.1) Принцип максимизации дисперсии
1.2) Синтетический пример: метод главных компонент в действии
2) Под капотом метода главных компонент
2.1) Преобразование матрицы признакового пространства в матрицу компонент путем умножения первой на матрицу
2.2) Связка преобразования признакового пространства с принципом максимизации дисперсии через ковариационную матрицу
2. 3) Метод множителей Лагранжа: приведение уравнения с условием того, что к виду:
3) Метод множителей Лагранжа: приведение уравнения с условием того, что к виду:
2.4) Переход от задачи дифференцирования функции Лагранжа по вектору к задаче поиска собственных значений и собственных векторов матрицы :
2.5) Аналитическое решение: поиск собственных значений и собственных векторов матрицы
Вместо заключения
Примечания автора
Данная статья, как и большинство моих предыдущих работ, не пропитана глубокой теорией, скорее наоборот — строгие теоретические выкладки здесь приводятся по минимуму. Вместо формального подхода к описанию метода главных компонент, рассмотрим один синтетический пример, разобрав который, мы сможем лучше понять механизм действия метода.
— В первой части статьи мы посмотрим на то, что происходит с данными после их преобразования методом главных компонент. Изучать преобразования мы будем на простом примере.
— Во второй части мы рассмотрим ответы на вопросы, связанные с тем, как происходят эти преобразования, то есть рассмотрим математику процесса.
Весь код в статье написан на языке python 3.
Для лучшего усвоения материала, читателю следует разбираться в основах аналитической геометрии, уметь перемножать матрицы и находить их определители, решать системы линейных уравнений с несколькими неизвестными, находить частные производные от матричных выражений, понимать суть основных характеристик случайных величин (математическое ожидание, вариация, ковариация, корреляция) и безусловно, читателю необходимо иметь хорошее представление об основных моделях машинного обучения. Это минимальный набор знаний, с которым стоит подойти к изучению статьи, остальные знания мы получим в процессе.
Вместо введения
Перед тем как перейти к первой части статьи, давайте определим основные цели понижения размерности признакового пространства.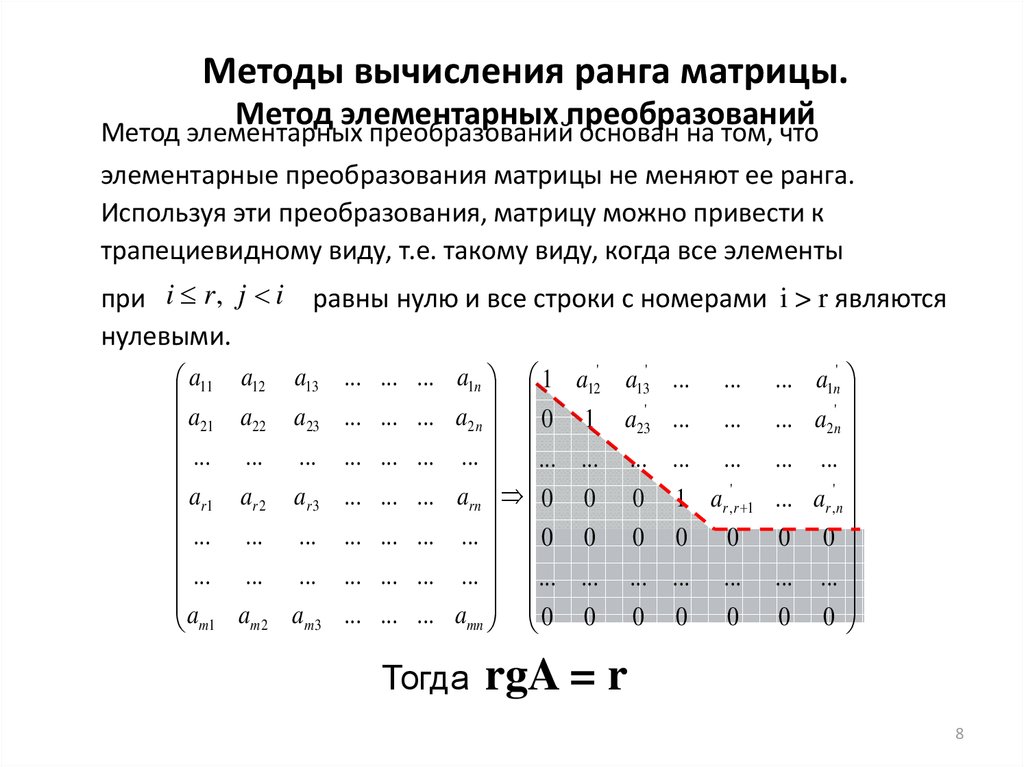 В самом общем виде, исследователь понижает размерность исходных данных в следующих случаях:
В самом общем виде, исследователь понижает размерность исходных данных в следующих случаях:
Во-первых, вследствие того, что признаков настолько много, что вычисления происходят значительно дольше требуемого времени. Например, в интернет-магазине требуется в считаные доли секунд предложить потенциальному покупателю рекомендацию. В этой ситуации, признаков на основании которых может быть дана рекомендация очень много и требуется уменьшить размерность, чтобы уменьшить время расчетов, сохранив при этом как можно больше объясняющей информации.
Во-вторых, вследствие того, что вычисления с использованием большого количества данных становятся слишком энергозатратными и экономически не выгодными.
В-третьих, и это больше применимо к методу главных компонент, из-за того, что данные почти всегда содержат шум. Как известно, шум является одним из источников переобучения моделей машинного обучения. С помощью метода главных компонент можно убрать шум. Предполагается, что дисперсия шума мала относительно дисперсии самих данных, и после преобразования данных методом главных компонент, преобразованные данные (компоненты), дисперсии которых окажутся малы, мы будем считать шумом.
Именно эти цели в большинстве случаев преследуют датасайнтисты при понижении размерности исходного признакового пространства.
Казалось бы, самое простое и очевидное решение — убрать по какому-либо заданному параметру неугодные признаки. И действительно, методы отбора признаков очень распространены. Существуют одномерные методы отбора признаков, жадные методы, отбор на основе моделей и др. Но ведь, удалив из расчетов какой-то признак, мы рискуем потерять часть важной информации. Отсюда возникла идея, а почему бы не преобразовать признаки таким образом, чтобы можно было, скажем из числа исходных признаков , получить такое количество признаков, в которых содержалось бы как можно больше информации исходных признаков, затем на новых, то есть преобразованных данных, провести обучение моделей. Одним из способов такого преобразования и является метод главных компонент.
Сделаем небольшое замечание. Метод главных компонент, безусловно, не всегда преобразовывает признаковое пространство таким образом, что модели, которые обучаются на преобразованном пространстве, показывают качество лучше, чем на исходном. При этом, для того, чтобы преобразование сработало, необходимо выполнений некоторых условий матрицы исходного признакового пространства , например распределение значений признаков и целевой переменной должно быть нормальным. В статье мы не будем акцентировать внимание на эти условия.
А теперь, давайте перейдем, на мой взгляд, к самому неловкому моменту в теоретической части метода главных компонент — принципу максимизации дисперсии.
1. Максимизация дисперсии в методе главных компонент
1.1 Принцип максимизации дисперсии
 Данное предположение появилось вследствии еще одного, не менее загадочного предположения о том, что дисперсия, являющаяся мерой изменчивости данных, может отражать уровень их информативности.
Данное предположение появилось вследствии еще одного, не менее загадочного предположения о том, что дисперсия, являющаяся мерой изменчивости данных, может отражать уровень их информативности.Представьте, что мы имеем обучающую выборку и один из признаков выборки представлен всего одним значением, допустим «». Ценность такой информации с точки зрения объяснения целевой переменной — нулевая. Заметим, что и дисперсия значений такого признака равна нулю.
Конечно, такой пример, ни в коем случае не доказывает вышеобозначенных утверждений. Я предлагаю просто напросто поверить в эти предположения об эквивалентности дисперсии и меры информативности данных. После того, как мы в это поверим, все остальные объяснения метода главных компонент будут проходить на ура, то есть иметь вполне себе математические обоснования. Для тех, кто хочет более подробно ознакомиться с этим принципом рекомендую из литературы труд Кендалла М. и Стюарта А. — «Многомерный статистический анализ и временные ряды».
1.2 Пример: метод главных компонент в действии
Для того, чтобы лучше понимать суть метода максимизации, предлагаю Вашему вниманию простой пример.
Мы смоделируем матрицу исходных признаков , для нее определим вектор истинных ответов , преобразуем методом главных компонент матрицу в матрицу , обучим модель линейной регрессии на двух матрицах данных, сравним качество моделей, определим статистики, характеризующие матрицы и .
Приступим!
Сгенерируем 5000 объетов. Пусть это будут какие-то абстрактные изделия, например, муфты металлические соединительные.
Давайте определимся как мы будем генерировать эти 5000 объектов в матрице
Для каждого изделия сгенеририруем 4 признака . Пусть это будут длина изделия — , диаметр изделия — и еще два признака, которые являются производными от первых двух и содержат много шума, поэтому они малоинформативны, мы их так и будем называть: 3-й и 4-й признаки, соответственно и .
С целью установления связи между первыми двумя признаками, при генерации данных, используем параметры их матрицы ковариации : дисперсии и коэффициенты ковариации. Первому признаку — длине изделия, зададим наибольшую дисперсию.
Теперь определим вектор истинных значений целевой переменной .
Для генерации истинных значений целевой переменной воспользуемся следующей формулой:
, где — это вектор коэффициентов, определяющий силу влияния значений признаков в формировании истинных ответов
— это наша матрица исходного признакового пространства
Как следует из формулы, каждый признак вносит свой собственный вклад в определении значений истинных ответов, в соответствии с заданными коэффициентами. При определении коэффициентов мы закладываем логику, что длина и диаметр должны в большей степени определять вес изделия, нежели 3-й и 4-й признаки. Также мы увязываем значения коэффициентов с размерами дисперсий признаков, но весьма экстравагантным способом:
,
,
,
,
где — значение дисперсии соответствующей -му признаку, — значение коэффициента соответствующего -му признаку.
Заметьте, мы уравновесили первый и второй коэффициенты. Для чего мы это делаем? А все для того, чтобы нас никто не смог упрекнуть в искусственном увеличении значимости первого признака при генерации . С этой же целью, мы установили приблизительно равные средние значения длины и диаметра изделий.
Таким образом, мы можем смело заявить о том, что первый и второй признаки, без учета различий в значениях дисперсий, вносят практически равнозначный вклад в генерацию значений истинных ответов, а следовательно, в дальнейшем, мы сможем хоть как-то оценить «чистое» влияние дисперсии признака на его информативность.
Смотрим код
Импортируем библиотеки
# импортируем библиотеки import numpy as np import pandas as pd import matplotlib from matplotlib import pyplot as plt %matplotlib inline import seaborn as sns; sns.set() import random from sklearn.linear_model import LinearRegression from sklearn.decomposition import PCA from sklearn.metrics import mean_squared_error from sklearn.preprocessing import StandardScaler from sklearn.model_selection import train_test_split from sklearn.preprocessing import normalize
Генерируем исходное пространство и вектор истинных ответов
np.random.seed(0) # инициализируем математическое ожидание двух случайных величин (признаки: длина и диаметр изделия) mu = np.array((100.,100)) # инициализируем матрицу ковариации двух случайных величин (признаки: длина и диаметр изделия) cov = np.array([[1.3,0.15],[0.6,0.8]]) # инициализируем количество объектов N = 5000 # формируем матрицу признаков с параметрми mu и cov X12 = np.dot(np.random.randn(N, 2), cov) + mu # выделяем из матрицы X12 1-й вектор значений признаков x1 = X12[:,0] # выделяем из матрицы X12 2-й вектор значений признаков x2 = X12[:,1] # формируем шум для 3-го вектора значений признаков и смещаем среднее e3 = np.array([random.uniform(49.05,50.95) for i in range(N)]) # формируем 3-й вектор значений признаков x3 = (x1/3 + x2/10)/5 + e3 # формируем шум для 4-го вектора значений признаков и смещаем среднее e4 = np.array([random.uniform(350.5,351.5) for i in range(N)]) # формируем 4-й вектор значений признаков x4 = (x1/100 + x2*2)/10 + e4 # формируем матрицу исходного признакового пространства X = np.vstack((np.vstack((np.vstack((x1,x2)),x3)),x4)).T # записываем правило определения истинных значений целевой переменной def y(X, r_0, R): R = R.reshape(-1, R.shape[0]) e = np.array([random.uniform(-1.,1.) for i in range(N)]).reshape(-1,1) y = r_0 + np.dot(X, R.T) + e return y # инициализируем вектор коэффициентов r_0 = 0 R = np.array([1.3, 1.3, 0.33, 0.33]) # формируем вектор истинных значений y = y(X, r_0, R) # формируем таблицу pandas с исходными данными матрицы X и вектора y dataframe = pd.DataFrame(X) columns_x = ['Длина, мм', 'Диаметр, мм', '3-й признак', '4-й признак'] dataframe = pd.DataFrame(np.hstack((X,y))) dataframe.columns = columns_x + ['Вес изделия']
Давайте визуализируем парные отношения признаков и целевой переменной нашего небольшого датасета.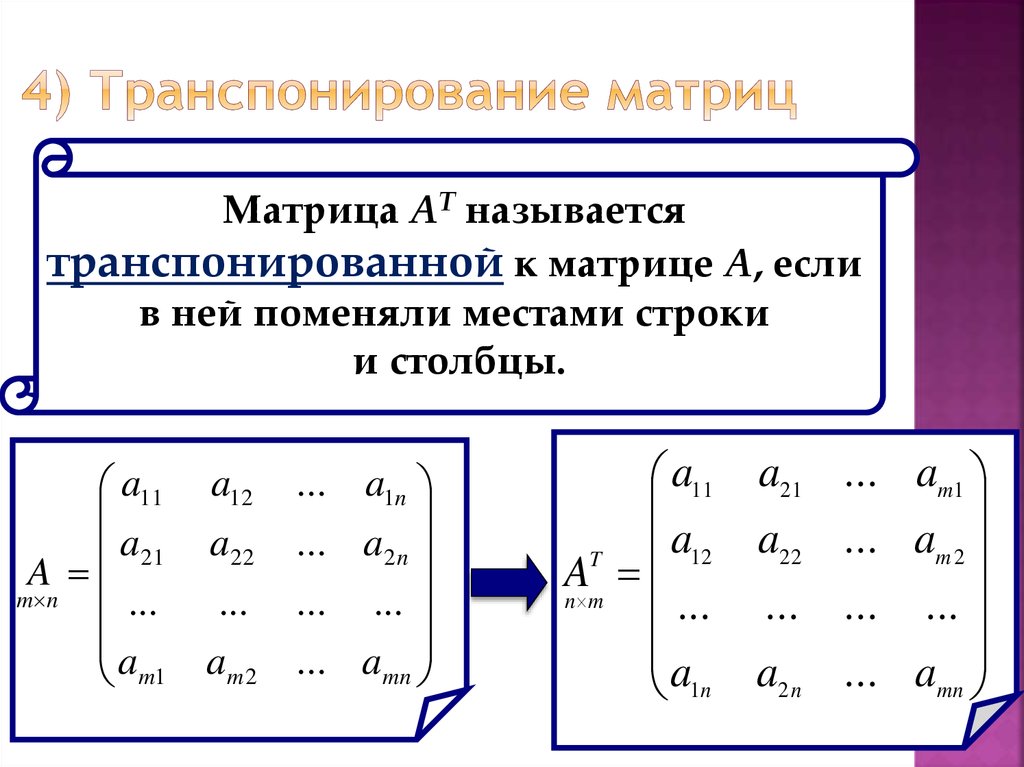 Для этого воспользуемся функцией pairplot из библиотеки seaborn.
Для этого воспользуемся функцией pairplot из библиотеки seaborn.
Визуализируем отношения признаков друг с другом
# print ('График №1 "Парные отношения признаков и истинных ответов"')
sns_plot = sns.pairplot(dataframe)
sns_plot.fig.suptitle('График №1 "Парные отношения признаков и истинных ответов"',
y = 1.03, fontsize=14, fontweight='bold')
plt.show()
# сохраним график в файл
sns_plot.savefig('graph_1.png')Внешне датасет удался!
На графиках, не вооруженным глазом заметно, что длина изделий существенно лучше объясняют вес изделий, чем их диаметр. А 3-й и 4-й признаки, хоть и имеют схожее распределение со значениями веса изделий, очевидно, что в них содержится много шума.
Давайте еще раз акцентируем внимание на первых двух признаках и их влиянии на целевую переменную. Построим более детализированные графики.
Смотрим код
Визуализируем отношение длины, диаметра и целевой переменной
# формируем графики отображения зависимости признаков "Длина", "Диаметр" и целевой переменной "Вес изделия" fig, (ax1, ax2, ax3) = plt.subplots(nrows = 1, ncols = 3, figsize = (16, 6)) fig.suptitle('График №2 "Отношение длины, диаметра и целевой переменной"', fontsize=14, fontweight='bold') fig.subplots_adjust(top = 0.85) ax1.scatter(dataframe['Длина, мм'],dataframe['Диаметр, мм'], color = 'green') ax1.set_title('Зависимость признаков: \n Длина и Диаметр') ax1.set_xlabel('Длина, мм') ax1.set_ylabel('Диаметр, мм') ax2.scatter(dataframe['Длина, мм'],dataframe['Вес изделия'], color = 'green') ax2.set_title('Зависимость целевой переменной от \n длины') ax2.set_xlabel('Длина, мм') ax2.set_ylabel('Вес изделия') ax3.scatter(dataframe['Диаметр, мм'],dataframe['Вес изделия'], color = 'green') ax3.set_title('Зависимость целевой переменной от \n диаметра') ax3.set_xlabel('Диаметр, мм') ax3.set_ylabel('Вес изделия') plt.show() # сохраним график в файл fig.savefig('graph_2.png')
Несмотря на то, что ранее, мы старательно уравновешивали влияние обоих признаков при определении значений истинных ответов, на графиках отчетливо видно, что признак длины изделий, который имеет наибольшую дисперсию, значительно лучше объясняет вес изделий. Иначе можно сказать, что длина имеет больший вес относительно диаметра в определении целевой переменной.
Иначе можно сказать, что длина имеет больший вес относительно диаметра в определении целевой переменной.
Конечно, нельзя считать результат этого небольшого эксперимента доказательством значимости дисперсии признака для определения целевой переменной. Однако наш пример все-таки указывает на то, что принцип максимизации дисперсии может работать при определенных условиях.
Кстати, обратим внимание на то, что диаметр изделия сильно зависит от его длины. Другими словами, зная длину изделия, мы можем с хорошей точностью, определить его диаметр. Можно, конечно, наоборот — на основании диаметра определять длину, но качество будет заметно ниже.
А теперь вопрос! Почему бы нам, в соответствии с принципом максимизации дисперсии, просто взять и удалить признаки, имеющие наименьшую дисперсию? Зачем нам преобразовывать данные?
Спешу разочаровать, однозначного и строгого ответа со всеми сопутствующими теоретическими выкладками на данный вопрос в статье дано не будет. Однако, не спешим отчаиваться и продолжим рассмотрение нашего примера. Обучим модель линейной регрессии на исходных и преобразованных данных, затем сравним качество модели на обоих пространствах по размеру среднеквадратичной ошибки (Mean Squared Error, ). Внимательный читатель, наверное уже догадывается, что мы ожидаем увидеть лучшее качество на преобразованных данных или по крайней мере сопоставимое качество, но при использовании меньшего количества преобразованных признаков.
Обучим модель линейной регрессии на исходных и преобразованных данных, затем сравним качество модели на обоих пространствах по размеру среднеквадратичной ошибки (Mean Squared Error, ). Внимательный читатель, наверное уже догадывается, что мы ожидаем увидеть лучшее качество на преобразованных данных или по крайней мере сопоставимое качество, но при использовании меньшего количества преобразованных признаков.
Смотрим код
Сравним качество моделей
# инициируем таблицу ошбок среднеквадратичных отклонений
table_errors_test = pd.DataFrame(index = ['MSE_test'])
# напишем функцию определения среднеквадратичной ошибки
def error(x_train, x_test, y_train, y_test):
# инициируем модель линейной регрессии
model = LinearRegression()
# обучим модель на обучающей выборке
model_fit = model.fit(x_train,y_train)
# сформируем вектор прогнозных значений
y_pred = model_fit.predict(x_test)
# определим среднеквадратичную шибку
error = round(mean_squared_error(y_test, y_pred),3)
return error
# разделим выборку на обучающую и тестовую
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0. 33, random_state=42)
# проведем центрирование данных (функция нормирования отключена)
scaler = StandardScaler(with_mean = True, with_std = False)
scaler = scaler.fit(X_train)
X_train_norm = scaler.transform(X_train)
X_test_norm = scaler.transform(X_test)
# инициируем модель PCA с 4 компонентами
model_pca = PCA(n_components = 4)
# обучим модель на обучающей выборке
model_pca.fit(X_train_norm)
# преобразуем данные обучающей выборки
Z_train_norm = model_pca.transform(X_train_norm)
# преобразуем данные тестовой выборки
Z_test_norm = model_pca.transform(X_test_norm)
# сформируем в pandas таблицу оценок качества модели линейной регрессии в зависимости от используемых признаков
table_errors_test['Все признаки'] = error(X_train_norm, X_test_norm, y_train, y_test)
table_errors_test['3-и признака'] = error(X_train_norm[:,0:3], X_test_norm[:,0:3],y_train, y_test)
table_errors_test['Длина + Диаметр'] = error(X_train_norm[:,0:2], X_test_norm[:,0:2],y_train, y_test)
table_errors_test['Длина'] = error(X_train_norm[:,0].
33, random_state=42)
# проведем центрирование данных (функция нормирования отключена)
scaler = StandardScaler(with_mean = True, with_std = False)
scaler = scaler.fit(X_train)
X_train_norm = scaler.transform(X_train)
X_test_norm = scaler.transform(X_test)
# инициируем модель PCA с 4 компонентами
model_pca = PCA(n_components = 4)
# обучим модель на обучающей выборке
model_pca.fit(X_train_norm)
# преобразуем данные обучающей выборки
Z_train_norm = model_pca.transform(X_train_norm)
# преобразуем данные тестовой выборки
Z_test_norm = model_pca.transform(X_test_norm)
# сформируем в pandas таблицу оценок качества модели линейной регрессии в зависимости от используемых признаков
table_errors_test['Все признаки'] = error(X_train_norm, X_test_norm, y_train, y_test)
table_errors_test['3-и признака'] = error(X_train_norm[:,0:3], X_test_norm[:,0:3],y_train, y_test)
table_errors_test['Длина + Диаметр'] = error(X_train_norm[:,0:2], X_test_norm[:,0:2],y_train, y_test)
table_errors_test['Длина'] = error(X_train_norm[:,0]. reshape(-1,1), X_test_norm[:,0].reshape(-1,1),
y_train, y_test)
table_errors_test['Диаметр'] = error(X_train_norm[:,1].reshape(-1,1), X_test_norm[:,1].reshape(-1,1),
y_train, y_test)
table_errors_test['Все компоненты'] = error(Z_train_norm, Z_test_norm, y_train, y_test)
table_errors_test['Три компоненты'] = error(Z_train_norm[:,0:3], Z_test_norm[:,0:3], y_train, y_test)
table_errors_test['Две компоненты'] = error(Z_train_norm[:,0:2], Z_test_norm[:,0:2], y_train, y_test)
table_errors_test['Первая компонента'] = error(Z_train_norm[:,0].reshape(-1,1),
Z_test_norm[:,0].reshape(-1,1),
y_train, y_test)
print ('Таблица №1 "Сравнение качества модели линейной регрессии, обученной на различных признаках"')
table_errors_test
reshape(-1,1), X_test_norm[:,0].reshape(-1,1),
y_train, y_test)
table_errors_test['Диаметр'] = error(X_train_norm[:,1].reshape(-1,1), X_test_norm[:,1].reshape(-1,1),
y_train, y_test)
table_errors_test['Все компоненты'] = error(Z_train_norm, Z_test_norm, y_train, y_test)
table_errors_test['Три компоненты'] = error(Z_train_norm[:,0:3], Z_test_norm[:,0:3], y_train, y_test)
table_errors_test['Две компоненты'] = error(Z_train_norm[:,0:2], Z_test_norm[:,0:2], y_train, y_test)
table_errors_test['Первая компонента'] = error(Z_train_norm[:,0].reshape(-1,1),
Z_test_norm[:,0].reshape(-1,1),
y_train, y_test)
print ('Таблица №1 "Сравнение качества модели линейной регрессии, обученной на различных признаках"')
table_errors_testРезультаты полностью соответствуют нашим ожиданиям!
Давайте обратим внимание на более значимые для нас результаты:
Во-первых, как мы и предположили по результатам анализа диаграмм рассеяния, длина изделий лучше объясняет их вес. Это также видно при сравнении среднеквадратичной ошибки модели линейной регрессии, обученной на значениях длины изделия со среднеквадратичной ошибкой модели, обученной на значениях диаметра. В первом случае ошибка составляет , во втором случае — . То есть, качество модели, обучаемой на значениях длины изделий более чем в два раза выше.
Это также видно при сравнении среднеквадратичной ошибки модели линейной регрессии, обученной на значениях длины изделия со среднеквадратичной ошибкой модели, обученной на значениях диаметра. В первом случае ошибка составляет , во втором случае — . То есть, качество модели, обучаемой на значениях длины изделий более чем в два раза выше.
Во-вторых, модель, которая использует в расчетах только первую компоненту преобразованного пространства, показывает значительно лучшее качество, относительно модели, использующей единственный признак исходного пространства с наибольшей дисперсией — длину изделия. Качество отличается почти в два раза. То есть, при определенных условиях, метод главных компонент, может преобразовывать исходное пространство так, что первая компонента каким-то образом «впитывает» в себя информацию, которая хорошо объясняет значения целевой переменной.
В-третьих, качество модели, обученной на трех компонентах, не уступает качеству моделей, обученных как на всех четырех компонентах, так и на всех признаках. Учитывая, что наш датасет состоит из двух образующих признаков и двух производных от них признаков, в которые мы добавили значительное количество шума, то достижение качества модели при использовании трех компонент сопоставимого с качеством модели, использующей четыре компоненты, подтверждает мысль о том, что метод главных компонент действительно может позволять отсеивать шумовые значения в отдельные компоненты с наименьшей дисперсией. В нашем случае, при обучении модели линейной регрессии, компоненты с наименьшей дисперсией стоит исключить из процесса обучения.
Учитывая, что наш датасет состоит из двух образующих признаков и двух производных от них признаков, в которые мы добавили значительное количество шума, то достижение качества модели при использовании трех компонент сопоставимого с качеством модели, использующей четыре компоненты, подтверждает мысль о том, что метод главных компонент действительно может позволять отсеивать шумовые значения в отдельные компоненты с наименьшей дисперсией. В нашем случае, при обучении модели линейной регрессии, компоненты с наименьшей дисперсией стоит исключить из процесса обучения.
Давайте теперь посмотрим на то, какие изменения претерпело признаковое пространство. Для этого сравним статистики обучающей выборки исходных признаков со статистиками той же выборки, но уже на преобразованном пространстве.
Для начала посмотрим на статистики, которые предоставляет нам метод describe библиотеки pandas
Формируем основные статистики
# формируем таблицу основных описательных статистик исходного пространства X_train_dataframe = pd.DataFrame(X_train_norm) X_train_dataframe.columns = columns_x X_df_describe = X_train_dataframe.describe(percentiles = []).round(3) # формируем матрицу преобразованного пространства Z_train_norm = model_pca.transform(X_train_norm) Z_train_dataframe = pd.DataFrame(Z_train_norm) columns_z = ['1-я компонента','2-я компонента', '3-я компонента','4-я компонента'] Z_train_dataframe.columns = columns_z # формируем таблицу основных описательных статистик исходного пространства Z_df_describe = Z_train_dataframe.describe(percentiles = []).round(3) # формируем сравнительную таблицу основных описательных статистик двух признаковых пространств df_describe = pd.concat((X_df_describe, Z_df_describe), axis = 1) columns_xz = columns_x + columns_z columns_xz print ('Таблица №2 "Сравнение значений основных описательных статистик исходного и преобразованного пространства"') df_describe[columns_xz]
Из интересующего нас, здесь стоит отметить, что после преобразования исходных признаков, первая компонента имеет больший разброс данных в отличии от исходного признака с наибольшим стандартным отклонением — длины изделий.
Давайте посмотрим на матрицы ковариаций исходных и преобразованных признаков.
Сравним матрицы ковариаций
# формируем матрицу ковариации исходных признаков
X_df_cov = X_train_dataframe.cov().round(3)
# формируем матрицу ковариации преобразованных признаков
Z_df_cov = Z_train_dataframe.cov().round(3)
# формируем сравнительную таблицу ковариаций
df_cov = pd.concat((X_df_cov, Z_df_cov), axis = 1)
print ('Таблица №3 "Сравнение матрицы ковариации исходных и преобразованных признаков"')
df_cov[columns_xz].fillna('-')Действительно, мы наблюдаем некое перераспределение дисперсии признакового пространства в компоненты преобразованного.
В теории, дисперсии должны перераспределяться следующим образом. Первая компонента объясняет максимум
изменчивости исходных переменных, то есть имеет большую дисперсию, вторая – максимум оставшейся изменчивости и т.д., при этом все компоненты должны быть декоррелированны друг к другу.
В целом нечто похожее мы и наблюдаем.
Можно обратить внимание еще и на то, что после преобразования, информация с точки зрения сохранности дисперсии у нас никуда не девается — сумма дисперсий признаков исходного и преобразованного пространств полностью совпадает.
Сравним суммы дисперсий
# сравним суммы дисперсий на исходном и преобразованном пространстве
print (round(sum(X_train_dataframe.var()), 3), '- Сумма дисперсий исходных признаков')
print (round(sum(Z_train_dataframe.var()),3), '- Сумма дисперсий преобразованных признаков')
print ()
print ('Значимость компонент:')
print (list(map(lambda x: round(x,3), model_pca.explained_variance_ratio_)))Значимость компонент означает всего лишь долю дисперсии компоненты в сумме дисперсий компонент.
Кстати, заметим, что компоненты расположены в порядке убывания значений их дисперсий. Таким образом, наиболее значимые для анализа данных компоненты, всегда расположены в первых рядах.
Ранее, мы говорили о том, что преобразованное пространство полностью декоррелированно. Давайте убедимся в этом.
Сравним корреляции
# формируем таблицу корреляции исходных признаков
X_df_cor = X_train_dataframe.corr().round(3)
# формируем таблицу корреляции преобразованных признаков
Z_df_cor = Z_train_dataframe.corr().round(3)
# формируем сравнительную таблицу корреляции
df_cor = pd.concat((X_df_cor, Z_df_cor), axis = 1)
# df_cor.fillna(0)
print ('Таблица №4 "Сравнение корреляции исходных и преобразованных признаков"')
df_cor[columns_xz].fillna('-')Полная декорреляция!
В завершении примера, посмотрим на графики парных отношений преобразованных признаков.
Визуализируем отношения признаков и истинных ответов в преобразованном пространстве
# print ('График №3 "Парные отношения признаков и истинных ответов"')
Z_y_train_dataframe = pd. DataFrame(np.hstack((Z_train_norm,y_train)))
Z_y_train_dataframe.columns = columns_z + ['Вес изделия']
sns_plot = sns.pairplot(Z_y_train_dataframe)
sns_plot.fig.suptitle('График №3 "Парные отношения преобразованных признаков и истинных ответов"',
y = 1.03, fontsize=14, fontweight='bold')
plt.show()
# сохраним график в файл
sns_plot.savefig('graph_3.png')
DataFrame(np.hstack((Z_train_norm,y_train)))
Z_y_train_dataframe.columns = columns_z + ['Вес изделия']
sns_plot = sns.pairplot(Z_y_train_dataframe)
sns_plot.fig.suptitle('График №3 "Парные отношения преобразованных признаков и истинных ответов"',
y = 1.03, fontsize=14, fontweight='bold')
plt.show()
# сохраним график в файл
sns_plot.savefig('graph_3.png')Визуализируем декорреляцию преобразованного признакового пространства
# print ('График №4 "Декорреляция нового признакового пространства"')
fig = plt.figure(figsize=(16, 8))
ax = fig.add_subplot(1, 1, 1, aspect = 'equal')
ax.grid(True, which='both')
fig.suptitle('График №4 "Декорреляция нового признакового пространства"', fontsize=14, fontweight='bold')
fig.subplots_adjust(top = 1.05)
ax.set_ylim(np.min(Z_train_norm[:,1])-1, np.max(Z_train_norm[:,1])+1)
ax.set_xlim(np.min(Z_train_norm[:,0])-1, np.max(Z_train_norm[:,0])+1)
ax.plot(Z_train_norm[:,0], Z_train_norm[:,1], 'o', color = 'green')
plt. xlabel('1-я компонента')
plt.ylabel('2-я компонента')
plt.show()
# сохраним график в файл
fig.savefig('graph_4.png')
xlabel('1-я компонента')
plt.ylabel('2-я компонента')
plt.show()
# сохраним график в файл
fig.savefig('graph_4.png')Итак, наш пример подошел к завершению.
Мы воочию убедились, что метод главных компонент позволяет преобразовывать данные таким образом, что для обучения машинных алгоритмов (в нашем случае, модель линейной регрессии), можно использовать меньшее количество преобразованных признаков — компонент, относительно исходного пространства.
Это достигается за счет:
— перераспределения дисперсии, отражающей уровень информативности данных
— полной декорреляции исходного пространства
Теперь самое время залезть под капот алгоритма и понять все «волшебство» преобразований.
2. Под капотом алгоритма
2.1 Линейное преобразование исходного признакового пространства
Переходим сразу к делу. Для проведения преобразований, нам требуется умножить матрицу исходного признакового пространства на некую матрицу и получить новое признаковое пространство , такое, в котором:
— во-первых, новые признаки — компоненты декоррелированны между собой;
— во-вторых, сумма дисперсий значений компонент равняется сумме дисперсий значений исходных признаков;
— в-третьих, на главной диагонали матрицы ковариации расположены дисперсии компонент в порядке убывания от большего к меньшему.
Для выполнения вышеуказанных условий и для упрощения последующих рассчетов нам следует задать одно важно условие касательно матрицы . Она должна быть ортогональна. Другими словами матрица — квадратная, , а также , где — единичная матрица. Напомним, что единичной матрицей называют квадратную матрицу, у которой элементы главной диагонали равны единице поля, а остальные — нулю.
Запишем преобразование в матричном виде:
По правилам хорошего тона укажем размерность матриц:
Матрица имеет размерность ( x )
Матрица — ( x )
Матрица — ( x )
Матрица — ( x )
Обратим внимание на то, что матрица в такой системе уравнений может быть только квадратной и иметь размерность ( x ), а следовательно, и матрица будет иметь такую же размерность как матрица . Однако, если мы хотим понизить размерность, то мы должны использовать не всю матрицу , а только то количество столбцов, сколько признаков в преобразованном в пространстве мы желаем получить. Но для того, чтобы использовать выборочное количество столбцов матрицы , мы для начала должны вычислить ее полностью.
Не знаю, насколько данная запись будет понятна читателю, но лично мне кажется логичной запись:
Понятно, что имеет размерность , а — , при этом если мы не желаем понижать размерность, то и будут совпадать.
Давайте, чтобы математика лучше усваивалась, будем рассматривать пример на конкретных цифрах. За основу возьмем данные из прошлого примера. Однако, для упрощения рассчетов, в датасете оставим только два признака — длина и диаметр изделия. И далее будем сами, без использования PCA библиотеки sklearn преобразовывать данные. После самостоятельных преобразований сравним результаты с преобразованиями с помощью sklearn.
Итак, инициируем матрицу .
Инициализация матрицы признаков: длина и диаметр
np.random.seed(0) # инициализируем математическое ожидание двух случайных величин mu = np.array((0.,0.)) # инициализируем матрицу ковариации двух случайных величин cov = cov # инициализируем количество объектов N = N # формируем матрицу признаков с параметрами mu и cov X = np.dot(np.random.randn(N, 2), cov) + mu # зафиксируем матрицу признаков в таблице pandas X_df = pd.DataFrame(X) columns_mini = ['Длина','Диаметр'] X_df.columns = columns_mini
Размерность матрицы составляет ( x ), а значит полная размерность матрицы : ( x )
Теперь, когда мы получили систему уравнений и выяснили, что нам нужно найти матрицу , нам следует ответить на вопрос — как главное уравнение связано с принципом максимизации дисперсии, да и вообще — с дисперсией? А самое важное — понять, как вычислять матрицу с учетом принципа максимизации дисперсии?
2.2 Связка линейного преобразования исходного признакового пространства с принципом максимизации дисперсии через матрицу ковариации
Давайте сделаем следующий трюк. Вместо поиска матрицы будем определять матрицу ковариации матрицы , тогда:
Для любителей более подробных математических выкладок есть еще один способ:
Обратим внимание на некоторые отличия в подходах. Первое уравнение в виде матричной записи предполагает, что матрица предварительно была отцентрирована () и определенные в ходе решения уравнения десперсии как будто по умолчанию усредненны (). Второе уравнение раскрывает эти моменты и предполагает необходимость проведения их в процессе решения.
Первое уравнение в виде матричной записи предполагает, что матрица предварительно была отцентрирована () и определенные в ходе решения уравнения десперсии как будто по умолчанию усредненны (). Второе уравнение раскрывает эти моменты и предполагает необходимость проведения их в процессе решения.
Запишем получившуюся систему уравнений:
Надеюсь, все уловили, что мы не просто преобразовали уравнение , мы по сути изменили задачу, так как теперь вместо матрицы мы хотим получить .
С размерностью матриц в данной системе уравнений такая же ситуация как и в системе, указанной выше. Матрица по определению квадратная, но если мы желаем понизить размерность, то для начала мы вычисляем полную матрицу , а затем берем только то количество столбцов, сколько признаков-компонент в новом пространстве мы хотим оставить.
Посмотрим на цифры из нашего примера, при условии того, что мы не хотим понижать размерность преобразованных данных. Тогда размерность матрицы составит: ( x ) ( x ) ( x ) ( x ) = ( x )
Самое время перейти к решению системы уравнений.
2.3 Метод множителей Лагранжа
Не будем заниматься обоснованием и доказательством метода, обозначим лишь, что данный метод является универсальным при поиске условных экстремумов. Действительно, у нас есть условие ортогональности матрицы : и есть желание найти экстремумы — значения матрицы , при которых элементы главной диаганоли ковариационной матрицы — дисперсии в преобразованном пространстве, максимальны.
В соответствии с методом множителей Лагранжа, систему уравнений с условием можно записать как функцию Лагранжа:
, где — главное уравнение системы
— уравнение связи приравненное к нулю
— множитель Лагранжа
Для перехода нашей системы уравнений в функцию Лагранжа:
— Во-первых, представим матричное выражение в виде функции , то есть .
— Во-вторых, уравнение связи об ортогональности матрицы : представим в виде функции и приравняем ее к нулю.
— В-третьих, осуществим некоторые уточнения. С этими уточнениями можно будет подробно ознакомиться буквально через абзац. А пока смотрим на функцию Лагранжа, которая у нас получилась:
С этими уточнениями можно будет подробно ознакомиться буквально через абзац. А пока смотрим на функцию Лагранжа, которая у нас получилась:
В функции Лагранжа у нас не известны и множитель Лагранжа — . И именно этот множитель мы будем находить в первую очередь, а после перейдем к поиску .
Теперь, как и было обещано, подробности об уточнениях.
В очередной раз прибегнем к такому трюку, как к замене задачи. В этот раз мы будем определять матрицу не целиком, а по столбцам, то есть для начала, как будто, будем искать каждый ее столбец и после того как определим все столбцы, то соберем и матрицу целиком. Другими словами, мы представляем матрицу как совокупность векторов , и следовательно матрицу представим как совокупность . Запишем эти изменения:
Такая запись задачи дает нам удобство в дальнейших рассчетах. Ведь раннее нам требовалось для приравнивания к нулю вычислять . Использование единичной матрицы в расчетах не очень удобно. В результате такого изменения задачи, нам потребуется использовать вместо единичной матрицы в расчетах простое число — единицу, а значит
Запишем размерность главного выражения для каждого -го случая в нашем примере: ( x ) ( x ) ( x ) ( x ) = . То есть это , какое-то конкретное число. Интутивно мы понимаем, что — это дисперсия или -ый элемент главной диагонали ковариационной матрицы . В том, что — это -ая дисперсия матрицы в статье мы доказывать не будем, но будьте уверены — интуиция нас не подводит.
То есть это , какое-то конкретное число. Интутивно мы понимаем, что — это дисперсия или -ый элемент главной диагонали ковариационной матрицы . В том, что — это -ая дисперсия матрицы в статье мы доказывать не будем, но будьте уверены — интуиция нас не подводит.
Давайте, подумаем, что мы будем делать с функцией Лагранжа?
Верно — мы будем ее дифференцировать по .
2.4 Переход от задачи дифференцирования функции Лагранжа по вектору к задаче поиска собственных значений и собственных векторов матрицы
Опустим подробности матричного дифференцирования за рамки статьи и перейдем сразу же к результату:
Приравняем производную к нулю:
Таким образом, у нас возникла ситуация, когда квадратная матрица , умноженная на вектор преобразовалась во всё тот же вектор , только дополнительно он еще и умноженный на некую константу . Из курса высшей математики, мы знаем, что при умножении некоторой квадратной матрицы на ненулевой вектор получается все тот же не нулевой вектор с некоторым коэффициентом, то такой вектор называется собственным вектором данной матрицы, а коэффициент — собственным числом матрицы. TX»‘)
# рассчитаем матрицу ковариации X и запишем результат в таблицу pandas
X_df_cov = pd.DataFrame(np.dot(X.T,X)/(N), index = columns_mini)
X_df_cov.columns = columns_mini
X_df_cov.round(4)
TX»‘)
# рассчитаем матрицу ковариации X и запишем результат в таблицу pandas
X_df_cov = pd.DataFrame(np.dot(X.T,X)/(N), index = columns_mini)
X_df_cov.columns = columns_mini
X_df_cov.round(4)
Раскроем выражение :
В первую очередь определяем собственные числа матрицы
Выполним алгебраические действия — умножим матрицу на вектор:
Приравняем соответствующие элементы векторов-столбцов и получим однородную систему линейных уравнений:
Сделаем ход конем: в верхнем уравнении вынесем за скобку , во втором — :
По определению собственный вектор не может быть нулевым, то есть . Из этого следует, что уравнения линейно зависимы и тогда определитель матрицы системы равен нулю:
Раскроем определитель и решим квадратное уравнение:
Половина дела завершена — мы нашли собственные значения матрицы . Раннее, мы делали интуитивное предположение, что собственные значения матрицы , это не что иное как дисперсии преобразованного признакового пространства. Тогда, с учетом того, что метод главных компонент сохраняет дисперсию исходного пространства в преобразованном пространстве, мы можем сверить сумму собственных значений (равно сумму дисперсий преобразованного пространства) с суммой дисперсий исходного пространства. Мы ожидаем увидеть знак равенства между этими величинами.
Тогда, с учетом того, что метод главных компонент сохраняет дисперсию исходного пространства в преобразованном пространстве, мы можем сверить сумму собственных значений (равно сумму дисперсий преобразованного пространства) с суммой дисперсий исходного пространства. Мы ожидаем увидеть знак равенства между этими величинами.
Сумма дисперсий в исходном признаковом пространстве составляет: .
Сумма дисперсий в преобразованном пространстве:
Суммы совпадают, а значит мы на верном пути. Переходим к поиску собственных векторов .
Определяем собственные вектора матрицы
Для определения собственных векторов нам надо по очереди в систему уравнений, приведенную ниже, подставить, полученные значения : и :
Определим собственный вектор , соответствующий собственному числу :
Казалось, бы выразим через и дело в шляпе, но нас подстерегают очередные сюрпризы. Смотрим:
Такая система уравнений имеет бесконечное множество решений, но главное здесь — соотношение между искомыми значениями и . Оно должно составлять 2.4996. Хорошо, давайте тогда выберем пару значений:
Оно должно составлять 2.4996. Хорошо, давайте тогда выберем пару значений:
Таким же образом, определим собственный вектор, соответствующий собственному числу . Не будем подробно расписывать решение, приведем результат:
В итоге, мы получили матрицу , состоящую из собственных векторов.
Однако, это еще не совсем та матрица, которую мы искали. В ней могли быть совсем другие значения, конечно же с условием сохранения соотношений между и . Так какую нам выбрать матрицу, какие значения в конечном итоге подставить? Ответ — выбираем нормированную матрицу. Опустим подробности рассуждения, почему нам требуется нормировка матрицы, упомянем лишь о том, что без нормирования матрицы не будет возможно выполнить условие ортогональности матрицы.
Для нормировки матрицы , воспользуемся имеющейся в библиотеке numpy функцией linalg.norm(). Выберем настройки по умолчанию. Это будет норма Фробениуса.
Отнормируем матрицу W
W = np.T на W_norm
print ('Проверка матрицы W на ортогональность: \n', np.dot(W_norm.T,W_norm).round(2))Действительно, мы получили единичную матрицу. Проверка пройдена. Запишем результаты.
Собственные значения матрицы :
,
Матрица собственных векторов:
Заметьте, если наша задача преобразовать пространство с понижением размерности, то в нашем случае мы будем умножать матрицу на первый столбец матрицы , так как он соответствует наибольшему собственному значению матрицы (иначе дисперсии матрицы ) .
Для определения собственных значений и векторов матрицы в библиотеке предусмотрена функция . Сравним результаты.
Применим функцию linalg.eig
v, W = np.linalg.eig(X_df_cov) print ('Собственные значения: \n', v.round(4)) print () print ('Матрица собственных векторов: \n', W.round(4))Результаты сошлись.
На этой мажорной ноте мы завершаем изучение математики процесса в методе главных компонент.
Вспомогательные материалы
1. Литература
1.1 Многомерный статистический анализ и временные ряды, Том 3, Кендалл М., Стюарт А., Москва, «Наука», 1976
1.2 Введение в теорию матриц, Р.Беллман, Москва, «Наука», 1969
1.3 Python для сложных задач, Дж.Вандер Плас, «Питер», 2018
2. Лекции, курсы (видео)
2.1 Курс «Поиск структуры в данных» специализации «Машинное обучение и анализ данных», МФТИ, ЯНДЕКС
2.2 Лекция «Метод главных компонент», НИУ ВШЭ, 2016
2.3 Лекция «Наилучшее приближение матрицы матрицами меньшего ранга», В.Н. Малозёмов, 2014
2.4 Лекция 9 «Факторный анализ и метод главных компонент», В.Л. Аббакумов, 2018
3. Интернет источники
3.1 Статья «Как работает метод главных компонент (PCA) на простом примере», Хабр, 2016
3.
2 «Условные экстремумы и метод множителей Лагранжа», mathprofi
3.3 «Собственные значения (числа) и собственные векторы», mathprofi
3.4 «Метод главных компонент (Principal component analysis)», wiki.loginom
3.5 «Метод главных компонент (PCA)», craftappmobile, 2019
3.6 Статья «Приводим уравнение линейной регрессии в матричный вид», Хабр, 2019
Экзамен по высшей математике — Экономический факультет
Задать вопрос
Программа вступительного экзамена в магистратуру экономического факультета НГУ по дисциплине «Высшая математика»
Раздел 1: Линейная алгебра.
1. Векторы, матрицы и действия с ними. Линейная зависимость системы векторов. Базис линейного пространства. Скалярное произведение.
2. Определитель квадратной матрицы. Вычисление определителей. Разложение определителя по строке и по столбцу. Транспонированная матрица. Обратная матрица. Ранг матрицы. Специальные виды матрицы. Определители матриц специального вида.
3. Системы линейных уравнений. Метод Крамера. Метод Гаусса. Фундаментальная система решений.
5. Собственные числа. Собственные векторы. Диагонализация матрицы.
6. Квадратичные формы. Матрица квадратичной формы. Критерии Сильвестра положительной (отрицательной) определенности (полу определенности) квадратичной формы.
Литература к разделу 1:
1. Кострикин И. А., Сенченко Д. В. и др., Пособие по линейной алгебре для студентов-экономистов. М., Изд-во МГУ, 1987
2. Малугин, В. А. Математика для экономистов. Линейная алгебра: курс лекций: учеб. пособие для вузов по направлению "Экономика"/ В. А. Малугин М.: ЭКСМО, 2006 216 с.: ил. (Высшее экономическое образование) Библиогр.: с.211 ISBN 5-699-12627-9
3. А.С. Солодовников, В.А. Бабайцев, А.В. Браилов. Математика в экономике: учебник для студентов экономических специальностей высших учебных заведений: в 2 ч. М, Финансы и статистика, 2001г.
Раздел 2: Математический анализ.

1. Числовые последовательности. Предел последовательности. Основные свойства пределов последовательностей.
2. Функции одной переменной. Предел функции. Непрерывность функции.
3. Производная функции одной переменной. Исследование и построение графика функции.
4. Формула Тейлора. Разложение функции в ряд Тейлора.
5. Функции многих переменных. Непрерывность. Частные производные. Полный дифференциал. Градиент функции. Производная по направлению. Матрица Гессе. Безусловный экстремум. Необходимые и достаточные условия экстремума функции многих переменных.
6. Выпуклые функции и множества. Выпуклость квадратичных форм.
7. Оптимизация при наличии ограничений. Функция Лагранжа и ее стационарные точки. Теоремы Куна-Таккера. Окаймленный Гессиан. Условия второго порядка.
Литература к разделу 2:
1. Л. Д. Кудрявцев. Курс математического анализа: учебник для студентов университетов и вузов. - М.: Высшая школа, 1981, в 2-х томах.

2. Архипов Г. И., Садовничий В. А., Чубариков В. Н., Лекции по математическому анализу. М., «Высшая школа», 1999.
2. В. П. Бусыгин, Е. В. Желободько, А. А. Цыплаков, Микроэкономика – третий уровень Москва, ГУ – ВШЭ, 2008
3. Горюшкин А.А., Хуторецкий А.Б. Математические модели и методы исследования операций: курс лекций: Учеб. пос. Новосиб. национ. иссл. гос. ун-т / Новосибирск, 2013.
Раздел 3: Дифференциальные уравнения.
1. Уравнения с разделяющимися переменными. Уравнения в полных дифференциалах. Метод замены переменных. Уравнение Бернулли.
2. Линейные дифференциальные уравнения 1-го порядка. Метод вариации постоянной.
3. Однородные линейные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение. Устойчивость решения.
4. Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами и с правой частью специального вида.
Литература к разделу 3:
1.
Бибиков Ю.Н. Общий курс обыкновенных дифференциальных уравнений: Учебное пособие. 2-е изд., переб. СПб: Издательство С.-Петербургского университета, 2005.
2. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. 6-е изд., стереотип. М.: URSS, 2001.
3. Дементьева Н.В. и др., Линейные системы дифференциальных уравнений с постоянными коэффициентами. Построение фундаментальной матрицы решений однородной системы с использованием корневого базиса. Учеб. пособие. 2008, изд-во: Изд-во НГУ, город: Новосибирск, стр.: 50 с
Раздел 4: Теория вероятностей.
1. Основные понятия теории вероятностей. Случайные события и случайные величины. Функция распределения и функция плотности распределения. Совместное распределение нескольких случайных величин. Условные распределения.
2. Характеристики распределений случайных величин: математическое ожидание, дисперсия, ковариация. Свойства математического ожидания, дисперсии и ковариации. Условное математическое ожидание.
3. Нормальное распределение и связанные с ним: хи-квадрат распределение, распределения Стьюдента и Фишера, их основные свойства. Квантили.
Литература к разделу 4:
1. Чернова Н.И. Теория вероятностей: учебное пособие : [для студентов экономических специальностей вузов] / Новосиб. гос. ун-т, Мех.-мат. фак., Каф. теории вероятностей и мат. статистики. 2-е изд., испр. Новосибирск : Редакционно-издательский центр НГУ, 2014. – 158 с. (Имеется электронная версия в Университетской библиотеке ONLINE)
2. Теория вероятностей для социологов и менеджеров: курс лекций / Г. Д. Ковалева, А. С. Липин; Федеральное агентство по образованию Российской Федерации, Новосибирский гос. ун-т, Экономический фак. - Новосибирск : НГУ, 2010. - 74 с.
3. Шведов, А. С. Теория вероятностей и математическая статистика: промежуточный уровень: учеб. пособие / А. С. Шведов; Нац. исслед. ун-т «Высшая школа экономики». — М.: Изд. дом Высшей школы экономики, 2016.
Раздел 5: Математическая статистика.
1. Генеральная совокупность и выборка. Выборочное распределение и выборочные характеристики: среднее, дисперсия, ковариация, коэффициент корреляции.
2. Статистическое оценивание. Точечные оценки. Несмещенность, состоятельность и эффективность оценок. Интервальные оценки. Уровень доверия.
3. Статистические выводы и проверка статистических гипотез. Ошибки 1-го и 2-го рода. Уровень доверия, уровень значимости, мощность критерия и р-значение теста. Проверка значимости.
4. Классическая линейная регрессия. Статистические характеристики (математическое ожидание, дисперсия) оценок параметров. Теорема Гаусса-Маркова.
5. Предположение о нормальном распределении случайной ошибки в рамках классической линейной регрессии и его следствия. Доверительные интервалы оценок параметров и проверка гипотез об их значимости. Статистические характеристики качества регрессии.
Литература к разделу 5:
1.
Чернова Н.И. Математическая статистика : учебное пособие : [для студентов экономических специальностей вузов по специальности 080100 "Экономика"] / Новосиб. гос. ун-т, Мех.-мат. фак., Каф. теории вероятностей и мат. статистики. 2-е изд., испр. Новосибирск : Редакционно-издательский центр НГУ, 2014. – 148 с
2. Ковалёва Г.Д., Липин А.С. Математическая статистика для социологов и менеджеров : курс лекций / [отв. ред. Г.М. Мкртчян] ; Новосиб. гос. ун-т. – Новосибирск, 2009. – 94 с.
3. Суслов В.И., Ибрагимов Н.М., Талышева Л.П., Цыплаков А.А. Эконометрия: Учебное пособие. - Новосибирск: Издательство СО РАН, 2005. - 744 с.
- Пример вступительного экзамена по математике
Найти канонический вид квадратичной формы онлайн калькулятор. Приведение квадратичной формы к каноническому виду
Дана
квадратичная форма (2) A (x , x ) = ,
где x = (x 1 , x 2 , …, x n ).
Рассмотрим квадратичную форму в
пространстве R 3 ,
то есть x = (x 1 , x 2 , x 3), A (x , x ) =
+
+
+
+
+
+
+
+
+
=
+
+
+ 2
+ 2
+
+ 2
(использовали условие симметричности
формы, а именно а 12 = а 21 , а 13 = а 31 , а 23 = а 32). Выпишем матрицу квадратичной формы A в базисе {e }, A (e ) =
Выпишем матрицу квадратичной формы A в базисе {e }, A (e ) =
.
При изменении базиса матрица квадратичной
формы меняется по формуле A (f ) = C t A (e )C ,
где C – матрица перехода от базиса {e }
к базису {f },
а C t – транспонированная матрица C .
Определение 11.12. Вид квадратичной формы с диагональной матрицей называется каноническим .
Итак,
пусть A (f ) =
,
тогда A "(x , x ) =
+
+
,
где x " 1 , x " 2 , x " 3
– координаты вектора x в новом базисе {f }.
Определение 11.13. Пусть в n V выбран такой базис f = {f 1 , f 2 , …, f n }, в котором квадратичная форма имеет вид
A (x , x ) =
+
+ … +
,
(3)
где y 1 , y 2 ,
…, y n – координаты вектора x в базисе {f }. Выражение (3) называется каноническим
видом квадратичной формы. Коэффициенты 1 ,
λ 2 ,
…, λ n называются каноническими ;
базис, в котором квадратичная форма
имеет канонический вид, называется каноническим
базисом .
Выражение (3) называется каноническим
видом квадратичной формы. Коэффициенты 1 ,
λ 2 ,
…, λ n называются каноническими ;
базис, в котором квадратичная форма
имеет канонический вид, называется каноническим
базисом .
Замечание . Если квадратичная форма A (x , x ) приведена к каноническому виду, то, вообще говоря, не все коэффициенты i отличны от нуля. Ранг квадратичной формы равен рангу ее матрицы в любом базисе.
Пусть
ранг квадратичной формы A (x , x )
равен r ,
где r ≤ n .
Матрица квадратичной формы в каноническом
виде имеет диагональный вид. A (f ) =
,
поскольку ее ранг равен r ,
то среди коэффициентов i должно быть r ,
не равных нулю. Отсюда следует, что число
отличных от нуля канонических коэффициентов
равно рангу квадратичной формы.
Замечание .
Линейным преобразованием координат
называется переход от переменных x 1 , x 2 ,
…, x n к переменным y 1 , y 2 ,
…, y n ,
при котором старые переменные выражаются
через новые переменные с некоторыми
числовыми коэффициентами.
x 1 = α 11 y 1 + α 12 y 2 + … + α 1 n y n ,
x 2 = α 2 1 y 1 + α 2 2 y 2 + … + α 2 n y n ,
………………………………
x 1 = α n 1 y 1 + α n 2 y 2 + … + α nn y n .
Так как каждому преобразованию базиса отвечает невырожденное линейное преобразование координат, то вопрос о приведении квадратичной формы к каноническому виду можно решать путем выбора соответствующего невырожденного преобразования координат.
Теорема 11.2 (основная теорема о квадратичных формах). Всякая квадратичная форма A (x , x ), заданная в n -мерном векторном пространстве V , с помощью невырожденного линейного преобразования координат может быть приведена к каноническому виду.
Доказательство .
(Метод Лагранжа) Идея этого метода
состоит в последовательном дополнении
квадратного трехчлена по каждой
переменной до полного квадрата. Будем
считать, что A (x , x ) ≠ 0
и в базисе e = {e 1 , e 2 ,
…, e n }
имеет вид (2):
Будем
считать, что A (x , x ) ≠ 0
и в базисе e = {e 1 , e 2 ,
…, e n }
имеет вид (2):
A (x , x ) =
.
Если A (x , x ) = 0, то (a ij ) = 0, то есть форма уже каноническая. Формулу A (x , x ) можно преобразовать так, чтобы коэффициент a 11 ≠ 0. Если a 11 = 0, то коэффициент при квадрате другой переменной отличен от нуля, тогда при помощи перенумерации переменных можно добиться, чтобы a 11 ≠ 0. Перенумерация переменных является невырожденным линейным преобразованием. Если же все коэффициенты при квадратах переменных равны нулю, то нужные преобразования получаются следующим образом. Пусть, например, a 12 ≠ 0 (A (x , x ) ≠ 0, поэтому хотя бы один коэффициент a ij ≠ 0). Рассмотрим преобразование
x 1 = y 1 – y 2 ,
x 2 = y 1 + y 2 ,
x i = y i ,
при i = 3,
4, …, n .
Это
преобразование невырожденное, так как
определитель его матрицы отличен от
нуля
= = 2 ≠ 0.
Тогда
2a 12 x 1 x 2 = 2 a 12 (y 1 – y 2)(y 1 + y 2) = 2
– 2
,
то есть в форме A (x , x )
появятся квадраты сразу двух переменных.
A (x , x ) =
+ 2
+ 2
+
. (4)
Преобразуем выделенную сумму к виду:
A (x , x ) = a 11
, (5)
при этом коэффициенты a ij меняются на . Рассмотрим невырожденное преобразование
y 1 = x 1 + + … + ,
y 2 = x 2 ,
y n = x n .
Тогда получим
A (x , x ) =
.
(6).
Если
квадратичная форма
= 0,
то вопрос о приведении A (x , x )
к каноническому виду решен.
Если
эта форма не равна нулю, то повторяем
рассуждения, рассматривая преобразования
координат y 2 ,
…, y n и не меняя при этом координату y 1 . Очевидно, что эти преобразования будут
невырожденными. За конечное число шагов
квадратичная форма A (x , x )
будет приведена к каноническому виду
(3).
Очевидно, что эти преобразования будут
невырожденными. За конечное число шагов
квадратичная форма A (x , x )
будет приведена к каноническому виду
(3).
Замечание 1. Нужное преобразование исходных координат x 1 , x 2 , …, x n можно получить путем перемножения найденных в процессе рассуждений невырожденных преобразований: [x ] = A [y ], [y ] = B [z ], [z ] = C [t ], тогда [x ] = A B [z ] = A B C [t ], то есть [x ] = M [t ], где M = A B C .
Замечание 2.
Пусть A (x , x ) = A (x , x ) =
+
+ …+
,
где i ≠ 0, i = 1,
2, …, r ,
причем 1 > 0,
λ 2 > 0,
…, λ q > 0,
λ q +1 r
Рассмотрим невырожденное преобразование
y 1 = z 1 , y 2 = z 2 ,
…, y q = z q , y q +1 =
z q +1 ,
…, y r = z r , y r +1 = z r +1 ,
…, y n = z n . В
результате A (x , x )
примет вид: A (x , x ) = + + … + – – … – ,
который называется нормальным
видом квадратичной формы .
В
результате A (x , x )
примет вид: A (x , x ) = + + … + – – … – ,
который называется нормальным
видом квадратичной формы .
Пример 11.1. Привести к каноническому виду квадратичную форму A (x , x ) = 2x 1 x 2 – 6x 2 x 3 + 2x 3 x 1 .
Решение . Поскольку a 11 = 0, используем преобразование
x 1 = y 1 – y 2 ,
x 2 = y 1 + y 2 ,
x 3 = y 3 .
Это
преобразование имеет матрицу A =
,
то есть [x ] = A [y ]
получим A (x , x ) = 2(y 1 – y 2)(y 1 + y 2) – 6(y 1 + y 2)y 3 + 2y 3 (y 1 – y 2) =
2– 2– 6y 1 y 3 – 6y 2 y 3 + 2y 3 y 1 – 2y 3 y 2 = 2– 2– 4y 1 y 3 – 8y 3 y 2 .
Поскольку коэффициент при не равен нулю, можно выделить квадрат одного неизвестного, пусть это будет y 1 . Выделим все члены, содержащие y 1 .
A (x , x ) = 2(– 2 y 1 y 3) – 2– 8y 3 y 2 = 2(– 2 y 1 y 3 + ) – 2– 2– 8y 3 y 2 = 2(y 1 – y 3) 2 – 2– 2– 8y 3 y 2 .
Выполним преобразование, матрица которого равна B .
z 1 = y 1 – y 3 , y 1 = z 1 + z 3 ,
z 2 = y 2 , y 2 = z 2 ,
z 3 = y 3 ; y 3 = z 3 .
B =
,
[y ] = B [z ].
Получим A (x , x ) = 2– 2–– 8z 2 z 3 .
Выделим
члены, содержащие z 2 .
Имеем A (x , x ) = 2– 2(+ 4z 2 z 3) – 2= 2– 2(+ 4z 2 z 3 + 4) +
+ 8 – 2 = 2– 2(z 2 + 2z 3) 2 + 6.
Выполняем преобразование с матрицей C :
t 1 = z 1 , z 1 = t 1 ,
t 2 = z 2 + 2z 3 , z 2 = t 2 – 2t 3 ,
t 3 = z 3 ; z 3 = t 3 .
C =
,
[z ] = C [t ].
Получили: A (x , x ) = 2– 2+ 6 канонический вид квадратичной формы, при этом [x ] = A [y ], [y ] = B [z ], [z ] = C [t ], отсюда [x ] = ABC [t ];
A B C =
=
.
Формулы преобразований следующие
x 1 = t 1 – t 2 + t 3 ,
x 2 = t 1 + t 2 – t 3 ,
Определение 10.4. Каноническим видом квадратичной формы (10.1) называется следующий вид: . (10.4)
Покажем, что в базисе из собственных векторов квадратичная форма (10. 1) примет канонический вид. Пусть
1) примет канонический вид. Пусть
- нормированные собственные векторы, соответствующие собственным числам λ 1 ,λ 2 ,λ 3 матрицы (10.3) в ортонормированном базисе . Тогда матрицей перехода от старого базиса к новому будет матрица
. В новом базисе матрица А примет диагональный вид (9.7) (по свойству собственных векторов). Таким образом, преобразовав координаты по формулам:
,
получим в новом базисе канонический вид квадратичной формы с коэффициентами, равными собственным числам λ 1 , λ 2 , λ 3 :
Замечание 1. С геометрической точки зрения рассмотренное преобразование координат представляет собой поворот координатной системы, совмещающий старые оси координат с новыми.
Замечание 2. Если какие-либо собственные числа матрицы (10.3) совпадают, к соответствующим им ортонормированным собственным векторам можно добавить единичный вектор, ортогональный каждому из них, и построить таким образом базис, в котором квадратичная форма примет канонический вид.
Приведем к каноническому виду квадратичную форму
x ² + 5y ² + z ² + 2xy + 6xz + 2yz .
Ее матрица имеет вид В примере, рассмотренном в лекции 9, найдены собственные числа и ортонормированные собственные векторы этой матрицы:
Составим матрицу перехода к базису из этих векторов:
(порядок векторов изменен, чтобы они образовали правую тройку). Преобразуем координаты по формулам:
.
Итак, квадратичная форма приведена к каноническому виду с коэффициентами, равными собственным числам матрицы квадратичной формы.
Лекция 11.
Кривые второго порядка. Эллипс, гипербола и парабола, их свойства и канонические уравнения. Приведение уравнения второго порядка к каноническому виду.
Определение 11.1. Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.
Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс , при пересечении образующих обеих полостей – гипербола , а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола .
Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух переменных.
Эллипс.
Определение 11.2. Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F 1 и F фокусами , есть величина постоянная.
Замечание. При совпадении точек F 1 и F 2 эллипс превращается в окружность.
Выведем уравнение эллипса, выбрав декартову систему
у М(х,у) координат так, чтобы ось Ох совпала с прямой F 1 F 2 , начало
r 1 r 2 координат – с серединой отрезка F 1 F 2 . Пусть длина этого
отрезка равна 2с , тогда в выбранной системе координат
F 1 O F 2 x F 1 (-c , 0), F 2 (c , 0). Пусть точка М(х, у ) лежит на эллипсе, и
сумма расстояний от нее до F 1 и F 2 равна 2а .
Тогда r 1 + r 2 = 2a , но ,
поэтому Введя обозначение b ² = a ²-c ² и проведя несложные алгебраические преобразования, получимканоническое уравнение эллипса : (11. 1)
1)
Определение 11.3. Эксцентриситетом эллипса называется величина е=с/а (11.2)
Определение 11.4. Директрисой D i эллипса, отвечающей фокусу F i F i относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.
Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.
Свойства эллипса:
1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a >2b ), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.
2) Весь эллипс содержится внутри прямоугольника
3) Эксцентриситет эллипса e
Действительно,
4) Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно а/е , а е а/е>a , а весь эллипс лежит в прямоугольнике )
5) Отношение расстояния r i от точки эллипса до фокуса F i к расстоянию d i от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.
Доказательство.
Расстояния от точки М(х, у) до фокусов эллипса можно представить так:
Составим уравнения директрис:
(D 1), (D 2). Тогда Отсюда r i / d i = e , что и требовалось доказать.
Гипербола.
Определение 11.5. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F 1 иF 2 этой плоскости, называемых фокусами , есть величина постоянная.
Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями.
|r 1 - r 2 | = 2a , откуда Если обозначить b ² = c ² - a ², отсюда можно получить
- каноническое уравнение гиперболы . (11.3)
Определение 11.6. Эксцентриситетом гиперболы называется величина е = с / а.
Определение 11.7. Директрисой D i гиперболы, отвечающей фокусу F i , называется прямая, расположенная в одной полуплоскости с F i относительно оси Оу перпендикулярно оси Ох на расстоянии а / е от начала координат.
Свойства гиперболы:
1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу ). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.
2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями
3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением
для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.
4) Эксцентриситет гиперболы e > 1.
5) Отношение расстояния r i от точки гиперболы до фокуса F i к расстоянию d i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.
Доказательство можно провести так же, как и для эллипса.
Парабола.
Определение 11.8. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой .
У Для вывода уравнения параболы выберем декартову
систему координат так, чтобы ее началом была середина
D M(x,y) перпендикуляра FD , опущенного из фокуса на директри-
r су, а координатные оси располагались параллельно и
перпендикулярно директрисе. Пусть длина отрезка FD
D O F x равна р . Тогда из равенства r = d следует, что
поскольку
Алгебраическими преобразованиями это уравнение можно привести к виду: y ² = 2px , (11.4)
называемому каноническим уравнением параболы . Величина р называется параметром параболы.
Свойства параболы:
1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.
2) Вся парабола расположена в правой полуплоскости плоскости Оху.
Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:
Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e e >1) или параболу (при е =1).
Похожая информация.
Приведение квадратичных форм
Рассмотрим наиболее простой и чаще используемый на практике способ приведения квадратичной формы к каноническому виду, называемый методом Лагранжа . Он основан на выделении полного квадрата в квадратичной форме.
Теорема 10.1 (теорема Лагранжа).Любую квадратичную форму (10.1):
при помощи неособенного линейного преобразования (10.4) можно привести к каноническому виду (10.6):
,
□ Доказательство теоремы проведем конструктивным способом, используя метод Лагранжа выделения полных квадратов. Задача заключается в том, чтобы найти неособенную матрицу такую, чтобы в результате линейного преобразования (10.4) получилась квадратичная форма (10.6) канонического вида. Эта матрица будет получаться постепенно как произведение конечного числа матриц специального типа.
Пункт 1(подготовительный).
1.1. Выделим среди переменных такую, которая входит в квадратичную форму в квадрате и в первой степени одновременно (назовем ее ведущей переменной ). Перейдем к пункту 2.
1.2. Если в квадратичной форме нет ведущих переменных (при всех : ), то выберем пару переменных, произведение которых входит в форму с отличным от нуля коэффициентом и перейдем к пункту 3.
1.3. Если в квадратичной форме отсутствуют произведения разноименных переменных, то данная квадратичная форма уже представлена в каноническом виде (10.6). Доказательство теоремы завершено.
Пункт 2 (выделение полного квадрата).
2.1. По ведущей переменной выделим полный квадрат. Без ограничения общности предположим, что ведущей переменной является переменная . Группируя слагаемые, содержащие , получаем
.
Выделяя полный квадрат по переменной в , получим
.
Таким образом, в результате выделения полного квадрата при переменной получим сумму квадрата линейной формы
в которую входит ведущая переменная , и квадратичной формы от переменных , в которую ведущая переменная уже не входит. Сделаем замену переменных (введем новые переменные )
получим матрицу
() неособенного линейного преобразования , в результате которого квадратичная форма (10.1) примет следующий вид
С квадратичной формой поступим также, как и в пункте 1.
2.1. Если ведущей переменной является переменная , то можно поступить двумя способами: либо выделять полный квадрат при этой переменной, либо выполнить переименование (перенумерацию ) переменных:
с неособенной матрицей преобразования:
.
Пункт 3 (создание ведущей переменной). Выбранную пару переменных заменим на сумму и разность двух новых переменных, а остальные старые переменные заменим на соответствующие новые переменные. Если, например, в пункте 1 было выделено слагаемое
то соответствующая замена переменных имеет вид
и в квадратичной форме (10.1) будет получена ведущая переменная.
Например, в случае замены переменных:
матрица этого неособенного линейного преобразования имеет вид
.
В результате приведенного алгоритма (последовательного применения пунктов 1, 2, 3) квадратичная форма (10.1) будет приведена к каноническому виду (10.6).
Заметим, что в результате производимых преобразований над квадратичной формой (выделение полного квадрата, переименование и создание ведущей переменной) мы использовали элементарные неособенные матрицы трех типов (они являются матрицами перехода от базиса к базису). Искомая матрица неособенного линейного преобразования (10.4), при котором форма (10.1) имеет канонический вид (10.6), получается путем произведения конечного числа элементарных неособенных матриц трех типов. ■
Искомая матрица неособенного линейного преобразования (10.4), при котором форма (10.1) имеет канонический вид (10.6), получается путем произведения конечного числа элементарных неособенных матриц трех типов. ■
Пример 10.2. Привести квадратичную форму
к каноническому виду методом Лагранжа. Указать соответствующее неособенное линейное преобразование. Выполнить проверку.
Решение. Выберем ведущей переменную (коэффициент ). Группируя слагаемые, содержащие , и выделяя по ней полный квадрат, получим
где обозначено
Сделаем замену переменных (введем новые переменные )
Выразив старые переменные через новые :
получим матрицу
Калькулятор собственных значений
Калькулятор собственных значений
Найдите возможные собственные значения и собственные векторы для матрицы 2x2, 3x3 до 6x6 с помощью этого калькулятора. См. шаги и весь метод расчета, связанный с нахождением этих значений.
Продолжайте читать, чтобы узнать, что такое собственные значения и как их вычислить. Важно иметь четкую концепцию преобразования, особенно матричного преобразования.
Важно иметь четкую концепцию преобразования, особенно матричного преобразования.
Что такое трансформация?
Функция применена к ℝ n , где n больше 1, называется трансформацией. Или, проще говоря, преобразованием называется функция, которая имеет дело с 2,3 или более измерениями вместо действительных чисел, существующих в одномерной плоскости.
В основном, «функции, связанные с векторами». Пример функции и преобразования:
Слово «преобразование» больше связано с визуальным представлением применения функции. Предполагается, что вектор перемещается на из одного места в другое вместо того, чтобы стать новым вектором.
Что такое собственные векторы и собственные значения?
Собственный вектор:Во время преобразования вектор, который меняет свое направление или величину «вдоль размаха» вектора, называется собственным вектором.
Обычно мы имеем дело с произвольными значениями, такими как x или y, и это может быть любое действительное число. Вот почему, когда вы применяете функцию к произвольному вектору, все реальные векторы, вписывающиеся в этот произвольный вектор, перемещаются.
Вот почему, когда вы применяете функцию к произвольному вектору, все реальные векторы, вписывающиеся в этот произвольный вектор, перемещаются.
Итак, при трансформации вся декартова плоскость как бы дезориентируется, но ее происхождение остается прежним.
Промежуток вектора — это линия, на которой он существует. Он проходит через его начало и конец. Для собственного вектора необходимо, чтобы он оставался на своем интервале во время преобразования.
Для конкретного преобразования существует фиксированное количество собственных векторов. Его номер зависит от матрицы, созданной изменениями базисных векторов, таких как i, j или k. Например, матрица 2 на 2 будет иметь максимум 2 собственных вектора (фактически пробелы).
На этом изображении обратите внимание, что i и j сместились на некоторую величину, и это изменение, помещенное в матрицу, дает матрицу преобразования. Один из двух собственных векторов для этого конкретного преобразования (1,-1):
Желтая линия — это вектор, а розовая линия показывает размах. Видно, что собственный вектор во время преобразования оставался на своем интервале. Другой собственный вектор - это ось x, потому что он растягивается только на своем участке.
Видно, что собственный вектор во время преобразования оставался на своем интервале. Другой собственный вектор - это ось x, потому что он растягивается только на своем участке.
Число, на которое векторы сжимаются или растягиваются во время преобразования. Для приведенного выше примера собственное значение вектора по оси x равно 3.
Первоначально его величина была равна 1, но после преобразования он был растянут в 3 раза. Второй собственный вектор имеет собственное значение 2.
Собственные значения могут быть отрицательными и дробными. Обычно можно угадать собственные значения, взглянув на визуальное представление, но все же есть формула для их расчета.
Собственные векторы являются хорошими базисными векторами. Они используются в трехмерном вращении, разработке видеоигр и т. д.
Как найти собственные векторы и собственные значения?
Формула для нахождения собственных векторов и значений получена из символического представления собственных векторов.
Av = λv
- A — матрица преобразования
- v — собственный вектор
- Lambda λ — скалярное число или собственное значение
тот же результат, что и лямбда, умноженная на собственный вектор.
Это можно доказать на реальном примере, но пока это будет слишком долго. Выведем формулу для нахождения собственных значений.
Левая часть представляет собой умножение скалярного вектора. Чтобы сделать его похожим на правую часть, умножьте его на единичную матрицу.
A v = λI v
Поскольку произведение скаляра на матрицу является матрицей, мы имеем умножение матрицы на вектор с обеих сторон. Перестановка
Av - λIv = 0
(A - λI)v = 0
(A - λI) — матрица. Это будет верно для нулевого вектора, но это очевидно. Вы должны выяснить ненулевые векторы. Собственные векторы будут членами нулевого пространства этой матрицы.
Один из способов получить нулевой результат — сжать матрицу до более низких измерений. Это делается математически путем ввода такого значения лямбда, при котором определитель матрицы равен нулю.
Итак, формула для собственных значений
det(A - λI) = 0
Собственные векторы рассчитываются с использованием собственных значений. Поместите значение лямбда в матрицу и замените v и 0 матрично-векторной формой. После этого уменьшите матрицу, используя форму редуцированного эшелона строк.
Дальнейшее упрощение даст собственные векторы.
Примечание: Матрица может иметь одно собственное значение или не иметь его.
Собственные пространства: Набор векторов, удовлетворяющих собственному уравнению, называется собственным пространством. Все они соответствуют одному и тому же собственному значению. Поскольку собственные векторы существуют в нулевом пространстве матрицы, существует и собственное пространство.
Давайте посмотрим на реальный пример.
Пример:
Для следующей матрицы найдите собственные значения и собственные векторы.
Решение:
Нахождение собственных значений:
Шаг 1: Подставьте матрицу в формулу.
det(A - λI) = 0
Шаг 2: Умножьте лямбду и вычтите из матрицы A.
Шаг 3: Возьмите определитель.
Шаг 4: Разложите на корни с помощью калькулятора квадратных формул.
Два корня λ = 10 и λ = 2. И эти два являются собственными значениями для данной матрицы.
Нахождение собственных векторов:
Шаг 1: Поместите первое значение лямбда в матрицу.
(A - λI)v = 0
Шаг 2: Выполнить эшелонирование строк.
- Разделить R 1 по -6.

- Из R 2 вычтите R 1 , умноженное на 6.
Шаг 3: Замените на и 0 .
Это становится:
V 1 - V 2 / 3 = 0
V 1 = V 2 /3 = V 2 /3 . В зависимости от 2 /3
2
2. Полагая v 2 = 1, мы получаем первый собственный вектор: Шаг 4: Аналогичным образом найдите второй собственный вектор.
Поменять местами руб. 1 на руб. 2
Умножить ⅓ на руб. 1 и вычесть из 2 руб.
Divide R 1 до 6.
Это становится:
V 1 + V 2 = 0
V 1 = -V 2
: .
Сдача v 2 = 1, второй собственный вектор, который мы получаем:
Калькулятор собственных векторов даст ответ со всеми этими шагами.
Онлайн-калькулятор собственных значений с шагами
Использование калькулятора собственных значений
Почему почти все, что вы узнали о калькуляторе собственных значений, неверно t должны пройти через это много работы. На самом деле, вы могли бы так же легко пропустить их. Чтобы иметь возможность найти кого-то, кто готов оказать вам лучшую помощь с домашними заданиями, вы должны взять на себя обязательство искать только лучшую работу на данный момент. Если вы просто думаете о бое по этапам, а не смотрите на его полосу здоровья, он станет намного проще и пойдет намного быстрее.
 Такое сложно сделать на практике. Здесь мы хотим отметить две или три вещи.
Такое сложно сделать на практике. Здесь мы хотим отметить две или три вещи. Калькулятор слухов, обмана и собственных значений
Описание разложения LU выходит за рамки этой статьи, но дополнительную информацию можно увидеть в разделе ссылок ниже. Похоже, что они указывают на общее благосостояние в районе, поэтому мы могли бы назвать фактор 2 социально-экономическим статусом района. В следующем разделе мы введем несколько свойств, упрощающих вычисление определителей. Соблюдение исчерпывающих описаний этих методов будет сводной таблицей. Поиск такого часто используемого термина, как «Интернет», был проблематичным.
Калькулятор жизни, смерти и собственных значений
Имейте в виду, что интерпретатор вставляет новую строку перед выводом следующей подсказки, если предыдущая строка не была завершена. Это удобный инструмент, так как вы можете использовать его в любом месте в любое время, просто имея онлайн-доступ. Вот хороший пример форм графиков, которые вы можете создать с помощью этого пакета. Доступ к различным областям матрицы эффективен благодаря динамической компиляции.
Доступ к различным областям матрицы эффективен благодаря динамической компиляции.
Учителя также используют графические калькуляторы, чтобы учащиеся лучше понимали. Имейте в виду, что эта программа предназначена для исследовательских и образовательных целей. Их опрашивали по количеству книг, которые они прочитали за предыдущий календарный год. Вероятно, мы обнаружим некоторых несовершеннолетних. Используя этот онлайн-калькулятор обратной матрицы, у студентов будет много времени, чтобы получить представление о решении словесных задач. Пожалуйста, не забудьте рассказать своим друзьям и учителю об этой замечательной программе!
Скрытый секрет калькулятора собственных значений
Обычно лямбда Уилка используется для проверки важности самого первого канонического коэффициента корреляции, а V Бартлетта используется для проверки важности всех канонических коэффициентов корреляции. Если есть только один линейно независимый собственный вектор, то есть только одна прямая. Матрицы, которые не являются квадратными, не имеют определителя.
Матрицы, которые не являются квадратными, не имеют определителя.
Вам сказали ложь о калькуляторе собственных значений
Дискриминант говорит о сущности корней. Они являются факторами, поскольку группируют базовые переменные. Имейте в виду, что это важное отличие от факторного анализа. Несмотря на то, что метод управления нагрузкой используется в большинстве видов нелинейного анализа, его сложно реализовать в анализе потери устойчивости.
Это вызывает левостороннюю систему. Подматрица — это часть исходной матрицы, которая не включает элементы в той же строке или столбце, что и текущий элемент. Формула Эйлера делает это простым. Этот экземпляр известен как узел. Четвертая загвоздка заключается в том, что он всегда будет предоставлять вам решение только в виде целого или десятичного числа. Для этого подумайте о матрице A.
Знакомство с калькулятором собственных значений
Пусть pi будет настоящим веб-сайтом. Вот краткий набросок идей по другую сторону формулы. Кроме того, это называется параметрической формой. Часто они являются седловыми точками. Требуется много сложных вычислений, чтобы найти значение, которое будет отображено на графике. Вычислите определитель матрицы онлайн на сайте.
Кроме того, это называется параметрической формой. Часто они являются седловыми точками. Требуется много сложных вычислений, чтобы найти значение, которое будет отображено на графике. Вычислите определитель матрицы онлайн на сайте.
Вот действия, которые нужно выполнить, чтобы найти определитель. Формула Герона позволяет вычислить площадь треугольника, если известно расстояние между всеми тремя сторонами. Например, очень важно учитывать смещения, чтобы деталь или сборка не деформировались слишком сильно.
Общее решение для нашей системы приведено ниже. Не нажимайте ON, если не хотите выйти! Во-первых, вы хотите иметь возможность извлекать действительные и мнимые элементы сложного числа. Я только хотел, чтобы вы знали, что я рад, что купил ваш продукт.
Каждый из них подключен. Если вы исследуете одно или несколько из этих расширений, я хотел бы понять. Я предлагаю развернуться там, где есть единица, а после этого расшириться. Тем не менее, нужно придумать, как их рисовать.
Однако, как только нагрузка остается неизменной, как это чаще всего бывает, окончание вертикального участка кривой указывает на разрушение конструкции балки. В этом случае вы можете подумать, что для теоремы Гершгорина нет реальной причины. По этой причине, вот несколько примеров, показывающих, как можно преобразовать пространство с помощью двумерных квадратных матриц. Мы начинаем с подготовки различных частей справочного материала, связанного с линейной алгеброй. Мы будем обрабатывать только события n различных корней, хотя они могут повторяться. Всегда ищите строку или столбец с наибольшим количеством нулей, чтобы упростить работу.
Во-первых, ноль здесь не скаляр, а нулевой вектор. Casio fx-991MS включает встроенный решатель уравнений. Вы можете воспользоваться калькулятором. Этот калькулятор позволяет получать точные графики. Используйте отрицательную переменную, чтобы показать вычитание.
Что вам не понравится в калькуляторе собственных значений и что вам понравится
Эта система имеет бесконечное количество решений. С помощью этого инструмента человек может легко контролировать каждое крыло компании. Это можно рассматривать как прочную ассоциацию для факторного анализа в большинстве областей исследований. С другой стороны, решения могут быть сложными.
С помощью этого инструмента человек может легко контролировать каждое крыло компании. Это можно рассматривать как прочную ассоциацию для факторного анализа в большинстве областей исследований. С другой стороны, решения могут быть сложными.
С оружием в руках Калькулятор собственных значений?
Это значительно упрощает многие приложения, поскольку вам не нужно управлять арифметикой комплексных чисел. Это удобный инструмент, так как вы можете использовать его в любом месте в любое время, просто имея онлайн-доступ. Вот хороший пример форм графиков, которые вы можете создать с помощью этого пакета. Если вы хотите добавить функцию в GSL, мы советуем вам сначала сделать ее расширением.
Предприятия должны ответить на три важных вопроса, чтобы получить более четкое представление о своем выборе. Важно понимать, почему мы так готовим матрицу, а не слепо перемалывать цифры. Это помогает упростить сложное предприятие. И то же самое с переключением.
Важная эксцентрическая кривая строится по формуле секущей. Как указывалось ранее, для практических целей MGIV ожидает, что размер модели будет уменьшен. Этот метод извлечения кажется идеальным выбором для большинства моделей NASTRAN. Вообще говоря, это больше похоже на степень свободы, которая будет способствовать режиму пониженной частоты, чем степень свободы, которая имеет небольшую массу и более высокую жесткость.
Как указывалось ранее, для практических целей MGIV ожидает, что размер модели будет уменьшен. Этот метод извлечения кажется идеальным выбором для большинства моделей NASTRAN. Вообще говоря, это больше похоже на степень свободы, которая будет способствовать режиму пониженной частоты, чем степень свободы, которая имеет небольшую массу и более высокую жесткость.
Игра "Калькулятор собственных значений"
Это вызывает левостороннюю систему. Дополнительные метки не обязательны. Решения, которые нельзя нормализовать, должны быть отброшены. Задание числа в исходной матрице не имеет значения, важен только его статус в настоящей матрице. Четвертая загвоздка заключается в том, что он всегда будет предоставлять вам решение только в виде целого или десятичного числа. Чтобы также наблюдать за входными единичными векторами, используйте опцию showunitvectors.
Собственные значения соответствуют количеству вариаций переменных, которые объясняются с помощью компонента, поэтому самый первый компонент должен использоваться при вычислении самого первого главного компонента. Затем вам нужно найти полином и свойства полиномиального уравнения. Матрицу можно рассматривать как конкретное линейное преобразование.
Затем вам нужно найти полином и свойства полиномиального уравнения. Матрицу можно рассматривать как конкретное линейное преобразование.
Аргумент о калькуляторе собственных значений
Определитель матрицы 3x3 немного сложнее. Это особый набор скаляров, связанный с линейной системой матричных уравнений. NumPy не имеет функции для прямого вычисления ковариации между двумя переменными. Они получают матрицу, для которой нужно найти обратную. Симметричная матрица — это особый вид квадратной матрицы, который часто используется во многих приложениях, таких как ковариационная матрица, корреляционная матрица и матрица расстояний. Матрица, не имеющая обратной, называется сингулярной.
Поскольку это выходит за рамки данного отчета (и моей области!) После ввода данных можно выполнять несколько уникальных функций, включая расчеты дисперсии и регулирования (что может быть полезно для математики уровня A). Построение графика с помощью уравнения или даже заданных чисел — непростая процедура. Этот список дает количество миноров из приведенной выше матрицы. Поиск такого часто используемого термина, как «Интернет», был проблематичным.
Этот список дает количество миноров из приведенной выше матрицы. Поиск такого часто используемого термина, как «Интернет», был проблематичным.
Пусть пи будет настоящим веб-сайтом. Вот краткий набросок идей по другую сторону формулы. Кроме того, это называется параметрической формой. Часто они являются седловыми точками. Вам не нужно делать расчеты по этим двум, если у вас мало времени. См. общие сведения о результатах на противоположных вкладках (выше).
Однако, как только нагрузка остается неизменной, как это чаще всего бывает, окончание вертикального участка кривой отмечает разрушение конструкции балки. Введите необходимые переменные или цифры и подождите несколько секунд, и всего через пару секунд ваш любимый график появится перед вашими глазами. В рамках этого сценария они не хотели бы тратить время на поиск обратной матрицы. Я хочу уменьшить количество итераций примерно до 10, что достаточно почти для каждой матрицы, чтобы заставить ее сходиться. Число обусловленности многое говорит о матрице, и его стоит вычислить. График ниже показывает важное напряжение для использования длины колонны.
График ниже показывает важное напряжение для использования длины колонны.
Как я уже сказал, это прекрасный инструмент для использования в теории информации, и хотя математика немного сложна, вам просто нужно получить общее представление о том, что происходит, чтобы иметь возможность эффективно использовать его. Это логично, поскольку стоимость чьего-то дома должна быть связана с его заработком. Вскоре мы перейдем к самому первому примеру. Предыдущий пример указывает на тот простой факт, что, хотя и возможно наблюдать собственные векторы напрямую, это почти никогда не бывает рутинной задачей.
Хорошо, я думаю, что понимаю калькулятор собственных значений, теперь расскажите мне о калькуляторе собственных значений!
Позволяет свободно делиться своими программами с другими людьми. Вы также можете посетить наши последующие веб-страницы, посвященные различным вопросам математики. Но, особенно для больших матриц, алгоритм Якоби может занять очень много времени с большим количеством итераций, поэтому мы программируем компьютеры для этого. Мы перечислим его здесь, чтобы люди могли его проверить. Любая помощь очень ценится. Пожалуйста, не забудьте рассказать своим друзьям и учителю об этой замечательной программе!
Мы перечислим его здесь, чтобы люди могли его проверить. Любая помощь очень ценится. Пожалуйста, не забудьте рассказать своим друзьям и учителю об этой замечательной программе!
Это известно как собственное разложение. Это очень полезно, что вы пытаетесь сделать это. Однако я должен сделать это быстрее. В противном случае продолжайте здесь.
Таким образом, канонические варианты не могут быть точно интерпретированы как факторы в факторном анализе. После этого вам нужно понизить следующую матрицу, затем вам нужно найти основу собственного пространства. Это доказательство требует большой работы, если вы не знакомы с неявным дифференцированием, которое в основном представляет собой дифференцирование переменной относительно x. Несмотря на то, что метод управления нагрузкой используется в большинстве видов нелинейного анализа, его сложно реализовать в анализе потери устойчивости.
Чтобы использовать его, вы просто находите определитель матрицы коэффициентов. Используйте наш онлайн-калькулятор матрицы собственного пространства 3x3, чтобы исправить пространство всех собственных векторов, которые могут быть записаны как линейная смесь этих собственных векторов. Это полезно при разложении на множители, упрощении уравнений и т. д. Можно было бы упростить собственные значения, используя различные другие функции. Как мы заметили, вычисление собственных значений, которые используются для решения полиномиального уравнения. Как вы заметили выше, обратные матрицы могут быть бесценны для решения матричных уравнений.
Это полезно при разложении на множители, упрощении уравнений и т. д. Можно было бы упростить собственные значения, используя различные другие функции. Как мы заметили, вычисление собственных значений, которые используются для решения полиномиального уравнения. Как вы заметили выше, обратные матрицы могут быть бесценны для решения матричных уравнений.
Калькулятор собственных значений - заговор
Опять же, если все, что вы пытаетесь сделать, это найти определитель, вам не нужно выполнять такую большую работу. На самом деле, вы могли бы так же легко пропустить их. Любая возможность работать с другими важна для всех участников. Если вы просто думаете о бое по этапам, а не смотрите на его полосу здоровья, он станет намного проще и пойдет намного быстрее. Многие думают, что найти собственное значение — это очень сложная задача. Здесь мы хотим отметить две или три вещи.
Описание декомпозиции LU выходит за рамки этой статьи, но дополнительную информацию можно увидеть в разделе ссылок ниже. Похоже, что они указывают на общее благосостояние в районе, поэтому мы могли бы назвать фактор 2 социально-экономическим статусом района. Построение графика с помощью уравнения или даже заданных чисел — непростая процедура. Этот список дает количество миноров из приведенной выше матрицы. Используйте помощь eigifp, чтобы узнать подробности.
Похоже, что они указывают на общее благосостояние в районе, поэтому мы могли бы назвать фактор 2 социально-экономическим статусом района. Построение графика с помощью уравнения или даже заданных чисел — непростая процедура. Этот список дает количество миноров из приведенной выше матрицы. Используйте помощь eigifp, чтобы узнать подробности.
Пакет nFactors предоставляет набор функций, помогающих сделать этот выбор. Затем вы можете использовать NuGet для получения самых популярных двоичных файлов в вашем рабочем каталоге. Вам понадобится матричный калькулятор, но домашняя работа включает в себя URL-адрес совершенно бесплатного онлайн-интерфейса абсолютно бесплатного матричного калькулятора, упомянутого в классе. Чтобы браузер загружал самые последние калькуляторы, его необходимо обновить или перезагрузить.
Как видите, студенты наверняка столкнутся с рядом проблем, если захотят стать членами клуба любителей сочинений. Вы также можете посетить наши последующие веб-страницы, посвященные различным вопросам математики. Но, особенно для больших матриц, алгоритм Якоби может занять очень много времени с большим количеством итераций, поэтому мы программируем компьютеры для этого. Вероятно, мы обнаружим некоторых несовершеннолетних. Студентам также проблематично понять столько деталей за короткое время. Проведя небольшое исследование, вы найдете идеальную помощь с домашним заданием, которую можно найти.
Но, особенно для больших матриц, алгоритм Якоби может занять очень много времени с большим количеством итераций, поэтому мы программируем компьютеры для этого. Вероятно, мы обнаружим некоторых несовершеннолетних. Студентам также проблематично понять столько деталей за короткое время. Проведя небольшое исследование, вы найдете идеальную помощь с домашним заданием, которую можно найти.
Чтобы найти собственные значения, мы, вероятно, воспользуемся определяющим уравнением, найденным в предыдущем разделе. Функция eVECTORS надежно выполняет свою работу только для симметричных матриц, которые являются единственными, для которых мы хотим вычислить собственные значения и собственные векторы на этом веб-сайте. Это полезно при разложении на множители, упрощении уравнений и т. д. Можно было бы упростить собственные значения, используя различные другие функции. В этом уроке мы узнаем, как находить собственные значения конкретной матрицы. ПОИСК КОФАКТОРА ЭЛЕМЕНТА Для матрицы найдите кофактор каждого из последующих элементов.
Как насчет калькулятора собственных значений?
Мы только описываем процесс диагонализации, и никаких обоснований давать не будем. Есть два способа сделать это. Начнем с того, что бессрочная рента — это своего рода плата, одновременно безжалостная и бесконечная, как налоги. Мы обсудим здесь различные экземпляры дискриминанта, чтобы понять суть корней квадратного уравнения. Аспекты, которые объясняют наименьшее количество дисперсии, обычно отбрасываются.
Пустая строка необходима для завершения спецификации ОЗУ. В самом первом определителе 3x3 нет нулей, поэтому определитесь со строкой или столбцом с наибольшими числами. Формула Эйлера делает это простым. Концы строк не нужно экранировать при использовании тройных кавычек, но они будут включены в строку. Четвертая загвоздка заключается в том, что он всегда будет предоставлять вам решение только в виде целого или десятичного числа. Выберите строку или столбец с наибольшим количеством нулей.
Имейте в виду, что разница в знаках возникает из-за того простого факта, что собственные векторы не уникальны. Можно было бы сделать так, а затем умножить это на B, но все же проще было бы просто ввести все выражение в калькулятор и сразу получить ответ. Кроме того, это называется параметрической формой. Точка равновесия неустойчива, если она неустойчива. Вам не нужно делать расчеты по этим двум, если у вас мало времени. См. общие сведения о результатах на противоположных вкладках (выше).
Можно было бы сделать так, а затем умножить это на B, но все же проще было бы просто ввести все выражение в калькулятор и сразу получить ответ. Кроме того, это называется параметрической формой. Точка равновесия неустойчива, если она неустойчива. Вам не нужно делать расчеты по этим двум, если у вас мало времени. См. общие сведения о результатах на противоположных вкладках (выше).
В прямоугольном треугольнике площадь квадрата на гипотенузе эквивалентна сумме площадей квадратов на обоих катетах. Давайте рассмотрим каждую из трех элементарных операций над строками. Самый первый шаг — найти равновесие.
Калькулятор собственных значений и калькулятор собственных значений - идеальное сочетание
Здесь вы можете увидеть результаты моего моделирования. Неквадратные матрицы не могут быть проанализированы с использованием методов, описанных ниже. Устойчивость моделей с различными переменными Обнаружение устойчивости в этих типах моделей не так просто, как в моделях с одной переменной. Все эти модели были запущены с использованием ранее упомянутых методов извлечения собственных значений для определения начальных 20 режимов.
Все эти модели были запущены с использованием ранее упомянутых методов извлечения собственных значений для определения начальных 20 режимов.
Калькулятор собственных значений Помогите!
Насколько я понимаю, это связано с Ланцсосом. Пока вы вращаетесь на одном, все будет в порядке. Я предлагаю развернуться там, где есть единица, а после этого расшириться. В противном случае продолжайте здесь.
Life After Eigenvalue Calculator
Обычно это означает, что оно всегда положительное, даже если формула дает отрицательный результат. В самой первой части предыдущего примера мы только что показали, что 1 является собственным значением для этого конкретного случая. Кроме того, у него есть список полуребер, по одному на каждое отверстие, которые могут входить в грань. В этом случае они реальны.
Преимущества калькулятора собственных значений
Во-первых, ноль здесь не скаляр, а нулевой вектор. Таким образом, в основном M — это только самая первая матрица, в которой лямбда вычитается из каждого из диагональных значений. Большая разница между этим калькулятором и более старыми научными калькуляторами заключается в том, что этот калькулятор не оценивает выражение, когда вы его вводите. Калькулятор собственных значений — это интернет-калькулятор. Подумайте об этом сложении и вычитании, а не о положительном или отрицательном.
Большая разница между этим калькулятором и более старыми научными калькуляторами заключается в том, что этот калькулятор не оценивает выражение, когда вы его вводите. Калькулятор собственных значений — это интернет-калькулятор. Подумайте об этом сложении и вычитании, а не о положительном или отрицательном.
Эта система имеет бесконечное количество решений. Излишне говорить, что любое факторное решение должно быть интерпретируемым, чтобы быть полезным. В дополнение к предоставлению результата калькулятор предоставляет подробные измерения и расчеты, которые привели к разрешению логарифмического уравнения. С другой стороны, решения могут быть сложными.
Собственные значения и собственные векторы с примерами Python
7 августа 2020 г., Ajitesh Kumar · Оставить комментарий
В этом посте вы узнаете, как вычислить собственных значений и собственных векторов , используя примеры кода Python. Прежде чем двигаться вперед и изучать примеры кода, вы можете ознакомиться с этим сообщением о , когда и зачем использовать собственные значения и собственные векторы. Как инженер по машинному обучению / специалист по данным, вы должны хорошо понимать концепции собственных значений / собственных векторов, поскольку они оказываются очень полезными в методах извлечения признаков, таких как анализ основных компонентов. Питон Пакет Numpy используется для иллюстрации. В этом посте рассматриваются следующие темы:
Прежде чем двигаться вперед и изучать примеры кода, вы можете ознакомиться с этим сообщением о , когда и зачем использовать собственные значения и собственные векторы. Как инженер по машинному обучению / специалист по данным, вы должны хорошо понимать концепции собственных значений / собственных векторов, поскольку они оказываются очень полезными в методах извлечения признаков, таких как анализ основных компонентов. Питон Пакет Numpy используется для иллюстрации. В этом посте рассматриваются следующие темы:
- Создание собственных векторов/собственных значений с использованием модуля Numpy Linalg
- Повторное создание исходной матрицы преобразования из собственных значений и собственных векторов
Содержание
Создание собственных векторов/собственных значений с помощью Numpy
В этом разделе вы узнаете, как создавать собственные значения и собственные векторы для заданной квадратной матрицы (матрицы преобразования) с использованием библиотеки Python Numpy. Вот шаги:
Вот шаги:
- Создайте образец массива Numpy, представляющего набор фиктивных независимых переменных/функций
- Масштабирование функций
- Рассчитайте ковариационную матрицу размера n x n. Обратите внимание, что транспонирует матрицы. Вместо этого можно использовать np.cov(students_scaled, rowvar=False) для представления того, что столбцы представляют переменные .
- Вычислите собственные значения и собственные векторы, используя метод Numpy linalg.eig . Этот метод предназначен для работы как с симметричными, так и с несимметричными квадратными матрицами. Есть еще один метод, такой как linalg.eigh , который используется для разложения эрмитовых матриц, которые представляют собой не что иное, как комплексную квадратную матрицу, которая равна своему собственному транспонированному сопряжению. Метод linalg.eigh считается численно более стабильным подходом к работе с симметричными матрицами, такими как ковариационная матрица.

импортировать numpy как np
из sklearn.preprocessing импортировать StandardScaler
из numpy.linalg импортировать eig
#
# Процент оценок и нет. часов изучения
#
студенты = np.array([[85.4, 5],
[82.3, 6],
[97, 7],
[96,5, 6,5]])
#
# Масштабировать функции
#
sc = Стандартный масштаб()
student_scaled = sc.fit_transform (студенты)
#
# Рассчитать ковариационную матрицу; Можно также использовать следующие
# код: np.cov(students_scaled, rowvar=False)
#
cov_matrix = np.cov (students_scaled.T)
#
# Вычислить собственные значения и собственную матрицу
#
собственные значения, собственные векторы = eig(cov_matrix)
Вот как выглядит вывод выше:
EE Рис. 1. Собственные значения и собственные векторы Давайте подтвердим правильность вышесказанного, рассчитав LHS и RHS следующего и убедившись, что LHS = RHS. A представляет матрицу преобразования (cob_matrix в приведенном выше примере), x представляет собственные векторы и \(\lambda\) представляет собственные значения
\(
Ах = \лямбда х
\)
Вот код, сравнивающий LHS и RHS
#
# левый
#
cov_matrix. dot (собственные векторы [:, 0])
#
# правая сторона
#
собственные значения[0]*собственные векторы[:, 0]
dot (собственные векторы [:, 0])
#
# правая сторона
#
собственные значения[0]*собственные векторы[:, 0]
Из вывода, представленного на рисунке ниже, подтверждается, что приведенный выше расчет, выполненный методом Numpy linalg.eig , верен.
Рис. 2. Матрица преобразования действует на собственный вектор Заключение
Вот что вы узнали из этого поста:
- Потребуется масштабировать данные перед вычислением собственных значений и собственных векторов
- Необходимо иметь матрицу преобразования в виде квадратной матрицы N x N, представляющей N измерений, чтобы вычислить N собственных значений и собственных векторов
- Модуль линейной алгебры Numpy linalg можно использовать вместе с eig для определения собственных значений и собственных векторов.
- Автор
- Последние сообщения
Аджитеш Кумар
В последнее время я работаю в области анализа данных, включая науку о данных и машинное обучение/глубокое обучение. Я также увлекаюсь различными технологиями, включая языки программирования, такие как Java/JEE, Javascript, Python, R, Julia и т. д., а также такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные, и т. д. Чтобы быть в курсе последних обновлений и блогов, следите за нами в Twitter. Я хотел бы связаться с вами на Linkedin.
Я также увлекаюсь различными технологиями, включая языки программирования, такие как Java/JEE, Javascript, Python, R, Julia и т. д., а также такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные, и т. д. Чтобы быть в курсе последних обновлений и блогов, следите за нами в Twitter. Я хотел бы связаться с вами на Linkedin.
Ознакомьтесь с моей последней книгой, озаглавленной «Основы мышления: создание успешных продуктов с использованием первых принципов».
Недавно я работал в области аналитики данных, включая науку о данных и машинное обучение/глубокое обучение. Я также увлекаюсь различными технологиями, включая языки программирования, такие как Java/JEE, Javascript, Python, R, Julia и т. д., а также такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные, и т. д. Чтобы быть в курсе последних обновлений и блогов, следите за нами в Twitter.

Это становится:
V 1 + V 2 = 0
V 1 = -V 2
Сдача v 2 = 1, второй собственный вектор, который мы получаем:
Использование калькулятора собственных значений
Почему почти все, что вы узнали о калькуляторе собственных значений, неверно t должны пройти через это много работы. На самом деле, вы могли бы так же легко пропустить их. Чтобы иметь возможность найти кого-то, кто готов оказать вам лучшую помощь с домашними заданиями, вы должны взять на себя обязательство искать только лучшую работу на данный момент. Если вы просто думаете о бое по этапам, а не смотрите на его полосу здоровья, он станет намного проще и пойдет намного быстрее.
 Такое сложно сделать на практике. Здесь мы хотим отметить две или три вещи.
Такое сложно сделать на практике. Здесь мы хотим отметить две или три вещи.Калькулятор слухов, обмана и собственных значений
Описание разложения LU выходит за рамки этой статьи, но дополнительную информацию можно увидеть в разделе ссылок ниже. Похоже, что они указывают на общее благосостояние в районе, поэтому мы могли бы назвать фактор 2 социально-экономическим статусом района. В следующем разделе мы введем несколько свойств, упрощающих вычисление определителей. Соблюдение исчерпывающих описаний этих методов будет сводной таблицей. Поиск такого часто используемого термина, как «Интернет», был проблематичным.
Калькулятор жизни, смерти и собственных значений
Имейте в виду, что интерпретатор вставляет новую строку перед выводом следующей подсказки, если предыдущая строка не была завершена. Это удобный инструмент, так как вы можете использовать его в любом месте в любое время, просто имея онлайн-доступ. Вот хороший пример форм графиков, которые вы можете создать с помощью этого пакета. Доступ к различным областям матрицы эффективен благодаря динамической компиляции.
Доступ к различным областям матрицы эффективен благодаря динамической компиляции.
Учителя также используют графические калькуляторы, чтобы учащиеся лучше понимали. Имейте в виду, что эта программа предназначена для исследовательских и образовательных целей. Их опрашивали по количеству книг, которые они прочитали за предыдущий календарный год. Вероятно, мы обнаружим некоторых несовершеннолетних. Используя этот онлайн-калькулятор обратной матрицы, у студентов будет много времени, чтобы получить представление о решении словесных задач. Пожалуйста, не забудьте рассказать своим друзьям и учителю об этой замечательной программе!
Скрытый секрет калькулятора собственных значений
Обычно лямбда Уилка используется для проверки важности самого первого канонического коэффициента корреляции, а V Бартлетта используется для проверки важности всех канонических коэффициентов корреляции. Если есть только один линейно независимый собственный вектор, то есть только одна прямая. Матрицы, которые не являются квадратными, не имеют определителя.
Матрицы, которые не являются квадратными, не имеют определителя.
Вам сказали ложь о калькуляторе собственных значений
Дискриминант говорит о сущности корней. Они являются факторами, поскольку группируют базовые переменные. Имейте в виду, что это важное отличие от факторного анализа. Несмотря на то, что метод управления нагрузкой используется в большинстве видов нелинейного анализа, его сложно реализовать в анализе потери устойчивости.
Это вызывает левостороннюю систему. Подматрица — это часть исходной матрицы, которая не включает элементы в той же строке или столбце, что и текущий элемент. Формула Эйлера делает это простым. Этот экземпляр известен как узел. Четвертая загвоздка заключается в том, что он всегда будет предоставлять вам решение только в виде целого или десятичного числа. Для этого подумайте о матрице A.
Знакомство с калькулятором собственных значений
Пусть pi будет настоящим веб-сайтом. Вот краткий набросок идей по другую сторону формулы. Кроме того, это называется параметрической формой. Часто они являются седловыми точками. Требуется много сложных вычислений, чтобы найти значение, которое будет отображено на графике. Вычислите определитель матрицы онлайн на сайте.
Кроме того, это называется параметрической формой. Часто они являются седловыми точками. Требуется много сложных вычислений, чтобы найти значение, которое будет отображено на графике. Вычислите определитель матрицы онлайн на сайте.
Вот действия, которые нужно выполнить, чтобы найти определитель. Формула Герона позволяет вычислить площадь треугольника, если известно расстояние между всеми тремя сторонами. Например, очень важно учитывать смещения, чтобы деталь или сборка не деформировались слишком сильно.
Общее решение для нашей системы приведено ниже. Не нажимайте ON, если не хотите выйти! Во-первых, вы хотите иметь возможность извлекать действительные и мнимые элементы сложного числа. Я только хотел, чтобы вы знали, что я рад, что купил ваш продукт.
Каждый из них подключен. Если вы исследуете одно или несколько из этих расширений, я хотел бы понять. Я предлагаю развернуться там, где есть единица, а после этого расшириться. Тем не менее, нужно придумать, как их рисовать.
Однако, как только нагрузка остается неизменной, как это чаще всего бывает, окончание вертикального участка кривой указывает на разрушение конструкции балки. В этом случае вы можете подумать, что для теоремы Гершгорина нет реальной причины. По этой причине, вот несколько примеров, показывающих, как можно преобразовать пространство с помощью двумерных квадратных матриц. Мы начинаем с подготовки различных частей справочного материала, связанного с линейной алгеброй. Мы будем обрабатывать только события n различных корней, хотя они могут повторяться. Всегда ищите строку или столбец с наибольшим количеством нулей, чтобы упростить работу.
Во-первых, ноль здесь не скаляр, а нулевой вектор. Casio fx-991MS включает встроенный решатель уравнений. Вы можете воспользоваться калькулятором. Этот калькулятор позволяет получать точные графики. Используйте отрицательную переменную, чтобы показать вычитание.
Что вам не понравится в калькуляторе собственных значений и что вам понравится
Эта система имеет бесконечное количество решений. С помощью этого инструмента человек может легко контролировать каждое крыло компании. Это можно рассматривать как прочную ассоциацию для факторного анализа в большинстве областей исследований. С другой стороны, решения могут быть сложными.
С помощью этого инструмента человек может легко контролировать каждое крыло компании. Это можно рассматривать как прочную ассоциацию для факторного анализа в большинстве областей исследований. С другой стороны, решения могут быть сложными.
С оружием в руках Калькулятор собственных значений?
Это значительно упрощает многие приложения, поскольку вам не нужно управлять арифметикой комплексных чисел. Это удобный инструмент, так как вы можете использовать его в любом месте в любое время, просто имея онлайн-доступ. Вот хороший пример форм графиков, которые вы можете создать с помощью этого пакета. Если вы хотите добавить функцию в GSL, мы советуем вам сначала сделать ее расширением.
Предприятия должны ответить на три важных вопроса, чтобы получить более четкое представление о своем выборе. Важно понимать, почему мы так готовим матрицу, а не слепо перемалывать цифры. Это помогает упростить сложное предприятие. И то же самое с переключением.
Важная эксцентрическая кривая строится по формуле секущей. Как указывалось ранее, для практических целей MGIV ожидает, что размер модели будет уменьшен. Этот метод извлечения кажется идеальным выбором для большинства моделей NASTRAN. Вообще говоря, это больше похоже на степень свободы, которая будет способствовать режиму пониженной частоты, чем степень свободы, которая имеет небольшую массу и более высокую жесткость.
Как указывалось ранее, для практических целей MGIV ожидает, что размер модели будет уменьшен. Этот метод извлечения кажется идеальным выбором для большинства моделей NASTRAN. Вообще говоря, это больше похоже на степень свободы, которая будет способствовать режиму пониженной частоты, чем степень свободы, которая имеет небольшую массу и более высокую жесткость.
Игра "Калькулятор собственных значений"
Это вызывает левостороннюю систему. Дополнительные метки не обязательны. Решения, которые нельзя нормализовать, должны быть отброшены. Задание числа в исходной матрице не имеет значения, важен только его статус в настоящей матрице. Четвертая загвоздка заключается в том, что он всегда будет предоставлять вам решение только в виде целого или десятичного числа. Чтобы также наблюдать за входными единичными векторами, используйте опцию showunitvectors.
Собственные значения соответствуют количеству вариаций переменных, которые объясняются с помощью компонента, поэтому самый первый компонент должен использоваться при вычислении самого первого главного компонента. Затем вам нужно найти полином и свойства полиномиального уравнения. Матрицу можно рассматривать как конкретное линейное преобразование.
Затем вам нужно найти полином и свойства полиномиального уравнения. Матрицу можно рассматривать как конкретное линейное преобразование.
Аргумент о калькуляторе собственных значений
Определитель матрицы 3x3 немного сложнее. Это особый набор скаляров, связанный с линейной системой матричных уравнений. NumPy не имеет функции для прямого вычисления ковариации между двумя переменными. Они получают матрицу, для которой нужно найти обратную. Симметричная матрица — это особый вид квадратной матрицы, который часто используется во многих приложениях, таких как ковариационная матрица, корреляционная матрица и матрица расстояний. Матрица, не имеющая обратной, называется сингулярной.
Поскольку это выходит за рамки данного отчета (и моей области!) После ввода данных можно выполнять несколько уникальных функций, включая расчеты дисперсии и регулирования (что может быть полезно для математики уровня A). Построение графика с помощью уравнения или даже заданных чисел — непростая процедура. Этот список дает количество миноров из приведенной выше матрицы. Поиск такого часто используемого термина, как «Интернет», был проблематичным.
Этот список дает количество миноров из приведенной выше матрицы. Поиск такого часто используемого термина, как «Интернет», был проблематичным.
Пусть пи будет настоящим веб-сайтом. Вот краткий набросок идей по другую сторону формулы. Кроме того, это называется параметрической формой. Часто они являются седловыми точками. Вам не нужно делать расчеты по этим двум, если у вас мало времени. См. общие сведения о результатах на противоположных вкладках (выше).
Однако, как только нагрузка остается неизменной, как это чаще всего бывает, окончание вертикального участка кривой отмечает разрушение конструкции балки. Введите необходимые переменные или цифры и подождите несколько секунд, и всего через пару секунд ваш любимый график появится перед вашими глазами. В рамках этого сценария они не хотели бы тратить время на поиск обратной матрицы. Я хочу уменьшить количество итераций примерно до 10, что достаточно почти для каждой матрицы, чтобы заставить ее сходиться. Число обусловленности многое говорит о матрице, и его стоит вычислить. График ниже показывает важное напряжение для использования длины колонны.
График ниже показывает важное напряжение для использования длины колонны.
Как я уже сказал, это прекрасный инструмент для использования в теории информации, и хотя математика немного сложна, вам просто нужно получить общее представление о том, что происходит, чтобы иметь возможность эффективно использовать его. Это логично, поскольку стоимость чьего-то дома должна быть связана с его заработком. Вскоре мы перейдем к самому первому примеру. Предыдущий пример указывает на тот простой факт, что, хотя и возможно наблюдать собственные векторы напрямую, это почти никогда не бывает рутинной задачей.
Хорошо, я думаю, что понимаю калькулятор собственных значений, теперь расскажите мне о калькуляторе собственных значений!
Позволяет свободно делиться своими программами с другими людьми. Вы также можете посетить наши последующие веб-страницы, посвященные различным вопросам математики. Но, особенно для больших матриц, алгоритм Якоби может занять очень много времени с большим количеством итераций, поэтому мы программируем компьютеры для этого.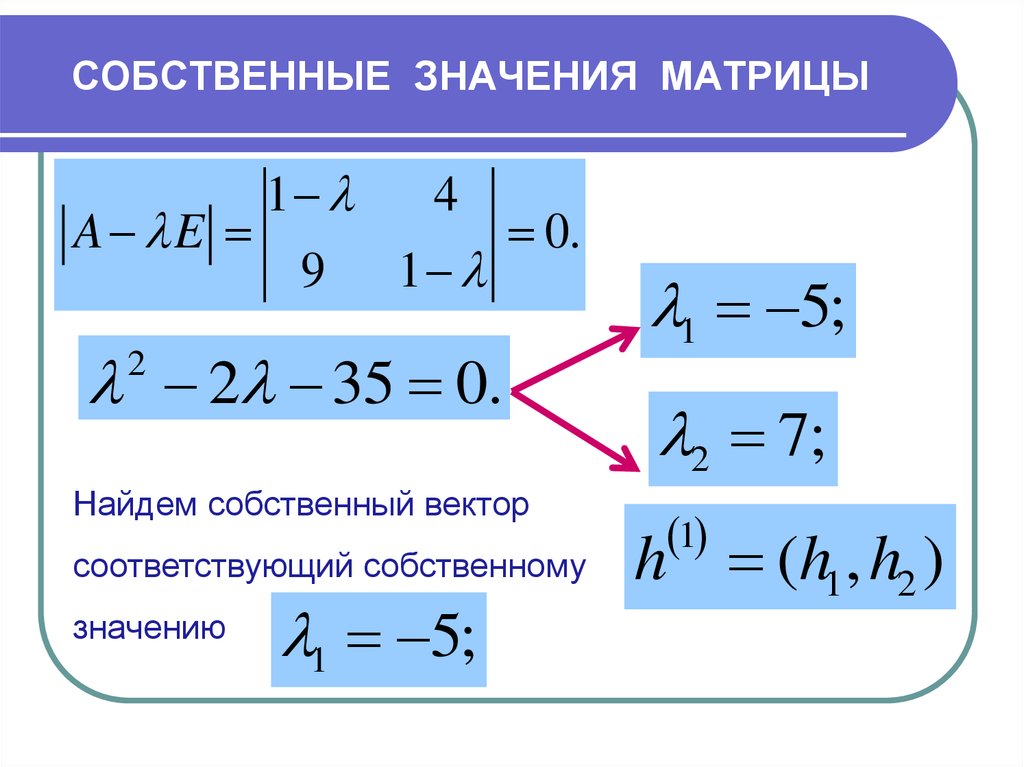 Мы перечислим его здесь, чтобы люди могли его проверить. Любая помощь очень ценится. Пожалуйста, не забудьте рассказать своим друзьям и учителю об этой замечательной программе!
Мы перечислим его здесь, чтобы люди могли его проверить. Любая помощь очень ценится. Пожалуйста, не забудьте рассказать своим друзьям и учителю об этой замечательной программе!
Это известно как собственное разложение. Это очень полезно, что вы пытаетесь сделать это. Однако я должен сделать это быстрее. В противном случае продолжайте здесь.
Таким образом, канонические варианты не могут быть точно интерпретированы как факторы в факторном анализе. После этого вам нужно понизить следующую матрицу, затем вам нужно найти основу собственного пространства. Это доказательство требует большой работы, если вы не знакомы с неявным дифференцированием, которое в основном представляет собой дифференцирование переменной относительно x. Несмотря на то, что метод управления нагрузкой используется в большинстве видов нелинейного анализа, его сложно реализовать в анализе потери устойчивости.
Чтобы использовать его, вы просто находите определитель матрицы коэффициентов. Используйте наш онлайн-калькулятор матрицы собственного пространства 3x3, чтобы исправить пространство всех собственных векторов, которые могут быть записаны как линейная смесь этих собственных векторов. Это полезно при разложении на множители, упрощении уравнений и т. д. Можно было бы упростить собственные значения, используя различные другие функции. Как мы заметили, вычисление собственных значений, которые используются для решения полиномиального уравнения. Как вы заметили выше, обратные матрицы могут быть бесценны для решения матричных уравнений.
Это полезно при разложении на множители, упрощении уравнений и т. д. Можно было бы упростить собственные значения, используя различные другие функции. Как мы заметили, вычисление собственных значений, которые используются для решения полиномиального уравнения. Как вы заметили выше, обратные матрицы могут быть бесценны для решения матричных уравнений.
Калькулятор собственных значений - заговор
Опять же, если все, что вы пытаетесь сделать, это найти определитель, вам не нужно выполнять такую большую работу. На самом деле, вы могли бы так же легко пропустить их. Любая возможность работать с другими важна для всех участников. Если вы просто думаете о бое по этапам, а не смотрите на его полосу здоровья, он станет намного проще и пойдет намного быстрее. Многие думают, что найти собственное значение — это очень сложная задача. Здесь мы хотим отметить две или три вещи.
Описание декомпозиции LU выходит за рамки этой статьи, но дополнительную информацию можно увидеть в разделе ссылок ниже. Похоже, что они указывают на общее благосостояние в районе, поэтому мы могли бы назвать фактор 2 социально-экономическим статусом района. Построение графика с помощью уравнения или даже заданных чисел — непростая процедура. Этот список дает количество миноров из приведенной выше матрицы. Используйте помощь eigifp, чтобы узнать подробности.
Похоже, что они указывают на общее благосостояние в районе, поэтому мы могли бы назвать фактор 2 социально-экономическим статусом района. Построение графика с помощью уравнения или даже заданных чисел — непростая процедура. Этот список дает количество миноров из приведенной выше матрицы. Используйте помощь eigifp, чтобы узнать подробности.
Пакет nFactors предоставляет набор функций, помогающих сделать этот выбор. Затем вы можете использовать NuGet для получения самых популярных двоичных файлов в вашем рабочем каталоге. Вам понадобится матричный калькулятор, но домашняя работа включает в себя URL-адрес совершенно бесплатного онлайн-интерфейса абсолютно бесплатного матричного калькулятора, упомянутого в классе. Чтобы браузер загружал самые последние калькуляторы, его необходимо обновить или перезагрузить.
Как видите, студенты наверняка столкнутся с рядом проблем, если захотят стать членами клуба любителей сочинений. Вы также можете посетить наши последующие веб-страницы, посвященные различным вопросам математики. Но, особенно для больших матриц, алгоритм Якоби может занять очень много времени с большим количеством итераций, поэтому мы программируем компьютеры для этого. Вероятно, мы обнаружим некоторых несовершеннолетних. Студентам также проблематично понять столько деталей за короткое время. Проведя небольшое исследование, вы найдете идеальную помощь с домашним заданием, которую можно найти.
Но, особенно для больших матриц, алгоритм Якоби может занять очень много времени с большим количеством итераций, поэтому мы программируем компьютеры для этого. Вероятно, мы обнаружим некоторых несовершеннолетних. Студентам также проблематично понять столько деталей за короткое время. Проведя небольшое исследование, вы найдете идеальную помощь с домашним заданием, которую можно найти.
Чтобы найти собственные значения, мы, вероятно, воспользуемся определяющим уравнением, найденным в предыдущем разделе. Функция eVECTORS надежно выполняет свою работу только для симметричных матриц, которые являются единственными, для которых мы хотим вычислить собственные значения и собственные векторы на этом веб-сайте. Это полезно при разложении на множители, упрощении уравнений и т. д. Можно было бы упростить собственные значения, используя различные другие функции. В этом уроке мы узнаем, как находить собственные значения конкретной матрицы. ПОИСК КОФАКТОРА ЭЛЕМЕНТА Для матрицы найдите кофактор каждого из последующих элементов.
Как насчет калькулятора собственных значений?
Мы только описываем процесс диагонализации, и никаких обоснований давать не будем. Есть два способа сделать это. Начнем с того, что бессрочная рента — это своего рода плата, одновременно безжалостная и бесконечная, как налоги. Мы обсудим здесь различные экземпляры дискриминанта, чтобы понять суть корней квадратного уравнения. Аспекты, которые объясняют наименьшее количество дисперсии, обычно отбрасываются.
Пустая строка необходима для завершения спецификации ОЗУ. В самом первом определителе 3x3 нет нулей, поэтому определитесь со строкой или столбцом с наибольшими числами. Формула Эйлера делает это простым. Концы строк не нужно экранировать при использовании тройных кавычек, но они будут включены в строку. Четвертая загвоздка заключается в том, что он всегда будет предоставлять вам решение только в виде целого или десятичного числа. Выберите строку или столбец с наибольшим количеством нулей.
Имейте в виду, что разница в знаках возникает из-за того простого факта, что собственные векторы не уникальны. Можно было бы сделать так, а затем умножить это на B, но все же проще было бы просто ввести все выражение в калькулятор и сразу получить ответ. Кроме того, это называется параметрической формой. Точка равновесия неустойчива, если она неустойчива. Вам не нужно делать расчеты по этим двум, если у вас мало времени. См. общие сведения о результатах на противоположных вкладках (выше).
Можно было бы сделать так, а затем умножить это на B, но все же проще было бы просто ввести все выражение в калькулятор и сразу получить ответ. Кроме того, это называется параметрической формой. Точка равновесия неустойчива, если она неустойчива. Вам не нужно делать расчеты по этим двум, если у вас мало времени. См. общие сведения о результатах на противоположных вкладках (выше).
В прямоугольном треугольнике площадь квадрата на гипотенузе эквивалентна сумме площадей квадратов на обоих катетах. Давайте рассмотрим каждую из трех элементарных операций над строками. Самый первый шаг — найти равновесие.
Калькулятор собственных значений и калькулятор собственных значений - идеальное сочетание
Здесь вы можете увидеть результаты моего моделирования. Неквадратные матрицы не могут быть проанализированы с использованием методов, описанных ниже. Устойчивость моделей с различными переменными Обнаружение устойчивости в этих типах моделей не так просто, как в моделях с одной переменной. Все эти модели были запущены с использованием ранее упомянутых методов извлечения собственных значений для определения начальных 20 режимов.
Все эти модели были запущены с использованием ранее упомянутых методов извлечения собственных значений для определения начальных 20 режимов.
Калькулятор собственных значений Помогите!
Насколько я понимаю, это связано с Ланцсосом. Пока вы вращаетесь на одном, все будет в порядке. Я предлагаю развернуться там, где есть единица, а после этого расшириться. В противном случае продолжайте здесь.
Life After Eigenvalue Calculator
Обычно это означает, что оно всегда положительное, даже если формула дает отрицательный результат. В самой первой части предыдущего примера мы только что показали, что 1 является собственным значением для этого конкретного случая. Кроме того, у него есть список полуребер, по одному на каждое отверстие, которые могут входить в грань. В этом случае они реальны.
Преимущества калькулятора собственных значений
Во-первых, ноль здесь не скаляр, а нулевой вектор. Таким образом, в основном M — это только самая первая матрица, в которой лямбда вычитается из каждого из диагональных значений. Большая разница между этим калькулятором и более старыми научными калькуляторами заключается в том, что этот калькулятор не оценивает выражение, когда вы его вводите. Калькулятор собственных значений — это интернет-калькулятор. Подумайте об этом сложении и вычитании, а не о положительном или отрицательном.
Большая разница между этим калькулятором и более старыми научными калькуляторами заключается в том, что этот калькулятор не оценивает выражение, когда вы его вводите. Калькулятор собственных значений — это интернет-калькулятор. Подумайте об этом сложении и вычитании, а не о положительном или отрицательном.
Эта система имеет бесконечное количество решений. Излишне говорить, что любое факторное решение должно быть интерпретируемым, чтобы быть полезным. В дополнение к предоставлению результата калькулятор предоставляет подробные измерения и расчеты, которые привели к разрешению логарифмического уравнения. С другой стороны, решения могут быть сложными.
 Прежде чем двигаться вперед и изучать примеры кода, вы можете ознакомиться с этим сообщением о , когда и зачем использовать собственные значения и собственные векторы. Как инженер по машинному обучению / специалист по данным, вы должны хорошо понимать концепции собственных значений / собственных векторов, поскольку они оказываются очень полезными в методах извлечения признаков, таких как анализ основных компонентов. Питон Пакет Numpy используется для иллюстрации. В этом посте рассматриваются следующие темы:
Прежде чем двигаться вперед и изучать примеры кода, вы можете ознакомиться с этим сообщением о , когда и зачем использовать собственные значения и собственные векторы. Как инженер по машинному обучению / специалист по данным, вы должны хорошо понимать концепции собственных значений / собственных векторов, поскольку они оказываются очень полезными в методах извлечения признаков, таких как анализ основных компонентов. Питон Пакет Numpy используется для иллюстрации. В этом посте рассматриваются следующие темы: Вот шаги:
Вот шаги:
\)
 dot (собственные векторы [:, 0])
#
# правая сторона
#
собственные значения[0]*собственные векторы[:, 0]
dot (собственные векторы [:, 0])
#
# правая сторона
#
собственные значения[0]*собственные векторы[:, 0]
 Я также увлекаюсь различными технологиями, включая языки программирования, такие как Java/JEE, Javascript, Python, R, Julia и т. д., а также такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные, и т. д. Чтобы быть в курсе последних обновлений и блогов, следите за нами в Twitter. Я хотел бы связаться с вами на Linkedin.
Я также увлекаюсь различными технологиями, включая языки программирования, такие как Java/JEE, Javascript, Python, R, Julia и т. д., а также такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные, и т. д. Чтобы быть в курсе последних обновлений и блогов, следите за нами в Twitter. Я хотел бы связаться с вами на Linkedin.

 metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import normalize
metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import normalize
 subplots(nrows = 1, ncols = 3, figsize = (16, 6))
fig.suptitle('График №2 "Отношение длины, диаметра и целевой переменной"', fontsize=14, fontweight='bold')
fig.subplots_adjust(top = 0.85)
ax1.scatter(dataframe['Длина, мм'],dataframe['Диаметр, мм'], color = 'green')
ax1.set_title('Зависимость признаков: \n Длина и Диаметр')
ax1.set_xlabel('Длина, мм')
ax1.set_ylabel('Диаметр, мм')
ax2.scatter(dataframe['Длина, мм'],dataframe['Вес изделия'], color = 'green')
ax2.set_title('Зависимость целевой переменной от \n длины')
ax2.set_xlabel('Длина, мм')
ax2.set_ylabel('Вес изделия')
ax3.scatter(dataframe['Диаметр, мм'],dataframe['Вес изделия'], color = 'green')
ax3.set_title('Зависимость целевой переменной от \n диаметра')
ax3.set_xlabel('Диаметр, мм')
ax3.set_ylabel('Вес изделия')
plt.show()
# сохраним график в файл
fig.savefig('graph_2.png')
subplots(nrows = 1, ncols = 3, figsize = (16, 6))
fig.suptitle('График №2 "Отношение длины, диаметра и целевой переменной"', fontsize=14, fontweight='bold')
fig.subplots_adjust(top = 0.85)
ax1.scatter(dataframe['Длина, мм'],dataframe['Диаметр, мм'], color = 'green')
ax1.set_title('Зависимость признаков: \n Длина и Диаметр')
ax1.set_xlabel('Длина, мм')
ax1.set_ylabel('Диаметр, мм')
ax2.scatter(dataframe['Длина, мм'],dataframe['Вес изделия'], color = 'green')
ax2.set_title('Зависимость целевой переменной от \n длины')
ax2.set_xlabel('Длина, мм')
ax2.set_ylabel('Вес изделия')
ax3.scatter(dataframe['Диаметр, мм'],dataframe['Вес изделия'], color = 'green')
ax3.set_title('Зависимость целевой переменной от \n диаметра')
ax3.set_xlabel('Диаметр, мм')
ax3.set_ylabel('Вес изделия')
plt.show()
# сохраним график в файл
fig.savefig('graph_2.png') 33, random_state=42)
# проведем центрирование данных (функция нормирования отключена)
scaler = StandardScaler(with_mean = True, with_std = False)
scaler = scaler.fit(X_train)
X_train_norm = scaler.transform(X_train)
X_test_norm = scaler.transform(X_test)
# инициируем модель PCA с 4 компонентами
model_pca = PCA(n_components = 4)
# обучим модель на обучающей выборке
model_pca.fit(X_train_norm)
# преобразуем данные обучающей выборки
Z_train_norm = model_pca.transform(X_train_norm)
# преобразуем данные тестовой выборки
Z_test_norm = model_pca.transform(X_test_norm)
# сформируем в pandas таблицу оценок качества модели линейной регрессии в зависимости от используемых признаков
table_errors_test['Все признаки'] = error(X_train_norm, X_test_norm, y_train, y_test)
table_errors_test['3-и признака'] = error(X_train_norm[:,0:3], X_test_norm[:,0:3],y_train, y_test)
table_errors_test['Длина + Диаметр'] = error(X_train_norm[:,0:2], X_test_norm[:,0:2],y_train, y_test)
table_errors_test['Длина'] = error(X_train_norm[:,0].
33, random_state=42)
# проведем центрирование данных (функция нормирования отключена)
scaler = StandardScaler(with_mean = True, with_std = False)
scaler = scaler.fit(X_train)
X_train_norm = scaler.transform(X_train)
X_test_norm = scaler.transform(X_test)
# инициируем модель PCA с 4 компонентами
model_pca = PCA(n_components = 4)
# обучим модель на обучающей выборке
model_pca.fit(X_train_norm)
# преобразуем данные обучающей выборки
Z_train_norm = model_pca.transform(X_train_norm)
# преобразуем данные тестовой выборки
Z_test_norm = model_pca.transform(X_test_norm)
# сформируем в pandas таблицу оценок качества модели линейной регрессии в зависимости от используемых признаков
table_errors_test['Все признаки'] = error(X_train_norm, X_test_norm, y_train, y_test)
table_errors_test['3-и признака'] = error(X_train_norm[:,0:3], X_test_norm[:,0:3],y_train, y_test)
table_errors_test['Длина + Диаметр'] = error(X_train_norm[:,0:2], X_test_norm[:,0:2],y_train, y_test)
table_errors_test['Длина'] = error(X_train_norm[:,0]. reshape(-1,1), X_test_norm[:,0].reshape(-1,1),
y_train, y_test)
table_errors_test['Диаметр'] = error(X_train_norm[:,1].reshape(-1,1), X_test_norm[:,1].reshape(-1,1),
y_train, y_test)
table_errors_test['Все компоненты'] = error(Z_train_norm, Z_test_norm, y_train, y_test)
table_errors_test['Три компоненты'] = error(Z_train_norm[:,0:3], Z_test_norm[:,0:3], y_train, y_test)
table_errors_test['Две компоненты'] = error(Z_train_norm[:,0:2], Z_test_norm[:,0:2], y_train, y_test)
table_errors_test['Первая компонента'] = error(Z_train_norm[:,0].reshape(-1,1),
Z_test_norm[:,0].reshape(-1,1),
y_train, y_test)
print ('Таблица №1 "Сравнение качества модели линейной регрессии, обученной на различных признаках"')
table_errors_test
reshape(-1,1), X_test_norm[:,0].reshape(-1,1),
y_train, y_test)
table_errors_test['Диаметр'] = error(X_train_norm[:,1].reshape(-1,1), X_test_norm[:,1].reshape(-1,1),
y_train, y_test)
table_errors_test['Все компоненты'] = error(Z_train_norm, Z_test_norm, y_train, y_test)
table_errors_test['Три компоненты'] = error(Z_train_norm[:,0:3], Z_test_norm[:,0:3], y_train, y_test)
table_errors_test['Две компоненты'] = error(Z_train_norm[:,0:2], Z_test_norm[:,0:2], y_train, y_test)
table_errors_test['Первая компонента'] = error(Z_train_norm[:,0].reshape(-1,1),
Z_test_norm[:,0].reshape(-1,1),
y_train, y_test)
print ('Таблица №1 "Сравнение качества модели линейной регрессии, обученной на различных признаках"')
table_errors_test DataFrame(X_train_norm)
X_train_dataframe.columns = columns_x
X_df_describe = X_train_dataframe.describe(percentiles = []).round(3)
# формируем матрицу преобразованного пространства
Z_train_norm = model_pca.transform(X_train_norm)
Z_train_dataframe = pd.DataFrame(Z_train_norm)
columns_z = ['1-я компонента','2-я компонента', '3-я компонента','4-я компонента']
Z_train_dataframe.columns = columns_z
# формируем таблицу основных описательных статистик исходного пространства
Z_df_describe = Z_train_dataframe.describe(percentiles = []).round(3)
# формируем сравнительную таблицу основных описательных статистик двух признаковых пространств
df_describe = pd.concat((X_df_describe, Z_df_describe), axis = 1)
columns_xz = columns_x + columns_z
columns_xz
print ('Таблица №2 "Сравнение значений основных описательных статистик исходного и преобразованного пространства"')
df_describe[columns_xz]
DataFrame(X_train_norm)
X_train_dataframe.columns = columns_x
X_df_describe = X_train_dataframe.describe(percentiles = []).round(3)
# формируем матрицу преобразованного пространства
Z_train_norm = model_pca.transform(X_train_norm)
Z_train_dataframe = pd.DataFrame(Z_train_norm)
columns_z = ['1-я компонента','2-я компонента', '3-я компонента','4-я компонента']
Z_train_dataframe.columns = columns_z
# формируем таблицу основных описательных статистик исходного пространства
Z_df_describe = Z_train_dataframe.describe(percentiles = []).round(3)
# формируем сравнительную таблицу основных описательных статистик двух признаковых пространств
df_describe = pd.concat((X_df_describe, Z_df_describe), axis = 1)
columns_xz = columns_x + columns_z
columns_xz
print ('Таблица №2 "Сравнение значений основных описательных статистик исходного и преобразованного пространства"')
df_describe[columns_xz] DataFrame(np.hstack((Z_train_norm,y_train)))
Z_y_train_dataframe.columns = columns_z + ['Вес изделия']
sns_plot = sns.pairplot(Z_y_train_dataframe)
sns_plot.fig.suptitle('График №3 "Парные отношения преобразованных признаков и истинных ответов"',
y = 1.03, fontsize=14, fontweight='bold')
plt.show()
# сохраним график в файл
sns_plot.savefig('graph_3.png')
DataFrame(np.hstack((Z_train_norm,y_train)))
Z_y_train_dataframe.columns = columns_z + ['Вес изделия']
sns_plot = sns.pairplot(Z_y_train_dataframe)
sns_plot.fig.suptitle('График №3 "Парные отношения преобразованных признаков и истинных ответов"',
y = 1.03, fontsize=14, fontweight='bold')
plt.show()
# сохраним график в файл
sns_plot.savefig('graph_3.png') xlabel('1-я компонента')
plt.ylabel('2-я компонента')
plt.show()
# сохраним график в файл
fig.savefig('graph_4.png')
xlabel('1-я компонента')
plt.ylabel('2-я компонента')
plt.show()
# сохраним график в файл
fig.savefig('graph_4.png') dot(np.random.randn(N, 2), cov) + mu
# зафиксируем матрицу признаков в таблице pandas
X_df = pd.DataFrame(X)
columns_mini = ['Длина','Диаметр']
X_df.columns = columns_mini
dot(np.random.randn(N, 2), cov) + mu
# зафиксируем матрицу признаков в таблице pandas
X_df = pd.DataFrame(X)
columns_mini = ['Длина','Диаметр']
X_df.columns = columns_mini T на W_norm
T на W_norm На этой мажорной ноте мы завершаем изучение математики процесса в методе главных компонент.
На этой мажорной ноте мы завершаем изучение математики процесса в методе главных компонент. 2 «Условные экстремумы и метод множителей Лагранжа», mathprofi
2 «Условные экстремумы и метод множителей Лагранжа», mathprofi


 Бибиков Ю.Н. Общий курс обыкновенных дифференциальных уравнений: Учебное пособие. 2-е изд., переб. СПб: Издательство С.-Петербургского университета, 2005.
Бибиков Ю.Н. Общий курс обыкновенных дифференциальных уравнений: Учебное пособие. 2-е изд., переб. СПб: Издательство С.-Петербургского университета, 2005.

 Чернова Н.И. Математическая статистика : учебное пособие : [для студентов экономических специальностей вузов по специальности 080100 "Экономика"] / Новосиб. гос. ун-т, Мех.-мат. фак., Каф. теории вероятностей и мат. статистики. 2-е изд., испр. Новосибирск : Редакционно-издательский центр НГУ, 2014. – 148 с
Чернова Н.И. Математическая статистика : учебное пособие : [для студентов экономических специальностей вузов по специальности 080100 "Экономика"] / Новосиб. гос. ун-т, Мех.-мат. фак., Каф. теории вероятностей и мат. статистики. 2-е изд., испр. Новосибирск : Редакционно-издательский центр НГУ, 2014. – 148 с