В случае если входная матрица a не является квадратной или вычисление обратной матрицы невозможно, то вызывается исключение LinAlgError.
Параметры: a — массив NumPy или подобнй массиву объект. Это может быть толко «квадратный» двумерный массив, т.е. квадратная матрица. Если это многомерный массив, то две его последние оси должны быть равны, в этом случае он рассматривается как массив матриц и обратная матрица вычисляется отдельно для каждой из них. Возвращает: результат — массив NumPy Обратная матрица или массив обратных матриц.
Примеры
Мы можем проверить правильность результата, опираясь на основное свойство обратной матрицы, т.е. np.dot(a, ainv) = np.dot(ainv, a) = np.eye(a.shape[0])
Понятие обратной матрицы может быть обобщено и для матриц над полем комплексных чисел:
Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы
Обратной матрицей A -1 матрицы A называют матрицу, удовлетворяющую следующему равенству:
где – E это единичная матрица.
Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы . Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.
Союзная ей матрица A*:
Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A* T :
Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A -1 , обратную матрице A:
Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:
Для начала найдем определитель матрицы A:
Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная. Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:
Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:
Союзная матрица будет иметь следующий вид:
Присоединенная матрица получается из союзной путем транспонирования:
Находим обратную матрицу:
➤ Пример на Python
Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию inv():
Рассмотрим свойства обратной матрицы.
Свойство 1 . Обратная матрица обратной матрицы есть исходная матрица:
➤Пример на Python
Свойство 2 . Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:
➤ Пример на Python
Свойство 3 . Обратная матрица произведения матриц равна произведению обратных матриц:
➤ Пример на Python
Ранг матрицыРанг матрицы является еще одной важной численной характеристикой. Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.
Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.
Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:
Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на Python воспользуемся функцией matrix_rank():
Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:
P.S.Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта . Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas.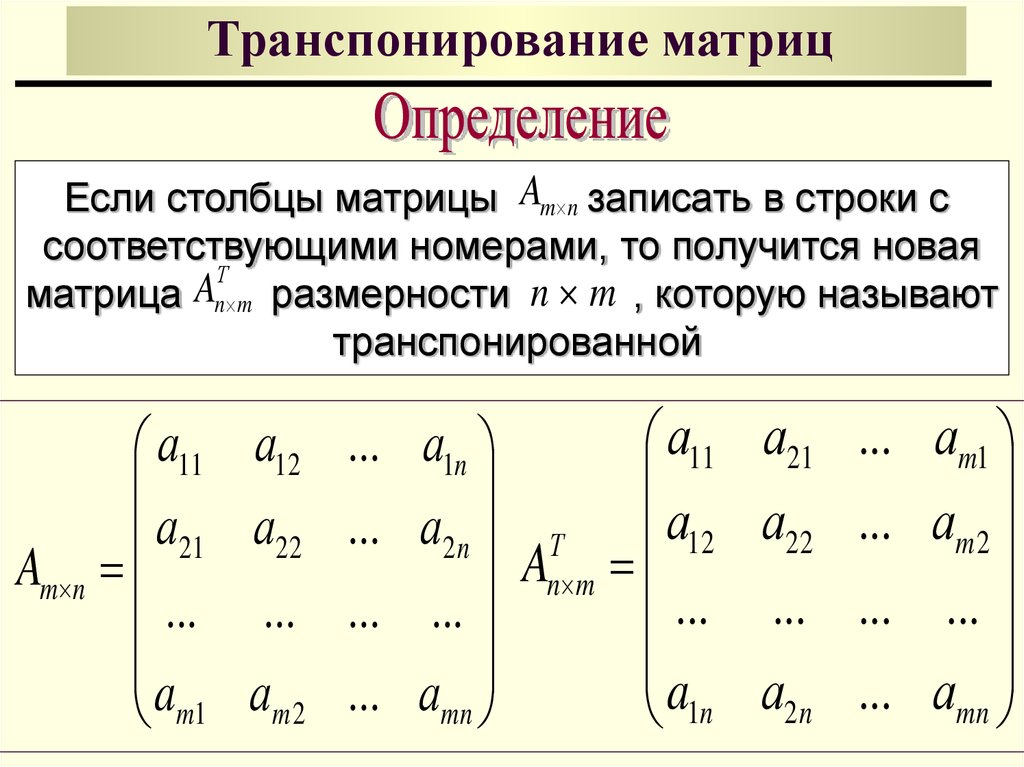 Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы : 1 комментарий
i want that help me
1) написать программу вычисляющую обратную матрицу
Работа с Matrix в Python
Для работы с Matrix Python нам необходимо импортировать модуль numpy. Матрица используется для операций с матрицей, которая может использоваться для научных целей, обработки изображений и т.д.
Как создать матрицу?
Согласно Википедии, матрица – это прямоугольный массив чисел, символов или выражений, упорядоченный по строкам и столбцам. Итак, в следующем коде мы будем инициализировать различные типы матриц.
Обычно матрица создается с помощью функции numpy.matix(). Мы можем использовать numpy.shape, чтобы узнать размер матрицы. Смотрите следующий пример кода матрицы.
Вы получите результат, как на следующем изображении.
Добавление матрицы
Код для сложения матриц достаточно сложен для написания вручную. Благодаря модулю numpy мы можем просто использовать оператор + для добавления матрицы. Итак, в следующем примере кода мы увидим, как писать код сложения вручную, а также с помощью оператора +.
Умножение и транспонирование матриц, обратная матрица
В предыдущем разделе мы обсудили преимущество Python Matrix в том, что он просто упрощает для нас задачу. Таким образом, мы можем просто умножить две матрицы, получить инверсию и транспонирование матрицы.
Как мы видели ранее, оператор + добавляет две матрицы, здесь мы можем просто использовать оператор * для умножения матриц. При этом количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.
Мы можем получить инверсию матрицы, используя функцию getI() и использовать getT() для транспонирования матрицы. Давайте посмотрим на пример:
Поскольку мы использовали случайные значения. Таким образом, элементы матрицы будут разными. Вывод вышеуказанного кода приведен ниже:
Вывод вышеуказанного кода приведен ниже:
«Обратная матрица» для студентов 2 курса СПО
Дисциплина – «Элементы высшей математики»
Курс -2
Практическая работа
Тема: «Обратная матрица»
Цель: формирование умений вычислять обратные матрицы;
закрепление умений вычислять определители второго и третьего порядков, составлять и вычислять алгебраические дополнения к элементам матрицы.
формирование общих компетенций, включающими в себя способность:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях.
ОК 6. Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.
Методические указания и теоретические сведения к практической работе
Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
А зачем нужно искать обратную матрицу?
Ели обратная матрица известна, то решение системы уравнений сводится к операции простого умножения матриц. При программировании задач 3D-графики и компьютерных игр обратные матрицы также находят широкое применение.
Матрица называется обратной по отношению к квадратной матрице A, если выполнено условие , где E – единичная матрица, порядок которой равен порядку матрицы A.
Невырожденная матрица – матрица, определитель которой не равен нулю. Вырожденная матрица – матрица, определитель которой равен нулю.
Обратная матрица существует тогда и только тогда, когда матрица A – невырожденная. Если обратная матрица существует, то она единственная.
Если обратная матрица существует, то она единственная.
Метод присоединённой (союзной) матрицы
Найти определитель матрицы A и убедиться, что ΔA≠0, т.е. что матрица А – невырожденная.
Составить алгебраические дополнения каждого элемента матрицы A и записать матрицу из найденных алгебраических дополнений.
Записать обратную матрицу по формуле
Матрица называется присоединённой (взаимной, союзной) к матрице A.
Союзной или присоединенной к матрице A называют матрицу , которая получается из матрицы A, если все ее элементы заменить соответствующими алгебраическими дополнениями и к полученной матрице применить операцию транспонирования. (Присоединенная матрица – это транспонированная матрица, составленная из алгебраических дополнений к элементам данной матрицы)
Пример 1.
Найти обратную матрицу к матрице
Решение. Вычисляем определитель матрицы:
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица к матрице находится по формуле:
Найдем (присоединенную) союзную матрицу , для этого вычислим алгебраические дополнения к элементам матрицы :
Таким образом, – матрица, составленная из алгебраических дополнений к элементам матрицы .
Итак, ,
Ответ:
Дисциплина – «Элементы высшей математики»
Курс -2
Практическая работа
Тема: «Обратная матрица»
Задание 1. Найти , если: а) ; б) .
Найти , если: а) ; б) .
Задание 2. Выполните проверку для задания 1.
Указание. Используйте формулу:
Задание 3. Докажите равенство для матриц из задания 1.
Задание 4. Определите, при каких x значениях существует матрица, обратная данной:
а)
; б) .
Задание 5. Показать, что матрица А является обратной для матрицы В, если:
а)
а) , .
б) .
Задание 6. Найти , если: а) ; б) /
Задание 7. Выполните проверку для матриц из задания 6.
Отчет о практической работе
1.Тема практической работы
2.Цель практической работы
3. Умения
Умения
В ходе выполнения практической работы я научился (закрепил умения) вычислять…
Я получил (совершенствовал) практические навыки…
4.Знания
5.Выводы
Мне было сложно выполнять…, потому, что…
Мне было несложно выполнять…, потому, что…
Теоретические вопросы
1.Вырожденные и невырожденные матрицы
2.Присоединенная (союзная) матрица
3.Обратная матрица
4.Алгоритм нахождения обратной матрицы
Опубликовано в группе «УРОК.РФ: группа для участников конкурсов»
| a=[[7,2,0],[3,1,0],[1,1,1]] | |
| b=[[0,2,3],[1,0,-2],[3,1,1]] | |
| # !/usr/bin/python | |
| # -*- coding: CP866 -*- | |
| # Нахождение обратной матрицы, и Детерминанта, примеры на Python | |
| import math # подключаем модуль математических функций | |
| def determinant(dim, data): # функция вычисления детерминанты | |
| if dim == 0: | |
| det = 0 | |
| if dim == 1: | |
| det = data[0] | |
| if dim == 2: | |
| det = data[0] * data[3] — data[2] * data[1] | |
| if dim == 3: | |
| det = data[0] * data[4] * data[8] + data[1] * data[5] * data[6] + data[2] * data[3] * data[7] — data[6] * data[ | |
| 4] * data[2] — data[7] * data[5] * data[0] — data[8] * data[3] * data[1] | |
| if dim > 3: | |
| det = 0 | |
| i = 0 | |
| for j in range(dim): | |
| det += data[i * dim + j] * cofactor(dim, data, i, j) | |
| return det | |
| def minor(dim, data, i, j): | |
| new_matrix = [] | |
| for k in range(dim * dim): | |
if (math. floor(k / dim) != i and k % dim != j): floor(k / dim) != i and k % dim != j): | |
| new_matrix.append(data[k]) | |
| return determinant(dim — 1, new_matrix) | |
| def cofactor(dim, data, i, j): # функция вычисления кофактора | |
| return math.pow(-1, i + j) * minor(dim, data, i, j) | |
| def cofactor_matrix(dim, data): # функция вычисления кофакторной матрицы | |
| new_matrix = [] | |
| for i in range(dim): | |
| for j in range(dim): | |
new_matrix. append(cofactor(dim, data, i, j)) append(cofactor(dim, data, i, j)) | |
| return new_matrix | |
| def transpose_matrix(dim, data):#транспонирование | |
| new_matrix = [] | |
| for i in range(dim): | |
| for j in range(dim): | |
| new_matrix.append(data[j * dim + i]) | |
| return new_matrix | |
| def adjoint_matrix(dim, data):#союзная матрица | |
| return transpose_matrix(dim, cofactor_matrix(dim, data)) | |
| matix = [[2, 2, 1, 2, 5], [1, 3, 3, 1, 3], [1, 2, 2, 1, 3], [4, 2, 2, 3, 8], [1, 5, 2, 1, 1]] # Пример матрицы | |
| matix = a | |
| data = [] # создаем пустую матрицу | |
| for i in range(len(matix)): # создаем счетчик итераций на основе размера матрицы matix | |
| for j in range(len(matix)): # создаем счетчик итераций на основе размера матрицы matix | |
| data = data + [matix[i][j]] # переводим квадратную матрицу matix в плоскую | |
| dim = len(matix) # размер матрицы | |
| dim2 = dim * dim # находим квадрат | |
| det = determinant(dim, data) # находим детерминанту | |
| print( | |
| ‘Детерминант: |A| =: ‘, det # | |
| ) | |
| print() | |
| print( | |
| ‘Обратная матрица : ‘) | |
| print() | |
| if det != 0: # если матрица имеет детерминант не равный нулю | |
| adj_matrix = adjoint_matrix(dim, data) # находим значение строк матрицы | |
| for n in range(dim2): # создаем счетчик итерации | |
| cs = int((adj_matrix[n]) / det) # находим значение ячейки матрицы | |
| if cs < 0: # условие при котором значение меньше нуля | |
| pr = » » # 3 пробела для форматирования | |
| else: # иначе | |
| pr = » » # 4 пробела для форматирования | |
| g = pr + str(cs) + » » # конкатинация пробелов и значения ячейки матрицы | |
| print( | |
| g), # выводим значение переменной g | |
| if (n % dim == dim — 1): # | |
| print () # пустая строка | |
| else: # иначе | |
| print( | |
| ‘Это вырожденная матрица, обратную матрицу найти невозможно’ ) # выводим сообщение о том что матрица вырождена |
Математика — Квадратный корень из матрицы
Поскольку квадратный корень из общей матрицы сложен, мы сначала попробуем несколько более простых случаев:
Корень из диагональной матрицы диагонали равны нулю.

В этом случае результат прост, мы просто берем корни отдельных диагональных членов.
| квадратный корень из: |
| = |
|
Корень симметричной матрицы
Симметричная матрица – это матрица, члены которой симметричны относительно диагональной оси, то есть элемент x ij имеет то же значение, что и элемент x ji
Для симметричной матрицы мы можно повернуть его, чтобы получить диагональную матрицу, затем взять корень диагональной матрицы, как указано выше, а затем повернуть ее обратно к исходным координатам. Эта матрица вращения является собственной матрицей или ортонормированным базисом [A], другими словами:
Эта матрица вращения является собственной матрицей или ортонормированным базисом [A], другими словами:
[D] = [Q] -1 [A] [Q]
где:
- [D] = диагональная матрица, диагональные члены являются собственными векторами A
- [A] = Симметричная матрица
- [Q] = Ортогональная матрица, столбцы являются собственными векторами A
- [Q] -1 = инверсия [Q]
Для получения дополнительной информации о диагонализации матриц см. эту страницу.
Таким образом, чтобы найти квадратный корень из [A], мы используем:
√[A] = [Q] √[D] [Q] -1
Пример
Мы хотим найти квадратный корень из:
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Программа
Существует ряд программ компьютерной алгебры с открытым исходным кодом. Я использовал Axiom, как установить Axiom здесь.
Я использовал Axiom, как установить Axiom здесь.
Я выделил красным цветом пользовательский ввод:
(1) -> m := matrix[[1,0,0],[0,1,0],[0,0,1]]
+1 0 0+
| |
(1) |0 1 0|
| |
+0 0 1+
Тип: Матрица (Целое число)
(2) -> собственные значения (м)
(2) [1]
Тип: Список (Союз (Дробь (Полином (Целое))),
ТакойЧто(Символ,Полином(Целое число))))
(3) -> собственные векторы (м)
+0+ +0+ +1+
| | | | | |
(3) [[eigval= 1,eigmult= 3,eigvec= [|0|,|1|,|0|]]]
| | | | | |
+1+ +0+ +0+
Тип: Список (Запись (eigval: Union (Дробь (Полином (Целое))),
Такой(Символ,Полином(Целое)))),
eigmult: NonNegativeInteger, eigvec:
Список(Матрица(Дробь(Многочлен(Целое))))))
(4) -> собственная матрица (m)
+1 0 0+
| |
(4) |0 1 0|
| |
+0 0 1+
Тип: Union(Matrix(Expression(Integer)),. |
Итак, в этом примере
√[A] = [Q] √[D] [Q] -1
| квадратный корень из: |
| = |
|
|
|
| что дает: |
| или |
|
, поскольку √1 = ±1
Однако этот метод, похоже, не находит других возможных корней, таких как: |
| или |
|
Они также возводятся в соответствие с требуемым значением, как мы можем видеть здесь:
(5) -> a := matrix[[0,0,1],[0,1,0],[1, 0,0]]
+0 0 1+
| |
(5) |0 1 0|
| |
+1 0 0+
Тип: Матрица (Целое число)
(6) -> а*а
+1 0 0+
| |
(6) |0 1 0|
| |
+0 0 1+
Тип: Матрица (Целое число)
(7) ->
|
Таким образом, в этом случае мы можем переупорядочить собственные векторы, чтобы сформировать другую собственную матрицу, но не все порядки являются корнями, например, это не соответствует требуемому значению:
(7) -> b := матрица [[0,0,1],[1,0,0],[0,1,0]]
+0 0 1+
| |
(7) |1 0 0|
| |
+0 1 0+
Тип: Матрица (Целое число)
(8) -> б*б
+0 1 0+
| |
(8) |0 0 1|
| |
+1 0 0+
Тип: Матрица (Целое число)
(9) ->
|
Корень общей матрицы
Я еще не придумал, как это сделать.
Оплачивайте счета через Интернет, лично и по телефону
От оплаты автомобиля до оплаты коммунальных услуг и ипотеки — оплата счетов через Western Union выполняется быстро, удобно и надежно, независимо от того, как вы решите платить.
Начать
Пригласи друга!
Вы оба получите электронный подарочный код Amazon.com на 20 долларов * .
Принять условия.
Подробнее
Простые шаги для онлайн-оплаты счетов
1
Зарегистрируйтесь и подтвердите свой бесплатный профиль
Войдите или Зарегистрируйтесь и подтвердите свой бесплатный профиль, чтобы оплачивать счета онлайн. Вы можете подтвердить свой профиль, используя водительские права США, паспорт или удостоверение личности государственного образца.
2
Найдите своего биллера
Найдите своего биллера, введя имя. От вашей ипотеки до счета за воду наша сеть, скорее всего, покроет вас.
3
Заполните обязательные поля
Просто укажите номер своего счета и сумму, которую вы хотите оплатить в счет.
4
Выберите безопасный способ оплаты
Наши услуги по оплате счетов позволяют удобно оплачивать кредитной/дебетовой картой 1 .
5
Готово! Счет оплачен
Мы вышлем вам электронное письмо с подтверждением и контрольным номером денежного перевода (MTCN) вашей транзакции для ваших записей.
Готов оплатить счета?
Начало работы
Дополнительные способы оплаты счетов с помощью Western Union
Оплачивайте счета на ходу
Оплачивайте счета в любое время и в любом месте с помощью приложения Western Union ® .
Загрузите приложениеПроизведите платеж лично
Посетите одно из 55 000 отделений агентов в США 2 , чтобы оплатить счет. Начните с приложения, и вы сможете сэкономить время при оплате в магазине — никаких форм для заполнения.
Поиск локацийОплатить по телефону
Нужно оплатить счет сейчас? Позвоните по номеру 1-800-634-3422 со своего домашнего или мобильного телефона и оплатите кредитной/дебетовой картой 1 .
Зарегистрируйтесь, чтобы начать оплачивать счета сегодня
Зарегистрируйтесь сейчасБыстрая и простая регистрация
Все, что вам нужно, это действующий адрес электронной почты и номер мобильного телефона, чтобы начать оплачивать счета через приложение , на WU.com или лично сегодня.
Отслеживание платежей
Мы предоставляем электронное письмо с подтверждением или квитанцию с номером отслеживания вашей транзакции.
Оплачивайте как вам удобно
Оплачивайте счета с помощью кредитной/дебетовой карты 1 онлайн или наличными в магазине.
Удобное расположение
Оплачивайте счета лично в ближайшем отделении Western Union ® .
Зарегистрируйтесь сейчас
Оплачивайте счета быстро в нашем приложении
Оплачивайте счета или начните оплачивать счета и оплачивайте в магазине.
Отслеживайте свои платежи в режиме реального времени.
Touch ID экономит ваше время благодаря быстрому входу в систему.
Отсканируйте QR-код, чтобы загрузить приложение WU.
Рейтинг на 15 сентября 2020 г.
Часто задаваемые вопросы об оплате счетов с помощью Western Union
Как оплачивать счета с помощью приложения Western Union ® ?
1. Если у вас уже есть приложение Western Union ® , войдите в систему, используя Touch ID или свои учетные данные. Если у вас еще нет нашего приложения, просто загрузите его в Apple App Store или Google Play Store. Новые пользователи могут выполнить шаги, чтобы зарегистрировать профиль с вашим адресом электронной почты. Вы можете подтвердить свой профиль, используя водительские права, паспорт или удостоверение личности государственного образца.
2. Когда вы войдете в наше приложение, выберите «Оплатить счета» и найдите своего биллера, введя его имя.
3. Укажите номер своего счета и сумму, которую вы хотите оплатить по счету.
4. Введите данные своей кредитной/дебетовой карты1.
5. Мы отправим вам электронное письмо с подтверждением и контрольным номером денежного перевода (MTCN) вашей транзакции для вашего учета.
Скачать приложение
Как оплачивать счета лично?
1. Найдите ближайшее отделение Western Union®.
2. Подойдите прямо к стойке и сообщите свой номер телефона, название компании, которую вы хотите оплатить, и номер вашего счета.
3. Оплата наличными или дебетовой картой, выпущенной банком США.
4. Мы отправим вам электронное письмо с подтверждением и контрольным номером денежного перевода (MTCN) вашей транзакции для вашего учета.
Ближайшее отделение Western Union®
Как оплачивать счета по телефону?
1. Позвоните по номеру 1-800-634-3422 (для испанского языка 1-800-325-4045) со своего домашнего или мобильного телефона. Нельзя пользоваться таксофоном.
Нельзя пользоваться таксофоном.
2. Следуйте инструкциям по оплате по телефону. Вам понадобится номер счета, указанный в выписке по счету.
3. Оплатите счет кредитной/дебетовой картой1, выпущенной банком в США.
4. Мы предоставим вам номер для отслеживания (MTCN). Сохраните это как подтверждение платежа.
Остались вопросы?
Свяжитесь с нашей службой поддержки клиентов или посетите нашу страницу часто задаваемых вопросов для получения дополнительной информации.
1 Если вы используете кредитную карту, может взиматься комиссия эмитента карты за выдачу наличных и соответствующие проценты. Чтобы избежать этих комиссий или снизить комиссию, используйте дебетовую карту или проверьте другие способы оплаты.
2 Данные сети по состоянию на 30 июня 2020 г.
* Применяются положения и условия. Применяются ограничения, см. amazon.com/gc-legal
Ассоциативные свойства матриц
Горячая математика Ассоциативное свойство сложения матриц. состояния :
состояния :
Позволять А , Б а также С быть м × н матрицы . Затем, ( А + Б ) + С знак равно А + ( Б + С ) .
Пример 1:
А знак равно [ 3 2 4 − 1 0 − 5 ] , Б знак равно [ − 2 3 − 1 4 2 0 ] , С знак равно [ 8 − 1 5 6 1 2 ]
Находить ( А + Б ) + С а также А + ( Б + С )
Находить ( А + Б ) + С :
( [ 3 2 4 − 1 0 − 5 ] + [ − 2 3 − 1 4 2 0 ] ) + [ 8 − 1 5 6 1 2 ] знак равно [ 1 5 3 3 2 − 5 ] + [ 8 − 1 5 6 1 2 ] знак равно [ 94 8 9 3 − 3 ]
Находить А + ( Б + С ) :
[ 3 2 4 − 1 0 − 5 ] + ( [ − 2 3 − 1 4 2 0 ] + [ 8 − 1 5 6 1 2 ] ) знак равно [ 3 2 4 − 1 0 − 5 ] + [ 6 2 4 10 3 2 ] знак равно [ 94 8 9 3 − 3 ]
Ассоциативное свойство умножения матриц состояния:
Позволять
А
,
Б
а также
С
быть
н
×
н
матрицы. Затем,
(
А
Б
)
С
знак равно
А
(
Б
С
)
.
Затем,
(
А
Б
)
С
знак равно
А
(
Б
С
)
.
Пример 2:
А знак равно [ 3 2 − 1 0 ] , Б знак равно [ − 2 3 4 2 ] , С знак равно [ − 1 5 1 2 ]
Находить
(
А
Б
)
С
а также
А
(
Б
С
)
.

 ..)
(5) ->
..)
(5) ->