Конспект урока по Геометрии «Средняя линия трапеции» 8 класс
Тема: «Средняя линия трапеции»
Цели урока:
1. Изучить понятие средней линии трапеции, доказательство свойства средней линии, учить применять теорему в нестандартных ситуациях при решении задач.
2. Формировать умение учащихся анализировать, обобщать, использовать элементы исследования, сравнения.
3. Развивать логическое мышление, воспитывать культуру математической речи
Ход урока:
1. Организационный момент
Ребята, послушайте, какая тишина!
Это в школе начались уроки.
Мы не будем тратить время зря,
И приступим все к работе.
Мы сюда пришли учиться,
Не лениться, а трудиться.
Работаем старательно,
Слушаем внимательно.
2. Мотивация урока.
Сегодня мы продолжим путешествие по прекрасной стране Геометрия.
Лучше разглядим ее красоту и совершенство. Девизом нашего урока будет: «С любовью к ее величеству — науке геометрии».
3. Актуализация опорных знаний. Проверка д/з.
1. Что называется средней линией треугольника?
2. Посмотрите на рисунок №1.
Отрезок МК – средняя линия треугольника АВС. Найдите длину отрезка МК, если АС равно 8 см.
Объясните почему?
Решим обратную задачу:
Длина отрезка МК равна 5 см. Чему равна длина стороны АС?
Объясните почему?
3. Придумайте сами задачу на нахождение средней линии треугольника.
4. Сформулировать свойство средней линии треугольника.
5. Стороны треугольника равны 2см, 4см и 6см. Чему равны средние линии этого треугольника?
3. Изучение нового материала.
Какой четырехугольник называется трапецией?
Назовите их основания и боковые стороны.
Свойства равнобедренной трапеции:
Углы при основании равны.
Диагонали равны.
Сумма противоположных углов равна 180º.
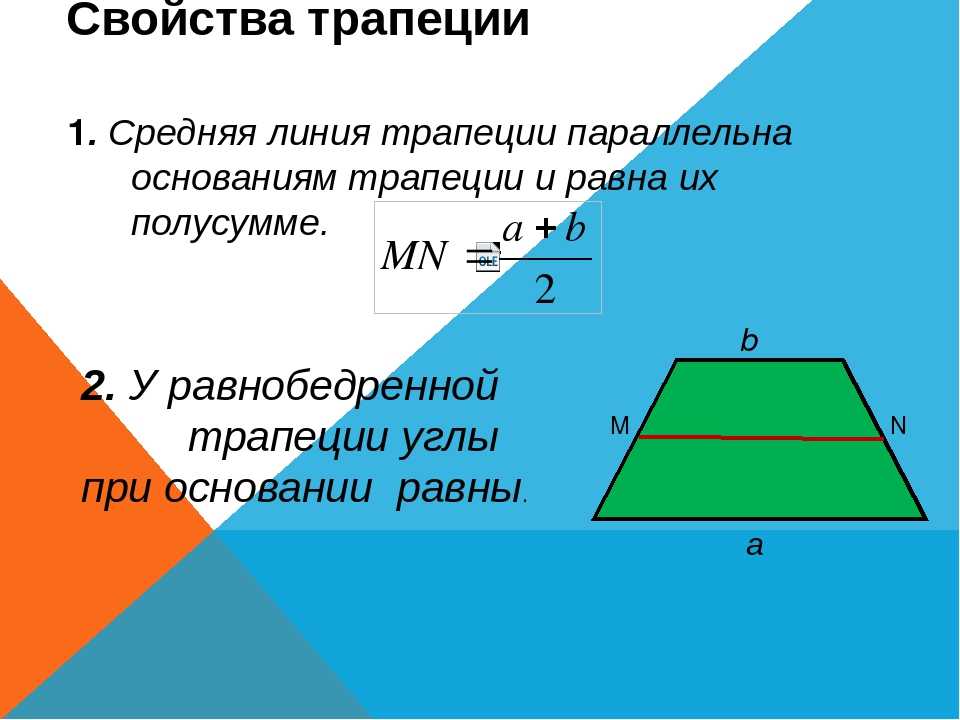
Введём понятие средней линии трапеции:
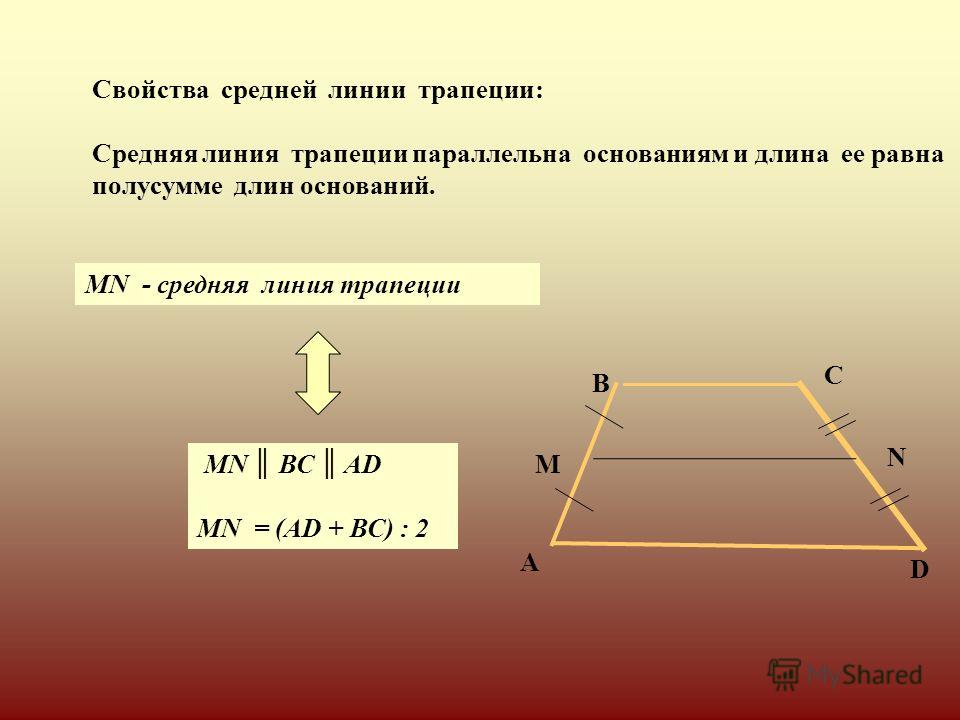
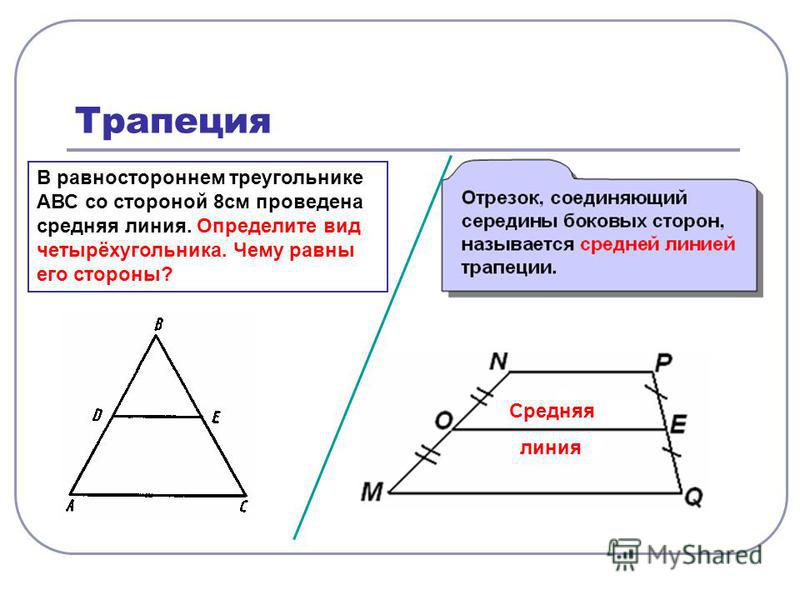
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
(В тетрадях учащиеся выполняют построения)
1) Верно ли определение: отрезок, соединяющий середины двух сторон трапеции, является средней линией? (Нет, отсутствует слово боковых сторон).
2) А сколько средних линий можно построить в трапеции? (Только одну).
3) Каким свойством обладает средняя линия трапеции? Измерьте основания трапеции и длину средней линии. Чему равна средняя линия? (Половине суммы оснований).
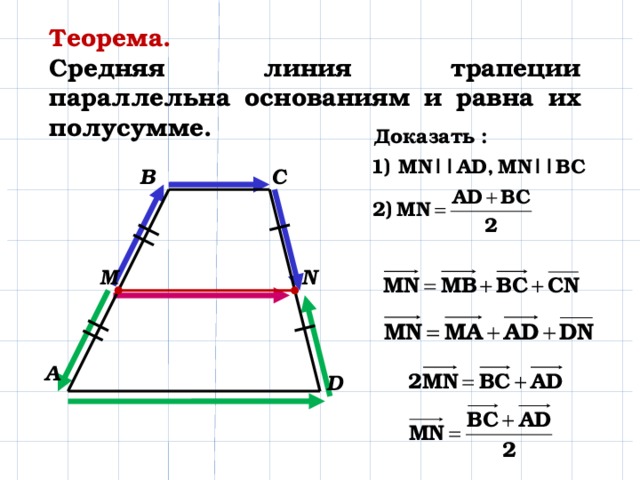
Попробуем доказать это свойство.
5. Закрепление нового материала.
6. Физкультминутка
Раз – потянуться
Два – нагнуться
Три – оглянуться
Четыре – присесть
Пять – руки вверх
Шесть – вперед
Семь – опустили
Восемь – сели
Девять – встали
Десять – снова сели
7.
Самостоятельная работа учащихся.
Работа в парах:
8. Подведение итогов урока. Д/з.
Рефлексия:
Наше занятие подходит концу. Пожалуйста, поделитесь с нами своими мыслями о сегодняшнем занятии (хотите одним предложением).
Вам для этого помогут слова:
-Я узнал…
-Я почувствовал…
-Я увидел…
-Я сначала испугался, а потом…
-Я заметил, что …
-Я сейчас слушаю и думаю…
-Мне интересно следить за…
Урок по теме «Средние линии треугольника и трапеции»
| Предмет: | Математика |
|---|---|
| Категория материала: | Конспекты |
| Автор: | Лиманская Инна Викторовна это Вы? |
Цели.
Обобщить и систематизировать изученный материал. Применять определения и свойства средних линий треугольника и трапеции при решении задач. Развивать внимание, познавательную активность, творческие способности. Воспитывать интерес к предмету.
Ход урока
І. Орг. момент
ІІ. Актуализация опорных знаний
1. Что называется средней линией треугольника?
2. Является ли отрезок МК средней линией треугольника АВС?
а)В
3 6
МК
6
4
А С
б)
В
5
М4
5
К
А
4
С
3. DЕ и КЕ – средние линии треугольника АВС. Является ли отрезок KD средней линией треугольника АВС?
В
ЕК
А DС
4. Сформулировать свойство средней линии треугольника.
5. Стороны треугольника равны 2см, 4см и 6см. Чему равны средние линии этого треугольника?
6. Найти периметр треугольника АВС.
В
К7Р
6 5
АМС
7. Какой четырехугольник называется трапецией?
8.
Какие четырехугольники являются трапециями? Назовите их основания и боковые стороны.
а)
В
С
ОDА
б)В
MON
АF C
9. Что называется средней линией трапеции?
10. Сформулировать свойство средней линии трапеции.
11. Найти х.
а) В5 С
=
М хК
=
АD
15
б)В6С
=
М8К
=
Ах D
12. В равностороннем треугольнике АВС со стороной 10см проведена средняя линия КЕ. Определить вид четырехугольника АКЕС. Чему равны стороны этого четырехугольника?
В
КЕ
АС
13. В5С
Е? H
М?N
F? Q
А 9 D
В
2
МR
EF
?
A C
ІІІ. Решение задач
1. Средняя линия трапеции делится диагоналями на три равные части. Найти большее основание трапеции. Если ее меньшее основание равно 6см.
2. В прямоугольной трапеции большее основание равно 21см. Высота, проведенная из вершины тупого угла, делит среднюю линию на отрезки, длины которых относятся как 3:2, считая от меньшей боковой стороны.
3. Средняя линия трапеции равна 11см, а высоты, проведенные из вершин тупых углов, делят боль шее основание на отрезки, длины которых относятся как 1:4:2. Найти основания трапеции.
ІV. Домашнее задание
Составить три задачи по готовым чертежам.
V. Итог урока
| Тип материала: | Документ Microsoft Word (docx) |
|---|---|
| Размер: | 26.03 Kb |
| Количество скачиваний: | 26 |
Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.
Теоремы о средней линии, трапеции и воздушные змеи — Дано: ∆HNS, O — середина HN, а E — середина
LAS по математике 9
Неделя 3 — Теоремы о средней линии, трапеции и воздушные змеи
Теорема о средней линии — соединяющий отрезок середины двух сторон треугольника параллельны третьей стороне и вдвое короче.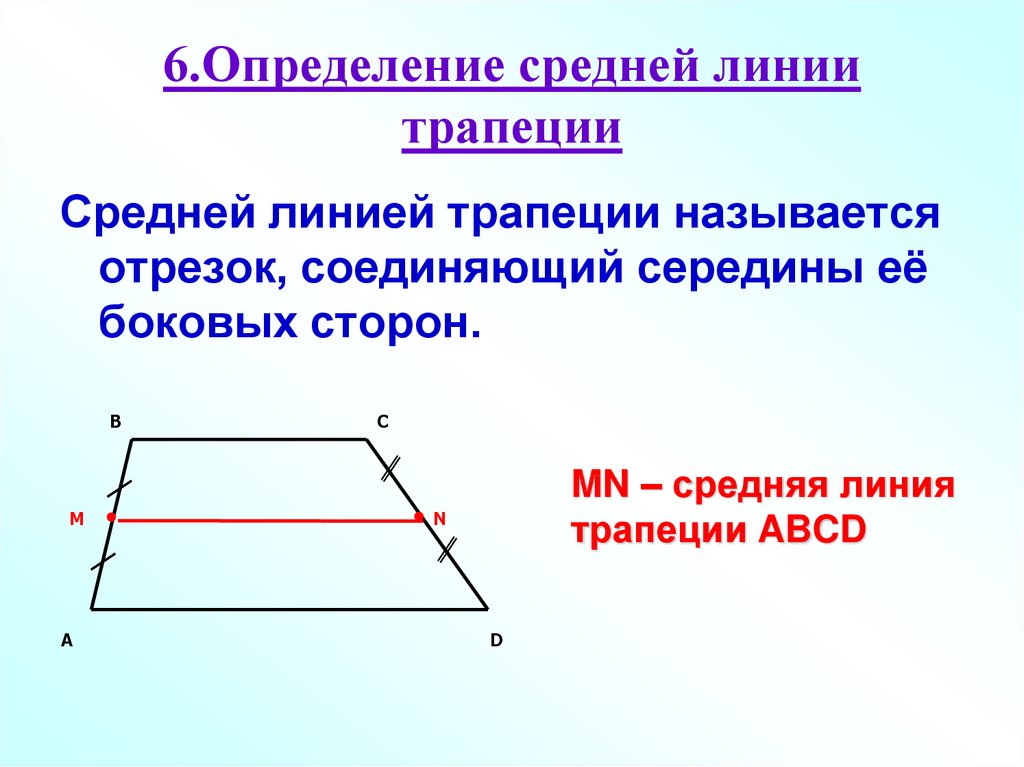
Дано: ∆HNS, O — середина HN, а E — середина NS
Докажите: OE//HS и OE=12HS
Утверждения
Обоснования
1. ∆HNS, O — середина HN, а E — середина
NS
2. В OE есть точка T такая, что OE≅ET
Постулат линии
3. NE≅ES
Определение средней точки
4. ♂2≅ В3
Теорема вертикальных углов
5. ∆Neo≅∆Set
SAS Postulate
6. ♂1≅ £
7. HN // ST.
Теорема обращения внутренних внутренних углов
8. OH≅ON
Определение середины
9. ON≅TS
10. OH≅TS
Переходное свойство
11. Четырехугольник HOTS является параллелограммом
Если противоположные стороны четырехугольника равны и параллельны, то он является
параллелограммом.
12. OE // HS
Определение параллелограммы
13. OE+ET = OT
Добавление сегмента Постулат
14. OE+OE = OT
Свойство замены
15. 2OE = OT
Дополнение Свойство
16.
HS≅OT
В параллелограмме любые две противоположные стороны равны.
17. 2OE=HS
Подстановочное свойство
18. OE=12HS
Делим обе стороны на два
Определение трапеции – четырехугольник с одной парой параллельных сторон.
Теорема о средней линии трапеции. Медиана трапеции параллельна каждому основанию, а ее длина составляет половину суммы длин
оснований.
Дано: Трапеция МИНС с медианой
TR, пересекающая диагональ IS в точке P.
Доказать: MS//TR//IN и TR=12(MS+IN)
Утверждения
Причины
1. Трапеция МИНС с медианой TR, пересекающая диагональ IS at P.
2. TP+PR=TR
Постулат сложения сегментов
3. TP//MS и TP=12MS RP//IN и RP=12IN
Теорема средней линии
4. MS//IN
Определение трапеции
5. MS//TP+RP//IN
Переходное свойство
6. MS//TR//IN
Свойство сложения
7. TR=12MS+12IN
Свойство замещения
8.
TR=12(MS+IN)
Разложение на множители
Определение равнобедренной ловушки трапеция, противоположные стороны которой равны.
Свойства равнобедренной трапеции
• Углы при основании равнобедренной трапеции равны.
Дано: равнобедренная трапеция AMOR с
MO//AR
Докажите: ∠A≅∠R и ∠AMO≅∠O
Заявления
Причины
1. Равнобедренная трапеция АМОР с МО//АР.
2. AM≅OR
Определение равнобедренной трапеции
3. Из M провести ME//OR, где E лежит на AR
Две точки определяют прямую
4. Четырехугольник MORE является параллелограммом
Определение Параллелограмм
5. ME≅OR
В параллелограмме любые две противоположные стороны равны
.
6. MA≅ME
Переходное свойство
7. ∆AME — равнобедренный треугольник
Определение равнобедренного треугольника
8. ∠A≅∠1
Углы при основании равнобедренных треугольников равны.
9.
∠1≅∠R
Теорема о соответствующих углах
10. ∠A≅∠R
Свойство переходности
11. ∠A и ∠AMO — дополнительные углы. ∠O и ∠R являются дополнительными
углами.
Теорема об одностороннем внутреннем угле
Свойства равнобедренной трапеции – Математика Blow the Blowfish
Добро пожаловать в четвертую часть второго урока «Свойства равнобедренной трапеции!» После прочтения этого урока вы должны использовать свойства равнобедренной трапеции для решения задач по геометрии и применять определение равнобедренной трапеции. и теоремы о свойствах равнобедренных трапеций. Прежде чем мы перейдем к свойствам равнобедренной трапеции, давайте сначала обсудим теорему о среднем отрезке трапеции.
ПРЕДВАРИТЕЛЬНЫЙ ТЕСТ
Что за ловушка!
Выполните описанную ниже процедуру и ответьте на следующие вопросы.
Материалы: высокосортная бумага, карандаш, линейка и транспортир
Процедура:
1.
Нарисуйте трапецию TRAP, где TRP ⊥ PA, TP = 5 см, TR = 4 см и PA = 8 см.
2. Обозначьте середины TP и RA как G и O соответственно.
3. Соедините G и O, чтобы сформировать сегмент.
Вопросы:
• Смотрит ли ГО параллельно основаниям трапеции?
• Измерить GO. Как долго это?
• Какова сумма оснований TRAP?
• Сравните сумму оснований и длину GO. Что ты нашел?
Теорема 6
- Медиана трапеции параллельна каждому основанию трапеции и ее длина равна половине суммы длин оснований трапеции.
Пример:
Трапеция MINS имеет медиану TR. Является ли TR||IN и TR||MS? Да, потому что по теореме 6 медиана трапеции параллельна каждому основанию трапеции. IN и MS — основания данной трапеции выше.
TR = 1/2(MS + IN)? Да, потому что согласно теореме 6 медиана трапеции равна половине суммы длин оснований трапеции.
* Медиана – отрезок, соединяющий середины катетов трапеции.
Теперь приступим к собственно уроку.
Теоремы о равнобедренной трапеции
Теорема 7
- Углы при основании равнобедренной трапеции равны.
Пример:
Равнобедренная трапеция AMOR. ∠A ≅ ∠R? Да, потому что по теореме 7 углы при основании равнобедренной трапеции равны.
Является ли ∠M ≅ ∠O? Да, потому что по теореме 7 углы при основании равнобедренной трапеции равны.
Теорема 8
- Противоположные углы равнобедренной трапеции дополнительные.
Пример:
Равнобедренная трапеция ARTS. Являются ли ∠R и ∠S дополнительными? Да, потому что согласно теореме 8 противолежащие углы равнобедренной трапеции являются дополнительными.
∠T и ∠A дополнительны? Да, потому что согласно теореме 8 противолежащие углы равнобедренной трапеции являются дополнительными.