ОГЭ 2015 математика демоверсия 9 класс | Геометрия
Добрый день, друзья!
Сегодня, когда многие из вас полностью отдаются отдыху на каникулах, мы продолжаем готовиться к предстоящим экзаменам в 2016 году.
И для этого решаем примеры и задачи из сборника ОГЭ 2015 математика демоверсия 9 класс.
Сегодня у нас на очереди задание № 1.
Дроби — простые, смешанные, неправильные, десятичные; а так же арифметические действия с ними.
Задание № 1. Вычислить значение выражения (19/12 + 11/18): 5/72.
Решение: в данном примере мы имеем дело с простыми дробями.
Сначала необходимо выполнить действие внутри скобок,
т.е. сложить две дроби с разными знаменателями.
Этому нам поможет основное свойство дроби,
которое говорит о том, что
числитель и знаменатель любой дроби можно умножить или разделить на одно и то же число, отличное от нуля.
Итак, ищем общий знаменатель для дробей 19/12 и 11/18.
Очевидно, что это будет число 36.
Поэтому, числитель и знаменатель первой дроби мы умножаем на 3,
а второй дроби — на 2.
57/36 + 22/36 = 79/36
Теперь мы должны выполнить второе действие —
деление одной дроби на другую.
Чтобы разделить дробь на дробь, необходимо вторую дробь представить в виде обратной, т.е. поменять местами числитель и знаменатель в этой дроби.
Затем произвести умножение дробей.
Числитель умножаем на числитель
и записываем в числителе произведения,
а знаменатель умножаем на знаменатель
и пишем в знаменателе произведения.
79/36 : 5/72 = 79/36 * 72/5 = 79*72/36*5 = 79*2 /5 = 158/5 = 316/10 = 31,6
Чтобы представить дробь 158/5 в виде десятичной
(а именно так необходимо писать в ответе варианта ОГЭ),
мы умножили числитель и знаменатель дроби на 2,
а затем числитель 316 разделили на 10.
Ответ: 31,6
Задание № 2. Вычислить значение выражения 0,0002•200•2000.
Решение: Любое число можно представить в виде произведения,
так называемой, мантиссы числа —
выражения, которое больше нуля, но меньше 10,
и разрядной единицы, т.
е. числа 10 в виде соответственной степени.Например, число 200 можно выразить как число 2,
умноженное на 100 или на 10².
Число 2000 выражаем как число 2, умноженное на 10³.
Попробуем таким же образом выразить число 0,0002.
На сколько его необходимо умножить,
чтобы здесь появилась мантисса (число от 0 до 9) — на 10000, или на 104
А чтобы получить число 0,0002 надо 2 умножить на 10
-4В итоге имеем: 0,0002•200•2000 = 2•10
4•2•10²•2•10³При перемножении чисел с одинаковыми основаниями,
но разными степенями, их степени складываются (-4+2+3=1),
а -основания — двойки — перемножаются.
Получаем окончательный результат: 8•10 = 80.
Ответ: 80.
Задание 3. Вычислить значение выражения (2 1/16 — 1 1/14) • 28.
Решение: Делаем то же, что и в задании № 1,
только сперва представим смешанные дроби в виде неправильных:
2 1/16 = 33/16 1 1/14 = 15/14
Теперь вычитаем из одной другую.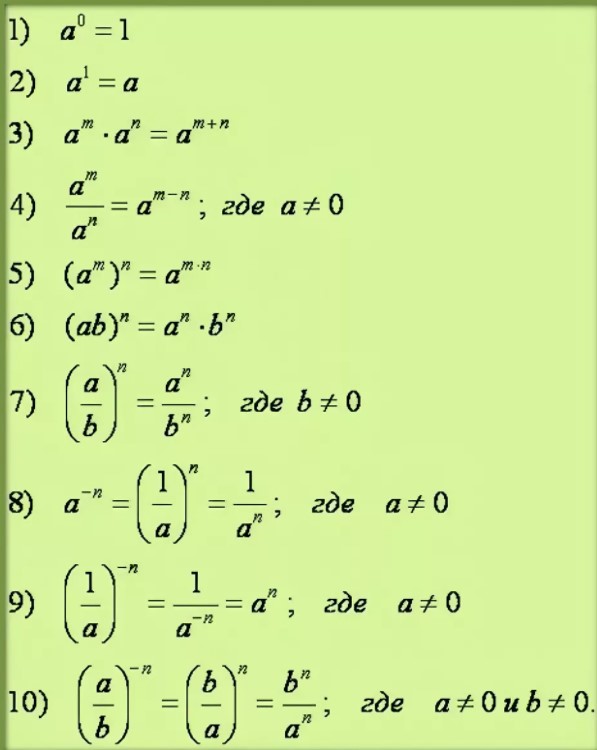
Общий множитель 112.
33/16 — 15/14 = 33*7/112 — 15*8/112 = (231 — 120)/112 = 111/112
Умножаем дробь на число:
111/112 • 28 = 111 •28/112 = 111/4 = 27,75
Ответ: 27,75
Задание № 4. Вычислить значение выражения 5,9•4,9/0,5
Решение: Перед нами десятичные дроби.
Для решения данного задания воспользуемся основным свойством дроби.
Умножим числитель и знаменатель дроби на 10 с тем,
чтобы избавиться от дроби в знаменателе.
Получим:
59•4,9/5 = 59•2•4,9/10 = 118•4,9/10 = 11,8•4,9
Для получения ответа нам осталось перемножить две десятичные дроби.
Умножаем в столбик два числа 118 и 49. Получаем 5782.
Поскольку мы перемножаем числа, у которых 2 знака после запятой,
то в результат нам необходимо внести корректировку.
А именно в число 5782 внести запятую, справа отсчитав 2 знака.
Получим 57,82.
Ответ: 57,82
Задание № 5. Вычислить значение выражения 5•10
-1 + 2•10-3 + 1•10-4Решение: это задание можно решать различными способами,
выберем один из них.
5•10-1 = 0,5
2•10-3 = 0,002
1•10-4 = 0,0001
А теперь складываем эти десятичные дроби: 0,5 + 0,002 + 0,0001 = 0,5021
Ответ: 0,5021.
Задание № 6. Вычислить значение выражения 0,2•(-3)³• — 0,1•(-3)² — 3
Решение:
во-первых — отрицательное число, возводимое в нечётную степень, останется отрицательным;
во-вторых — отрицательное число, возводимое в чётную степень,
станет положительным;
в-третьих — если перед скобкой стоит знак минус, то при раскрытии скобок, выражение, стоящее в скобке, меняет знак на противоположный.
0,2•(-27) — 0,1•(+9) — 3 = — 5,4 — 0,9 — 3.
Перед нами сумма трёх отрицательных чисел.
— общий знак выражения будет минус;
— складываем модули этих чисел 5,4 + 0,9 + 3 = 9,3
Ответ: — 9,3
На сегодня всё.
Успехов и до новых задач!
Если показатели одинаковые а основания разные. Умножение и деление чисел со степенями
В прошлом видеоуроке мы узнали, что степенью некоего основания называется такое выражение, которое представляет собой произведение основания на самого себя, взятого в количестве, равном показателю степени.
Изучим теперь некоторые важнейшие свойства и операции степеней.
Например, умножим две разные степени с одинаковым основанием:
Представим это произведение в полном виде:
(2) 3 * (2) 2 = (2)*(2)*(2)*(2)*(2) = 32
Вычислив значение этого выражения, мы получим число 32. С другой стороны, как видно из этого же примера, 32 можно представить в виде произведения одного и того же основания (двойки), взятого в количестве 5 раз. И действительно, если пересчитать, то:
Таким образом, можно с уверенностью прийти к выводу, что:
(2) 3 * (2) 2 = (2) 5
Подобное правило успешно работает для любых показателей и любых оснований. Это свойство умножения степени вытекает из правила сохранности значения выражений при преобразованиях в произведении. При любом основании а произведение двух выражений (а)х и (а)у равно а(х + у). Иначе говоря, при произведении любых выражений с одинаковым основанием, итоговый одночлен имеет суммарную степень, образующуюся сложением степени первого и второго выражений.
Представляемое правило прекрасно работает и при умножении нескольких выражений. Главное условие — что бы основания у всех были одинаковыми. Например:
(2) 1 * (2) 3 * (2) 4 = (2) 8
Нельзя складывать степени, да и вообще проводить какие-либо степенные совместные действия с двумя элементами выражения, если основания у них являются разными.
Как показывает наше видео, в силу схожести процессов умножения и деления правила сложения степеней при произведении прекрасно передаются и на процедуру деления. Рассмотрим такой пример:
Произведем почленное преобразование выражения в полный вид и сократим одинаковые элементы в делимом и делителе:
(2)*(2)*(2)*(2)*(2)*(2) / (2)*(2)*(2)*(2) = (2)(2) = (2) 2 = 4
Конечный результат этого примера не так интересен, ведь уже в ходе его решения ясно, что значение выражения равно квадрату двойки. И именно двойка получается при вычитании степени второго выражения из степени первого.
Чтобы определить степень частного необходимо из степени делимого вычесть степень делителя.
Правило работает при одинаковом основании для всех его значений и для всех натуральных степеней. В виде абстракции имеем:
(а) х / (а) у = (а) х — у
Из правила деления одинаковых оснований со степенями вытекает определение для нулевой степени. Очевидно, что следующее выражение имеет вид:
(а) х / (а) х = (а) (х — х) = (а) 0
С другой стороны, если мы произведем деление более наглядным способом, то получим:
(а) 2 / (а) 2 = (а) (а) / (а) (а) = 1
При сокращении всех видимых элементов дроби всегда получается выражение 1/1, то есть, единица. Поэтому принято считать, что любое основание, возведенное в нулевую степень, равно единице:
Вне зависимости от значения а.
Однако будет абсурдно, если 0 (при любых перемножениях дающий все равно 0) будет каким-то образом равен единице, поэтому выражение вида (0) 0 (ноль в нулевой степени) просто не имеет смысла, а к формуле (а) 0 = 1 добавляют условие: «если а не равно 0».
Решим упражнение. Найдем значение выражения:
(34) 7 * (34) 4 / (34) 11
Так как основание везде одинаково и равно 34, то итоговое значение будет иметь такое же основание со степенью (согласно вышеуказанных правил):
Иначе говоря:
(34) 7 * (34) 4 / (34) 11 = (34) 0 = 1
Ответ: выражение равно единице.
Степень с отрицательным показателем. Деление степеней с одинаковым основанием. 4. Уменьшите показатели степеней 2a4/5a3 и 2/a4 и приведите к общему знаменателю. Основание и аргумент первого логарифма — точные степени. Данное свойство распространяется на степень произведения трех и большего количества множителей. Следовательно, am−an>0 и am>an, что и требовалось доказать. Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями.
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке. То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным. Вычисление значения степени называют действием возведения в степень. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).
После того как определена степень числа, логично поговорить про свойства степени.
В этой статье мы дадим основные свойства степени числа, при этом затронем все возможные показатели степени. Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров. Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами.
Приведем пример, подтверждающий основное свойство степени. Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Основное свойство дроби позволяет записать равенство am−n·an=a(m−n)+n=am.
Переход к новому основанию
То есть, свойство натуральной степени n произведения k множителей записывается как (a1·a2·…·ak)n=a1n·a2n·…·akn. Для наглядности покажем это свойство на примере. Доказательство можно провести, используя предыдущее свойство. Например, для любых натуральных чисел p, q, r и s справедливо равенство.
Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. Достаточно очевидно, что для любого натурального n при a=0 степень an есть нуль. Действительно, 0n=0·0·…·0=0. К примеру, 03=0 и 0762=0. Переходим к отрицательным основаниям степени. Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m, где m — натуральное.
Переходим к доказательству этого свойства. Докажем, что при m>n и 0По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств. Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно. При этом условию p>q будет соответствовать условие m1>m2, что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями.
Операции с корнями. Расширение понятия степени.
До сих пор мы рассматривали степени только с натуральным показателем;нодействиясостепенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения. Если мы хотим, чтобы формула a m: a n=a m — nбыла справедлива при m = n,нам необходимо определение нулевой степени. Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать.
Вынесение показателя степени из логарифма
Если основания разные, эти правила не работают! Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств. Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.
Часто в процессе решения требуется представить число как логарифм по заданному основанию.
Свойства степеней, формулировки, доказательства, примеры.
Число n может быть абсолютно любым, ведь это просто значение логарифма. Она так и называется: основное логарифмическое тождество. Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением. В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма.
Примеры решения примеров с дробями, содержащими числа со степенями
Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице. 1 = 0 — это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a0 = 1 — это прямое следствие из определения. Вот и все свойства. Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.
Логарифмическая единица и логарифмический ноль
2.
a-4 есть a-2 первый числитель. В этом случае советуем поступать следующим образом. Это действие третьей ступени. Например, основное свойство дроби am·an=am+n при упрощении выражений часто применяется в виде am+n=am·an. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0n=0, а при знакомстве с делением мы условились, что на нуль делить нельзя. Из полученного равенства am−n·an=am и из связи умножения с делением следует, что am−n является частным степеней am и an. Этим доказано свойство частного степеней с одинаковыми основаниями.
Аналогично, если q=0, то (ap)0=1 и ap·0=a0=1, откуда (ap)0=ap·0. В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. Эти неравенства по свойствам корней можно переписать соответственно как и. А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно.
Деление степеней с одинаковым основанием.
Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями.
3.a-3 есть a0 = 1, второй числитель. В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. Теперь рассмотрим их на конкретных примерах и попробуем доказать.
Таким образом мы доказали, что при делении двух степеней с одинаковыми основаниями, их показатели надо вычитать. После того как определена степень числа, логично поговорить про свойства степени.
Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров. Например, основное свойство дроби am·an=am+n при упрощении выражений часто применяется в виде am+n=am·an. Приведем пример, подтверждающий основное свойство степени. Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке.
Свойства степеней с натуральными показателями
Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Из полученного равенства am−n·an=am и из связи умножения с делением следует, что am−n является частным степеней am и an. Этим доказано свойство частного степеней с одинаковыми основаниями. Для наглядности покажем это свойство на примере. Например, для любых натуральных чисел p, q, r и s справедливо равенство. Для большей ясности приведем пример с конкретными числами: (((5,2)3)2)5=(5,2)3+2+5=(5,2)10.
Сложение и вычитание одночленов
Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. Достаточно очевидно, что для любого натурального n при a=0 степень an есть нуль. Действительно, 0n=0·0·…·0=0. К примеру, 03=0 и 0762=0. Переходим к отрицательным основаниям степени. Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m, где m — натуральное.
Переходим к доказательству этого свойства. Докажем, что при m>n и 0Осталось доказать вторую часть свойства. Следовательно, am−an>0 и am>an, что и требовалось доказать. Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами.
Если p=0, то имеем (a0)q=1q=1 и a0·q=a0=1, откуда (a0)q=a0·q. По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств. Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно.
При этом условию p>q будет соответствовать условие m1>m2, что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Эти неравенства по свойствам корней можно переписать соответственно как и. А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно.
Основные свойства логарифмов
Вычисление значения степени называют действием возведения в степень.
1. Если Вы теперь аккуратно воспользуетесь свойствами степеней (при возведении степени в степень показатели…
То есть показатели степени действительно вычитаются, но, поскольку в знаменателе у степени показатель отрицательный, при вычитании минус на минус даёт плюс, и показатели складываются. Вспомним, что называется одночленом, и какие операции можно делать с одночленами. Напомним, что для приведения одночлена к стандартному виду необходимо вначале получить численный коэффициент, перемножив все численные множители, а после этого перемножить соответствующие степени.
Переход к новому основанию
То есть, мы должны научиться различать подобные и не подобные одночлены. Сделаем вывод: подобные одночлены имеют одинаковую буквенную часть, и такие одночлены можно складывать и вычитать.
Спасибо Вам за отзыв. Если наш проект вам понравился и вы готовы помочь или принять участие в нём, перешлите информацию о проекте знакомым и коллегам. В предыдущем видео говорилось,что в примерах с одночленами может быть только умножение:»Найдем отличие этих выражений от предыдущих.
Само понятие одночлена как математической единицы подразумевает только умножение чисел и переменных, если есть другие операции, выражение уже не будет одночленом. Но вместе с тем между собой одночлены можно складывать, вычитать, делить… Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.
Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают! Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
То есть, свойство натуральной степени n произведения k множителей записывается как (a1·a2·…·ak)n=a1n·a2n·…·akn. Правил относительно сложения и вычитания степеней с одинаковыми основаниями не существует.
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной
сумме степеней слагаемых.Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
5}$. Ответ: $\frac{2x}{1}$ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.
Урок на тему: «Правила умножения и деления степеней с одинаковыми и разными показателями. Примеры»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
3=8$.
Экспоненциальные правила и объединение подобных членов
Экспоненциальные правила
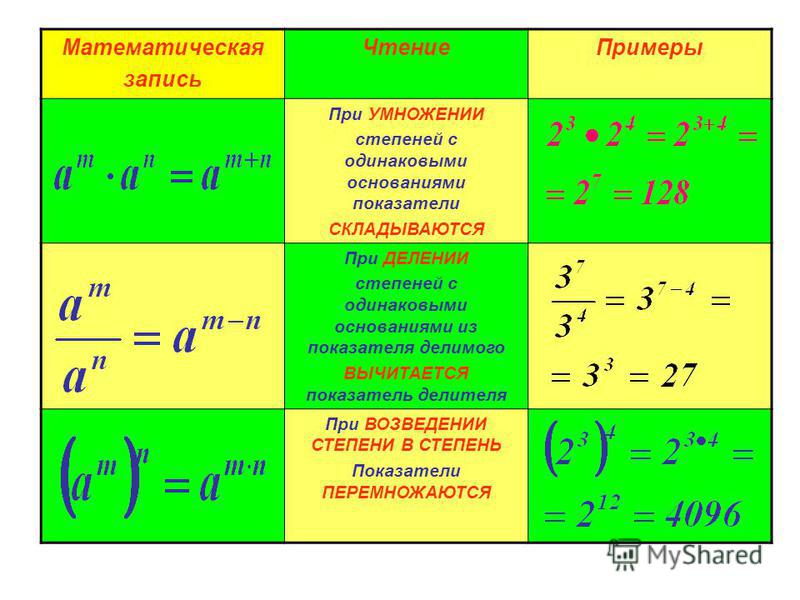
Сложение/вычитание : Можно добавлять только термины с одной и той же базовой переменной И одним и тем же показателем степени. База и показатель степени остаются прежними, а коэффициенты (числа впереди) добавляются. (Помните, что если коэффициента нет, там есть 1 с маскирующими сверхспособностями — она исчезает при умножении.) | Умножение: Когда вы умножаете термины с одной и той же переменной, вы добавляете показатели степени. Это потому, что х в квадрате на самом деле х * х. Если вы затем умножите это на x*x*x, вы получите в общей сложности 5 умноженных x. |
| Деление: Когда вы делите члены с одинаковыми основаниями, вы вычитаете. Есть множество способов взглянуть на отрицательные показатели степени при делении, но оба приведут вас к одному и тому же ответу. Вы можете вычитать точно так же, как и раньше, но не забывайте, что минус минус — это то же самое, что плюс плюс. Вы также можете переместить термин с отрицательным показателем на другую сторону дроби и отбросить отрицательный (это работает для перемещения вверх или вниз). Теперь у нас есть простое умножение. | Возведение степени в степень: Когда вы возводите степень в степень, вы умножаете степени. Сила продукта: Обязательно распределите показатель степени по всему продукту. Нулевой показатель: Не забывайте, что все, что возведено в степень 0, равно 1. (у x1 есть маскирующие сверхспособности) |
Вы можете двигаться в любом направлении (вверх или вниз), но мы, как правило, хотим, чтобы наш ответ заканчивался положительной экспонентой. Как вы можете видеть в этом примере, мы вычли меньшее число из большего, и ответ оказался в этой части дроби.
Видео Сала Кана, Tarrou’s Chalk Talk и MathROBERG
Свойства показателей степени: умножение и степень | Свойства показателей степени |
Отрицательные показатели и мощность нуля | Упрощение частных с отрицательными показателями |
Отрицательные показатели |
Практика положительных и отрицательных выражений
Предыдущая тема | Выберите единицу измерения | Следующая тема |
Авторские права на эти видео принадлежат Khan Academy, Tarrou’s Chalk Talk и MathROBERG.
4. Операции с экспонентами: Подкасты, которые распространяются как чума (это хорошо…)
Глава 4. Операции с экспонентами: Подкасты, которые распространяются как чума (это хорошо…)
Не могли бы вы умножить это еще раз? Мог вы умножаете это снова?
Есть еще один способ выразить повторяющееся умножение.
и снова и снова, не повторяясь.
Экспоненты — это способ повторяющегося умножения . Но это еще не все
степени, в том числе некоторые меньшие, чем обычно числа (и мы не просто
средние дроби). В этой главе вы освежите в памяти оснований , корней 9.0013 ,
и радикалов , все не получая
арестованы за любые сидячие протесты. И, как обычно, ноль и единица приходят со своими проблемами… так что прыгайте
в феерию возведения в степень подкастинга.
У Адди есть подкаст
Примечание
Кхм, эксцентричная
Подкасты Адди о сумасшедших знаменитостях.
В последнее время у Адди стало намного больше слушателей. Чтобы взять его следующий уровень, ей нужно новое оборудование, чтобы еще лучше подкаст… но на это уходит много денег.
У Адди есть веб-сайт для размещения ее подкастов, и она хочет
размещайте рекламу на своем сайте, чтобы собрать средства на новое снаряжение.
Она выстроилась в очередь
возможные спонсоры, но они не помогут, пока Адди не докажет, что может
получить реальный трафик на ее сайте. Адди необходимо:
…отслеживать ежедневные посещения ее веб-сайта в течение следующих 2 недели.
…докажите, что ее сайт может генерировать не менее 5 000 000 посещений в следующие 2 недели!
Примечание
Ого, это много.
Давайте мобилизуем слушателей Адди
Адди знает, что у нее есть большие поклонники. Вот письмо, над которым она работала отправить ей 3 топ слушатели :
Смогут ли Адди и Алекс получить достаточно просмотров?
Алекс предложил отправить еще одну серию электронных писем для Адди. Он начнет с 3 друзей, как и она, и попытается помочь получить 5 000 000 просмотров за 14 дней.
Чтобы вычислить общее количество попаданий, вам нужно вычислить
как сложить обе группы, с которыми работает Адди.
В главе 2 вы объединили как
условия, чтобы помочь Полу в его путешествии, и это та же самая идея. Вы можете
помните из главы 2, что термин — это любая часть уравнения, скрепленного вместе.
с умножением или делением. Поскольку экспонента — это просто сокращение
версия умножения, что означает экспоненциальные члены с тем же основанием и тем же
экспоненты подобны термам.
С показателями степени вы можете комбинировать термины, имеющие одну и ту же основу. Давайте попробуем и посмотрим, как это работает:
Потому что (3 14 ) 2 это умножение, а не сложение.
Термин — это нечто, скрепленное умножением, что означает что весь экспоненциальный член рассматривается как группа.
Примечание
3 14 — это один термин, а не два.
Когда вы группируете два похожих термина вместе, вы добавляете эти термины
все вместе. Но если вы возьмете эти два термина и воспользуетесь показателями (что 2 в конце
(3 14 ) 2 ), затем
вы размножаетесь, а это не то, чего мы хотим.
Смотри:
Ну, это сработает, но это много троек…
Запись умножения вручную будет работать; это просто не очень удобно. Смотри, какой длинной получается эта штука:
Но смотри, узор есть! Вот что это означает:
Экспоненты с одинаковым основанием подобны ТЕРМИНЫ.
Это означает, что их можно складывать, вычитать, умножать и разделенный.
Пробное подразделение:
Алекс сходит с ума по своей сестре
Алекс не отправлял никаких писем своему друзья до третьего дня. Это означает, что у него есть только 12 дней, чтобы получить слово из. Удастся ли Адди?
Злодей всегда найдется…
The Movie Podcast узнал о плане Эдди по увеличению числа подписчиков,
и им это не нравится. Спонсорство, которое Эдди пытается получить… ну,
это деньги из кармана Movie Podcast. Так что теперь они дерутся
назад.
Каждый, кто попал в Подкаст Кино страница вместо страницы Startalk Podcast отнимает потенциальные хиты. Что это значит для шансов Адди получить новое спонсорство? по рукам?
Различные основы = НЕ похожие термины.
Термины с разными основаниями не похожи на термины (независимо от показатель). Просто у них нет ничего общего. Как экспоненциальный термины, они не умножают одно и то же число, независимо от того, сколько раз.
Примечание
Как мы видели ранее, они подобны терминам только в том случае, если основание И показатель степени совпадают.
Вы не можете складывать показатели степени с разными основаниями
Если мы просто поговорим о той части уравнения Адди, которая имеет два терминов, это выглядит так:
Вы знаете, что вы не можете сложить или вычесть эти два, потому что
они не похожи на термины. Умножение и деление тоже не работают.
Экспоненциальные члены, умноженные вместе, просто записываются вместе,
вот так:
Порядок операций говорит о показателях ПЕРВЫЙ
Нельзя разделять основания и комбинировать разные показатели потому что каждое основание должно оставаться со своим показателем степени. Получатель чего-то операции говорят, что показатели идут от до умножение. Это означает, что показатели степени должны быть упрощены , прежде чем их можно будет комбинировать с что-то другое.
Сила мозга
Проверьте это с реальными числами — попробуйте 3 2 и 4 3 . Может ты показываешь это (3 2 )(4 3 ) нет то же, что и ((3)(4)) (2)(3) , без работы до конца ответ?
Адди нужен еще один раунд электронные письма.
Но сколько ей нужно отправить? У Адди осталось всего 9 дней
и ей нужно выяснить, сколько писем ей нужно для начала
сегодня, чтобы компенсировать кампанию Movie Podcast.
Нам нужно работать с экспонентой «назад»
Вернемся к уравнению Адди. у нас разные информация на этот раз: количество нужных нам хитов и количество дней осталось:
Теперь мы заполним то, что мы знаем:
Корень является ПРОВЕРКОЙ показатель степени
Нам нужна операция, которая может раскрыть показатель степени. Так когда у нас есть экспонента, что является основанием для получения определенного ответа? Хорошо, это корень . Когда найдешь корень чего-то, вы находите номер , который может умножайте снова и снова, чтобы получить окончательное число.
Для Адди нам нужно взять корень девятой степени с обеих сторон ее уравнение. Это изолирует x и дайте нам числовое значение на другой стороне.
9 дней спустя…
Вы помогли Адди получить большой проверять!
Сайт Эдди прошел 5 000 000 посещений, никаких проблем.