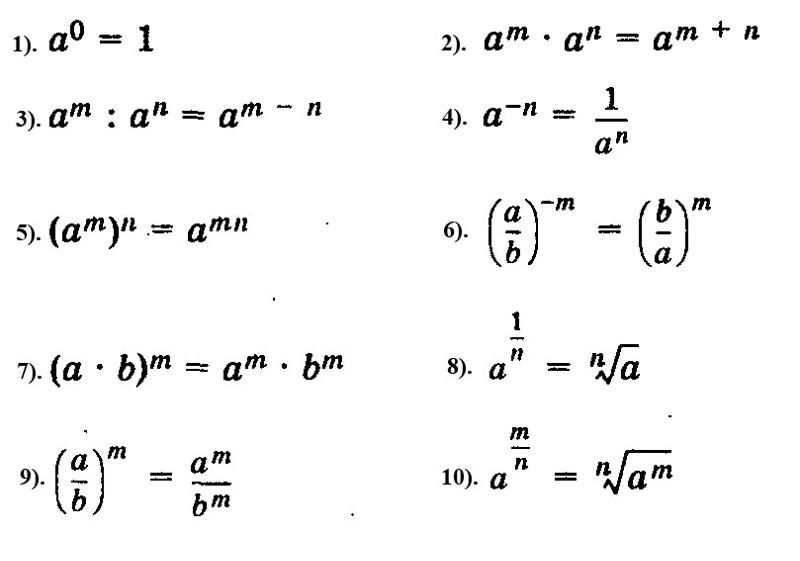7 класс. Алгебра. Степень с натуральным показателем и ее свойства. — Возведение в степень .
Комментарии преподавателяНа этом уроке мы изучим возведение степени в степень. Вначале вспомним определение степени и теоремы об умножении и делении степеней с одинаковым основанием. Далее будет сформулирована теорема о возведении степени в степень. Затем мы приведем примеры ее использования на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач и будем решать типичные примеры с помощью всех теорем.
Напоминание:
Основные определения:
Здесь a – основание степени,
n – показатель степени,
– n-ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:
При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
На этом уроке будет рассмотрена следующая теорема.
Теорема 3. Для любого числа а и любых натуральных n и k справедливо равенство:
Вывод: частные случаи подтвердили правильность формулы . Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.
По определению степени:
Применим теорему 1:
Итак, мы доказали: , где а – любое число, n и k – любые натуральные числа.
Другими словами, чтобы возвести степень в степень показатели нужно перемножить, а основание оставить неизменным.
Пример 1: Упростить.
Для решения следующих примеров воспользуемся свойством .
а)
б)
в)
Комментарий к примеру 1.
Мы написали, что , но в то же время , так как .
Аналогично, .
В качестве основания может быть любое допустимое алгебраическое выражение:
Пример 2:Упростить.
а)
б)
Пример 3: Вычислить.
а)
б)
в)
г). Комментарий:
д). Комментарий:
е). Комментарий:
Пример 4: Упростить.
Для решения следующих примеров будем пользоваться теоремами 1, 2, 3.
а)
б)
в)
г)
д) или быстрее
е) =
Пример 5: Вычислить:
а)=
На этом уроке мы изучим умножение степеней с одинаковыми показателями. Сначала вспомним основные определения и теоремы об умножении и делении степеней с одинаковыми основаниями и возведении степень в степень. Затем сформулируем и докажем теоремы об умножении и делении степеней с одинаковыми показателями. А затем с их помощью решим ряд типичных задач.
Тема: Степень с натуральным показателем и ее свойства
Урок: Умножение и деление степеней с одинаковыми показателями
Напоминание:
Основные определения:
Здесь a — основание степени,
n — показатель степени,
— n-ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n иk справедливо равенство:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:
При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
Теорема 3. Для любого числа а и любых натуральных n иk справедливо равенство:
Все перечисленные теоремы были о степенях с одинаковыми основаниями, на этом уроке будут рассмотрены степени с одинаковыми показателями.
Рассмотрим следующие примеры:
Распишем выражения по определению степени.
1)
2)
Вывод: из примеров можно заметить, что , но это еще нужно доказать. Сформулируем теорему и докажем ее в общем случае, то есть для любых а и b и любого натурального n.
Теорема 4
Для любых чисел а и b и любого натурального n справедливо равенство:
Доказательство теоремы 4.
По определению степени:
.
Итак, мы доказали, что .
Чтобы перемножить степени с одинаковыми показателями, достаточно перемножить основания, а показатель степени оставить неизменным.
Сформулируем теорему для деления степеней с одинаковыми показателями.
Теорема 5
Для любого числа а и b () и любого натурального n справедливо равенство:
Доказательство теоремы 5.
Распишем и по определению степени:
Итак, мы доказали, что .
Чтобы разделить друг на друга степени с одинаковыми показателями, достаточно разделить одно основание на другое, а показатель степени оставить неизменным.
Пример 1: Представить в виде произведения степеней.
Для решения следующих примеров воспользуемся теоремой 4.
а)
б)
в)
Для решения следующего примера вспомним формулы:
г)
д)
е)
ж)
Обобщение теоремы 4:
з)
и)
к)
л)
Пример 2: Запишите в виде степени произведения.
а)
б)
в)
г)
Пример 3: Запишите в виде степени с показателем 2.
а)
б)
Пример 4: Вычислить самым рациональным способом.
а)
б)
Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/stepen-s-naturalnym-pokazatelem-i-eyo-svojstva/vozvedenie-stepeni-v-stepen-formula-a-sup-n-sup-sup-k-sup-a-sup-nk-sup?konspekt&chapter_id=2
http://interneturok.ru/ru/school/algebra/7-klass/stepen-s-naturalnym-pokazatelem-i-eyo-svojstva/umnozhenie-i-delenie-stepeney-s-odinakovymi-pokazatelyami?konspekt&chapter_id=2
Источник видео: http://www.youtube.com/watch?v=YgxoKBgwok0
Формулы сокращённого умножения. — Студопедия
Поделись
ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ, РАЦИОНАЛЬНЫХ, ИРРАЦИОНАЛЬНЫХ, СТЕПЕННЫХ ВЫРАЖЕНИЙ
Теоретические сведения.
КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ ИЗ ЧИСЛА, ИХ СВОЙСТВА.
Корень n – степени: , n — показатель корня, а –подкоренное выражение
Если n – нечетное число, то выражение имеет смысл при а
Если n – четное число, то выражение имеет смысл при
Арифметический корень:
Корень нечетной степени из отрицательного числа:
ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ
1.
Правило извлечения корня из произведения:
2.Правило извлечения корня из дроби:
3. Правило извлечения корня из корня:
4. Правило вынесения множителя из под знака корня:
5. Внесение множителя под знак корня:
,
6. Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число.
7. Правило возведения корня в степень.
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
= ,a – основание степени, n – показатель степени
Свойства:
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным.
2. При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным.
3. При возведении степени в степень показатели перемножаются.
4. При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают.
5. Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга.
6. Если
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
1.
2.
3.
4.По определению:
Свойства:
1.
2.
3.
4.
5.
6. Пусть r рациональное число , тогда
7 .Для любого рациональных чисел r и s из неравенства > следует
> при a>1 при
Формулы сокращённого умножения.
Пример 1. Упростите выражение .
Решение
Применим свойства степеней (умножение степеней с одинаковым основанием и деление степеней с одинаковым основанием): .
Ответ: 9m7 .
Пример 2.Сократить дробь:
Решение.Так область определения дроби все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем .Сократив дробь, получим .Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби и равны при х ≠ 1 и х ≠ -2.
Пример 3.Сократить дробь:
Пример 4.Упростить:
Пример 5.Упростить:
Пример 6. Упростить:
Пример 7. Упростить:
Пример 8.Упростить:
Пример 9. Вычислить: .
Решение.
Пример 10.Упростить выражение:
Решение.
Пример 11.Сократить дробь , если
Решение. .
Пример 12.Освободиться от иррациональности в знаменателе дроби
Решение.
В знаменателе имеем иррациональность 2-й степени, поэтому помножим и числитель, и знаменатель дроби на сопряженное выражение, то есть сумму чисел и , тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.
Добавление показателей – методы и примеры
Алгебра – один из основных курсов математики. Чтобы понять алгебру, важно знать, как использовать экспоненты и радикалы. Добавление показателей является частью программы по алгебре, и по этой причине для учащихся важно иметь более прочную основу в математике.
Многие студенты часто путают сложение степеней со сложением чисел , и, следовательно, делают ошибки. Эти недоразумения обычно влекут за собой разницу в значении таких терминов, как возведение в степень и показатель степени.
Прежде чем углубляться в советы о том, как добавлять показатели степени, давайте начнем с определения терминов степени. Начнем с того, что показатель степени — это просто многократное умножение числа само на себя.
В математике эта операция называется возведением в степень. Таким образом, возведение в степень — это операция с числами в форме b n , где b называется основанием, а число n — показателем степени, или индексом, или степенью . Например, x 4 содержат 4 в качестве показателя степени, а x называется базовым.
Экспоненты иногда называют степенями чисел. Показатель степени представляет количество раз, которое число должно быть умножено само на себя. Например, x 4 = x × x × x × x.
Чтобы сложить показатели, и показатели, и переменные должны быть одинаковыми. Вы добавляете коэффициенты переменных, оставляя показатели без изменений. Добавляются только термины с одинаковыми переменными и степенями. Это правило также согласуется с умножением и делением показателей.
Ниже приведены шаги для добавления показателей степени:
- Проверьте члены, если они имеют одинаковые основания и показатели степени
Например, 4 2 +4 2 , эти члены имеют одинаковое основание 4 и показатель степени 2.
- Вычислите каждый член отдельно, если они имеют разные основания или степени
Например, 3 2 + 4 3 , эти члены имеют разные показатели степени и основания.
- Сложите результаты вместе.
Сложение показателей степени с разными показателями степени и основаниями
Сложение показателей степени выполняется путем сначала вычисления каждого показателя степени, а затем добавления:
Пример 1
- 4 2 + 2 5 = 4–4 + 2=2=2 = 16 + 32 = 48
- 8 3 + 99 + 32 = 48
- 8 3 + . 2 = (8)(8)(8) + (9)(9) = 512 + 81 = 593
- 3 2 + 5 3 = (3)(3) + (5)(5)(5) = 9 + 125 = 134
- 6 2 + 6 3 9 032
- 3 4 + 3 6 = 81 + 729 = 810.
Добавление экспонентов с теми же основаниями и показателями
Общая формула приведена как:
B N + B N = 2B .
n
Пример 2
- 4 2 + 4 2 = 2⋅4 2 = 2om4 % = 32
- 8 3 + 8 3 + 8 3 = 3 (8 3 ) = 3 * 512 = 1536
- 3 2 + 3 2 = 2(3 2 ) = 2 * 9 = 18
- 5 2 + 5 2 = 2(5 2 ) = 2 * 25 = 50. с разными базами?
Добавление отрицательных показателей выполняется путем вычисления каждого показателя отдельно, а затем добавления:
a -n + b -M = 1/A N + 1/B M
Пример 3
4 -2 + 2 -5 = 1/4 2 + 1/2. 5 = 1/(4⋅4)+1/(2⋅2⋅2⋅2⋅2) = 1/16+1/32 = 0,09375
Как сложить дробь с разными основаниями и показателями?
Добавление дробных показателей степени выполняется путем вычисления каждого показателя степени отдельно, а затем добавления:
a n/m + b k/j .
Пример 4
3 3/2 + 2 5/2 = √ (3 3 ) + √ (2 5 ) = √ (27) + √ (32). = 5,196 + 5,657 = 10,853
Как сложить дробные показатели с одинаковыми основаниями и одинаковыми дробными показателями?
B N/M + B N/M = 2B N/M
Пример 5
4 2/3 + 4 2/3 = 2 % 2/3 = 2 ⋅ 3 √ (4 2 ) = 5,04
Как сложить переменные с разными показателями степени?
Добавление показателей выполняется путем вычисления каждого показателя отдельно и последующего сложения:
x n + x m
Как сложить переменные с одинаковыми показателями?
x N +x N = 2x N
Пример 6
x 2 + x 2 = 2 + x 2 = 2 .
0013 x 2 Пример 7
(4 -1 + 8 -1 ) ÷ (2/3) -1 1 (3/2)
= (2 + 1)/8 ÷ 3/2
= (3/8 ÷ 3/2)
= (3/8 ÷ 2/3)
= ¼
Пример 8
Упрощение: (1/2) -2 + (1/3) -2 + (1/4) -2
Решение:
(1/2) -2 + (1/3) -2 + (1/4) -2
= (2/1) 2 + (3/1) 2 + (4/1) 2
= (2 2 + 3 2 + 4 1 2 90 + 9 + 16)
= 29Основные операции — Полномочия | Shmoop
Основные операции — Полномочия | ШмупМагазин не будет работать корректно в случае, если куки отключены.
Похоже, в вашем браузере отключен JavaScript. Для наилучшего взаимодействия с нашим сайтом обязательно включите Javascript в своем браузере.
Предыдущий СледующийПолномочия
Будучи юными любителями математики, мы сложили пять четвёрок следующим образом:
4 + 4 + 4 + 4 + 4
Затем мы научились писать короче, например так:
4 × 5
Повторное сложение может быть записано как умножение.
Теперь, когда мы все выросли в математике, у нас также есть более короткий способ записи многократного умножения. Если мы хотим умножить 5 четыре раза, мы можем написать 5 × 5 × 5 × 5. Но более короткий способ — использовать степени.
Степени , также известные как экспоненты , представляют собой короткий способ записи длинных строк умножения.
Вместо 5 × 5 × 5 × 5 напишите 5 4 , что означает «умножить четыре пятерки вместе». Мы произносим 5 4 как «5 в четвертой степени».
Или как насчет экономии времени: разве 10 9 написать проще, чем ?
Возьмите увеличительное стекло и давайте посмотрим поближе на 10 9 . Большое число 10 — это по основанию . Это число, которое многократно умножается. Меньшее число, скрывающееся в верхнем правом углу, — это показатель степени . Это немного застенчиво, но это говорит нам, сколько оснований мы умножаем. Основание равно 10, а показатель степени равен 9, поэтому мы умножаем девять десятков вместе. И это одно большое число. Именно для этого экспоненты наиболее полезны: запись очень больших чисел.
Важные правила полномочий
- Любое число в степени 0 равно 1.
- Любое число в степени 1 равно самому себе.
- Когда вы видите число, возведенное в отрицательную степень , возьмите обратное число (переверните дробь), а затем измените степень с отрицательной на положительную.
- Любое число в степени 0 равно 1.
0013 x 2 
