сторона | это… Что такое сторона?
сущ., ж., употр. наиб. часто
Морфология: (нет) чего? стороны́, чему? стороне́, (вижу) что? сто́рону, чем? стороно́й, о чём? о стороне́; мн. что? сто́роны, (нет) чего? сторо́н, чему? сторона́м, (вижу) что? сто́роны, чем? сторона́ми, о чём? о сторона́х
пространство, направление
1. Стороной называется пространство, которое находится в каком-либо направлении от кого-либо, чего-либо, а также само это направление. Правая, левая сторона чего-либо. | Противоположные стороны.
2. Стороной называется направление движения кого-либо, чего-либо. В сторону леса.
3. Стороны света (горизонта) — это восток, запад, юг, север.
4. Если кто-либо отпускает, посылает кого-либо на все четыре стороны, то это означает, что кто-либо предоставляет кому-либо свободу в выборе направления своего движения, не препятствует чьему-либо уходу и т. п.
5. Стороной называют пространство, которое расположено слева или справа от средней линии чего-либо. Левая сторона улицы. | Теневая, солнечная сторона улицы. | Чётная, нечётная сторона улицы. | По обе стороны дороги. | По ту сторону забора.
6. Стороной называют направление вправо или влево от кого-либо, чего-либо. Вытянуть руки в стороны. | Посмотреть в сторону.
7. Он шёл по улице, удивляясь, как сильно изменился родной город, внимательно глядя по сторонам в надежде встретить хоть кого-нибудь знакомого.
Если кто-либо оглядывается, смотрит по сторонам, то это означает, что этот человек осматривает пространство вокруг себя.
8. Если кто-либо смотрит по сторонам, значит, он невнимателен, не следит за чем-либо. Иванов, ты опять смотришь по сторонам, ну-ка быстро к доске!
9. Если какой-либо предмет одежды съехал, сбился на сторону, то это означает, что он самопроизвольно сместился с привычного места на теле человека. Пальто распахнуто, шапка съехала на сторону, что случилось?
10. Если что-либо находится в сторону, в стороне от чего-либо, то это означает, что что-либо расположено в некотором отдалении от чего-либо.
11. Если кто-либо говорит что-либо в сторону, то это означает, что этот человек произносит что-либо тихо, слегка отвернувшись, как будто сказанное не предназначается собеседнику.
12. Если о ком-либо говорят, что он — человек со стороны, то это означает, что этот человек является чужим, не воспринимается кем-либо как свой, близкий. Вопреки ожиданиям сотрудников на это место взяли человека со стороны.
13. Если один из супругов гуляет на стороне, пошёл на сторону, то это означает, что он (она) имеет любовницу (любовника), изменяет партнеру.
14. Когда кто-либо продаёт товар на́ сторону, он делает это незаконно и не тому, кому он был предназначен.
отношение к делу
15. Если кто-либо держится, остаётся в стороне от кого-либо, чего-либо, то это означает, что этот человек избегает контактов с кем-либо, не принимает участия в чём-либо.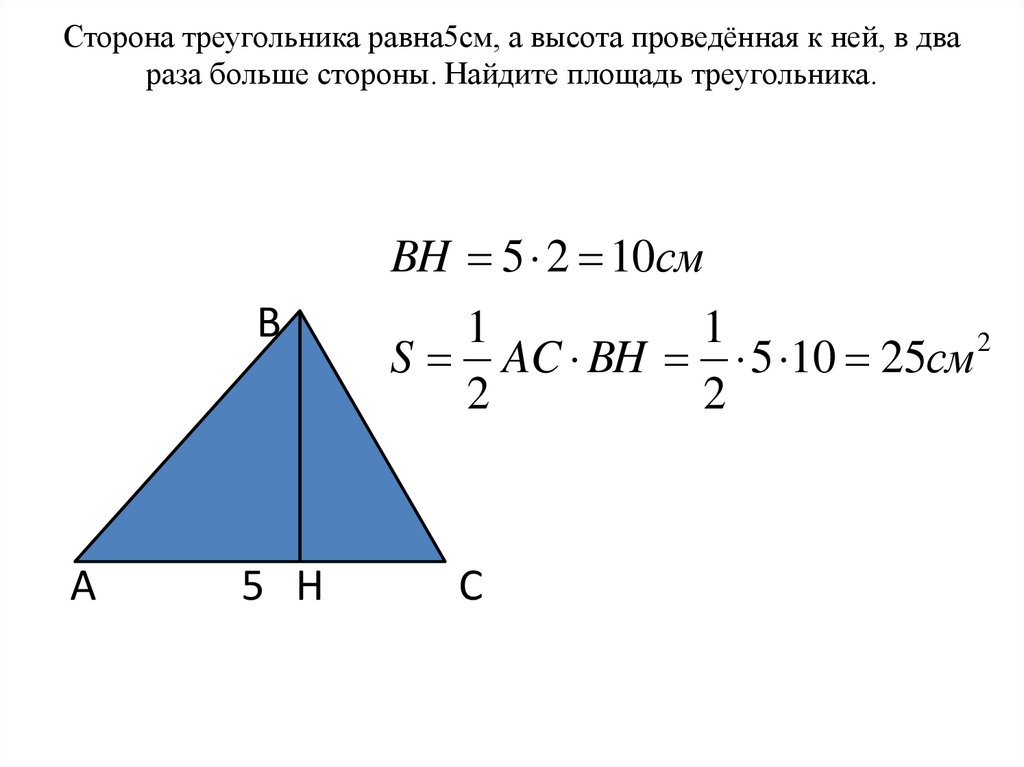
16. Если кто-либо уводит разговор в сторону от чего-либо, то это означает, что этот человек уклоняется от обсуждения главного.
17. Если кто-либо смотрит на что-либо со стороны, то это означает, что этот человек имеет нейтральное мнение о чём-либо. Смотреть на себя со стороны. | Это было заметно со стороны.
18. Если кто-либо говорит, что его
19. Если кто-либо предлагает оставить в стороне какие-либо вопросы при обсуждении чего-либо, то это означает, что этот человек не хочет касаться какой-либо темы в разговоре с кем-либо.
20. Если кто-либо предлагает отбросить в сторону что-либо, то это означает, что этот человек хочет отказаться от чего-либо, ставшего негодным, ненужным, неважным.
21. Если какая-либо проблема, ситуация рассматривается кем-либо со всех сторон, то это означает, что при её обсуждении учитываются все возможные составляющие, перспективы и т. п.
22. Стороной называется одна из поверхностей какого-либо предмета; боковая часть чего-либо. Лицевая сторона материи.
23. В геометрии стороной называют отрезок прямой линии, который частично ограничивает площадь геометрической фигуры. Равенство сторон в прямоугольном треугольнике. | Стороны многоугольника. | Сторона квадрата.
24. Стороной называют составную часть, элемент чего-либо. Существенная сторона дела.
| Экономическая сторона проблемы. | Юридическая сторона дела.
25. Стороной называется отдельная черта, которая частично характеризует что-либо. Техническая сторона проекта.
взаимоотношения
26. Стороной называется каждая из групп людей, которые находятся во взаимодействии или противостоянии друг другу. Третья сторона. | Враждующие стороны. | Договаривающиеся стороны. | Заинтересованная сторона. | Прения сторон в суде. | По договору купли-продажи одна сторона (продавец) обязуется передать вещь (товар) в собственность другой стороне (покупателю).
27. Дядей и т. п. со стороны матери называют родственника по материнской линии.
28. Если кто-либо тянет кого-либо на свою сторону, то это означает, что этот человек пытается убедить кого-либо в своей правоте, сделать кого-либо участником какой-либо группы людей, которая по своим интересам противопоставлена другой.
29. Если кто-либо на стороне кого-либо, то это означает, что этот человек поддерживает кого-либо в его действиях против кого-либо, спорах с кем-либо.
30. Если кто-либо встаёт на сторону кого-либо; принимает (держит, берёт) сторону кого-либо, то это означает, что этот человек выражает своё единомыслие, единодушие с кем-либо, защищает кого-либо в конфликте, споре и т. п.
31. Оборотной (другой) стороной медали называют до времени скрытые, не проявленные отрицательные моменты какого-либо успешного, удачного дела, действия, процесса и т. п.
32. Выражение шутки в сторону употребляется как призыв к серьёзному обсуждению чего-либо.
Дождь прошёл стороной.
34. Выражение с одной стороны…, с другой стороны… употребляется для противопоставления двух фактов, обстоятельств и т. п.
• сторо́нка сущ., ж.
Задачи для тех, кто любит геометрию и схемы
У нас накопилось так много задач про геометрию, что мы решили выпустить отдельную подборку с ними. Для решения нужны или простые формулы со школы, или смекалка (она у вас есть).
Погнали чертить.
Задачка от Джеффа Безоса. На размышление даётся 30 секунд
Перед вами очередная задачка с собеседований в крупные IT-компании. Вот сама задача:
Кабель длиной 80 метров висит на двух столбах. Высота каждого столба — 50 метров. Каково расстояние между столбами, если центр провисающего кабеля находится:
а) на высоте 20 метров от земли — вариант для технарей;
б) на высоте 10 метров от земли — вариант для гуманитариев.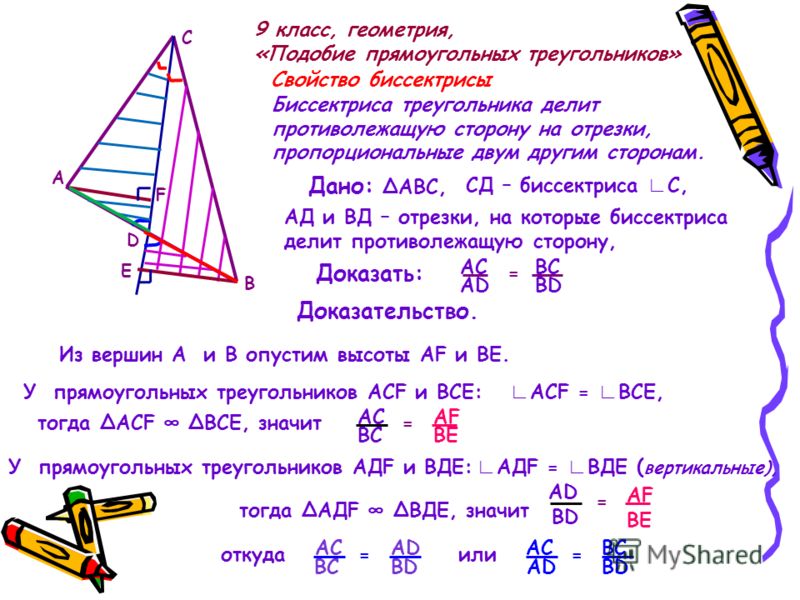
Для решения можно использовать инженерный калькулятор с расширенными функциями.
В задаче нет никакого подвоха, но для решения нужно хорошо знать математику, углы и угловые функции. Попробуйте сначала решить её самостоятельно, а потом загляните в решения.
Первое, что мы сделаем, — поднимем уровень земли, чтобы он касался провода. Так как до центра провиса 20 метров, то высота столбов тоже уменьшится на эти 20 метров:
Расстояние между столбами у нас при этом осталось тем же самым.
Так как кабель провисает по центру, нам достаточно найти расстояние от края до середины и умножить его на 2 — так мы найдём полное расстояние между столбами.
❗️ Самая важная часть.
Так как провисающий кабель похож на гиперболу, то мы для решения будем использовать не тригонометрические функции, которые работают с прямыми и окружностями, а гиперболические, график которых похож на гиперболу.
Если нужно точное описание этих функций — вот оно:
Сначала поработаем с высотой столба.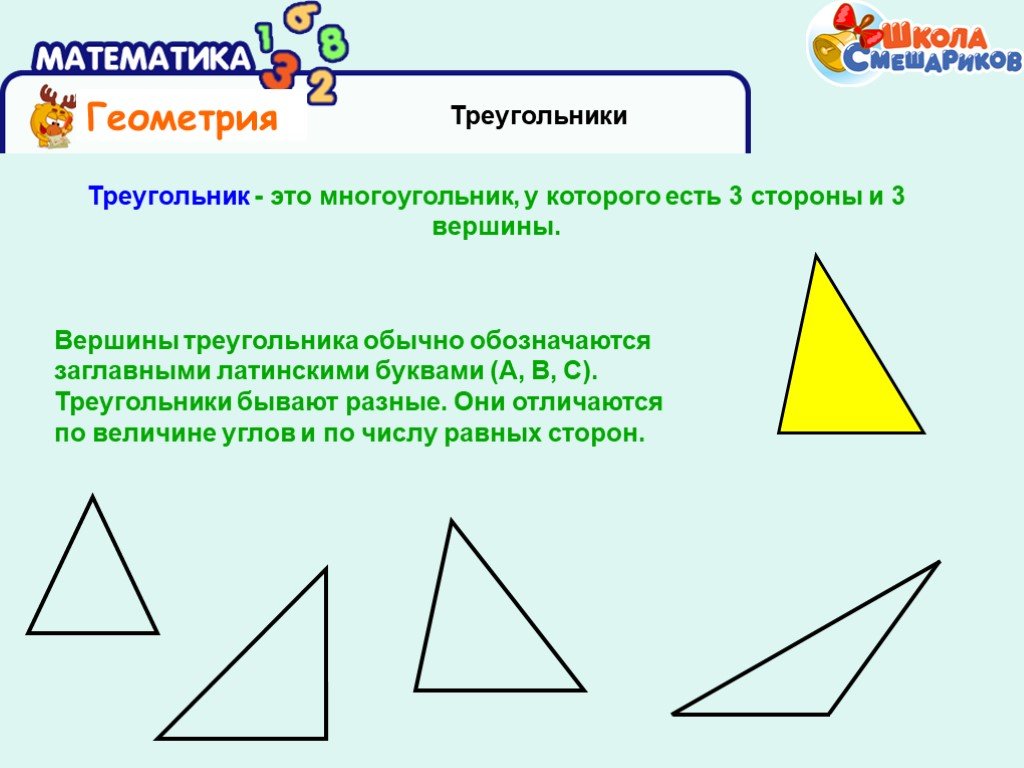
Запишем формулу для расстояния, затем добавим на рисунок те данные, которые мы уже знаем, и раскроем формулу:
Получилось сложно, но половина уже готова
Теперь составим второе уравнение, в котором используем значение длины кабеля. Так как он провисает ровно посередине, то его длина от края до точки перегиба — 40 метров.
Добавляем свойство о том, что разность квадратов гиперболического синуса и косинуса равна единице:
Раскрываем скобки, приводим всё к классическому квадратному уравнению и, решая его, получаем ответ: a = 35/3.
Это значение подставляем в формулу гиперболического синуса, чтобы посчитать половину длины кабеля:
Решаем это уравнение на калькуляторе и получаем ответ: x ≈ 22,7. Это половина расстояния между столбами, а полное расстояние ≈ 45,4 метра.
Ответ: если высота до центра провиса равна 20 метров, то расстояние между столбами составляет примерно 45,4 метра.
У гуманитариев кабель длиной 80 метров провисает на минимальной высоте 10 метров от земли.
При этом высота столба 50 метров. Значит, если провести новый «уровень земли» (красным), верхняя часть столба будет равняться 40 метрам.
Посмотрите на рисунок. Нет ли здесь ошибки?
Если верхняя часть столба 40 метров и длина кабеля до середины — тоже 40 метров, то какой это треугольник? Может ли такой треугольник существовать?
Простая задача про круги, которая выглядит сложной
Дано: есть три одинаковых круга с диаметром в 1 метр. Круги соприкасаются друг с другом, а вокруг них натянута эластичная лента.
Что нужно: найти длину этой ленты.
Кажется, что это очень сложная задача, где нужно знать сложные формулы расчёта кривизны и точек натяжения, но на деле всё будет гораздо проще. Если знаете английский — посмотрите оригинальный ролик, там классная анимация:
Строим внутренний треугольник
Первое, что мы сделаем, — соединим центры всех кругов в один треугольник:
В геометрии есть такое правило, что если круги касаются друг друга, то через их центры можно провести прямую линию, и точка касания кругов будет лежать на этой линии.
Раз у нас диаметр равен 1, то радиус каждого круга равен 0,5. Обозначим это на рисунке:
Получается, что длина каждой стороны треугольника равна 0,5 + 0,5 = 1. Запомним это и идём дальше.
Строим проекцию
От каждой вершины треугольника проведём под прямым углом линии к ленте:
Получились прямоугольники. У прямоугольников противоположные стороны равны, поэтому раз стороны треугольника равны единице, то и эти отрезки на ленте тоже будут равны единице:
Осталось найти длину оставшихся секций:
Вычисляем длину секций
Здесь нам поможет знание о том, что полный оборот внутри круга — это 360 градусов.
Так как во внутреннем треугольнике все стороны равны, то это равносторонний треугольник. А раз так, то углы в нём равны 60 градусов. Добавим сюда по два прямых угла по 90 градусов из прямоугольников:
Решаем уравнение: 90 + 60 + 90 + X = 360 → X = 120 градусов.
Но 120 градусов — это ровно треть круга, а у нас таких частей как раз три:
Это значит, что из них можно составить один целый круг.
При этом мы знаем, что у этого круга радиус 0,5, а диаметр тогда равен единице. Этого достаточно, чтобы посчитать длину окружности: L = π × d → L = 3,14.
Складываем это число с длинами трёх отрезков и получаем полную длину: 3 + π
Как найти площадь прямоугольника?
Старая задачка для тех, кто устал от сложных расчётов: найдите площадь маленького прямоугольника внутри большого прямоугольника (он выделен синим):
Чтобы решить эту задачу, обозначим ширину синего прямоугольника за X. Заодно уберём метры и квадратные метры, чтобы не мешали:
Отлично, у нас появилась ширина у тех прямоугольников, у которых известна площадь. Осталось добавить высоту Y — так как большая фигура тоже прямоугольник, то высота всех внутренних прямоугольников также будет одинаковой:
Теперь, когда у нас есть размеры и площади прямоугольников, мы можем составить два равенства:
(7 − x) × Y = 20
(8 − X) × Y = 25
Получилось два уравнения с двумя неизвестными, а значит, их можно объединить в систему и решить:
7Y − XY = 20
8Y − XY = 25
Вычтем первое уравнение из второго:
(8Y − 7Y) − (XY − XY) = 25 − 20
Y = 25 − 20 = 5.
Теперь подставим это значение в первое уравнение:
7 × 5 − 5X = 20
35 − 5X = 20 → 5X = 35 − 20 → 5X = 15 → X = 3.
В самом начале мы обозначили ширину синего прямоугольника за X, а потом высоту — за Y. Значит, его площадь будет равна X × Y. А раз мы уже знаем оба эти значения, то получается, что площадь синего треугольника равна 3 × 5 = 15 квадратных метров.
Задача про периметр и забывчивого монтажника
Одному монтажнику поставили задачу — подготовить кабель для камер видеонаблюдения на первом этаже здания. Само здание прямоугольное, а стены между комнатами делят этаж на 4 комнаты-прямоугольника. В техническом условии было написано, что кабель в каждой комнате должен идти точно по периметру стен, поэтому монтажник измерил периметр каждой комнаты и записал всё на листочке. Но он спешил, поэтому в магазине обнаружил, что забыл записать периметр последней комнаты:
Помогите монтажнику найти периметр последнего прямоугольника, чтобы ему не пришлось лишний раз возвращаться на объект.
Обозначим буквами стороны каждого прямоугольника:
Теперь, когда у нас есть обозначения сторон, запишем то, что нам уже известно:
2а + 2с = 17
2b + 2c = 15
2b + 2d = 18
Периметр последнего прямоугольника равен 2a + 2d — эту сумму мы и будем искать в решении.
Возьмём первое уравнение и посчитаем, чему равно 2c, чтобы подставить это во второе уравнение:
2c = 17 − 2a → подставляем во второе уравнение
2b + 17 − 2a = 15 → 2b − 2a = 15 − 17 → 2b − 2a = −2
Теперь отсюда выясним, чему равно 2b, и подставим это в третье уравнение:
2b − 2a = −2 → 2b = 2a − 2 → подставляем в третье уравнение:
2a − 2 + 2d = 18
2a = 2d = 18 + 2
2a + 2d = 20
Но периметр последней комнаты как раз равен 2a + 2d, а значит, он равен 20.
Мэтимэтикс.
Задача про три участка и роутер
Для решения этой задачи потребуется вспомнить тригонометрию. Вспомним же её!
Три брата купили квадратные участки в лесном посёлке.
Участки одинакового размера. Длина каждого участка — 100 метров, а расположены они треугольником:
Братья решили сэкономить на интернете и поставить один роутер на троих. Чтобы найти точку, одинаково близкую ко всем участкам, они вплотную обвели три квадрата в круг и поставили роутер точно в центре получившегося круга.
Но братья не учли, что сигнал роутера дотягивается только на 130 метров, а дальше интернет теряется. Хватит ли братьям этого роутера или нужно взять мощнее?
Чтобы понять, хватит ли братьям этого роутера, нужно выяснить, какого радиуса круг у них получился. Если радиус будет меньше, чем радиус покрытия роутера, то всё в порядке, а если нет — роутер придётся менять.
Первым делом проведём через круг три диаметра, каждый из которых будет проходить через вершину треугольника. Длина каждой стороны треугольника — тоже 100 метров, так как он образован сторонами квадрата:
Раз все три линии в равностороннем треугольнике пересекаются в одной точке, то каждая линия — одновременно биссектриса (делит угол пополам) и медиана (делит противоположную сторону пополам), а ещё она проходит под прямым углом к противоположной стороне.
А раз участки квадратные, то и противоположную сторону эта линия тоже пересекает под прямым углом и тоже делит ту сторону пополам:
Теперь посмотрим поближе на центральный треугольник, а точнее — на один из маленьких треугольников, который получился в результате. Так как каждая синяя линия — это биссектриса, а в равностороннем треугольнике все углы по 60 градусов, то левый угол будет равен 30 градусам. Мы знаем, что сумма всех углов треугольника равна 180 градусов, и у нас уже есть два угла — 30 и 90 градусов. Это значит, что верхний угол будет равен 180 − 90 − 30 = 60 градусов:
Зная всё это, найдём длину короткого катета по формуле X = tg(30) × 50 = 1/√3 × 50 = 50/√3
Теперь вернёмся ко всему рисунку и посмотрим на другой треугольник, где одна из сторон — это радиус круга.
Мы уже знаем, что синие линии делят квадраты пополам, а значит, нижняя сторона треугольника равна 50 метрам. Также мы знаем, что внизу у нас прямой угол, а значит, зелёная сторона треугольника тоже равна 100 метрам:
Получается, что у нас есть прямоугольный треугольник с катетами 50 метров и (100 + 50/√3) метров, и нужно узнать длину гипотенузы.
По теореме Пифагора сумма квадратов катетов равна квадрату гипотенузы:
a² + b² = c²
Подставим сюда наши значения и решим уравнение:
50² + (100 + 50/√3)² = r²
r = √(50² + (100 + 50/√3)²)
r = √(2500 + (100 +28,86)²) = √(2500 +16606,83) = 138,22
Выходит, что радиус круга (138 метров), который граничит со всеми участками, меньше, чем радиус действия роутера (130 метров). Значит, братьям нужно брать роутер помощнее или ставить всё своё оборудование ближе к роутеру.
Задача про треугольник и неполные размеры
Задачка на логику и геометрию, как в школе. Это не нужно в ИТ, но иногда нужно отвлекаться.
Вот картинка, тут всё понятно. Нужно найти площадь треугольника.
Так как у нас в треугольник вписан квадрат, это значит, что обе его стороны находятся под прямым углом к основанию треугольника:
А раз так, то угол, который образуется при пересечении наклонной линии, совпадает с углом наклона этой линии к основанию:
Если у треугольников есть два одинаковых угла, то такие треугольники называются подобными.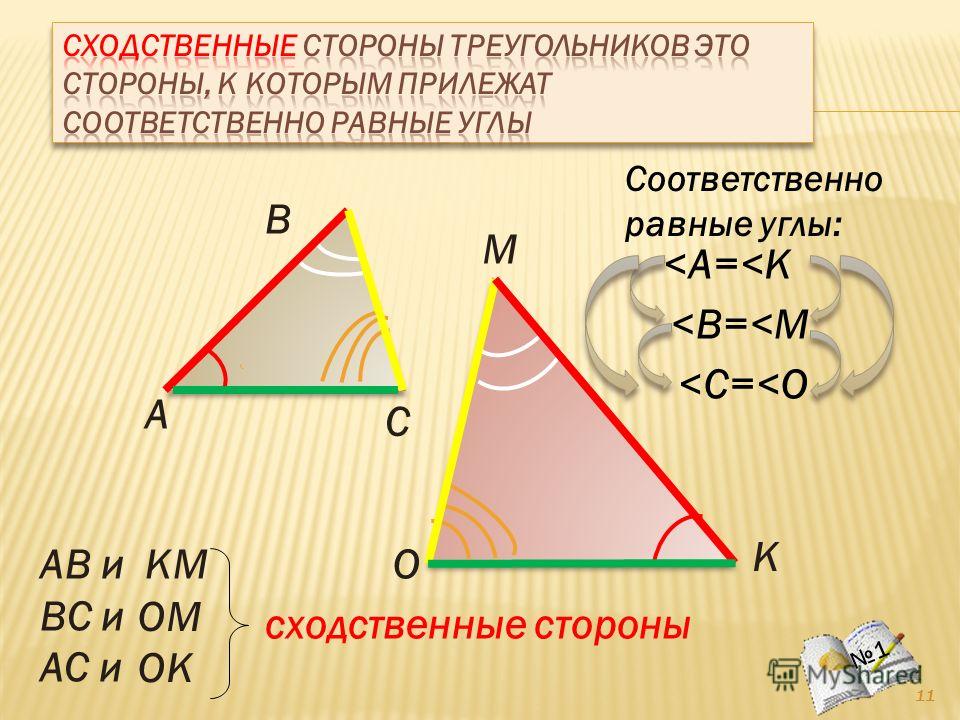
А раз они подобные, то и соотношение сторон у них будет одно и то же. Обозначим сторону квадрата за X:
Теперь построим соотношение:
5 / X = X / 20 ← решим это уравнение
X² = 5 × 20 = 100
X = 10
Зная сторону квадрата, можно легко найти площадь всего треугольника:
(5 + 10) × (10 + 20) / 2 = 15 × 30 / 2 = 255
Представим, что мы ничего не знаем про тригонометрию, углы и подобие треугольников. Возьмём наш рисунок и мысленно достроим его до прямоугольника:
Так как у квадрата все углы прямые, то и синие линии у нас тоже пересекаются под прямыми углами между собой и с внешним прямоугольником. Это значит, что мы можем перенести известные размеры на оранжевый прямоугольник:
Зная длину и ширину, посчитаем его площадь — 5 × 20 = 100.
Теперь посмотрим на рисунок так: у нас есть прямоугольник, разделённый пополам по диагонали. Это значит, что площадь нижних треугольников совпадает с площадью верхних треугольников:
Но раз у нас часть площадей в верхнем и нижнем треугольнике одинаковая, их можно вычесть из обеих частей:
Получается, что площадь оранжевого прямоугольника совпадает с площадью квадрата.
А мы знаем, что площадь прямоугольника равна 100; получается, чтобы найти сторону квадрата, нужно извлечь квадратный корень:
√100 = 10
Значит, сторона квадрата равна 10. Этого достаточно, чтобы посчитать всю площадь треугольника:
(5 + 10) × (10 + 20) / 2 = 15 × 30 / 2 = 255
Непростая задача про диагональ квадрата
Если вы уже окончили школу, попробуйте решить эту задачку в уме, используя формулу длины диагонали квадрата:
d = X√2,
где X — это длина стороны квадрата.
Теперь условия: есть квадрат с длиной стороны x. Из нижнего левого угла провели под каким-то углом линию длиной 12 сантиметров:
После этого повернули на 90 градусов и провели вторую линию длиной 3 сантиметра:
А потом повернули ещё на 90 градусов и провели линию точно до правого верхнего угла. Её длина оказалась равна 9 сантиметрам:
Нужно найти X, то есть длину стороны квадрата.
Чтобы найти решение, нам придётся выйти за рамки квадрата и использовать свойства перпендикулярных линий и прямых углов.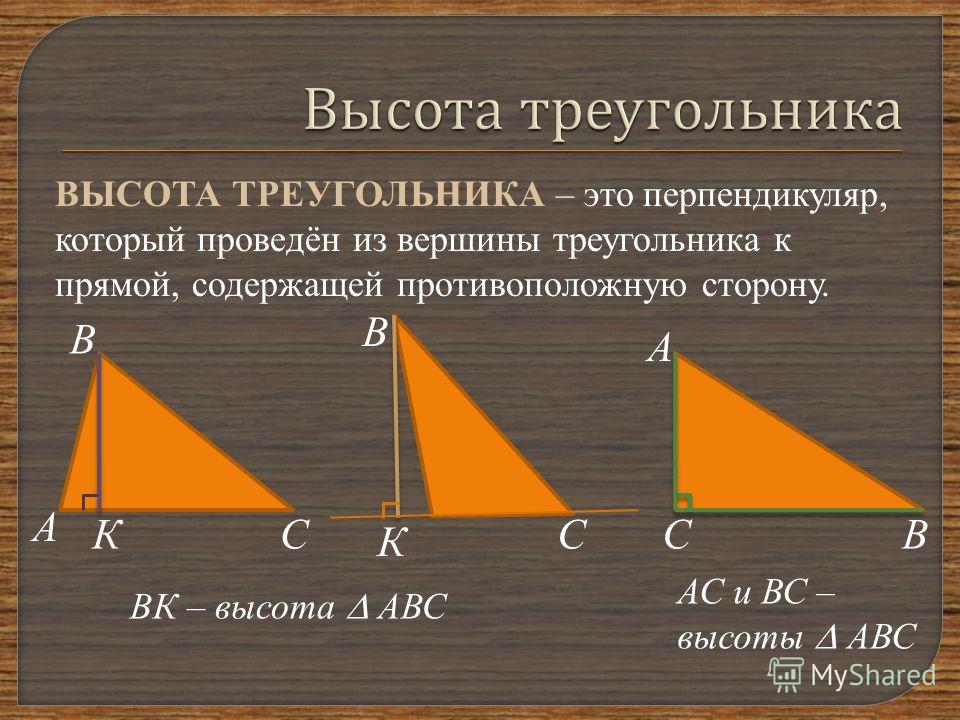
Возьмём два отрезка, 9 и 12 сантиметров и на противоположных концах тоже под прямым углом построим отрезки по 3 сантиметра:
Теперь достроим недостающие линии в каждом прямоугольнике — 9 и 12 сантиметров — и тоже под прямым углом. Так как везде получились углы по 90 градусов, то перед нами два прямоугольника с общей стороной 3 сантиметра:
Если их объединить, то у нас получится прямоугольник длиной 9 + 12 = 21 сантиметр и шириной 3 сантиметра. Проведём диагональ в этом прямоугольнике:
А теперь важное замечание: так как углы прямоугольника совпадают с углами квадрата, то диагональ прямоугольника — это диагональ квадрата и их длины равны. По теореме Пифагора a² + b² = c² найдём диагональ:
21² + 3³ = с² → 441 + 9 = с² → с² = 450
с = √450 = 15√2
Тут нам пригодится формула длины диагонали квадрата: с = X√2. Но у нас c = 15√2, получается, что X = 15 — это и есть длина стороны квадрата.
Текст:
Михаил Полянин
Редактор:
Максим Ильяхов
Художник:
Алексей Сухов
Корректор:
Ирина Михеева
Вёрстка:
Кирилл Климентьев
Соцсети:
Виталий Вебер
Соответствие сторон в геометрии
Соответствие сторон в геометрии — это два или более отрезка двух фигур одинаковой длины.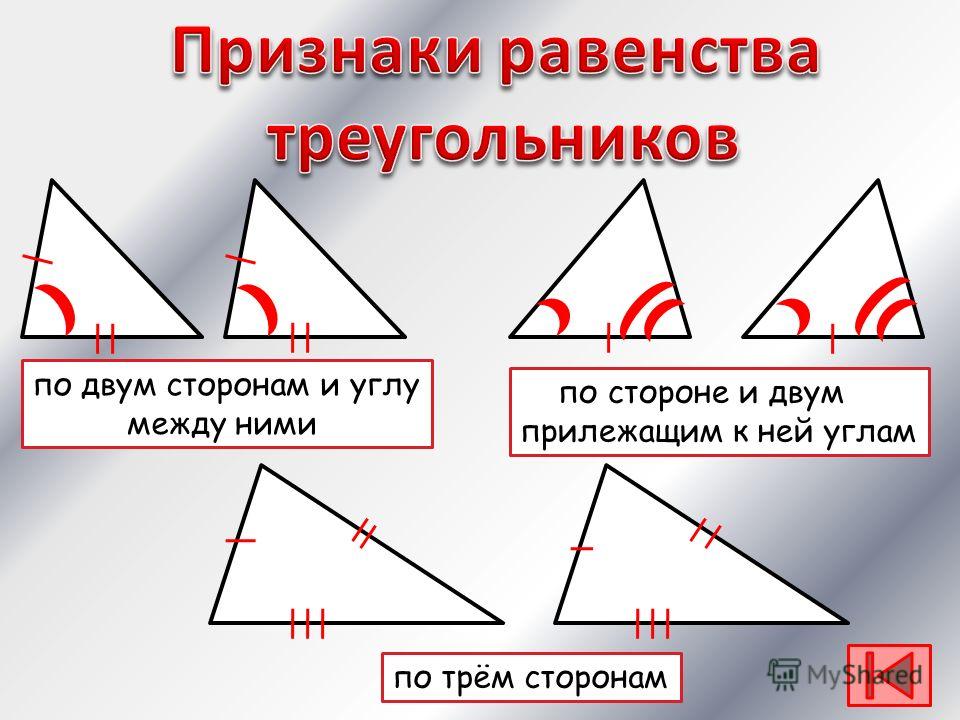
Например, на приведенной ниже диаграмме отрезок AB имеет ту же длину, что и отрезок PQ. Это соотношение верно и для всех других пар соответствующих сторон.
Причина, по которой это важно, заключается в том, что это означает, что если вы знаете размеры одной фигуры, вы можете использовать эту информацию для предсказания другой фигуры. Например, если бы мы знали, что треугольник ABC в два раза шире треугольника PQR, мы могли бы заключить, что отрезок PQ будет вдвое длиннее отрезка AB.
Существует несколько различных способов определения соответствующих сторон в геометрии. Самый распространенный метод – использование углов. Если два угла на одной фигуре конгруэнтны, то есть имеют одинаковую меру, то стороны, образующие эти углы, также будут конгруэнтны. Вот почему в приведенном выше примере мы можем с уверенностью сказать, что отрезки AB и PQ являются соответствующими сторонами, даже если мы не знаем их точных длин.
Другой способ определить соответствующие стороны — использовать соотношения и пропорции. Если вы знаете отношение двух соответствующих сторон на одной фигуре, то вы можете использовать это отношение, чтобы найти значение соответствующей стороны на другой фигуре. Например, допустим, мы знаем, что отношение соответствующих сторон в треугольниках XYZ и LMN равно 3:5. Мы можем использовать эту информацию, чтобы составить пропорцию и найти x: 9.0003
3/х = 5/12
3/х * 12/5 = 1
36 = 5x
7,2 = х
Итак, мы знаем, что треугольник XYZ имеет ширину 7,2 единицы.
Соответствующие стороны — важное понятие в геометрии, потому что они позволяют нам делать предсказания о фигурах на основе известной информации. Есть несколько различных способов определить соответствующие стороны, но наиболее распространенным методом является использование углов. Другой способ определить их — использовать соотношения и пропорции. Спасибо за прочтение!
Что такое пример соответствующих сторон?
Если две стороны многоугольника параллельны, то они называются соответствующими сторонами.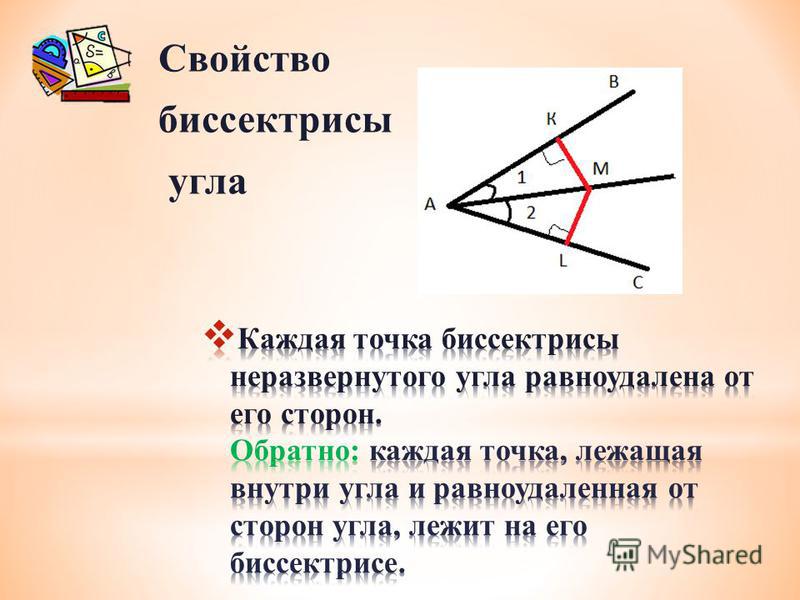
Соответствующие стороны также иногда называют «совпадающими сторонами» или «конгруэнтными сторонами». На рисунке ниже две синие линии параллельны и, следовательно, являются соответствующими сторонами.
Как найти соответствующие стороны?
Чтобы найти соответствующие стороны, вам нужно сначала определить, какие стороны параллельны. Как только вы определили параллельные стороны, вы можете сопоставить их. На рисунке ниже две синие линии параллельны и, следовательно, являются соответствующими сторонами. Две зеленые линии также параллельны, поэтому они также являются соответствующими сторонами.
Какой пример альтернативных внутренних углов?
Если два угла расположены по разные стороны от секущей, но по одну сторону от параллельных прямых, то они являются параллельными внутренними углами.
Какой пример альтернативных внешних углов?
Если два угла расположены по разные стороны от секущей и по разные стороны от параллельных прямых, то они являются параллельными внешними углами.
Какой пример последовательных внутренних углов?
Если два угла расположены по одну сторону от секущей и по одну сторону от параллельных прямых, то они являются последовательными внутренними углами.
Какие 3 соответствующие стороны?
Три соответствующие стороны — это две параллельные стороны и сторона, которая находится между ними. На картинке ниже три соответствующие стороны — это две синие стороны и зеленая сторона.
Что является примером трансверсали?
Секущей называется линия, пересекающая две или более других прямых.
Что такое соответствие в геометрии?
Термин «соответствующий» может иметь разные значения в геометрии, в зависимости от контекста. Иногда это относится к углам или сторонам, которые находятся в одном и том же относительном положении, а иногда к элементам одинакового размера и формы.
Например, соответствующие углы — это углы, находящиеся в одном и том же относительном положении.
Если две прямые пересечь секущей, то углы по одну сторону от этой секущей будут в том же относительном положении, что и углы по другую сторону. Соответствующие углы могут быть либо смежными, либо несмежными.
Аналогично, соответствующие стороны — это стороны, которые находятся в одном и том же относительном положении. Если две фигуры имеют одинаковую форму, то стороны будут в одинаковом относительном положении. Например, если два треугольника имеют одинаковую форму, то стороны будут соответствовать друг другу.
Наконец, соответствующие детали — это детали одинакового размера и формы. Две фигуры могут иметь соответствующие части, даже если они не имеют одинаковой общей формы. Например, два круга могут иметь соответствующие части, даже если они имеют разную форму. Термин «соответствующий» часто используется при обсуждении подобных цифр.
Теорема AAS (угловая сторона) (видео и примеры)
Написано
Малкольм МакКинси
Внепровозглашенный факт
Paul Mazzola
AAS (Angle-gheck.
-Side) теоремаТеорема AAS утверждает, что если два угла и не включенная в них сторона одного треугольника конгруэнтны соответствующим частям другого треугольника, то эти треугольники конгруэнтны.
Обратите внимание, что здесь написано «не включенная сторона», что означает, что вы берете два последовательных угла, а затем переходите к следующей стороне (в любом направлении). Вы не принимаете сторону между этими двумя углами! ( Если бы вы это сделали, вы бы использовали постулат ASA ).
Угол-Угол-Сторона определение Математика — это чистая наука, поэтому вас почти никогда не останавливают на улице и не заставляют проверить два треугольника на конгруэнтность. Однако если бы вы были им, вы могли бы проверить треугольники на конгруэнтность пятью способами. Знание как можно большего количества методов помогает вам, давая вам гибкость в решении любой ситуации, будь то остановка на улице или тупик в классе. Этот метод называется 90 114 Angle Angle Side или теоремой 9 AAS.
0115 .
Доказательство конгруэнтности треугольников
Существует пять методов проверки конгруэнтности треугольников, хотя один из них ограничен для использования с прямоугольными треугольниками. Вот все пять:
Боковой Боковой Боковой (SSS)
Боковой Угол Боковой (SAS)
Угол Боковой Угол — (ASA)
Эта нога зарезервирована (HL) для прямоугольных треугольников.
Уголок Боковой угол — (AAS)
В других уроках мы проиллюстрировали другие методы, и нет, мы не просто случайным образом переставили «Угол» и «Сторона» всеми возможными способами. Обратите внимание, например, что вы не можете найти угол, угол, угол в качестве доказательства конгруэнтности (которое зарезервировано для подобия), и вы не можете состряпать постулат о боковом и боковом углах.
Какой бы термин вы ни увидели зажатым между другими, эта часть включает . Включенный угол или сторона физически находятся между другими сторонами треугольника.
Таким образом, Side Angle Side (SAS) означает одну сторону, угол рядом с этой стороной, а затем сторону рядом с этим углом. Эта сторона там, совсем одна, а не между углами.
Для каждого метода тестирования вы проверяете три части, указанные между двумя треугольниками. Если соответствующие части конгруэнтны для этих трех частей, два треугольника конгруэнтны. Эти методы проверки или доказательства позволяют установить соответствие, проверяя только половину частей (с трех возможных сторон и трех возможных углов).
Теорема AAS
Возможно, в вашем учебнике это называется теоремой или может быть названо постулатом; не беспокойтесь об этом! Держите в уме концепцию, а не суетливые слова, пытаясь доказать конгруэнтность треугольников.
Чтобы продемонстрировать настоящие треугольники, ниже мы с гордостью представляем △GUM и △RED .
Теорема Ааса — конгруэнтные и последовательные треугольники Конгруэнтны ли они? Обратите внимание на маленькие штриховки, обозначающие все совпадения, которые в математическом сокращении используют символ ≅ .
Конгруэнтные детали являются:
ϩG≅ Вор
тнам. 2
.0115
Из этих треугольников мы знаем, что два внутренних угла конгруэнтны (и являются последовательными или рядом друг с другом), но мы ничего не знаем о стороне между ними. Вместо этого, казалось бы, бесполезно, мы узнаем, что другая сторона конгруэнтна.
Просмотрев наш набор инструментов, полный методов проверки сходства треугольников, мы можем попробовать каждый из них:
Сторона Сторона Сторона (SSS) — Это не сработает, потому что мы не знаем обо всех трех сторонах
Угол стороны Сторона (SAS) — это тоже не сработает, потому что мы знаем два угла, а не две стороны
Угол Сторона Угол (ASA) — сначала это выглядит многообещающе, но сторона, о которой мы знаем, не является включенной стороной; он торчит там, за одним из двух известных углов
Нога гипотенузы (HL) — Забудьте об этом! Это зарезервировано для прямоугольных треугольников, которых у нас нет
Угол Угол Сторона (AAS) — Это билет! Это тот (единственный), который мы можем использовать!
Почему работает теорема ААС?
Скажите, пожалуйста, сколько в сумме составляют внутренние углы всех треугольников?
Мы надеемся, что вы сказали 180° , потому что это правильный ответ.
Если вы знаете два угла треугольника, то вы знаете три угла треугольника. Это не магия; это математика:
Решение ∠U теперь дает вам два угла с включенной стороной. Ты это видел? Мы обогнули ту сторону, которая только что торчала, совершенно одна, и поместили ее между двумя определенными углами, ∠G и ∠U . Итак, там, где когда-то у нас был ААС, мы пробежались по треугольнику и превратили его в АСА, что уже является постулатом.
Если два угла и прилежащая к ним сторона одного треугольника конгруэнтны двум соответствующим углам и прилежащей к ним стороне другого треугольника, то эти два треугольника конгруэнтны.
Пример теоремы AAS
Здесь мы предлагаем два новых треугольника: △LEG и △ARM . Обратите внимание на все маленькие штриховки, указывающие на конгруэнтность углов и сторон:
Пример конгруэнтности AAS PostulateϪl ≅ ▲
ϩ ≅ Ϫr
Сторона
Сторона
555555 555 55 5 .
, что еще ты знаешь?Мы надеемся, что вы сказали, что Ϫg ≅ Ϫm, , потому что:
180 ° − Вор — ВЕ = ♂
180 ° −x — or = strm = or = or = stm = or = or = or = stm.
∠G ≅ ∠M
Что это позволяет вам делать сейчас? Deploy ASA and declare the two triangles congruent, since:
∠L ≅ ∠A
Side LG ≅ Side AM
∠G ≅ ∠M
What real геометры делают
Вам не нужно доказывать конгруэнтность третьего угла, а затем развертывать ASA, так как у нас есть, готовая и ожидающая, теорема AAS. Так что настоящие математики и геометры просто прыгают прямо к ААС и объявляют два треугольника конгруэнтными.
Если вам нужно объяснить эту теорему другому студенту, другу или случайному незнакомцу на улице, вы не можете совершить прыжок из двух углов в загадочный третий без объяснения причин.
, что еще ты знаешь?