Строить график функции онлайн: Построение графика функции онлайн

alexxlab / / Разное

Построить график функции y 3 в степени. Калькуляторы для построения графика функции

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.


На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.


Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

  1. Введите ваше уравнение в поле после знака «=».
  2. Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.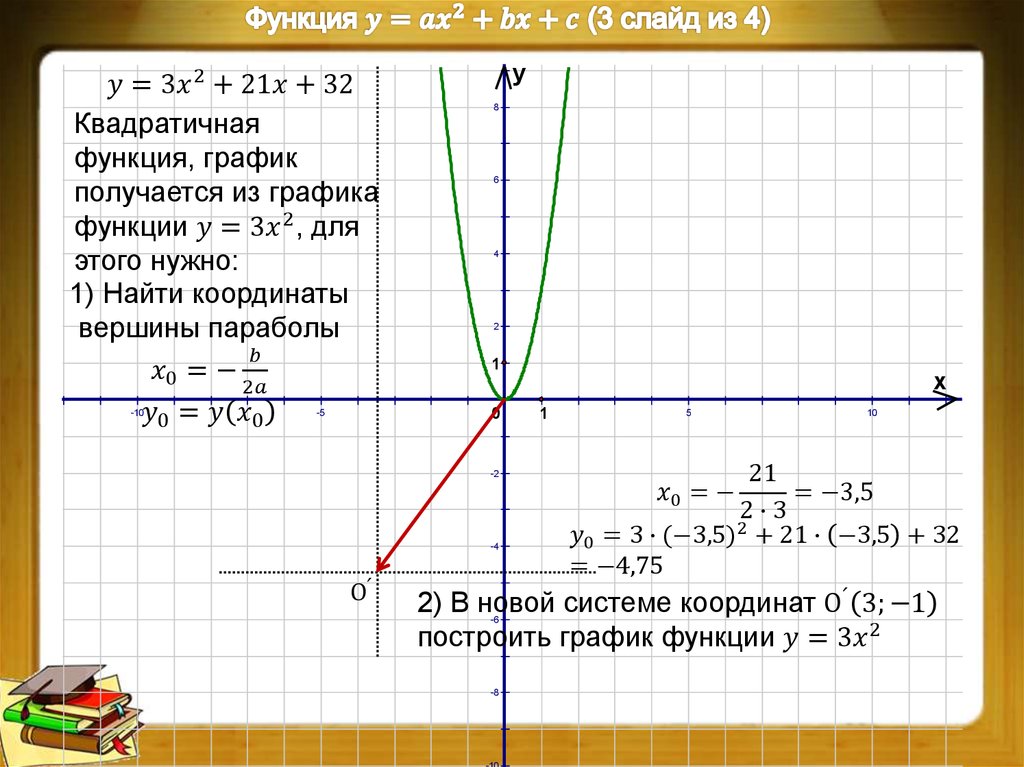


В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

  1. Выберите необходимый способ задания графика.
  2. Введите уравнение.
  3. Задайте интервал.
  4. Нажмите кнопку «Построить» .


Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

  1. Найдите в списке необходимую вам функцию.
  2. Щелкните на нее левой кнопкой мыши
  3. При необходимости введите коэффициенты в поле «Функция:» .
  4. Нажмите кнопку «Построить» .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.


Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).

Инструкция:

  1. В левом столбце кликните правой кнопкой мыши по свободной строке.
  2. В нижнем левом углу нажмите на значок клавиатуры.
  3. На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
  4. График строится в реальном времени.

Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.

Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений.

3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).

В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция

у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .

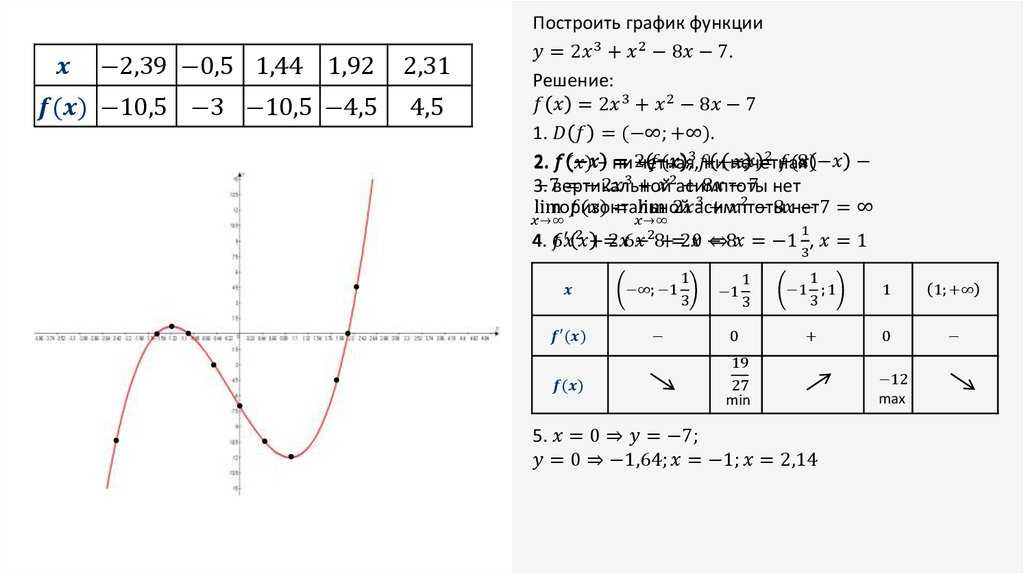
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:


Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.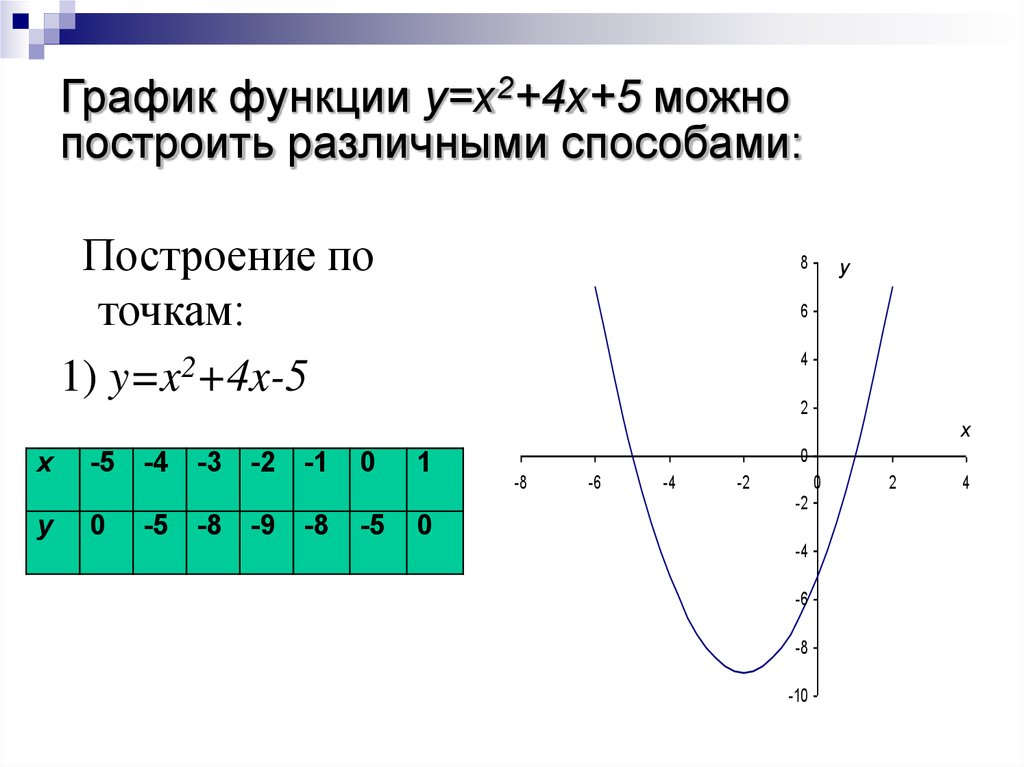

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:


Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

.

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

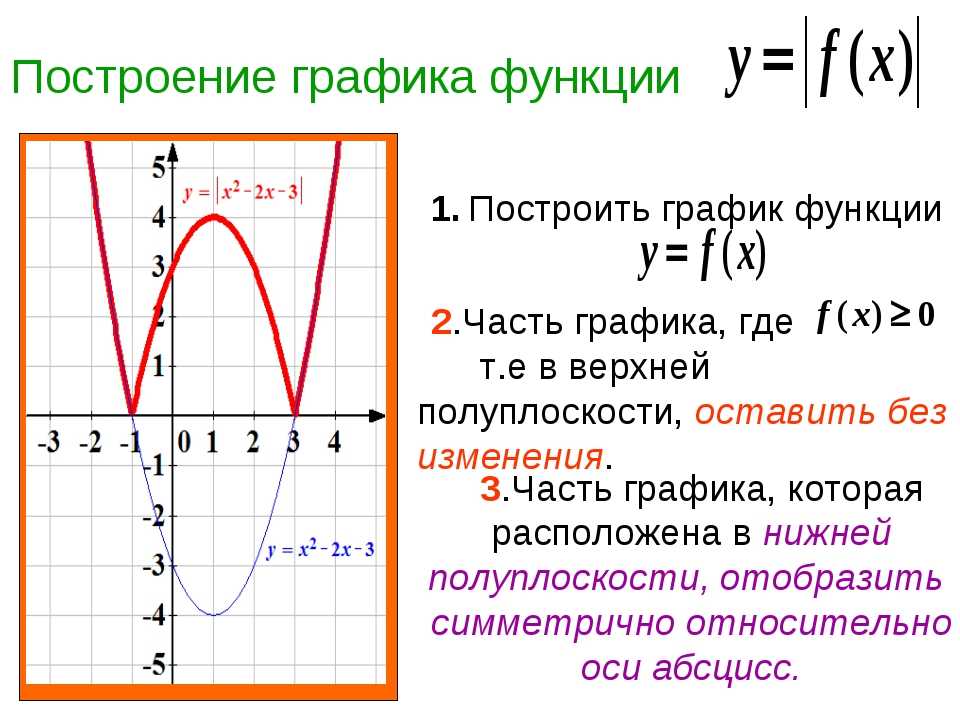
График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции

у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

Пример 2. Построить график функции у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции

у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x).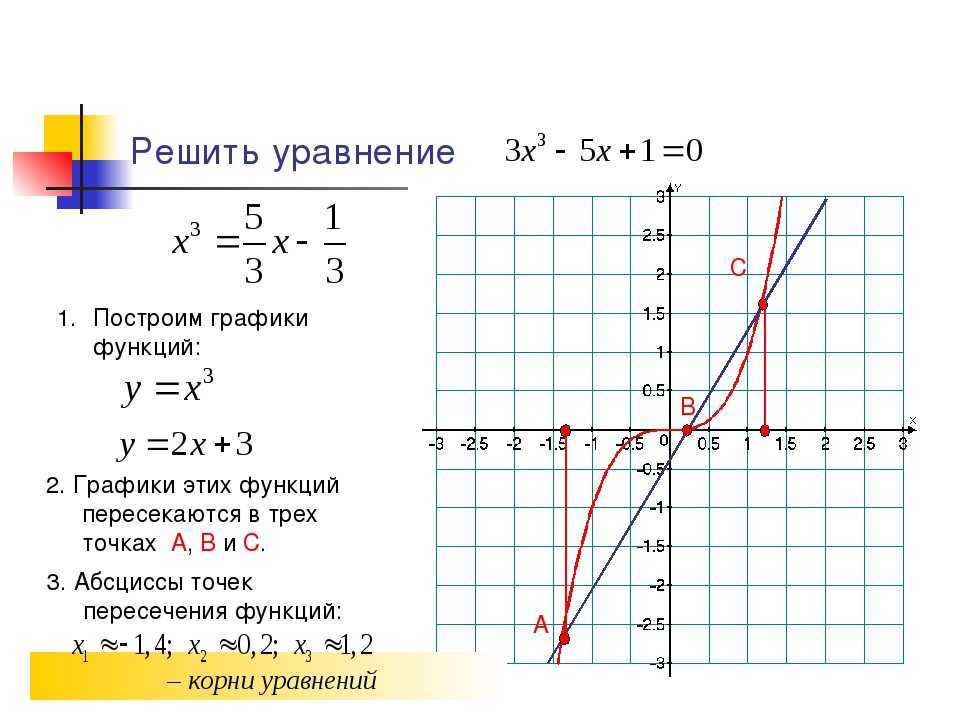 если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

  • Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

  • Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
  • Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
  • Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
  • Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

  • В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
  • В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

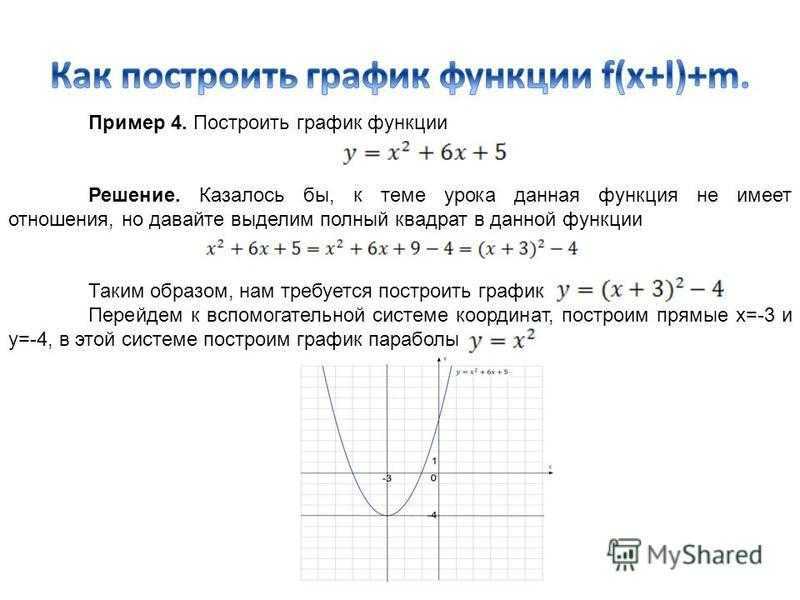
Как построить график функции в Эксель Онлайн

При помощи онлайн-редактора таблиц «Эксель-онлайн.РФ» можно строить различные графики, в том числе графики функции. Причём эти графики могут быть построены как на основе уже имеющихся у вас данных, так и на основе вычислений, сделанных прямо в «Эксель-онлайн.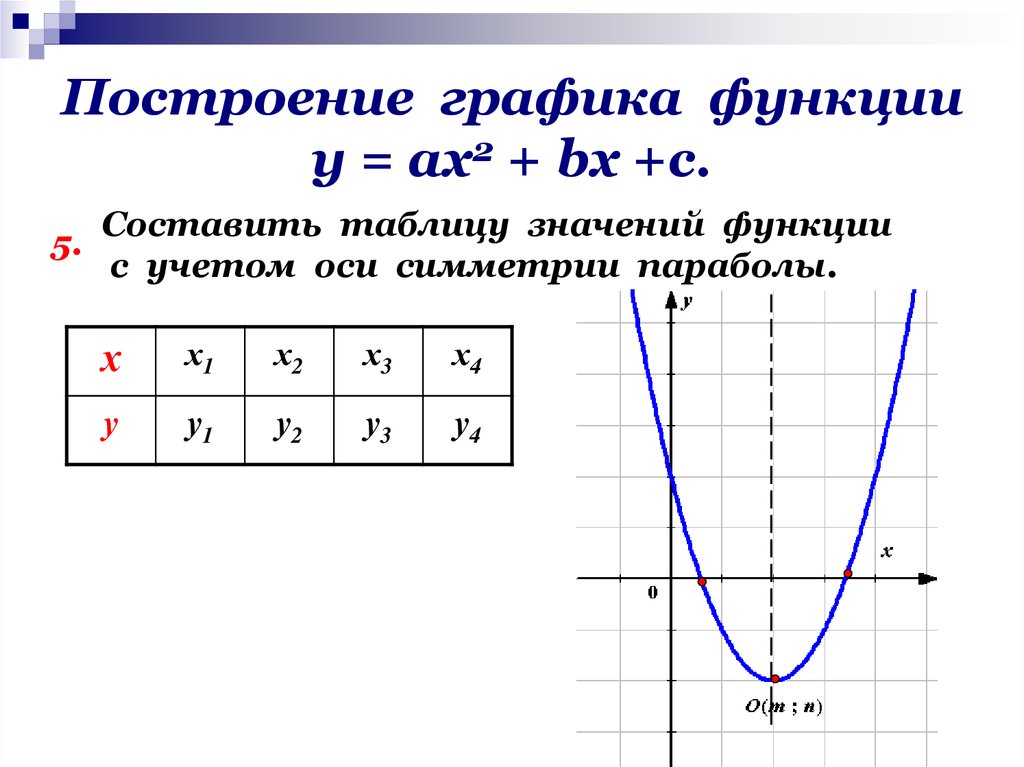 РФ».

Пример графика зависимости функции от аргумента

Разберём построение графика на примере типичной алгебраической зависимости — зависимости функции от аргумента, где аргумент — это «X», а значение функции — «Y».

Аргументом (X) назначим время, за которое автомобиль проезжает 100 км, для простоты и удобства счёта пусть это будет 1 час. В свою очередь, значением функции (Y) в данном случае выступит количество пройденных километров.

Итак, за 1 час (X) наша машина преодолеет расстояние 100 км (Y), соответственно за 2 ч. — 200 км, за 3 ч. — 300 км, а за 4 — 400 км.

Построение графика зависимости функции от аргумента
  1. Для начала работы вам нужно удалить текст в верхнем левом углу и ввести свои данные или же загрузить уже готовый документ.
  2. Затем выделите все ячейки с нужными цифрами.
  3. Откройте вкладку «Вставить» на панели инструментов (вверху экрана) и нажмите иконку с подписью «График».
  4. Выберите из списка наиболее подходящий вариант, допустим, «Объёмный график».
  5. Нажмите ЛКМ, и график автоматически появится в вашей таблице.
Варианты построения графиков

Также при помощи онлайн-редактора таблиц «Эксель-онлайн.РФ» вы можете создавать другие различные варианты графиков: график с накоплением, нормированный график с накоплением, график с маркерами, график с маркерами и накоплением, нормированный график с маркерами и накоплением.

Кроме того, в нашем редакторе можно делать гистограммы, диаграммы и многие другие виды графического представления данных, доступные в классическом Excel.

Изменить тип или вид графика, диапазон отображаемых данных

Изменить тип или вид графика можно, выделив уже сформированный график и нажав ПКМ. После этого откроется меню, при помощи которого вы оперативно отформатируете данные, сможете быстро наглядно сравнить — какое графическое исполнение будет наиболее актуальным в вашем случае.

Здесь же предусмотрена функция «Выбрать данные», благодаря которой возможно выделение диапазона данных, которые необходимо видеть на графике.

Построение графика функции онлайн

Функция f ()

График:

от до

Точки пересечения:

показывает?

Введите:

{ здесь кусочно-определенная функция

Примеры функций для построения графиков

Приведенные выше примеры также содержат:

  • модуль или абсолютное значение: absolute(x) или |x|
  • квадратные корни sqrt(x),
    кубических корней cbrt(x)
  • тригонометрические функции:
    sinus sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
  • экспоненциальные функции и показатели exp(x)
  • обратные тригонометрические функции:
    арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x)
  • натуральные логарифмы ln(x),
    десятичных логарифмов log(x)
  • гиперболические функции:
    гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
  • обратные гиперболические функции:
    гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс ath(x), гиперболический арккотангенс acoth(x)
  • другие тригонометрические и гиперболические функции: секанс
    sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксикансек asech(x), гиперболический арккосеканс acsch(x)
  • функции округления:
    округлить до пола(x), округлить до потолка(x)
  • знак числа:
    знак(х)
  • для теории вероятностей:
    функция ошибок erf(x) (интеграл вероятности), Функция Лапласа laplace(x)
  • Факториал х :
    х! или факториал(х)
  • Гамма-функция gamma(x)
    • 95
    — возведение в степень
    х + 7
    — дополнение
    х — 6
    — вычитание
    Вещественные числа
    вставка как 7,5 , № 7,5
    Константы
    Пи
    — число Пи
    и
    — основание натурального логарифма
    я
    — комплексный номер
    оо
    — символ бесконечности

    Чтобы увидеть подробное решение,
    поделитесь со всеми своими друзьями-студентами:

    Графические математические функции в Python

    «графический калькулятор», такой как Desmos или WolframAlpha.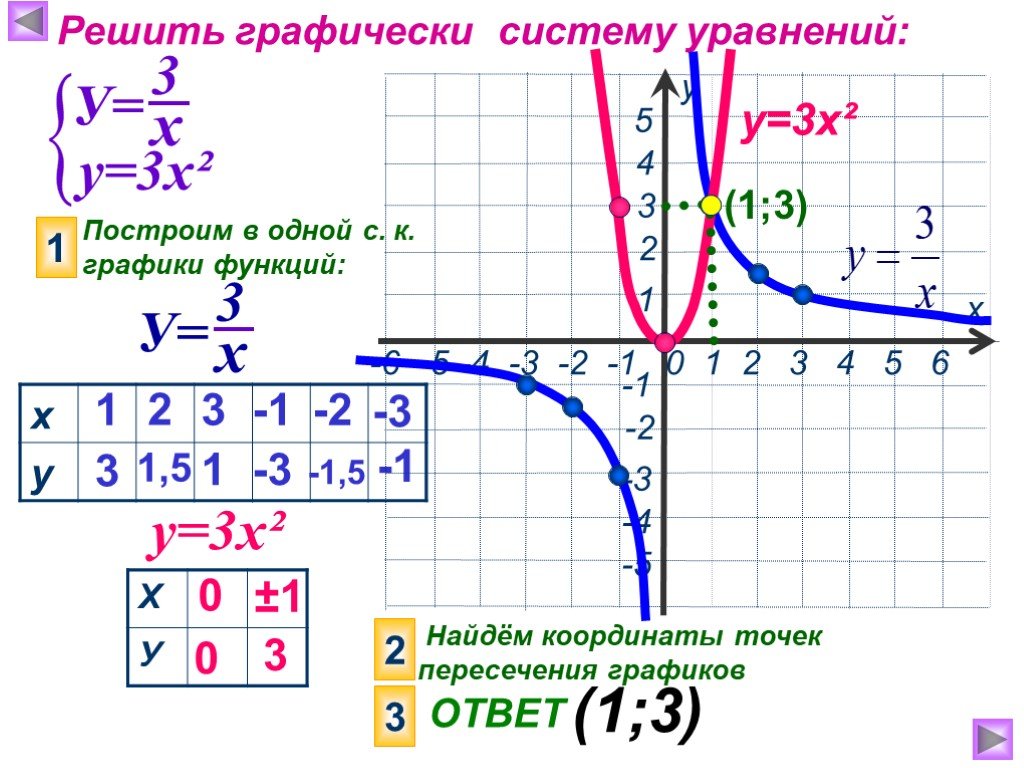 Использование этого способа означает, что вам нужно настроить координаты Matplotlib и выполнить несколько дополнительных шагов.

    Рекламные объявления

    Первая проблема, с которой мы сталкиваемся, — это вопрос о том, как построить математическую функцию. Если мы используем функцию построения графика в SymPy, которая может использовать Matplotlib в качестве серверной части, эта проблема будет решена для нас, но как мы настроим ее для простой функции Python, если мы хотим отображать результаты этой функции, примененной к диапазон значений?

    Более того, после того, как мы проработаем это, мы столкнемся с некоторыми дополнительными проблемами форматирования, которые нам необходимо решить.

    • Если мы неправильно настроим размер графика, по умолчанию MatPlotlib может дать нам сжатый график, тогда как часто нам нужен квадратный график с одинаковыми экстентами для осей X и Y.
    • По умолчанию Matplotlib не будет отображать для нас линии осей X и Y (но их легко добавить)
    • Нам, вероятно, понадобятся какие-то метки на оси или, возможно, сетка, поскольку это делали на миллиметровке, которую мы так любили (?) в старшей школе.

    Мы бегло рассмотрели некоторые из этих проблем в статье Создание интерактивного графика Python с использованием Matplotlib в Jupyter, но наше внимание было сосредоточено на настройке интерактивности.

    В этой статье мы хотим использовать более пошаговый подход, чтобы подробно объяснить каждую фазу для читателей, которые могут захотеть — или даже нуждаются — использовать matplotlib для работы в качестве несколько «настроенного вручную» графического калькулятора.

    Advertisements

    Опять же, Matplotlib — это низкоуровневый инструмент, и такого рода вещи гораздо проще выполнить в инструменте, больше предназначенном для символьной математики (например, SymPy) или графическом калькуляторе (например, Desmos). Тем не менее, по пути мы многое узнаем о настройке Matplotlib, поэтому стоит понять, как это сделать.

    Мы начинаем недалеко от начала Евклида 2300 лет назад. Начнем с простых точек и линий.

    Построение линии в Matplotlib

    Начнем с простой линейной функции. Мы помним из курса алгебры травма , что линейная функция — это просто функция, график которой представляет собой прямую линию, в виде:

    В Python легко увидеть, как можно закодировать такую ​​функцию, с некоторыми значениями по умолчанию для m (наклон) и b (пересечение с осью y):

     по линейному определению (x, m=2, b = -1):
     """Функция для построения произвольной точки (x) на линии."""
     return m * x + b

    В качестве краткого отступления вспомним, что математически функция отображает одно числовое значение в другое. Строго говоря, это то, что функция делает и в компьютерных науках, хотя часто то, что мы называем функцией, на самом деле является подпрограммой, которая не возвращает значение, как «функция» Python print .

    Advertisements

    Построение графика этой функции со значениями по умолчанию (y = 2x -1) очень просто в Desmos, как мы видим здесь. В Matplotlib, чтобы получить из него строку в Python, нам сначала нужно получить какие-то значения для X, поэтому у нас будет линия, а не одна точка. К счастью, для отрезка нам нужны только две точки. В этом примере мы будем использовать списки Python, а не массивы NumPy.

     x_values ​​= [-5, 5]

    Теперь, когда у нас есть значения x, нам нужно применить нашу функцию, чтобы сопоставить их со значениями y. Мы можем сделать это, используя простой для понимания, и построить функцию, используя matplotlib

     import matplotlib.pyplot as plt
y_values ​​= [линейный (x) для x в x_values]
plt.plot(x_values, y_values)

    Вывод:

    Как видите, макет по умолчанию оставляет много возможностей для улучшения. Нам потребуются функции для рисования осей, создания квадратной сетки и установки размера делений сетки. Все они будут принимать минимальный и максимальный диапазон для использования.

    Рекламные объявления

    Чтобы выбрать диапазон для использования, давайте просто заметим, осмотрев его визуально, что 12 x 12 будет в данном случае «достаточно большим» для значений.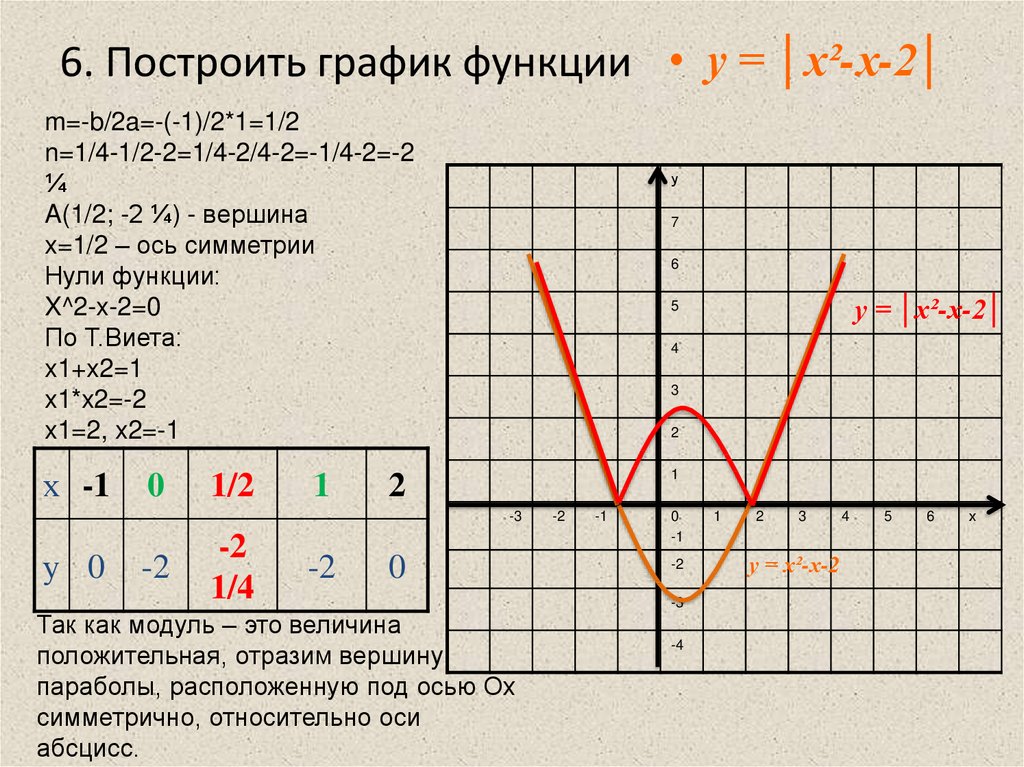 Но сначала давайте определим каждую функцию.

    Чтобы сделать сетку квадратной, мы дважды вызываем функцию оси Matplotlib.

     по определению configure_graph_grid (grid_min, grid_max):
    """Установить квадратную ось сетки"""
    
    # Сделайте его квадратным и установите ограничения
    плт.ось('квадрат')
    plt.axis(( grid_min, grid_max, grid_min, grid_max))

    По сути, вызов этой функции дает нам квадратный лист бумаги нужного размера. Теперь давайте превратим его в «миллиметровку», нарисовав на нем прямоугольники.

     по определению set_ticks (оси, min_val, max_val, tick_size = 1):
    """Устанавливает степень детализации полей. По умолчанию 1"""
    ticks = [x для x в диапазоне (min_val, max_val, tick_size)]
    axes.set_xticks(тики)
    axes.set_yticks(ticks)

    Хорошо, теперь у нас есть диаграмма. Затем, как вы помните из старшей школы, «достаньте свои линейки. Пришло время нарисовать эти оси X и Y».

    Реклама

     def plot_axes(grid_min, grid_max):
    """Постройте оси x и y, сначала x, затем y"""
    plt. plot([grid_min, grid_max], [0,0], color=".3")
    plt.plot([0,0],[grid_min, grid_max], цвет=".3")
    plt.grid()

    Мы почти у цели. Теперь мы готовы использовать эти функции и написать еще немного кода. В частности, мы:

    • Устанавливаем минимальное и максимальное значения сетки. Ранее мы говорили, что подойдет -12, 12
    • Установите размер фигуры (в дюймах). Мы выберем шесть (хотя мы можем уменьшить его на нашем снимке экрана).
    • Вызов нужных нам функций.
    • Постройте график:
     min_val, max_val = -12, 12
рис, оси = plt.subplots (figsize = (6,6))
configure_graph_grid (min_val, max_val)
plot_axes (min_val, max_val)
set_ticks (оси, min_val, max_val)
line = plt.plot(x_values, y_values)

    Вывод теперь намного проще для понимания, чем наш первый график:

    Рекламные объявления

    каждый x) равен 2, а точка пересечения y равна -1.

    Нелинейный график в Matplotlib

    Теперь, когда у нас есть большая часть кода для настройки графика, мы хотим попробовать свои силы в нелинейном графике.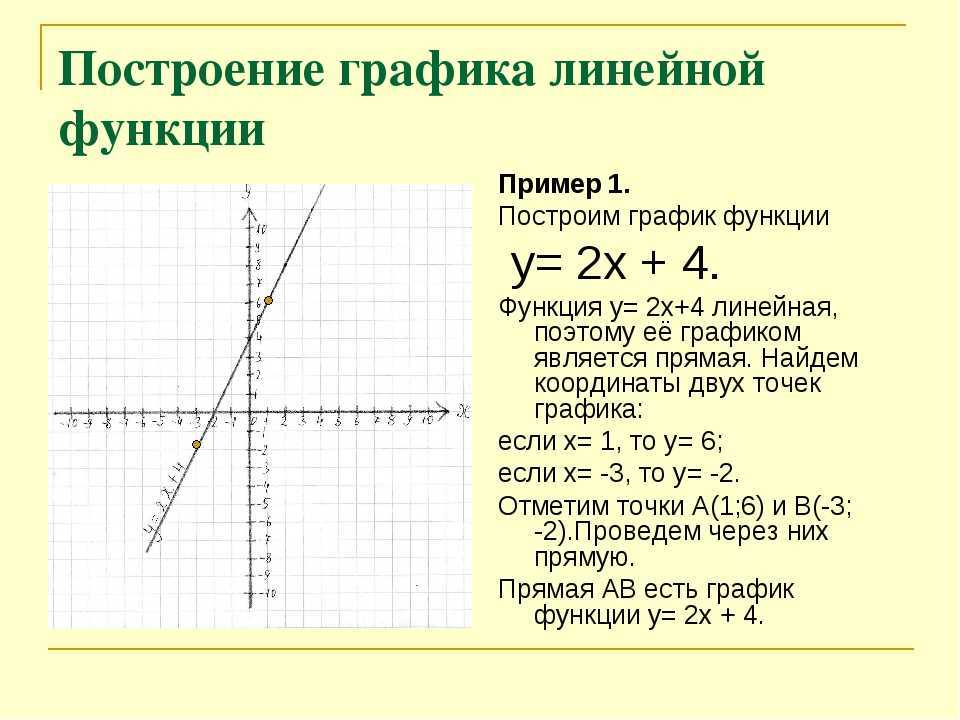 Нелинейные сюжеты привносят пару новых морщин. Во-первых, для кривой нам нужно нанести более двух точек. Это легко реализовать с помощью функции NumPy linspace . Это немного сложнее, используя список Python (но не так уж плохо). Здесь мы показываем обе версии. Нам нужен диапазон в 100 точек в каждом случае, равномерно распределенный между -5 и 5.

     импортировать numpy как np
x_as_array = np.linspace (-5, 5, 100)
x_as_list = [(val / 10) для val в диапазоне (-50, 51)]

    Используя linspace , мы просто передаем нужные параметры. Чтобы настроить его как список, мы использовали понимание списка с функцией диапазона, но поскольку диапазон имеет дело с целыми числами, нам нужно было масштабировать «вверх», чтобы получить 100 целых чисел в правильном диапазоне, а затем разделить результат на 10, чтобы получить от -5 до +5 с шагом 0,1.

    Advertisements

    Вторая проблема, с которой нам нужно разобраться, — это возможность существования асимптоты, то есть функции, при которой f(x) приближается к бесконечности в пределе.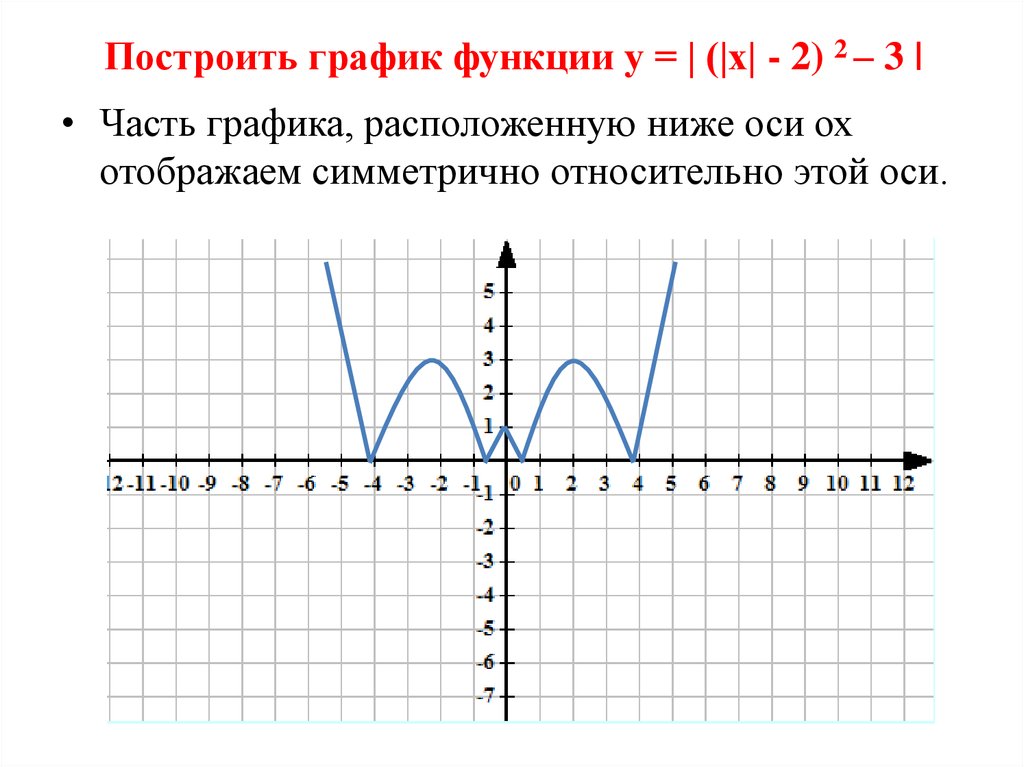

    У меня случайно была такая функция в некоторых заметках по исчислению, которые я взял в SymPy:

    Если мы реализуем это как функцию Python, мы должны быть осторожны, чтобы не допустить деления на ноль (поскольку именно в этом случае вызывает асимптоту).

    Для этой цели подойдет следующий код. Если знаменатель равен нулю, мы возвращаем NaN (не число). В противном случае мы делим x на знаменатель, как показано в приведенной выше функции.

     из импорта математики нан
def function_with_asympotes(x):
    """Реализовать дробную функцию с возможным нулем в знаменателе"""
    номинал = (х + 3) * (х - 1)
    если номинал:
        возврат х / номинал
    еще:
        вернуть нан

    Используя функции конфигурации, которые мы написали ранее, все, что осталось сделать сейчас, это настроить наш массив Y, вызвав функцию в цикле так же, как мы сделали это для нашей линейной функции. Затем мы вызываем наши функции конфигурации и строим график, как и раньше. Собрав все это вместе, код для построения графика нашей линейной функции выглядит так:

     x_array = np.linspace(-5, 5, 100)
y_array = np.array([function_with_asympotes(x) для x в x_array])
минимальное_значение, максимальное_значение = -12, 12
рис, оси = plt.subplots (figsize = (6,6))
configure_graph_grid (min_val, max_val)
plot_axes (min_val, max_val)
set_ticks (оси, min_val, max_val)
строка = plt.plot(x_array, y_array)

    Получилось достаточно удовлетворительно, хотя и не совсем идеально. Вертикальные асимптоты равны -3 и 1 (два значения, при которых знаменатель равен нулю). На этом графике не похоже, что они простираются до бесконечности, но значения правильные. Для сравнения, вот как это начертил SymPy:

    Рекламные объявления

    Заключительные мысли

    На этом этапе мы показали, как использовать Matplotlib в качестве своего рода графического калькулятора «сделай сам». Конечно, как мы уже подчеркивали, это не самый простой инструмент для этого.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *