Формула суммы n первых членов геометрической прогрессии 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 13.
Сумма первых n-членов геометрической прогрессии.
Всем привет. Сегодня мы выведем формулу суммы первых n-членов геометрической прогрессии.
Расскажу историю о награде изобретателя шахматной игры. По преданию, индийский принц, восхищенный остроумием игры и разнообразием возможных положений шахматных фигур, призвал к себе ее изобретателя, и сказал ему: «Я желаю достойно наградить тебя за прекрасную игру, которую ты придумал. Я достаточно богат, что исполнить любое твое желание». Изобретатель попросил в награду столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую в 2 раза больше, т. е. 2 зерна, на третью еще в 2 раза больше, т. е. 4 зерна, и т. д. до 64-й клетки. Говорят, что принц рассмеялся, услышав, какую награду попросил у него ученый. Так сколько же зерен должен был получить изобретатель шахмат?
Так сколько же зерен должен был получить изобретатель шахмат?
Итак, получим последовательность 1; 2; 4; 8; 16; 32; 64;…
А это геометрическая прогрессия (bn):
Возникает необходимость найти сумму 64-х слагаемых: S64 = 1+2+4+8+16+32+64+…
Это очень сложно и громоздко…
Давай выведем формулу суммы первых n-членов (Sn) для геометрической прогрессии (bn). Обозначим сумму (Sn):
Sn =b1+b2+b3+b4+…+bn (1).
Умножим обе части этого равенства на q, получим:
Snq=b1q+b2q+b3q+…+bnq
Учитывая, что
b2=b1q, b3=b2q, …., bn =bn-1q, получим:
Snq=b 2+b3+b4+…. bn-1q+ bn+bnq (2)
bn-1q+ bn+bnq (2)
Вычтем почленно из равенства (2) равенство (1) и приведем подобные члены:
Snq- Sn= (b2+b3+b4+…+ bn+ bnq) – (b1+b2+b3+b4+…+bn)= bnq- b1, в левой части вынесем общий множитель за скобку и получим:
Sn(q-1)= bnq- b1, отсюда
S n = bnq-b1q-1; q≠1
При решении многих задач удобно пользоваться формулой, записанной в другом виде, подставим вместо bn формулу n-го члена bn=b1qn-1
S n=bnq-b1q-1= b1qn-1q-b1q-1= b1qn-b1q-1= S n=b1(qn-1)q-1, если q≠1.
Итак,
|
Sn=b1(qn-1)q-1 |
Вернемся к задаче о вознаграждении и вычислим количество зерен:
S64 =1(264-1)2-1=264-1= 18 446 744 073 709 551 615 ≈ 18,4 ∙ 1018
Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли.
Давай рассмотрим несколько примеров:
(bn) – геометрическая прогрессия, где
b1=2, b2= -4. Найдем сумму первых 8 членов геометрической прогрессии:
S n=b1(qn-1)q-1 , q=b2b1=-2,
S8=2((-2)8-1)-2-1=2(256-1)-3=-170
Ответ: 170
Рассмотрим еще один пример:
Найдем сумму десяти первых членов геометрической прогрессии: 3; 6; 12; 24;….
Найдите S10 = ?
S n =b1(qn-1)q-1, q=b2b1=63=2
S10=b1(qn-1)q-1 = 3(210-1)2-1 = 3(210 – 1)=
3 ∙ (1024 — 1) = 3 ∙ 1023 = 3069.
Ответ: 3069
В следующей задаче найдем сумму первых семи членов геометрической прогрессии, в которой второй член равен 6 и четвертый – равен 54, если известно, что все ее члены положительны.
Итак, чтобы найти сумму семи членов, необходимо найти знаменатель данной прогрессии. Для этого найдем третий член, воспользовавшись свойством геометрической прогрессии, получим:
Для этого найдем третий член, воспользовавшись свойством геометрической прогрессии, получим:
b32=b2∙b4
b32=6∙54=324
b3=18 или b3=-18
По условию задачи все члены прогрессии положительны, значит третий член равен 18.
Ответ:18
Найдем знаменатель и первый член геометрической прогрессии:
q=b3b2=186=3, значит b1=b2q=63=2
Теперь найдем сумму:
S7=b1q7-1q-1=237-13-1=2187-1=2186
Ответ: 2186
Алгебра Формула суммы первых n-членов геометрической прогрессии
Материалы к уроку
Конспект урока
Согласно легенде, индийский принц решил наградить изобретателя шахмат и предложил ему самому выбрать награду. Изобретатель шахмат попросил в награду за свое изобретение столько зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую – в два раза больше, то есть два зерна, на третью – еще в два раза больше, то есть четыре зерна, и так далее до шестидесяти четвертой клетки. Каково же было удивление принца, когда он узнал, что такую, казалось бы, скромную просьбу невозможно выполнить.
Каково же было удивление принца, когда он узнал, что такую, казалось бы, скромную просьбу невозможно выполнить.
Действительно, число зерен, о которых идет речь, является суммой шестидесяти четырех членов геометрической прогрессии, первый член которой равен единице, а знаменатель равен двум. Обозначим эту сумму через эс: эс равно один плюс два плюс два квадрат плюс два куб и так далее.. плюс два в шестьдесят третьей степени.
Умножим обе части записанного равенства на знаменатель прогрессии, получим следующее выражение…
Вычтем почленно из второго равенства первое и проведем упрощения…..
Получим, что эс равно два в шестьдесят четвертой степени.. минус один.
Можно подсчитать, что масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.
Выведем теперь формулу суммы первых эн членов произвольной геометрической прогрессии. Воспользуемся тем же приемом, с помощью которого была вычислена сумма эс.
Пусть дана геометрическая прогрессия бэ энное. Обозначим сумму первых ее членов через эс энное..
Умножим обе части этого равенства на ку…
Учитывая, что бэ первое умноженное на ку равно бэ второму, бэ второе умноженное на ку равно бэ третьему, бэ третье умноженное на ку равно бэ четвертому и так далее, бэ с индексом эн минус один умноженное на ку равно бэ энному, получим что эс энное умноженное на ку равно сумме бэ второго, бэ третьего, бэ четвертого, бэ энного и бэ энного ку.
Вычтем почленно из последнего равенства сумму эн ее членов…..
Получим равенство: произведение эс энного на разность ку и один равно разности произведения бэ энного на ку и бэ первого.
Отсюда следует, что при ку не равном единице, сумма эн членов геометрической прогрессии задается следующей формулой…
Мы получили формулу суммы первых эн членов геометрической прогрессии, в которой ку не равно единице. Если ку равно единице, то все члены прогрессии равны первому члену и сумма эн членов равна эн умноженному на бэ первое.
При решении многих задач удобно пользоваться формулой суммы первых эн членов геометрической прогрессии, записанной в другом виде. Подставим в формулу суммы первых эн членов геометрической прогрессии вместо бэ энного выражение бэ первое умноженное на ку степени эн минус один. Получим формулу следующего вида…
Пример первый. Найдем сумму первых девяти членов геометрической прогрессии, в которой бэ первое равно двум, ку равно одной второй.
Так как известны первый член и знаменатель прогрессии, то удобно пользоваться второй формулой нахождения суммы. Подставив в нее данные, получим, три целые сто двадцать семь сто двадцать восьмых.
Пример второй. Найдем сумму один плюс икс плюс икс квадрат и так далее плюс икс степени эн минус один, где икс не равен единице, слагаемые которой являются членами геометрической прогрессии один, икс, икс квадрат и так далее…
Первый член прогрессии равен единице, а знаменатель равен икс. Так как икс степени эн минус один является членом этой прогрессии с номером эн, то задача состоит в нахождении суммы первых эн ее членов. Воспользуемся первой формулой для нахождения суммы. Подставим в нее исходные данные и получим сумму, равную отношению разности икс степени эн.. и один к разности икс и один.
Воспользуемся первой формулой для нахождения суммы. Подставим в нее исходные данные и получим сумму, равную отношению разности икс степени эн.. и один к разности икс и один.
Пример третий. Найдем сумму первых восьми членов геометрической прогрессии, если известно, что третий член прогрессии равен восьми, а пятый член прогрессии равен тридцати двум.
Зная третий и пятый члены прогрессии, можно найти знаменатель прогрессии. Так пятый член прогрессии будет равен произведению третьего члена прогрессии и квадрата знаменателя прогрессии, то квадрат знаменателя прогрессии будет равен четырем, значит, знаменатель равен двум или минус двум.
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.
Если ку равно минус двум, то первый член будет равен двум и сумма прогрессии будет равна пятистам десяти.
Если ку равно минус двум, то первый член равен двум, а сумма будет равна минус ста семидесяти.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Дано: (cn) — геометрическая прогрессия, c1 = 1; q=-2; Найти: S9 Решение: S9 = . S9 = = = 171 |
геометрических последовательностей и рядов | безграничная алгебра |
Геометрические последовательности
Геометрическая последовательность — это упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на константу, называемую
ррр
, обыкновенное отношение.
Цели обучения
Вычислите
nnn
-й член геометрической прогрессии, зная начальное значение
aaa
и знаменатель 9{ n-1 }an=arn−1
.Ключевые термины
- геометрическая последовательность : Упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое обыкновенным отношением.
 Также известна как геометрическая прогрессия.
Также известна как геометрическая прогрессия.
Определение геометрических последовательностей
Геометрическая прогрессия, также известная как геометрическая последовательность, представляет собой упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое знаменателем 9.0005
ррр
. Например, последовательность
2,6,18,54,⋯2, 6, 18, 54, \cdots2,6,18,54,⋯
является геометрической прогрессией со знаменателем
333
. Точно так же
10,5,2,5,1,25,⋯10,5,2,5,1,25,\cdots10,5,2,5,1,25,⋯
является геометрической последовательностью со знаменателем
12\displaystyle{\frac{1} {2}}21
.
Таким образом, общая форма геометрической прогрессии такова:
a,ar,ar2,ar3,ar4,⋯a, ar, ar^2, ar^3, ar^4, \cdotsa,ar,ar2,ar3 ,ar4,⋯ 9{ n-1 }an=arn−1
Такая геометрическая последовательность также следует рекурсивному соотношению:
an=ran−1a_n=ra_{n-1}an=ran−1
для каждого целого числа
n≥1. n\ge 1.n≥1.
n\ge 1.n≥1.
Поведение геометрических последовательностей
Как правило, чтобы проверить, является ли данная последовательность геометрической, просто проверяют, имеют ли все последовательные элементы последовательности одинаковое соотношение. Обычное отношение геометрического ряда может быть отрицательным, что приводит к чередующейся последовательности. Чередующаяся последовательность будет иметь числа, которые переключаются между положительными и отрицательными знаками. Например:
1,-3,9,-27,81,-243,⋯1,-3,9,-27,81,-243, \cdots1,-3,9,-27,81,-243,⋯
представляет собой геометрическую прогрессию со знаменателем
−3-3−3
.
Поведение геометрической последовательности зависит от значения знаменателя. Если обыкновенное отношение:
- Положительное, все члены будут иметь тот же знак, что и исходный член .
- Отрицательный, условия будут чередоваться между положительными и отрицательными
- Больше, чем
111
, будет экспоненциальный рост до положительной бесконечности (+∞+\infty+∞
) 111
, прогрессия будет постоянной последовательностью- Между
−1-1−1
и111
, но не000
будет экспоненциальный спад в сторону000
−1-1−1
, последовательность представляет собой чередующуюся последовательность (см. чередующуюся серию)
чередующуюся серию)- Менее
−1-1−1
, для абсолютных значений наблюдается экспоненциальный рост в сторону положительной и отрицательной бесконечности (из-за знакопеременного знака)
Геометрические последовательности (со знаменателем, не равным
−1-1−1
,
111
или
000
) показывают экспоненциальный рост (или убывание, а не экспоненциальный рост) ) арифметической прогрессии, такой как
4,15,26,37,48,⋯4, 15, 26, 37, 48, \cdots4,15,26,37,48,⋯
(с общей разностью
111111
). Этот результат был получен Т.Р. Мальтуса в качестве математической основы его принципа народонаселения. Обратите внимание, что два вида прогрессии связаны: возведение в степень каждого члена арифметической прогрессии дает геометрическую прогрессию, а логарифмирование каждого члена геометрической прогрессии с положительным знаменателем дает арифметическую прогрессию. 9{2}=acb2=ac
9{2}=acb2=ac
Суммирование первых n членов геометрической последовательности
Используя знаменатель и первый член геометрической последовательности, мы можем суммировать ее члены.
Цели обучения
Вычислить сумму первых
nnn
членов геометрической последовательности
Ключевые выводы
Ключевые моменты
- Члены геометрического ряда образуют геометрическую прогрессию, что означает, что отношение последовательных членов в ряду постоянно . 9{ n } }{ 1-r } }s=a1−r1−rn .
Ключевые термины
- геометрический ряд : Бесконечная последовательность чисел, которые нужно сложить, члены которой находятся путем умножения предыдущего члена на фиксированное, ненулевое число, называемое обыкновенным отношением.
- геометрическая прогрессия : Ряд чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное, отличное от нуля число, называемое обыкновенным отношением.

Геометрические ряды являются примерами бесконечных рядов с конечными суммами, хотя не все из них обладают этим свойством. Исторически сложилось так, что геометрические ряды играли важную роль в раннем развитии исчисления и продолжают занимать центральное место в изучении сходимости рядов. Геометрические ряды используются в математике, и они имеют важные приложения в физике, технике, биологии, экономике, информатике, теории массового обслуживания и финансах. 9{ n } }}n=0∑∞zn
Эту концепцию можно изобразить с помощью диаграммы:
Бесконечный геометрический ряд: Каждый из фиолетовых квадратов получается путем умножения площади следующего большего квадрата на
14\displaystyle{\frac{1}{4}}41
. Площадь первого квадрата
12⋅12=14\displaystyle{\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}}21⋅21 =41
, а площадь второго квадрата равна
14⋅14=116\displaystyle{\frac{1}{4} \cdot \frac{1}{4} = \frac{1}{16 }}41⋅41=161
.
Ниже приведены несколько геометрических рядов с различными обыкновенными отношениями. Поведение термов зависит от знаменателя
rrr
:
4+40+400+4000+…4+40+400+4000+\dots4+40+400+4000+…
имеет обыкновенное отношение101010
9+3+1+13+19+…\displaystyle{9+3+1+\frac{1}{3}+\frac{1}{9}+\dots}9+3+1+31 +91+…
имеет знаменатель13{\frac{1}{3}}31
3+3+3+3+…3+3+3+3+\точки3+3+3+3+…
имеет обыкновенное отношение111
1−12+14−18+…\displaystyle{1-\frac{1}{2}+\frac{1}{4} -\frac{1}{8}+\dots}1−21 +41−81+…
имеет знаменатель−12-\frac{1}{2}−21
3−3+3−3+…3-3+3-3+\dots3−3+3−3+…
имеет знаменатель−1-1−1
Значение
ррр
предоставляет информацию о характере ряда:
- Если
ррр
находится между−1-1−1
и+1+1+1
, члены ряда становятся все меньше и меньше, в пределе стремясь к нулю, и ряд сходится к сумме. Рассмотрим последовательность, в которой
Рассмотрим последовательность, в которойrrr
равно половине(12,14,18,⋯ ){\left(\frac{1}{2}, \frac{1}{4}, \frac{1}{8} }, \cdots \right)}(21,41,81,⋯)
, сумма которых равна единице. - Если
rrr
больше111
или меньше−1-1−1
, члены ряда становятся все больше и больше по величине. Сумма слагаемых также становится все больше и больше, а в ряду нет суммы. Ряд расходится. - Если
ррр
равно111
, то все члены ряда одинаковы. Ряд расходится. - Если
rrr
равно−1-1−1
, термы попеременно принимают два значения(например, 2,−2,2,−2,2,−2,⋯ )\left(\text{e.g.} , 2,-2,2,-2,2,-2,\cdots \right)(например,2,−2,2,−2,2,−2,⋯)
. Сумма членов колеблется между двумя значениями(например, 2,0,2,0,2,0,⋯ )\left(\text{например}, 2,0,2,0,2,0,\cdots \right)(например,2,0,2,0,2,0,⋯)
. Это другой тип расхождения, и снова в ряду нет суммы. 9{ п } { 1-р } \end{выравнивание} }s=a+ar+ar2+ar3+⋯+arn−1=k=0∑n−1ark=a1−r1−rn, где
aaa
— первый член ряда , а
ррр
— обыкновенное отношение.

Следовательно, используя обыкновенное отношение и первый член последовательности, мы можем просуммировать первые
nnn
членов.
Пример
Найдите сумму первых пяти членов геометрической прогрессии
(6,18,54,162,⋯ )\left(6, 18, 54, 162, \cdots \right)(6,18,54,162,⋯) 9{ 5 } }{ 1-3 } \\ &= 6\cdot\frac {{-242} }{-2} \\ &= 6 \cdot 121 \\ &= 726 \end{выравнивание} }s=a1−r1−rn=6⋅1−31−35=6⋅−2−242=6⋅121=726
Бесконечный геометрический ряд
Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами.
Цели обучения
Вычислить сумму бесконечного геометрического ряда и распознать момент сходимости геометрического ряда0027
- сходятся : приближение к конечной сумме.
- геометрический ряд : Бесконечная последовательность суммированных чисел, члены которых постепенно изменяются с обыкновенным отношением.

Геометрический ряд — это бесконечный ряд, члены которого находятся в геометрической прогрессии или последовательные члены которого имеют общее отношение. Если члены геометрического ряда стремятся к нулю, сумма его членов будет конечной. Когда числа близки к нулю, они становятся незначительно малыми, что позволяет вычислить сумму, несмотря на то, что ряд бесконечен.
Говорят, что геометрический ряд с конечной суммой сходится. Ряд сходится тогда и только тогда, когда абсолютное значение знаменателя меньше единицы:
∣r∣<1\left | г \ право | < 1∣r∣<1
Далее следует пример бесконечного ряда с конечной суммой. Мы вычислим сумму
sss
следующего ряда:
s=1+23+49+827+⋯\displaystyle{s = 1+\frac { 2 }{ 3 } +\frac { 4 }{ 9 } +\frac { 8 }{ 27 } + \cdots}s=1+32+94+278+⋯
Этот ряд имеет обыкновенное отношение
23\displaystyle{\frac{2}{3}}32
.
 Если мы умножим на это обыкновенное отношение, то начальный член
Если мы умножим на это обыкновенное отношение, то начальный член111
станет
23\displaystyle{\frac{2}{3}}32
,
23\displaystyle{\frac{2 {3}}32
становится
49\displaystyle{\frac{4}{9}}94
и так далее:
23s=23+49+827+1681+⋯\displaystyle{ \ frac {2} {3} s = \ frac { 2 }{ 3 } + \ frac { 4 } { 9} +\frac { 8 }{ 27 } +\frac { 16 }{ 81 } + \cdots}32s=32+94+278+8116+⋯
Этот новый ряд совпадает с предыдущим оригинал, за исключением того, что первый член отсутствует. Вычитание нового ряда
23s\displaystyle{\frac{2}{3}s}32s
из исходного ряда,
sss
отменяет все члены в оригинале, кроме первого:
s−23s =1∴s=3\displaystyle{ \начать{выравнивать} s-\frac{2}{3}s &=1 \\ \поэтому s &= 3 \end{выравнивание} }s−32s∴s=1=3 9п\стрелка вправо 0\\ &= \frac{a}{1-r} \end{выравнивание} }s=a1−r1−rn→a1−r1as rn→0=1−ra
Следовательно, для
∣r∣<1|r|<1∣r∣<1
, мы можем записать бесконечную сумму как:
s=a1−r\displaystyle{s = \frac{a}{1-r}}s=1−ra
Пример
Найдите сумму бесконечной геометрической прогрессии постоянное отношение между каждым членом и тем, что ему предшествует:
г = 3264 = 12 \ Displaystyle { \начать{выравнивать} г &= \ гидроразрыв {32} {64} \\ &= \фракция{1}{2} \end{выравнивание} }r=6432=21
Замените
a=64a=64a=64
и
r=12\displaystyle r= \frac{1}{2}r=21
в формула суммы бесконечного геометрического ряда:
s=641−12=6412=128\displaystyle{ \начать{выравнивать} s &= \frac{64}{1-\frac{1}{2}} \\ &= \frac{64}{\frac{1}{2}} \\ &= 128 \end{выравнивание} }s=1−2164=2164=128
Применение геометрического ряда
Геометрические ряды имеют приложения в математике и естественных науках и являются одним из простейших примеров бесконечных рядов с конечными суммами.

Цели обучения
Применение геометрических последовательностей и рядов к различным физическим и математическим темам
Ключевые выводы
Ключевые моменты
Ключевые термины
- геометрические ряды : бесконечная последовательность суммированных чисел, члены которых постепенно изменяются с обыкновенным отношением.
- фрактал : природное явление или математический набор, демонстрирующий повторяющийся узор, который можно увидеть в любом масштабе.
Геометрические ряды сыграли важную роль в раннем развитии исчисления и продолжают оставаться центральной частью изучения сходимости рядов. Геометрические ряды используются во всей математике. Они имеют важные приложения в физике, технике, биологии, экономике, информатике, теории массового обслуживания и финансах.
Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами, хотя не все они обладают этим свойством.

Повторяющееся десятичное число
Повторяющуюся десятичную дробь можно рассматривать как геометрический ряд, обыкновенное отношение которого равно степени
110\displaystyle{\frac{1}{10}}101
. Например:
0,7777⋯=710+7100+71000+710000+⋯\displaystyle{0,7777 \cdots = \frac{7}{10} + \frac{7}{100}+ \frac{7}{1000} + \frac{7}{10000}+ \cdots}0,7777⋯=107+1007+10007+100007+⋯
Формулу суммы геометрического ряда можно использовать для преобразования десятичной дроби в дробь:
0,7777⋯=a1−r=7101−110=(710)(910)=(710)(109)=79 \displaystyle{ \начать{выравнивать} 0,7777 \cdots &= \frac { a }{ 1-r } \\ &= \frac { \frac{ 7 }{ 10 } }{ 1-\frac{ 1 }{ 10 } } \\ & = \ гидроразрыва {\ влево (\ гидроразрыва {7} {10} \ справа)} {\ влево (\ гидроразрыва {9} {10} \ справа)} \\ &= \left(\frac{7}{10}\right)\left(\frac{10}{9}\right)\\ &= \фракция {7} {9} \end{выравнивание} }0,7777⋯=1−ra=1−101107=(109)(107)=(107)(910)=97
Формула работает для любого повторяющегося термина.
 Еще несколько примеров:
Еще несколько примеров:0,123412341234⋯=a1−r=1234100001−110000=(123410000)(999
0)=(123410000)(100009999)=12349999\displaystyle{ \начать{выравнивать} 0,123412341234 \cdots &= \frac { a }{ 1-r } \\ &= \frac { \frac{1234}{10000} }{1-\frac{1}}{10000}} \\ & = \ гидроразрыва {\ влево (\ гидроразрыва {1234} {10000} \ справа)}} {\ влево (\ гидроразрыва {9999} {10000} \ справа)} \\ &= \влево(\frac{1234}{10000}\вправо)\влево(\frac{10000}{9999}\вправо)\\ &= \фракция { 1234 }{ 9999 } \end{выравнивание} }0,123412341234⋯=1−ra=1−100001100001234=(100009999)(100001234)=(100001234)(999
0)=999
= 0 0,09009−1100=(9100)(99100)=(9100)(10099)=999=111\displaystyle{ \начать{выравнивать} 0,00909 \cdots &= \frac { a }{ 1-r } \\ &= \frac { \frac{9}{100} }{1-\frac{1}}{100}} \\ & = \ гидроразрыва {\ влево (\ гидроразрыва {9} {100} \ справа)}} {\ влево (\ гидроразрыва {99} {100} \ справа)} \\ &= \left(\frac{9}{100}\right)\left(\frac{100}{99}\right)\\ &= \фракция { 9 }{ 99} \\ &= \фракция{1}{11} \end{выравнивание} }0,00909⋯=1−ra=1−10011009=(10099)(1009)=(1009)(99100)=999=1110.
 143814381438⋯=a1 −r = 1438100001−110000 = (143810000) (999
143814381438⋯=a1 −r = 1438100001−110000 = (143810000) (9990) = (143810000) (100009999) = 14389999 \ displaystyle { \начать{выравнивать} 0,143814381438 \cdots &= \frac { a }{ 1-r } \\ &= \frac { \frac{1438}{10000} }{1-\frac{1}}{10000}} \\ & = \ гидроразрыва {\ влево (\ гидроразрыва {1438} {10000} \ справа)} {\ влево (\ гидроразрыва {9999} {10000} \ справа)} \\ &= \left(\frac{1438}{10000}\right)\left(\frac{10000}{9999}\справа)\\ &= \фракция {1438} {9999} \end{выравнивание} }0,143814381438⋯=1−ra=1−100001100001438=(100009999)(100001438)=(100001438)(999
0)=999
=
⋯ 0,9999 9101−110 = (910) (910) = (910) (109) = 99 = 1 \ displaystyle { \начать{выравнивать} 0,9999 \cdots &= \frac { a }{ 1-r } \\ &= \ frac { \ frac { 9 }{ 10 } }{ 1- \ frac { 1 }{ 10 } } \\ & = \ гидроразрыва {\ влево (\ гидроразрыва {9} {10} \ справа)} {\ влево (\ гидроразрыва {9} {10} \ справа)} \\ &= \left(\frac{9}{10}\right)\left(\frac{10}{9}\right)\\ &= \фракция { 9n — 110n−1.

Квадратура параболы Архимеда
Архимед использовал сумму геометрического ряда для вычисления площади, ограниченной параболой и прямой линией. Его метод состоял в том, чтобы разбить область на бесконечное число треугольников.
Теорема Архимеда: Разбиение Архимедом параболического отрезка на бесконечное число треугольников.
Теорема Архимеда утверждает, что общая площадь под параболой равна
43\displaystyle{\frac{4}{3}}34
площади синего треугольника. Он определил, что каждый зеленый треугольник имеет
18\displaystyle{\frac{1}{8}}81
площадь синего треугольника, каждый желтый треугольник имеет
18\displaystyle{\frac{1}{8 }}81
площадь зеленого треугольника и так далее. Если предположить, что площадь синего треугольника равна
111
, то общая площадь представляет собой бесконечный ряд:
1 + 2 (18) + 4 (18) 2 + 8 (18) 3 + ⋯ \ displaystyle {1 + 2 \ влево ( \ frac { 1 }{ 8 } \ right ) +4 { \ влево ( \ frac { 1 }{ 8 } \right ) }^{ 2 }+8{ \left ( \frac { 1 }{ 8 } \right ) }^{ 3 }+ \cdots}1+2(81)+4( 81)2+8(81)3+⋯
Первый член представляет площадь синего треугольника, второй член — площади двух зеленых треугольников, третий член — площади четырех желтых треугольников и так далее.
 Упрощение дробей дает:
Упрощение дробей дает:1+14+116+164+⋯\displaystyle{1+ \frac{1}{4}+ \frac{1}{16}+ \frac{1}{64}+ \cdots }1+41+161+641+⋯
Это геометрический ряд со знаменателем
14\displaystyle{\frac{1}{4}}41
, а дробная часть равна
13\displaystyle{\frac{1}{3}}31
.
Фрактальная геометрия
Снежинка Коха: Внутренняя часть снежинки Коха состоит из бесконечного количества треугольников.
Снежинка Коха представляет собой фрактальную форму с внутренней частью, состоящей из бесконечного количества треугольников. При изучении фракталов геометрические ряды часто возникают как периметр, площадь или объем самоподобной фигуры. В случае снежинки Коха ее площадь можно описать геометрическим рядом.
Построение снежинки Коха: первые четыре итерации: каждая итерация добавляет набор треугольников снаружи фигуры.

Площадь внутри снежинки Коха можно описать как объединение бесконечного числа равносторонних треугольников. На приведенной выше диаграмме треугольники, добавленные во второй итерации, имеют точно
13\displaystyle{\frac{1}{3}}31
размер стороны самого большого треугольника, и поэтому они имеют ровно
19\displaystyle{\frac{1}{9}}91
площадь. Точно так же каждый треугольник, добавленный во второй итерации, имеет 9{ 3 }+ \cdots}1+3(91)+12(91)2+48(91)3+⋯
Первый член этого ряда представляет площадь первого треугольника, второй член общая площадь трех треугольников, добавленных во второй итерации, третий член — общая площадь двенадцати треугольников, добавленных в третьей итерации, и так далее. За исключением начального члена
111
, этот ряд является геометрическим с постоянным отношением
r=49\displaystyle{r = \frac{4}{9}}r=94
.
 Первый член геометрического ряда равен 9.0005
Первый член геометрического ряда равен 9.0005a=319=13\displaystyle{a = 3 \frac{1}{9} = \frac{1}{3}}a=391=31
, поэтому сумма:
1+ a1−r=1+131−49=85\displaystyle{ \начать{выравнивать} 1+ \frac { a }{ 1-r } &=1+ \ frac { \frac{1}{3} }{ 1- \frac{4}{9} } \\ &= \фракция{8}{5} \end{выравнивание} }1+1−ra=1+1−9431=58
Таким образом, снежинка Коха имеет
85\displaystyle{\frac{8}{5}}58
из площадь основания треугольника.
Парадоксы Зенона
Парадоксы Зенона — это набор философских проблем, придуманных древнегреческим философом для поддержки доктрины о том, что истина противоречит нашим чувствам. Проще говоря, один из парадоксов Зенона гласит: существует точка А, которая хочет переместиться в другую точку В. Если А перемещается только на половину расстояния между ней и точкой В за раз, она никогда туда не попадет, потому что вы можете продолжать делить оставшееся пространство пополам навсегда.
 Ошибка Зенона состоит в предположении, что сумма бесконечного числа конечных шагов не может быть конечной. Теперь мы знаем, что его парадокс неверен, о чем свидетельствует сходимость геометрического ряда с
Ошибка Зенона состоит в предположении, что сумма бесконечного числа конечных шагов не может быть конечной. Теперь мы знаем, что его парадокс неверен, о чем свидетельствует сходимость геометрического ряда сr=12\displaystyle{r = \frac{1}{2}}r=21
. Эта проблема была решена современной математикой, которая может применить концепцию бесконечного ряда для нахождения суммы пройденных расстояний.
Лицензии и авторство
Контент под лицензией CC, совместно используемый ранее
- Курирование и пересмотр. Автор : Boundless.com. Лицензия : Общедоступное достояние: Неизвестно Авторские права
Контент под лицензией CC, конкретное указание авторства
- Геометрическая последовательность. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- IB Математика (HL)/Алгебра. Предоставлено : Wikibooks.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - геометрическая последовательность. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Геометрическая последовательность. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Геометрическая серия. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- геометрический ряд. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Геометрическая серия. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
- Геометрические ряды. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Геометрическая прогрессия.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Бесконечная серия. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- геометрический ряд. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Геометрический ряд. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
- Парадоксы Зенона. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Геометрическая прогрессия. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Геометрическая серия. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- аннуитет.
 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike - фрактал. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- геометрический ряд. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Геометрическая серия. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
- Снежинка Коха. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Геометрическая серия. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Geometric_series. Лицензия : Общественное достояние: неизвестно Авторское право
- Мозаика сходства Коха.
 Предоставлено : Википедия. Лицензия : Общественное достояние: Не известно Авторское право
Предоставлено : Википедия. Лицензия : Общественное достояние: Не известно Авторское право
Формула геометрического ряда — ChiliMath
Помните, что последовательность — это просто список чисел, а последовательность — это сумма списка чисел. Геометрическая последовательность — это такой тип последовательности, что при делении каждого члена на предыдущий член получается обычное отношение.
Это означает, что у нас есть r =\Large {{{a_{n + 1}}} \over {{a_n}}} для любых последовательных или смежных терминов.
Ниже приведен пример геометрической последовательности. Обратите внимание, что когда каждый член (кроме первого) делится на предыдущий член, получается знаменательное отношение 2.
Теперь, если мы сложим члены последовательности, она станет рядом!
Вместо того, чтобы складывать члены последовательности методом грубой силы, есть формула, которую мы можем использовать, чтобы легко найти сумму конечной геометрической последовательности.

Обратите внимание, что для использования формулы нам нужны три вещи. Нам нужен первый член, знаменатель и количество членов. По сравнению с формулой арифметического ряда нам не требуется последний член.
Давайте рассмотрим несколько примеров!
Пример 1: Найдите сумму первых пяти (5) членов геометрической прогрессии.
2,6,18,54,…
Это простая задача, и она предназначена для того, чтобы мы могли проверить ее с помощью ручного расчета.
Во-первых, давайте проверим, действительно ли это геометрическая прогрессия. Разделите каждое слагаемое на предыдущее слагаемое.
{\ Большой {{6 \более 2}}} = 3
{\ Большой {{18} \более 6}} = 3
{\ Большой {{54} \более {18}}} = 3
Имеет знаменатель 3, что означает, что это геометрическая прогрессия!
Нам нужно сложить первые 5 слагаемых, но, похоже, нам не хватает еще одного слагаемого. Давайте сгенерируем пятый член, умножив четвертый член на знаменатель, таким образом, 54 х 3 = 162.

Поскольку у нас есть все члены в последовательности, теперь мы можем их сложить. Мы можем сделать это вручную или в уме, потому что это относительно небольшие числа.
2 + 6 + 18 + 54 + 162 = \boxed{242}
Итак, мы получили число 242. Давайте воспользуемся формулой, чтобы проверить правильность нашего ответа.
В геометрической последовательности первый член равен 2, знаменатель равен 3, и в последовательности пять членов, что означает, что наше n равно 5.
{a_1} = 2
r = 3
n = 5
Подставьте эти значения в формулу и упростите.
Наши ответы совпадают! Следовательно, сумма первых пяти членов данной геометрической прогрессии равна 242.
Пример 2: Найдите сумму первых десяти (10) членов геометрической прогрессии, если {a_1} = 3 и r=2 .
Эта задача проста, потому что дана вся информация для формулы. Ваш учитель может дать что-то подобное, просто чтобы проверить, знаете ли вы формулу арифметического ряда и, что более важно, знаете ли вы, как ее использовать.

Давайте соберем известную нам информацию.
Первый член равен 3, это означает, что {a_1} = 3.
Обычное отношение равно 2, это означает, что r=2.
Количество терминов 10, значит n=10.
Подставьте эти значения в формулу и упростите.
Следовательно, сумма первых десяти (10) членов геометрической прогрессии равна 3069.
Пример 3: Найдите сумму первых шести (6) членов геометрического ряда.
36 — 12 + 4 + …
Если мы наблюдаем последовательность, члены чередуются в знаках, что предполагает, что обыкновенное отношение должно быть отрицательным. Кроме того, поскольку абсолютное значение членов уменьшается, это означает, что отношение commo является дробным.
Первое слагаемое, очевидно, равно 36.
Обычное отношение равно \large{ — {1 \over 3}}, потому что
\large{{{ — 12} \over {36}} = — {1 \over 3}}
\large{{4 \over { — 12}} = — {1 \over 3}}
Мы ищем сумму первых шести членов, таким образом, n=6.

Теперь мы готовы подставить эти значения в формулу. Только будьте осторожны при работе с дробями. Это единственная дополнительная трудность в этой задаче. В остальном действуйте как обычно.
Следовательно, сумма первых шести (6) членов геометрической прогрессии равна \large{{{728} \over {27}}}.
Пример 4: Найдите сумму геометрического ряда ниже.
7 + 21 + 63 + …+15,309
На первый взгляд проблема может показаться пугающей. Но поверьте мне, это не так уж и плохо. Когда вы изучите основную стратегию того, как подходить к этому типу проблем, вы поймете, что на самом деле это очень просто. Поверь мне, ты получишь это!
Начнем с того, что мы знаем. Что ж, мы знаем первый член, который равен 7. Обычное отношение равно 3. Попробуйте разделить термин на предшествующий ему член. Мы должны получать 3 каждый раз. Другое дело, что мы не знаем, сколько членов нужно добавить, что равно n в формуле. Однако указан последний член, равный 15 309.
 . Мы будем использовать наши предыдущие знания о геометрической последовательности, чтобы найти количество членов в последовательности n, если мы знаем последний член. Это наш план!
. Мы будем использовать наши предыдущие знания о геометрической последовательности, чтобы найти количество членов в последовательности n, если мы знаем последний член. Это наш план!Вот формула геометрической последовательности:
Мы знаем значения последнего члена, равного a_n=15,309, первого члена, равного a_1=7, и обыкновенного отношения, равного r=3. Подставьте эти значения в формулу и найдите n.
Значит, в геометрическом ряду 8 членов. Теперь у нас есть вся необходимая информация для решения исходной задачи.
Найдем первые восемь (8) членов геометрического ряда.
7 + 21 + 63 + …+15,309
Первый член равен 7. Обычное отношение равно 3. Всего в последовательности восемь (8) членов.
Следовательно, сумма данного геометрического ряда равна 22 960.
Пример 5: Найдите сумму геометрического ряда ниже.
— 1 + 2 — 4 + … — 4,096
Эта задача очень похожа на №4. Я просто хочу сделать еще одну задачу для мастерства.

Давайте идентифицируем соответствующую информацию из данного геометрического ряда.
Первый член равен -1. Поскольку члены чередуются знаками, мы ожидаем, что обыкновенное отношение будет отрицательным.
{\Large{2 \over { — 1}}} = — 2
{\Large{{ — 4} \over 2}} = — 2
Итак, да, обычное отношение равно -2. Мы не знаем количество членов, но нам дано значение последнего члена, равное -4096. Используя последний член, мы можем воспользоваться формулой геометрической последовательности, чтобы найти количество членов в ряду. 9{n — 1}}} при изменении n от 1 до 9».
Давайте сгенерируем несколько членов заданного геометрического ряда в виде суммирования. Чтобы получить первый член, начните с n = 1, подставьте его в формулу, а затем упростите. Чтобы получить второй член, подставьте n=2 в формулу и упростите. Чтобы получить третий член, оцените n=3 в формуле и так далее. Пропустите средние члены, но сделайте последний член, то есть когда n = 9.
Если вы все сделали правильно, вы должны получить что-то похожее ниже.
9{n — 1}}} = 2 + 6 + 18 + … + 13 122
Первый член равен 2. Значимое отношение равно 3. И в ряду 9 членов.
Пример 7: Найдите второй член {a_2} в геометрическом ряду такой, что {S_n} ={\large {{2186} \over {81}}}, r ={\large {1 \over 3 }} и n=7.
Если мы рассмотрим формулу геометрического ряда, станет очевидно, что у нас есть вся информация, кроме первого члена {a_1}. Кстати, мы решаем для a_1, так что ничего страшного. Найдя значение первого члена, мы можем найти второй член, просто умножив первый член на обыкновенное отношение.
Подставьте известные значения, затем найдите a_1.
Поскольку первый член равен 18, второй член находится путем умножения первого члена на знаменатель.
{a_2} = {a_1}r = 18\left( {{1 \over 3}} \right) = 6
Следовательно, второй член равен 6.
Вам также может быть интересно:
Геометрические ряды Практические задачи с ответами
Формула бесконечного геометрического ряда
Формула геометрического ряда
Формула арифметической последовательности
Формула арифметического ряда
Геометрический ряд | Колледж Алгебра
Результаты обучения
- Запишите первые n членов геометрической прогрессии.

- Определить, существует ли сумма бесконечного геометрического ряда.
- Назовите сумму сходящегося бесконечного геометрического ряда.
- Решите задачу о ренте, используя геометрический ряд.
Так же, как сумма членов арифметической прогрессии называется арифметической последовательностью, сумма членов геометрической последовательности называется
.{k}[/latex]
Показать решение
Пример: решение прикладной задачи с геометрическим рядом
Начальная зарплата сотрудника на новой работе составляет 26 750 долларов. Он получает 1,6% ежегодного повышения. Найдите его общий заработок через 5 лет.
Показать решение
Попробуйте
Начальная зарплата сотрудника на новой работе составляет 32 100 долларов. Она получает 2% ежегодного повышения. Сколько она заработает к концу 8 лет?
Показать решение
Использование формулы для суммы бесконечного геометрического ряда
До сих пор мы рассматривали только конечные ряды. Сумма бесконечного ряда определена, если ряд является геометрическим и [latex]-1 Формула суммы бесконечного геометрического ряда с [латекс]-1 [латекс]S= \dfrac{{a}_{1}}{1-r}[/latex] Найдите сумму, если она существует, для следующего: Показать решение В начале раздела мы рассмотрели задачу, в которой пара ежемесячно инвестировала определенную сумму денег в фонд колледжа в течение шести лет. Аннуитет — это инвестиция, при которой покупатель производит последовательность периодических равных платежей. Чтобы найти сумму ренты, нам нужно найти сумму всех платежей и начисленных процентов. В примере пара инвестирует 50 долларов каждый месяц. Это стоимость первоначального депозита. Счет оплачен 6% годовых процентов , начисляемых ежемесячно. Мы можем найти значение аннуитета сразу после последнего депозита, используя геометрический ряд с [латекс]{а}_{1}=50[/латекс] и [латекс]r=100,5\%=1,005[/ латекс]. После первого депозита стоимость аннуитета составит 50 долларов. Посмотрим, сможем ли мы определить сумму в фонде колледжа и заработанные проценты. 9{72}\right)}{1 — 1,005}\приблизительно 4\text{,}320,44[/latex] После внесения последнего депозита на счету пары будет в общей сложности 4 320,44 доллара США. Обратите внимание, что пара совершила 72 платежа по 50 долларов каждый, что в сумме составляет [латекс]72\влево(50\вправо) = 3600 долларов[/латекс]. Это означает, что из-за аннуитета пара заработала 720,44 доллара в свой фонд колледжа. {\infty} 2k[/латекс], где верхний предел суммирования равен бесконечности. Поскольку члены не стремятся к нулю, сумма ряда неограниченно возрастает по мере добавления новых членов. Следовательно, сумма этого бесконечного ряда не определена. Когда сумма не является действительным числом, мы говорим, что ряд 9n[/latex] становятся очень маленькими и приближаются к 0. Каждый последующий член влияет на сумму меньше, чем предыдущий. По мере того, как каждый последующий член приближается к 0, сумма членов приближается к конечному значению. Члены любого бесконечного геометрического ряда с [латекс]-1
{\infty} 2k[/латекс], где верхний предел суммирования равен бесконечности. Поскольку члены не стремятся к нулю, сумма ряда неограниченно возрастает по мере добавления новых членов. Следовательно, сумма этого бесконечного ряда не определена. Когда сумма не является действительным числом, мы говорим, что ряд 9n[/latex] становятся очень маленькими и приближаются к 0. Каждый последующий член влияет на сумму меньше, чем предыдущий. По мере того, как каждый последующий член приближается к 0, сумма членов приближается к конечному значению. Члены любого бесконечного геометрического ряда с [латекс]-1 ОПРЕДЕЛЕНИЕ ОПРЕДЕЛЕНИЯ СУММЫ БЕСКОНЕЧНОГО ГЕОМЕТРИЧЕСКОГО РЯДА
Как сделать:
Имея первые несколько членов бесконечного ряда, определите, существует ли сумма ряда. 
A Общее примечание: ФОРМУЛА СУММЫ БЕСКОНЕЧНОГО ГЕОМЕТРИЧЕСКОГО РЯДА
Как:
Дан бесконечный геометрический ряд, найти его сумму. Пример: нахождение суммы бесконечного геометрического ряда
Аннуитеты
 Чтобы найти процентную ставку за период платежа, нам нужно разделить годовую процентную ставку (APR) в размере 6% на 12. Таким образом, ежемесячная процентная ставка составляет 0,5%. Мы можем умножить сумму на счете каждый месяц на 100,5%, чтобы найти стоимость счета после начисления процентов.
Чтобы найти процентную ставку за период платежа, нам нужно разделить годовую процентную ставку (APR) в размере 6% на 12. Таким образом, ежемесячная процентная ставка составляет 0,5%. Мы можем умножить сумму на счете каждый месяц на 100,5%, чтобы найти стоимость счета после начисления процентов.

 П. учитель математики
П. учитель математики



 Также известна как геометрическая прогрессия.
Также известна как геометрическая прогрессия. чередующуюся серию)
чередующуюся серию)
 Рассмотрим последовательность, в которой
Рассмотрим последовательность, в которой

 Если мы умножим на это обыкновенное отношение, то начальный член
Если мы умножим на это обыкновенное отношение, то начальный член

 Еще несколько примеров:
Еще несколько примеров: 143814381438⋯=a1 −r = 1438100001−110000 = (143810000) (999
143814381438⋯=a1 −r = 1438100001−110000 = (143810000) (999
 Упрощение дробей дает:
Упрощение дробей дает:
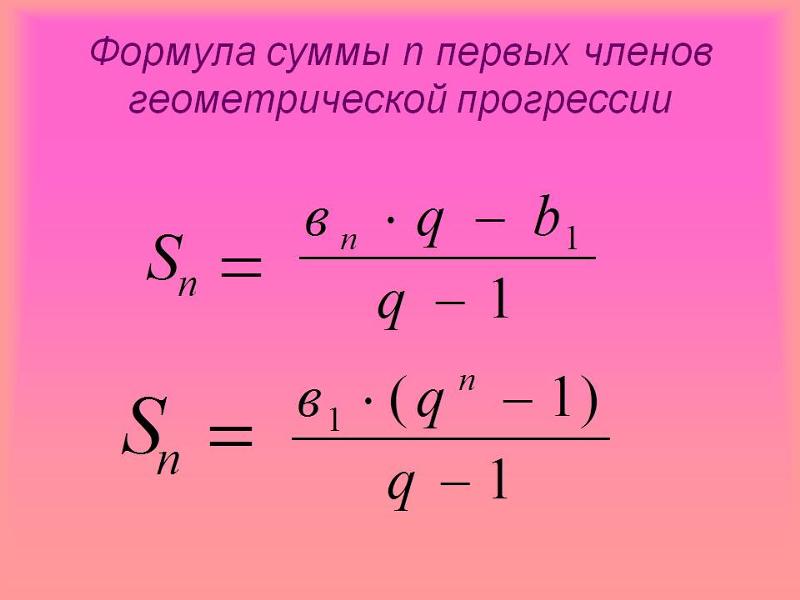 Первый член геометрического ряда равен 9.0005
Первый член геометрического ряда равен 9.0005 Ошибка Зенона состоит в предположении, что сумма бесконечного числа конечных шагов не может быть конечной. Теперь мы знаем, что его парадокс неверен, о чем свидетельствует сходимость геометрического ряда с
Ошибка Зенона состоит в предположении, что сумма бесконечного числа конечных шагов не может быть конечной. Теперь мы знаем, что его парадокс неверен, о чем свидетельствует сходимость геометрического ряда с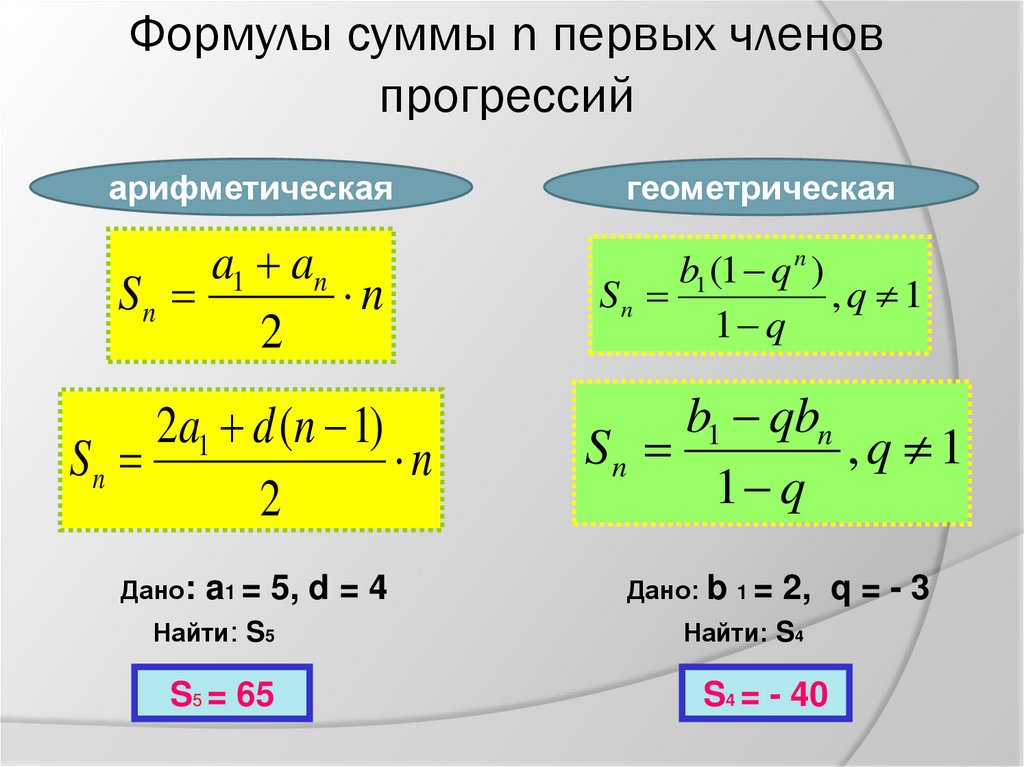 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Википедия. Лицензия : Общественное достояние: Не известно Авторское право
Предоставлено : Википедия. Лицензия : Общественное достояние: Не известно Авторское право 



 . Мы будем использовать наши предыдущие знания о геометрической последовательности, чтобы найти количество членов в последовательности n, если мы знаем последний член. Это наш план!
. Мы будем использовать наши предыдущие знания о геометрической последовательности, чтобы найти количество членов в последовательности n, если мы знаем последний член. Это наш план!