После этого можно сделать замену $x+\frac{b}{2a}=t$, в результате чего данный тип интегралов можно свести к табличным или их сумме.
Интегралы — Математика — Смотреть онлайн видео уроки для начинающих бесплатно!
В категории Интегралы собраны бесплатные онлайн видео уроки по этой теме. Интеграл (integer — целый) – это математический символ, который используется в исчислении, является аналогом операции суммирования. Интегрирование – это процесс нахождения интеграла функции, действие, обратное дифференцированию. Формально, это деление площади фигуры на прямоугольные полоски и нахождение предела сумм этих площадей. Определённый интеграл функции f (x) с нижним пределом а и верхним пределом b представляет собой площадь части графика функции, которая ограничена осью абсцисс, кривой у = f(x) и двумя прямыми х = а и х = b. Если значения а и b не заданы, то интеграл называется неопределенным. Изучение интегралов по видео урокам будет полезно как для начинающих, так и для более опытных математиков.
Видеоуроки из рубрики Интегралы Вы можете смотреть бесплатно в любое удобное время. К некоторым видео урокам по интегралам приложены дополнительные материалы, которые можно скачать. Приятного Вам обучения!
Новые · Лучшие · Популярные
Смотреть урок онлайн
Метод замены переменной при решении неопределенных интегралов
В этом видео уроке рассказывается о том, как использовать метод замены переменной при решении неопределенных интегралов. В первой части обучения будет рассмотрена схема применения данного метода. Метод замены переменной является основным методом решения неопределенных интегралов. Его еще часто называют методом подстановки. После изучения теоретической части, полученные знания будут применяться на практических заданиях. С этой целью, в данном видео уроке представлено решение нескольких примеров…
Смотреть урок онлайн
Простейшие интегралы.
Решение с помощью таблицыЭто видео посвящено вопросу о том, как решать простые интегралы при помощи таблицы. Для начала вспомним определение первообразной. Функция F(x) является первообразной для функции f(x) на определенном промежутке, если для любого значения x данного промежутка справедливо равенство F (x)= f(x). Сформулируем определение неопределенного интеграла. Неопределённый интеграл — это совокупность всех первообразных функции f(x). При этом используется следующая запись: интеграл f(x)dx=F(x)+C, где f(x…
Смотреть урок онлайн
Определенный интеграл (11 класс). Понятие, решение примера
Видео урок «Определенный интеграл (11 класс). Понятие, решение примера» посвящен вопросу о понятии определенного интеграла как площади криволинейной трапеции. Пусть на отрезке ab задана непрерывная функция y=f(x). Попробуем определить площадь фигуры, границами которой являются: сверху — график функции y=f(x), по бокам — вертикальные прямые x=a и x=b, снизу — ось абсцисс.
Смотреть урок онлайн
Что такое интеграл
В этом видео мы поговорим об интеграле. Этим зверем из высшей математики часто пугают несчастных детей, но тебе, если ты посмотрел мои видео про производную и первообразную, этот серый волк будет совсем не страшен. Определенный интеграл равен всего лишь навсего разности первообразных, которая в свою очередь совпадает с площадью под графиком производной. За страшным словом скрывается простая суть: слово интеграл переводится как сумма. Помните — сумма прямоугольников. А действия по нахождению…
Смотреть урок онлайн
Решение интегралов с квадратичной функцией, примеры
Видео «Решение интегралов с квадратичной функцией, примеры» посвящено вопросу о том, как правильно выполнять интегрирование выражений, в состав которых входит квадратичная функция.
Смотреть урок онлайн
Несобственные интегралы 2 рода — от неограниченных (разрывных) функций
В этом онлайн уроке рассказывается о том, что собой представляют несобственные интегралы 2 рода — от неограниченных (разрывных) функций. Допустим, задана функция, которая непрерывна на определенном промежутке, причем её предел с одной стороны равен бесконечности, т.е. функция в этой точке терпит разрыв второго рода. При рассмотрении определенного интеграла с пределами соответствующими этому промежутку возникает вопрос, к какому значению он стремиться. В данном видео уроке будет рассмотрен…
Смотреть урок онлайн
Интегралы с бесконечными пределами (несобственные 1 рода)
Видео «Интегралы с бесконечными пределами (несобственные 1 рода)» посвящено вопросу о том, что такое интегралы с бесконечными пределами и каков их геометрический смысл, решение примера.
Допустим, что задан определенный интеграл от непрерывной функции с верхним пределом интегрирования равным B. Представим себе, что значение этого интеграла численно равно площади криволинейной трапеции. При увеличении значения предела B, площадь этой трапеции также увеличивается. Возникает вопрос, к какому…
Смотреть урок онлайн
Как найти объем тела вращения через вычисление определенного интеграла
В этом видео уроке рассказывается о том, как найти объем тела вращения через вычисление определенного интеграла. Допустим, дана криволинейная трапеция, которая ограничена сверху графиком непрерывной функции, а по бокам — вертикальными прямыми линиями. При вращении данной плоской фигуры вокруг оси абсцисс, образуется объемная фигура. С помощью определенного интеграла можно вычислить объем этого тела. Здесь будет представлена формула, по которой вычисляется объем тела вращения. В первом случае…
Смотреть урок онлайн
Как найти длину дуги кривой через вычисление определенного интеграла
Онлайн урок «Как найти длину дуги кривой через вычисление определенного интеграла» посвящен вопросу о методе, с помощью которого можно определить длину дуги кривой.
Одним из приложений определенного интеграла является нахождение длин дуг кривых. Здесь будет представлена формула, с помощью которой можно найти длину дуги кривой. Для решения данной задачи с помощью этой формулы необходимо знать функцию, которой задана кривая и абсциссы точек, между которыми измеряется длина кривой. В данном видео…
Смотреть урок онлайн
Метод интегрирования по частям в определенном интеграле — формула, пример решения
Это видео посвящено вопросу о том, как использовать метод интегрирования по частям при решении определенного интеграла, формула, пример использования. Если вы уже освоили данный метод при решении неопределенных интегралов, то вам не составит труда научиться его использовать и для вычисления определенного интеграла. Также необходимо уметь применять формулу Ньютона-Лейбница. Здесь представлена формула, по которой будет проводиться вычисление интеграла. Применение метода интегрирования по частям.
..
1 2
Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.
Неопределенный интеграл с примерами решения
Содержание:
- Простейшие неопределенные интегралы
- Примеры с решением:
- Первообразная и неопределенный интеграл
- Преобразования неопределенных интегралов
Неопределенным интегралом называется совокупность всех первообразных. Первообразной данной функции на некотором промежутке называется такая функция производная которой на всем промежутке равна данной функции Можно показать, что разные первообразные одной и той же функции отличаются на постоянную величину. Таким образом, если мы знаем одну из первообразных заданной функции то неопределенный интеграл
Эту формулу можно также записать в другом виде:
из которого следует, что интегрирование является операцией, обратной дифференцированию.
Так же как техника дифференцирования опирается на знание таблицы производных, так и вычисление интегралов невозможно без знания таблицы основных интегралов.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Эта таблица фактически является переписанной наоборот (с небольшими изменениями) таблицей производных.
Относительно приводимой таблицы можно сделать следующие замечания. Полезно запомнить распространенный частный случай формулы 3 при
В восьмой формуле можно пользоваться любым из выражений, стоящих справа ( производные функции и равны). То же самое замечание относится и к девятой формуле (производные функций и также равны между собой).
Возможно вам будут полезны данные страницы:
Знакочередующиеся ряды |
Сходимость знакочередующихся рядов |
Найти неопределенный интеграл: примеры решения |
Пределы: примеры решения |
Последние четыре формулы относятся к так называемым гиперболическим функциям ( — гиперболический синус, — гиперболический косинус гиперболический тангенс, — гиперболический котангенс). Этим функциям в учебной литературе обычно уделяется незначительное внимание, хотя в приложениях они используются довольно часто. Следующий раздел будет посвящен гиперболическим функциям, что компенсирует имеющийся пробел в учебниках.
Наконец приведем известную задачу Л. Д. Ландау, которую он давал на экзамене по теоретическому минимуму для отбора физиков-теоретиков в свои группы. Она относится к самому первоначальному понятию и обозначению неопределенного интеграла. |
Простейшие неопределенные интегралы
Непосредственное использование таблицы основано на свойстве линейности неопределенного интеграла:
Иа этого свойства следует, что если нам удалось представить подынтегральную функцию в виде линейной комбинации функций, интегралы от которых известны, то интеграл от этой функции равен линейной комбинации соответствующих табличных интегралов. Рассмотрим применение этого метода на примерах.
Примеры с решением:
На участке выполнено неравенство следовательно, и первообразная подынтегральной функции
На участке имеем и поэтому следовательно, первообразная подынтегральной функции Из условия непрерывности функции в точке находим соотношение между постоянными
т.е. Опуская индекс у константы получаем следующий ответ:
Первообразная и неопределенный интеграл
Определение.
Первообразной от заданной функции называется функция такая, что ее дифференциал равен т. е.
Например, функция является первообразной от функции так как Площадь криволинейной трапеции (в соответствии с § 4 гл. IX) является первообразной от функции график которой ограничивает эту криволинейную трапецию, так как
Пример 1.
Покажем, что функция есть первообразная от функции В самом деле, производная равна следовательно, дифференциал равен Поэтому есть первообразная от
Определение первообразной можно дать в другой, эквивалентной форме: первообразной от функции называется функция имеющая своей производной
Обратим внимание на то, что первообразная от данной функции существует не одна. Например, как было указано, есть первообразная от но, взяв функцию где —любое постоянное число, получим, что т. е. также является первообразной от
Можно было бы доказать, что и обратное предложение верно, т. е. если функции и являются первообразными от функции то они отличаются друг от друга на постоянное слагаемое.
Из сказанного следует, что операция нахождения первообразной, во-первых, является операцией, обратной дифференцированию, и, во-вторых, эта операция неоднозначная, т. е. в результате ее применения можно получить различные функции, отличающиеся на постоянные слагаемые.
Определение. Совокупность всех первообразных от заданной функции называется неопределенным интегралом от этой функции.
Неопределенный интеграл обозначается так и читается: неопределенный интеграл от функции Если — одна из первообразных функций то любая другая из первообразных от той же функции будет равна
где —любое число. Следовательно
Из определения первообразной и неопределенного интеграла следует, что
В самом деле,
Выпишем формулы, справедливость которых проверяется дифференцированием.
Проверим формулу 10. Возьмем дифференциал от левой части равенства, получим [в силу формулы (Б)]
Таким образом, мы убеждаемся в том, что левая часть есть первообразная от функции Теперь возьмем дифференциал от правой части равенства 10:
Убеждаемся в том, что правая часть равенства есть первообразная от функции часть может отличаться от правой только на постоянное слагаемое, но это постоянное у нас и написано в правой части формулы 10.
Итак, формула 10 верна.
Преобразования неопределенных интегралов
Подобно тому, как в алгебре даются правила, позволяющие преобразовывать алгебраические выражения с целью их упрощения, так и для неопределенного интеграла существуют правила, позволяющие производить его преобразования.
Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от каждого члена в отдельности, т. е.
Постоянный множитель можно вынести за знак интеграла, т. е
(—постоянная величина).
Формула интегрирования по частям, а именно:
Докажем формулу
Возьмем дифференциал от правой части равенства
Применяя формулу 4 из таблицы § 2 гл. IX, получим
Член преобразуем по формуле 5 той же таблицы:
а член по формуле (Б) § 1 этой главы равен
Собирая все вместе, будем иметь
т. е. мы получили то, что получается при дифференцировании левой части равенства (III).
Аналогично проверяются формулы (I) и (II).
Пример 2.
Применяя правило интегрирования I и формулы 1 и 5 из таблицы интегралов, получаем
Пример 3.
Применяя правило II и формулу 6 из таблицы интегралов, получаем
Пример 4.
В таблице интегралов, приведенных в § 1, такого интеграла нет. Вычислим его, интегрируя по частям; для этого перепишем данный интеграл следующим образом:
Положив применим правило интегрирования по частям:
Но так как то, применяя формулу 1 таблицы интегралов получим Окончательно получаем
Пример 4.
Рассмотрим Положим и Тогда так как Применяя интегрирование по частям, будем иметь
Основные правила интеграции
Обзор
[Вернитесь к началу страницы]
Как и в случае дифференцирования, существуют некоторые основные правила, которые мы можем применять при интегрировании функций.
Если вы знакомы с материалом первых нескольких страниц этого раздела, вы уже должны усвоить идею о том, что интеграция и дифференциация противоположны друг другу. Это означает, что когда мы интегрируем функцию, мы всегда можем дифференцировать результат, чтобы получить исходную функцию. К сожалению, обратное неверно. Как только мы продифференцируем функцию, любой постоянный член этой функции просто исчезнет, потому что производная любого постоянного члена равна нулю. Это то, что нам нужно иметь в виду, когда мы думаем о том, как мы будем интегрировать функцию, потому что это означает, что наш ответ всегда будет содержать константу неизвестного значения. Мы называем эту константу постоянная интегрирования , C .
Мы уже говорили о силовом правиле для интеграции в другом месте этого раздела. Это правило, по сути, является обратным степенному правилу, используемому при дифференцировании, и дает нам неопределенный интеграл переменной, возведенной в некоторую степень.
Чтобы освежить вашу память, формула правила мощности интеграции выглядит следующим образом:
| ∫ | ax n d x = a | x n +1 | + C |
| n +1 |
Эта формула дает нам неопределенный интеграл от переменной x , возведенной в степень n , умноженной на постоянный коэффициент a (обратите внимание, что n не может быть равно минус один , потому что в этом случае в знаменателе в правой части формулы будет стоять ноль). Одного этого правила достаточно, чтобы мы могли интегрировать полиномиальные функции одной переменной. Мы просто интегрируем каждое слагаемое по отдельности — знак плюс или минус перед каждым слагаемым не меняется. Неопределенные интегралы некоторых общих выражений показаны ниже.
Обратите внимание, что в этих примерах и представляют собой константу, x представляют собой переменную, а и представляют собой 9.0007 Число Эйлера (приблизительно 2,7183). Обратите также внимание на то, что первые три примера в таблице получены из применения правила мощности.
Неопределенные интегралы некоторых общих функций
Постоянное значение a :
| ∫ | a d x = ax + C |
Переменная x :
| ∫ | x d x = | x 2 | + C |
| 2 |
The square of a variable x 2 :
| ∫ | x 2 D x = | x 3 | + C |
| 3 |
.
0007 x :
| ∫ | 1 | d x = ln ( x ) + C |
| x |
The exponential function e x :
| ∫ | E x D x = E x + C |
. Другие экспонентные функции A 7 . Другие экспонентные функции A 34: 4.0005 Косиральный цвет из переменного Cos ( x ): Основные правила интегрирования, которые мы опишем ниже, включают в себя степень , постоянный коэффициент (или постоянный множитель ), сумма и разность правил. Мы приведем несколько простых примеров, чтобы продемонстрировать, как работают эти правила. [Вернитесь к началу страницы] Степенное правило интегрирования, как мы видели, является обратным степенному правилу, используемому при дифференцировании. Давайте рассмотрим пару примеров использования этого правила. Предположим, мы хотим найти неопределенный интеграл от x 3 . Применяя степенное правило, получаем: n √ a = a 1 / n 3 √ x = x 1 / 3 Теперь мы можем применить правило степени, чтобы получить: [Вернитесь к началу страницы] Правило постоянного коэффициента (иногда называемое правилом постоянного множителя ) по существу говорит нам, что неопределенный интеграл от c · ƒ( x ), где ƒ( x ) — некоторая функция, а c представляет собой постоянный коэффициент, равный неопределенному интегралу от ƒ( x ), умноженному на c . Правило постоянного коэффициента по существу позволяет нам игнорировать постоянный коэффициент в выражении, пока мы интегрируем остальную часть выражения. Например, предположим, что мы хотим найти неопределенный интеграл выражения 5 x 2 . Правило постоянных коэффициентов говорит нам, что неопределенный интеграл этого выражения равен неопределенному интегралу от x 2 умножить на пять . Другими словами: Теперь мы просто применяем правило степени к x 2 : [Вернитесь к началу страницы] Правило суммы говорит нам, как мы должны интегрировать функции, являющиеся суммой нескольких членов. В этот момент вам может быть интересно, почему правило написано именно так. Здесь очень важно понимать, что в функции, являющейся суммой двух (или более) членов, каждый член может рассматриваться как самостоятельная функция, даже постоянный член. Предположим, мы хотим найти неопределенный интеграл полиномиальной функции ƒ( х ) = 6 х 2 + 8 х + 10. Применяя правило сумм, получаем: [Вернитесь к началу страницы] Правило различия говорит нам, как мы должны интегрировать функции, которые включают различие двух или более терминов. По сути, это то же самое, что и правило сумм, поскольку оно говорит нам, что мы должны интегрировать каждый член в сумму отдельно . Единственное отличие состоит в том, что порядок, в котором появляются термины, имеет решающее значение и не должен изменяться. Формально это правило можно сформулировать следующим образом: Давайте посмотрим на пример. Интегралы и производные являются частью раздела математики, называемого исчислением. Связь между этими двумя очень важна и называется основной теоремой исчисления. [4] Теорема гласит, что интеграл можно обратить производной, подобно тому, как сложение можно обратить вычитанием. Интеграция помогает при попытке размножить единицы в задаче. Например, если задача со скоростью (расстояние/время) {\ displaystyle \ left ({\ tfrac {\ text {distance}} {\ text {time}}} \ right)} требует ответа только с расстоянием, одно решение заключается в интегрировании по времени. Это означает умножение на время, чтобы сократить время в (расстояние-время) × время {\ displaystyle \ left ({\ tfrac {\ text {distance}} {\ text {time}}} \ right) \ times {\ text {time} }}. Это делается путем сложения вместе небольших фрагментов графика скорости. Срезы имеют ширину, близкую к нулю, но бесконечное сложение их вместе приводит к тому, что они складываются в одно целое. Сложение этих срезов дает уравнение, производным которого является первое уравнение. Интегралы — это способ сложить вместе множество крошечных вещей вручную. Это похоже на суммирование: 1+2+3+4….+n{\displaystyle 1+2+3+4….+n}. Разница с интегрированием в том, что мы также должны добавить все десятичные дроби между ними. [4] В другой раз интегрирование полезно при нахождении объема твердого тела. Он может бесконечно складывать двумерные (без ширины) срезы твердого тела — до тех пор, пока не появится ширина. Это означает, что объект теперь имеет три измерения: исходные два и ширину. Это дает объем описываемого трехмерного объекта. По основной теореме исчисления интеграл является первообразной. dx{\displaystyle dx} в конце показывает, что мы интегрируем относительно x , то есть по мере изменения x . Можно увидеть, что это обратное дифференцирование. Однако при интегрировании добавляется константа C. Это называется константой интегрирования. [1] Это требуется, потому что дифференцирование целого числа дает нуль, поэтому интегрирование нуля (который можно поставить в конце любого подынтегрального выражения) дает целое число C. Значение этого целого числа можно найти, используя заданные условия.
9{\,}{\frac {f'(x)}{f(x)}}dx=\ln {|f(x)|}+C} Две вертикальные полосы обозначают абсолютное значение; знак (положительный или отрицательный) у f (x) {\ displaystyle f (x)} игнорируется. Это потому, что натуральный логарифм отрицательных чисел не имеет значения. Интеграл суммы функций представляет собой сумму интеграла каждой функции. то есть, Однако для линейных интегралов площадь представляет собой двумерную поверхность, которая «изгибается в трех измерениях». Он волнистый, как занавеска, а не полностью плоский, как в примере выше: Линейный интеграл Это делается путем введения следующего набора параметрических уравнений для определения кривой CCC в плоскости xyxyxy: x=x(t),y=y(t). Только А
А и Б
А и С
только Б
Б и С
только С
Все они
Ни один из них Вывод этих уравнений следующий: Во-первых, имеется кривая CCC в плоскости xyxyxy, определяемая набором параметризованных уравнений x(t)x(t)x(t) и y(t) y(t)y(t), заканчивающийся в точках t=at=at=a и t=b:t=b:t=b: Затем кривая CCC расширяется в трех измерениях с помощью функции z=f(x,y),z = f(x,y),z=f(x,y), определяющей «занавес» между f(x, y)f(x,y)f(x,y) и z=0z=0z=0 и лежащих на кривой C:C:C: Теперь интеграл определяется аналогично плоскому интегралу (y=f(x)). Площадь = f (x, y) ΔS, \ text {Площадь} = f (x, y) \ Delta S, Площадь = f (x, y) ΔS, , где ΔS \Delta S∆S — это ширина каждого из этих отрезков при приближении к нулю: ∆S→0.\Delta S \rightarrow 0.∆S→0. 92}\, dt.Area=∫t=at=bf(x(t),y(t))(dtdx)2+(dtdy)2dt. Каким образом приведенный выше результат обобщается на путь, который существует не только в плоскости xyxyxy, но также изменяется в направлении zzz. Например, американские горки или уравнение, которое зависит от z?z?z? Основные отличия заключаются в том, что f(x,y)f(x,y)f(x,y) теперь также является функцией zzz, поэтому f(x,y,z)f(x,y, z)f(x,y,z), и что ΔS\Delta SΔS, определенное выше, теперь необходимо обобщить на три измерения. Шаг 3: У нас есть и поскольку f(x,y)=xy,f(x,y) = xy,f(x,y)=xy, f(3sin(t),3cos(t))=9cos(t )sin(t).f\big(3\sin(t),3\cos(t)\big) = 9\cos(t)\sin(t).f(3sin(t),3cos(t ))=9{t=\pi}\cos(t)\sin(t)\, dt \\
&= \в коробке{0}.
\end{align}Area=9∫t=0t=πcos(t)sin(t)(−sin(t))2+(cos(t))2dt=9∫t=0t=π cos(t)sin(t)dt=0.
Именно этого мы и ожидали из-за симметрии задачи. □_\квадрат□ А
Б
С
Д
Два из них
Три из них
Все эти
Ни один из этих 92. Какой набор параметрических уравнений позволит построить подобный эллипс? A. x(t)=Rcos(t),y(t)=Rsin(t)2x(t) = R\cos(t), y(t) = \frac{R\sin (t)}{2}x(t)=Rcos(t),y(t)=2Rsin(t) B. x(t)=Rsin(t),y(t)=Rcos (t)2x(t) = R\sin(t), y(t) = \frac{R\cos(t)}{2}x(t)=Rsin(t),y(t)=2Rcos (t) C. x(t)=Rcos(t),y(t)=2Rsin(t)x(t) = R\cos(t), y(t) = 2R\ sin(t)x(t)=Rcos(t),y(t)=2Rsin(t) D. x(t)=2Rcos(t),y(t)=Rsin(t) x(t) = 2R\cos(t), y(t) = R\sin(t)x(t)=2Rcos(t),y(t)=Rsin(t) 92 dx + 5xy\, dy\большое) ? ∮C(y2dx+5xydy)? Теперь рассмотрим реальную проблему: Предположим, есть грабитель банка, который хочет найти ключ, а затем использовать его, чтобы открыть сейф. Хитрость в том, что когда он получает ключ, он включает сигнал тревоги, который приводит в действие радиационную бомбу, излучающую излучение с постоянной скоростью, пока он не откроет сейф, после чего излучение прекращается. Теперь он хочет оптимизировать свой маршрут, чтобы получить минимально возможную дозу радиации. 92}.(Общее излучение)=R2T. Итак, теперь вопрос… Какой из следующих путей позволит грабителю схватить ключ и открыть сейф с наименьшим радиационным облучением? (Предположим, что какой бы путь он ни выбрал, он будет двигаться с постоянной скоростью.) Рассмотрим эти три варианта: A. Дуга окружности с центром в (1,1)(1,1)(1,1) Очевидно, перед грабителем стоит вопрос, как провести наименьшее количество времени под воздействием радиации, но при этом оставаться достаточно далеко от источника радиации. Интуитивно понятно, что A отсутствует, так как это не только более длинный маршрут, чем B , но и приближает его к радиации. Однако B и C не так очевидны. B — это самый прямой маршрут (прямая линия), он дает ему наименьшее количество общего времени воздействия радиации, но приближает его к радиации немного ближе, чем С . В качестве альтернативы, C держит его подальше от радиации, но это дает ему немного больше общего времени воздействия радиации. Итак, какой путь лучше? Здесь пригодится линейный интеграл каждого пути. Итак, начнем с C . Хотя здесь можно было бы взять линейный интеграл, это было бы не очень интересно, поскольку, хотя он и движется по дуге, он остается на том же расстоянии от источника излучения в начале координат, поэтому суммарное облучение EEE составит 92} = T,EC=R2T=12T=T, , где TTT – это общее время, затрачиваемое на то, чтобы добраться туда. Поскольку WLOG его скорость можно принять равной 1, это просто длина дуги, или π2:\frac{\pi}{2}:2π: EC=π2. Теперь о пути B… Для этого потребуется линейный интеграл , поскольку грабитель находится на разных расстояниях от излучения и, следовательно, получает разное количество излучения в разных точках своего пути. Ясно, что в точке (12,12)\big(\frac{1}{2},\frac{1}{2}\big)(21,21) излучение будет максимальным, а при (0,1)(0,1)(0,1) и (1,0)(1,0)(1,0) лучевая нагрузка будет минимальной (для данного конкретного пути). Итак, качественно излучение по пути будет выглядеть так: Суммарное облучение на пути B , EBE_BEB, представленное площадью под кривой (синяя область), это то, что можно оценить с помощью линейного интеграла: 9\circ45∘ угол траектории. Это дает x(t)=t2,y(t)=1−t2.x(t) = \frac{t}{\sqrt{2}},\quad y(t) = 1 — \ frac{t}{\sqrt{2}}.x(t)=2t,y(t)=1−2t. Итак, dxdt=12,dydt=−12.\frac{dx}{dt} = \frac{1}{\sqrt{2}},\quad \frac{dy}{dt} = — \ frac{1}{\sqrt{2}}. ∫ A x D x = A x + C + C 9008 + C 99008 + C 9008 + C 9008 . 
Логарифм переменной LN ( x ):
9 ). переменной sin ( x ): ∫ LN ( x ) D x = x LN ( x ) — x + C ∫ SIN ( x ) D x = -cos ( x ) + C 44
∫ cos ( x ) d x = sin ( x ) + C Правило силы
Это дает нам неопределенный интеграл от переменной, возведенной в степень. Вот еще раз правило мощности: ∫ ax n d x = a x n +1 + C n +1 ∫ x 3 D x = x 4 + C + 0 4 777777999999999999999999999999999999999999999900 + C . 
Иногда не так очевидно, что мы можем использовать степенное правило для нахождения неопределенного интеграла функции. Предположим, например, что мы хотим найти неопределенный интеграл выражения 3 √ x . Как мы используем правило мощности для интеграции функции кубического корня? Это на самом деле довольно легко. Все, что нам нужно сделать, это переписать выражение так, чтобы мы получили х в степени. Существует стандартная формула, которая позволяет выразить n -й корень числа как в индексной форме (т. е. как , возведенное в степень):4
Применяя эту формулу к
3 √ x , мы получаем: ∫ x 1 / 3 d x = 3 x 4 / 3 + C 4 Правило постоянного коэффициента
Формально мы можем выразить это следующим образом: ∫ c ƒ( x ) d x = c ∫ ƒ( x ) d x ∫ 5 x 2 d x = 5 ∫ x 2 d x 5 ∫ x 2 d x = 5 x 3 + C 3 Правило суммы
По сути, это говорит нам, что мы должны интегрировать каждый член в сумму отдельно , а затем просто сложить результаты вместе. Порядок, в котором термины появляются в результате, не важен. Формально мы можем сформулировать это следующим образом: ∫ (ƒ( x ) + g ( x )) d x = ∫ ƒ( x ) d x + ∫ г ( x ) d x ∫ (6 x 2 + 8 x + 10) d x = ∫ 6 x 2 d x + ∫ 8 x d x + ∫ 10 d x
9. ∫ 7 x 08
2 + 8 x + 10) D x = 2 x 3 + 4 x 2 + 10 x + C 
Правило разницы ∫ (ƒ ( x ) — G ( x )) D x = ∫ ƒ ( x ) D x 9008 — 4040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040404040. 40404040404040404040404. ƒ ). г ( x ) d x 
Предположим, мы хотим найти неопределенный интеграл полиномиальной функции ƒ( х ) = 4 х 3 — 18 х — 7. Применяя правило сумм, получаем: ∫ (4 x 3 — 18 x — 7) d x = ∫ 4 x 3 d x — ∫ 18 х д х — ∫ 7 д х
.
Правила суммы и разности по сути являются одним и тем же правилом. Если мы хотим интегрировать функцию, которая содержит как сумму, так и разность ряда терминов, главное помнить, что мы должны интегрировать каждый термин отдельно и быть осторожным, чтобы сохранить порядок, в котором появляются термины. ∫ 7 х (00 7 х 0008 2 + 8 x + 10) D x = x 4 — x 2 — 7 x + C 
{\,}} в виде длинной буквы «S». [1] [2] [3]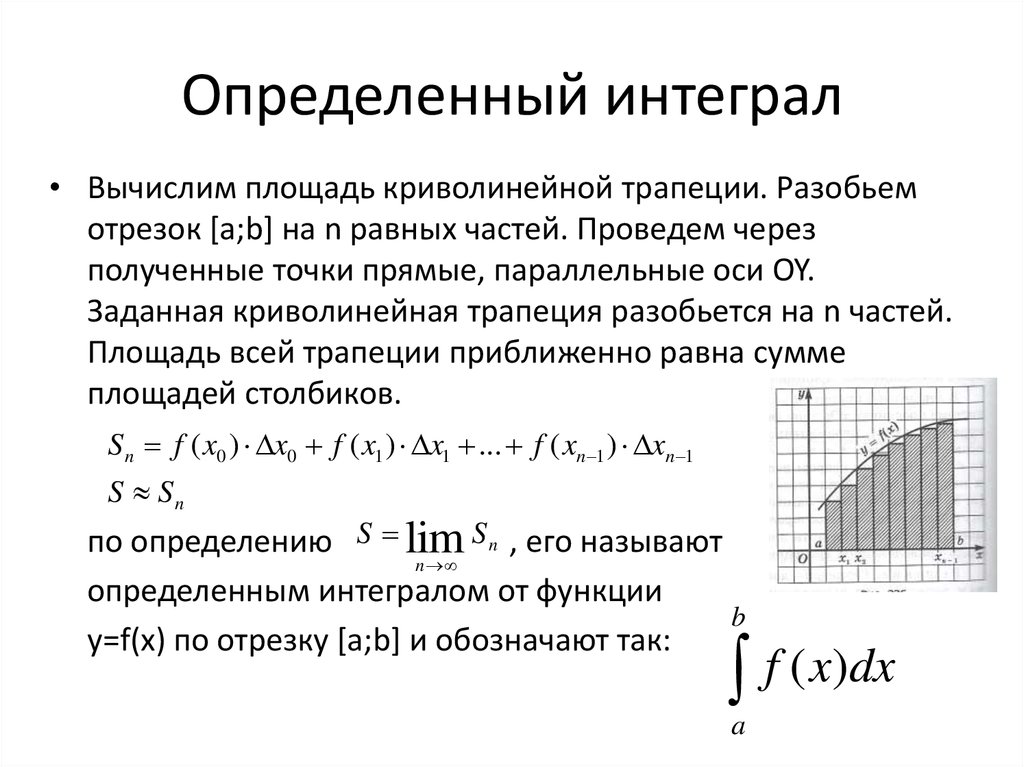 
Это называется суммой Римана. Содержание
Первообразная[изменить | изменить источник]
9{n+1}}{n+1}}+C} Сумма функций[изменить | изменить источник]
9{а}ф(х)\,дх}
ISBN 0-582-54539-0 . Линейный интеграл | Brilliant Math & Science Wiki
Содержание
x=x(t), \ четырехугольник y=y(t).x=x(t),y=y(t). 92}\, dt.Area=∫t=at=bf(x(t),y(t),z(t))(dtdx)2+(dtdy)2+(dtdz)2 дт.
\big(y = f(x)\big).(y=f(x)). Определите ширину каждого небольшого вертикального сегмента поверхности, изображенной выше, как ΔS\Delta SΔS. Площадь каждого из этих сегментов равна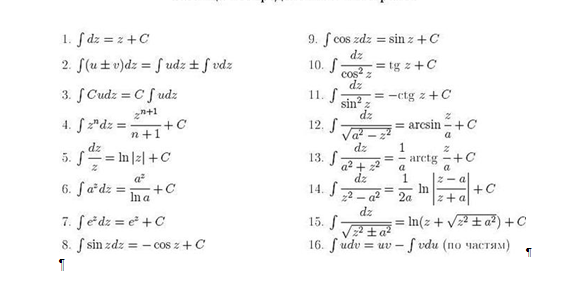
2}.ds=(dtdx)2+(dtdy)2+(dtdz)2. 92}\, dt.Area=∫t=0t=πf(3sin(t),3cos(t))(dtdx)2+(dtdy)2dt.
x2+4y2=R2.
B. Прямой маршрут из (0,1)(0 ,1)(0,1) до (1,0)(1,0)(1,0)
C. Дуга окружности с центром в точке (0,0)(0,0)(0,0).
Ой!
E_C = \frac{\pi} {2}.EC=2π.