Элементарная алгебра
Элементарная алгебра
ОглавлениеГлава I. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ§ 2. Понятия кольца и поля § 3. Упорядоченные поля § 4. Понятие функции и аналитического выражения § 5. Элементарные функции и их классификация § 6. Метод математической индукции Глава II. ОБЩИЕ СВЕДЕНИЯ ОБ УРАВНЕНИЯХ § 1. Понятие уравнения. Решения уравнения § 2. Классификация уравнений, изучаемых в элементарной математике § 3. Равносильность уравнений § 4. Преобразование уравнений при их решении Глава III. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ С ОДНИМ НЕИЗВЕСТНЫМ § 1. Алгебраические уравнения n-й степени с одним неизвестным § 2. Корни квадратного трехчлена § 3. Исследование квадратного трехчлена над полем действительных чисел § 4. Двучленные уравнения § 5. Трехчленные уравнения, приводящиеся к квадратным § 6. Симметрические уравнения § 7. Алгебраическое уравнение n-й степени с рациональными коэффициентами § 8.  Частные приемы решения уравнений высших степеней§ 9. Дробно-рациональные уравнения Глава IV. ТЕОРИЯ СОЕДИНЕНИЙ § 2. Перестановки § 3. Сочетания § 4. Размещения § 5. Перестановки с повторениями § 6. Сочетания с повторениями § 7. Размещения с повторениями Глава V. БИНОМ НЬЮТОНА И ПОЛИНОМИАЛЬНАЯ ТЕОРЕМА § 1. Бином Ньютона § 2. Биномиальные коэффициенты и их основные свойства § 3. Треугольник Паскаля § 4. Полиномиальная теорема § 5. Вычисление сумм степеней первых n чисел натурального ряда Глава VI. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Многочлен от нескольких переменных и его каноническая форма § 2. Однородный многочлен от n переменных и число его членов § 3. Число членов в каноническом представлении многочлена от n переменных § 4. Тождественность двух многочленов § 6. Применение метода неопределенных коэффициентов при выполнении алгебраических действий над многочленами Глава VII.  СИСТЕМЫ УРАВНЕНИЙ С НЕСКОЛЬКИМИ НЕИЗВЕСТНЫМИ§ 1. Понятие системы уравнений § 2. Равносильность систем уравнений § 3. Уравнения и системы уравнений, являющиеся следствием данной системы уравнений § 4. Основные элементарные методы решения систем уравнений § 5. Решение нелинейных систем алгебраических уравнений элементарными методами 1. Решение системы двух уравнений с двумя неизвестными, из которых одно—второй степени, а другое — первой. 2. Решение системы двух уравнений второй степени с двумя неизвестными, которые не имеют членов первой степени. 3. Решение системы двух уравнений второй степени с двумя неизвестными в общем виде. 4. Решение системы двух однородных уравнений с двумя неизвестными. 5. Решение системы двух уравнений с двумя неизвестными, одно из которых однородное, а второе не однородное. 7. Решение нелинейной системы алгебраических уравнений, в состав которой входят линейные уравнения. 8. Решение нелинейной системы алгебраических уравнений, левая часть одного из которых представляется в виде произведения.  § 6. Графическое решение нелинейных систем алгебраических уравнений с двумя неизвестными Глава VIII. НЕРАВЕНСТВА § 1. Основные свойства неравенств § 2. Тождественные неравенства § 3. Применение неравенств для определения наибольших и наименьших значений § 4. Решение неравенств § 5. Решение алгебраических неравенств с одним неизвестным первой и второй степени § 6. Решение систем алгебраических неравенств первой степени с двумя неизвестными § 7. Применение неравенств для задания числовых и точечных множеств § 1. Корни с натуральными показателями в поле действительных чисел § 2. Тождественные преобразования иррациональных выражений в поле действительных чисел § 3. Решение иррациональных уравнений и систем, в состав которых входят иррациональные уравнения, в поле действительных чисел Глава X. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ В ПОЛЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 1.  {2n+1} $$Представьте число в виде суммы степеней основания с коэффициентами:1203 в третьей степени счисления, 43020 в пятой степени счисления, 70652 в 8 степени счисленияРешение: 1. 1203:3=401 ост 0 401:3=133 ост 2 133:3=44 ост. 1 44:3=14 ост. 2 14:3=4 ост. 2 4:3=1 ост.1 1:3=0 ост.1 1122120₃ 2. 43020:5=8604 ост. 0 8604:5=1720 ост. 4 1720:5=344 ост.0 344:5=68 ост.4 68:5=13 ост.3 13:5=2 ост.3 2:5=0 ост.2 2334040₅ 3. 70652:8=8831 ост.4 8831:8=1103 ост.7 1103:8=137 ост.7 137:8=17 ост.1 17:8=2 ост.1 2:8=0 ост.2 211774₈ Доказательство суммы степеней Бернулли | Марко Тавора, доктор философии.Как вычислить сумму p степеней n первых целых чиселИзображение Garik Barseghyan с Pixabay. Среди своих значительных достижений известный швейцарский математик Якоб Бернулли (1655–1705), один из многих выдающихся математиков в своей семье (семья Бернулли дала начало восьми всемирно известным математикам), в 1713 г. Сумма, известная как формула Фаульхабера (названная в честь немецкого математика Иоганна Фаульхабера (1580–1635)), результат которой Бернулли опубликовал под названием Summae Potestatum , равно , заданному следующим выражением 5 Уравнение : сумма p -й степени первых n положительных целых чисел, известная как формула Фаульхабера. Как отмечено в этих исключительных лекциях по теории чисел, вычисления становятся намного более аккуратными, если записать сумму, начинающуюся с индекса m = 0 и заканчивающуюся индексом m = n -1. При таком альтернативном выборе индексов сумма становится следующей: Уравнение 2: Уравнение. 1 записывается суммой, начиная с индекса m =0 ноль и заканчивая индексом m = n -1. Выбор этого нового набора индексов «очищает» вычисления.Теперь рассмотрим так называемую производящую функцию S ( n , t ), степенной ряд, который имеет суммы в уравнениях. 1 и 2 как коэффициенты: Уравнение 3: Производящая функция имеет суммы, заданные уравнениями. 1 и 2 в качестве коэффициентов. Согласно Википедии, производящая функция «представляет собой способ кодирования бесконечной последовательности чисел, рассматривая их как коэффициенты степенного ряда». Подставляя уравнение. 2 в уравнении 3 мы получаем двойную сумму: Уравнение 4: Ур. 3 после замены уравнения. 2., где к — целое число. После нескольких шагов алгебры, используемых для перестановки сумм, мы можем переформулировать уравнение. 4 следующим продуктом двух функций: Уравнение 5: Уравнение. 4 переписан как произведение двух функций. Это выражение получается после перестановки сумм и выполнения некоторых простых (но не очень наглядных) алгебраических действий.Уравнение 5 получается перестановкой двойной суммы в уравнении. 4 и проделав некоторые простые (но не очень наглядные) алгебраические действия. Теперь первый делитель S ( n , t ) может быть тривиально записано в виде степенного ряда с использованием разложения Тейлора экспоненциальной функции: Уравнение 6: Разложение степенного ряда экспоненциальной функции. (вам просто нужно вычесть 1 из левой части уравнения 6 и разделить обе части на x ). Пропуская несколько шагов (во избежание беспорядка), производящая функция S ( n , t ) становится следующим сложным выражением: 3 после использования временного ряда экспоненциальной функции и уравнения. 7 (который содержит числа Бернулли). Теперь следующим шагом является определение так называемых полиномов Бернулли: Уравнение 9: Определение полиномов Бернулли, показанных на рис. 3 ниже.На рисунке ниже показано несколько примеров полиномов Бернулли, соответствующих различным значениям чисел Бернулли. Рисунок 3: Полиномы Бернулли для нескольких значений чисел Бернулли (источник).Сравнивая исходное выражение для производящей функции S ( n , t ) с уравнением 8 и используя определение многочленов Бернулли, получаем: Уравнение 10: Окончательное выражение для суммы p степеней n первых целых чисел, которые нам нужны. Обратите внимание, что производящую функцию можно изящно записать так: Уравнение 11: Окончательное выражение для производящей функции, выраженное через многочлены Бернулли и числа Бернулли.В предыдущей статье (см. ниже) я вывел первые пять чисел Бернулли. Они задаются следующим образом: Уравнение 12: Первые пять чисел Бернулли, полученные в этой статье. Рисунок 4: Слева японский математик Кова Секи. Справа страница из его работы Кацуё Сампо (1712), где он сводит в таблицу биномиальные коэффициенты и числа Бернулли.О суммах рядов обратных величинВеликий математик Эйлер и его замечательные открытияв направленииdatascience.com Использование уравнения. 9 мы получаем некоторые полиномы Бернулли (см. рис. 3): Уравнение 13: Первые полиномы Бернулли. Теперь у нас есть все необходимые инструменты! Ниже приведены два простых примера суммы, которую мы ищем, но все остальные случаи могут быть получены тривиально:0005 Уравнение 14: Два простых примера сумм p степеней n первых целых чисел. На моем Github и личном веб-сайте www.marcotavora.me есть другие интересные материалы как по математике, так и по другим темам, таким как физика, наука о данных и финансы. Проверь их! Сумма последовательных степеней (3-я, 4-я, 5-я и 6-я) КалькуляторСумма последовательных кубов, 4-х степеней, 5-х степеней, 6-х степеней и т. д. известна как сумма степеней. Сумма мощностей от 1 до н мощностью р (1 р + 2 р + 3 р + … + н р ) обозначается S р (н). Для положительных целых значений p и n значение S p (n) может быть найдено путем вычисления многочлена от n . Зная, как суммировать степени от 1 до n , вы можете найти сумму степеней между любыми двумя значениями a и b . Эти уравнения объясняются ниже, и вы также можете использовать калькулятор суммы мощностей слева. Уравнения суммы степеней Сумма последовательных кубов от 1³ до n³ равна квадрату n -го треугольного числа. S₃(n) = n²(n+1)²/4 = [n(n+1)/2]² = [T(n)]² Сумма четвертых степеней равна S₄(n) = n(n+1)(2n+1)(3n² + 3n — 1)/30 Сумма 5-х степеней равна S₅(n) = n²(n+1)²(2n² + 2n — 1)/12 Сумма шестых степеней равна S₆(n) = n(n+1)(2n+1)(3n⁴ + 6n³ — 3n + 1)/42 Сумма последовательных степеней отA P до B PСумма любой последовательности подряд от A P до B P ( ( ( ( ( . ) и S p (a) плюс a p . ) Пример: Найдите сумму всех пятых степеней от 100⁵ до 120⁵, включая конечные точки. S₅(120) — S₅(100) + 100⁵ Fun Facts О суммах степеней 0. 1. Если вы знаете многочлены S₀(n), S₁(n), S₂(n),…, S p-1 (n), то можно найти S p (n), разложив сумму Σ j=1…n (1+j) p+1 на отдельные степенные суммы . Σ j=1…n (1+j) p+1 = Σ k=0…p+1 [Σ j=1…n C(p+1,k)j k ] = Σ k=0…p+1 C(p+1,k)S k (n) где C(p+1,k) биномиальный коэффициент p +1 выбрать к . Если продолжить упрощать выражение, то получим Σ j=1…n (1+j) p+1 — S p+1 (n) = Σ k= 0…p C(p+1,k)S k (n) (n+1) p+1 — 1 = Σ k=0…p C (p+1,k)S k (n) (n+1) p+1 — 1 — Σ k=0. [ (n+1) p+1 — 1 — Σ k=0…p-1 C(p+1,k)S k (n) ] / (p+1) = S p (n) См. вывод формула квадратного пирамидного числа для примера использования этой техники. 2. Бесконечная сумма обратных величин S₃(n) равна 4π²/3 — 12. Это можно доказать следующим образом: Σ n=1…∞ ) = Σ n=1…∞ 4/[n²(n+1)²] = Σ n=1…∞ [-8/n + 8/(n +1) + 4/n² + 4/(n+1)²] = -8Σ n=1…∞ [1/n — 1/(n+1)] + 4Σ n=1…∞ 1/n² + 4Σ n =2…∞ 1/n² = -8Σ n=1…∞ [1/n — 1/(n+1)] + 8Σ n=1… ∞ 1/n² — 4 Первая часть этого выражения представляет собой телескопическую сумму, которая сводится к -8. |
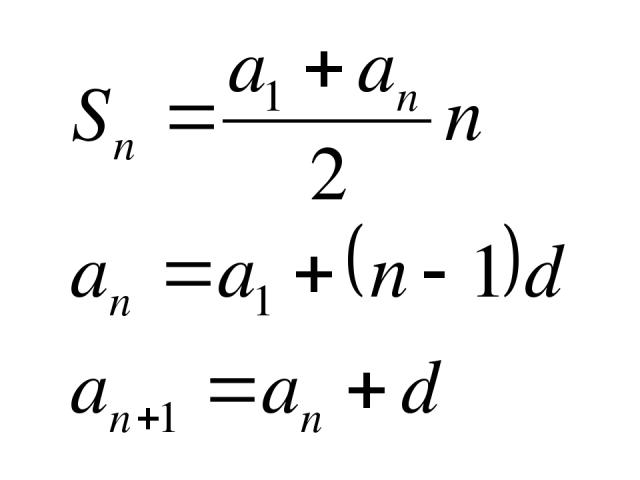выражение для суммы p степеней n первых целых чисел (которые он назвал Summae Potestatum). Его решение, имеющее вид полиномиальной функции n степени ( p + 1), содержит коэффициенты, включающие вездесущие и ныне известные числа Бернулли (последовательность дробных чисел, которые встречаются во многих областях как математики, так и теоретическая физика).
Фаульхабер был эрудитом, обучался на ткача, работал на укреплениях нескольких городов, среди прочего строил водяные колеса и геометрические инструменты для военных (источник).
Чтобы написать второй член S ( n , t ), нужно ввести ранее упомянутые числа Бернулли. Функция t /(e ᵗ -1) в уравнении. 5 становится:
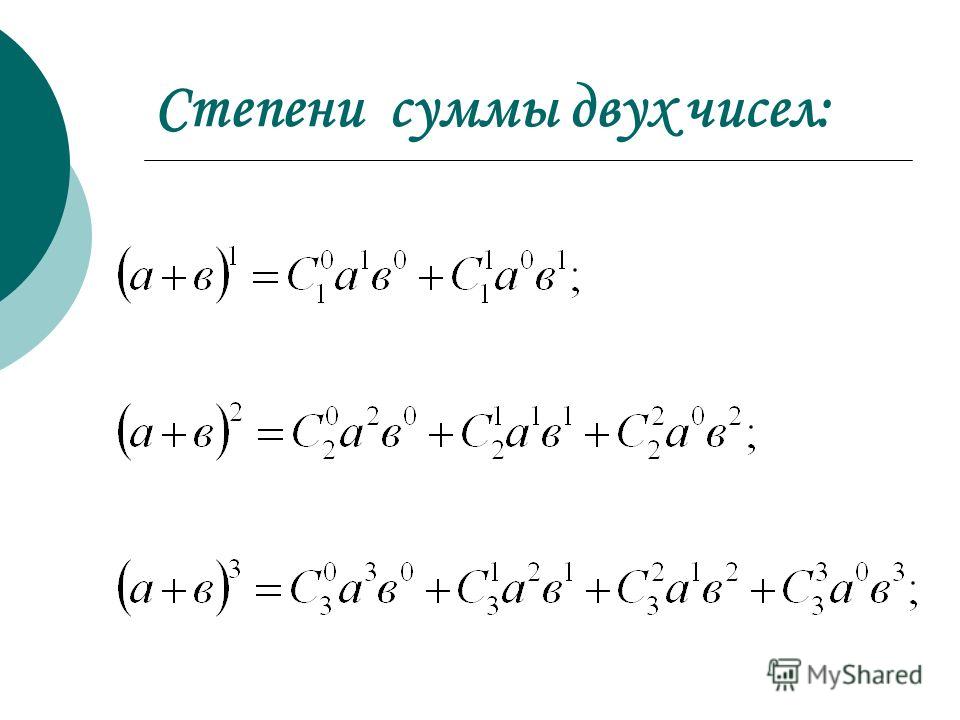То есть
S₀(n) — это сумма нулевых степеней от 1⁰ до n⁰. Поскольку любое ненулевое число, возведенное в 0-ю степень, равно 1, S₀(n) = (1)(n) = n.
..p-1 