Элементы высшей математики
Элементы высшей математики
ОглавлениеПРЕДИСЛОВИЕЧАСТЬ ПЕРВАЯ.  § 1. Ось § 2. Вектор § 3. Направленные углы § 4. Проекция вектора с оси на ось § 5. Векторные цепи § 6. Цепи углов § 7. Проекции вектора на две взаимно перпендикулярные оси § 8. Угол между двумя лекторами. Условия параллельности и перпендикулярности S 9. Упражнения и контрольные вопросы Глава 2. КООРДИНАТЫ § 1. Метод координат § 2. Основные задачи, решаемые методом координат § 3. Упражнения Глава 3. ФУНКЦИИ § 1. Переменные в постоянные § 2. Понятие о функциональной зависимости § 3. Классификация математических функций § 4. Обзор и графическое изображение простейших функции одного аргумента § 5. Обратные функции § 6. Понятие об уравнении линии § 7. Упражнения Глава 4. ПРЯМАЯ § 1. Уравнение прямой, проходящей через данную точку § 2. Общее уравнение прямой § 3. Частные случаи § 4. Переход к уравнению с угловым коэффициентом § 5. Построение прямой § 6. Определение угла между двумя прямыми § 7.  Условие совпадения прямых§ 8 Пересечение прямых § 9. Расстояние от точки до прямой § 10. Другой подход к выводу уравнения прямой § 11. Прямая, проходящая через две точки § 12. Уравнение прямой в отрезках на осях § 13. Задачи на прямую линию Глава 5. ПРОСТЕЙШИЕ КРИВЫЕ. ПРЕОБРАЗОВАНИЕ КООРДИНАТ § 1. Окружность § 2. Эллипс. Построение посредством нитн. Зависимость между полуосями и полуфокусным расстоянием § 3. Построение эллипса по точкам § 4. Уравнение эллипса § 5. Связь эллипса с окружностью § 6. Директрисы эллипса § 7. Гипербола. Построение посредством нити § 8. Построение гиперболы по точкам § 9. Уравнение гиперболы § 10. Асимптоты. Геометрическое значение b § 11. Директрисы гиперболы § 12. Парабола. Построение по точкам § 14. Преобразование координат § 15. Пример на упрощение уравнения кривой путем параллельного переноса осей § 16. Поворот осей § 17. Общий случай § 18.  Полярные координаты§ 19. Спираль Архимеда § 20. Логарифмическая спираль § 21. Примеры на составление полярных уравнений кривых § 22. Выражение прямоугольных координат через полярные § 23. Уравнение лемнискаты § 24. Параметрическое задание линий § 25. Построение графика § 26. Циклоида § 27. Упражнения Глава 6. ВЕКТОРЫ, ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ § 1. Оси, векторы, углы § 2. Проекции § 3. Проекции на три взаимно перпендикулярные оси. Длина вектора через проекции § 4. Простейшие зависимости, содержащие величину вектора, проекции и направляющие косинусы § 5. Проекция вектора на оси. Косинус угла между двумя векторами. Скалярное произведение векторов § 6. Координаты § 7. Выражение проекций вектора через координаты конца и начала § 8. Выражение длины вектора через координаты концов. Расстояние между двумя точками § 9. Деление отрезка в данном отношении § 10. График уравнения с двумя переменными § 11.  Поверхность как след, образуемый перемещением некоторой деформируемой плоской кривой§ 12. Цилиндрические поверхности § 13. Обратная задача. Уравнение шаровой поверхности § 14. Уравнение плоскости, проходящей через данную точку § 15. Общее уравнение плоскости § 16. Частные случаи § 17. Выяснение расположения плоскости относительно осей § 18. Угол между плоскостями. Условие параллельности. Условие перпендикулярности § 19. Условие совпадения плоскостей § 20. Расстояние от точке до плоскости § 22. Прямая, проходящая через данную точку § 23. Прямая, проходящая через две точки § 24. Переход от системы уравнений прямой в общем виде к системе в виде пропорций § 25. Угол между прямыми. Условие параллельности. Условие перпендикулярности § 26. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности § 27. Простейшие поверхности. Эллипсоид § 28. Другие простейшие поверхности § 29.  Кривая в пространстве как пересечение двух поверхностей§ 30. Параметрические уравнения § 31. Винтовая линия § 32. Параметрические уравнения в механике § 33. Переход от параметрического представления к общему и обратно § 34. Преобразование координат § 35. Упражнения ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ § 1. Бесконечно малые § 2. Понятие предела переменной величины § 3. Понятие бесконечно большой § 4. Свойства бесконечно малых § 5. Основные свойства пределов § 6. Предел непрерывной функции § 7. Геометрическое истолкование непрерывности § 8. Свойство непрерывной функции § 9. Предел функции, зависящей от нескольких переменных § 10. Особые случаи разыскания предела § 11. Замечательный тригонометрический предел § 12. Признак существования предела § 13. Сходимость бесконечных рядов § 14. Простейшие признаки сходимости § 15. Основание натуральных логарифмов § 16. Порядок бесконечно малых § 17.  x.§ 9. Производные произведения и частного. Производные tg x и ctg x. § 10. Производные обратных тригонометрических функций § 11. Сводка основных формул § 12. Дифференциал § 13. Основные формулы для дифференциалов § 15. Высшие дифференциалы § 16. Дифференцирование неявных функций § 17. Дифференцирование функций, заданных параметрическим способом § 18. Преобразование дифференциалов к новой переменной § 19. Упражнения Глава 3. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ § 1. Непрерывность первой производной § 2. Возрастание и убывание функций. Максимум и минимум § 3. Приложение к построению графиков § 4. Наибольшее и наименьшее значения функции § 5. Прикладные задачи на наибольшее и наименьшее значения § 6. Направление выпуклости, точки перегиба § 7. Приложение к построению графиков § 8. Построение графиков разрывных функций § 9. Признак максимума и минимума, основанный на исследовании знака первой производной § 10.  Признак максимума и минимума, основанный на исследовании знака второй и высших производных§ 11. Асимптоты § 12. Дифференциал дуги § 13. Направляющие косинусы касательной § 14. Радиус кривизны, центр кривизны § 15. Дифференциал дуги и направляющие косинусы касательной для кривой в пространстве § 16. Упражнения Глава 4. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ § 1. Функции многих переменных. Область определения. Непрерывность § 2. Частные производные и полный дифференциал § 3. Частные производные и полный дифференциал сложной функции многих переменных § 4. Дифференцирование неявных функций § 5. Частные производные и полные дифференциалы высшего порядка § 6. Упражнения ЧАСТЬ ТРЕТЬЯ. ОСНОВЫ ТЕОРИИ ЧИСЕЛ Глава 1. ТЕОРИЯ ДЕЛИМОСТИ § 2. Общий наибольший делитель § 3. Общее наименьшее кратное § 4. Простые числа § 5. Единственность разложения на простые сомножители § 6. Непрерывные дроби и их связь с алгоритмом Евклида Вопросы к главе 1 Глава 2.  § 1. Функции [x] и {x} § 2. Мультипликативные функции § 3. Число делителей и сумма делителей § 4. Функция Мёбиуса § 5. Функция Эйлера Вопросы к главе II Глава 3. СРАВНЕНИЯ § 2. Свойства сравнений, подобные свойствам равенств § 3. Дальнейшие свойства сравнений § 4. Полная система вычетов § 5. Приведенная система вычетов § 6. Теоремы Эйлера и Ферма Вопросы к главе 3 Глава 4. СРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ § 2. Сравнения первой степени § 3. Система сравнений первой степени § 4. Сравнения любой степени по простому модулю § 5. Сравнения любой степени по составному модулю Вопросы к главе 4 Глава 5. СРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ § 2. Символ Лежандра § 3. Символ Якоби § 4. Случай составного модуля Вопросы к главе 5 Глава 6. ПЕРВООБРАЗНЫЕ КОРНИ И ИНДЕКСЫ § 2. Первообразные корни по модулям § 3. Разыскание первообразных корней по модулям § 4. Индексы по модулям § 5.  a§ 7. Индексы по любому составному модулю Вопросы к главе 6 Глава 7. ХАРАКТЕРЫ § 2. Важнейшие свойства характеров Вопросы к главе 7 РЕШЕНИЯ ВОПРОСОВ Решения к главе 2 Решения к главе 3 Решения к главе 4 Решения к главе 5 Решения к главе 6 ОТВЕТЫ К ЧИСЛЕННЫМ ПРИМЕРАМ |
Производная постоянной функции — константы
Правила дифференцирования функций, содержащих постоянные
Здесь мы рассмотрим следующие правила, связанные с дифференцированием функций, содержащих постоянные:
(1) ;
(2) ,
где C – постоянная, u – дифференцируемая функция от независимой переменной :
.
Вначале мы докажем эти правила. Затем приведем примеры вычисления производных.
Производная постоянной функции
Выясним, чему равна производная постоянной функции. Для этого применим определение производной:
(3) .
Пусть функция является постоянной, которую обозначим как :
.
То есть не зависит от x. Значения переменной y одинаковы при любых значениях переменной x и равны . Тогда
;
;
.
То есть производная постоянной функции равна нулю:
.
Вынесение постоянной за знак производной
Теперь докажем правило (2). То есть если является дифференцируемой функцией от переменной x (на некотором множестве ее значений), то при дифференцировании, постоянный множитель можно выносить за знак производной:
(2) .
Доказательство
Поскольку является дифференцируемой функцией, то существует производная этой функции:
.
Рассмотрим функцию от независимой переменной x следующего вида:
.
По определению производной
.
То есть
.
Что и требовалось доказать.
Примеры
Все примеры Проиллюстрируем применение рассмотренных правил (1) и (2). Далее будут рассмотрены примеры, в которых нужно найти производные функций, зависящих от переменной x.
⇓, ⇓, ⇓, ⇓, ⇓.
Пример 1
Найти производную функции
.
Решение
Функция не содержит переменную x. Поэтому она является постоянной. Поскольку производная постоянной функции равна нулю, то производная заданной функции равна нулю:
.
Ответ
.
Пример 2
Найти производную функции от переменной x:
.
Решение
Здесь является постоянной. Выносим ее за скобки и используем таблицу производных:
.
Ответ
.
Пример 3
Найдите производную:
.
Решение
Применим свойство логарифма
.
Тогда
.
Выносим постоянную 6 за скобки и применяем таблицу производных:
.
Ответ
.
Пример 4
Продифференцировать функцию от переменной x:
.
Решение
Применим свойство экспоненты
.
Тогда
.
Но является постоянной, не зависящей от переменной величиной. Выносим ее за скобки и используем таблицу производных:
.
Ответ
.
Пример 5
Продифференцировать по переменной x функцию, состоящую из корней:
.
Решение
Преобразуем корни в степенную функцию, применяя свойства корней:
;
;
;
;
.
Выносим постоянную за скобки и применяем правило дифференцирования степенной функции из таблицы производных:
.
Тогда
.
Приведем корни к одинаковой степени и упростим результат:
.
Ответ
.
Исчисление. Есть ли символ для «взятия производной от чего-то»?
Задавать вопрос
спросил
Изменено 5 лет, 9 месяцев назад
Просмотрено 9к раз
$\begingroup$
92+4x+9$ в исходную $f(x)$, а затем взять производную.
$\endgroup$
2
$\begingroup$
Чаще всего выбирают $\frac{d}{dx}$. Если переменная понятна из контекста, вы можете использовать простую $D$.
Если у вас есть несколько переменных и вы хотите дифференцировать только по одной, лучше всего записать ее как частную производную с $\frac{\partial}{\partial x}$ или $\partial_x$. 92+4x+9)_x$, но я бы настоятельно рекомендовал вместо этого использовать $\frac{d}{dx}$.
Существует несколько видов производных, и хорошо использовать нотацию, совместимую с ними (использует аналогичный синтаксис). $\frac{d}{dx}$ легко заменить на $\frac{\partial}{\partial x}$, $\nabla$, $\Delta$ или $d$.
$\endgroup$
2
$\begingroup$
Да, есть.
Поскольку $f’$ представляет собой производную от $f$, вы можете использовать штрих-символ следующим образом: 92+14x+4$$
Я уже видел, как его использовали таким образом. Также обратите внимание, что если вы не сбиваете с толку читателя, вы можете придумать свои собственные обозначения, если это будет полезно.
$\endgroup$
$\begingroup$
Подобно тому, как символ $$\int(\cdots)\;dx$$ обозначает первообразную чего-то (выражение, где стоит «$\cdots$»), так и символ $$\frac{d}{dx }(\cdots)$$ обозначает производную от чего-то (опять же, выражение, где стоит «$\cdots$»). 92-27x+1)’ = 26x-27$$
Другими словами, $$(\cdots)’\equiv \frac{d}{dx}(\cdots)$$
$\endgroup$
Интерпретация знака производной – The Math Doctors
(Новый вопрос недели)
Иногда, когда мы изучаем новый предмет, в данном случае исчисление, поверхностно простой вопрос может сбить с толку.
И это может быть хорошо! Давайте рассмотрим вопрос о производной, который, хотя и не использует очень сложные понятия, бросает вызов учащемуся, который заставляет глубже задуматься о понятии, требуя различий, которые рутинный вопрос не требует от ученика. 92) + 1)
галлона на милю при движении со скоростью x миль в час по гладкой сухой дороге.
- Если водитель говорит вам, что хочет ехать со скоростью 20 миль в час, что вы должны ему сказать?
- Если водитель хочет ехать со скоростью 40 миль в час, что ему сказать?
Мне нужно руководство по решению этого вопроса.
В первой части мы должны взять x = 20 миль в час в G'(x), чтобы получить G'(x) = -1/200?
Книжный ответ 1/200, иди быстрее.
Во-первых, что здесь говорит нам знак минус.
Во второй части получаем G'(40) = 1/400.
Книжный ответ: G'(40) = 1/400, иди медленнее.
Спасибо в ожидании.
В вопросе необходимо уточнить или исправить некоторые моменты; и сама проблема, если предположить, что о ней было сообщено полностью, немного неясна в отношении того, какой ответ ожидается.
2} + 1 \right).$$ Это правильная производная, независимо от того, была ли она предоставлена как часть задачи или предоставлена Ахтаром как часть его работы. (Интересный побочный вопрос: каковы единицы измерения производной? Это «галлоны на милю, на милю в час» или \(\frac{\text{gal/mi}}{\text{mi/hr} }\) – ставка ставки по отношению к ставке, которая будет частью трудности в этой задаче!)
Нам не сообщают подробности об уровне знаний ученика, но мы можем предположить:
Похоже, что эта проблема ставится в преддверии задач минимизации/максимизации и, возможно, даже до того, как ученик станет умеет дифференцировать, так как задача дает производную. Все, что требуется от ученика, — это оценить G'(x) по определенному значению, а затем понять, как знак G'(x) соотносится с реальным миром.
Не совсем понятно, что на самом деле запрашивается и к чему относится первый ответ; «1/200» не может быть G(20), что равно 0,3, поэтому мы должны интерпретировать это как «G'(20) = 1/200», что не совсем правильно.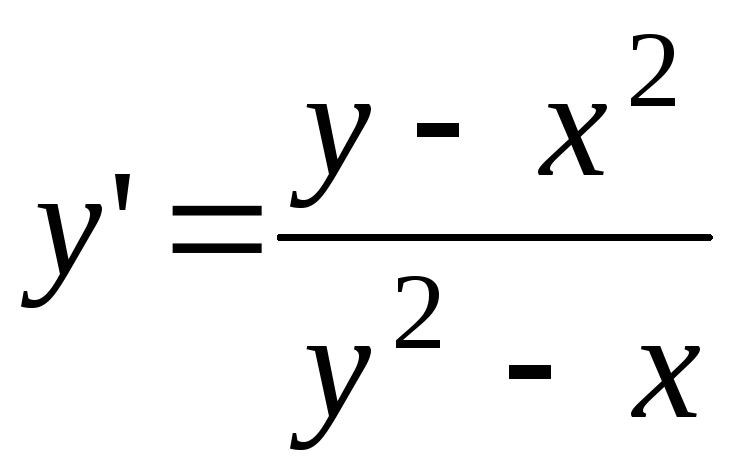
Как сказал Ахтар, это -1/200. (Возможно, они действительно сказали, что это абсолютное значение производной.) Второй ответ дает нам представление о цели: решить, будет ли лучше двигаться быстрее или медленнее.
Если ответ книги на первую часть говорит G'(20) = 1/200, это неверно; вы правильно поняли эту часть. Это вторая задача, которая смущает вас.
Обратите внимание, что G(x) означает : это уровень расхода топлива в галлонах на милю при скорости x миль/час. Как вы думаете, чего хотел бы добиться менеджер? Я бы сказал, что он или она захочет сэкономить деньги за счет использования меньшего количества топлива в заданной поездке (на фиксированное расстояние).
В свете этой цели вы можете понять, почему в первом случае вы сказали водителю ехать быстрее? Если это все еще не ясно, расскажите мне о своих рассуждениях, и мы можем подумать об этом дальше.
Итак, нам нужно решить, будет ли увеличение или уменьшение скорости уменьшать расход топлива.
Ахтар ответил:
Спасибо, сэр. Если G(x) представляет скорость расхода топлива, то чему равно G'(x)? Это скорость изменения расхода топлива ? Если это так, то G'(20) = -1/200 = -0,005, это очень низкая скорость изменения . Итак низкое потребление , тогда почему мы предлагаем ехать быстрее.
Во второй части G'(40) = 1/400 = 0,0025, так что это выше по сравнению с первой частью, поэтому понятно, что нужно двигаться медленнее, чтобы сэкономить деньги за счет низкого потребления … .. но, сэр, объясните первую часть.
Ахтар вычислил производную и обнаружил, что G'(20) = -0,005, а G'(40) = 0,0025. Но он интерпретирует их так, как если бы они были скоростью потребления, а не скоростью изменения .0142 норма расхода. Поначалу это нелегко интерпретировать, особенно потому, что слово «скорость» используется не как скорость по отношению ко времени (в милях в час, как мы привыкли), а по отношению к скорости.
Вероятно, также не помогает то, что x здесь представляет не положение, а скорость! Здесь есть много вещей, которые незнакомы и требуют, чтобы мы замедлились и переосмыслили их значение.
Доктор Рик ответил:
Да, G'(x) представляет скорость изменения расхода топлива (относительно скорости). Если бы скорость изменения была постоянной, G'(x) = -0,005 означало бы, что на каждые увеличит скорость грузовика на 1 милю/час, скорость расхода топлива уменьшит на 0,005 галлона/милю.
Итак, G’ говорит нам не о том, сколько топлива мы используем, а о том, насколько (и в каком направлении) это количество изменит , если мы изменим нашу скорость. Отрицательное значение означает, что потребление уменьшится (улучшится), если мы увеличим нашу скорость.
Аналогично во второй части, при каждом увеличении скорости на 1 милю/час уровень расхода топлива будет увеличить на 0,0025 галлона/милю.
Это меньшая скорость изменения, чем в первой части (с точки зрения расстояния от нуля, то есть абсолютного значения G'(x)). Так что если бы решение принималось на основании насколько изменяется расход топлива, то причин менять скорость во второй части было бы еще меньше, чем в первой.
Это меньшая скорость изменения, чем в первой части (с точки зрения расстояния от нуля, то есть абсолютного значения G'(x)). Так что если бы решение принималось на основании насколько изменяется расход топлива, то причин менять скорость во второй части было бы еще меньше, чем в первой.Внимание Ахтара к размеру (абсолютному значению) G’ неуместно:
Но важная часть — это направление изменения, то есть признак производной. В первой части увеличение скорости приводит к снижению расхода топлива, чего и хочет менеджер. Во второй части увеличение скорости приводит к увеличению расхода топлива на ; едет медленнее вызывает снижение расхода топлива. Итак, во второй части менеджер говорит притормозить.
Вот откуда приходят ответы. Лучшая скорость больше 20 миль в час и меньше , чем 40 миль в час.
Этого достаточно, чтобы ответить на вопрос, но давайте рассмотрим вашу мысль о том, что G'(x) = -1/200 является « очень низкой скоростью изменения ».
У нас может быть плохое представление о величине скорости изменения расхода топлива — мы не часто об этом говорим. Чтобы помочь нам об этом подумать, я построил график G(x):При x = 20 миль/час (а также при x = 40 миль/час) расход топлива составляет 0,3 галлона/милю. . Мы могли бы также сказать, что «пробег» грузовика на этих скоростях составляет 1/0,3 = 10/3 = 3,33 мили на галлон; то есть грузовик проедет только 3,33 мили на каждом галлоне топлива. (Пробег — более знакомая мне цифра в США, и это очень маленькое число по сравнению с автомобилем, где мы хотели бы проехать 30 миль или больше на галлоне бензина. Я могу поверить, однако , что 3,33 мили на галлон разумно для большого грузовика.)
Таким образом, как при 20, так и при 40 милях в час расход топлива одинаков, и это относительно большое число. (При 30 милях на галлон расход составит 1/30 = 0,0333 галлона на милю, что намного меньше, чем в нашей истории.)
Теперь сравните с минимальным расходом топлива, который я нашел и обозначил примерно как 0,283 галлона/милю при скорости около 28,284 мили/час.
$$x = \sqrt{800} = 28,284$$
Учащийся на данный момент еще не дошел до точки нахождения этого минимума и, следовательно, не может сказать сколько быстрее или медленнее идти, только направление в котором изменить скорость для снижения расхода топлива. Да, увеличение скорости всего на 1 милю в час мало что даст, но экономия складывается. Надеюсь, это поможет.
Итак, что мы узнали?
Когда проблема сбивает с толку, нам нужно решить, на какой части сосредоточиться, в данном случае на знаке. Мы должны тщательно обдумать, что это значит, и применить это к цели. И это тщательное размышление, мы надеемся, приведет к лучшему пониманию в будущем.
Увеличив скорость на 8,284 мили/час, мы уменьшили расход топлива на 0,3 – 0,283 = 0,017 галлона на милю. Если грузовик проедет 100 миль, мы сэкономим 1,7 галлона топлива. В этом 100-мильном путешествии мы используем 28,3 галлона, а не 30 галлонов, экономия 5,7%, которую менеджер, вероятно, не считает незначительной. 92 = 800$$