Быстрый подсчет суммы ряда или из алгебры в геометрию | by Vladislav Kopylov
Как можно максимально эффективно вычислить сумму ряда чисел от 1 до n? Допустим, есть ряд чисел от 1 до 6. Надо вычислить его сумму. Делается это очень легко: 1+2+3+4+5+6 = 21. Ничего сложного!
Визуальное представление ряда от 1 до 6Но если нужно подсчитать сумму ряда от 1 до 10 000 или от 1 до 100 000, или от 1 до 10 000 000, то тут столкнемся с трудностью. Во-первых, в уме их быстро не подсчитать. Во-вторых, если производить вычисления будет машина, то потребуется произвести количество вычислений равное длине последовательности.
Поэтому нужно найти более эффективный способ выполнить это.
У суммы ряда есть интереса особенность, если внимательно посмотреть на рисунок выше, то можно заметить что числа в такой последовательности представляют собой геометрическую фигуру, а именно прямоугольный треугольник. Для подтверждения верности нашего предположения, объединим две суммы ряда.
У нас получается идеальный прямоугольник или два прямоугольных треугольника.
Следовательно, для того что бы вычислить сумму последовательности нужно вычислить площадь прямоугольного треугольника. Это значит, что рассчитать сумму ряда можно по следующей формуле, где n максимальное число в последовательности:
Используем формулу на практике. Нам нужно вычислить сумму последовательности от 1 до 10. Для этого нужно решить следующее простое уравнение:
Теперь рассмотрим на примере насколько эффективно вычислять сумму последовательности через площадь.
Для этого запрограммируем обе формулы: вычисление через сумму и вычисление через площадь треугольника. Для программирования используем язык ruby. Скажем машине что бы она вычислила несколько сумм последовательностей подряд с пределом от 2 до 100 000. А-ля:
- Вычисли сумму последовательности от 1 до 2
- Потом, вычисли сумму последовательности от 1 до 3
- Потом, вычисли сумму последовательности от 1 до 4
- …
- и наконец, от 1 до 100 000
Сначала вычислим методом сложения, а потом вычислим с помощью площади треугольника.
Запомним время которое потребовалось для выполнения задач и выведем его что бы увидеть разницу. Вычисления проводились на компьютере с процессором Intel Core i5 (1,4GHz).
Получается, что при вычислением методом сложения мы затратили 370 секунд, а при вычислением методом расчета площадь треугольника всего 0,02 секунды. Разница на лицо!
Для любопытства, запустим вычисления суммы последовательностей с пределом от 2 до 10 000 000 через площадь треугольника и зафиксируем время выполнения, что бы узнать сколько времени займет это вычисление. Удастся ли нам нагрузить машину дольше чем на одну секунду? Для вычислений этого потребовалось всего 1,7 секунд 😀.
Итог: некоторые задачки решаются намного эффективнее если посмотреть на них под другим углом. Это рождает более эффективные решения которые экономят ресурсы. При вычислений небольших чисел, например последовательности от 1 до 6, разница практические не ощутима, каким способом мы бы не решали. Но с увеличением объема вычислений разница будет видна все больше и больше.
чему она равна и как ее вычислить
Натуральных чисел бесконечно много, но несмотря на это ученые знают, чему равна их сумма. Но почему сумма всех натуральных чисел представляет собой такое странное число — -1/12?
Никита Шевцев
Wikimedia Commons
Думаете, что если сложить все натуральные числа, то получится бесконечность? Индийский математик еще в начале века показал, что эта сумма будет равна -1/12. Погрузимся в дебри математики и разберемся, что не так с этим значением
Натуральные числа представляют собой целые положительные числа от единицы и до бесконечности. Сумма таких чисел представляет собой классический расходящийся ряд, бесконечная сумма которого должны быть равна бесконечности. Однако существуют способы присвоить сумме этого ряда конечное значение. Но как вычислить сумму натуральных чисел?
Способы посчитать сумму всех натуральных чисел
Считать сумму расходящихся рядов математики научились еще в XIX веке.
Итак, откуда же нам тогда известно, что сумма натуральных чисел равна -1/12? Все благодаря трудам нескольких гениальных математиков, именами которых и названы ряды и функции, о которых мы поговорим ниже. Для того, чтобы вычислить сумму натуральных чисел есть метод, который называется регуляризацией дзета-функции Римана. Дзета-функция Римана представляет собой функцию от комплексного переменного s, которая определяется рядом Дирихле.
Вычислить сумму натуральных чисел при помощи дзета-фукнции
Значение дзета-функции от s равно бесконечной сумме ∑n-s, где суммирование происходит по n от 1 до бесконечности.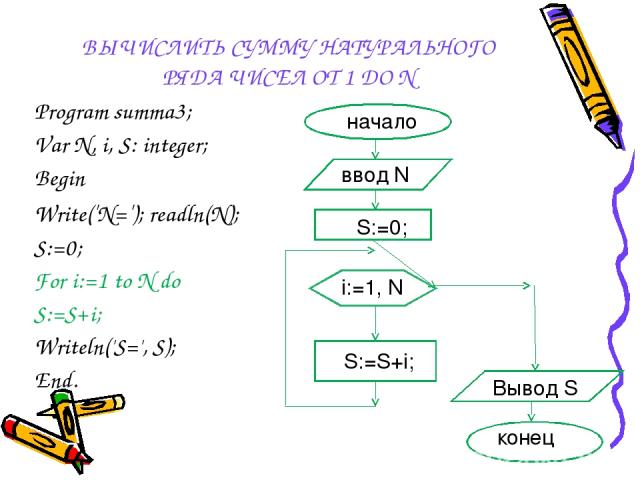
Если мы возьмем значение дзета-функции от -1, значение членов ряда станет равным натуральным числам: 1-1 = 1, (1/2)-1 = 2, (1/3)-1 = 3… Дзета-функция от -1 в этом случае равна 1 + 2 +3…, то есть сумме всех натуральных чисел.
График мнимой и вещественной части дзета-функции можно увидеть на рисунке ниже. Используя соотношение между дзета-функцией Римана и эта-функцией Дирихле можно довольно легко вычислить значение первой. В результате получается, что дзета-функция Римана от -1 равна -1/12. Такое значение получается благодаря тому, что из плоскости вещественных чисел мы переходим в комплексную плоскость. Таким образом, вычислить сумму натуральных чисел при помощи такого метода оказывается довольно просто.
Зачем нужна сумма всех натуральных чисел?
Если вы дочитали до этого момента, тогда для вас есть приятный бонус — интересный факт. На первый взгляд кажется, что это вычисление суммы ряда натуральных чисел довольно абстрактно и не несет никакой практической пользы.
Но на самом деле сумма этого ряда фигурирует в теории струн и даже помогает описать эффект Казимира, заключающийся во взаимном притяжении проводящих незаряженных тел в вакууме под действием квантовых флуктуаций. Так что, если в школе задания вроде «найдите сумму всех натуральных чисел» казались вам странными, теперь вы знаете, что результаты этих задач имеют практическое применение.
Используйте функцию СУММ для суммирования чисел в диапазоне
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Дополнительно…Меньше
Вы можете использовать простую формулу для суммирования чисел в диапазоне (группе ячеек), но функцию СУММ проще использовать, когда вы работаете с несколькими числами. Например, =СУММ(A2:A6) с меньшей вероятностью содержит опечатки, чем =A2+A3+A4+A5+A6.
Вот формула, которая использует два диапазона ячеек : =СУММ(A2:A4,C2:C3) суммирует числа в диапазонах A2:A4 и C2:C3.
Вы должны нажать Enter, чтобы получить общее количество 39787.
Чтобы создать формулу:
Введите =СУММ в ячейке, за которой следует открывающая скобка ( .
Чтобы ввести первый диапазон формул, который называется аргумент (фрагмент данных, необходимый для запуска формулы), введите A2:A4 (или выберите ячейку A2 и перетащите через ячейку A6).
Введите запятую (,), чтобы отделить первый аргумент от следующего.
Введите второй аргумент, C2:C3 (или перетащите, чтобы выбрать ячейки).
Введите закрывающую скобку ) , а затем нажмите Enter.
Каждый аргумент может быть диапазоном, числом или ссылкой на одну ячейку, разделенными запятыми.
=СУММ(A2:A4,2429,10482)
=СУММ(4823;A3:A4;C2:C3)
=СУММ(4823,12335,9718,С2:С3)
=СУММ(А2,А3,А4,2429,10482)
Совет: Если вам нужно суммировать столбцы или строки чисел рядом друг с другом, используйте автосумму для суммирования чисел.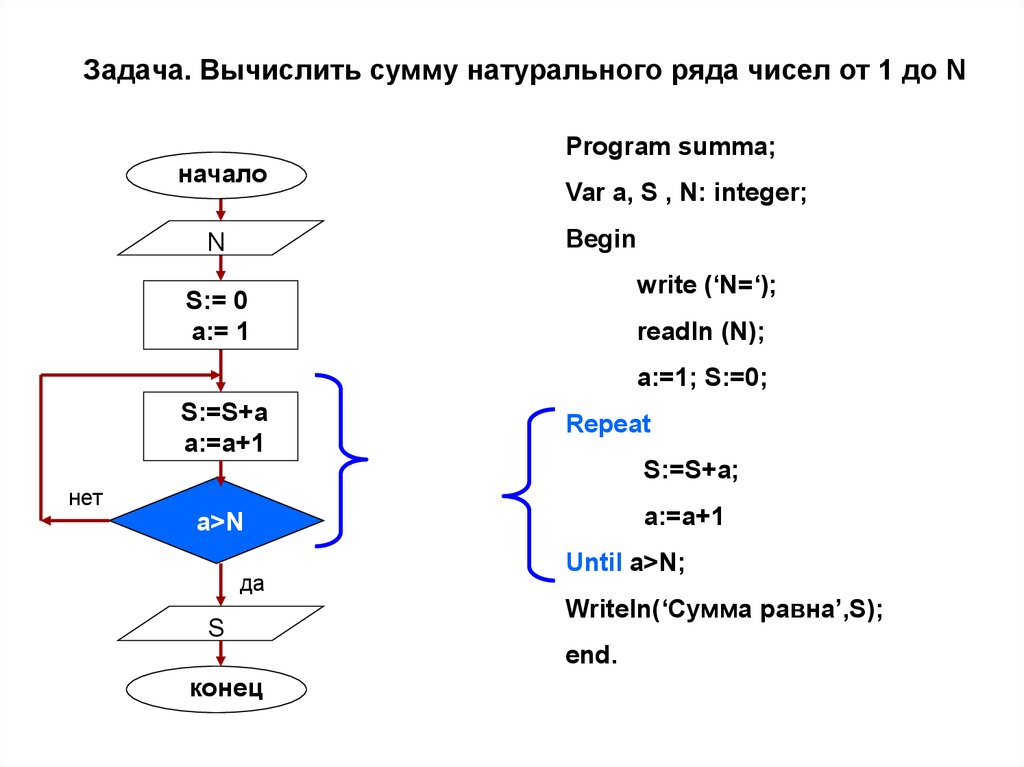
Попробуйте
Если вы хотите поиграть с нашими образцами данных, вот некоторые данные для использования.
Чтобы увидеть, как работает функция СУММ, скопируйте следующую таблицу на рабочий лист и вставьте ее в ячейку A1.
Данные | ||
-5 | ||
15 | ||
30 | ||
‘5 | ||
ИСТИНА | ||
Формула | Описание | Результат |
=СУММ(3, 2) | Добавляет 3 и 2. | 5 |
Добавляет 5, 15 и 1. Текстовое значение «5» сначала преобразуется в число, а логическое значение ИСТИНА сначала преобразуется в число 1. | 21 | |
=СУММ(A2:A4) | Складывает значения в ячейках с A2 по A4. | 40 |
=СУММ(A2:A4, 15) | Складывает значения в ячейках с A2 по A4, а затем добавляет к этому результату 15. | 55 |
=СУММ(A5,A6, 2) | Складывает значения в ячейках A5 и A6, а затем добавляет 2 к этому результату. Поскольку нечисловые значения в ссылках не переводятся — значение в ячейке A5 (‘5) и значение в ячейке A6 (ИСТИНА) обрабатываются как текст — значения в этих ячейках игнорируются. | 2 |
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
Последовательности и серии: терминология и обозначения
ExamplesArith. и гео. Посл.Ариф. СерияГео. Серия
Пурпурная математика
«Последовательность» (называемая «последовательностью» в британском английском) — это упорядоченный список чисел; числа в этом упорядоченном списке называются «элементами» или «терминами» последовательности.
«Серия» — это то, что получается при сложении всех членов последовательности; сложение, а также результирующее значение называются «суммой» или «суммированием». Например, «1, 2, 3, 4» — это последовательность с элементами «1», «2», «3» и «4»; соответствующий ряд представляет собой сумму «1 + 2 + 3 + 4», а значение ряда равно 10,9.0003
Последовательность может быть названа или упомянута заглавной буквой, такой как «A» или «S». Члены последовательности обычно называются примерно так: « a i » или « a n », где буква в нижнем индексе « i » или « n » является «индексом» или прилавок. Таким образом, второй член последовательности может быть назван « a 2 » (произносится как «ай-суб-два»), а « a 12 » будет обозначать двенадцатый член.
Содержание продолжается ниже
MathHelp.com
Последовательность также может быть записана в терминах ее терминов. Например, последовательность терминов a i с индексом от i = 1 до i
Последовательность терминов, начинающаяся с индекса 3 и продолжаться вечно можно было бы записать как:
{ a n } n=3 ∞
В некоторых книгах используется обозначение в скобках; другие используют обозначение фигурных скобок.
В любом случае, они говорят о списках терминов. Начальное значение счетчика называется «нижним индексом»; конечное значение называется «верхним индексом». Форматирование соответствует английскому: нижний индекс пишется под верхним индексом, как показано выше. (Множественное число слова «index» — «indices», произносится как INN-duh-seez.)
Примечание. Иногда последовательности начинаются с индекса 9.0241 n = 0, поэтому первое слагаемое на самом деле a 0 . Тогда второй член будет a 1 . Первый указанный термин в таком случае будет называться «нулевым» термином. Такой способ нумерации терминов используется, например, в массивах Javascript. Или, как во втором примере выше, последовательность может начинаться со значения индекса больше 1. Не предполагайте, что каждая последовательность и серия будут начинаться с индекса n = 1.
Когда последовательность не имеет фиксированного числовой верхний индекс, но вместо этого «уходит в бесконечность» («бесконечность» обозначается этим символом восьмерки сбоку, ∞), последовательность называется «бесконечной» последовательностью.
Бесконечные последовательности обычно имеют конечные нижние индексы. То есть они начнут с некоторого конечного счетчика, например 9.0241 i = 1.
Как упоминалось выше, последовательность A с элементами a n может также упоминаться как «{ a n }», но вопреки тому, что вы, возможно, узнали. в других контекстах этот «набор» на самом деле является упорядоченным списком, а не неупорядоченным набором элементов. (В вашей книге могут использоваться некоторые обозначения, отличные от тех, которые я показываю здесь. К сожалению, обозначения, похоже, еще не полностью стандартизированы для этой темы. Просто старайтесь всегда убедиться, что какой бы ресурс вы ни использовали, ясны определения терминов и символов этого ресурса.) В наборе нет определенного порядка элементов, и повторяющиеся элементы обычно отбрасываются как бессмысленные дубликаты. Таким образом, следующий набор:
{1, 2, 1, 2, 1, 2, 1, 2}
…сократится до (и эквивалентно):
{1, 2}
С другой стороны, следующее последовательность:
{ a n } = {1, 2, 1, 2, 1, 2, 1, 2}
. .. не может быть переупорядочена или «упрощена» каким-либо образом.
Члены последовательности могут быть просто перечислены, как показано выше, или же они могут быть определены правилом. Часто это правило связано с индексом. Например, в последовательности A = { a i } = {2 i + 1}, i -й член определяется правилом «2 i + 1», поэтому первые несколько членов:
а 1 = 2(1) + 1 = 3
а 2 = 2(2) + 1 = 5
а 90 7 0 3 90 3 = 2(0) 3 = 2(2) …и так далее. Иногда правило для последовательности таково, что следующий член последовательности определяется в терминах предыдущих членов. Этот тип последовательности называется «рекурсивной» последовательностью, а правило называется «рекурсией». Самая известная рекурсивная последовательность — это последовательность Фибоначчи (fibb-oh-NAH-chee). Его правило рекурсии выглядит следующим образом:
а 1 = а 2 = 1;
a n = a n −1 + a n −2 for n ≥ 3
What this rule says is that the first two terms of the обе последовательности равны 1; тогда каждый член после первых двух находится путем сложения двух предыдущих членов. Таким образом, третий член, a 3 , находится путем сложения a 3−1 = a 2 и a 3−2 = a 1 . Первые несколько членов последовательности Фибоначчи:
1, 1, 2, 3, 5, 8, 13
Для обозначения последовательности мы используем либо латинскую заглавную букву «S», либо греческую букву, соответствующую заглавная буква «S», которая называется «сигма» (SIGG-muh):
Чтобы показать суммирование, скажем, членов последовательности с первого по десятый { a n }, мы бы написали следующее:
Как и в случае с последовательностями, « n = 1» называется «нижним индексом», говоря нам, что « n » — это счетчик и что счетчик начинается с «1»; «10» называется «верхним индексом», говоря нам, что a 10 будет последним членом, добавленным в этот ряд; « a n » означает термины, которые мы будем добавлять. Все это произносится как «сумма от n, равного одному до десяти, a-sub-n». Символ суммирования выше означает следующее:
a 1 + a 2 + a 3 + a 4 + a 5 + a 6 + a 7 + a 8 + a 9 + a 10
Выписанная выше форма называется «расширенной» формой ряда, в отличие от более компактной «сигмы» .
Для индекса можно использовать любую букву, но i , j , k , m и n , вероятно, используются чаще, чем любые другие буквы.
Есть несколько правил, которые могут помочь упростить или оценить серию. Если каждый член ряда умножается на одно и то же значение, вы можете вынести это значение из ряда. Это означает следующее:
Это означает, что если вам сказали, что сумма некоторого конкретного ряда имеет значение, скажем, 15, и что каждый член этого ряда умножается, скажем, на 2, вы можете найти значение как:
Другое правило для рядов состоит в том, что если членами ряда являются суммы, то вы можете разделить ряд сумм на сумму рядов. Другими словами:
Если вы суммируете только несколько первых членов ряда, а не все (возможно, бесконечно много), это называется «взятием (или нахождением) частичной суммы». Если бы, скажем, вам сказали найти сумму только первых восьми членов ряда, вы бы «нашли восьмую частичную сумму».
Последовательности и ряды наиболее полезны, когда есть формула для их членов. Например, если формула для термов a n последовательности определяется как « a n = 2 n + 3″, то вы можете найти значение любого члена, подставив значение n в формулу . Например, a 8 = 2(8) + 3 = 16 + 3 = 19. Словами « a n = 2 n + 3» можно прочитать как « n ». -й член задается как два-энн плюс три». Слово « n -th» произносится как «ENN-eth» и означает просто «общий термин 9».0241 a n , где я еще не указал значение n .