Теорема о соответственных углах / Параллельные прямые / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Параллельные прямые
- Теорема о соответственных углах
Теорема
| Если две параллельные прямые пересечены секущей, то соответственные углы равны. |
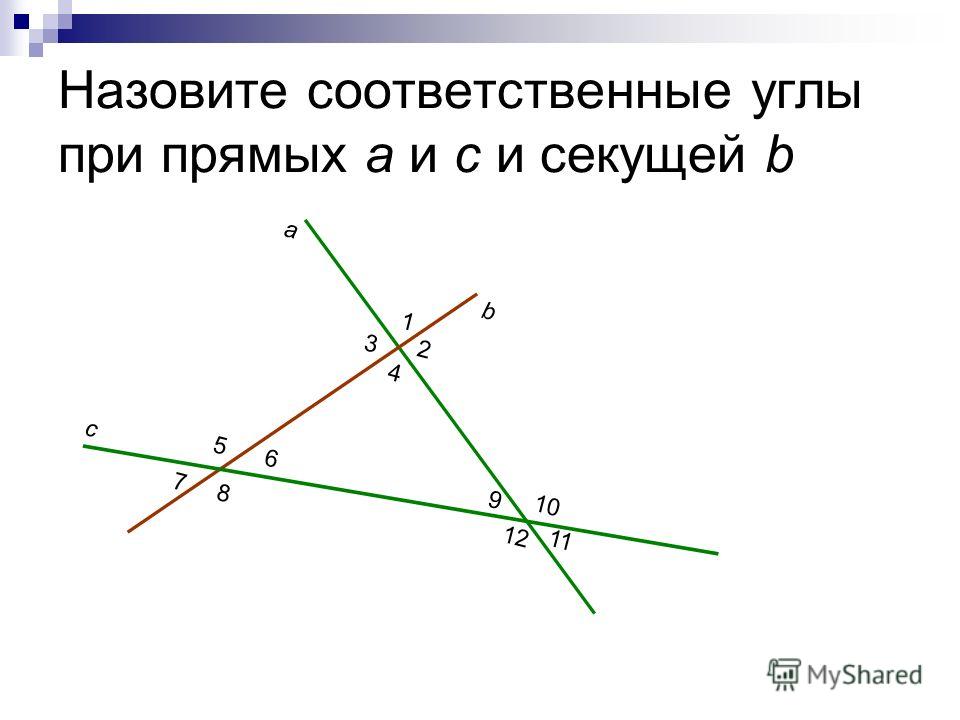
Дано: , — секущая, 1 и 2 — соответственные (Рис.1).
Доказать: 1 = 2.
Доказательство:
По условию , значит накрест лежащие углы 1 и 3 равны, т.е. 1 = 3 (по теореме о накрест лежащих углах).
Из равенств 1 = 3 и 2 = 3 следует, что 1 = 2. Что и требовалось доказать.
Советуем посмотреть:
Параллельные прямые
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Аксиомы геометрии
Аксиома параллельных прямых
Теорема о накрест лежащих углах
Теорема об односторонних углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Параллельные прямые
Правило встречается в следующих упражнениях:
7 класс
Задание 205, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 389, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 428, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 447, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 586, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 588, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 589, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 850, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 873, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Две параллельные прямые — свойства и признаки
Поможем понять и полюбить математику
Начать учиться
Если в задаче есть параллельные прямые — это большая удача, ведь они дают много равных углов, с помощью которых можно вычислить практически все, что угодно.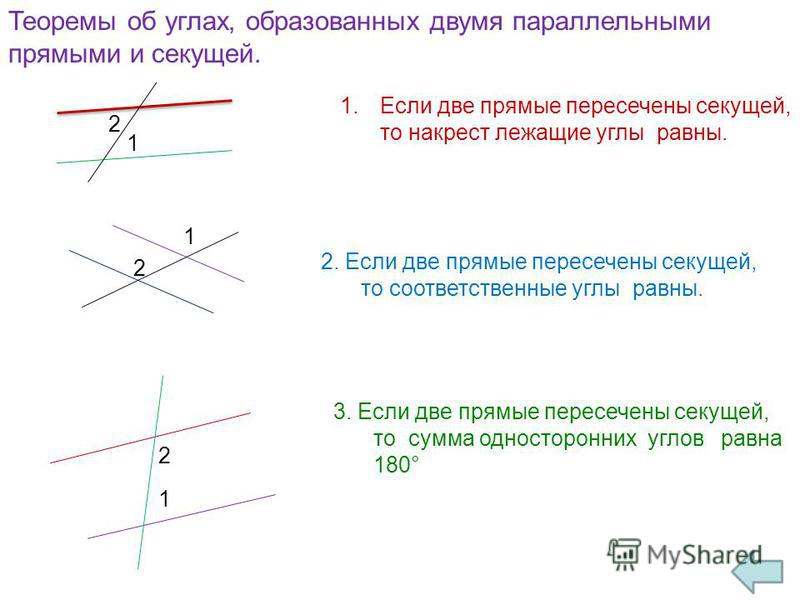
Сейчас мы разберемся, какие еще бонусы дает установление параллельности, и чем это может быть полезно при решении задач.
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b. |
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой.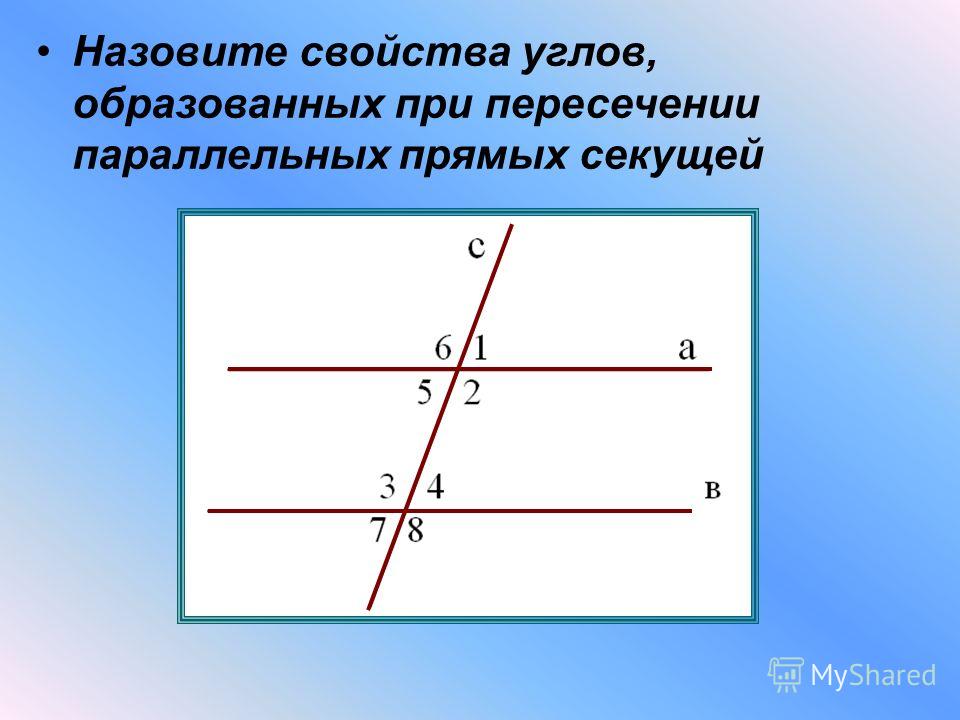
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна. |
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой.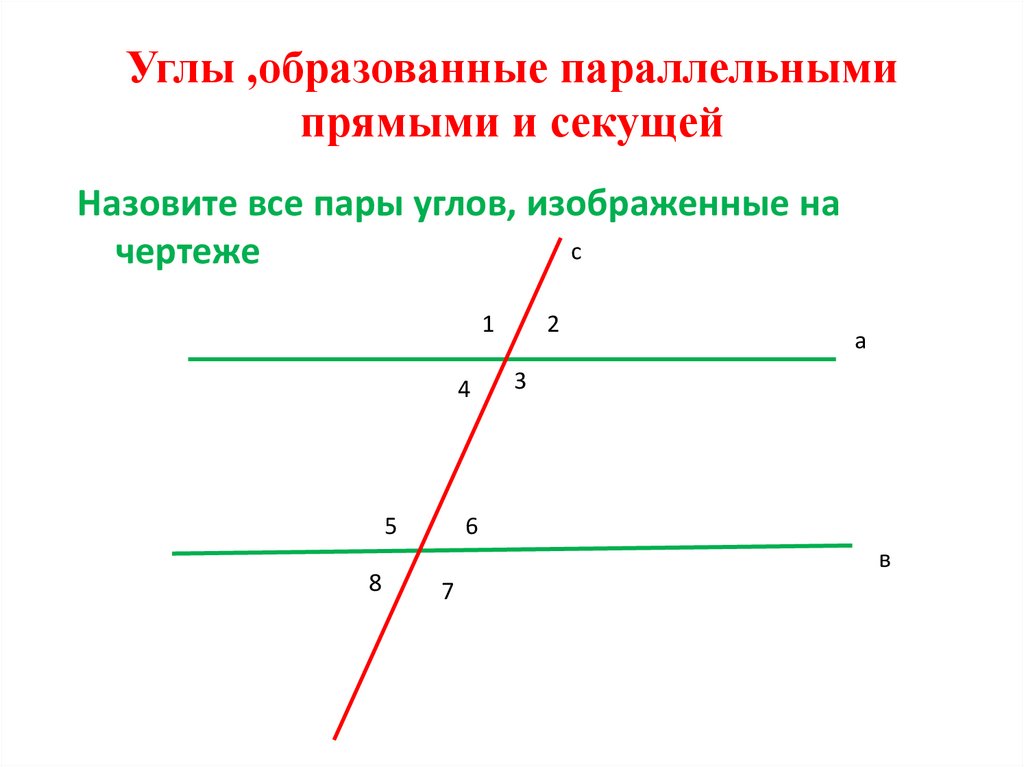
К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
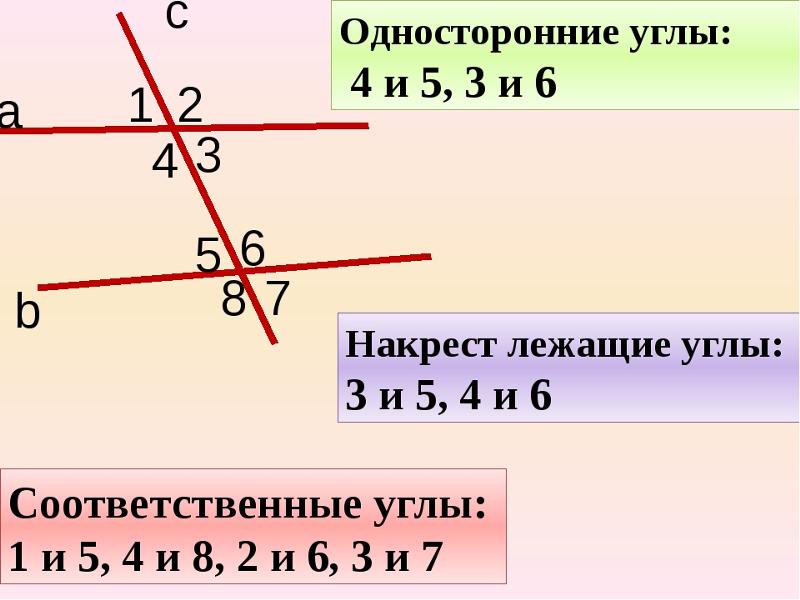
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
- два внутренних односторонних угла образуют в сумме 180°:
∠4 + ∠5 = 180°; ∠3 + ∠6 = 180°.
- два внутренних накрест лежащих угла равны между собой:
∠3 = ∠5, ∠4 = ∠6.
- два соответственных угла равны между собой:
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой. |
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
В данном случае ∠3 и ∠MPK являются вертикальными, следовательно ∠MPK = ∠3 = 92°.
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
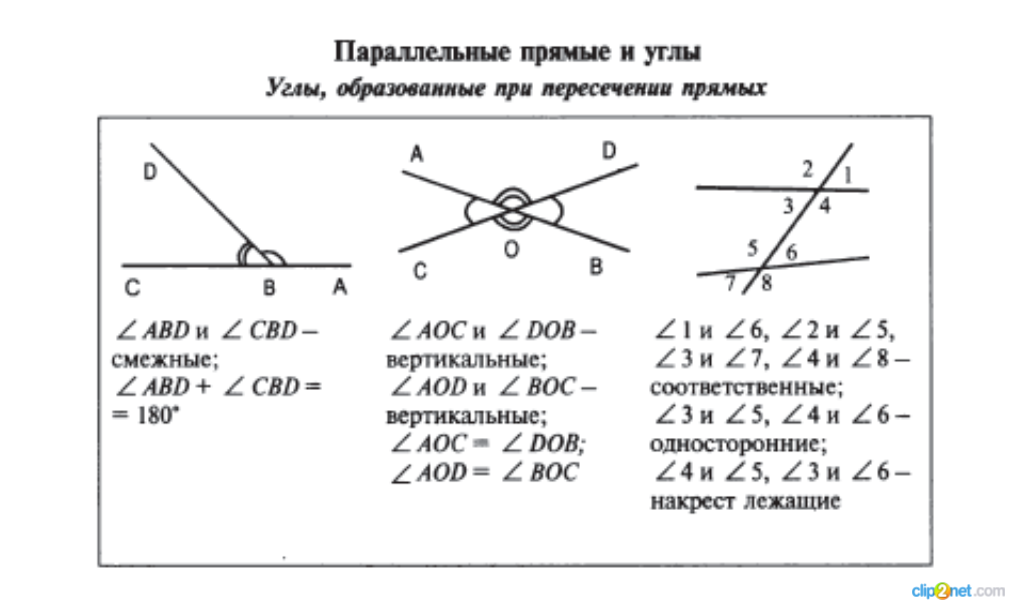
DK = 2DM = 2 х 27 = 54 (см)
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Яна Кононенко
К предыдущей статье
140.7K
Показательные уравнения
К следующей статье
171.6K
Таблица производных функций
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Соответствующие углы – определение и теорема с примерами
Определение
Соответствующие углы – это пары углов, которые занимают одно и то же относительное положение на каждом пересечении, когда секущая пересекает две параллельные прямые.
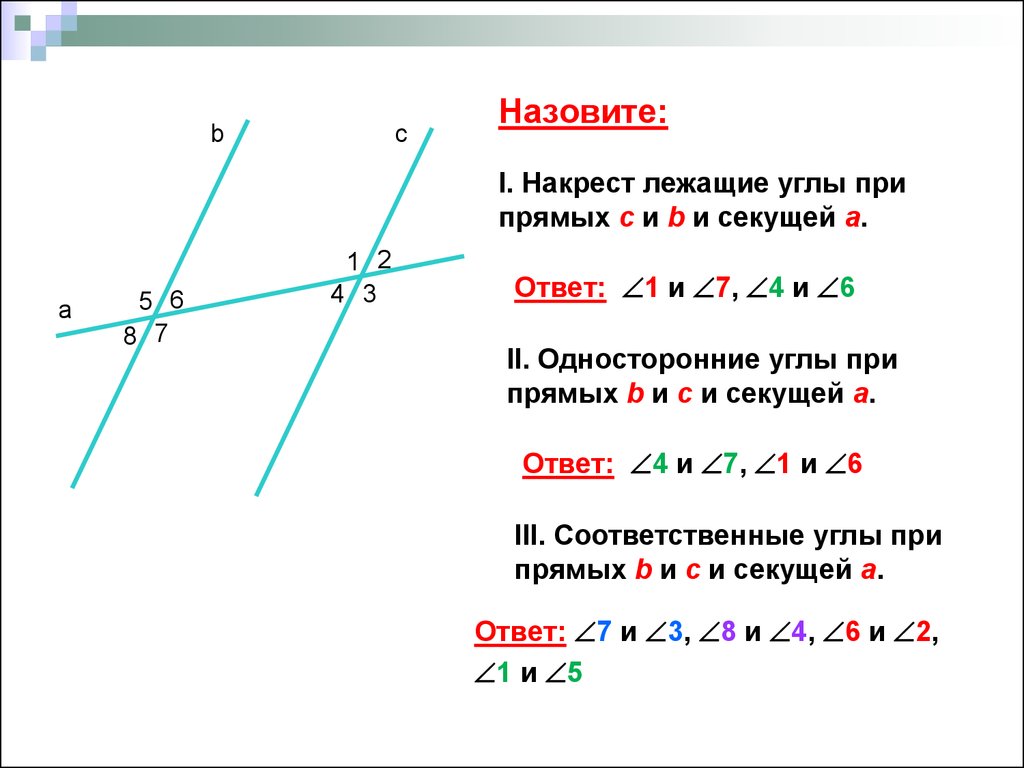
На приведенном выше рисунке показаны две параллельные прямые AB и CD, пересекаемые поперечной GH. Пары соответствующих углов на данном рисунке:
∠1 и ∠5
∠3 и ∠6
∠4 и ∠7
∠2 и ∠8
Соответствующие углы равны, если секущая пересекает хотя бы две параллельные прямые.
На данном рисунке AB∥CD,
Таким образом,
∠1 = ∠5, ∠3 = ∠6, ∠4 = ∠7, ∠2 = ∠8
Соответствующие углы, образованные при пересечении секты в хотя бы две непараллельные прямые не равны и также не имеют отношения друг к другу.
Свойства
- Находится на одной стороне поперечной
- Состоит из одного внутреннего и одного внешнего угла
- Они равны, если секущая пересекает две параллельные прямые
- Они не связаны, если секущая пересекает две непараллельные прямые
- Они являются дополнительными, если секущая перпендикулярно пересекает две параллельные прямые.
- Внешние углы по одну сторону от секущей являются дополнительными, если две прямые параллельны.
То же самое и с внутренними углами.
То же самое и с внутренними углами.Типы соответствующих углов
Два типа соответствующих углов:
1) Соответствующий внутренний угол : Находится на внутренней стороне пересечения между параллельными линиями и поперечными.
2) Соответствующий внешний угол : Находится на внешней стороне пересечения между параллельными линиями и поперечными.
Теорема о соответствующих углах
Теорема о соответствующих углахДокажите теорему о соответствующих углах
Чтобы доказать:
∠1 = ∠5, ∠3 = ∠6, ∠4 = ∠7, ∠2 = ∠8
Доказательство:
Дано, PQ и RS — две параллельные прямые, пересекаемые поперечной IJ.
Теперь, если PQ∥ RS
Тогда по теореме о соответствующих углах мы можем написать
∠1 = ∠5
∠3 = ∠6
∠4 = ∠7
∠2 = ∠8
Отсюда доказано 9004 8
Запомнить : Таким образом, единственный способ доказать конгруэнтность соответствующих углов — это параллельность данных прямых.
Таким образом, теорема о соответствующих углах верна без доказательства.
Теорема обращения соответствующих углов
Теорема обращения соответствующих угловДокажите теорему обращения соответствующих углов
Доказать:
PQ∥ RS
Доказательство: 90 005
Дано, ‘PQ’, ‘RS’ два прямые, пересекаемые секущей IJ, и ∠1 = ∠5, ∠3 = ∠6, ∠4 = ∠7, ∠2 = ∠8 — пары соответствующих углов
. Тогда по теореме, обращенной к внутренним углам,
PQ∥ RS
Отсюда доказано
Вспомните : Таким образом, единственный способ доказать параллельность данных прямых — это просто конгруэнтность соответствующих углов. Таким образом, теорема, обратная о соответствующих углах, принимается как истинная без доказательства.
Как найти соответствующие углы
Давайте рассмотрим несколько примеров, чтобы лучше понять концепцию.
Найдите недостающие углы на данном рисунке.
Учитывая, что ∠3 = 45°
Решение:
Дано, ∠3 = 45°
∠3 = ∠4 (вертикально противоположные углы)
Следовательно, ∠4 = 45°
Теперь
∠4 =∠7 = 45° (соответствующие углы)
∠3 =∠6 (соответствующие углы)
Следовательно, ∠6 = 45°
Теперь,
∠1 + ∠4 = 180° (дополнительные углы)
∠1 + 45° = 180°
∠1 = 180° – 45°
∠1 = 135°
Аналогично,
∠1 = ∠2 (вертикально противоположные углы)
Следовательно, ∠2 = 135°
Опять же,
∠1 = ∠5 (соответствующие углы)
Следовательно, ∠5 = 135°
Аналогично,
∠2 = ∠8 (соответствующие углы)
Следовательно, ∠8 = 135°
Два соответствующих угла измеряют (2x +10)° и 70°. Найдите значение х.
Решение:
Согласно теореме о соответствующих углах, два соответствующих угла равны.
Таким образом,
(2x +10) ° = 70 °
2x = 70 °- 10 °
x = 60 °/2
x = 30 °
.
Два соответствующих угле 14 и 4y + 6. Найдите модуль соответствующего угла.
Решение:
Согласно теореме о соответствующих углах, два соответствующих угла равны.
Таким образом,
6y-14 = 4y + 6
6y – 4y = 6 + 14
2y = 20
y = 10
Таким образом, величина равна
6y-14 = 6 x 10 – 14 = 46°
- Окна имеют горизонтальные и вертикальные решетки, образующие несколько квадратов. Каждая вершина образует соответствующие углы
- Мост, стоящий на опоре, в которой опоры соединены друг с другом так, что соответствующие углы равны
- Конструкция железнодорожного пути, в которой соответствующие углы сохранены равными
- Углы, образованные кубиком Рубика
Часто задаваемые вопросы
Q1. Соответствующие углы дополнительные
Ans . Соответственные углы являются дополнительными только в том случае, если секущая перпендикулярно пересекает две параллельные прямые.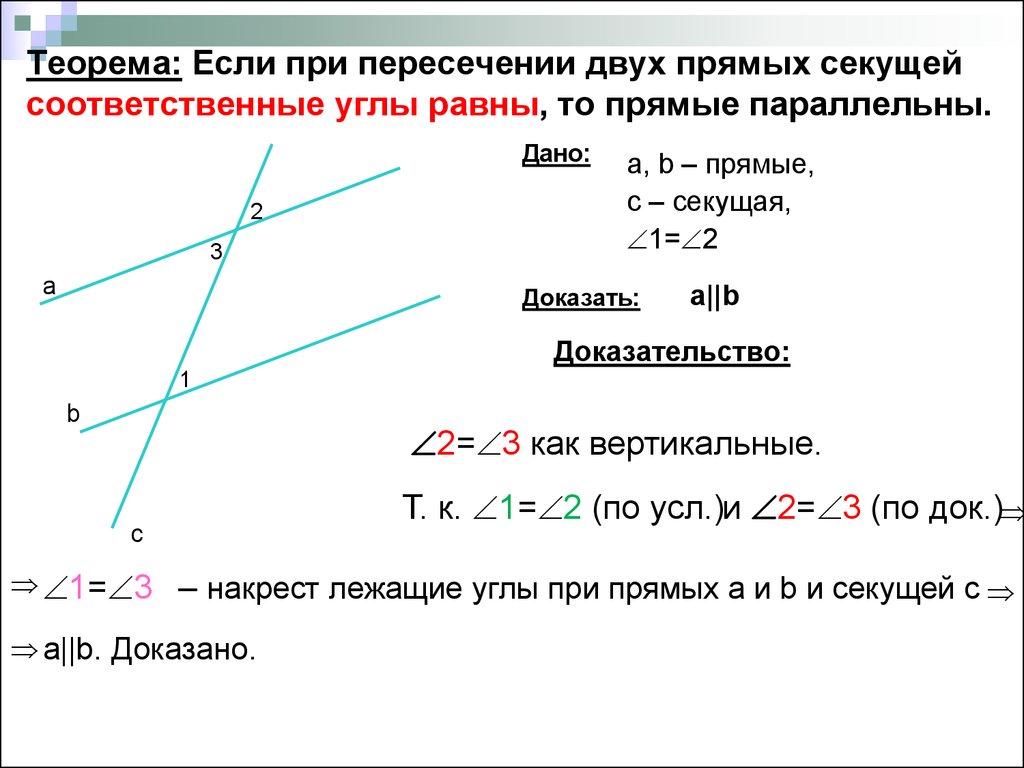
Линии и углы — Определения и свойства | Учебник по геометрии
Вот некоторые основные определения и свойства линий и углов в геометрии. Эти концепции проверяются на многих конкурентных вступительных экзаменах, таких как GMAT, GRE, CAT.
Эти основные понятия геометрии образуют основу, на которой могут быть построены более сложные идеи. Не волнуйтесь, если вы не сталкивались с ним ранее.
Мы начнем с самых простых идей, а затем построим на их основе другую родственную теорию.
Добавьте эту страницу в закладки для быстрого доступа к ней, чтобы вы могли вернуться к ней в любое время, когда почувствуете, что вам нужен курс повышения квалификации по линиям и углам.
Отрезок линии : Отрезок линии имеет две конечные точки определенной длины.
Луч : Луч имеет одну конечную точку и бесконечно простирается в одном направлении.
Прямая линия : Прямая линия не имеет ни начальной, ни конечной точки и имеет бесконечную длину.
Острый угол : Угол между 0° и 90° является острым углом, ∠A на рисунке ниже.
Тупой угол : Угол между 90° и 180° является тупым углом, ∠B, как показано ниже.
Прямой угол : Угол, равный 90°, является прямым углом, ∠C, как показано ниже.
Прямой угол : Угол, равный 180°, является прямым углом, ∠AOB на рисунке ниже.
Дополнительные углы :
На рисунке выше ∠AOC + ∠COB = ∠AOB = 180°
Если сумма двух углов равна 180°, то такие углы называются дополнительными углами с.
Два прямых угла всегда дополняют друг друга.
Пара смежных углов, сумма которых является прямым углом, называется линейной парой.
Дополнительные углы :
∠COA + ∠AOB = 90°
Если сумма двух углов равна 90°, то эти два угла называются дополнительными углами.
Смежные углы :
Углы, имеющие общую сторону и общую вершину, называются смежными углами.
На приведенном выше рисунке ∠BOA и ∠AOC являются смежными углами. Их общее плечо — OA, а общая вершина — «O».
Вертикально противоположные углы :
При пересечении двух прямых углы, образованные противоположно друг другу в точке пересечения (вершине), называются вертикально противоположными углами.
На рисунке выше
x и y — это две пересекающиеся линии.
∠A и ∠C составляют одну пару вертикально противоположных углов, а
∠B и ∠D составляют другую пару вертикально противоположных углов.
Перпендикулярные линии: Когда между двумя линиями имеется прямой угол, говорят, что линии перпендикулярны друг другу.
Здесь говорят, что прямые OA и OB перпендикулярны друг другу.
Параллельные прямые :
Здесь A и B — две параллельные прямые, пересекаемые прямой p.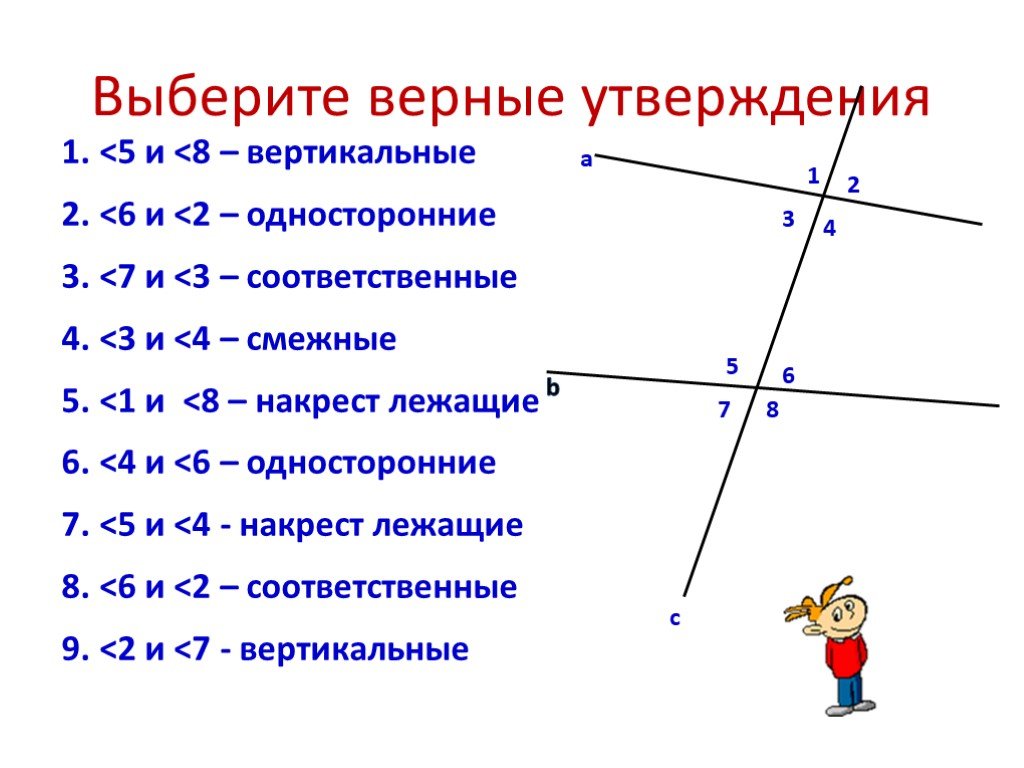
Прямая p называется секущей, которая пересекает две или более прямых (не обязательно параллельных прямых) в различных точках.
Как видно на рисунке выше, при пересечении секущей двух прямых образуется 8 углов.
Рассмотрим детали в табличной форме для удобства.
| Типы уголков | Уголки |
| Внутренние уголки | ∠3, ∠4, ∠5, ∠6 |
| Наружные уголки | ∠1, ∠2, ∠7, ∠8 |
| Вертикально противоположные углы | (∠1, ∠3), (∠2, ∠4), (∠5, ∠7), (∠6, ∠8) |
| Соответствующие углы | (∠1, ∠5), (∠2, ∠6), (∠3, ∠7), (∠4, ∠8) |
| Внутренние альтернативные углы | (∠3, ∠5), (∠4, ∠6) |
| Внешние альтернативные углы | (∠1, ∠7), (∠2, ∠8) |
| Внутренние уголки на одной стороне поперечного сечения | (∠3, ∠6), (∠4, ∠5) |
При пересечении секущей двух параллельных прямых
- Соответствующие углы равны.
- Вертикально противоположные углы равны.
- Альтернативные внутренние углы равны.
- Альтернативные внешние углы равны.
- Пара внутренних углов по одну сторону от секущей является дополнительной.
Можно сказать, что прямые параллельны, если мы можем проверить хотя бы одно из вышеупомянутых условий.
Давайте рассмотрим несколько примеров.
Пример 1. Если прямые m и n параллельны друг другу, то определить углы ∠5 и ∠7.
Раствор :
Определение одной пары позволяет найти все остальные углы. Ниже приводится один из многих способов решения этого вопроса.
∠2 = 125°
∠2 = ∠4, так как они являются вертикально противоположными углами.
Следовательно, ∠4 = 125°
∠4 — один из внутренних углов по ту же сторону от трансверсали.
Следовательно, ∠4 + ∠5 = 180°
125 + ∠5 = 180 → ∠5 = 180 – 125 = 55°
∠5 = ∠7, так как вертикально противоположные углы.
Следовательно, ∠5 = ∠7 = 55°
Примечание : Иногда свойство параллельности линий может не упоминаться в условии задачи, и линии могут казаться параллельными друг другу; но их может и не быть. Важно определить, параллельны ли две линии, проверив углы, а не по внешнему виду.
Пример 2. Если ∠A = 120° и ∠H = 60°. Определить, параллельны ли прямые.
Решение :
Дано ∠A = 120° и ∠H = 60°.
Поскольку смежные углы являются дополнительными, ∠A + ∠B = 180°
120 + ∠B = 180 → ∠B = 60°.
Дано, что ∠H = 60°. Мы видим, что ∠B и ∠H — внешние альтернативные углы.
Когда внешние параллельные углы равны, прямые параллельны.
Следовательно, прямые p и q параллельны.
Мы можем проверить это, используя другие углы.
Если ∠H = 60°, ∠E = 120°, поскольку эти два угла лежат на прямой, они являются дополнительными.
Теперь ∠A = ∠E = 120°. ∠A и ∠E — соответствующие углы.