Мир математики: Таблица квадратов
Когда-то уже довольно давно, когда я училась классе в восьмом, моя учительница математики на кружке показала, как в столбик можно извлекать квадратные корни. Вычислить корень можно с произвольной точностью, найти сколько угодно цифр в его десятичной записи, даже если он получается иррациональным. Алгоритм запомнился, а вопросы остались. Непонятно было, откуда взялся метод и почему он дает верный результат. В книжках этого не было, а может, просто не в тех книжках искала. В итоге, как и многое из того, что на сегодняшний день знаю и умею, вывела сама. Делюсь своим знанием здесь. Кстати сказать, до сих пор не знаю, где приведено обоснование алгоритма)))
Итак, сначала на примере рассказываю, “как работает система”, а потом объясняю, почему она на самом деле работает.
Возьмем число (число взято “с потолка”, только что в голову пришло).
1.
2. Извлекаем квадратный корень из первой группы цифр слева – в нашем случае это (ясно, что точно корень может не извлекаться, берем число, квадрат которого максимально близок к нашему числу, образованному первой группой цифр, но не превосходит его). В нашем случае это будет число. Записываем в ответ – это старшая цифра корня.
3. Возводим число, которое стоит уже в ответе — это — в квадрат и вычитаем из первой слева группы цифр – из числа . В нашем случае остается .
4. Приписываем справа следующую группу из двух цифр: . Число , которое уже стоит в ответе, умножаем на , получаем .
5. Теперь следите внимательно.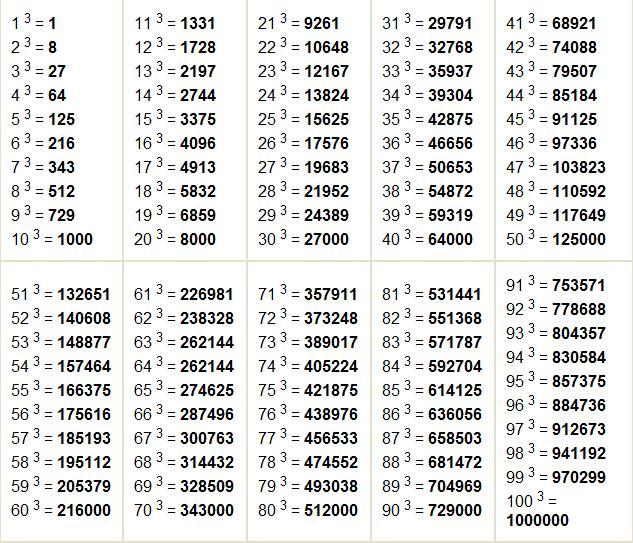
6. Из вычитаем произведение , получаем .
7. Далее повторяем знакомые операции: приписываем к справа следующую группу цифр , умножаем на , к полученному числу приписываем справа одну цифру, такую, чтобы при умножении на нее получилось число, меньшее , но наиболее близкое к нему – это цифра – следующая цифра в десятичной записи корня.
8. Далее у нас в числе стоит десятичная точка, ставим такую же в результате после цифры . Продолжаем процесс, снося по две цифры после точки. Ясно, что можно сносить и два нуля.
Вычисления запишутся следующим образом:
А теперь обещанное объяснение. Алгоритм основан на формуле
Первый раз вычитаем квадрат, дальше, приписывая по одной цифре к результату, к числу под корнем, тем самым, приписываем две десятичных цифры. Отсюда разбиение на пары (видно из формулы). Вычтя квадрат, необходимо вычитать дальше числа вида , где – удвоенный известный на данный момент результат, приписывая к нему цифру, получаем , умножаем на эту же самую цифру, имеем .
Как вычислить корень из числа без калькулятора? Быстро и легко вычислить корень из большого числа
Автор j2jglobali На чтение 5 мин. Просмотров 675 Опубликовано
Во многих ситуациях необходимо вычислить корень из числа без калькулятора, например, на экзамене. Вам может показаться это довольно сложной задачей, которая занимает уйму времени, особенно если дано дробное или крупное число.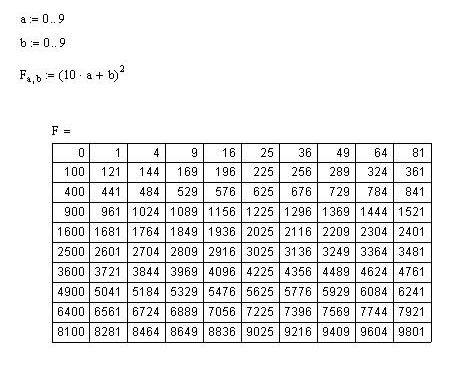
В этой статье мы опровергнем этот миф и покажем, как быстро вычислить корень из числа в уме несколькими способами.
Содержание
- Способ разложения на множители.
- Способ, который подойдет для любого числа с целым корнем
- Способ для вычисления корней с остатком
- Способ оценки
Способ разложения на множители.
Для этого способа необходимо выучить несколько признаков делимости:
- На 2 делятся четные числа
- На 3 делятся числа, сумма цифр в которых поделится на 3, например, 123. Здесь к 1 прибавляем 2 и 3, получив 6. Это число делится на 3.
- На 4 делятся числа последние две цифры которых являются нулями, например, 100. А также число, последние две цифры которого являются двузначным числом, делимым на 4, например, 216.
Исходя из признаков делимости, выбираем цифру на которую будет делиться число 12 816. В нашем случае это 4. Далее просто делим 12 816 на 4 в столбик. Получаем 324. Его можно разделить либо 3, либо на 4.
Весомой разницы нет. Мы разделим на 4, потому что так быстрее. Получаем 81 и из таблицы умножения знаем, что 81 = 9².
Выписываем все делители под знак корня и делаем их квадратными (4*4 = 4²; 81 = 9²).
Корень числа, как известно, равен данному числу в квадрате, поэтому выносим 4 и 9 из-под корня без квадрата. Далее просто перемножаем эти числа и получаем ответ. В нашем случае – это 36.
Данный способ хоть и простой, но может не подойти ко всем числам, ведь некоторые из них делятся только на двузначные или трехзначные числа.
Способ, который подойдет для любого числа с целым корнем
Этот способ сложнее, но благодаря ему можно вычислить корень из большого числа.
Для него нужно знать квадраты чисел от 1 до 9.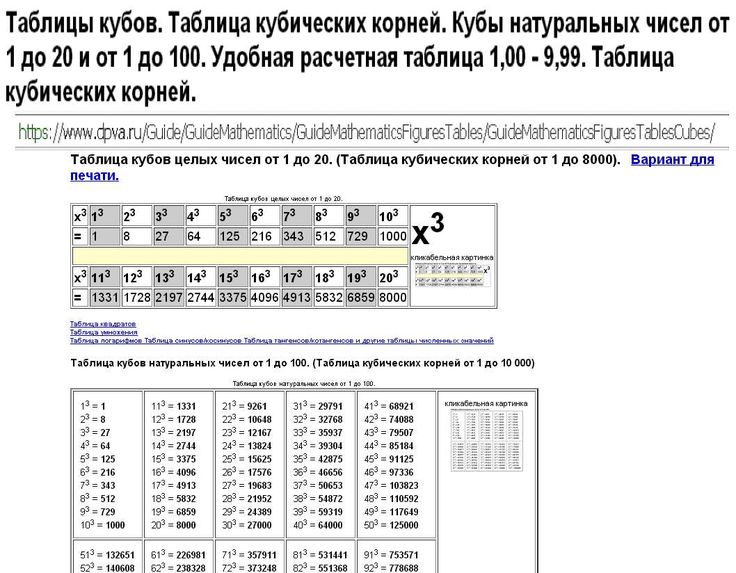
Нам понадобится только последняя цифра квадрата. Например, квадрат 6 – 36. Запишем только шестерку. И так с каждой цифрой.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 |
Для нахождения корня, мы воспользуемся формулой: (десятки + единицы) ²= десятки² + 2*десятки*единицы + единицы²
Суть метода тяжело раскрыть на словах, поэтому продемонстрируем на примере.
Допустим, нам необходимо вычислить корень из числа 8 464. Сначала мы разбиваем число на группы двузначных чисел справа налево.
Находим цифру, квадрат которой является минимальным приближенным к двузначному числу слева. Здесь это 9. Записываем цифру в результат и вычитаем из 84 квадрат девятки. То есть 84-81.
Получаем цифру три и располагаем ее справа от столбца. Туда же выписываем двузначное число, которое расположено правее – 64.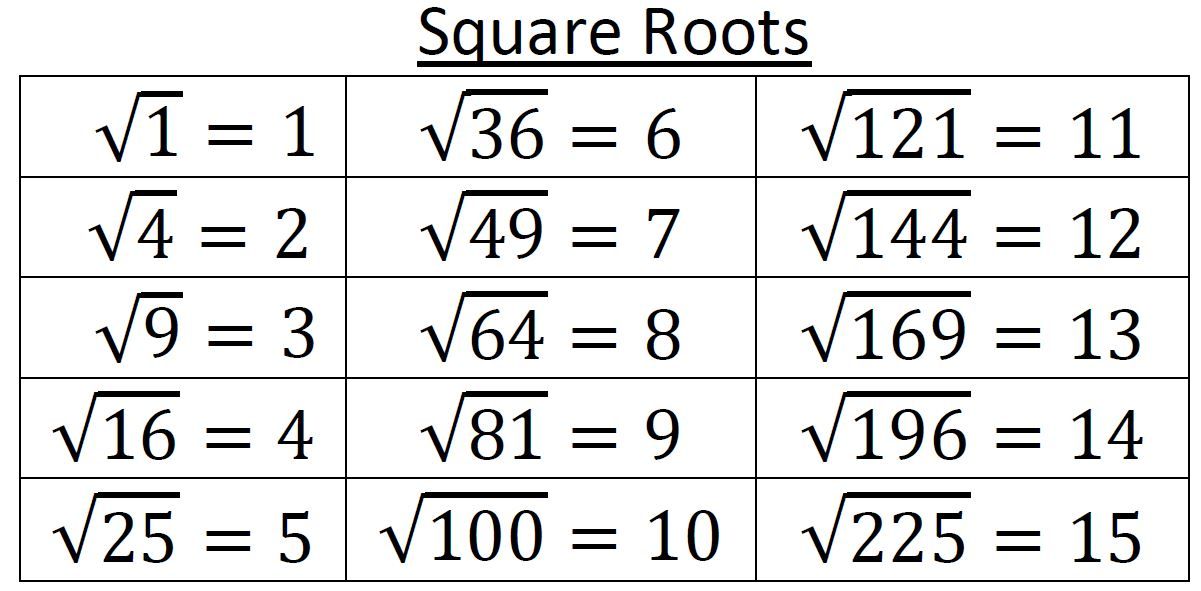
Слева от столбца пишем девятку, умноженную на два, оставив две клеточки, как показано на картинке.
Далее в эти две клеточки выписываем цифру, с помощью которой, образуется трехзначное число, умножив которое на вписанную цифру, должно получиться такое же число, что и справа от столбца или наименьшее приближенное к нему.
Цифру, которой мы воспользовались (в этом случае – 2) выписываем в результат после девятки и получаем решение.
Если число пятизначное, шестизначное или более, нужно проделать процедуру из последних, указанную в последних трех абзацах, еще один раз. Продемонстрирую это на втором примере.
Возьмем пятизначное число 84 681 и разделим его на блоки двузначных чисел справа налево. В числе с пятью знаками слева остается одна цифра, и это нормально. Находим цифру, квадрат которой является минимальным приближенным числом к восьми. Это 2. Пишем ее после знака равно.
Из восьми вычитаем квадрат двойки – четверку. Выписываем разницу справа от столбика, а слева пишем двойку, умноженную на 2.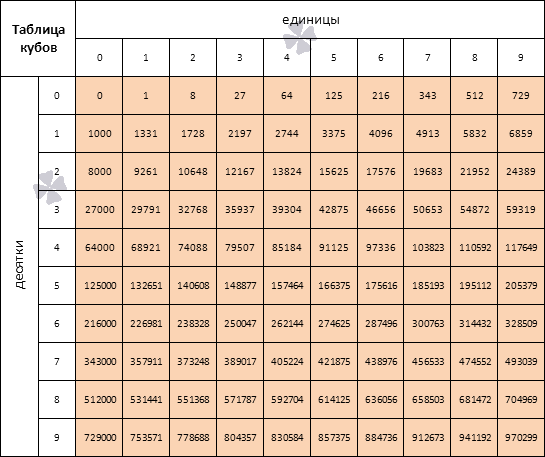
Сносим второй блок, который расположен правее и получаем число 446 справа от столбца.
Находим такую цифру, приписав которую к четверке и умножив полученное двузначное число на нее же, получится минимальное число приближенное к 446. Это девятка. Запишем ее в результат после двойки.
49 умножим на 9 и получим 441. Запишем его справа от столбца, под 446.
Вычтем из 446 число 441. Запишем разницу и снесем следующее двузначное число – 81. Получим 581.
Слева от столбика напишем произведение 29 (число после знака равно) и двойки. Далее воспользуемся табличкой, которую составили ранее: трехзначное число справа оканчивается единицей. Квадрат цифры 1 и 9 тоже ею оканчивается. Применив логическое мышление, можно понять, что число слева от столбца должно оканчиваться единицей. Следовательно, получаем число 581 и умножаем его на 1.
Числа справа и слева от столбца сходятся, значит все решено правильно. Припишем единицу к 29 в ответе и получим 291. Это число и является решением.
Стоит понимать, что способ не сработает если корнем окажется число с остатком!
В большинстве случаев корень является числом с остатком. Этот метод поможет найти такой корень.
Он работает по принципу разложения числа на множители. Покажем на примере.
Допустим, нужно найти корень из 45. Раскладываем это число на множители (можно воспользоваться способом из начала статьи или сделать это самостоятельно). 45 = 5*9. Девять является квадратом трех, следовательно нужно вынести 3 из-под знака корня. Пятерка же не является квадратом какого-либо числа, поэтому она остается под корнем.
Ту же операцию можно проделать и с числом 320, которое можно разделить на множители 64 и 5. 64 – квадрат восьми, поэтому последнее выносится из-под корня, а 5 остается под ним.
Способ оценки
Способ подойдет для быстрого вычисления корня из четырехзначного числа. Чтобы его применить, нужно знать или иметь доступ к таблице квадратов из второго способа.
Выбираем самое маленькое приближенное к 6084 двузначное круглое число и, полагаясь на однозначные числа, возводим его в квадрат.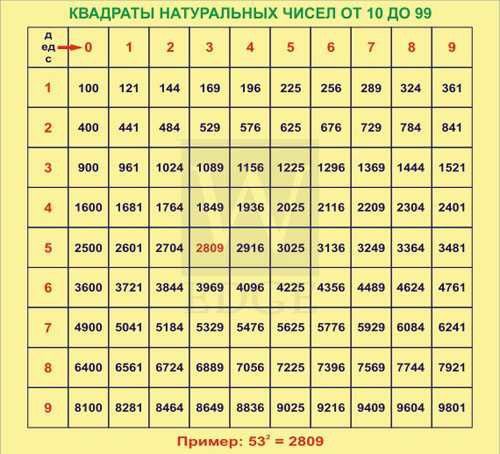
Так же поступаем и с наибольшим числом, приближенным к 6084.
Таким образом, мы получаем диапазон чисел, между которыми нужно искать ответ.
Узнать вторую цифру можно воспользовавшись таблицей представленной выше.
Просмотрев ее, становится понятно, что это либо 2 либо 8.
Воспользовавшись цифрой 2, получим число 72. 72 в квадрате = 5184. Поэтому такой ответ нам не подходит остается цифра восемь.
Получаем ответ 78.
Квадратный корень от 1 до 100
Квадратный корень от 1 до 100 — это список квадратных корней всех чисел от 1 до 100. Квадратный корень может иметь как отрицательные, так и положительные значения. Положительные значения квадратных корней от 1 до 100 находятся в диапазоне от 1 до 10.
В квадратных корнях от 1 до 100 числа 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100 являются полными квадратами. а остальные числа являются несовершенными квадратами, т.е. их квадратный корень будет иррациональным. Квадратный корень от 1 до 100 в радикальной форме выражается как √x, а в экспоненциальной форме он выражается как (x) ½ .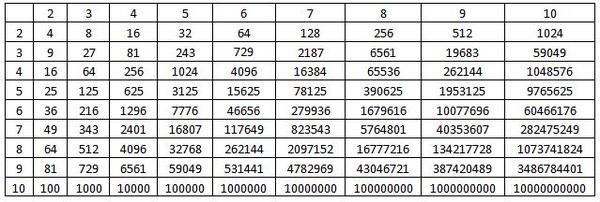
Изучение квадратного корня от 1 до 100 поможет вам быстро упростить длинные уравнения, занимающие много времени. Значение квадратных корней от 1 до 100 до 3 знаков после запятой указано в таблице ниже.
Ученикам рекомендуется тщательно запомнить эти значения квадратного корня от 1 до 100 для более быстрого выполнения математических вычислений. Нажмите на кнопку загрузки, чтобы сохранить копию в формате PDF.
В таблице ниже показаны значения квадратных корней от 1 до 100 для идеальных квадратов.
В таблице ниже показаны значения от 1 до 100 квадратных корней для неполных квадратов.
Каково значение квадратного корня от 1 до 100?
Значение квадратного корня от 1 до 100 представляет собой число (x 1/2 ), умноженное само на себя дает исходное число. Он может иметь как отрицательные, так и положительные значения. В диапазоне от 1 до 100 квадратные корни из 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100 являются целыми числами (рациональными), а квадратные корни из 2, 3, 5, 6, 7 , 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35 , 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 82, 83, 84, 85, 86 , 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98 и 99 — десятичные числа, которые не являются ни конечными, ни повторяющимися (иррациональными).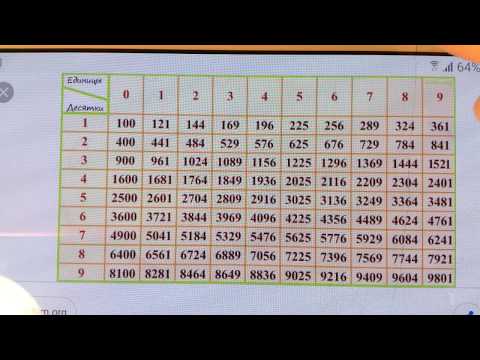
Какие существуют методы вычисления квадратных корней от 1 до 100?
Существует два метода, обычно используемых для вычисления значения квадратного корня от 1 до 100. Для полных квадратов (1, 4, 9, 16, 25, 36, 49, 64, 81 и 100) мы можем использовать простые методом факторизации и для неполных квадратов (2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19)., 20, 21, 22, 23, 24, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46 , 47, 48, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 65, 66, 67, 68, 69, 70, 71, 72, 73 , 74, 75, 76, 77, 78, 79, 80, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98 и 99) можно использовать метод длинного деления.
Если извлечь квадратный корень от 1 до 100, сколько из них будет иррациональным?
Цифры 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46 , 47, 48, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 65, 66, 67, 68, 69, 70, 71, 72, 73 , 74, 75, 76, 77, 78, 79, 80, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98 и 99 — несовершенные квадраты.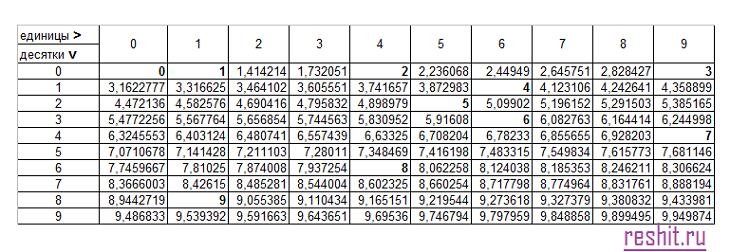
Следовательно, их квадратный корень будет иррациональным числом (не может быть выражено в виде p/q, где q ≠ 0).
Каково значение 21 плюс 2 квадратного корня 784?
Значение √784 равно 28. Итак, 21 + 2 × √784 = 21 + 2 × 28 = 77. Следовательно, значение 21 плюс 2 квадратного корня из 784 равно 77.
Сколько чисел в квадратных корнях от 1 до 100 рациональны?
Числа 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100 являются полными квадратами, поэтому их квадратные корни будут целыми числами, т.е. могут быть выражены в виде p/q, где q ≠ 0 , Следовательно, квадратный корень из чисел 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100 являются рациональными числами.
Какие значения квадратных корней от 1 до 100 находятся между 2 и 3 включительно?
Значения квадратных корней от 1 до 100 между 2 и 3 равны √4 (2), √5 (2,236), √6 (2,449), √7 (2,646), √8 (2,828) и √9 (3 ).
Используя таблицу квадратных корней, найдите квадратные корни из следующих 1110…
Перейти к
- Квадраты и квадратные корни.
- Квадраты и квадратные корни. Упражнение 3.2.
- Квадраты и квадратные корни. Упражнение 3.3.
- Квадраты и квадратные корни. Упражнение 3.4.
- Квадраты и квадратные корни. Упражнение 3.5.
- Квадраты и квадратные корни. Упражнение 3.6.
- Квадраты и квадратные корни. Упражнение 3.7.
- Квадраты и квадратные корни. Упражнение 3.8.
- Квадраты и квадратные корни. Упражнение 3.9.
Упражнение 3.7.- Рациональное число
- Полномочия
- Квадраты и квадратные корни
- Куб и кубические корни
- Игра с числами
- Алгебраические выражения и тождества
- Факторизация
- Отдел алгебраических выражений
- Линейное уравнение с одной переменной
- Прямые и обратные варианты
- Время и работа
- Процент
- Скидка на убыток и налог на добавленную стоимость
- Сложные проценты
- Понимание многоугольников фигур
- Понимание фигур Четырехугольники
- Понимание фигур Специальные типы четырехугольников
- Практическая геометрия
- Визуализация фигур
- Площадь трапеции и многоугольника
- Объем Площадь Прямоугольный Куб
- Площадь поверхности и объем правого кругового цилиндра
- Классификация и табулирование данных
- Классификация и табулирование данных Графическое представление данных в виде гистограмм
- Графическое представление данных в виде круговых диаграмм или круговых диаграмм
- Вероятность обработки данных
- Введение в графики
Главная >
РД Шарма Решения
Класс 8
Математика
>
Глава 3.
Квадраты и квадратные корни
>
Квадраты и квадратные корни. Упражнение 3.9.
>
Вопрос 20
Вопрос 20 Квадраты и квадратные корни Упражнение 3.9
Используя таблицу квадратного корня, найдите квадратные корни из следующих чисел:
1110
Ответ:
Из таблицы квадратного корня мы знаем, что
Квадратный корень из 1110: корень 1110 это 33.317
стенограмма видео
«привет дорогой студент я Sunita и я
от лидера обучения, и я здесь, чтобы
показать вам, как сделать сумму
используя таблицу квадратного корня прямо так
с помощью таблицы квадратного корня найти
квадратный корень из 1110
поэтому всякий раз, когда мы должны использовать квадратный корень
таблица первый шаг
состоит в том, чтобы сделать факторизацию числа
Итак, давайте проведем факторизацию
данный номер
используя простые множители, так что 1110
так что начну с первого прайма
фактор два
так вот я получаю 555
мой следующий главный фактор будет три три
те
три восьмых и три пятерки
тогда я перейду к 5 5 3 15
и 7 и так как 37 простое число
у нас больше нет простых множителей, поэтому
это первичная факторизация
так что мы можем выразить это число в
с точки зрения его простых множителей
будет 1110 является продуктом
2 3 5
и 37 так что если нам нужно
найти квадратный корень из 1110
нам нужно найти квадратный корень из этого
продукт правильный, поэтому позвольте мне разделить
условия сейчас
это равно квадратному корню из 2
умножается на
квадратный корень из 3 умножить на квадрат
корень из 37
умножить на квадратный корень из 5.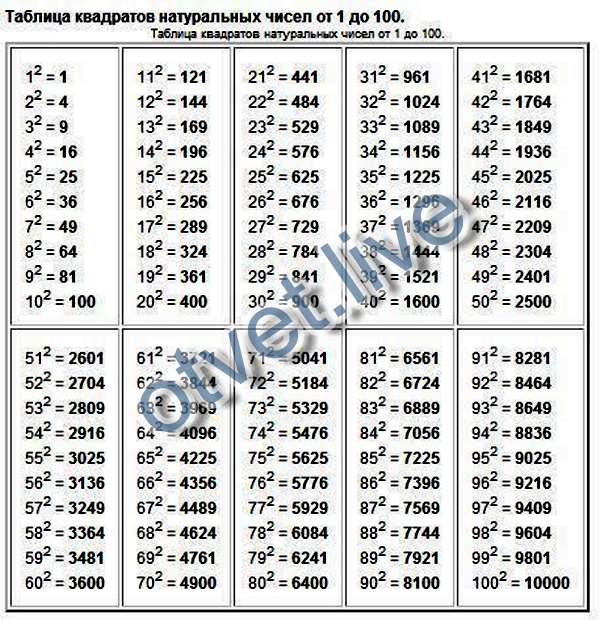
я
просто поменял местами 37 и 5 на
цель расчета все прямо сейчас
из таблицы квадратного корня, которую я уже имел
скопировал
значения квадратных корней из этих
числа
2 3 5 и 37 так что они мне понадобятся
здесь
так что давайте начнем умножение так
здесь у меня есть первые два члена
квадратный корень из 2 в квадратный корень из 3
будет 1,41
умножить на 1,5
для целей расчета я
округление до второго десятичного знака
так что позвольте мне сделать умножение здесь
1,73 умножить на 1,41
так вот у меня 173 во второй строке я
будет четыре тройки двенадцать
четыре семерки это 28 и 129четыре
четыре плюс два шесть
в третьем ряду у меня будет 173
снова теперь я добавляю числа вверх
у меня 3 9 13
14 и 2 ладно сейчас я ставлю свою десятичную
точка на месте
это 2.4 все в порядке, так что я напишу, что
здесь
снова я буду округлять до
второе десятичное место так
я оставлю 2.44
ладно ладно теперь позвольте мне сделать второй
часть, которая
квадратный корень из 37, умноженный на
квадратный корень из 5 значения здесь так
квадратный корень из 37
6,08
поэтому я напишу это здесь 6.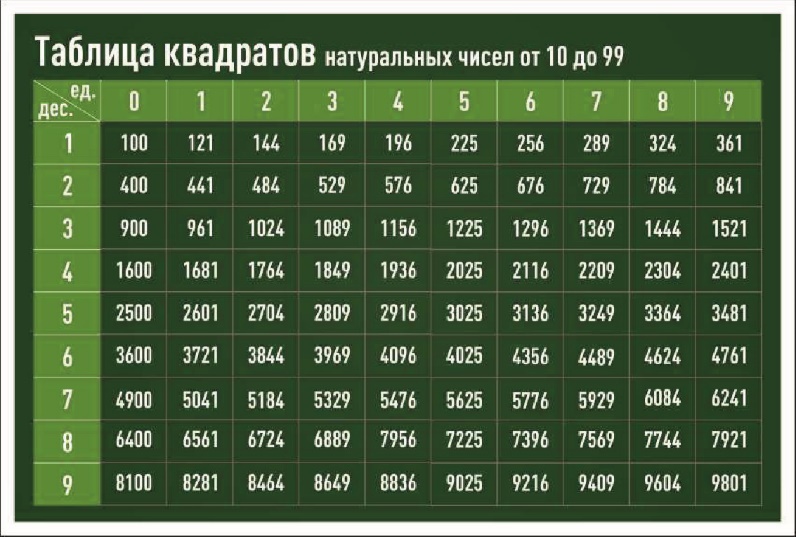
08
умножить на квадратный корень из 5
2.34 я округляю до двух знаков после запятой
места
так позвольте мне сделать умножение
умножается на
две целых три четверти, так что я здесь
32 и шесть четверок равно 24
во второй строке я снова получу э
24 восемь троек это 24 и
шесть три шестерки восемнадцать третий
линия я получу
ну восемь двоек шестнадцать
а шесть двоек это двенадцать так
я просто суммирую это, я собираюсь получить
2
7 12 8 в
10 и 2 12
2 и 1 3 и 1 4 и 1
и есть четыре десятичных знака, так что
это 14.2272
который я напишу как 14.23
нет, извините, да 2 3 правильно, так что это мой
окончательное умножение
14,23 умножить на 2,44
вот у меня 12 четыре двойки восемь
и один девять четыре четыре шестнадцать
четыре единицы четыре и один пять
второй ряд четыре тройки двенадцать
фотографии восемь и один девять четыре четыре
шестнадцать
четыре единицы четыре и один пять
последний ряд две тройки шесть два
двойки четыре
две четверки восемь и две единицы
два
так что я добавляю, я получаю 2 11
9и 1 10 и 6 16 и 6 22
6 и 4 10 и 7 17 8 и 1 9 и 5
14 2 и 1 3
правильно, и у меня есть 4 десятичных знака, так что мой
ответ
34,72
таким образом, путем умножения квадратных корней из
физическое лицо
факторы 2 3 5 и 37
я получаю свой ответ как 34,72
надеюсь ты понял решение
оставить комментарий в разделе комментариев
и
регулярно посещайте наш канал, чтобы узнать больше
такое домашнее задание
решения, и вы можете подписаться на нашу
канал для обновлений
спасибо»
Похожие вопросы
Используя таблицу квадратных корней, найдите квадратные корни из следующего: 7
Используя таблицу квадратных корней, найдите квадратные корни из следующих чисел: 15
Используя таблицу квадратных корней, найдите квадратные корни следующего:74
Используя таблицу квадратных корней, найдите квадратные корни следующего:82
Используя таблицу квадратных корней, найдите квадратные корни следующего:198
Используя таблицу квадратных корней, найдите квадратные корни следующего: 540
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
квадраты и квадратные корни упражнения 3.