Поиск материала «Четырехзначные математические таблицы, Брадис В.М., 1990» для чтения, скачивания и покупки
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Четырехзначные MATEMATИЧЕСКИЕ ТАБЛИЦЫ 12.71 12.
B. M. БРАДИС. Четырехзначные MATEMATИЧЕСКИЕ ТАБЛИЦЫ. 13-е издание, стереотипное. Москва. 2010. удк 51(083.4) ББК 22.13. Брадис, В. М. . Четырехзначные.
edu.glavsprav.ru
- Четырехзначные математические таблицы — Брадис В.М.
Четырехзначные математические таблицы — Брадис В.М. Рекомендуется использовать с 7 класса. Необходимая книга для школьника или студента, решающего задачи по геометрии. Значения, приводимые в математических таблицах, иногда бывают точными, но чаще приближенными, представляя собой результаты округления точных значений.
 Для учащихся старших классов общеобразовательных учебных заведений. Список таблиц — синусы-косинусы — тангенсы-котангенсы — тангенсы углов, близких к 90°, котангенсы малых углов — длина…
Для учащихся старших классов общеобразовательных учебных заведений. Список таблиц — синусы-косинусы — тангенсы-котангенсы — тангенсы углов, близких к 90°, котангенсы малых углов — длина…11klasov.net
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- Скачать таблицы брадиса косинус синус тангенс бесплатно
Глоссарий. К содержанию. Скачать Таблицы Брадиса. Таблицы Брадиса (pdf). Таблица Брадиса синусы и косинусы
edu.glavsprav.ru
- Четырёхзначные математические таблицы для сред. школы.
В.М.Брадис.
fremus.narod.ru
- Таблица Брадиса скачать бесплатно
Если у вас дома не оказалось так необходимого всем школьникам учебного пособия, то на нашем сайте вы можете как помотреть, так и скачать таблицу Брадиса в любом удобном для вашего чтения формате.
Данная книга представляет собой самый полный сборник всех «Четырехзначных математических таблиц» синусов, косинусов, тангенсов, квадратов, логарифмов и пр… В общей сложности всего около двадцати двух видов. В ней вы так же найдёте как пользоваться таблицей Брадиса .
xn—-7sbabaccz5af0a8dqc8d.xn--p1ai
- Таблица Брадиса: скачать, распечатать (doc, pdf) полная версия…
Таблицы Брадиса — это математический справочник, в котором собраны таблицы, необходимые для работ по курсу математики и для практических вычислений, не требующих высокой точности. Составил таблицы Брадиса Владимир Модестович, советский математик и педагог, член-корреспондент Академии педагогических наук РСФСР. Скачать и распечатать полную версию таблиц Брадиса в формате pdf.
trafaret-decor.ru
- Таблица Брадиса: синусы и косинусы, тангенсы, котангенсы
Таблица Брадиса — это таблица, которая поможет при вычислениях в решении задач как в школе (на математике, алгебре, геометрии и физике в старших классах), так и в вузах.
 На этой странице четырехзначные математические онлайн таблички для синусов, косинусов, тангенсов и котангенсов. Пользоваться таблицами просто. Пример : найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5.
На этой странице четырехзначные математические онлайн таблички для синусов, косинусов, тангенсов и котангенсов. Пользоваться таблицами просто. Пример : найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5.uchim.org
- Брадис В.М. / Четырехзначные математические таблицы.
Название: Четырехзначные математические таблицы. Автор: Брадис В.М. Аннотация: Книга содержит таблицы квадратов, квадратных корней, кубов, синусов и косинусов, тангенсов и котангенсов, мантиссы десятичных логарифмов и др. Всего 22 таблицы.
Название: Математические модели социальных систем Автор: А.К. Гуц, В.В. Коробицын, А.А. Лаптев. Л.А. Паутова, Ю.В. Фролова Аннотация: Учебное. Владимиров В.С. / Таблицы интегралов комплекснозначных функций p-адических аргументов.
www.
 vixri.ru
vixri.ru - Таблицы Брадиса | Учебно-методическое пособие по математике
Использование таблиц для решения задач. Вашему вниманию представляю интегрированный урок информатики и математики. Проведение интегрированных уроков в учебном процессе способствует развитию межпредметные связи, где информатика выступает…
Презентация для уроков, а также внеурочной деятельности по химии. Может быть использована как межпредметный материал…. В.М. Брадис и его замечательные таблицы. В презентации представлен дополнительный материал к урокам геометрии по теме «Решение треугольников».
nsportal.ru
- Таблица Брадиса
Здесь указаны четырехзначные математические таблицы Брадиса. По сути это просто вычисленные значения некоторых тригонометрических функций и уравнений, например таких, как синус от угла (sin), косинус от угла (cos), тангенс (tg), также таблицу логарифмов, квадратных корней и кубов.
 На данной странице вы посмотреть и скачать в формате pdf по отдельности каждые таблицы Брадиса, или скачать (посмотреть) полную таблицу Брадиса. Все приведенное ниже — бесплатно.
На данной странице вы посмотреть и скачать в формате pdf по отдельности каждые таблицы Брадиса, или скачать (посмотреть) полную таблицу Брадиса. Все приведенное ниже — бесплатно.www.kontrolnaya-rabota.ru
- Четырехзначные математические таблицы. Брадис В.М.
Четырехзначные математические таблицы. Брадис В.М. 13-е изд., стер.
Список таблиц — синусы-косинусы — тангенсы-котангенсы — тангенсы углов, близких к 90°, котангенсы малых углов — длина окружности диаметра D — площадь круга диаметром D — радианная мера — тригонометрические функции от аргумента в радианах — мантиссы десятичных логарифмов — значения функции 10x — логарифмы синусов малых углов, логарифмы косинусов углов, близких к 90° — логарифмы.
www.at.alleng.org
- В.Брадис. Четырехзначные математические таблицы для.
 ..
..В.Брадис. Четырехзначные математические таблицы для средней школы (djvu). Скачать книгу бесплатно (djvu, 1.22 Mb). Читать «В.Брадис.
libcats.org
- Таблицы Брадиса (.zip.pdf — 5,2Mb) — Инженерный справочник…
Вы сейчас находитесь в каталоге: Таблицы Брадиса. Значения тригонометрических, логарифмических функций. Прочее. Таблицы Брадиса (.zip.pdf — 5,2Mb).
dpva.ru
- Четырёхзначные математические таблицы | Брадис…
Список таблиц — синусы-косинусы — тангенсы-котангенсы — тангенсы углов, близких к 90°, котангенсы малых углов — длина окружности диаметра D — площадь круга диаметром D — радианная мера — тригонометрические функции от аргумента в радианах — мантиссы десятичных логарифмов — значения функции 10x — логарифмы синусов малых углов, логарифмы косинусов углов, близких к 90° — логарифмы.
.. Таблицы приведены в 47-м издании.
libcats.org
- Четырёхзначные математические таблицы (1976) | учебники…
В.М. Брадис. Четырёхзначные математические таблицы для средней школы. Пособие для учащихся. 47-е издание.
Общие правила вычисления. Таблица I. Точные произведения двузначных чисел. Указания к таблице I.
bibliobraz.su
- Книга Четырёхзначные математические таблицы ( Брадис…)
Читать онлайн книгу Четырёхзначные математические таблицы автора Брадис В.М.
bookree.org
- Школа пифагора — четырехзначные математические таблицы
Памятки по Математике Великие Математики Теория Чисел Математическая Логика.
Четырехзначные Математические Таблицы Брадиса. Презентации по Математике.

xn—-7sbbao2ali0aghq2c8b.xn--p1ai
- Четырехзначные математические таблицы для средней школы…
«Значения, приводимые в математических таблицах, иногда бывают точными, но чаще приближенными, представляя собой результаты округления точных значений, и содержат погрешности, не превосходящие половины единицы разряда последней цифры. Если значение взято не прямо из таблицы, а найдено посредством интерполяции (см. с. 85—90), погрешность может быть больше, но в подавляющем большинстве случаев не превосходит единицы разряда последней цифры.
www.nehudlit.ru
- Таблицы Брадиса (.zip.pdf — 5,2Mb) — таблицы Tehtab.ru
Дополнительная информация от TehTab.ru: Таблица Брадиса тригонометрические функции sin x, cos x, tg x от аргумента в радианах.
Таблица Брадиса — десятичные логарифмы синусов малых углов, десятичные логарифмы косинусов углов, близких к 90° Значения тригонометрических функций.

tehtab.ru
- Таблица Брадиса — СИНУСЫ И КОСИНУСЫ | Математика
Таблица брадиса — синусы и косинусы даёт значение синуса любого острого угла, содержащего целое число градусов и десятых долей градуса, на пересечении строки, имеющей в заголовке (слева) соответствующее число градусов, и столбца, имеющего в заголовке (сверху) соответствующее число минут.
Ниже вы можете скачать таблицу брадиса — синусы и косинусы в виде изображений. _ Источник информации: Брадис В.М. Четырехзначные математические таблицы: Для средней школы. /
infotables.ru
- Таблица Брадиса для синуса и косинуса
Таблица Брадиса для синуса и косинуса.
Таблица Брадиса для тангенса и котангенса.
elenasuchkova.ucoz.ru
- Таблицы Брадиса (формат djvu) — синусы, косинусы, котангенсы.
 ..
..А ведь когда-то без них, ни один курсовик невозможно было сделать! Вместе с логарифмической линейкой основной инструмент при расчетах был. Таблица Брадиса — синусы, косинусы, котангенсы и тангенсы. Таблица Брадиса — таблица поможет при вычислениях в решении конструкторских задач. В формате djvu четырехзначные математические таблицы для синусов, косинусов, тангенсов и котангенсов.
DWG.ru
- Четырехзначные математические таблицы для средней школы
Брадис В.
Категория: КНИГИ ДЛЯ ДЕТЕЙ. 15.50 Mb. Только что пользователи скачали эти книги
libcats.org
- Таблица Брадиса косинусов, синусов, тангенсов, котангенсів
Таблица Брадиса — это таблица, которая поможет при вычислениях в решении задач как в школе (на математике, алгебре, геометрии и физике в старших классах), так и в вузах. На этой странице четырехзначные математические онлайн таблички для синусов, косинусов, тангенсов и котангенсов.
 Пользоваться. таблицами просто. Пример : найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5.
Пользоваться. таблицами просто. Пример : найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5.MyComp.su
- Таблица Брадиса для школьников и студентов
Таблица Брадиса необходима для вычислений, связанных со значениями тригонометрических функций. Обратите внимание, что здесь представлены усовершенствованные таблицы, значения которых основаны на современных (более точных) алгоритмах вычисления. Как пользоваться таблицей Брадиса. Наглядная инструкция.. Таблица Брадиса для синуса и косинуса. Обратите внимание на то, что значения синусов и косинусов углов не может быть больше 1.
UrokMatematiki.ru
- Брадис В.М. Четырехзначные математические таблицы
Список таблиц.
 Общие правила вычисления Точные произведения двузначных чисел Значения дробей вида 1/n Квадраты Квадратные корни Кубы Длина окружности диаметра d Площадь круга диаметра d Синусы и косинусы Тангенсы и котангенсы Тангенсы углов, близких к 90°, и котангенсы малых углов Радианная мера Тригонометрические функции от аргумента в радианах Мантиссы десятичных логарифмов Значения функции 10х (десятичные антилогарифмы) Логарифмы синусов малых углов и косинусов.
Общие правила вычисления Точные произведения двузначных чисел Значения дробей вида 1/n Квадраты Квадратные корни Кубы Длина окружности диаметра d Площадь круга диаметра d Синусы и косинусы Тангенсы и котангенсы Тангенсы углов, близких к 90°, и котангенсы малых углов Радианная мера Тригонометрические функции от аргумента в радианах Мантиссы десятичных логарифмов Значения функции 10х (десятичные антилогарифмы) Логарифмы синусов малых углов и косинусов.www.studmed.ru
- Скачать полную таблицу Брадиса в формате pdf (можно для…)
Полная таблица Брадиса в формате pdf. На этой странице Вы можете скачать таблицу Брадиса в формате pdf абсолютно бесплатно здесь ссылка.
www.kontrolnaya-rabota.ru
- Четырёхзначные таблицы В.М. Брадиса — презентация, доклад…
Вы можете изучить и скачать доклад-презентацию на тему Четырёхзначные таблицы В.
 М. Брадиса. Презентация на заданную тему содержит 11 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
М. Брадиса. Презентация на заданную тему содержит 11 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!В 1921 году Брадис издаёт «Таблицы четырёхзначных логарифмов и натуральных тригонометрических величин», в дальнейшем меняет название на «Четырёхзначные математические таблицы».
myslide.ru
- Таблица Брадиса синусы и косинусы: скачать… — 3mu.ru
Данная таблица Брадиса, которую можно скачать и распечатать в хорошем качестве, поможет вам в ваших вычислениях. Скачать таблицу Брадиса синусы и косинусы. Вся таблица поместилась на двух листах А4 формата, которые можно распечатать на отдельных листах или с двух сторон одного листа. Скачать таблицу Брадиса синусов и косинусов можно в PDF или DOCx форматах. (PDF — 1 страница, 2 страница; DOCx — 1 страница, 2 страница).
 Если данный материал был вам полезен, вы всегда можете поддержать наш сайт.
Если данный материал был вам полезен, вы всегда можете поддержать наш сайт.3mu.ru
- Презентация по математике «Брадис Владимир Модестович.»
Математик Владимир Модестович Брадис (1890 – 1975) еще в начале 20-го века придумал способ, позволяющий до минимума сократить утомительные расчеты, которые приходилось производить каждому инженеру до появления калькуляторов. Он выбрал несколько наиболее необходимых для практических расчетов функций и посчитал все их значения в широком интервале аргументов с приемлемой точностью, четыре значащих цифры. Результаты своих расчетов В.М.Брадис представил в виде таблиц.
nsportal.ru
- Почему таблица Брадиса — четырехзначная?
Таблица Брадиса или тригонометрическая таблица, которая представляет собой сборник значений углов в градусном и радиальном измерении. Фактически является сборником таблиц, которые содержат посчитанные значения для синусов (sin), косинусов (cos), тангенсов (tg), котангенсов (ctg) и их производных.
 Эти значения рассчитаны до четвертого знака после запятой. Поэтому сборник и называется «Четырёхзначные математические таблицы». Ниже рассмотрим основные таблицы.
Эти значения рассчитаны до четвертого знака после запятой. Поэтому сборник и называется «Четырёхзначные математические таблицы». Ниже рассмотрим основные таблицы.themechanic.ru
- Таблица Брадиса — математическое пособие, в котором…
Практические примеры использования таблицы. Что такое таблица Брадиса. Использование калькуляторов при сложных расчетах (например, формулах с применением логарифмов) сегодня считается стандартом по умолчанию.
Свое название они получили от брошюры «Четырехзначные математические таблицы», составленной Владимиром Брадисом. Книга неоднократно переиздавалась в советское время большими тиражами (до 500 000 экземпляров) и широко использовалась в учебном процессе — на уроках алгебры, геометрии и физики.
wiki.fenix.help
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Четырехзначные математические таблицы, Брадис В.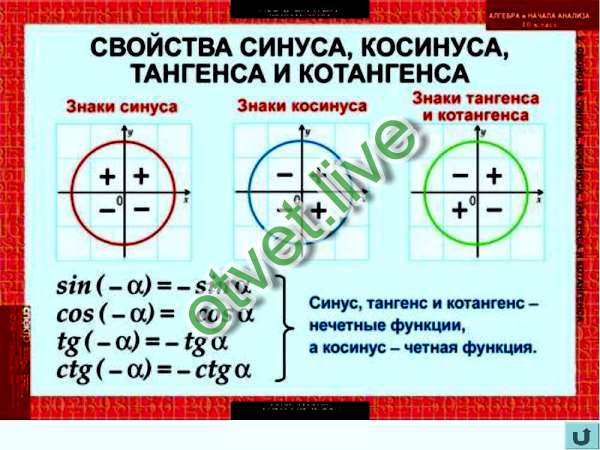 М., 1990»
М., 1990»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 107 тыс. ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
4.5: Другие тригонометрические функции и тождества
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 89303
- Мэтью Болкинс, Дэвид Остин и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли
Мотивирующие вопросы
- Какие другие \(3\) тригонометрические функции и как они связаны с функциями косинуса, синуса и тангенса?
- Как ведут себя графики функций секанса, косеканса и котангенса и как эти графики соотносятся с графиками функций косинуса, синуса и тангенса?
- Что такое тригонометрическое тождество и почему тождества важны?
Функции синуса и косинуса, первоначально определенные в контексте точки, пересекающей единичный круг, также являются центральными в тригонометрии прямоугольного треугольника. Они позволяют нам найти недостающую информацию в прямоугольных треугольниках простым способом, когда мы знаем один из непрямых углов и одну из трех сторон треугольника или две стороны, где одна является гипотенузой. Кроме того, мы определили функцию тангенса в терминах функций синуса и косинуса, а функция тангенса предлагает дополнительные возможности для поиска недостающей информации в прямоугольных треугольниках. Мы также видели, как обратные функции ограниченного синуса, косинуса и тангенса позволяют нам находить недостающие углы в самых разных условиях, включая прямоугольные треугольники.
Они позволяют нам найти недостающую информацию в прямоугольных треугольниках простым способом, когда мы знаем один из непрямых углов и одну из трех сторон треугольника или две стороны, где одна является гипотенузой. Кроме того, мы определили функцию тангенса в терминах функций синуса и косинуса, а функция тангенса предлагает дополнительные возможности для поиска недостающей информации в прямоугольных треугольниках. Мы также видели, как обратные функции ограниченного синуса, косинуса и тангенса позволяют нам находить недостающие углы в самых разных условиях, включая прямоугольные треугольники.
Одним из мощных аспектов тригонометрии является то, что предмет дает нам возможность рассмотреть одну и ту же идею с разных точек зрения. Например, мы заметили, что функции \(f(t) = \cos(t)\) и \(g(t) = \sin(t+\frac{\pi}{2})\) на самом деле та же функция; в качестве другого, для значений \(t\) в области \((-\frac{\pi}{2}, \frac{\pi}{2})\text{,}\) мы знаем, что запись \( y = \tan(t)\) равносильно написанию \(t = \arctan(y)\text{. }\). Какую перспективу мы выбираем, часто зависит от контекста и предоставленной информации.
}\). Какую перспективу мы выбираем, часто зависит от контекста и предоставленной информации.
Хотя почти на каждый вопрос, связанный с тригонометрией, можно ответить, используя функции синуса, косинуса и тангенса, иногда бывает удобно использовать три связанные функции, которые связаны с тремя другими возможными сочетаниями отношений сторон в прямоугольных треугольниках.
Рисунок определения \(\PageIndex{1}\): Функции секанса, косеканса и котангенса.
- Для любого действительного числа \(t\), для которого \(\cos(t) \ne 0\text{,}\) мы определяем секанс \(t\text{,}\), обозначаемый \(\ sec(t)\text{,}\) по правилу
\[ \sec(t) = \frac{1}{\cos(t)}\text{.} \nonumber \]
- Для любого действительного числа \(t\), для которого \(\sin(t) \ne 0\text{,}\) мы определяем косеканс числа \(t\text{,}\), обозначаемый \(\csc( t)\text{,}\) по правилу
\[ \csc(t) = \frac{1}{\sin(t)}\text{.} \nonumber \]
- Для любого действительного числа \(t\), для которого \(\sin(t) \ne 0\text{,}\) мы определяем котангенс числа \(t\text{,}\), обозначаемый \(\cot( t)\text{,}\) по правилу
\[ \cot(t) = \frac{\cos(t)}{\sin(t)}\text{.
 } \nonumber \]
} \nonumber \]
В частности, обратите внимание, что, как и функция тангенса, секанс, косеканс и котангенс также полностью определяются в терминах функций синуса и косинуса. В контексте прямоугольного треугольника с углом \(\theta\text{,}\) мы знаем, как думать о \(\sin(\theta)\text{,}\) \(\cos(\theta) \text{,}\) и \(\tan(\theta)\) как отношения сторон треугольника. Теперь мы можем сделать то же самое с другими тригонометрическими функциями:
\begin{align*} \sec(\theta) &= \frac{1}{\cos(\theta)} = \frac{1}{\frac{\text{adj}}{\text{hyp} }} = \frac{\text{hyp}}{\text{adj}}\\ \csc(\theta) &= \frac{1}{\sin(\theta)} = \frac{1}{\ frac{\text{opp}}{\text{hyp}}} = \frac{\text{hyp}}{\text{opp}}\\ \cot(\theta) &= \frac{\cos(\ theta)}{\sin(\theta)} = \frac{\frac{\text{adj}}{\text{hyp}}}{\frac{\text{opp}}{\text{hyp}}} = \frac{\text{adj}}{\text{opp}} \end{align*}
Рисунок \(\PageIndex{2}\): Прямоугольный треугольник с углом \(\theta\text{.}\) С помощью этих трех дополнительных тригонометрических функций у нас теперь есть выражения, учитывающие все шесть возможных комбинаций двух сторон треугольника. прямоугольный треугольник в соотношении.
прямоугольный треугольник в соотношении.
Предварительный просмотр \(\PageIndex{1}\)
Рассмотрим прямоугольный треугольник с гипотенузой длины \(61\) и катетом длины \(11\text{.}\) Пусть \(\alpha\) быть углом, противоположным стороне длины \(11\text{.}\) Найдите точную длину другой стороны, а затем определите значение каждой из шести тригонометрических функций, вычисленных в \(\alpha\text{.}\ ) Кроме того, каковы точные и приблизительные размеры двух непрямых углов в треугольнике?
Соотношения в прямоугольных треугольниках
Поскольку функции синуса и косинуса используются для определения каждой из остальных четырех тригонометрических функций, отсюда следует, что мы можем преобразовать информацию, известную о других функциях, обратно в информацию о функциях синуса и косинуса. Например, если мы знаем, что в некотором треугольнике \(\csc(\alpha) = \frac{5}{3}\text{,}\) следует, что \(\sin(\alpha) = \frac{ 3}{5}\text{.}\) Отсюда мы можем обычным способом определить недостающую информацию в заданном треугольнике.
Также часто можно просмотреть данную информацию в контексте единичного круга. С ранее предоставленной информацией о том, что \(\csc(\alpha) = \frac{5}{3}\text{,}\), естественно рассматривать \(\alpha\) как угол в прямоугольном треугольнике, лежащий напротив катета длины \(3\) с гипотенузой, равной \(5\text{,}\), поскольку \(\csc(\alpha) = \frac{\text{hyp}}{\text{opp}} \text{.}\) Теорема Пифагора затем говорит нам, что сторона, примыкающая к \(\alpha\), имеет длину \(4\text{,}\), как видно из \(\треугольника OPQ\) в Рисунок \(\PageIndex{3}\)
Рисунок \(\PageIndex{3}\) Прямоугольный треугольник \(3\)-\(4\)-\(5\). Но мы могли бы также рассматривать \(\sin(\alpha) = \frac{3}{5}\) как \(\sin(\alpha) = \frac{\frac{3}{5}}{1} \text{,}\) и, таким образом, представьте, что прямоугольный треугольник имеет гипотенузу \(1\) и вертикальный катет \(\frac{3}{5}\text{.}\) Этот треугольник похож на первоначально рассмотренный \(3\)-\(4\)-\(5\) прямоугольный треугольник, но его можно рассматривать как лежащий внутри единичного круга.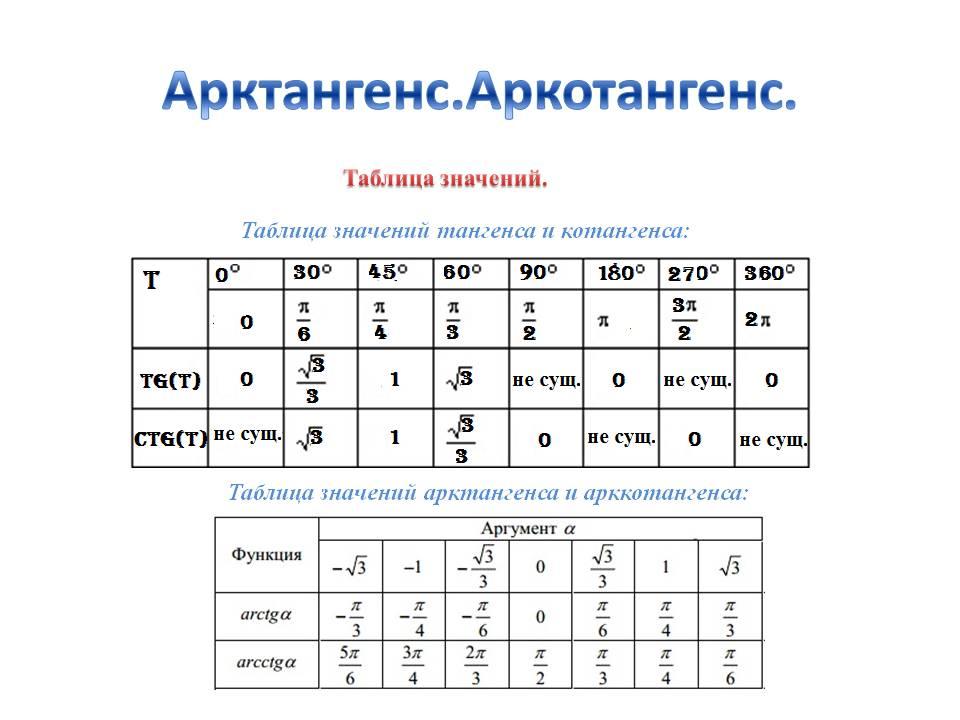 Перспектива единичного круга особенно ценна, когда используются такие соотношения, как \(\frac{\sqrt{3}}{2}\text{,}\) \(\frac{\sqrt{2}}{2}\text {,}\) и \(\frac{1}{2}\) возникают в прямоугольных треугольниках.
Перспектива единичного круга особенно ценна, когда используются такие соотношения, как \(\frac{\sqrt{3}}{2}\text{,}\) \(\frac{\sqrt{2}}{2}\text {,}\) и \(\frac{1}{2}\) возникают в прямоугольных треугольниках.
Activity \(\PageIndex{2}\)
Предположим, что \(\beta\) — это угол в стандартном положении с конечной стороной в квадранте II, и вы знаете, что \(\sec(\beta) = -2 \text{.}\) Без использования каких-либо вычислительных устройств определите точные значения пяти других тригонометрических функций, вычисленных в \(\beta\text{.}\)
Свойства секанса, косеканса и котангенса функции
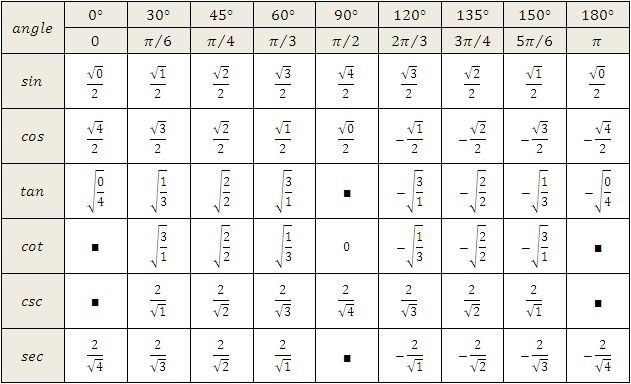
Как и функция тангенса, функции секанса, косеканса и котангенса определяются в терминах функций синуса и косинуса, поэтому мы можем определить точные значения этих функций в каждой из специальных точек на единичной окружности. Кроме того, мы можем использовать наше понимание единичного круга и свойств функций синуса и косинуса, чтобы определить ключевые свойства этих других тригонометрических функций. Начнем с исследования секущей функции.
Начнем с исследования секущей функции.
Используя тот факт, что \(\sec(t) = \frac{1}{\cos(t)}\text{,}\), заметим, что в любом месте \(\cos(t) = 0\text{, }\) значение \(\sec(t)\) не определено. Мы обозначаем такие случаи в следующей таблице как «u». Во всех остальных точках значение функции секущей является просто обратной величиной функции косинуса. Так как \(|\cos(t)| \le 1\) для всех \(t\text{,}\), то \(|\sec(t)| \ge 1\) для всех \(t\ ) (для которого определено значение секанса).
| \(т\) | \(0\) | \(\ гидроразрыва {\pi}{6}\) | \(\ гидроразрыва {\pi}{4}\) | \(\ гидроразрыва {\pi}{3}\) | \(\ гидроразрыва {\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\frac{3\pi}{4}\) | \(\frac{5\pi}{6}\) | \(\пи\) |
| \(\cos(t)\) | \(1\) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(\ гидроразрыва{1}{2}\) | \(0\) | \(-\frac{1}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) |
| \(\сек(т)\) | \(1\) | \(\frac{2}{\sqrt{3}}\) | \(\sqrt{2}\) | \(2\) | и | \(-2\) | \(-\sqrt{2}\) | \(-\frac{2}{\sqrt{3}}\) | \(-1\) |
| \(т\) | \(\frac{7\pi}{6}\) | \(\frac{5\pi}{4}\) | \(\frac{4\pi}{3}\) | \(\frac{3\pi}{2}\) | \(\frac{5\pi}{3}\) | \(\frac{7\pi}{4}\) | \(\frac{11\pi}{6}\) | \(2\пи\) |
| \(\cos(t)\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{1}{2}\) | \(0\) | \(\frac{1}{2}\) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(0\) |
| \(\сек(т)\) | \(-\frac{2}{\sqrt{3}}\) | \(-\sqrt{2}\) | \(-2\) | и | \(2\) | \(\sqrt{2}\) | \(\frac{2}{\sqrt{3}}\) | \(1\) |
Таблица 4. 5.4 и Таблица 4.5.5 помогают нам определить тренды функции секущей. Знак \(\sec(t)\) соответствует знаку \(\cos(t)\) и, таким образом, положителен в квадранте I, отрицателен в квадранте II, отрицателен в квадранте III и положителен в квадранте IV.
5.4 и Таблица 4.5.5 помогают нам определить тренды функции секущей. Знак \(\sec(t)\) соответствует знаку \(\cos(t)\) и, таким образом, положителен в квадранте I, отрицателен в квадранте II, отрицателен в квадранте III и положителен в квадранте IV.
Кроме того, мы наблюдаем, что по мере приближения \(t\)-значений в первом квадранте к \(\frac{\pi}{2}\text{,}\) \(\cos(t)\) приближается к \(0\) (при этом будучи всегда положительным). Поскольку числитель функции секущей всегда равен \(1\text{,}\), а его знаменатель приближается к \(0\) (в то время как знаменатель остается положительным), это означает, что \(\sec(t)\) неограниченно возрастает как \(t\) приближается к \(\frac{\pi}{2}\) с левой стороны. Как только \(t\) немного больше, чем \(\frac{\pi}{2}\) в квадранте II, значение \(\cos(t)\) становится отрицательным (и близким к нулю). Это заставляет значение \(\sec(t)\) уменьшаться без ограничений (отрицательно и все дальше от \(0\)) при \(t\), приближающемся к \(\frac{\pi}{2}\) с правой стороны.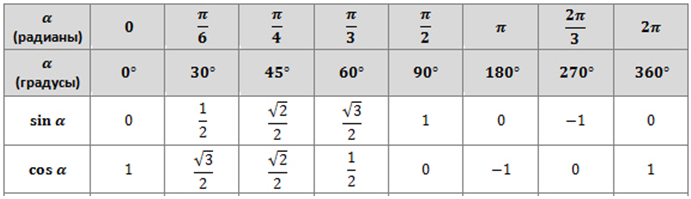 Таким образом, мы видим, что \(p(t) = \sec(t)\) имеет вертикальную асимптоту в точке \(t = \frac{\pi}{2}\text{;}\) периодичность и знаковое поведение \ (\cos(t)\) означает, что это асимптотическое поведение функции секущей будет повторяться.
Таким образом, мы видим, что \(p(t) = \sec(t)\) имеет вертикальную асимптоту в точке \(t = \frac{\pi}{2}\text{;}\) периодичность и знаковое поведение \ (\cos(t)\) означает, что это асимптотическое поведение функции секущей будет повторяться.
Нанеся данные в таблицу вместе с ожидаемыми асимптотами и интуитивно соединив точки, мы видим график функции секущей в Рисунок \(\PageIndex{6}\)
Рисунок \(\PageIndex{6}\ ) График функции секущей со специальными точками, исходящими из единичного круга, плюс функция косинуса (пунктирная, голубого цвета).Как из таблицы, так и из графика видно, что функция секущей имеет период \(P = 2\pi\text{.}\) Подведем итог нашей недавней работы следующим образом.
Свойства функции секанса.
Для функции \(p(t) = \sec(t)\text{,}\)
- ее областью определения является множество всех действительных чисел, кроме \(t = \frac{\pi}{2} \pm k\pi\), где \(k\) — любое целое число;
- его диапазоном является множество всех действительных чисел \(y\) таких, что \(|y| \ge 1\text{;}\)
- его период равен \(P = 2\pi\text{.
 }\)
}\)
Упражнение \(\PageIndex{3}\)
В этом упражнении мы разрабатываем стандартные свойства функции косеканса, \(q(t) = \csc(t)\text{.}\)
Рисунок \(\PageIndex{7}\) Оси построения графика \(q(t) = \csc(t)\text{.}\)- Заполните таблицы 4.5.8 и 4.5.9, чтобы определить точные значения функции косеканса в особых точках единичной окружности. Введите «\(u\)» для любого значения, при котором \(q(t) = \csc(t)\) не определено.
| \(т\) | \(0\) | \(\ гидроразрыва {\pi}{6}\) | \(\ гидроразрыва {\pi}{4}\) | \(\frac{4\pi}{3}\) | \(\ гидроразрыва {\pi}{2}\) | \(\frac{2\pi}{3}\) \(\frac{\sqrt{3}}{2}\) | \(\frac{3\pi}{4}\) \(\frac{\sqrt{2}}{2}\) | \(\frac{5\pi}{6}\) \(\frac{1}{2}\) | \(\пи\) \(0\) |
| \(\sin(t)\) | \(0\) | \(\ гидроразрыва{1}{2}\) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(-\frac{\sqrt{3}}{2}\) | \(1\) | ||||
| \(\csc(t)\) | \(\) | \(\) | \(\) | \(\) | \(\) | \(\) | \(\) | \(\) | \(\) |
| \(т\) | \(\frac{7\pi}{6}\) | \(\frac{5\pi}{4}\) | \(\frac{4\pi}{3}\) | \(\frac{3\pi}{2}\) | \(\frac{5\pi}{3}\) | \(\frac{7\pi}{4}\) | \(\frac{11\pi}{6}\) | \(2\пи\) |
| \(\sin(t)\) | \(-\frac{1}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{1}{2}\) | \(0\) |
| \(\csc(t)\) | \(\) | \(\) | \(\) | \(\) | \(\) | \(\) | \(\) | \(\) |
2.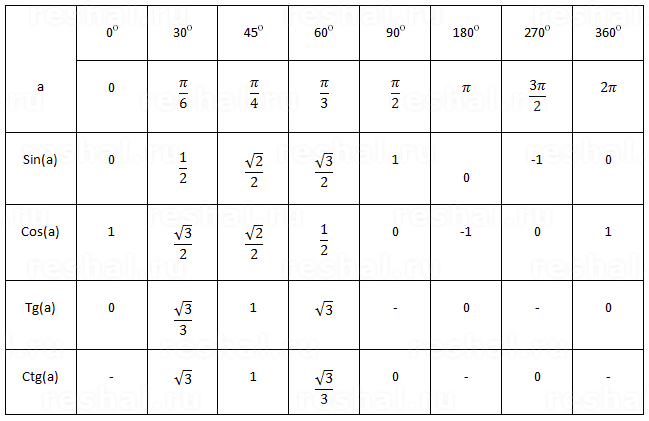 В каких квадрантах число \(q(t) = \csc(t)\) положительно? отрицательный?
В каких квадрантах число \(q(t) = \csc(t)\) положительно? отрицательный?
3. При каких \(t\)-значениях \(q(t) = \csc(t)\) имеет вертикальную асимптоту? Почему?
4. Какова область определения функции косеканса? Каков его диапазон?
5. Нарисуйте точный помеченный график \(q(t) = \csc(t)\) на осях, показанных на рис. 4.5.7, включая особые точки, исходящие из единичной окружности.
6. Каков период функции косеканса?
Упражнение \(\PageIndex{4}\)
В этом упражнении мы разрабатываем стандартные свойства функции котангенса, \(r(t) = \cot(t)\text{.}\)
- Завершено Таблица 4.5.10 и Таблица 4.5.11 для определения точных значений функции котангенса в особых точках на единичной окружности. Введите «u» для любого значения, при котором \(r(t) = \cot(t)\) не определено.
| \(т\) | \(0\) | \(\ гидроразрыва {\pi}{6}\) | \(\ гидроразрыва {\pi}{4}\) | \(\frac{\pi}{3}\) \(\frac{\sqrt{3}}{2}\) \(\frac{1}{2}\) \(\frac{ 3}{\sqrt{3}}\) | \(\frac{\pi}{2}\) \(1\) \(0\) u | \(\frac{2\pi}{3}\) \(\frac{\sqrt{3}}{2}\) \(-\frac{1}{2}\) \(- \frac{3}{\sqrt{3}}\) | \(\frac{3\pi}{4}\) \(\frac{\sqrt{2}}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-1\) | \(\frac{5\pi}{6}\) \(\frac{1}{2}\) \(-\frac{\sqrt{3}}{2}\) \(- \frac{1}{\sqrt{3}}\) | \(\pi\) \(0\) \(-1\) \(0\) |
| \(\sin(t)\) | \(0\) | \(\ гидроразрыва{1}{2}\) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | ||||||
| \(\cos(t)\) | \(1\) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | ||||||
| \(\загар(т)\) | \(0\) | \(\frac{1}{\sqrt{3}}\) | \(1\) | ||||||
| \(\кроватка(т)\) |
| \(т\) | \(\frac{7\pi}{6}\) | \(\frac{5\pi}{4}\) | \(\frac{4\pi}{3}\) | \(\frac{3\pi}{2}\) | \(\frac{5\pi}{3}\) | \(\frac{7\pi}{4}\) | \(\frac{11\pi}{6}\) | \(2\пи\) |
| \(\sin(t)\) | \(-\frac{1}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{1}{2}\) | \(0\) |
| \(\cos(t)\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{1}{2}\) | \(0\) | \(\ гидроразрыва{1}{2}\) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(1\) |
| \(\загар(т)\) | \(\frac{1}{\sqrt{3}}\) | \(1\) | \(\frac{3}{\sqrt{3}}\) | и | \(-\frac{3}{\sqrt{3}}\) | \(-1\) | \(-\frac{1}{\sqrt{3}}\) | \(0\) |
| \(\кроватка(т)\) |
- В каких квадрантах число \(r(t) = \cot(t)\) положительно? отрицательный?
- При каких \(t\)-значениях \(r(t) = \cot(t)\) имеет вертикальную асимптоту? Почему?
- Какова область определения функции котангенса? Каков его диапазон?
- Нарисуйте точный помеченный график \(r(t) = \cot(t)\) на осях, указанных на рисунке \(\PageIndex{12}\) , включая особые точки, исходящие из единичной окружности.
 .
.
6. На интервалах, где функция определена в каждой точке интервала , всегда ли \(r(t) = \cot(t)\) возрастает, всегда убывает или ни то, ни другое?
7. Каков период функции котангенса? 92 + 2x + 1\text{,} \nonumber \]
, поскольку это уравнение верно для любого значения \(x\text{,}\), а левая и правая части уравнения просто выглядят по-разному. но вполне эквивалентные выражения.
Тригонометрические тождества — это просто тождества, включающие тригонометрические функции. Хотя существует большое количество таких тождеств, которые можно изучить, мы решили сосредоточиться на тех из них, которые оказываются наиболее полезными при изучении исчисления. Наиболее важным тригонометрическим тождеством является фундаментальное тригонометрическое тождество, которое является тригонометрическим переформулированием теоремы Пифагора. 92(\theta) \text{.} \nonumber \]
Эти тождества оказываются полезными в исчислении, когда мы разрабатываем формулы для производных функций тангенса и котангенса.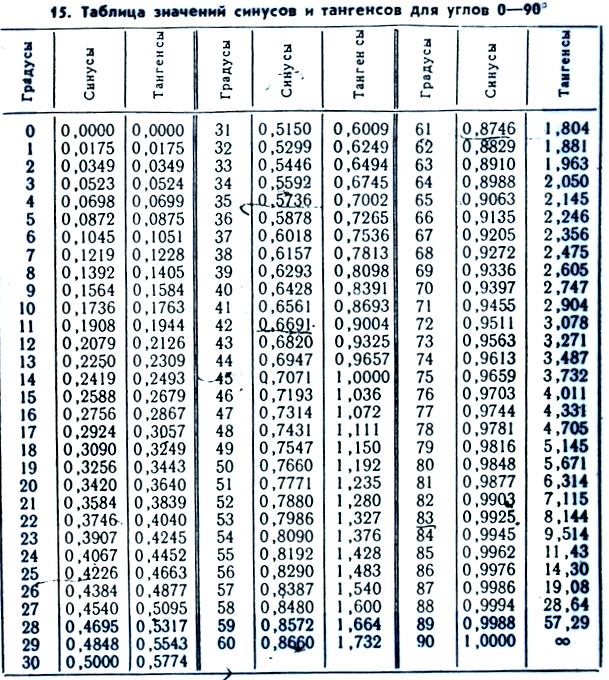
В исчислении также полезно знать пару других стандартных тождеств для сумм углов или двойных углов. Мы просто констатируем эти тождества без каких-либо оснований. Для получения дополнительной информации о них см. Раздел 10.4 в College Trigonometry, Stitz and Zeager 1 .
Дополнительную информацию о бесплатных текстах Stitz и Zeager можно найти по адресу 92(\тета)\текст{.}\)
Упражнение \(\PageIndex{5}\)
В этом упражнении мы исследуем, как идентичность суммы двух углов для функции синуса помогает нам по-другому взглянуть на среднюю скорость изменения функции синуса.
Напомним, что для любой функции \(f\) на интервале \([a,a+h]\text{,}\) ее средняя скорость изменения равна
\[AV_{[a,a+h]} = \frac{f(a+h)-f(a)}{h}\text{.} \nonumber \]
- Пусть \(f(x) = \sin(x)\text{.
 }\) Используйте определение \(AV_{[a,a+h]}\) для записи выражения для средней скорости изменения функции синуса на интервале \([a+h,a]\text{.}\)
}\) Используйте определение \(AV_{[a,a+h]}\) для записи выражения для средней скорости изменения функции синуса на интервале \([a+h,a]\text{.}\) - Применить идентичность суммы двух углов для функции синуса, \(\sin(\alpha + \beta) = \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta) \text{,}\) в выражение \(\sin(a+h)\text{.}\)
- Объясните, почему ваша работа в пунктах (а) и (б) вместе с алгеброй показывает, что
\[ AV_{[a,a+h]} = \sin(a) \cdot \frac{\cos(h)-1}{h} — \cos(a) \frac{\sin(h)} {ч}\текст{.} \номер\]
- В исчислении мы переходим от средней скорости изменения к мгновенной скорости изменения, приближая \(h\) к \(0\) в выражении для средней скорости изменения. Используя вычислительное устройство в радианном режиме, исследуйте поведение
\[ \frac{\cos(h)-1}{h} \nonumber \]
, когда \(h\) приближается к \(0\text{.}\) Что происходит? Точно так же, как \(\frac{\sin(h)}{h}\) ведет себя при малых значениях \(h\text{?}\) Что это говорит нам о \(AV_{[a,a+ h]}\) для функции синуса, когда \(h\) приближается к \(0\text{?}\)
Резюме
- Функции секанса, косеканса и котангенса определяются соответственно как обратные функции косинуса, синуса и тангенса.
 То есть,
То есть,\[ \sec(t) = \frac{1}{\cos(t)}, \csc(t) = \frac{1}{\sin(t)}, \text{ и } \cot(t ) = \frac{1}{\tan(t)}\text{.} \nonumber \]
- График функции котангенса аналогичен графику функции тангенса, за исключением того, что он убывает на каждом интервале, на котором он определен, в каждой точке интервала и имеет вертикальные асимптоты везде, где \(\tan(t) = 0 \) и равен нулю везде, где \(\tan(t)\) имеет вертикальную асимптоту.
Графики функций секанса и косеканса отличаются от графиков функций косинуса и синуса несколькими способами, в том числе тем, что их областью значений является множество всех действительных чисел \(y\), таких что \(y \ge 1\) и они имеют вертикальные асимптоты везде, где функция косинуса и синуса соответственно равна нулю.
- Тригонометрическое тождество — это уравнение, включающее тригонометрические функции, которое истинно для каждого значения переменной, для которой определены тригонометрические функции.
 2(t)\) совпадает (во всех точках, где определено \(f\)) с функцией, значение которой всегда \(1\текст{.}\)
2(t)\) совпадает (во всех точках, где определено \(f\)) с функцией, значение которой всегда \(1\текст{.}\)
Упражнения
4.
Пусть угол \(\beta\) в квадранте II удовлетворяет условию \(\cos(\beta) = -\frac{12}{13}\text{.}\) Определить значения других пяти тригонометрических функций, вычисленные в \(\beta\) точно и без оценки какой-либо тригонометрической функции на вычислительном устройстве.
Как изменятся ваши ответы, если \(\бета\) находится в квадранте III?
5.
Для каждого из следующих преобразований стандартных тригонометрических функций используйте свое понимание преобразований, чтобы определить область определения, диапазон, асимптоты и период функции с тщательным обоснованием. Затем проверьте свои результаты, используя Desmos или другая графическая утилита.
- \(\ displaystyle f (t) = 5 \ sec (t- \ frac {\ pi} {2}) + 3 \)
- \(\displaystyle g(t) = -\frac{1}{3}\csc(2t) — 4\)
- \(\ displaystyle h (t) = -7 \ tan (t + \ frac {\ pi} {4}) + 1 \)
- \(\displaystyle j(t) = \frac{1}{2}\cot(4t) — 2\)
6.
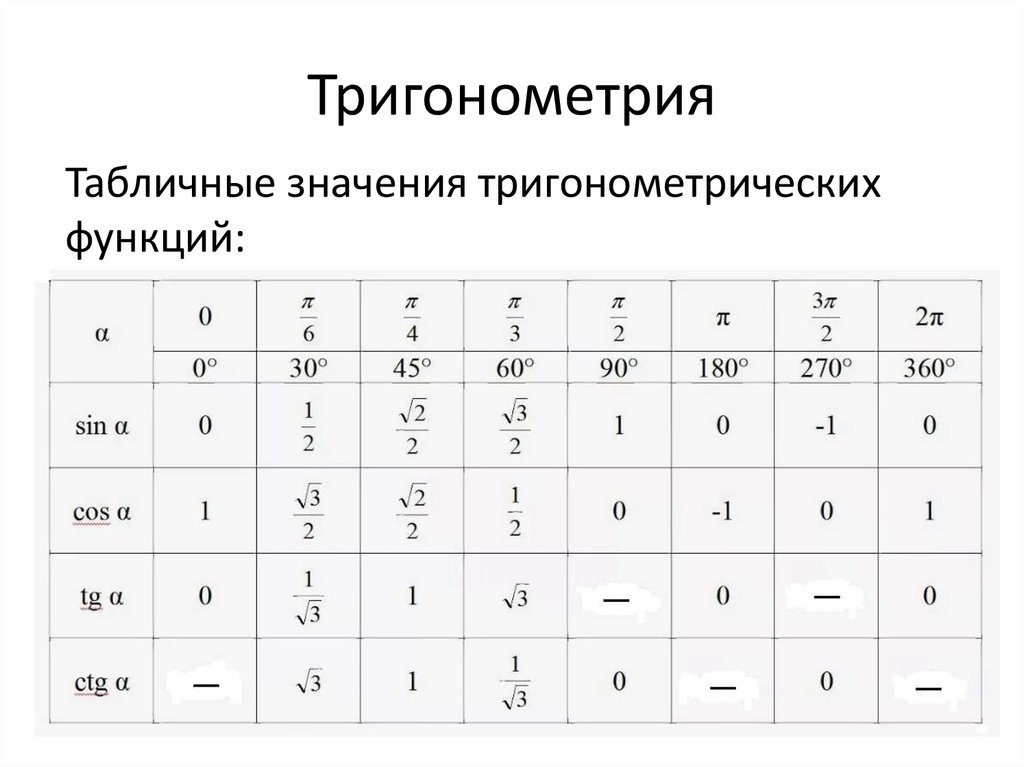
В прямоугольном треугольнике с гипотенузой 1 и вертикальным катетом \(x\text{,}\) с углом \(\theta\) напротив \(x\text{,}\) определите простейшее выражение, которое вы может для каждой из следующих величин через \(x\text{.}\)
- \(\displaystyle \sin(\theta)\)
- \(\displaystyle\сек(\тета)\)
- \(\displaystyle\csc(\тета)\)
- \(\displaystyle\загар(\тета)\)
- \(\displaystyle \cos(\arcsin(x))\)
- \(\displaystyle\cot(\arcsin(x))\)
Эта страница под названием 4.5: Другие тригонометрические функции и тождества распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Мэтью Болкинсом, Дэвидом Остином и Стивеном Шликером (ScholarWorks @Grand Valley State University) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Активное исчисление
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- источник@https://activecalculus.
 org/prelude
org/prelude
- источник@https://activecalculus.
Искусство решения задач
Тригонометрия — изучение отношений между длинами сторон и углами треугольников через тригонометрические функции . Это фундаментальный раздел математики, и его открытие проложило путь к бесчисленным известным результатам.
В соревновательной математике тригонометрия является неотъемлемой частью как геометрии, так и алгебры. Многие важные результаты в геометрии записаны в терминах тригонометрических функций, таких как закон синусов и закон косинусов; многие другие, такие как теорема Стюарта, легче всего доказать с помощью тригонометрии. В алгебре выражения, включающие тригонометрические функции, часто появляются на конкурсах. Они решаются умным использованием бесчисленных тождеств тригонометрических функций, которые могут упростить громоздкие уравнения.
Вне соревнований по математике тригонометрия является основой большей части анализа. В частности, Анализ Фурье почти полностью написан на языке тригонометрических функций.
Содержание
- 1 Определения
- 1.1 Определение прямоугольного треугольника
- 1.2 Определение единичной окружности
- 1.3 Определение серии Тейлора
- 2 приложения в геометрии
- 2.1 Закон синусов
- 2.2 Закон косинусов
- 3 Тригонометрические тождества
- 4 См. также
Определения
Тригонометрические функции могут быть определены несколькими эквивалентными способами. Определение, которое обычно преподают первым, — это определение прямоугольного треугольника из-за простоты доступа. Курс геометрии от среднего до олимпиадного обычно использует определение тригонометрии единичного круга. Помимо математики соревнований, определение тригонометрии в виде ряда Тейлора предпочтительнее, чтобы расширить тригонометрию на сложную область.
Определение прямоугольного треугольника
Определение прямоугольного треугольника в тригонометрии включает отношения между сторонами прямоугольного треугольника по отношению к заданному углу. Приведенные ниже определения будут относиться к углу с длинами сторон, указанными на диаграмме. Поскольку угол должен быть меньше, чтобы треугольник оставался прямым, эти определения работают только для острых углов.
Приведенные ниже определения будут относиться к углу с длинами сторон, указанными на диаграмме. Поскольку угол должен быть меньше, чтобы треугольник оставался прямым, эти определения работают только для острых углов.
- Синус : Синус угла , обозначаемый , определяется как отношение стороны, противоположной гипотенузе.
- Косинус : Косинус угла , обозначаемый , определяется как отношение стороны, прилегающей к гипотенузе.
- Тангенс : Тангенс угла, обозначенный как , определяется как отношение стороны, противоположной стороне, к стороне, прилегающей к .
Обычная мнемоника, чтобы помнить, что это SOH-CAH-TOA , где S INE = O PPOSITE / H Ypotenus T угол = O точка / A точка
Более необычными являются обратные тригонометрические функции, перечисленные ниже.
- Косеканс : Косеканс угла, обозначенный как , определяется как величина, обратная синусу .

- Секанс : Секанс угла , обозначенный , определяется как величина, обратная косинусу .
- Котангенс : Котангенс угла , обозначенный , определяется как величина, обратная тангенсу .
Определение прямоугольного треугольника чаще всего преподается на вводных занятиях по геометрии из-за его простоты. Однако он имеет свои ограничения. Он работает только в том случае, если он правильный, а это означает, что тригонометрические функции определяются только при остром угле.
Несмотря на то, что тригонометрия определяется с помощью прямоугольных треугольников, она так же полезна при использовании для остроугольных и тупоугольных треугольников. Закон синусов и закон косинусов, упомянутые ниже, обобщают определение прямоугольного треугольника, включая все треугольники.
Определение единичной окружности
Рассмотрим единичную окружность, окружность радиусом 1 с центром в начале координат. Начиная с , пройдите расстояние против часовой стрелки по единичному кругу, как показано на диаграмме. Координаты этой точки определены как .
Координаты этой точки определены как .
Как и другие тригонометрические функции, определяется как отношение к , а косеканс, секанс и котангенс определяются как обратные величины синуса, косинуса и тангенса соответственно.
Преимущество этого определения в том, что оно совпадает с определением прямоугольного треугольника для острых углов, но расширяет их область действия с острых углов на все углы с действительными значениями. Таким образом, это определение обычно предпочтительнее в настройках геометрии от промежуточного до олимпийского.
Определение ряда Тейлора
Ряды Тейлора для синуса и косинуса используются в качестве определения синуса и косинуса в анализе, особенно сложном анализе. Такое определение тригонометрических функций дает конкретный способ расширить определение тригонометрии с действительных чисел на полную комплексную плоскость. Ряды Тейлора для синуса и косинуса показаны ниже:
Эти определения не используются в школьных математических соревнованиях; однако они появляются на Патнэме и других университетских соревнованиях.
Применение в геометрии
Хотя тригонометрия полезна на любом уровне, на промежуточных соревнованиях особенно любят вопросы по геометрической тригонометрии. Помимо упомянутых
Закон синусов
Закон синусов гласит, что в любой , где сторона напротив , напротив , напротив , и радиус описанной окружности . Закон синусов особенно удобен в задачах, связанных с радиусом описанной окружности, поскольку он чрезвычайно широко используется в промежуточной геометрии.
Закон косинусов
Закон косинусов гласит, что в любой , где находится сторона, противоположная , противолежащая и противолежащая . Это обобщение теоремы Пифагора и используется для доказательства нескольких известных результатов, таких как формула Герона и теорема Стюарта. Тем не менее, его применение ограничено по сравнению с законом синусов, поскольку использование закона косинусов может стать тяжелым для алгебры. Полезно запомнить общие, «более приятные» значения синуса и косинуса, так как это может пригодиться в соревнованиях, особенно если вы хотите применить к задачам либо это, либо закон синусов.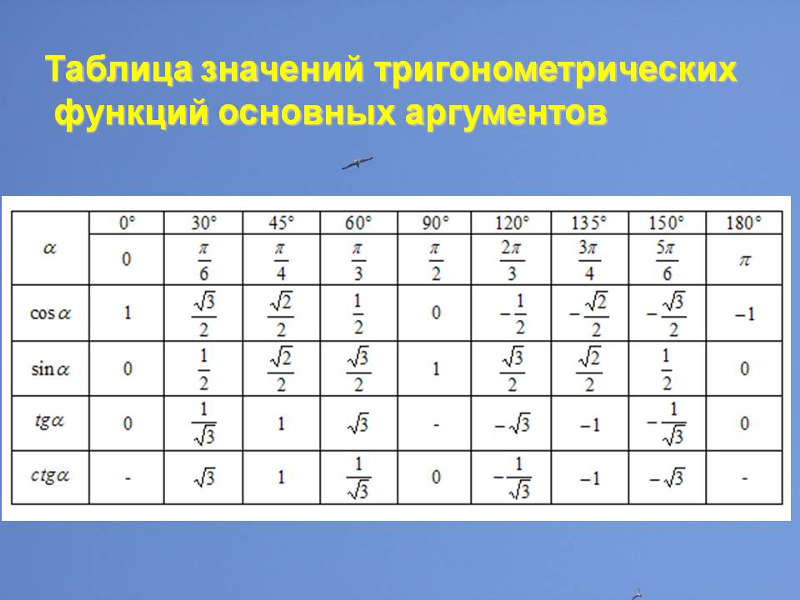

 Для учащихся старших классов общеобразовательных учебных заведений. Список таблиц — синусы-косинусы — тангенсы-котангенсы — тангенсы углов, близких к 90°, котангенсы малых углов — длина…
Для учащихся старших классов общеобразовательных учебных заведений. Список таблиц — синусы-косинусы — тангенсы-котангенсы — тангенсы углов, близких к 90°, котангенсы малых углов — длина…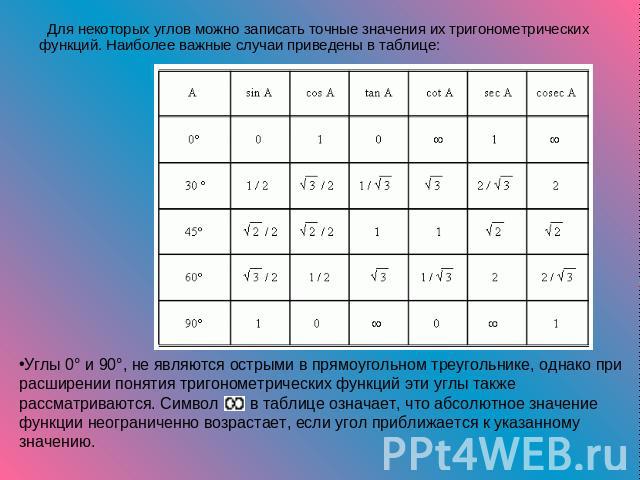
 На этой странице четырехзначные математические онлайн таблички для синусов, косинусов, тангенсов и котангенсов. Пользоваться таблицами просто. Пример : найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5.
На этой странице четырехзначные математические онлайн таблички для синусов, косинусов, тангенсов и котангенсов. Пользоваться таблицами просто. Пример : найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5.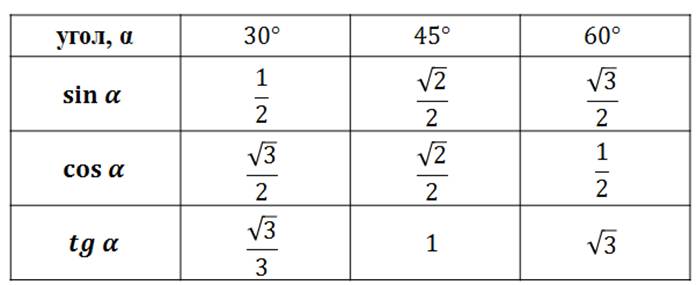 vixri.ru
vixri.ru На данной странице вы посмотреть и скачать в формате pdf по отдельности каждые таблицы Брадиса, или скачать (посмотреть) полную таблицу Брадиса. Все приведенное ниже — бесплатно.
На данной странице вы посмотреть и скачать в формате pdf по отдельности каждые таблицы Брадиса, или скачать (посмотреть) полную таблицу Брадиса. Все приведенное ниже — бесплатно.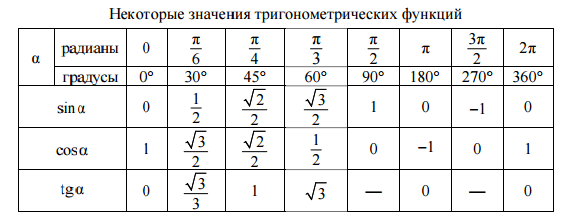 ..
..


 ..
..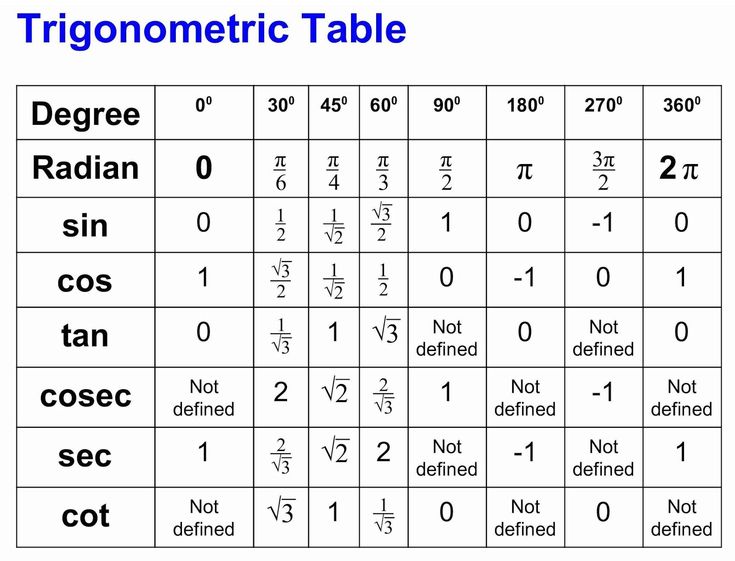 Пользоваться. таблицами просто. Пример : найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5.
Пользоваться. таблицами просто. Пример : найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5.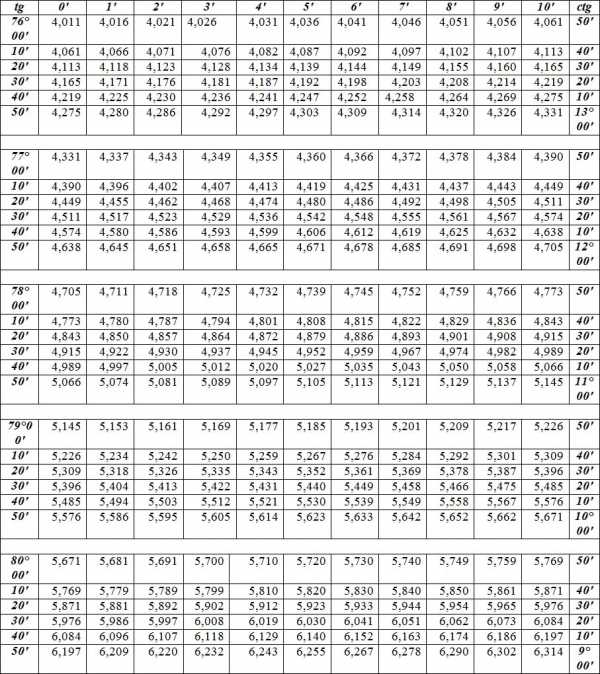 Общие правила вычисления Точные произведения двузначных чисел Значения дробей вида 1/n Квадраты Квадратные корни Кубы Длина окружности диаметра d Площадь круга диаметра d Синусы и косинусы Тангенсы и котангенсы Тангенсы углов, близких к 90°, и котангенсы малых углов Радианная мера Тригонометрические функции от аргумента в радианах Мантиссы десятичных логарифмов Значения функции 10х (десятичные антилогарифмы) Логарифмы синусов малых углов и косинусов.
Общие правила вычисления Точные произведения двузначных чисел Значения дробей вида 1/n Квадраты Квадратные корни Кубы Длина окружности диаметра d Площадь круга диаметра d Синусы и косинусы Тангенсы и котангенсы Тангенсы углов, близких к 90°, и котангенсы малых углов Радианная мера Тригонометрические функции от аргумента в радианах Мантиссы десятичных логарифмов Значения функции 10х (десятичные антилогарифмы) Логарифмы синусов малых углов и косинусов.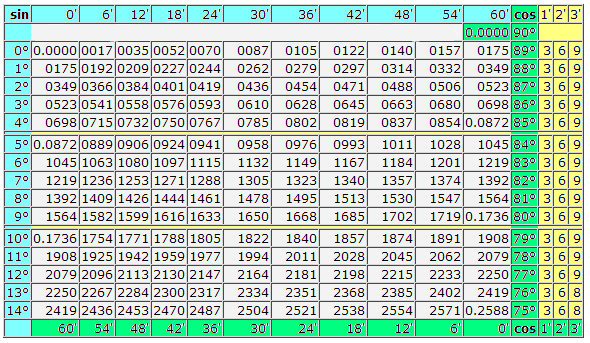 М. Брадиса. Презентация на заданную тему содержит 11 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
М. Брадиса. Презентация на заданную тему содержит 11 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки! Если данный материал был вам полезен, вы всегда можете поддержать наш сайт.
Если данный материал был вам полезен, вы всегда можете поддержать наш сайт. Эти значения рассчитаны до четвертого знака после запятой. Поэтому сборник и называется «Четырёхзначные математические таблицы». Ниже рассмотрим основные таблицы.
Эти значения рассчитаны до четвертого знака после запятой. Поэтому сборник и называется «Четырёхзначные математические таблицы». Ниже рассмотрим основные таблицы.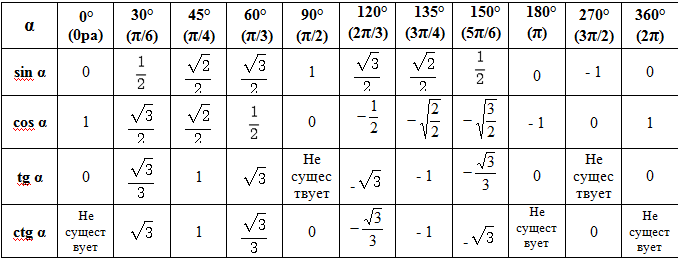 } \nonumber \]
} \nonumber \]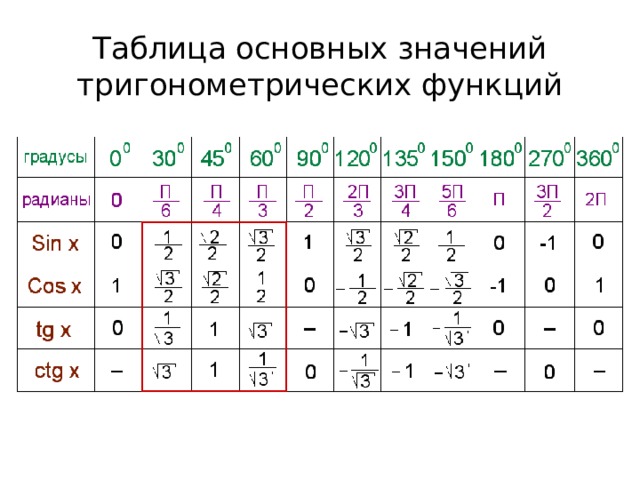 5.5. Значения функций косинуса и секанса в особых точках единичной окружности (квадранты III и IV).
5.5. Значения функций косинуса и секанса в особых точках единичной окружности (квадранты III и IV).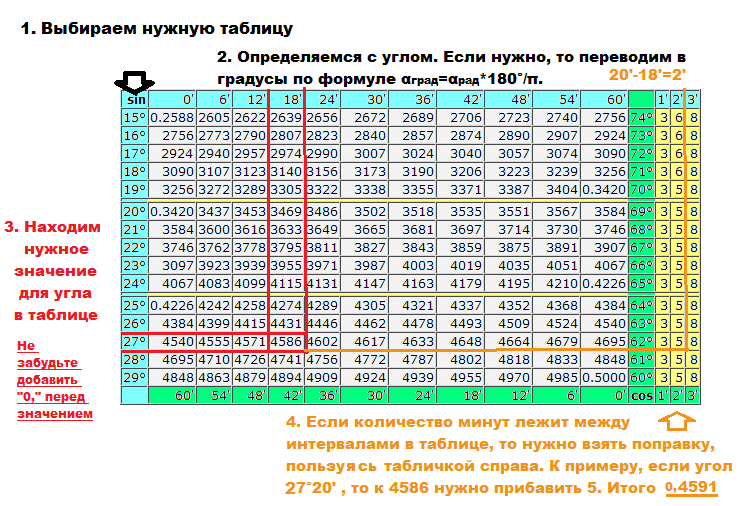 }\)
}\) 5.9. Значения функции синуса в особых точках единичной окружности (квадранты III и IV).
5.9. Значения функции синуса в особых точках единичной окружности (квадранты III и IV). 5.11. Значения функций синуса, косинуса и тангенса в особых точках единичной окружности.
5.11. Значения функций синуса, косинуса и тангенса в особых точках единичной окружности. .
. }\) Используйте определение \(AV_{[a,a+h]}\) для записи выражения для средней скорости изменения функции синуса на интервале \([a+h,a]\text{.}\)
}\) Используйте определение \(AV_{[a,a+h]}\) для записи выражения для средней скорости изменения функции синуса на интервале \([a+h,a]\text{.}\)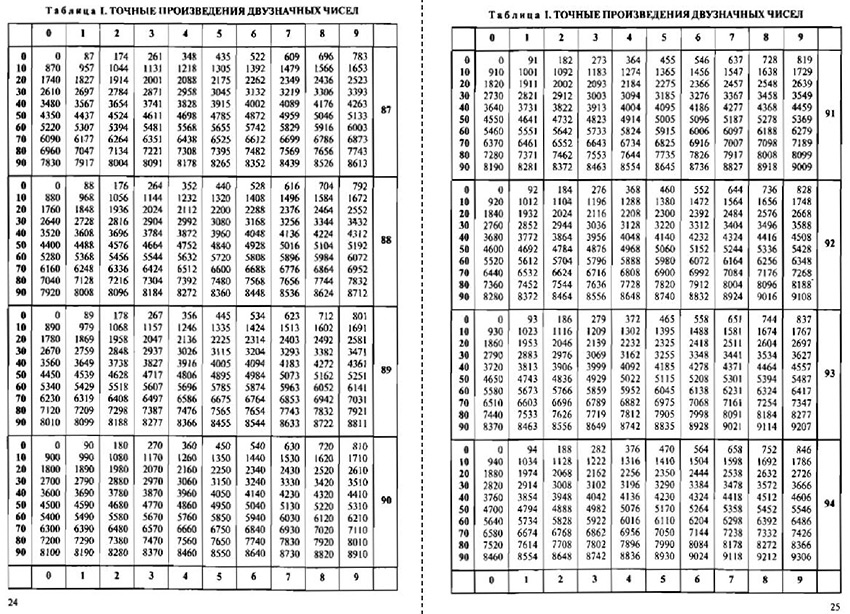 То есть,
То есть,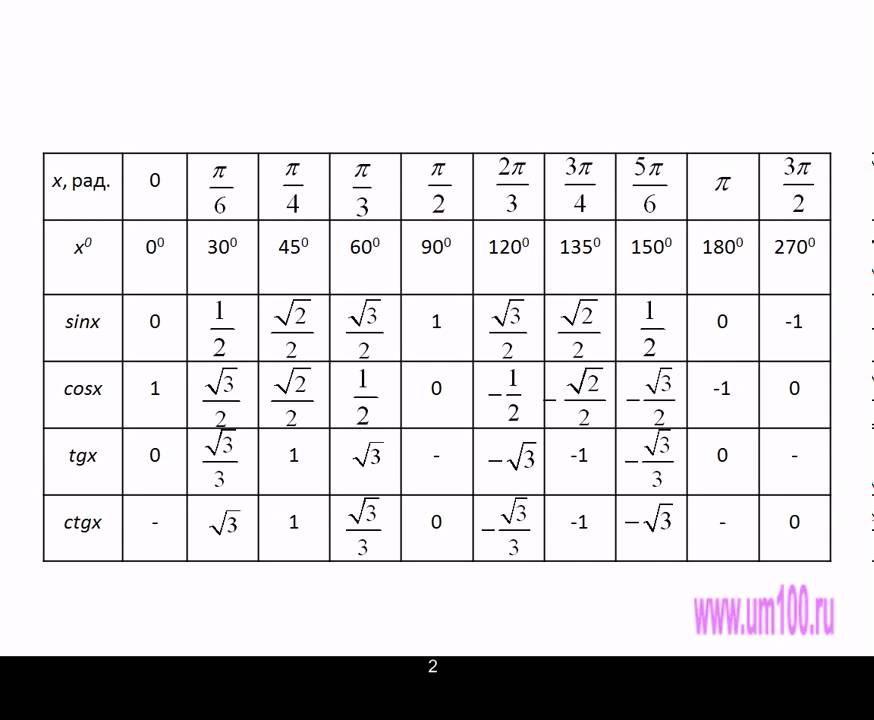 2(t)\) совпадает (во всех точках, где определено \(f\)) с функцией, значение которой всегда \(1\текст{.}\)
2(t)\) совпадает (во всех точках, где определено \(f\)) с функцией, значение которой всегда \(1\текст{.}\)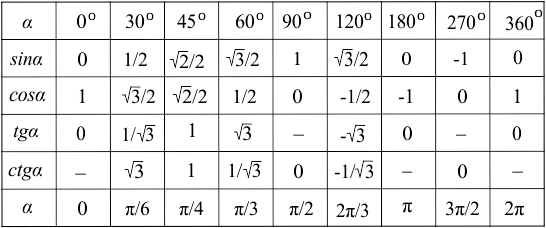 org/prelude
org/prelude