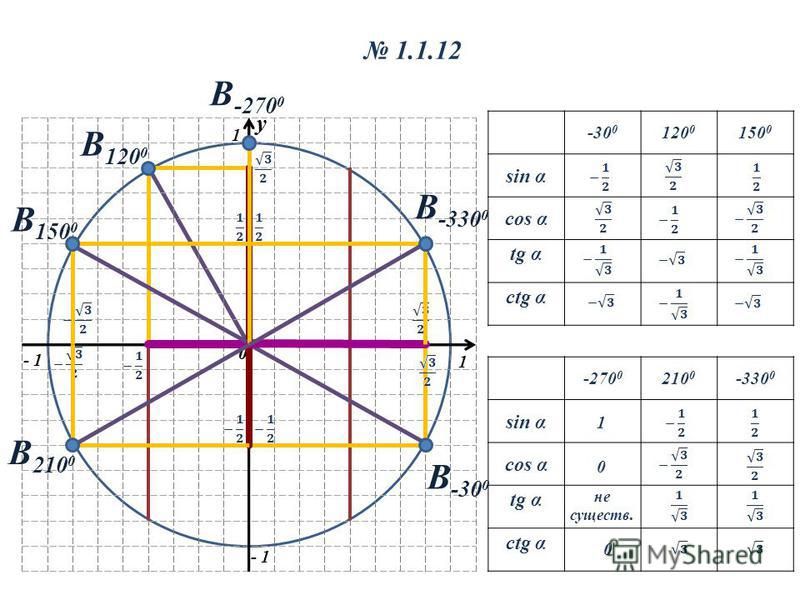
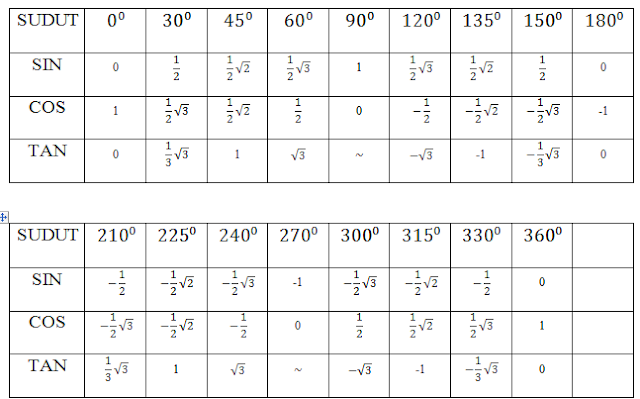
Sin Cos Tan Таблица: значения, формулы, примеры
Тригонометрические функции sin, cos и tan являются основными функциями, которые мы учитываем при решении любых тригонометрических вопросов. В этой статье обсуждается таблица sin cos tan и способы получения из нее значений.
Значение тригонометрии используется для измерения значения углов и сторон прямоугольного треугольника. Основное внимание уделяется решению значений sin, tan и cos тригонометрических задач.
Формула sin cos и tan определяется двумя или тремя сторонами прямоугольного треугольника.
Содержание
- Таблица Sin Cos Tan
- Как определить значения Sin Cos Tan?
- Решенные примеры с использованием табличной формулы Sin Cos Tan
- шагов для создания тригонометрической таблицы
Таблица Sin Cos Tan
Тригонометрические функции sin, cos и tan являются основными функциями, которые мы рассматриваем при решении любых тригонометрических вопросов.
«Таблица sin cos tan» состоит из значений sin, cos и tan стандартных углов 0°, 30°, 45°, 60° и 9°.0°, а иногда и другие углы, такие как 180°, 270° и 360°.
Ниже представлена таблица, которую можно использовать для определения углов.
Таблица sin cos и tan помогает найти значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 90°. Он состоит из тригонометрических соотношений – синуса, косинуса, тангенса, косеканса, секанса, котангенса.
sin θ = Противоположный/Гипотенуза
cos θ = Прилегающий/Гипотенуза
tan θ = Противоположный/Прилегающий
Как найти значения Sin Cos Tan?
Следующие шаги помогут запомнить тригонометрические значения.
- Сначала разделите числа 0,1,2,3 и 4 на 4, а затем извлеките положительные корни из всех этих чисел.
- Мы получаем значения коэффициентов синусов, т. е. 0, ½, 1/√2, √3/2 и 1 для углов 0°, 30°, 45°, 60° и 90°
- Запишите значения синуса в градусах в обратном порядке, чтобы получить значения косинуса для тех же углов.
- Как мы знаем, тангенс — это отношение sin и cos, например, tan θ = sin θ/cos θ. Таким образом, мы можем получить значения коэффициента тангенса для конкретных углов.
Примеры решения с использованием формулы таблицы Sin Cos Tan
Примеры решения с использованием формулы таблицы Sin Cos Tan помогут понять концепцию формул, приведенных в приведенной выше таблице. Проверьте решенные вопросы, данные ниже создаваться с тригонометрическими функциями в первом столбце, такими как sin, cos, tan, cosec, sec, cot.
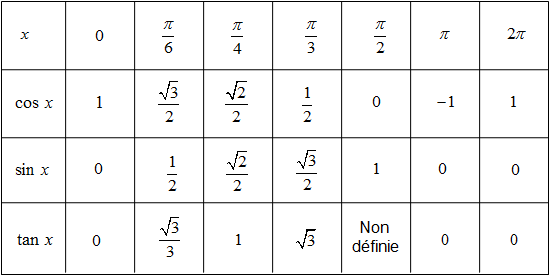
Определите значение Sec: Значение sec может быть получено всеми распространенными значениями cos. Значение sec на 0° противоположно cos на 0°
Таблица тригонометрических отношений, формулы, определения, мнемоника, задачи
Шесть тригонометрических отношений для прямоугольного треугольника: синус (sin), косеканс (Cos), тангенс (Tan), косеканс (Cos), секанс (Sec), Котангенс(Cot) соответственно.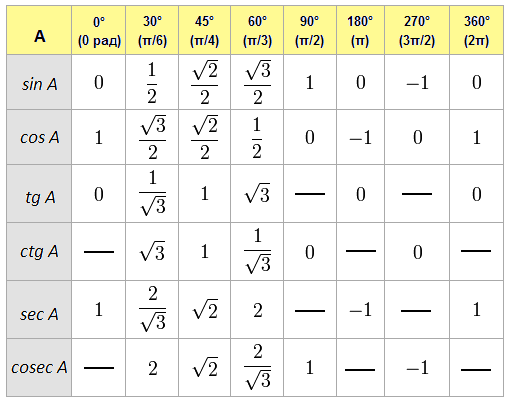
Мы изучим формулы sin, cos, tan для этих тригонометрических соотношений и простые способы их запоминания.
Определение тригонометрии : Раздел математики, который занимается измерением сторон и углов треугольника и задачами, основанными на них.
Отношение сторон прямоугольного треугольника к его острым углам.
Возьмем прямоугольный треугольник APM, как показано на рисунке. Здесь ∠PAM (или, короче, угол A) — острый угол. Обратите внимание на положение стороны PM относительно угла A. Она обращена к ∠ A. Назовем ее стороной, противоположной углу A. AP — гипотенуза прямоугольного треугольника, а сторона AM — часть ∠ A. Итак, мы назовем его стороной, прилегающей к углу A.
∠ A = θ, AP = r (гипотенуза) и PM = y (перпендикуляр), AM = x (основание), ∠ PMA = 90 o
Угол : Фигура, полученная путем вращения данного луча вдоль его конечной точки.
Измерение угла : Величина поворота луча от начального положения до конечного положения.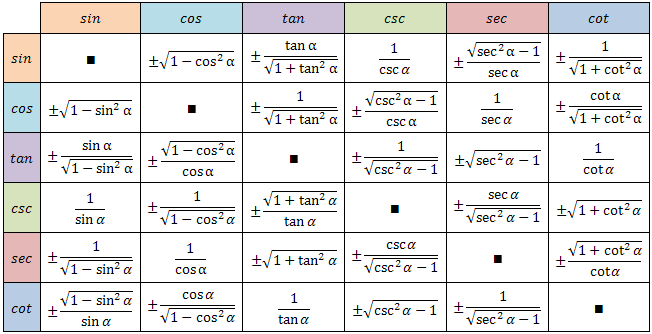
Гипотенуза Определение : самая длинная сторона прямоугольного треугольника, лежащая напротив прямого угла.
Перпендикулярно: под углом 90° к заданной линии, плоскости, поверхности или земле.
Основание: Сторона, на которой стоит прямоугольный треугольник, известна как его основание
Тригонометрические отношения угла θ в треугольнике APM определяются следующим образом.
Противоположный над гипотенузой – Sin, Прилегающий к гипотенузе – Cos , Противоположный над прилежащим – Tan, Гипотенуза над противоположным – Cosec, Гипотенуза над прилежащим – Sec и Прилегающий к противоположному – Котангенс,
Соотношения, определенные выше, обозначаются как sin θ, cos θ, tan θ, cosec θ, sec θ и кроватка θ соответственно. Обратите внимание, что коэффициенты cosec θ, sec θ и cot θ соответственно обратны отношениям sin θ, cos θ и tan θ.
Противоположность SIN : COSECANT
противоположность COS: SECANT
противоположность TAN : COTANGENT
противоположность Cosecant: SIN
противоположность Котангенту : TAN
Противоположность SECANT : COSECANT
TRIG MNEMONICS — S OME P EOPE H AVE, C H B HASS H AIR111111111111111111111111111111111111111111111111111111111111111111111111111111111111. канат B мчится.
Здесь, S ome P eople H ave для
- S in θ= P erpendicular/ H
C urly B отсутствие H воздух для
- C os θ= B ase/ ase/ H ypotenuse.
T сквозной P трос B рывок для
- T и θ= P эрпендикулярный/2 B
Тригонометрические отношения некоторых конкретных углов
Мы уже знаем о равнобедренном прямоугольном треугольнике и прямоугольном треугольнике с углами 30º, 60º и 90º.
Можем ли мы найти sin 30º или tan 60º или cos 45º и т.д. с помощью этих треугольников?
Существует ли sin 0º или cos 0º?
Триггерные отношения дополнительных углов
Мы знаем, что дополнительные углы — это пара углов, сумма которых равна 90°. Подобно 40° и 50°; 60° и 30°; 20° и 70°; 15° и 75°; и т. д.
- sin (90° – θ) = cos θ
- раскладушка (90° – θ) = tanθ
- cos (90° – θ) = sin θ
- сек (90° – θ) = cosec θ
- желтовато-коричневый (90° – θ) = раскладушка θ
- cosec (90° – θ) = θ сек.
Происхождение тригонометрических соотношений
Первое использование понятия «синус» в том виде, в котором мы его используем сегодня, было в работе Арьябхатьям Арьябхаты в 500 г. н.э. Арьябхата использовал слово ардха-джья для полу- аккорд, который со временем был сокращен до джья или джива. Когда Арьябхатиям был переведен на арабский язык, слово джива было сохранено как есть. Слово джива было переведено как синус, что означает кривая, когда арабская версия была переведена на латынь. Вскоре слово синус, также использовавшееся как синус,
стало обычным явлением в математических текстах по всей Европе. Английский профессор астрономии Эдмунд Гюнтер (1581–1626) впервые употребил сокращенное обозначение «грех».
Термины «косинус» и «тангенс» возникли гораздо позже. Функция косинуса возникла из-за необходимости вычислить синус дополнительного угла. Арьябхатта назвал это котиджйа. Название cosinus произошло от Эдмунда Гюнтера. В 1674 году английский математик сэр Джонас Мур впервые использовал сокращенную запись «cos».
Sin Cos Tan — это основные функции, используемые в тригонометрии, и они основаны на прямоугольном треугольнике.
Решенные примеры по отношениям триггеров:
Пример-1 . Если тангенс A = 3/4, найдите другое тригонометрическое отношение угла A.
Решение:
Учитывая тангенс A = 3/4
Следовательно, тангенс A = Противоположная сторона/Смежная сторона = 3/4
Следовательно, противоположная сторона : смежная сторона = 3:4
Для угла A, противоположная сторона = BC = 3 k
Прилежащая сторона = AB = 4 k (где k — любое положительное число)
Теперь у нас есть в треугольнике ABC (по теореме Пифагора)
Пример 2: Если ∠ A и ∠ P — острые углы такие, что sin A = sin P, затем докажите, что ∠ A = ∠ P
Решение: Дан sin A = sin P
Пример 3: В ∆ABC прямой угол находится в точке B, AB = 5 см и ∠ACB = 30 o . Определить длины сторон ВС и АС.