Тема 3
Решение большинства неравенств сводится к решению соответствующих уравнений. Рассмотрим решение линейных и квадратных неравенств, а также специальный метод решения неравенств — метод интервалов.
Всякое значение неизвестного, при котором данное неравенство обращается в верное числовое неравенство, называется решением неравенства.
Решить неравенство — значит найти все его решения или доказать, что их нет.
Неравенства вида , где х — неизвестное, а и b — некоторые действительные числа называются неравенствами первой степени или линейными неравенствами.
Неравенства вида , где называются неравенствами второй степени с одной неизвестной или квадратными неравенствами.
Примерные задания
Линейные неравенства
Задание 1
Укажите наименьшее целое решение неравенства —х+0,5(х+4)<4.
Решение: Сначала раскроем скобки. —х+0,5х+2<4. При решении линейных неравенств обычно переносят неизвестные слагаемые в левую часть неравенства, а известные – в правую, и приводят подобные слагаемые. -0,5х<2. Обе части неравенства делим на отрицательное число. Не забываем, что знак неравенства меняется на противоположный. х>-4.
Наименьшим целым решением является число (-3), а не (-4).
Ответ: -3.
Задание 2
Найдите число целых решений неравенства
Решение: Исходное неравенство называется двойным неравенством. Его можно решать разными способами.
1-й способ.
2-й способ (с помощью системы).
Исходное неравенство равносильно системе неравенств
Решим первое неравенство.
.
Решим второе неравенство.
x<8.
Отметим решения и первого и второго неравенства на координатной прямой.
Решением системы неравенств будет промежуток .
Количество целых чисел, входящих в промежуток, равно 16.
Ответ: 16.
Квадратные неравенства
Решение квадратных неравенств
состоит из 5 этапов:
1. Вводим соответствующую функцию .
Вводим соответствующую функцию .
2.Определяем направление ветвей параболы.
3.Находим нули функции, т. е. решаем уравнение .
4.Если уравнение имеет корни, то отмечаем корни на координатной прямой и схематически рисуем параболу в соответствии с направлением ветвей.
5.Находим решение неравенства с учетом смысла знака неравенства.
Задание 3
Решите неравенство .
Решение:
1. Пусть .
2. Так как а=-1, то ветви параболы направлены вниз.
3. Решим уравнение .
Его корни: х=1; х= -3.
4. Отметим числа 1 и (-3) на координатной прямой и построим эскиз графика функции.
5. Так как знак неравенства , то решением его будет отрезок .
Ответ:
Решить неравенство .
Решение:
1. Имеем .
2. Ветви параболы направлены вниз.
3. Уравнение решений не имеет (Д<0). Парабола не пересекает ось абсцисс.
4.
Так как знак неравенства (<), то решением его являются все числа.
Ответ: .
Область определения выражения
Значения переменной, при которых выражение имеет смысл, называют допустимыми значениями переменной.
Множество всех допустимых значений переменной называют областью определения выражения.
Задание 4
При каких значениях х имеет смысл выражение .
Решение: Так как выражение имеет смысл при и выражение имеет смысл при , то составим и решим систему
Отметим решение на координатной прямой.
Областью определения исходного выражения будет объединение промежутков
Ответ:
Метод интервалов
Задание 5
Решим неравенство
Решение: Так как числитель дробного выражения отрицателен, то решение исходного неравенства сводится к решению неравенства . Решим неравенство методом интервалов. Рассмотрим функцию y=(-x+5)(x2-4). Найдем нули функции, т.е. решим уравнение  Отметим нули функции на координатной прямой.
Отметим нули функции на координатной прямой.
В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль функции, т.е. через точки -2; 2; 5, ее знак меняется.
Определим знак функции в каком-нибудь из четырех промежутков. Например, рассмотрим f(0)=(-0+5)(02-4)=5(-4)=-20<0, значит в промежутке (-2; 2) значения функции отрицательны.
Далее происходит чередование знаков.
Итак, мы решаем методом интервалов неравенство . Решением неравенства будет объединение промежутков .
Ответ:
Задание 6
Решить неравенство
Решение: Рассмотрим функцию y=x4-9x2. Ее нули 0; -3; 3. Отметим эти числа на координатной прямой и определим знак функции, например, на промежутке (0; 3).
Ее нули 0; -3; 3. Отметим эти числа на координатной прямой и определим знак функции, например, на промежутке (0; 3).
Найдем значение функции в точке 1,
f(1)=1-9<0.
так как , то число 0 является, говорят, нулем двойной кратности. При переходе через него знак функции не меняется.
У исходной функции только 0 является нулем двойной кратности, поэтому и при переходе через точку
(-3) знак функции меняется.
Решением исходного неравенства является не только объединение промежутков , но и точка 0.
Ответ:
Скачать задания контрольной работы № 3
Желаю успехов!
Нина Васильевна
Примечание: При выполнении заданий контрольной работы вы можете воспользоваться учебниками:
-
Алгебра.
 Учебник для 9 класса общеобразовательных учреждений / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Телековского.
Учебник для 9 класса общеобразовательных учреждений / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Телековского. -
Алгебра. Учебник для 9 класса общеобразовательных учреждений / Ш.А. Алимов, Ю.М. Колягин и др.
-
Алгебра 9 класс. Учебник для общеобразовательных учреждений / А.Г. Мордкович.
Посмотреть ответы…
Бесплатные видеоуроки от проекта «Инфоурок»
Большая коллекция из 3243 видеоурока по 20 предметам и различным темам
УченикВероника
УчительЕвгения Вадимовна
Отличный учитель, который всегда вовлекает ученика в процесс, и сам проявляет заинтересованность в успехах ученика. Интересно слушать и работать!
УченикВероника
УчительДарья Максимовна
Дарья Максимовна замечательный, отзывчивый педагог!Обьясняет простым и доступным язык любую сложную тему- это большой плюс!! Спасибо большое моему репетитору, так как я уверена, что ОГЭ сдам на отлично !!
УченикДарья
УчительЕлизавета Владимировна
Очень качественные и продуктивные занятия.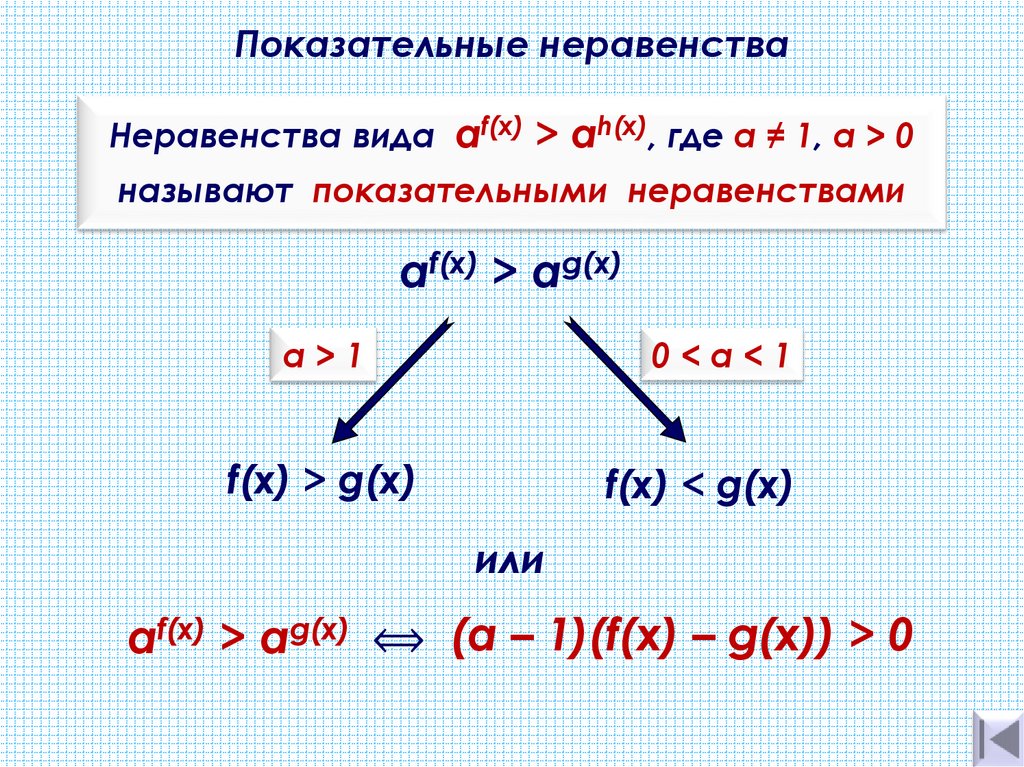 Занимаюсь не долго, но уже чувствуется прогресс. Очень милый и добрый преподаватель. Всё понятно объясняет. Мне, очень нравится заниматься математикой с Елизаветой Владимировной.
Занимаюсь не долго, но уже чувствуется прогресс. Очень милый и добрый преподаватель. Всё понятно объясняет. Мне, очень нравится заниматься математикой с Елизаветой Владимировной.
УченикКарина
УчительАндрей Юрьевич
Мне понравилось заниматься с Андреем Юрьевичем. Впервые встречаю репетитора, который прежде учить языку, рассказывает про его истоки – географию, культуру, историю. Мне очень откликается такой подход. Видно, что преподаватель с большим опытом. Я очень довольна первым занятием! Буду продолжать заниматься с данным преподавателем.
УченикМия
УчительТатьяна Александровна
Ответственная, настойчивая, харизматичная, пунктуальная, высокий уровень проф подготовки, терпеливая. Наша девочка довольна, проявляет явный интерес к урокам и продвинулась в изучаемой теме. Большое спасибо вам и преподавателю Татьяне Александровне.
УченикАлёна
УчительЕлена Петровна
Прекрасный преподаватель. После восьми занятий английский стал намного лучше, многое узнала. Все понятно в объяснении, уроки на позитиве. Благодарна за работу. Искренне рекомендую.
Все понятно в объяснении, уроки на позитиве. Благодарна за работу. Искренне рекомендую.
УченикКатя
УчительЕлена Александровна
Все понравилось приятно работать с учителем. Как по мне лучше чем Елена Александровна я еще не видела учителя по русскому языку.
УченикДиана
УчительДиана Михайловна
У Дианы Михайловны занимаются английским языком две дочери: Есения и Ксения. Девочкам очень нравится преподаватель и наполнение уроков, материал преподносится в очень интересной форме, а все объяснения понятны и доступны. Девочки уже показали успехи в изучении английского языка в школе.
УченикДмитрий
УчительСветлана Анатольевна
Дмитрий прошел со Светланой Анатольевной 4 занятия и уже виден прогресс! Мальчик по натуре немного застенчивый, поначалу был немногословен, но уже хорошо разговаривает на уроках, что говорит о профессионализме педагога.
УченикАрина
УчительИрина Сергеевна
Спасибо огромное. Очень рады, что нашли этот ресурс для занятий. Ирина Сергеевна объясняет все быстро, понятно и динамично. Всего за несколько занятий наверстали упущенное по химии и прошли дальше. Обязательно будем обращаться в дальнейшем.
Ирина Сергеевна объясняет все быстро, понятно и динамично. Всего за несколько занятий наверстали упущенное по химии и прошли дальше. Обязательно будем обращаться в дальнейшем.
УченикЕлизавета
УчительРимма Николаевна
У Елизаветы есть успехи, занимается с удовольствием и заинтересованностью. Римма Николаевна очень интересно преподносит материал. Очень нравится учитель, занимаемся с удовольствием.
УченикАртём
УчительНина Ивановна
Нам понравилась Нина Ивановна, хороший человек и прекрасный педагог. Очень ответственная, трудолюбивая и толковая. Сразу нашла подход к ученику. Доходчиво объяснит любую тему. Преподаватель, в отличии от многих репетиторов не просто отбывает время, а действительно помогает.
УченикЭдуард
УчительЖанна Сергеевна
Замечательный педагог, нашла подход с первых занятий. Все очень доходчиво и понятно объясняет. Ребенку очень нравится, просит дополнительные часы для занятий.
УченикЛюдмила
УчительРита Ивановна
Добрый день! Рита Ивановна очень профессионально оценила все пробелы моего сына и нам бы хотелось продолжить с ней обучение! Занятия очень хорошие, учитель понятно все объясняет, всем рекомендую.
УченикСветлана
УчительОльга Олеговна
Спасибо Ольге Олеговне за проведённый урок в праздничный день. Здоровья, процветания, побольше радостных событий в жизни, благополучия, успехов и удачи в таком не лёгком и таком нужном труде!!! Спасибо за урок, всё понравилось!
УченикИрина
УчительТатьяна Николаевна
Очень грамотный педагог, хорошо подходит к вопросам с которыми обращаемся, подход к ребенку очень понравился, буквально на 5-8 урок у ребенка был уже прогресс и теперь любит математику. На урок математики приходим с удовольствием, подтянули свои недочеты, решаем быстро примеры, а главное сами. Спасибо за знания!
УченикПолина
УчительСветлана Михайловна
Светлана Михайловна очень хороший учитель, за урок мы разбираем много вопросов и обсуждаем правила русского языка в каждом конкретном примере. Занимаюсь с удовольствием!
УченикМария
УчительДарья Александровна
Замечательный, приятный и внимательный преподаватель. Ребенок сначала засмущался от непривычного формата урока, но Дарья Александровна, в итоге, смогла завоевать внимание и доверие дочери. Обязательно будем продолжать обучение! Спасибо!
Обязательно будем продолжать обучение! Спасибо!
УченикАнтон
УчительСветлана Васильевна
Репетитор быстро оценила проблемы, порекомендовала способы восполнения пробелов. Продолжим заниматься дальше, так как Светлана Васильевна доступно объясняет материал, и все сразу становится понятным. Классный репетитор, советую!
УченикСофия
УчительГалина Михайловна
Добрый день! Галина Михайловна — замечательный педагог! Мне все было очень понятно и вообще было приятно общаться! Была непонятна тема : ,, Не /ни с глаголами ,,. После того, как Галина Михайловна объяснила, все трудности были сняты. Огромное спасибо !!! 🙏
УченикЛеонид
УчительЕлена Александровна
На уроке педагог работала по индивидуальной программе, выявила пробелы в знаниях и все доходчиво разъяснила. Сложные темы, объяснили легко и понятно, сыну все очень понравилось!
УченикГалина
УчительТамара Иосифовна
Замечательный педагог и очень доброжелательный человек!!! Тамара Иосифовна очень доходчиво объяснила непонятные для меня моменты, причем из разных тем, за один урок!!! Урок проходил в спокойной и дружественной обстановке. Спасибо большое!!! Очень понравилось!!!
Спасибо большое!!! Очень понравилось!!!
УченикМария
УчительВладимир Григорьевич
Спасибо большое, Вы лучший преподаватель по информатике. Как хорошо, что есть такая замечательная платформа. Спасибо всем, кто ее организовал и Вам лично. Всем друзьям и знакомым буду рекомендавать! онлайн-уроки.
УченикОльга
УчительИрина Ивановна
Очень понравился урок! Ирина Ивановна с первых минут расположил к себе ребёнка так, что даже мой непоседливый и не очень настроенный на учебу пятиклассник увлекся так, что не заметил, как пролетели 45мин. Спасибо! С удовольствием продолжим занятия!
УченикФёдор
УчительНаталия Анатольевна
Как родитель могу сказать, что самое важное — это расположить к себе ребенка. Уже после первого занятия с Наталией Анатольевной я увидела желание заниматься в глазах своей дочери. Занятие проходило очень комфортно. Понравилось, как построена программа проверочного урока.
УченикПолина
УчительМарина Михайловна
Мне очень понравилось вводное занятие, спасибо большое. За пол часа Марина Михайловна с помощью разговора поняла все мои слабые места и помогла многие из них подправить и понять. Я хочу заниматься с ней и далее.
За пол часа Марина Михайловна с помощью разговора поняла все мои слабые места и помогла многие из них подправить и понять. Я хочу заниматься с ней и далее.
УченикАйсултан
УчительГалина Дмитриевна
Здравствуйте! У нас был пробный урок с Галиной Дмитриевной по математике. Занимались именно логическими задачами. Учитель имеет очень хороший подход к детям и у нее есть своя отработанная хорошая методика. Хорошо объясняет, приятная. Спасибо!
УченикВиктор
УчительЮлия Анатольевна
Спасибо большое учитель объясняет очень хорошо там где ты что либо не поймёшь педагог тебе всё объяснит как раз педагог сказала повторить всё то что мне говорил предыдущий репетитор СПАСИБО БОЛЬШОЕ !!!
УченикМаксим
УчительАлёна Юрьевна
Благодарим за интересное и познавательное занятие! Преподаватель четко и внимательно ведет занятие, обращает внимание на моменты, которые необходимо доработать. Профессионально! Приятно общаться.
УченикАлександр
УчительАнастасия Сергеевна
Добрый день! Мы безумно рады, что нам посчастливилось найти такого замечательного и удивительного педагога, как Анастасия Сергеевна! Она очень интересно проводит урок, ребёнок безумно рад. Сразу чувствуется, что человек талантливый. С нетерпением ждём новый урок.
Сразу чувствуется, что человек талантливый. С нетерпением ждём новый урок.
УченикЕкатерина
УчительСергей Васильевич
Спасибо за урок! Занятие очень понравилось, Сергей Васильевич все понятно и интересно обьясняет, во время урока была доброжелательная атмосфера. Также учитель посоветовал некоторые книги и способы подготовки к экзамену. Спасибо!!!
УченикКарина
УчительГулез Гаджимурадовна
Нравятся все педагоги с которыми мы занмаемся, все обладают высоким уровнем профессионализма,используют интересные и современные методы и технологии обучения. Имеет хороший уровень научно-методической подготовки. Ребенок занимается с большим интересом. Будем заниматься с Вами до окончания школы, сейчас мы в 4 классе)
УченикФеона
УчительНаталия Михайловна
За 45 минут узнала и поняла больше, чем за полгода в школе. Учитель объясняет очень понятно, доходчиво, выше школьного уровня. Однозначно этот урок не последний. С Уважением, Феона.
УченикЕкатерина
УчительНаталья Васильевна
Спасибо, Наталья Васильевна! Профессионально, четко, по делу. Педагог очень терпеливая, спокойная, уверенная. Занятие очень понравилось и ребенку и мне, маме.
Педагог очень терпеливая, спокойная, уверенная. Занятие очень понравилось и ребенку и мне, маме.
УченикМаксим
УчительАлександр Александрович
Спасибо большое Александру Александровичу. Очень быстро нашел подход к ребёнку , а так же увлек математикой! Ребёнку было комфортно общаться. Надеемся встретиться на следующих занятиях.
УченикМарина
УчительНиколай Васильевич
Николай Васильевич помог за короткий срок восполнить пробелы в знаниях, за что очень благодарны! Уроки очень интересные! Будем обращаться еще к нему.
УченикМарина
УчительАлександр Сергеевич
Занятия ребенку с Александром Сергеевичем очень нравятся. Все схватывает, доволен уроками. С репетитором нашли общий язык. Мы очень благодарны Александру Сергеевичу! Хороший педагог. Спасибо.
УченикЕлизавета
УчительАлёна Игоревна
Дети понимают всё, абсолютно. В школе не понимают ничего, а с Вашими репетиторами понимают всё. Сдвиги очень большие. Алёна Игоревна хороший педагог. Все занятия результативные.
Все занятия результативные.
УченикДжу Уван Ми
УчительГалина Михайловна
Плохо знаю русский язык, и постоянно делаю многие ошибки в тексте и в работе. Только благодаря достуным объяснениям учителя я мог самостоятельно находить ошибки. Большое спасибо за Вашу работу и сердечные помощи в изучении русского языка!
УченикРоман
УчительИрина Алексеевна
Мой сын занимался с Ириной Алексеевной, очень понравилось, всё спокойно и понятно было показано, рассказано. Очень профессионально и качественно выстроены занятия, учитель доброжелателен, ребенку интересно заниматься.
УченикЖеня
УчительОльга Сергеевна
Ольга Сергеевна — профессинал своего дела. Высококвалифицированный педагог. По английскому нужно было именно аудирование и речь, 100% подобрали репетитора по нашему запросу. Педагог строгий — то, что нужно моему ребёнку. Мы очень довольны!
УченикНикита
УчительСарвар Шодиевич
До этого никогда не занимался у репетиторов, думал что буду сидеть ничего не понимать и всё время уйдёт зря. Однако Сарвар Шодиевич очень понятно объясняет, не подчёркивает ваши «незнания» и до упора старается всё разъяснить. Могу с уверенностью посоветовать этого репетитора каждому, кто хочет разобраться в алгебре и геометрии.
Однако Сарвар Шодиевич очень понятно объясняет, не подчёркивает ваши «незнания» и до упора старается всё разъяснить. Могу с уверенностью посоветовать этого репетитора каждому, кто хочет разобраться в алгебре и геометрии.
УченикВиктор
УчительЮлия Анатольевна
Спасибо большое учитель объясняет очень хорошо там где ты что либо не поймёшь педагог тебе всё объяснит как раз педагог сказала повторить всё то что мне говорил предыдущий репетитор СПАСИБО БОЛЬШОЕ !!!
УченикЭльмира
УчительЛюдмила Евгеньевна
Выражаю благодарность центру где есть такие сильные и ответственные учителя. Отдельная благодарность Людмиле Евгеньевне за опыт за знания.
УченикДарья
УчительОльга Александровна
Ольга Александровна отлично объясняет темы, с ребенком нашла общий язык моментально. Дочь занимается с удовольствием, пробелы подтянули за пару уроков. Спасибо Вам большое!
УченикОлеся
УчительГузалия Робертовна
Сыну очень понравилось заниматься с Гузалией Робертовной. Очень внимательный и доброжелательный педагог, который сразу видит слабые стороны. Всячески поощряет ребёнка и помогает поднять самооценку. Большое спасибо!
Очень внимательный и доброжелательный педагог, который сразу видит слабые стороны. Всячески поощряет ребёнка и помогает поднять самооценку. Большое спасибо!
УченикДарья
УчительМария Никитична
Нравится, как преподает Мария Никитична (по программе школы + присутствует игровая минутка, ученице на занятиях не бывает скучно) Уровень знаний повысили до 5-ки, значительно расширили словарный запас. Все устраивает, рекомендует знакомым и в целом рада, что такая платформа существует.
УченикОлеся
УчительДаниил Станиславович
Спасибо. Урок понравился. Даниил Станиславович заинтересовал английским языком. Составили предположительные темы для занятий после новогодних праздников
УченикГеоргий
УчительЕкатерина Станиславовна
Грамотный, добрый, располагающий к себе педагог. С ребёнком Екатерина Станиславовна установила хороший контакт. Преподносит информацию очень доступно. Занятие проходит разнообразно, в том числе в игровой форме. Рекомендуем 5+
УченикНиколя
УчительАлла Валентиновна
Алла Валентиновна отличный преподаватель! Выявила все пробелы в знаниях Константина по русскому языку и работает над их устранением. Также помогает в работе над текущими темами урока. Уже прошли несколько занятий и продолжаем заниматься. нашла общий язык с сыном. Все нравится. Хотим заниматься дальше!
Также помогает в работе над текущими темами урока. Уже прошли несколько занятий и продолжаем заниматься. нашла общий язык с сыном. Все нравится. Хотим заниматься дальше!
УченикПолина
УчительСветлана Григорьевна
Светлана Григорьевна просто супер учитель!!!! Все очень понятно и хорошо объясняет, прохожу с ней темы по географии 6 класса. На уроке с ней очень интересно. Уже 2 урока — одно удовольствие!!!
УченикНаталья
УчительСергей Александрович
Классный репетитор, все темы разбираются на 5+, будем обязательно продолжать обучение, также рекомендуем всем ученикам!
УченикМаксим
УчительНадежда Викторовна
Замечательный педагог, с которым нравится заниматься. Максим готовится к сдаче ОГЭ по русскому языку и занимается с репетитором с начала ноября прошлого года. За это время успели повторить пройденный материал и изучить несколько тем нового материала. Надежда Викторовна объясняет материал в доступной форме. Максим продолжит с ней занятия.
УченикАлександра
УчительИрина Борисовна
Отличный репетитор ! Ирина Борисовна обьясняет сложные темы простым и доступным языком ! Сердечно благодарю педагога за грамотность и профессионализм !!!!
УченикФеона
УчительЯнина Александровна
Преподаватель компетентный, объясняет понятно, выше школьного уровня. Быстро заполняет пробелы в знаниях. Будем сотрудничать. С Уважением, Феона.
Быстро заполняет пробелы в знаниях. Будем сотрудничать. С Уважением, Феона.
УченикМадина
УчительМария Анатольевна
Очень чётко и понятно объяснила Мария Анатольевна. Спасибо вам. Не смотря первый раз, пробную занятия, она прям очень понравилась дочке и естественно мне💐. В дальнейшем обязательно будем заниматься с ней и подниматься.
УченикВероника
УчительЕвгения Вадимовна
Отличный учитель, который всегда вовлекает ученика в процесс, и сам проявляет заинтересованность в успехах ученика. Интересно слушать и работать!
УченикВероника
УчительДарья Максимовна
Дарья Максимовна замечательный, отзывчивый педагог!Обьясняет простым и доступным язык любую сложную тему- это большой плюс!! Спасибо большое моему репетитору, так как я уверена, что ОГЭ сдам на отлично !!
УченикДарья
УчительЕлизавета Владимировна
Очень качественные и продуктивные занятия. Занимаюсь не долго, но уже чувствуется прогресс. Очень милый и добрый преподаватель. Всё понятно объясняет. Мне, очень нравится заниматься математикой с Елизаветой Владимировной.
Всё понятно объясняет. Мне, очень нравится заниматься математикой с Елизаветой Владимировной.
УченикКарина
УчительАндрей Юрьевич
Мне понравилось заниматься с Андреем Юрьевичем. Впервые встречаю репетитора, который прежде учить языку, рассказывает про его истоки – географию, культуру, историю. Мне очень откликается такой подход. Видно, что преподаватель с большим опытом. Я очень довольна первым занятием! Буду продолжать заниматься с данным преподавателем.
Неравенство с одной переменной | Определение, примеры, правила, решение, резюме
Введение В алгебре неравенство — это математическое выражение, в котором используется символ неравенства для обозначения связи между двумя утверждениями. Обе стороны знака неравенства имеют разные выражения. Это означает, что выражение в левой части должно быть больше или меньше выражения в правой части, или наоборот. Буквальные неравенства — это когда связь между этими двумя алгебраическими выражениями определяется с помощью символов неравенства. «Неравенство существует, когда два действительных числа или алгебраических выражения связаны символами «>», «», .> », например, x>3 (x должен быть больше 3)
«Неравенство существует, когда два действительных числа или алгебраических выражения связаны символами «>», «», .> », например, x>3 (x должен быть больше 3)
Если в неравенстве есть только одна переменная, оно называется открытым предложением или неравенством с одной переменной. Одно переменное неравенство может быть линейным или более высокого порядка. Именно для дальнейшего обсуждения мы обсуждаем одно переменное линейное неравенство или одно переменное квадратичное неравенство. Итак, сначала определим эти однопеременные неравенства, а затем метод их решения.
Линейное неравенство с одной переменной Определение: Линейное неравенство — это математическое выражение, которое сравнивает два линейных выражения и объявляет одно больше или меньше другого. Линейные уравнения с одной переменной — это уравнения, которые записываются в виде ax + b = 0, где a и b — два целых числа, а x — переменная, и существует только одно решение. 8x + 3 = 8, в частности, является линейным уравнением только с одной переменной. В результате у этого уравнения есть только одно решение: x = 97/2. Вот несколько хороших примеров линейных неравенств, которые рассматриваются в этом разделе:
8x + 3 = 8, в частности, является линейным уравнением только с одной переменной. В результате у этого уравнения есть только одно решение: x = 97/2. Вот несколько хороших примеров линейных неравенств, которые рассматриваются в этом разделе:
- 3x > 6
- 8x + 6 < 4x
- 145x + 9>16 − 2x + 1
- 5x ≥ 1
- X < 6
Это однопеременное линейное неравенство с переменной x. Степень x равна единице, поэтому это называется линейным неравенством, и из-за одной переменной они являются линейными неравенствами с одной переменной.
92 – z = 7
Когда вещественное число заменяется переменной в линейном неравенстве, результатом является истинное утверждение. Линейные неравенства могут иметь неограниченное число решений или вообще не иметь их. Если существует бесконечно много возможностей, изобразите набор на отрезке прямой и/или используйте обозначение интервала, чтобы проиллюстрировать ответ.
Линейные неравенства могут иметь неограниченное число решений или вообще не иметь их. Если существует бесконечно много возможностей, изобразите набор на отрезке прямой и/или используйте обозначение интервала, чтобы проиллюстрировать ответ.
Чтобы вычислить неравенство с одной переменной, преобразуйте его в выражение (математическую фразу со знаком «=») и решите. На числовой прямой напишите решение, которое часто называют «граничной точкой». Числовая линия в этой точке делится на две части. Для обстоятельств, связанных или, граничная точка включается в решение; для случаев, связанных строго > или, это исключено. Граничные точки, входящие в решения, обозначены на числовой прямой в виде сплошных закрашенных кружков, а исключенные решения показаны в виде незакрашенных кружков. После этого выберите число из каждой зоны, разделенной граничной точкой, и посмотрите, верно оно или нет в исходном неравенстве. Если это так, то любое целое число в этой области является решением неравенства.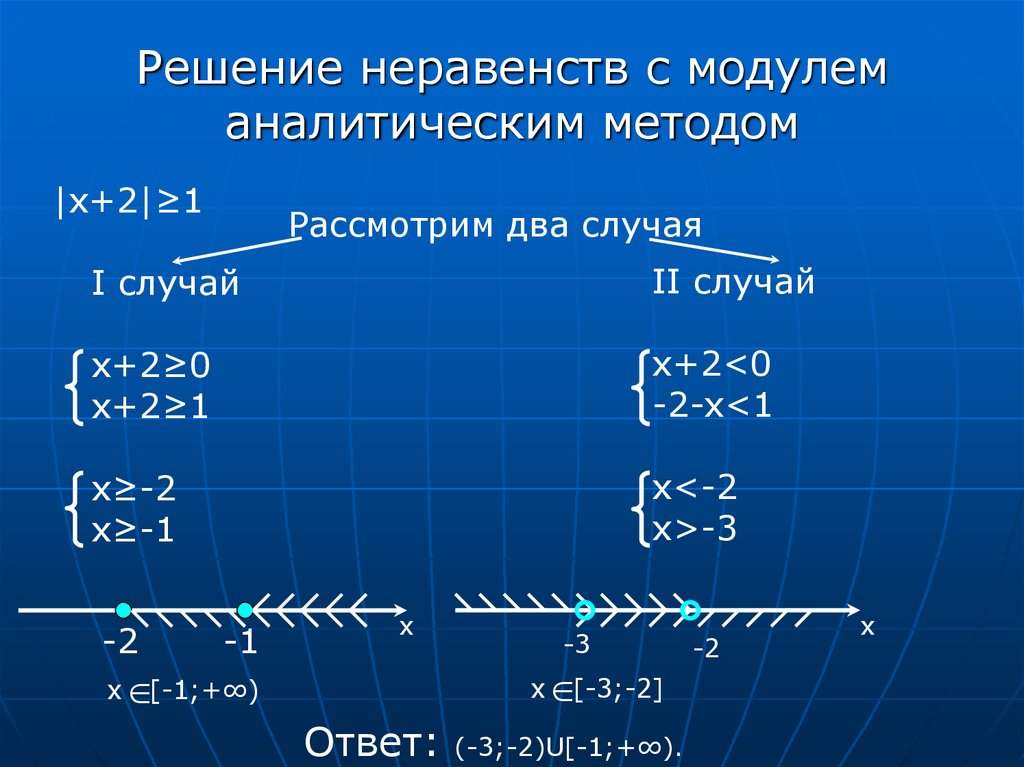 Если оно ложно, то в этой области нет числа, которое может решить неравенство.
Если оно ложно, то в этой области нет числа, которое может решить неравенство.
При решении линейного неравенства с одной переменной необходимо соблюдать некоторые правила.
Правила:-Решение неравенств следует тому же набору критериев, что и решение математического уравнения. При умножении или делении на отрицательное число есть одно исключение.
Чтобы устранить неравенство, мы можем:
- К обеим сторонам добавить одинаковое число.
- Уменьшите одинаковые суммы с обеих сторон уравнения.
- Обе стороны должны быть умножены на одно и то же положительное значение.
- Вычтите одинаковое положительное значение с обеих сторон.
- Измените знак и умножьте обе части на одно и то же отрицательное значение.
- Измените знак и разделите обе части на одно и то же отрицательное число.
Например
Если у нас есть
X + 5 > -2
Если мы умножим это неравенство на -2, то мы получим
-2x – 10 < 4
Сравните эти значения, умножьте на -2 признак неравенства.
Теперь посмотрите несколько примеров решения линейного неравенства с одной переменной
Следовательно, неравенства также можно решать путем деления или умножения обеих частей на переменную. Например, чтобы решить неравенство 5x > 3, умножьте обе части на 5, чтобы получить x > 35. Однако когда мы умножаем или делим на отрицательное целое число, происходит нечто необычное. Например, мы знаем, что 5 больше 3. Однако, если обе части неравенства 5>3 умножить на -2, мы получим 10>6. Мы знаем, что это не так, потому что -10 меньше -6.
Когда мы умножаем или делим неравенство на отрицательное число, это происходит, и мы должны поменять знак, чтобы неравенство стало верным. Чтобы умножить 2 > 4 на -3, например, мы умножаем 2 и 4 на -3 каждое, затем меняем знак на знак <, в результате чего 6 < 12.
Примеры:- Пример 1Решите это уравнение: 6x – (x + 10) <0
Нам нужно отделить переменную с одной стороны от знака неравенства, чтобы решить неравенство. Мы используем те же фундаментальные подходы, которые использовались для решения уравнения для выделения фактора. Большинство неравенств можно решить, добавив или удалив константу из одной части уравнения.
Мы используем те же фундаментальные подходы, которые использовались для решения уравнения для выделения фактора. Большинство неравенств можно решить, добавив или удалив константу из одной части уравнения.
Превратите задачу в уравнение и решите ее.
6х – х – 10 = 0
5 x – 10 = 0
5x = 10 из этого следует x = 10/5, поэтому x = 2
Следовательно, мы разделяем реальную линию на два интервала
(-∞, 2 ) (2 , ∞)
Теперь мы выберем одну тестовую точку в каждом тестовом интервале и проверим знак неравенства, а затем решим, какой интервал включает решение.
| Интервал проверки | контрольная точка | знак неравенства0135 -25-10 <0 |
| ( 2,∞ ) | 5 | 25 – 10 > 0 |
Следовательно, интервал (-∞, 2) удовлетворяет области решения. Итак, это необходимое решение.
На числовой строке запишите решение (граничную точку).
Решение -2 -1 0 1 2
Мы используем закрашенную точку, поскольку x = 2 также является решением неравенства (< ). В исходном неравенстве проверьте число по обе стороны от граничной точки. Раздел, содержащий данные, подтверждающие истинность неравенства, должен быть выделен.
В исходном неравенстве проверьте число по обе стороны от граничной точки. Раздел, содержащий данные, подтверждающие истинность неравенства, должен быть выделен.
4x > 24 было исходной проблемой.
Разделите обе части на 4
4x / 4 > 24 / 4
x > 6
x > 6 — это упрощенная версия этого неравенства.
Пример 3Здание одного дома стоит на четыре этажа выше другого здания. Найдите количество этажей в каждом здании, если общее количество этажей в обоих зданиях равно 24.
Метод
Мы знаем, что x = количество этажей одного здания, которое выше другого, и x + 8 = другая высота здания.
(x + 8) + x = 24
2x + 8 = 24
2x = 24 – 8
2x = 16
x = 16/2
x = 8+,8 одно здание 16 этажей, а другие 8.
Следовательно, с одной переменной большинство линейных уравнений имеют ровно одно решение. По крайней мере в одном примере линейное уравнение может иметь неограниченное количество решений, но в этом случае каждое действительное целое число является решением. 2 +bx + c <0
2 +bx + c <0
Термины с более низкой степенью, чем вторая, могут существовать или не существовать. Член первой степени и постоянный член являются членами более низкой степени в квадратном уравнении, чем квадратный член. В формуле
Методы решенияНеравенство можно решить как алгебраически, так и графически. Это намного сложнее, чем линейный пример, и может включать более одного уникального периода. Шаги, описанные ниже, можно использовать для решения квадратных неравенств.
Решение квадратного неравенства :Пошаговое руководство Алгебраически
Реорганизуйте неравенство так, чтобы большинство частей выражения, выраженных как f ( x ), находились на одной стороне, а соединяло их только неравенство до нуля. Например, f ( x ) 0 r f ( x ) > 0. Чтобы определить решения уравнения, решите f ( x ) = 0 с помощью факторизации или иным образом. Выберите контрольные точки для каждого интервала таким образом, чтобы были представлены значения чуть ниже, между и больше, чем решения уравнения.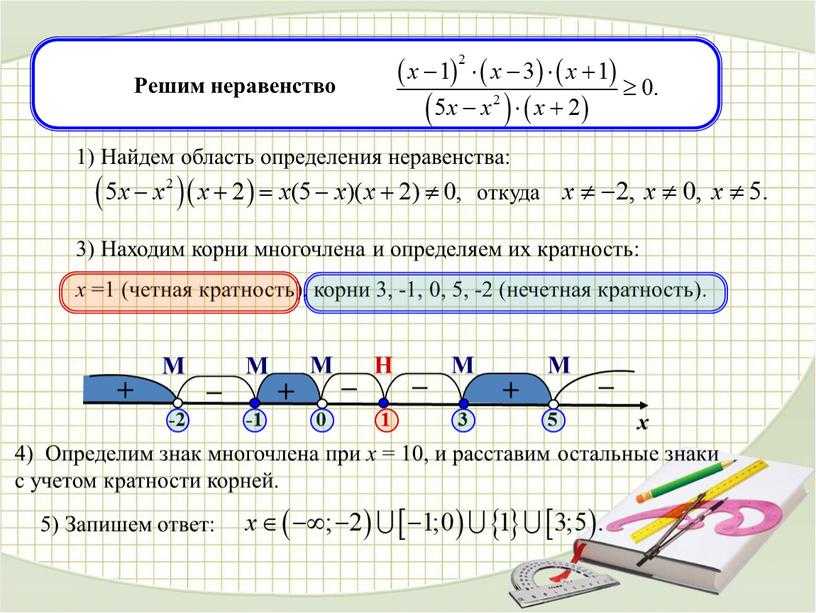 Диаграмму знаков также можно использовать для определения того, будут ли интервалы положительными или отрицательными. Определите, какие интервалы удовлетворяют неравенству.
Диаграмму знаков также можно использовать для определения того, будут ли интервалы положительными или отрицательными. Определите, какие интервалы удовлетворяют неравенству.
Мы также можем обобщить эти шаги следующим образом:
- Используйте это действие для решения квадратного неравенства:
- Решите неравенство, как если бы это было уравнение.
- Истинные решения уравнения служат граничными точками для формулировки неравенства.
- Если исходное неравенство содержит равенство, сделать границы сплошными кругами; в противном случае сделайте их открытыми кругами.
- Выберите точки из каждой из зон, созданных граничными точками. В исходном неравенстве замените эти «контрольные точки» на эти «контрольные точки».
- Когда контрольная точка соответствует исходному неравенству, область, в которой она расположена, является частью решения.
- Показать решение графически и в виде набора решений.

Решить задачу (x – 3)(x + 2) > 0
Записать ее неравенство в виде уравнения
(x – 3)(x + 2) = 0 (x – 3)(x + 2) = 0 (x – 3)(x + В результате свойства нулевого произведения, уравнение
Проведите демаркационную линию. Таким образом, поскольку исходное неравенство не включало равенство, точки разделительной линии открыты круги
Выберите точки из нескольких областей, для которых было разработано уравнение.
Проверьте контрольные точки, чтобы убедиться, что они удовлетворяют исходному неравенству.
(x – 3)(x + 2) = 0
Отсюда следует, что (x – 3) = 0 или (x + 2) = 0
X = 3 или x = -2
Интервалы яичек равны
(-∞,-2) и -2 , 3 , ( 3 , ∞)
Теперь проверим знаки в каждом проверяемом интервале неравенства
| Проверяемые интервалы | Контрольная точка | (x – 3)(x + 2) знак | ||||
| (-∞,-2) | -5 | (-5 – 3)(-5 +2) >0 Положительный | 6 | 6 | 6 | |
| (-2 , 3) | 0 | (0 – 3)(0 + 2) <0 Знак минус | ||||
| (3, ∞) | 5 | (5 -2 + 2 — )>0Positive |
Следовательно, вложенные интервалы (-∞, -2) и (3,∞) удовлетворяют условию неравенства. Таким образом, их объединение является искомым множеством решений неравенства. 92+121 никогда не пересекает ось X, как показано ниже. Решение представляет собой пустое множество, записанное в виде интервала.
Таким образом, их объединение является искомым множеством решений неравенства. 92+121 никогда не пересекает ось X, как показано ниже. Решение представляет собой пустое множество, записанное в виде интервала.
В результате наш ответ на это неравенство — пустое множество.
В предыдущих двух примерах мы решали квадратные неравенства с правой частью неравенства, равной нулю. Хотя обе части неравенства имеют ненулевые выражения, неравенство сначала должно быть упрощено до точки, где первая сторона становится равной нулю.
Отсюда заключаем
Интервал или объединение интервалов является решением квадратного неравенства. Мы могли бы использовать терминологию разности множеств, чтобы записать его как дополнение одного интервала, когда он представляет собой объединение двух интервалов.
Шаги алгебраического решения квадратного неравенства следующие: f(x) > 0
Перестройте неравенство так, чтобы все члены выражения находились на одной стороне, например, используя неравенство, связывающее это с нулем.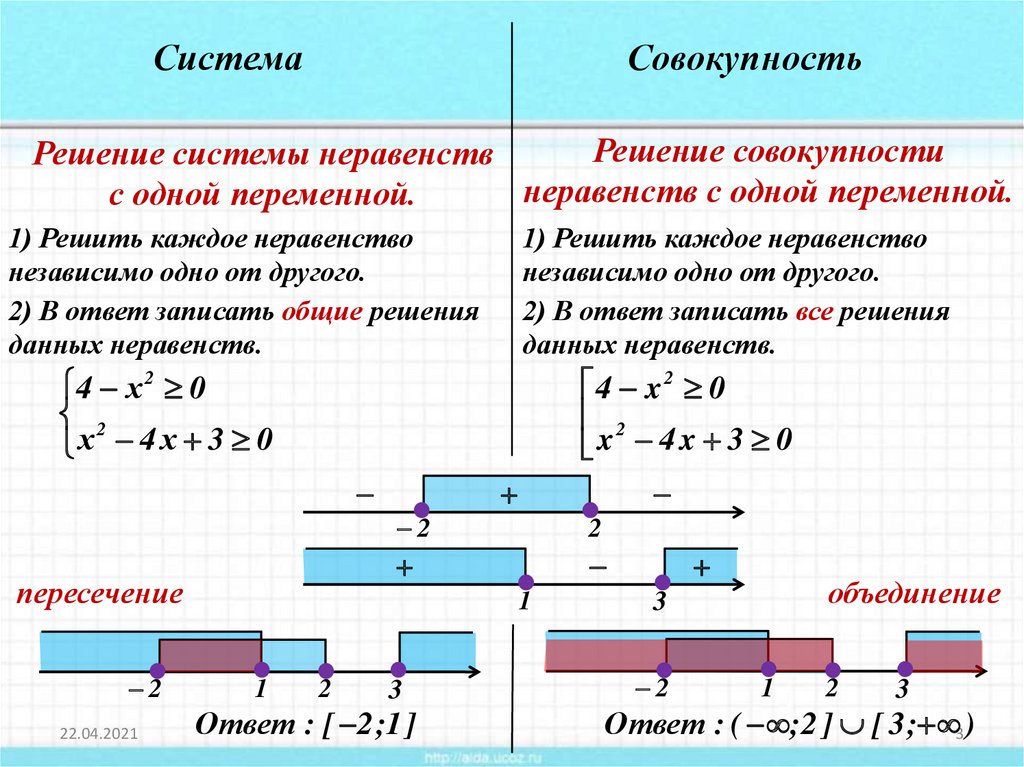 F(x) = 0
F(x) = 0
Фактор неравенства путем определения корней выражения. Ф(х)
Используя контрольные точки в каждом интервале или диаграмму знаков, найдите интервалы, удовлетворяющие неравенству. Также можно построить график функции.
Следуйте приведенным ниже инструкциям, чтобы решить квадратное неравенство графически.
Переформулируйте неравенство так, чтобы все члены выражения находились на одной стороне, а неравенство соединяло их с нулем; Например.
Чтобы найти корни выражения, факторизируйте неравенство по установке.
Используя корни уравнения, начертите график уравнения и определите направление кривой параболы. Если вы изменили исходное неравенство, чтобы изменить знак значения x, будьте особенно осторожны: вместо исходного неравенства используйте коэффициент x в измененной форме неравенства, чтобы определить форму кривой.
Определите, какие интервалы удовлетворяют неравенству.
Ключевые точкиСледовательно, вообще
- Линейное неравенство с одной переменной имеет бесконечное число решений.
 В результате ответы обычно представляются в виде графика на числовой прямой.
В результате ответы обычно представляются в виде графика на числовой прямой. - Типичный график линейного неравенства представляет собой половину числовой прямой со всеми точками слева или справа от граничного значения, а заштрихованная область показывает решения неравенства.
- В случае строгого неравенства (или >) граничное значение обозначается незакрашенным кружком (), а в случае нестрогого неравенства (или) граничное значение обозначается сплошным кружком ( •).
- Метод тестового значения или стандартная форма могут быть использованы для определения того, какую сторону значения границы следует заштриховать.
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Факты о неравенстве для детей
Факты из Детской энциклопедии
Неравенство — это когда один объект:
- Меньше другого (означает, что a меньше, чем b )
- Больше, чем другие (означает, что a больше, чем b )
- Не меньше другого (означает, что a не меньше b , то есть либо больше, либо равно b )
- Не больше другого (означает, что a не больше b , или меньше или равно б )
Неравенство иногда используется для обозначения утверждения, что одно выражение меньше, больше, не меньше или не больше другого.
Содержание
- Работа с неравенствами
- Различные виды неравенств
- Четыре способа решения неравенств
- Примеры решения неравенств
- Связанные страницы
Работа с неравенствами
Неравенство 1 Это решение уравнения x+4>12
Неравенство в математике – это когда два решения или ответа сравниваются на большее или меньшее. Это когда два или еще много решений сравниваются не в равной степени. Решить неравенство означает найти его решения. Когда вы подставляете число в переменную, и утверждение верно, то это решение. Когда вы подставляете число в переменную, а утверждение неверно, тогда число не является решением утверждения.
Решение неравенства — это поиск решения заданной переменной. Это нахождение относительного порядка множества. У неравенства может быть много решений, но обычно мы ищем только действительные числа. Правильный способ чтения неравенства — слева направо, как и в других уравнениях, но единственное отличие состоит в том, что для каждого уравнения действуют разные правила.
Например, рассмотрим неравенство x+4>12, где x — действительное число. Во-первых, нужно найти x и убедиться, что это действительно решение. Ответ будет x>8, и это истинное утверждение. Это выражение относится к местоположению x в наборе действительных чисел. Числовая линия — это один из способов показать положение относительно всех других действительных чисел. (См. рисунок Неравенство 1)
Различные виды неравенств
Линейное неравенство Пример линейного неравенства
Существует пять различных видов неравенств:
- , меньше или больше или равно, больше. Это то, что если мы заменим неравенство отношением равенства, то результатом будет линейное уравнение.
- Второй вид — это комбинации неравенств, которые должны удовлетворять неравенствам. Здесь сначала нужно иметь число в наборах решений, чтобы числа, удовлетворяющие неравенствам, были значениями пересечения двух наборов решений.
- Третий тип — это неравенства, включающие абсолютные значения, что означает, что значения можно перефразировать как комбинации неравенств, включающие абсолютные значения.

- Четвертый вид называется полиномиальным неравенством, что означает, что оно непрерывно и что его графики не имеют скачков и изломов.
- Последнее, но не менее важное, это рациональное неравенство, которое означает, что оно представляет собой форму деления одного многочлена на другой многочлен. Другими словами, графики рациональных функций не имеют разрывов и не представлены нулями знаменателя.
абсолютное значение Пример, показывающий абсолютное значение
Четыре способа решения неравенств
Пример добавления неравенств.
Существует четыре способа решения квадратных уравнений:
- Прибавьте или вычтите одинаковое число с обеих сторон.
- Сдвиньте стороны и измените положение знака неравенства.
- Умножить одно и то же число с обеих сторон.
- Разделите одно и то же положительное или отрицательное число на обе части.
пример умножения неравенства
Кроме того, для решения неравенства потребуется два шага. Первый заключается в упрощении с помощью обратной операции сложения или вычитания. Второй — упростить больше, используя обратную величину умножения или деления. Обратите внимание, что при умножении или делении неравенства на отрицательное число знак неравенства необходимо перевернуть.
Первый заключается в упрощении с помощью обратной операции сложения или вычитания. Второй — упростить больше, используя обратную величину умножения или деления. Обратите внимание, что при умножении или делении неравенства на отрицательное число знак неравенства необходимо перевернуть.
Примеры решения Неравенства
Неравенство 2 Решение уравнения -6y<-12
Неравенство — это математическое утверждение, объясняющее, что два значения не равны и различны. Уравнение a ≠ b означает, что a не равно b . Неравенство одинаково для любого уравнения, с той (единственной) разницей, что в неравенстве используется не знак равенства, а символы неравенства. Неравенство b>a означает, что b больше, чем a. Ограничения скорости, отметки и другие используют неравенство для их выражения.
При решении неравенства человеку необходимо иметь верное утверждение. Когда вы делите или умножаете неравенство с отрицательным числом с обеих сторон, утверждение неверно.

 Учебник для 9 класса общеобразовательных учреждений / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Телековского.
Учебник для 9 класса общеобразовательных учреждений / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Телековского.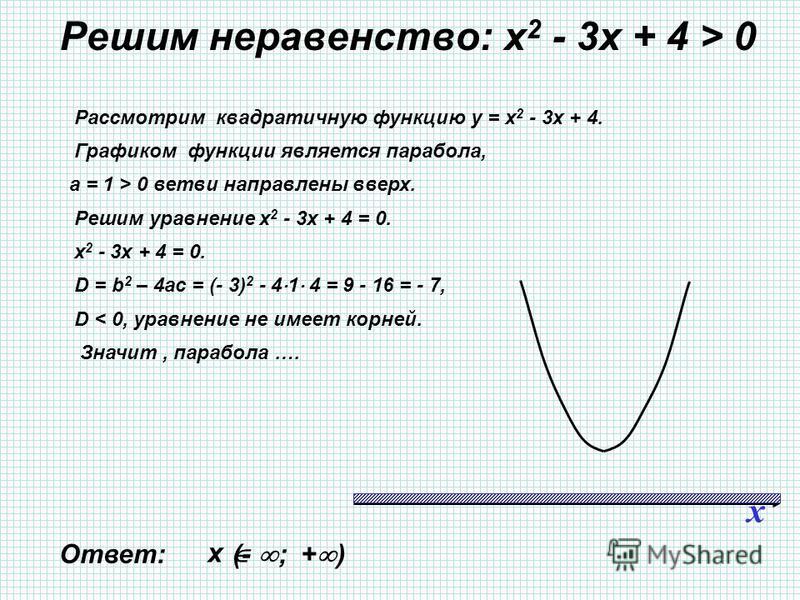
 В результате ответы обычно представляются в виде графика на числовой прямой.
В результате ответы обычно представляются в виде графика на числовой прямой.