Алгебра 7-9 классы. 25. Числовые неравенства. Свойства числовых неравенств. Оценки
- Подробности
- Категория: Алгебра 7-9 классы
СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ
Понятие числового неравенства: а > b — это значит, что а — b — положительное число; а < b — это значит, что а — b — отрицательное число. Числовые неравенства обладают рядом свойств, знание которых поможет нам в дальнейшем работать с неравенствами.
Для чего нужно уметь решать уравнения, вы знаете: до сих пор математическая модель практически любой реальной ситуации, которую мы рассматривали, представляла собой либо уравнение, либо систему уравнений. На самом деле встречаются и другие математические модели — неравенства, просто мы пока таких ситуаций избегали.
На самом деле встречаются и другие математические модели — неравенства, просто мы пока таких ситуаций избегали.
Знание свойств числовых неравенств будет полезно и для исследования функций. Например, с неравенствами связаны такие известные вам свойства функций, как наибольшее и наименьшее значения функции на некотором промежутке, ограниченность функции снизу или сверху. С неравенствами связано и свойство возрастания или убывания функции, о котором пойдет речь в одном из следующих параграфов. Так что, как видите, без знания свойств числовых неравенств нам не обойтись. Да вы и сами уже могли убедиться в необходимости умения работать с неравенствами.
Свойство 1.
Если а>b и b > с, то а > с.
Доказательство. По условию, а > b, т. е. а — b — положительное число. Аналогично, так как b > с, делаем вывод, что b — с — положительное число.
Сложив положительные числа а — b и b — с, получим положительное число. Имеем (а — b) + (b — с) = а — с. Значит, а — с — положительное число, т. е. а > с, что и требовалось доказать.
Свойство 1 можно обосновать, используя геометрическую модель множества действительных чисел, т, е. числовую прямую. Неравенство а > b означает, что на числовой прямой точка а расположена правее точки b, а неравенство b > с — что точка b расположена правее точки с (рис. 115). Но тогда точка а расположена на прямой правее точки с, т. е. а > с.
Свойство 1 обычно называют свойством транзитивности (образно говоря, от пункта а мы добираемся до пункта с как бы транзитом, с промежуточной остановкой в пункте
Свойство 2.
Если а > b, то а + с > b + с.
Свойство 3.
Если а>b и m > 0, то am > bm;
если a > b u m < 0,то am < bm.
Смысл свойства 3 заключается в следующем: если обе части неравенства умножить на одно и то же положительное число, то знак неравенства следует сохранить; если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства следует изменить (< на >,> на < ).
То же относится к делению обеих частей неравенства на одно и то же положительное или отрицательное число m, поскольку деление на m всегда можно заменить умножением на . Из свойства 3, в частности, следует, что, умножив обе части неравенства а > b на — 1, получим
— а <-b. Это значит, что если изменить знаки у обеих частей неравенства, то надо изменить и знак неравенства: если а > Ь, то — а < — b.
Свойство 4.
Если а > b и с > d, то а + с > b + d.
Доказательство.
I способ. По условию, а > b и с > d, значит, а — b и с — d — положительные числа. Тогда и их сумма, т. е. (а — b) + (с — d) — положительное число.
Так как
(а — b) + (с — d) = (а + с) — (b + d),
то и
а + с > b + d.
II способ. Так как а> b, то, согласно свойству 2, а + с > b + с. Аналогично, так как с > d, то с + b > d + b.
Итак, a + c > b + c, b + c > b + d. Тогда, в силу свойства транзитивности, получаем, что а + с > b + d.
Свойство 5.
Если а, b, с, d — положительные числа и a > b, с > d, то ас > bd.
Доказательство. Так как а > b и с > 0, то ас > bс. Аналогично, так как с > d и b > 0
, то cb > db.Итак, ас > bc, bc > bd. Тогда, согласно свойству транзитивности, получаем, что ас > bd.
Обычно неравенства вида а > b, с > d (или а < с, с < d) называют неравенствами одинакового смысла, а неравенства а > b и с < d — неравенствами противоположного смысла. Свойство 5 означает, что при умножении неравенств одинакового смысла, у которых левые и правые части — положительные числа, получится неравенство того же смысла.
Свойство 6.
Если а и b — неотрицательные числа и а> b, то аn> bn, где n — любое натуральное число.
Смысл свойства 6 заключается в следующем:
Дополнение к свойству 6. Если n — нечетное число, то для любых чисел а и b из неравенства а > b следует неравенство того же смысла аn > bn.
Вы обратили внимание на то, что в приведенных доказательствах мы пользовались по сути дела всего двумя идеями? Первая идея — составить разность левой и правой частей неравенства и выяснить, какое число получится: положительное или отрицательное. Вторая идея — для доказательства нового свойства использовать уже известные свойства.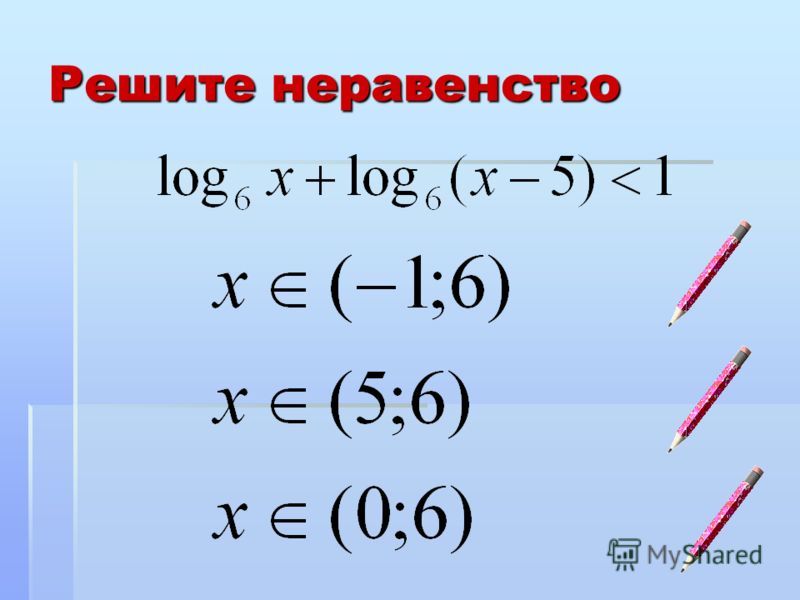 Так поступают и в других случаях доказательств числовых неравенств.
Так поступают и в других случаях доказательств числовых неравенств.
Пример 1.
Пусть а и b — положительные числа и а > b Доказать, что
Решение. Рассмотрим разность Имеем
По условию, а, b, а — b — положительные числа. Значит, — отрицательное число, т.е. откуда следует, что
Пример 2.
Пусть а — положительное число. Доказать, что
Решение. Рассмотрим разность Имеем
Получили неотрицательное число, значит,
Заметим, что если a = 1; если же а ≠ 1, то
Числовые неравенства
- Основные свойства числовых неравенств
- Сложение и вычитание неравенств
- Умножение неравенств
- Двойные неравенства
- Строгие и нестрогие неравенства
- Способы доказательства неравенств
Если числа a и b равны между собой, то a — b
 Если же числа a и b не равны между собой, то разность a — b либо положительна, либо отрицательна.
Если же числа a и b не равны между собой, то разность a — b либо положительна, либо отрицательна.Если разность a — b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a — b отрицательна, то говорят, что число a меньше числа b; записывается это таким образом:
a . (2)
Например, 5 > 3, поскольку разность 5 — 3 = 2 положительна; — 7
Записи (1) и (2) называются числовыми неравенствами, а знаки > и
Числовые неравенства допускают простую геометрическую интерпретацию. Будем изображать числа точками числовой прямой. Пусть числу a соответствует точка А, а числу b — точка В. Тогда, если а > b, то точка А будет лежать правее точки В. Если же a , то точка А будет лежать левее точки В.
До сих пор мы говорили лишь о таких неравенствах, обе части которых представляют собой вполне определенные числа. (Правда, для общности рассуждений мы обозначали эти числа буквами.) Однако в математике часто приходится иметь дело и с такими неравенствами, отдельные члены которых, выраженные с помощью букв, могут принимать различные числовые значения, например,
\(\sqrt{a}\) > a, (3)
1/a > 3, (4)
a — 1 a, (5)
\(\sqrt{a}\) + \(\sqrt{b}\)
Допустимыми значениями букв, входящих в неравенство, называются такие значения этих букв, при которых обе части неравенства имеют смысл.
Очевидно, что допустимыми значениями a в неравенстве (3) служат все положительные числа и нуль, в неравенстве (4) — все числа, кроме нуля, в неравенстве (5) — все числа. Для неравенства (6) допустимые значения a и b складываются из всевозможных пар неотрицательных чисел.
Рассмотрим подробнее неравенство (3). Оно, как мы уже говорили, определено для всех неотрицательных значений a. Однако не каждое из указанных чисел удовлетворяет этому неравенству. Действительно, при a = 0,25 \(\sqrt{a}\) = 0,5. Поскольку 0,5 > 0,25, то число a = 0,25 удовлетворяет неравенству (3). А вот число 4 ему уже не удовлетворяет, поскольку \(\sqrt{4}\)
Неравенство, которому удовлетворяют все допустимые значения входящих в него букв, называется тождественным неравенством.
Примером такого неравенства может служить хотя бы неравенство (5). При любом значении a a — 1 a. Неравенство (4) нельзя отнести к тождественным неравенствам; ему не удовлетворяет, например, значение a = 1: 1/1
Основные свойства числовых неравенств
- Если a > b, то b , и, наоборот, если a , то b > а.
Доказательство.
 Пусть a > b. По определению это означает, что число (a — b) положительно. Если мы перед ним поставим знак минус, то полученное число — (a — b) будет, очевидно, отрицательным. Поэтому — (a — b) b — а b .
Пусть a > b. По определению это означает, что число (a — b) положительно. Если мы перед ним поставим знак минус, то полученное число — (a — b) будет, очевидно, отрицательным. Поэтому — (a — b) b — а b .Обратное утверждение предлагаем учащимся доказать самостоятельно.
Доказанное свойство неравенств допускает простую геометрическую интерпретацию: если точка А лежит на числовой прямой правее точки В, то точка В лежит левее точки А, и наоборот.
- Если a > b, a b > c, то a > с.
Геометрически это свойство состоит в следующем. Пусть точка А (соответствующая числу a) лежит правее точки В (соответствующей числу b), а точка В, в свою очередь, лежит правее точки С (соответствующей числу с). Тогда точка А и подавно будет лежать правее точки С.
Приведем алгебраическое доказательство этого свойства неравенств.

Пусть a > b, a b > с. Это означает, что числа (a — b) и (b- с) положительны. Сумма двух положительных чисел, очевидно, положительна. Поэтому (a — b) + (b- с) > 0, или a — с > 0. Но это и означает, что a > с.
- Если a > b, то для любого числа с a + с > b + с, a — c > b — с.
Иными словами, если к обеим частям числового неравенства прибавить или от обеих частей отнять одно и то же число, то неравенство не нарушится.
Доказательство. Пусть a > b. Это означает, что a — b > 0. Но a — b = (a + с) — (b + с). Поэтому (a + с) — (b + с) > 0. А по определению это и означает, что a + с > b + с. Аналогично показывается, что a — c > b — с.

Например, если к обеим частям неравенства 5 > 4 прибавить 11/2, то получим
61/2 > 51/2. Отнимая от обеих частей данного неравенства число 5, получим 0 > — 1.Следствие. Любое слагаемое одной части числового неравенства можно перенести в другую часть неравенства, поменяв знак этого слагаемого на противоположный.
Пусть, например, a + b > с. Требуется доказать, что a > с — b. Для доказательства от обеих частей данного неравенства достаточно отнять число b.
- Пусть a > b. Если с > 0, то аc > bc. Если же с , то ас .
Иными словами, если обе части числового неравенства умножить на положительное число, то неравенство не нарушится;
если обе части неравенства умножить на отрицательное число, то знак неравенства изменится на противоположный.
Короче это свойство формулируется таким образом:
Неравенство сохраняется при почленном умножении на положительное число и изменяет знак на противоположный при почленном умножении на отрицательное число.
Например, умножив неравенство 5 > 1 почленно на 7, получим 35 > 7. Почленное умножение того же неравенства на — 7 дает — 35
Доказательство 4-го свойства.
Пусть а > b. Это означает, что число а — b положительно. Произведение двух положительных чисел а — b и с, очевидно, также положительно, т. е. (a — b) с > 0, или
aс — bс > 0. Поэтому aс > bс.Аналогично рассматривается случай, когда число с отрицательно. Произведение положительного числа a — b на отрицательное число с, очевидно, отрицательно, т. е.
(а — b) с 0; поэтому aс — bс 0, откуда aс .
Следствие. Знак неравенства сохраняется при почленном делении на положительное число и изменяется на противоположный при почленном делении на отрицательное число.
Это вытекает из того, что деление на число с =/= 0 равносильно умножению на число 1/c.
Сложение и вычитание неравенств
Про два неравенства, имеющие одинаковые знаки неравенства (оба знак > или оба знак одинакового смысла. Например, неравенства a > b и 3 > 2 — одинакового смысла, так как оба они имеют один и тот же знак > ; неравенства a и, a также одинакового смысла, поскольку имеют один и тот же знак
Если одно из неравенств имеет знак >, а другое знак противоположного смысла. Например, 16 > 0 и 5 a — неравенства противоположного смысла.
Теорема 1. Неравенства одинакового смысла можно почленно складывать.
Доказательство. Пусть a > b и с > d. Докажем, что a + с > b + d.
Так как a > b и с > d, то числа (a — b) и (с — d) положительны. Сумма двух положительных чисел также положительна: (a — b) + (с — d) > 0.
Но (a — b) + (с — d) = (a + с) — (b + d).
Поэтому число (a + с) — (b + d) положительно. А это и означает, что a + с > b + d.
Случай, когда складываются неравенства a и с , предлагаем учащимся рассмотреть самостоятельно.
Примеры:
$$ \frac{+\begin{cases}0 > -100\\65 > 64\end{cases}}{65 > -36} \;\;\;\; \frac{+\begin{cases}14 Теорема 2. Два неравенства противоположного смысла можно почленно вычитать, оставляя знак того неравенства из которого мы вычитаем.
Например:
$$ \frac{-\begin{cases}2 > 0\\-3 -6} \;\;\;\; \frac{-\begin{cases}10 2\end{cases}}{7 Доказательство. Пусть a > b и с . Покажем, что a — c > b — d.
Почленное умножение неравенства c на — 1 дает — с > — d. Сложив это неравенство с данным неравенством a > b, получим a — c > b — d.
Случай, когда a и с > d, предлагаем учащимся рассмотреть самостоятельно.
Замечание. Неравенства одинакового смысла почленно вычитать, вообще говоря, нельзя. Например, если бы мы из неравенства 2 > 0 вычли почленно неравенство 0 > — 5, то пришли бы к противоречию: 2 больше 5.
Умножение неравенств
Теорема. Неравенства одинакового смысла с положительными частями можно почленно умножать.
Доказательство. Пусть a > b и с > d, причем числа a, b, с и d положительны. Докажем, что aс > bd.
Докажем, что aс > bd.
Умножив неравенство a > b почленно на положительное число с, получим aс > bc. Умножив затем неравенство с > d почленно на положительное число b, получим bc > bd. Теперь имеем: aс > bc, a bc > bd. Но тогда по второму основному свойству неравенств (§ 10) должно быть aс > bd.
Аналогично может быть рассмотрен случай, когда a и c .
Примеры:
$$ \frac{\cdot \begin{cases}2 > 1\\6 > 4\end{cases}}{12 > 4} \;\;\;\; \frac{\cdot \begin{cases}5 > 3\\100 > 10\end{cases}}{500 > 30}\;\;\;\; \frac{\cdot \begin{cases}1
Следствие 1. Если a > b, причем числа a и b положительны, то для любого натурального п
an > bn.
Действительно, умножая почленно неравенство a > b само на себя, получим a2 > b2. Умножая затем почленно полученное неравенство на исходное неравенство a > b, получим a3 > b3 и т. д.
Следствие 2. Если числа a и b положительны и
an > bn (1)
(п — натуральное число), то a > b.
Действительно, возможен один из трех случаев: a = b, a и a > b.
Если а = b, то аn = bn.
При a мы имели бы b > а, и потому по следствию 1 bn > an . И то и другое противоречит неравенству (1).
И то и другое противоречит неравенству (1).
Остается признать, что а > b.
Пример. Определить, какое число больше: \(\sqrt{5}\) + \(\sqrt{6}\) или \(\sqrt{3}\) + \(\sqrt{8}\).
Возвысим оба числа в квадрат:
(\(\sqrt{5}\) + \(\sqrt{6}\))2 = 5 + 2\(\sqrt{30}\) + 6 = 11 + 2\(\sqrt{30}\) ;
(\(\sqrt{3}\) + \(\sqrt{8}\))2 = 3 + 2\(\sqrt{24}\) + 8 = 11 + 2\(\sqrt{24}\)
Квадрат первого числа больше квадрата второго числа. Так как эти числа положительны, то по следствию 2
\(\sqrt{5}\) + \(\sqrt{6}\) > \(\sqrt{3}\) + \(\sqrt{8}\):
Двойные неравенства
Иногда приходится иметь дело с двойными неравенствами. Так называются неравенства вида
a’ .
По существу, эта формула объединяет в себе два неравенства: a’ и a . Этим и объясняется название «двойное неравенство».
Двойные, неравенства обладают всеми теми свойствами, о которых мы говорили в § 10-12, когда рассматривали обычные неравенства. Например, к каждой части двойного неравенства можно прибавить любое число k:
Например, к каждой части двойного неравенства можно прибавить любое число k:
a’ + k . (1)
Каждую часть двойного неравенства можно умножить на любое положительное число k:
ka’ . (2)
Каждую часть двойного неравенства можно умножить и на любое отрицательное число l, поменяв при этом знаки неравенства на противоположные:
la’ > la > la». (3)
Строгие и нестрогие неравенства
Когда хотят записать, что число a не меньше числа b (другими словами, a больше или равно b), то используют знак > и пишут a > b. Например, a2 + 1 > 1, | х | > 0 и т. д.
Если нужно записать, что число a не больше числа b (другими словами, a меньше или равно b), то используют знак и пишут a b. Например, 1 1 + a2, — | х |
Например, 1 1 + a2, — | х |
Соотношения a > b и a b, так же как и соотношения a > b и a , называются неравенствами. Неравенства, содержащие знак > или знак строгими, а неравенства, содержащие знак > или знак , — нестрогими. Например, неравенства π π > 6 — строгие, а неравенства 17 > 17 и 3 4 — нестрогие.
Все выведенные выше свойства строгих числовых неравенств легко распространяются и на нестрогие неравенства.
Например, если a > b, то b a; если a > b, то а + с > b +с и т. д.
Способы доказательства неравенств
Доказать неравенство, содержащее некоторые буквы, — это значит показать, что ему удовлетворяют любые допустимые или специально указанные значения этих букв. 2}{2} $$
2}{2} $$
Но (\(\sqrt{a}\) — \(\sqrt{b}\))2> 0.
Поэтому \(\frac{a + b}{2} — \sqrt{ab} \geq 0 \). А это и означает, что \(\frac{a + b}{2} \geq \sqrt{ab}\).
Знак равенства в формуле (1) имеет место тогда и только тогда, когда \(\sqrt{a}\) — \(\sqrt{b}\) = 0, т. е при a = b.
2-й способ. Предположим, что данное неравенство верно. Тогда, умножив обе его части на 2, получим:
a + b > 2 \(\sqrt{ab}\).
Перенесем 2 \(\sqrt{ab}\) в левую часть:
a + b — 2 \(\sqrt{ab}\) > 0.
Наконец, перепишем полученное неравенство в виде
(\(\sqrt{a}\) — \(\sqrt{b}\))2> 0. (2)
Последнее неравенство, очевидно, верно для любых положительных чисел a и b, причем равенство в нем достигается тогда и только тогда, когда a = b. Таким образом, данное неравенство мы свели к очевидному неравенству. Теперь, производя все рассуждения в обратном порядке, мы докажем данное неравенство.
Теперь, производя все рассуждения в обратном порядке, мы докажем данное неравенство.
Для любых, положительных чисел a и b имеем:
(\(\sqrt{a}\) — \(\sqrt{b}\))2> 0,
или
a — 2 \(\sqrt{ab}\) + b > 0.
Знак равенства при этом имеет место тогда и только тогда, когда a = b. Перенося — 2\(\sqrt{ab}\) в правую часть, получаем a + b > 2\(\sqrt{ab}\), откуда \(\frac{a + b}{2} \geq \sqrt{ab}\).
Сразу трудно было догадаться, что при доказательстве неравенства (1) нужно исходить из очевидного неравенства (2). Вот почему предварительно нам пришлось сделать допущение, что неравенство (1) верно, и получить при этом допущении неравенство (2).
Пример 2. Доказать, что если произведение положительных чисел х и у равно 1, то (1 + x)(1 + у) > 4.
Доказательство. Полагая в только что доказанном неравенстве
$$ \frac{a + b}{2} \geq \sqrt{ab}$$
a = 1, b = х, получим \(\frac{1 + x}{2} \geq \sqrt{x}\) или 1 + х > 2\(\sqrt{x}\)
Аналогично показывается, что 1 + y > 2\(\sqrt{y}\). Почленное умножение полученных неравенств дает:
(1 + х)(1+у) > 2\(\sqrt{x}\) •2\(\sqrt{y}\),
или
(1 + х)(1+у) > 4\(\sqrt{xy}\).
Но по условию ху = 1. Поэтому
(1 + х)(1+у) > 4.
Решение неравенств путем умножения или деления — Easy Peasy All-in-One Homeschool
На этом уроке вы научитесь решать неравенства, связанные с умножением или делением. Вы снова будете использовать свои знания о решении уравнений в качестве основы для решения неравенств.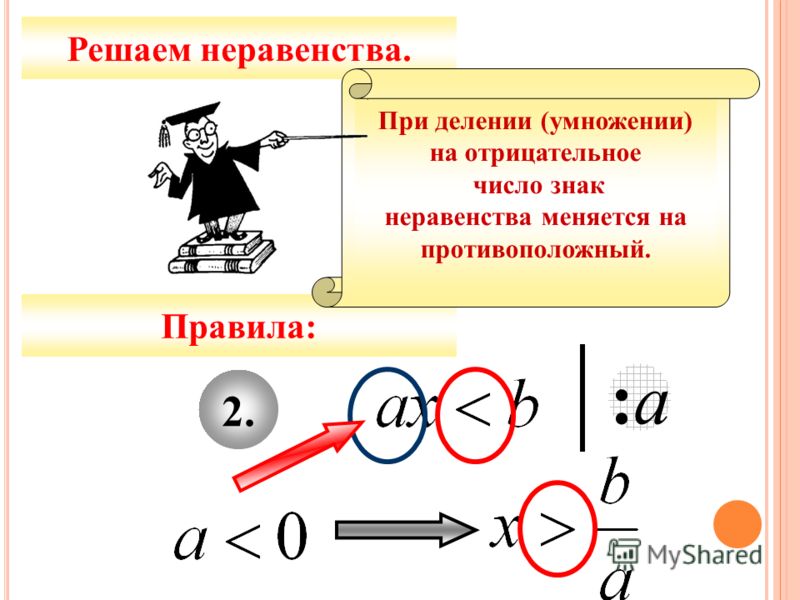 Есть одно важное правило, которое будет применяться к умножению и делению неравенства, в котором участвуют отрицательные числа. Внимательно изучите приведенную ниже таблицу свойств, чтобы понять это важное правило.
Есть одно важное правило, которое будет применяться к умножению и делению неравенства, в котором участвуют отрицательные числа. Внимательно изучите приведенную ниже таблицу свойств, чтобы понять это важное правило.
Попробуйте несколько из них, чтобы ознакомиться с этим правилом.
Практика
Каждый раз знак сохраняется, а числа умножаются. Проверьте неравенство, чтобы убедиться, что новое неравенство является точным. Это должно быть неточным каждый раз, когда неравенство умножается на отрицательное число.
Неравенство: 3 < 4
Умножить каждую сторону на: 2
Новое неравенство: 6 < 8 точно
Неравенство: 5 > 2
Умножьте каждую сторону на: -3
Новое неравенство: -15> -6 Неакурата
Неравенство: -1 ≤ 5
Умножение каждой стороны на: 4
Новое неравенство: -4 ≤ 200017 Точно
Неравенство: 3 ≥ -10
Умножить каждую сторону на: -2
Новое Неравенство: -6 ≥ 20 неточное
Неравенство: 1 < 8
Новое Неравенство: 1 < 8
Умножить каждую сторону на 0:0:0 -2
Неравенство9:00:0 8 < -64 неточное
Неравенство: -3 ≤ 10
Умножьте каждую сторону на: -2
Новое неравенство: 6 ≤ -20 Неточный
Неравенство: 4 <8
Разделите каждую сторону на: 4
Новое неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: неравенство: 1 <2 Точно
Неравенство: 9 ≥ -12
Разделите каждую сторону на: -3
Новое неравенство: -3 ≥ 4 naccurate
Неравенство: 20> 100003
Разделите каждую сторону на: 5: 5
Новое неравенство: 4 > 2 точно
Неравенство: -8 < -4
Разделить каждую сторону на: -2
Новое неравенство: 4 < 2 неточно
Неравенство: -24 ≤ 90 разделить на каждую сторону 16
3
Новое неравенство: 6 ≤ -4 Неакуратное
Неравенство: 12> -6
Разделите каждую сторону на: -6
Новое неравенство: -2> 1 Неточный
Теперь мы неравенство путем умножения.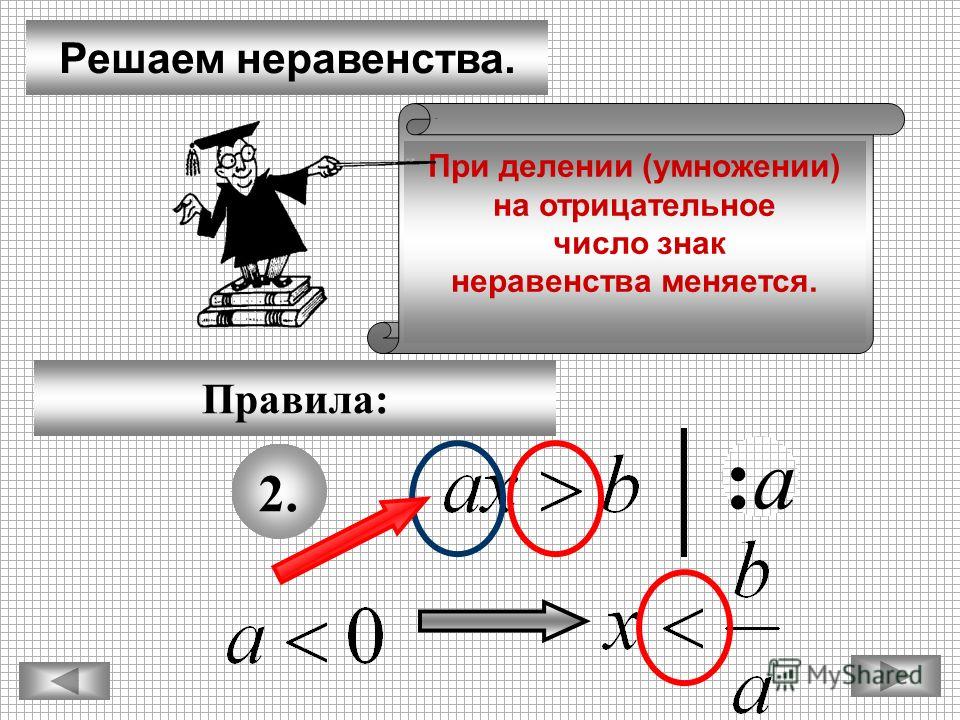
Четверо друзей отправились на обед в популярный ресторан и решили разделить стоимость еды. Доля каждого человека составляет не более 15 долларов. Неравенство
можно использовать для нахождения p, цены их обеда в долларах. Каково множество решений неравенства и что оно представляет в этой ситуации?
Стратегия
Используйте обратные операции для решения неравенства, как если бы вы решали уравнение.
Решение
Теперь интерпретируйте решение. Это имеет смысл, потому что если доля каждого человека не превышала 15 долларов, то весь обед не может стоить больше 60 долларов.
Также стоит рассмотреть пример решения неравенства делением.
Расследовать Уэбб — аквалангист. Его высота по сравнению с уровнем моря изменяется с постоянной скоростью -30 футов в минуту. Он начал с поверхности воды, и сейчас его высота составляет менее -120 футов. Как долго Уэбб спускался?
Как долго Уэбб спускался?
Стратегия
Для этого вам нужно перевести слова в неравенство. Пусть m обозначает минуты, в течение которых он спускался.
Скорость изменения (-30), умноженная на m (минуты), меньше (<) -120
-30m < -120
Используйте обратные операции для решения неравенства.
Разделите обе части на -30 И переверните символ неравенства .
м > 4
Решение
Интерпретировать набор решений. Вопрос заключается в том, как долго он спускался, чтобы достичь глубины менее 120 футов под поверхностью, а m представляет собой минуты. Это означает, что он снижался более 4 минут, чтобы достичь уровня менее -120. Подставить число из набора решений, 5 минут.
-30(5) < -120
-150 < -120 Правильно!
(источник)
Искать:Задать вопрос
Прежде чем задать вопрос, проверьте страницу часто задаваемых вопросов! Группа поддержки Или найдите определенное место или группу уровня Список групп facebook
EP Шестерня
Большое разнообразие дизайнов и продуктовСледите за EP на Facebook
EP на других языках
Kinderleicht Lernen
Использование EP для говорящих по-испански
Следите за блогом по электронной почте
Введите свой адрес электронной почты, чтобы следить за этим блогом и получать уведомления о новых сообщениях по электронной почте.
Адрес электронной почты:
Мои романы и книги
Чудесные истории Ли – не будем бояться
Отказ от ответственности
Задания, набор ссылок, структура учебной программы и файлы, созданные этим сайтом, принадлежат этому владельцу блога и не могут быть скопированы и опубликованы на другом сайте или использованы для какой-либо коммерческой выгоды.
Copyright 2023 Lee Giles
Все права защищены
GMAT Алгебра | Как работают отрицательные числа в неравенствах GMAT
By Dominate the GMAT / 23 мая 2013 г. / Блог
Одна из тем по алгебре, тестируемая на GMAT, — это неравенств . Во многих отношениях неравенства довольно просты и очевидны. Как правило, вы просто обращаетесь с ними как с обычными алгебраическими уравнениями при поиске возможных значений переменных. Например, сравните следующее (уравнение № 1 и неравенство № 1):
Уравнение №1: 2 x + 5 = 17
+ 5 < 17
Чтобы решить, вы делаете то же самое — вычитаете по 5 с обеих сторон и делите на 2, и знак неравенства остается прежним. Таким образом, x < 6.
Таким образом, x < 6.
Основное различие между неравенством № 1 и уравнением № 1 заключается в том, что в этом неравенстве существует бесконечное число возможных значений для 9.0223 x , что будет удовлетворять параметрам, установленным неравенством. В то время как в уравнении № 1 есть только одно значение для 90 223 x 90 224 во всей вселенной чисел, для которого 2 90 223 x 90 224 + 5 = 17 (т. е. 6), в неравенстве № 1 есть несколько ответов. На самом деле подойдет любое значение x меньше 6.
Довольно просто, правда?
Ну, в конце концов, это GMAT, так что вы знаете, что чем сложнее задачи, тем выше вероятность того, что составители теста расставят для вас ловушки. На самом деле, есть две основные вещи, на которые следует обращать внимание в более сложных вопросах, когда речь идет о неравенстве GMAT:
1. Неравенства с двумя переменными
Неравенства с двумя переменными сами по себе не являются «трюками», но они вносят дополнительный уровень сложности, с которым вам нужно убедиться, что вы знаете, как с ним справляться. Хорошая новость заключается в том, что это довольно просто: таблицы неравенства делают подобные проблемы безвредными. Ознакомьтесь с нашей статьей «Математика GMAT — неравенства с двумя переменными» , чтобы узнать все, что вам нужно знать, чтобы освоить этот важный вариант неравенства GMAT.
Хорошая новость заключается в том, что это довольно просто: таблицы неравенства делают подобные проблемы безвредными. Ознакомьтесь с нашей статьей «Математика GMAT — неравенства с двумя переменными» , чтобы узнать все, что вам нужно знать, чтобы освоить этот важный вариант неравенства GMAT.
2. Деление на отрицательные числа
Одно из малоизвестных и часто забываемых правил математики, которое упускают из виду многие студенты GMAT, заключается в том, что при делении неравенства на отрицательное число знак неравенства меняет направление. На самом деле, закрепим это как правило:
Правило: При делении неравенства на отрицательное число знак неравенства меняет направление.
Давайте посмотрим на вариант вышеприведенного неравенства, чтобы понять, как это работает:
Неравенство №2: -2 x + 5 < 17
Единственная тонкая разница между Неравенством №2 и Неравенством №1 заключается в том, что в Неравенстве №2 коэффициент переменной x равен отрицательному 2. И тем не менее, в этом вся разница в мире.
И тем не менее, в этом вся разница в мире.
Вы начинаете так же: вычтите 5 из обеих сторон, так что теперь -2 x < 12. Однако следующим шагом будет деление обеих сторон на минус 2, чтобы изолировать x . Как следует из приведенного выше правила, это меняет знак неравенства. Итак, правильный ответ x > 6 , а не «меньше 6», как в неравенстве № 1 выше.
Это одно из тех правил, которые вы можете доказать себе, подставив кучу чисел для x , посмотрев на них на числовой прямой и подтвердив себе, что «да», на самом деле знак неравенства соответствует . наоборот при делении на отрицательное число. ИЛИ вы можете просто запомнить правило и понять, что GMAT — это, в конце концов, средство для достижения цели, и пока знание этого правила поможет вам получить еще пару правильных ответов в день экзамена, это все, что имеет значение. Все, что работает для вас.
Как это правило проверяется на GMAT
Эту небольшую информацию о том, как отрицательные числа влияют на неравенства, можно проверить в любом разделе GMAT, посвященном количественным показателям или разделам Integrated Reasoning, и тем не менее, скорее всего, вы встретите ее на данных GMAT.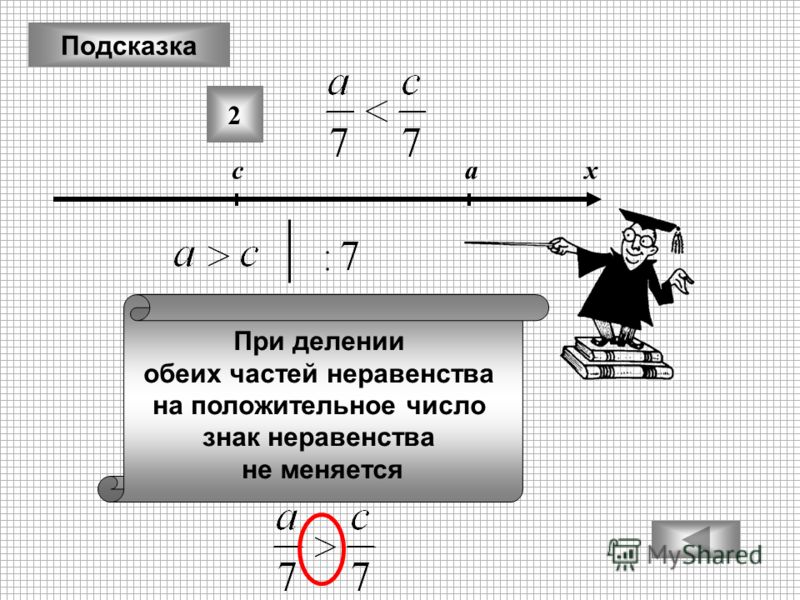 вопросы достаточности. Поэтому важно, чтобы вы использовали свой черновик и следовали методологии, изложенной в «Достаточность данных — часть 1» , чтобы убедиться, что вы не совершите ошибку по невнимательности, упустив это тонкое правило.
вопросы достаточности. Поэтому важно, чтобы вы использовали свой черновик и следовали методологии, изложенной в «Достаточность данных — часть 1» , чтобы убедиться, что вы не совершите ошибку по невнимательности, упустив это тонкое правило.
Чтобы увидеть, как это работает, попробуйте ответить на этот пример вопроса о достаточности данных GMAT:
Если ab < ac, что больше, b или c?
(1) а < 0
(2) с < 0
Что вы думаете?
Что ж, очевидный способ продолжить — просто разделить обе части неравенства в основе вопроса на «a» и получить, что b < c. Для многих студентов вы бы тут же остановились и пришли к выводу, что, конечно же, b меньше, чем c , поэтому у вас достаточно информации, чтобы ответить на вопрос.
Проблема, конечно, в том, что мы не знаем, является ли или положительным или отрицательным! Если а положительно, то, конечно же, b < c, если вы разделите обе части неравенства на а . Однако что, если и отрицательные? В этом случае, как мы видели в приведенном выше правиле, знак неравенства меняется на противоположный, потому что теперь вы делите неравенство на отрицательное число. В этом случае b > c. Итак, нам потребуется дополнительная информация о природе числа 9.0223 и для определения достаточности.
Однако что, если и отрицательные? В этом случае, как мы видели в приведенном выше правиле, знак неравенства меняется на противоположный, потому что теперь вы делите неравенство на отрицательное число. В этом случае b > c. Итак, нам потребуется дополнительная информация о природе числа 9.0223 и для определения достаточности.
Конечно же, теперь ответ должен прыгать прямо со страницы:
(1) Достаточно . Это именно то, что мы заранее определили, что нам нужно было знать. Если а < 0, то с заведомо меньше b.
(2) Недостаточно . Знак c не имеет отношения к ответу на вопрос.
Итак, правильный ответ А.
Заключение
Сложность этого «трюка» с изменением знака неравенства при делении на отрицательные числа заключается не столько в понимании самого правила, сколько в том, чтобы следить за ним в день теста. Легко напевать на GMAT, отвечая на вопросы, а затем увидеть вопрос о неравенстве и манипулировать им как обычным уравнением, не замечая того тонкого факта, что в какой-то момент при решении неравенства вам придется делить на отрицательное число.

 Пусть a > b. По определению это означает, что число (a — b) положительно. Если мы перед ним поставим знак минус, то полученное число — (a — b) будет, очевидно, отрицательным. Поэтому — (a — b) b — а b .
Пусть a > b. По определению это означает, что число (a — b) положительно. Если мы перед ним поставим знак минус, то полученное число — (a — b) будет, очевидно, отрицательным. Поэтому — (a — b) b — а b .


