Противоположно направленные векторы: Коллинеарные, равные, противоположные векторы — урок. Геометрия, 9 класс.

Вопросы к главе IV

1. Справедливо ли утверждение: а) любые два противоположно направленных вектора коллинеарны; б) любые два коллинеарных вектора сонаправлены; в) любые два равных вектора коллинеарны; г) любые два сонаправленных вектора равны; д) если а↑↓b, b↑↓c, то a↑↓c; е) существуют векторы а, b и с такие что а и с не коллинеарны, b и с не коллинеарны, а a и b коллинеарны?

а) Да, так как они лежат на параллельных прямых. б) Нет, они могут быть противоположно направлены. в) Да. г) Нет, например a и 2a. д) Нет, a↑↑c. е) Да, например три стороны параллелограмма.

2. Точки A и С симметричны относительно точки О и AD = BC. Симметричны ли точки В и D относительно точки О?

Да, так как ABCD — параллелограмм и BD — его диагональ, а О — центр.

3. Точки A и С симметричны относительно прямой а и AD = BC. Могут ли точки В и D быть: а) симметричными относительно прямой а; б) несимметричными относительно прямой а?

а) Да, (рис. 226 а), б) Да, (рис. 226 б).

4. Точки A и С, а также точки В и D симметричны относительно плоскости α. Могут ли векторы АВ и CD быть: а) равными; неравными?

а) Да; б) Да.

5. Известно, что векторы а и a+b коллинеарны. Коллинеарны ли векторы а и b?

Да, так как a и a — (a + b) коллинеарны.

6. Может ли длина суммы двух векторов быть меньше длины каждого из слагаемых?

Да, например

7. Может ли длина суммы нескольких ненулевых векторов быть равной сумме длин этих векторов?

Да, если все векторы сонаправлены.

8. Может ли длина разности двух ненулевых векторов быть равной сумме длин этих векторов?

Да, если эти векторы противоположно направлены.

9. Может ли длина разности двух ненулевых векторов быть равной разности длин этих векторов?

Да, если эти векторы сонаправлепы.

10. Может ли длина суммы двух ненулевых векторов быть равна длине разности этих векторов?

Да, если эти векторы перпендикулярны.

11. На какое число нужно умножить ненулевой вектор а, чтобы получить вектор b, удовлетворяющий следующим условиям:

а) На 1; б) на — 3; в) на — k; г) на 0.

12. Известно, что AB = k⋅CD, причем точки А, В и С не лежат на одной прямой. При каком значении k прямые AC и BD являются: а) параллельными; б) пересекающимися? Могут ли прямые АС и BD быть скрещивающимися?

а) Эти прямые параллельны при k = 1 б) При k ≠ 1 и k ≠ 0 эти прямые пересекаются. Прямые АС и BD не могут быть скрещивающимися, т. к. лежат в одной плоскости.

13. Компланарны ли векторы: а) а, b, 2а, 3b; б) а, b, a+b, а — b?

а, б) Да, эти векторы лежат в плоскости, проходящей через вектора a и b.

14. Известно, что векторы а, b и с компланарны. Компланарны ли векторы: а) а, 2b, 3с; б) а+b, а+2с, 2b — Зс?

Да.

15. Точки А, В и С лежат на окружности, а точка О не лежит в плоскости этой окружности. Могут ли векторы ОА, ОВ и ОС быть компланарными?

Нет, так как если эти вектора лежат в одной плоскости, то точка О лежит в плоскости ABC, но точка О не лежит в этой плоскости.

Источник:

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №0
к главе «Глава IV. Векторы в пространстве § 3. Компланарные вектора ».

Все задачи

← 375. В тетраэдре ABCD точки К и М — середины ребер АВ и CD Докажите, что середины отрезков КС, KD, МА и MB являют ся вершинами некоторого параллелограмма.

376. Лан параллелепипед MNРQМ1N1P1Q1. Докажите, что: →

Векторы в пространстве

Векторы в пространстве

вход

Содержание

I . Понятие вектора в пространстве

II . Коллинеарные векторы

III . Компланарные векторы

IV . Действия с векторами

V. Разложение вектора

VI . Базисные задачи

Проверь себя

Помощь в управлении презентацией

Выход

Понятие вектора в пространстве

Вектор(направленный отрезок) –

отрезок, для которого указано какой из его концов считается началом, а какой – концом.

Длина вектора – длина отрезка AB.

В

M

А

Коллинеарные векторы

Два ненулевых вектора называются коллинеарными , если они лежат на одной

прямой или параллельных прямых.

Среди коллинеарных различают:

• Сонаправленные векторы
• Противоположно направленные векторы

Сонаправленные векторы

Сонаправленные векторы — векторы, лежащие

по одну сторону от прямой, проходящей через их начала.

Нулевой вектор считается сонаправленным с любым вектором.

• Равные векторы

Равные векторы

Равные векторы — сонаправленные векторы,

длины которых равны.

От любой точки можно отложить вектор,

равный данному, и притом только один.

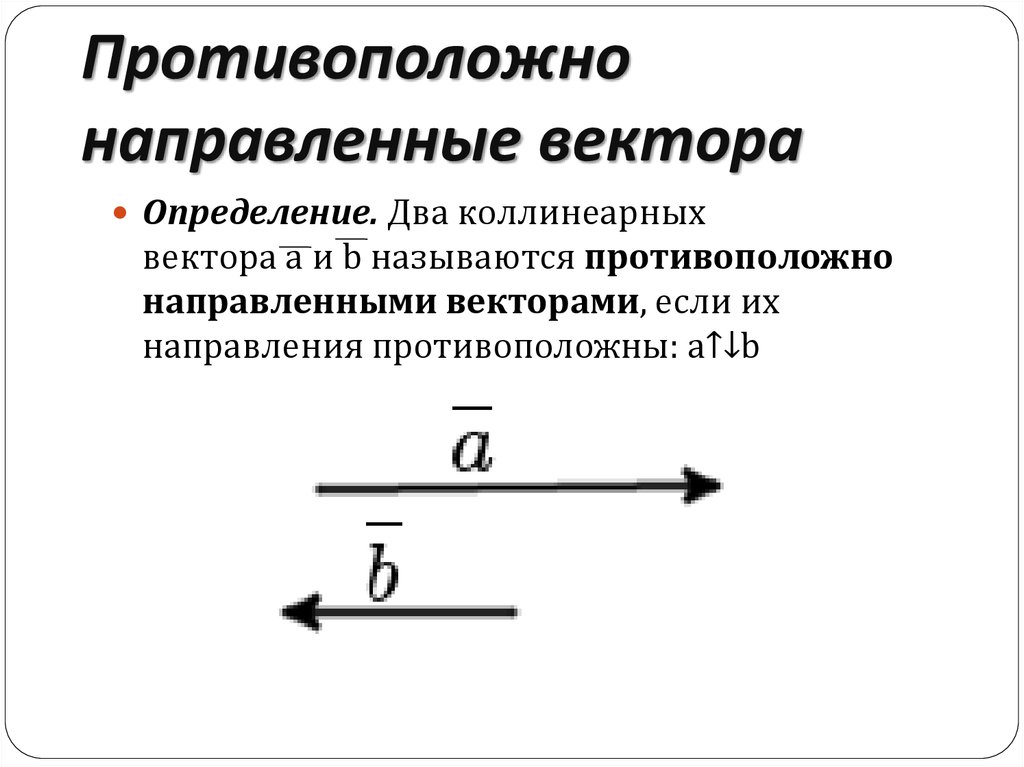
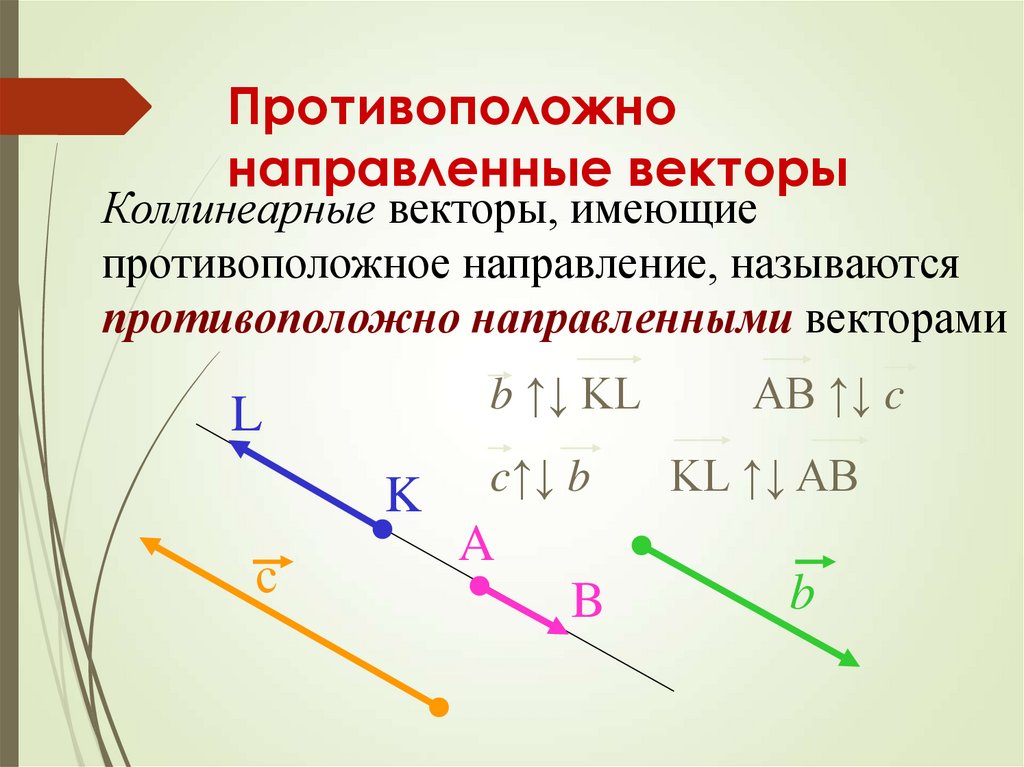
Противоположно направленные векторы

Противоположно направленные векторы – векторы, лежащие по разные стороны от прямой, проходящей через их начала.

• Противоположные векторы

Противоположные векторы

Противоположные векторы – противоположно направленные векторы, длины которых равны.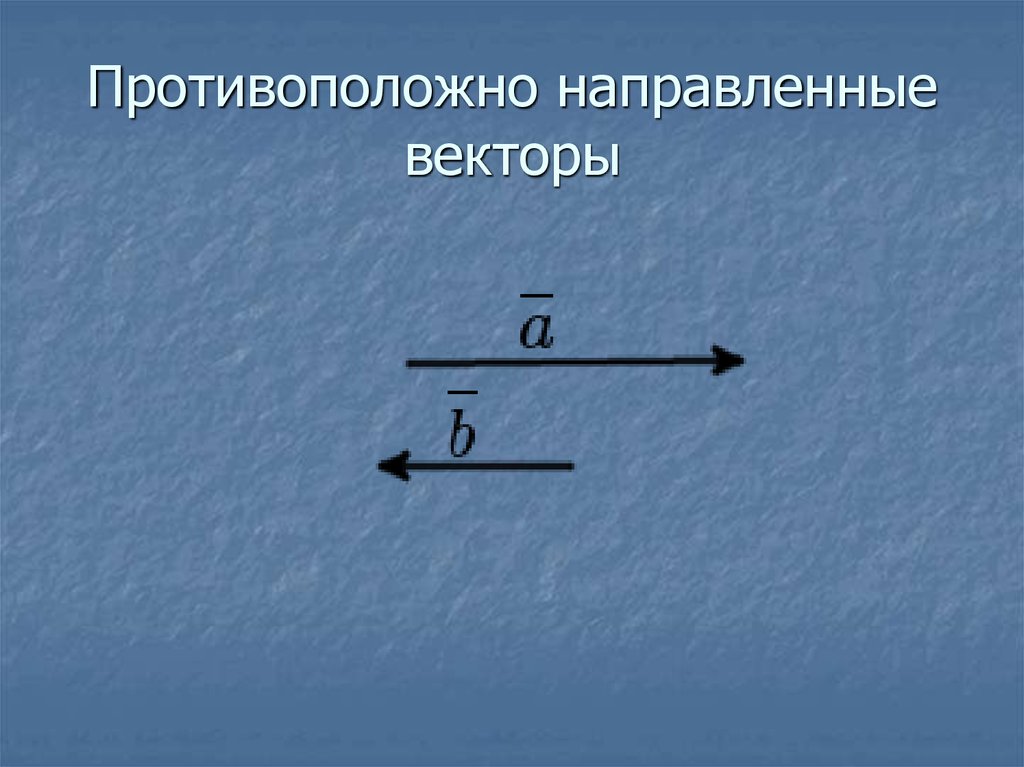

Вектором, противоположным нулевому,

считается нулевой вектор.

Признак коллинеарности

Доказательство

Доказательство признака коллинеарности

Определение компланарных векторов

Компланарные векторы – векторы, при откладывании которых от одной и той же точки пространства, они будут лежать в одной плоскости.

Пример:

B 1

C 1

A 1

D 1

B

C

А

D

О компланарных векторах

Любые два вектора всегда компланарны.

Три вектора, среди которых имеются два коллинеарных, компланарны.

α

если

Признак компланарности

Доказательство

Задачи

Задачи на компланарность

• Компланарны ли векторы:

а)

б)

Справка Решение

• Известно, что векторы , и компланарны. Компланарны ли векторы:

а)

б)

Справка Решение

Решение

Решение

Решение

Доказательство признака компланарности

B 1

С

B

A

A 1

O

Свойство компланарных векторов

Действия с векторами

• Сложение
• Вычитание
• Умножение вектора на число
• Скалярное произведение

Сложение векторов

• Правило треугольника
• Правило параллелограмма
• Правило многоугольника
• Правило параллелепипеда
• Свойства сложения

Правило треугольника

B

А

C

Правило треугольника

B

А

C

Для любых трех точек А, В и С справедливо равенство:

Правило параллелограмма

B

А

C

Свойства сложения

Правило многоугольника

Сумма векторов равна вектору, проведенному

из начала первого в конец последнего(при последовательном откладывании).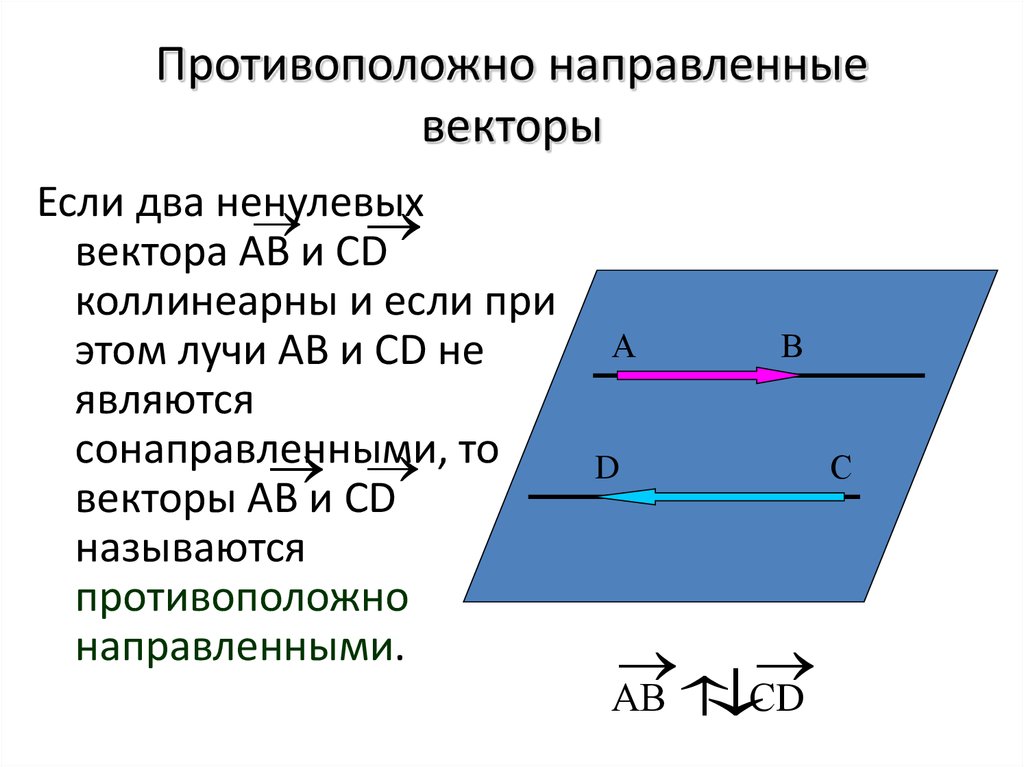

B

C

A

Пример

E

D

Пример

B 1

C 1

A 1

D 1

B

C

A

D

Правило параллелепипеда

Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той же точки и лежащих на трех измерениях параллелепипеда.

B 1

C 1

A 1

D 1

B

C

А

D

Свойства

B 1

C 1

A 1

D 1

B

C

А

D

Вычитание векторов

• Вычитание
• Сложение с противоположным

Вычитание

Разностью векторов и называется такой

вектор, сумма которого с вектором равна

вектору .

Вычитание

B

A

Правило трех точек

C

Правило трех точек

Любой вектор можно представить как разность двух векторов, проведенных из одной точки.

B

А

K

Сложение с противоположным

Разность векторов и можно представить как сумму вектора и вектора, противоположного вектору .

А

B

O

Умножение вектора на число

Свойства

• Произведением нулевого вектора на любое число считается нулевой вектор.
• Произведение любого вектора на число нуль есть нулевой вектор.

Свойства

Скалярное произведение

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Справедливые утверждения

Вычисление скалярного произведения в координатах

Свойства скалярного произведения

Справедливые утверждения

• скалярное произведение ненулевых векторов

равно нулю тогда и только тогда, когда эти векторы перпендикулярны

• скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату

его длины

Вычисление скалярного произведения в координатах

Доказательство

Доказательство формулы скалярного произведения

B

α

O

A

A

B

O

O

B

A

Доказательство формулы скалярного произведения

Свойства скалярного произведения

1 0 .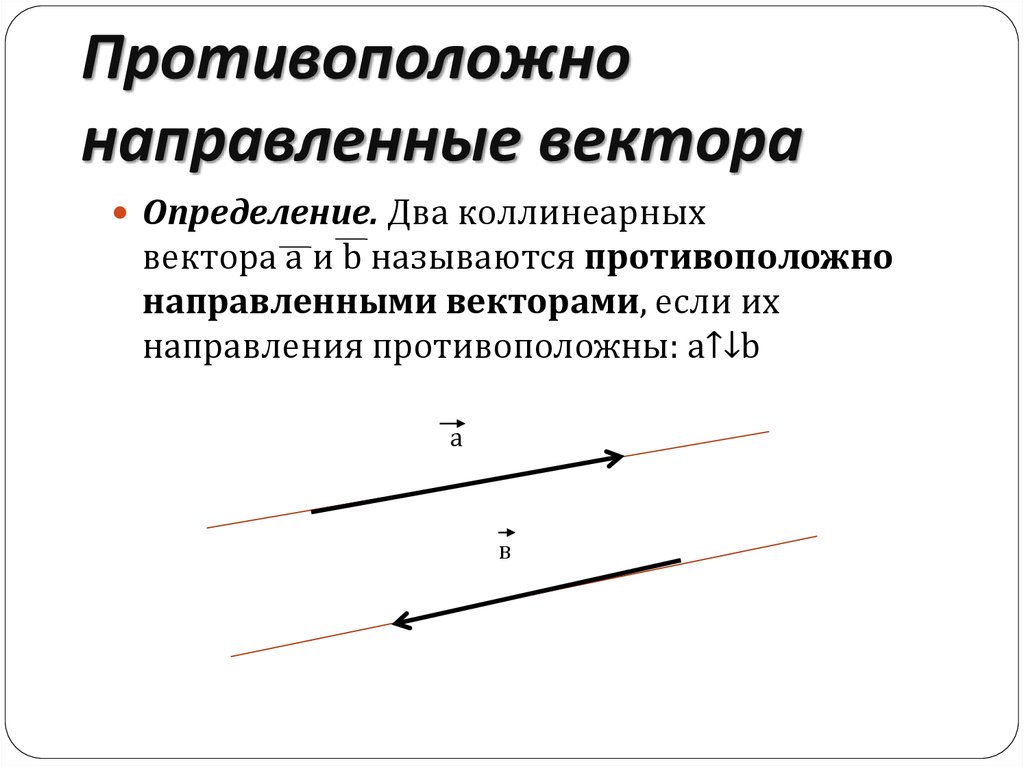

2 0 .

3 0 .

4 0 .

(переместительный закон)

(распределительный закон)

(сочетательный закон)

Разложение вектора

• По двум неколлинеарным векторам
• По трем некомпланарным векторам

Разложение вектора по двум неколлинеарным векторам

Теорема.

Любой вектор можно разложить по двум

данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

Доказательство

Доказательство теоремы

• Пусть коллинеарен .

Тогда , где y – некоторое число. Следовательно,

т.е. разложен по векторам и .

P

B

O

A

A 1

Доказательство теоремы

• не коллинеарен ни вектору , ни вектору .

Отметим О – произвольную точку.

Доказательство теоремы

Докажем, что коэффициенты разложения определяются единственным образом.

Допустим:

Тогда:

—

Разложение вектора по трем некомпланарным векторам

Если вектор p представлен в виде

где x, y, z – некоторые числа, то говорят, что вектор

разложен по векторам , и .

Числа x, y , z называются коэффициентами разложения.

Теорема

Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.

Доказательство

Доказательство теоремы

P

С

B

P 1

P 2

O

A

Доказательство теоремы

Докажем, что коэффициенты разложения определяются единственным образом.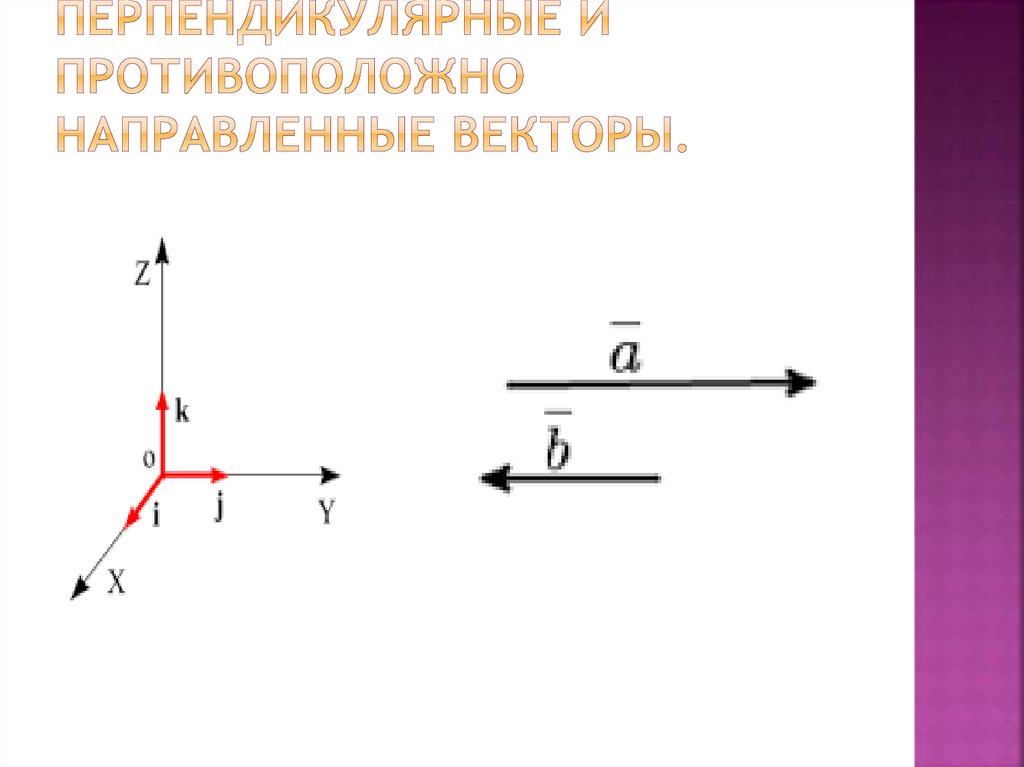

Допустим:

Тогда:

—

Базисные задачи

Вектор, проведенный в середину отрезка

Вектор, проведенный в точку отрезка

Вектор, соединяющий середины двух отрезков

Вектор, проведенный в центроид треугольника

Вектор, проведенный в точку пересечения

диагоналей параллелограмма

Вектор, лежащий на диагонали параллелепипеда

Вектор, проведенный в середину отрезка,

равен полусумме векторов, проведенных из той же точки в его концы.

С

A

B

O

Доказательство

Доказательство

С

A

B

O

Вектор, проведенный в точку отрезка

Точка С делит отрезок АВ в отношении т : п .

С

A

m

n

B

O

Доказательство

Доказательство

С

A

m

n

B

O

Вектор, соединяющий середины двух отрезков,

равен полусумме векторов, соединяющих их концы.

N

С

N

D

С

D

B

B

M

M

A

A

Доказательство

Доказательство

N

С

D

B

M

A

Вектор, проведенный в центроид треугольника,

равен одной трети суммы векторов, проведенных из этой точки в вершины треугольника.

Центроид – точка пересечения медиан треугольника.

O

С

M

A

B

Доказательство

Доказательство

O

С

M

K

A

B

Вектор, проведенный в точку пересечения диагоналей параллелограмма,

равен одной четверти суммы векторов, проведенных из этой точки в вершины параллелограмма.

O

C

B

M

A

D

Доказательство

O

Доказательство

C

B

M

A

D

Вектор, лежащий на диагонали параллелепипеда,

равен сумме векторов, лежащих на трех его ребрах, исходящих из одной вершины.

C 1

B 1

A 1

D 1

B

C

A

D

Доказательство

Доказательство

B 1

C 1

A 1

D 1

B

C

A

D

Помощь в управлении презентацией

• управление презентацией осуществляется с помощью левой клавиши мыши
• переход от одного слайда к другому и на гиперссылки по одиночному щелчку
• завершение презентации при нажатии кнопки выход

переход к следующему слайду

возврат к содержанию

возврат к подтеме

возврат с гиперссылок

Проверь себя

• Устные вопросы
• Задача 1 . Задача на доказательство
• Задача 2. Разложение векторов
• Задача 3. Сложение и вычитание векторов
• Задача 4. Скалярное произведение

Устные вопросы

Справедливо ли утверждение:

а) любые два противоположно направленных вектора коллинеарны?

б) любые два коллинеарных вектора сонаправлены?

в) любые два равных вектора коллинеарны?

г) любые два сонаправленных вектора равны?

д)

е) существуют векторы , и такие, что

и не коллинеарны, и не коллинеарны, а

и коллинеарны?

Ответы

Ответы

а) ДА

б) НЕТ (могут быть и противоположно направленными)

в) ДА

г) НЕТ (могут иметь разную длину)

д) ДА

е) ДА

Задача 1. Задача на доказательство

B 1

C 1

A 1

D 1

M 2

M 1

B

C

А

D

Решение

Решение

B 1

C 1

A 1

D 1

M 2

M 1

B

C

А

D

Задача 2. Разложение векторов

Разложите вектор по , и :

а)

б)

в)

г)

Решение

D

B

A

N

C

Решение

а)

б)

в)

г)

Задача 3. Сложение и вычитание

Упростите выражения:

а)

б)

в)

г)

д)

е)

Решение

Решение

а)

б)

в)

г)

д)

е)

Задача 4. Скалярное произведение

Вычислить скалярное произведение векторов:

C 1

B 1

A 1

D 1

B

C

A

D

Решение

Задача 4. Скалярное произведение

Вычислить скалярное произведение векторов:

B 1

C 1

O 1

A 1

D 1

B

C

A

D

Решение

Решение

Решение

Решение

B 1

C 1

O 1

A 1

D 1

B

C

A

D

Как найти единичный вектор, противоположно направленный \\[v=\\left( 1,3,-4 \\right)\\]?

Последняя обновленная дата: 25 января 2023 г.

•

Общее представление: 214,2K

•

Просмотр сегодня: 4,08K

Ответ

Проверено

214.2K+ виды

HINT: 9003 мы должны найти единичный вектор, направленный противоположно \[v=\left( 1,3,-4 \right)\].. Сначала мы можем увидеть, что заданное имеет противоположное направление, где мы можем умножить a знак минус к заданному вектору. Затем мы можем написать формулу для единичного вектора и расширить ее, мы можем изменить ее на противоположно направленную и мы можем вычислить оставшуюся часть, чтобы получить ответ для единичного вектора.

Полное пошаговое решение:
Мы знаем, что данный вектор равен
\[v=\left( 1,3,-4 \right)\]
Теперь мы можем написать вектор, противоположный приведенному выше вектору изменив его знак, мы получим
\[-v=-<1,3,-4>\]…….. (1)
Теперь мы можем написать формулу для противоположного единичного вектора. {2} }}\] 9{2}}}}\left( —<1,3,-4> \right)\]
Теперь мы можем упростить описанный выше шаг, мы получим
\[\Rightarrow -\dfrac{1}{26}<1 ,3,-4>\]
Следовательно, единичный вектор, противоположно направленный \[v=\left( 1,3,-4 \right)\], равен \[-\dfrac{1}{26}< 1,3,-4>\].

Примечание: Учащиеся делают ошибки при написании величины, которая находится в формуле, где величина представляет собой квадратный корень из суммы квадратов заданных величин. Мы также должны помнить, что единичный вектор — это величина, умноженная на вектор. Следует также отметить, что данное является противоположно направленным, где мы можем умножить отрицательный знак на данный вектор.

Недавно обновленные страницы

Если ab и c единичные векторы, то left ab2 right+bc2+ca2 математика класса 12 JEE_Main

Стержень AB длиной 4 единицы перемещается горизонтально, когда математика класса 11 JEE_Main

Оценить значение intlimits0pi cos 3xdx A 0 B 1 класс 12 математика JEE_Main

Что из следующего верно цианид с А Этиловый спирт класс 12 по химии JEE_Main

Если ab и c единичные векторы, то влево ab2 right+bc2+ca2 математика класса 12 JEE_Main

Стержень AB длиной 4 единицы перемещается горизонтально, когда математика класса 11 JEE_Main

Вычислить значение intlimits0pi cos 3xdx A 0 B 1 математика класса 12 JEE_Main

Что из следующего является правильным 1 nleft S чашка T справа класс 10 математика JEE_Main

Какова площадь треугольника с вершинами Aleft математика класса 11 JEE_Main

KCN легко реагирует с образованием цианида с A Этил спирт 12 класс химия JEE_Main

Сомнения в тренде

Вектор — Математическая энциклопедия

геометрический

Направленный отрезок прямой в евклидовом пространстве, один конец которого (точка $A$) называется началом координат, а другая (точка $B$) называется концом вектора. Такой вектор можно обозначить $ \mathbf a $, $ \overline{а}\; $, $\vec{a}$, или $ \overline{ {AB }}\; $. Вектор, начало и конец которого совпадают, называется нулевым вектором и обычно обозначается $\mathbf 0 $. Вектор характеризуется своим модулем (или длиной), который равен длине отрезка $AB$ и обозначается $ | \mathbf а | $, и по его направлению: от $A$ до $В$. Вектор $ \overline{BA}\; $ называется вектором, противоположным $ \overline{AB}\; $. Вектор с длиной, равной единице, называется единичным вектором. Любое направление может быть назначено нулевому вектору. Два вектора называются коллинеарными, если они расположены на одной прямой или на двух параллельных прямых; они называются компланарными, если лежат в одной плоскости или в двух параллельных плоскостях. Два коллинеарных вектора называются одинаково (противоположно) направленными, если их конечные точки находятся по одну сторону (по разные стороны) от прямой, соединяющей их начала, или по одну сторону от их общего начала. Два вектора $ \overline{AB}\; $ и $ \overline{ {A ^ \prime B ^ \prime }}\; $ на одной прямой называются одинаково (противоположно) направленными, если один из лучей $AB$, $ А ^ \простой Б ^ \простой $ полностью включено (не) в другое. Два вектора называются равными, если они имеют одинаковые модули и одинаково направлены (такие векторы также известны как свободные векторы). Все нулевые векторы называются равными.

Помимо свободных векторов, т. е. векторов, начало которых нематериально, в механике и физике часто рассматривают векторы, характеризуемые своей длиной, направлением и местом своего начала (точки приложения). Класс равных векторов, лежащих на одной прямой, называется скользящим вектором. Также рассматриваются связанные векторы, которые называются равными, если они имеют не только равные модули и одинаковые направления, но и общую точку приложения. Векторное исчисление, которое представляет собой изучение операций, выполняемых над векторами, основано на свободных векторах, поскольку два заданных свободных вектора эквивалентны заданному скользящему вектору или заданному связанному вектору.

Понятие вектора возникло как математическая абстракция объектов, которые характеризуются величиной и направлением, такими как смещение, скорость и напряженность магнитного или электрического поля.

Понятие вектора может быть введено аксиоматически (ср. Векторное пространство).

Комментарии

Геометрический вектор, как определено выше, исходит из таких понятий, как сила в механике, величина, которая имеет величину, направление и точку приложения. Математическая установка — это установка аффинного пространства, которое является векторным пространством «с точностью до места его начала» или, точнее, просто транзитивным групповым действием $ \phi $ (лежащей в основе аддитивной группы) векторного пространства $ L $ на множестве $A$. Простая транзитивность определяет отображение $ \theta : A \times A \rightarrow L $ характеризуется $\phi(\theta(x,y),x)=y$. Написание $ \vec{xy} $ для $\тета(x,y)$, $ \vec{ху} $ — свободный вектор, определяемый связанным вектором или геометрическим вектором, $ ( x, y) $ или $ ( x, \vec{xy} ) $( которая имеет точку приложения $ x $ а направление и величина задаются $ \vec{xy} $). Для трех точек $ x, y , z \in A $ есть $ \vec{xy} + \vec{yz} + \vec{zx} = 0 $ в $L$, которое называется отношением Шаля (ср.