trigonometrija_21_P-1 — презентация онлайн
Похожие презентации:
Градусная и радианная меры угла. Вращательное движение. Синус, косинус, тангенс и котангенс
Радианная мера угла. Синус, косинус, тангенс числа
Угол поворота. Радианная мера угла
Алгебра и начала анализа. (10 класс)
Радианная мера угла
Угол поворота. Радианная мера угла
Тригонометрия
Начала тригонометрии
Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс)
Тригонометрическая окружность. Тригонометрические функции
Тригонометрические формулы
Глава V стр.115-164
Радианная мера угла
п.21 стр. 115-118
Немного из истории…
1. Древние вавилоняне и египтяне изучали
тригонометрию как часть астрономии;
разделили окружность на 360
2. Древние индийцы: ввели названия
«синус», «косинус», составили таблицы
синусов, косинусов
3. IX-XVвв – Средний и Ближний восток:
составляли таблицы котангенса, тангенса,
окружности
Учёные, которые внесли свой вклад в развитие тригонометрии
Архимед
Жозеф Луи
Лагранж
Фалес
Тригонометрия
(«три» — три, «гониа» — угол,
«метриа» — измеряю)
раздел математики,
изучающий
соотношение сторон
и углов в треугольнике
Тригономе́трия (от греч.
τρίγονο(треугольник) и греч. μετρειν (измерять),
то есть измерение треугольников) —
раздел математики, в котором
изучаются тригонометрические
функции и их приложения к геометрии.
Градусная мера угла
=1
1 – цена одного деления
окружности, разделенной на
360 частей
7. Числовая окружность
Числовая окружность – это единичнаяокружность, точки которой соответствуют
определенным действительным числам.
Единичной окружностью называют
окружность радиуса 1.
8. Общий вид числовой окружности
Каждой точке прямойставится в
соответствие некоторая
точка окружности.
Центральный угол,
опирающийся на дугу,
длина которого равна
радиусу окружности,
называется углом в один
радиан.
10. Радианная мера угла
у90°
Р
1 радиан это центральный
угол, длина дуги которого
равна радиусу окружности
0
180°
О
0°
360°
х
180
57 °
1 радиан =
180°= рад
180° развёрнутый угол
270°
90° прямой угол
2
360° полный угол 2
Единицы
измерения углов
Радианы
Градусы
радиан=180
Перевод из радианной меры
в градусную:
180
1 радиан
0
180
рад
0
Перевод из градусной меры
в радианную:
1
0
0
180
180
рад
рад
Перевод из градусной меры в
радианную:
0
180
Перевод из радианной меры в
градусную:
180
0
№1: Переведите в радианную меру
углы:
0
1) 45
2) 15
3) 72
180
№1: Переведите в радианную меру
углы:
0
4) 225
5) 360
6) 150
180
№ 2.
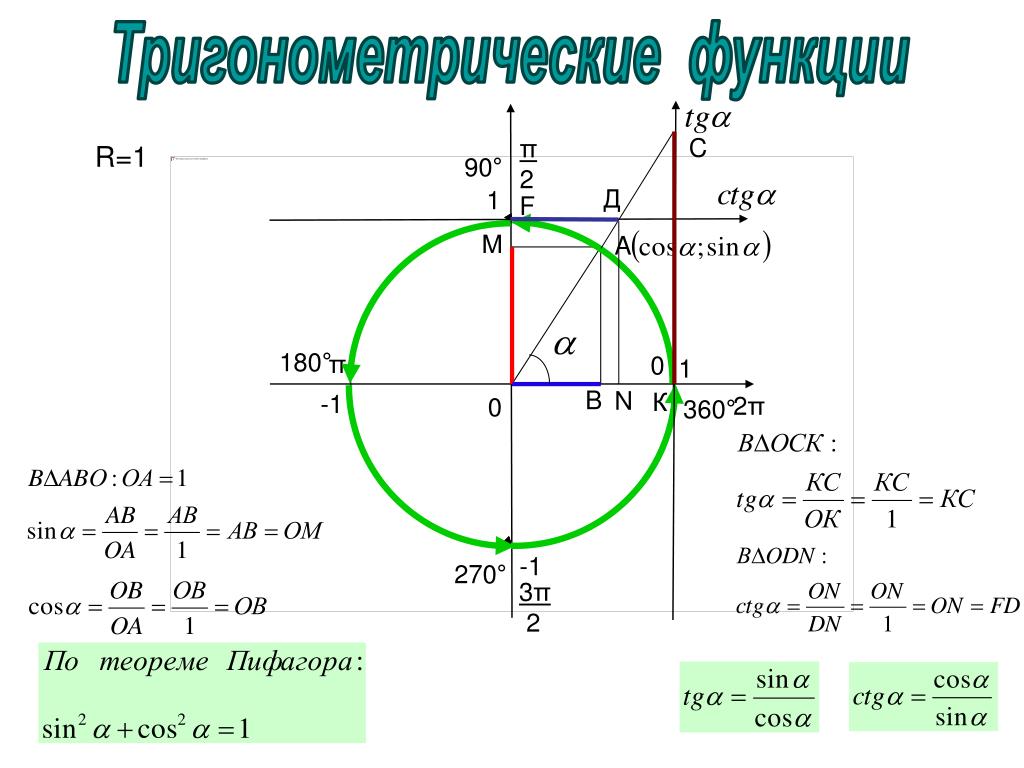Перевести в градуснуюмеру углы и построить:
1)
2)
3)
3
4
9
180
0
Перевести в градусную меру
0
углы и построить:
180
3
4)
5
7
5)
6
6) 5
19. Поворот точки вокруг начала координат п. 22 стр. 119-123
Задание:1.Изучить п. 22. стр. 119-120.
2.Разобрать задачу 1 стр.122.
3.Решить № 416(2,4),417(2,4) стр. 123
English Русский Правила
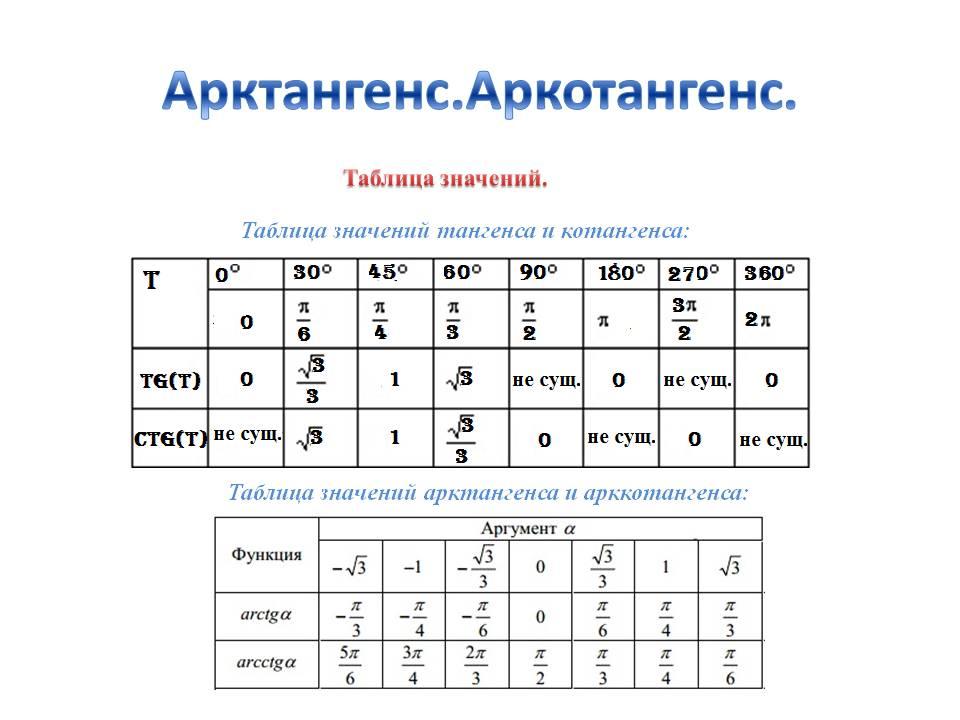
Тригонометрическая таблица — определение, как создать, примеры и часто задаваемые вопросы
Тригонометрическая таблица — это стандартная таблица, которая помогает нам находить значения тригонометрических соотношений для стандартных углов, таких как 0°, 30°, 45°, 60° и 90°. °. Тригонометрическая таблица содержит все шесть тригонометрических соотношений: синус, косинус, тангенс, косеканс, секанс, котангенс. Тригонометрические функции, также известные как гониометрические функции, угловые функции или круговые функции, — это функции, которые устанавливают связь между углом и отношением двух сторон прямоугольного треугольника.
Тригонометрические функции полезны для изучения различных типов углов, треугольников и других объектов.
Определение тригонометрической таблицы
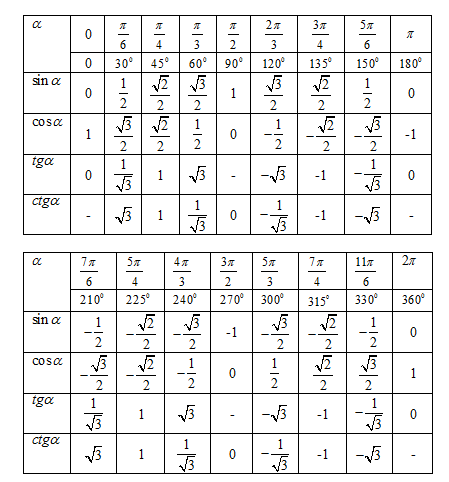
Табличное представление значений всех шести тригонометрических функций для их общих углов называется тригонометрической таблицей. Значение различных тригонометрических отношений можно узнать с помощью приведенной ниже таблицы:
Тригонометрические функции
Тригонометрия имеет 6 основных тригонометрических функций: синус, косинус, тангенс, косеканс, секанс и котангенс. Теперь давайте рассмотрим тригонометрические функции. Для любого прямоугольного треугольника с перпендикуляром (P), основанием (B) и гипотенузой (H) шесть тригонометрических функций следующие:0003
Советы по изучению тригонометрических соотношенийСинус: Определяется как отношение перпендикуляра к гипотенузе и представляется как sin θ
Косинус: Определяется как отношение основания к гипотенузе и представляется как cos θ
Тангенс: Определяется как отношение синуса и косинуса угла.
Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как tan θ
Косеканс: Это величина, обратная sin θ, и представляется как cosec θ.
Секанс: Это величина, обратная cos θ, обозначается как sec θ.
Котангенс: Это величина, обратная тангенсу θ, и представляется как cot θ.
Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как tan θИзучите приведенную ниже таблицу, чтобы легко запомнить тригонометрические соотношения.
| Некоторые люди имеют вьющиеся черные волосы, чтобы создать красоту0056 |
|---|
| cos θ (кудрявый) = основание (черный) / гипотенуза (волосы) |
| загар θ (к) = перпендикуляр (производство) / основание (красота) |
Как создать тригонометрическую таблицу?
Изучите следующие шаги, чтобы создать тригонометрическую таблицу стандартных углов.
Шаг 1: Создайте таблицу
Создайте таблицу и перечислите все углы, такие как 0°, 30°, 45°, 60° и 90°, в верхней строке. Введите все тригонометрические функции sin, cos, tan, cosec, sec и cot в первый столбец.
Шаг 2: Оцените значение для всех углов функции sin.
Для нахождения значений функции sin разделите 0, 1, 2, 3 и 4 на 4 и возьмите под корень каждого значения соответственно как
Для значения sin 0° = √( 0/4) = 0
Аналогично,
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/ 4) = √3/2
sin 90° = √(4/4) = 1
| sin 0° | sin 30° | SIN 45 ° | SIN 60 ° | SIN 90 ° | ||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1/a Оценить значение для всех углов функции cos Значение функции cos противоположно значению функции sin, т.
Шаг 4: Оценка значения для всех углов функции тангенса Значение функции тангенса равно функции sin, деленной на функцию cos, т. е. tan x = sin x / cos x . Значение всех углов в функции тангенса рассчитывается как tan 0 ° = sin 0 ° / cos 0 ° = 0/1 = 0, аналогично
Шаг 5: Оценить значение для всех углов от функции COSEC 9000 3 9000 3 9000 3 функция равна обратной функции sin.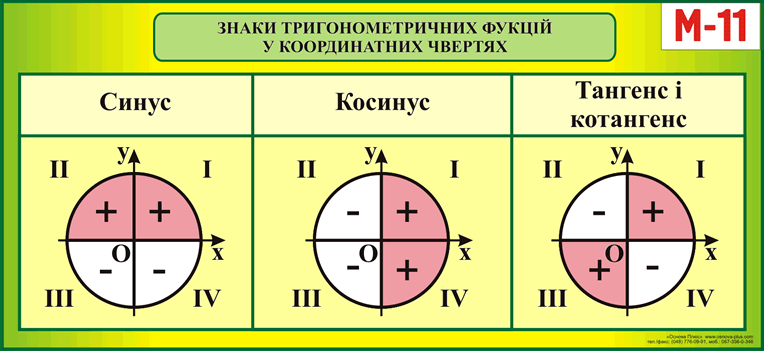 Значение cosec 0° получается путем взятия обратной величины sin 0°cosec 0° = 1 / sin 0° = 1 / 0 = не определено. Similarly,
Шаг 6: Оцените значение для всех углов функции sec Значение функции sec равно обратному значению функции cos. Значение sec 0° получается путем взятия обратной величины cos 0° с 0 ° = 1 / cos 0 ° = 1 /1 = 1. Аналогично,
Шаг 7: Оценить значение для всех углов от Cot Fecund функция равна обратной функции тангенса. с 0 ° = 1 / cos 0 ° = 1 /1 = 1. Аналогично,
Расположите все полученные значения тригонометрической таблицы в тригонометрическую таблицу. Тригонометрические тождества (дополнительные и дополнительные углы)
Также чек 9212 Решенные примеры по тригонометрии Пример 1: Если sin θ = 4/5, то найти все тригонометрические значения. Решение:
Пример 2: Найдите значение COS 45 ° + 2 sin 60° – тангенс 60°. Решение:
Пример 3. Найдите значение cos 75°. Решение:
Часто задаваемые вопросы по тригонометрии ТаблицаВопрос 1: Что такое тригонометрия? Ответ:
Вопрос 2. Что такое тригонометрическая таблица? Ответ:
Вопрос 3: Что такое стандартные углы в тригонометрической таблице? Ответ:
Вопрос 4: Каково значение тангенса 45 градусов? Ответ:
Wndsn Quadrant TelemetersГрафические телеметрические компьютеры Wndsn: Низкотехнологичные, высокоэффективные номограммы расстояний и высот от лаборатории прикладных наук Wndsn 2021-12-02: 5-е издание руководства Quadrant Telemeter теперь доступно в нашем магазине и на Amazon. Телеметры Wndsn Quadrant Учебные пособия Использование и применение
Лучший инструмент тот, который у тебя с собой, на тебе.
При навигации в неблагоприятных условиях нам нужно больше, чем просто догадки, чтобы благополучно вернуться домой. Модель наихудшего случая, основанная на нашем исследовании высоких частот, — это реальность, в которой электричество и сети передачи данных недоступны или недоступны. В Wndsn мы задаемся вопросом, что происходит, когда гаснет свет. Мы спрашиваем, что нам понадобится, что нельзя импровизировать. Если электроника перестанет работать, все наши привычные стратегии и технологические решения станут недоступны. С дальномерами можно импровизировать, но с правильными инструментами мы можем повысить точность на один или даже два порядка, чтобы увидеть разницу между поиском и обнаружением. Решение состоит в том, чтобы вернуться в эпоху электричества и поискать проверенные и верные знания, которые были достаточно хороши для поколений. Ответ очевиден: низкие технологии. Военно-морские силы по всему миру до сих пор предлагают своим гардемаринам обучение секстанту, зная, что всегда есть место для искусства и науки низкотехнологичной (но высоко полезной) навигации. Секстант и его предшественники, традиционная астрономическая навигация, геодезия, триангуляция, а также аналоговые методы навигации составляют ДНК наших телеметров. О Wndsn Лаборатория прикладных наук Wndsn, базирующаяся в Берлине, разрабатывает и производит низкотехнологичных инструментов и приборов с высокими эксплуатационными характеристиками с целью предоставления или улучшения «того, что нельзя импровизировать» в маловероятных сценариях с высокой степенью воздействия там, где это наиболее необходимо, но обычно недоступно или недопустимо. Wndsn создает специальные инструменты и многоцелевые инструменты, решения для измерения и освещения для применения в городской разведке, враждебных театрах военных действий, зонах стихийных бедствий и исследованиях на открытом воздухе. Кроме того, разработка сувениров об экспедициях и нашивок с боевым духом, чтобы отметить междисциплинарные исследования и достижения. Wndsn производит продукты архивного качества, разработанные с намерением сочетать методы, проверенные веками, объединяя раннюю историю науки с передовыми современными методами, что приводит к культовым, неподвластным времени, высокофункциональным конструкциям. Патчи морального духа Wndsn продуманы до мелочей — ни одна линия не оставлена на произвол судьбы, ни один элемент не является простым наполнителем. Они служат инфографикой, инструкциями по работе с инструментами Wndsn, магическими символами, а также функциональными маркерами. |
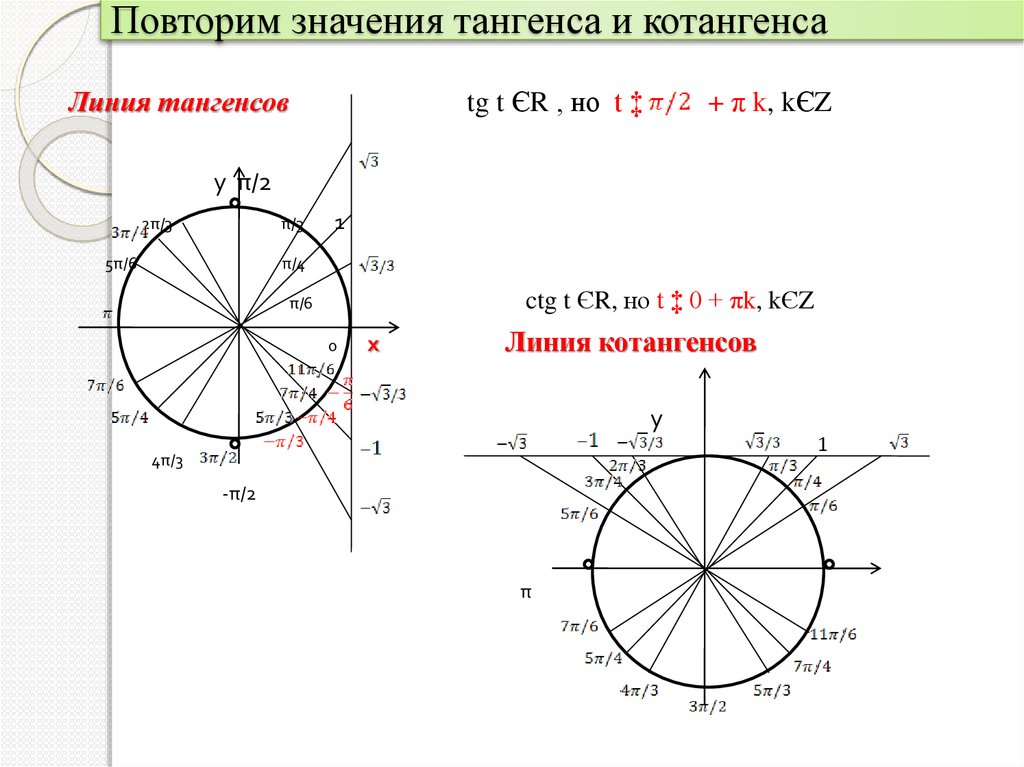е. cos 0° = sin 90°, cos 30° = sin 60° и cos 45° = sin 45°, поэтому
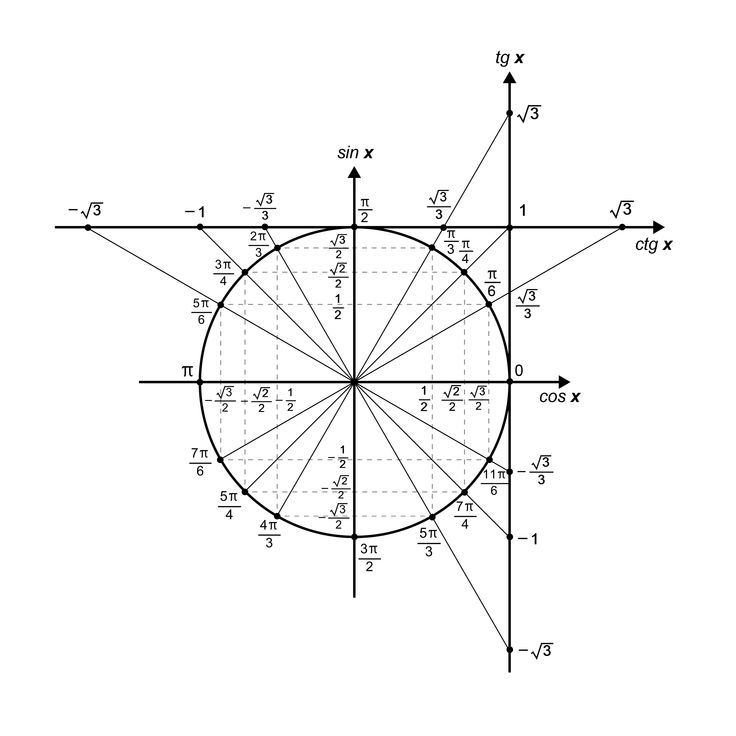Значение cot 0° получается путем взятия обратной величины cos 0°
Телеметры Wndsn — это номограммы расстояний и высот размером с бумажник, разработанные в лаборатории прикладных наук Wndsn. Телеметры Wndsn сочетают в себе тысячелетний опыт гражданского строительства, геодезии, навигации и астрономии в одном надежном, низкотехнологичном, высокофункциональном приборе, который можно взять с собой куда угодно, он автономен и не зависит от внешних современных технологий. Wndsn Telemeters — это инструменты для наблюдения невооруженным глазом, которые предлагают различные средства измерения углового размера, а также графические компьютеры, предоставляющие функции для обработки или преобразования измеренных значений. Их цель — помочь вам ориентироваться по известным ориентирам или астрономическим объектам, перепроверить значения, полученные разными способами, или в экстренных ситуациях, когда другие методы не работают или недоступны. 
Могут быть обстоятельства, когда вы не можете определить расстояние с помощью карты или где вы находитесь без карты. Поэтому очень важно изучить методы, с помощью которых вы можете точно определять шаг, измерять, использовать субтенсию или оценивать расстояния на земле. 
Полученные продукты представляют собой измерительные, расчетные и исследовательские инструменты, основанные на девизе «Ex Mensura, Scientia» — знание из измерения.