Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376184 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
RU
- Class
RU
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |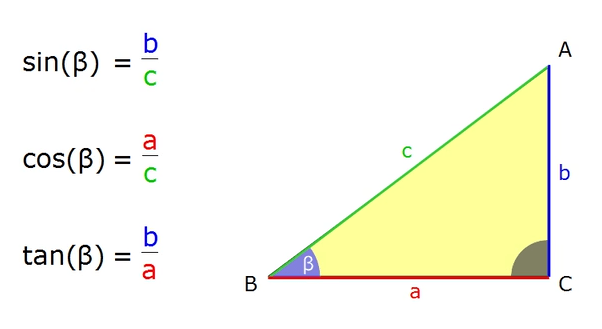
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |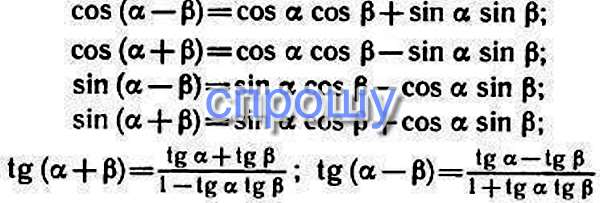
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |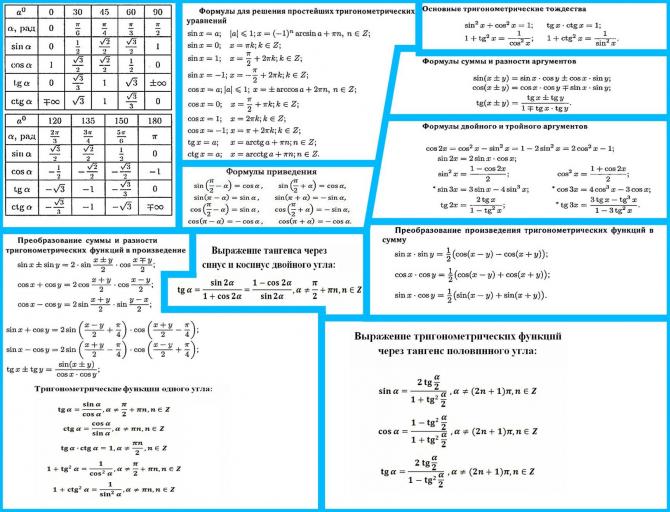
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |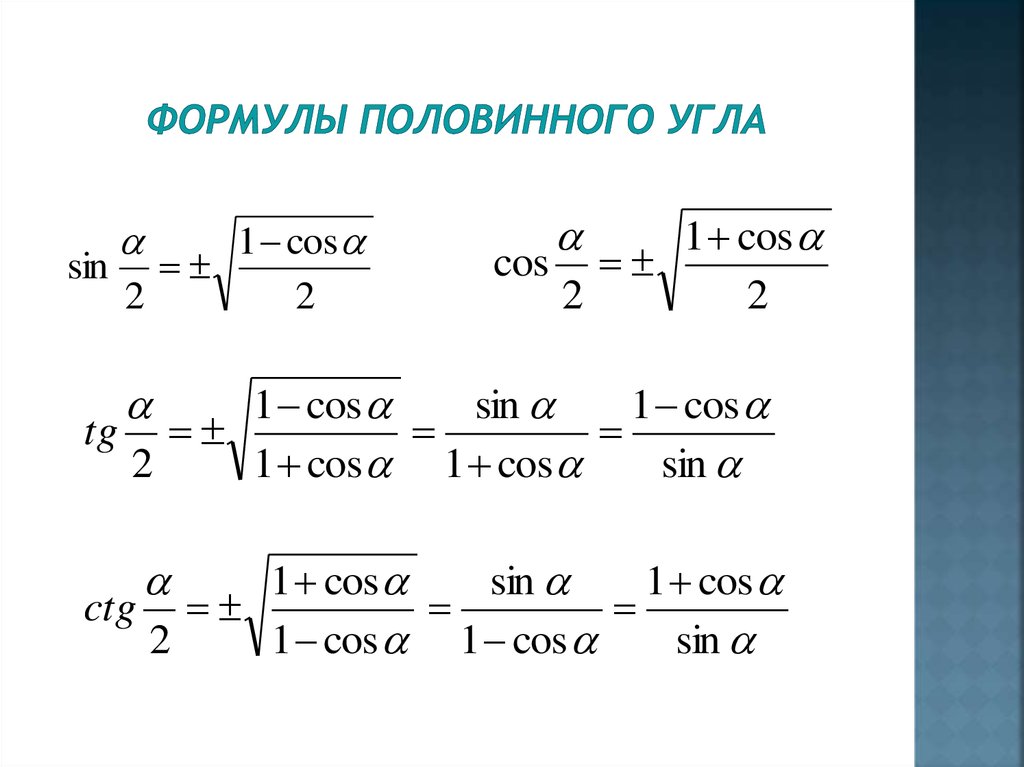
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |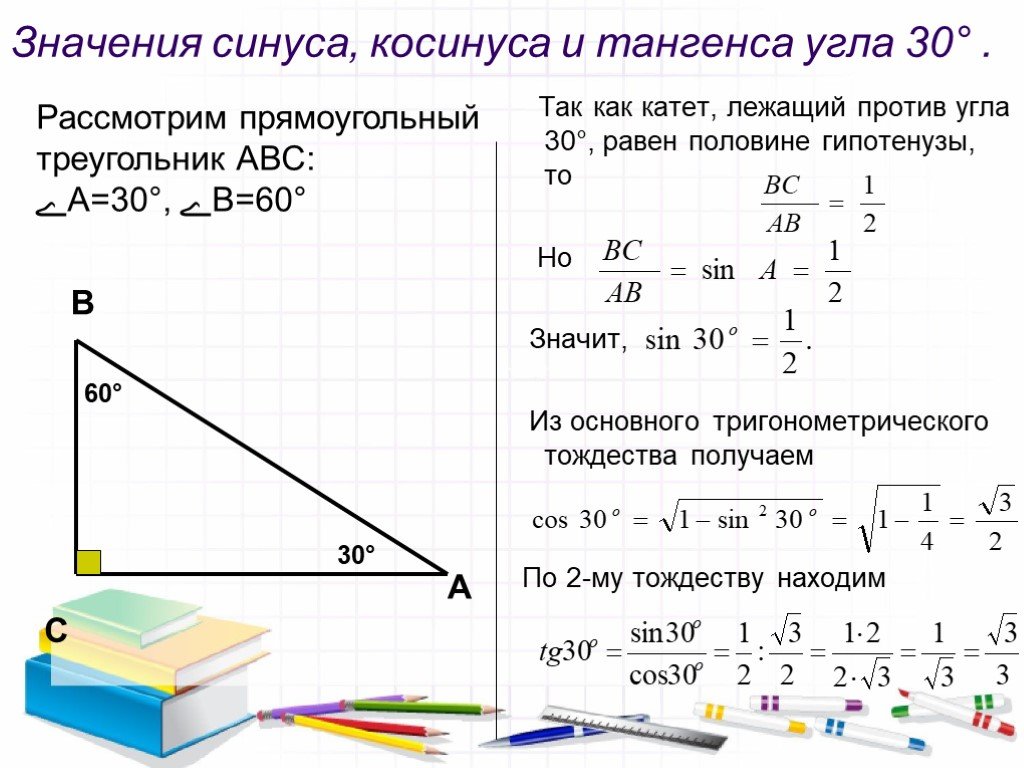
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |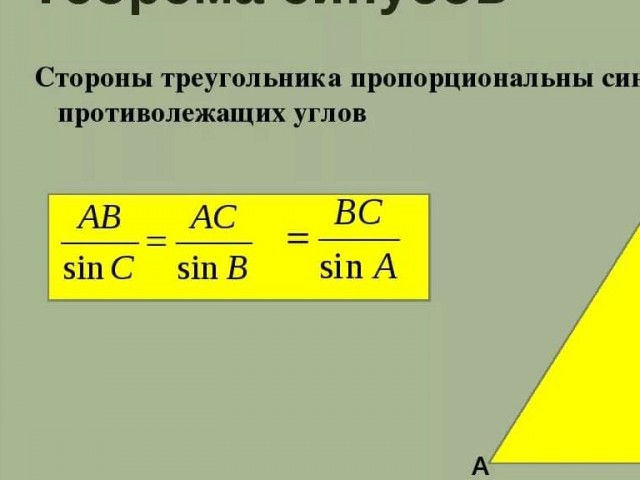
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Вопрос Видео: Тождества для степеней косинуса
Стенограмма видео
Выразите cos в шестой степени 𝜃 через cos шесть 𝜃, cos пять 𝜃, cos четыре 𝜃, cos три 𝜃, cos два 𝜃, cos 𝜃 и любые постоянные сроки.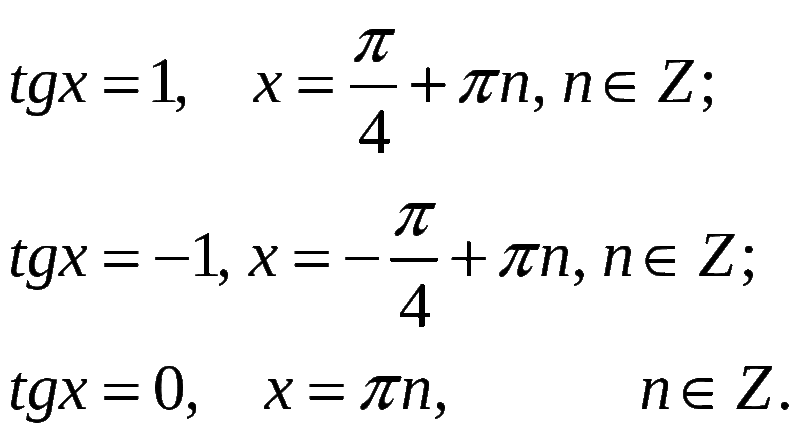
В этом вопросе мы хотим найти выражение для cos в шестой степени 𝜃. И это выражение должно состоять из членов, которые включают только целое число, кратное значениям 𝜃, и постоянные члены. В некоторых вопросах, подобных этому, можно найти выражения для каждой из этих формул множественных углов для косинуса, а затем получить наш ответ, равный тому, что мы хотим, в данном случае косинус в шестой степени 𝜃. Однако для этого нам нужно будет сделать это для каждой из формул множественного угла в вопросе. Таким образом, хотя этот метод и возможен, он потребует очень много времени и потребует множества проб и ошибок.
Вместо этого нам нужно вспомнить, что мы можем найти подобные выражения, используя теорему де Муавра. Итак, чтобы ответить на этот вопрос, мы начнем с того, что вспомним теорему де Муавра. Одна версия этого говорит, что для любого целочисленного значения 𝑛 и действительного числа 𝜃, cos 𝜃 плюс 𝑖 грех 𝜃, все возведенные в 𝑛-ю степень, равны косу 𝑛𝜃 плюс 𝑖 грех 𝑛𝜃.
Однако, если бы мы попытались напрямую использовать это выражение для ответа на наш вопрос, у нас могли бы возникнуть трудности. Поскольку мы хотим найти выражение для cos в шестой степени 𝜃, нам нужно установить 𝑛 равным шести, чтобы в нашем выражении появился cos в шестой степени. Однако, когда мы распределяем 𝑛-ю степень по нашим скобкам, мы получим кос-термы пятой степени, кос-термы четвертой степени, вплоть до кос-членов нулевой степени.
Кажется, что избавиться от всех этих терминов будет очень сложно. Поэтому вместо этого нам нужно будет вспомнить очень полезный результат. Если мы назовем комплексное число в наших скобках 𝑧, то теорема де Муавра говорит нам, что 𝑧 в 𝑛-й степени равно косинусу 𝑛𝜃 плюс 𝑖 греху 𝑛𝜃. И затем мы можем использовать теорему де Муавра, чтобы найти два полезных результата: 𝑧 в 𝑛-й степени плюс один над 𝑧 в 𝑛-й степени равен двум cos от 𝑛𝜃 и 𝑧 в 𝑛-й степени минус один над 𝑧 в 𝑛-й степени равен к двум 𝑖 греху 𝑛𝜃. И чтобы доказать эти результаты, мы напрямую используем теорему де Муавра, которая, как мы помним, верна для любого целочисленного значения 𝑛.
И мы знаем, что единица на 𝑧 в 𝑛-й степени такая же, как 𝑧 в отрицательной степени 𝑛.
Эти результаты очень полезны, и их стоит запомнить. Мы собираемся сосредоточиться на верхнем результате, который мы собираемся использовать, чтобы найти выражение для cos в шестой степени 𝜃. Мы начинаем с установки нашего значения 𝑛 равным единице в этом выражении. Это дает нам два cos 𝜃 равно 𝑧 плюс один больше 𝑧. И помните, вопрос требует, чтобы мы нашли выражение для cos в шестой степени 𝜃, поэтому мы собираемся возвести обе части этого уравнения в шестую степень. В левой части нашего уравнения мы можем упростить, взяв шестую степень обоих наших двух факторов. Это дает нам два в шестой степени, умноженные на cos в шестой степени 𝜃. И мы можем упростить это, поскольку мы знаем, что два в шестой степени равно 64.
Таким образом, левая часть нашего уравнения упрощается и дает нам 64 cos в шестой степени числа 𝜃. И в правой части нашего уравнения у нас есть сумма двух чисел, возведенных в степень.
Мы можем сделать это, используя биномиальную формулу. Напомним, это говорит нам о том, что для любого положительного целого числа 𝑚, 𝑎 плюс 𝑏, возведенных в 𝑚-ю степень, равно сумме от 𝑟 равно нулю до 𝑚 из 𝑚 выбрать 𝑟, умноженное на 𝑎 в степени 𝑟, умноженное на 𝑏 в степени 𝑚 минус 𝑟. Таким образом, мы можем использовать это, чтобы распределить показатель степени шести по правой части нашего уравнения. Мы получаем, что шесть выбирают ноль 𝑧 в шестой степени плюс шесть выбирают один раз 𝑧 в пятой степени умножают на единицу больше 𝑧 плюс шесть выбирают два раза 𝑧 в четвертой степени умножают на единицу больше 𝑧 все в квадрате. И затем мы продолжаем добавлять термины этой формы до шести, выбираем шесть, умножаем на единицу и 𝑧 все возводим в шестую степень.
Помните, вопрос требует, чтобы мы нашли выражение для cos в шестой степени 𝜃. Но он хочет этого с точки зрения нескольких углов 𝜃. Мы можем изменить это, чтобы получить cos в шестой степени 𝜃. Однако правая часть этого выражения выражена в терминах 𝑧; это еще не с точки зрения cos углов 𝜃.
Это означает, что нам нужно упростить правую часть нашего уравнения. Мы будем делать это по срокам. В нашем первом члене шесть выбирают ноль равным единице, поэтому первый член — это просто 𝑧 в шестой степени. В нашем втором члене шесть выбирают один равно шести, а 𝑧 в пятой степени, умноженное на единицу над 𝑧, можно упростить, используя наши законы показателей. Это равно 𝑧 в четвертой степени. Итак, наш второй член равен шести 𝑧 в четвертой степени.
В нашем третьем члене шесть выбирают два равно 15, а 𝑧 в четвертой степени, умноженное на единицу в квадрате 𝑧, равно 𝑧 в четвертой степени в квадрате 𝑧, что равно 𝑧 в квадрате. Итак, наш третий член равен 15𝑧 в квадрате. Точно так же мы можем упростить и остальные члены этого разложения. Получаем 20, 15 больше 𝑧 в квадрате, шесть больше 𝑧 в четвертой степени и один больше 𝑧 в шестой степени. И теперь мы можем заметить кое-что интересное. Мы можем упростить это выражение, используя теорему Муавра. Например, у нас есть первый член в этом расширении плюс последний член в этом расширении — это 𝑧 в шестой степени плюс единица сверх 𝑧 в шестой степени.
Установив 𝑛 равным шести в нашем полезном результате, мы знаем, что это равно удвоенному cos шести 𝜃. И это не единственный раз, когда этот результат появляется в нашем дополнении. Мы можем использовать это еще два раза.
Итак, мы объединим термины в нашем расширении, чтобы получить 𝑧 в шестой степени плюс один больше 𝑧 в шестой степени плюс шесть 𝑧 в четвертой степени плюс шесть больше 𝑧 в четвертой степени плюс 15𝑧 в квадрате плюс 15 больше 𝑧 в квадрате плюс 20. И прежде чем мы применим теорему Муавра, мы можем заметить кое-что интересное. В нашем первом наборе скобок мы можем убрать общий множитель шесть. И точно так же в нашем третьем наборе скобок мы можем убрать общий множитель 15. Это дает нам следующее выражение. И теперь мы можем упростить все три набора скобок, используя теорему Муавра. Установив 𝑛 равным шести, мы знаем, что 𝑧 в шестой степени плюс один сверх 𝑧 в шестой степени равно двум из шести 𝜃. Если 𝑛 равно четырем, 𝑧 в четвертой степени плюс один сверх 𝑧 в четвертой степени равно двум, потому что четыре 𝜃.
А если 𝑛 равно двум, 𝑧 в квадрате плюс один на 𝑧 в квадрате равно двум производным от двух 𝜃.
Итак, подставив эти выражения в и вспомнив, что нам нужно умножить на наши коэффициенты, и нам еще нужно добавить 20 в конце, мы получаем 64 cos в шестой степени 𝜃 равно двум cos из шести 𝜃 плюс 12 cos из четыре 𝜃 плюс 30 потому что два 𝜃 плюс 20. И теперь это почти в том виде, в котором мы хотим. Все, что нам нужно сейчас, это переставить так, чтобы cos в шестой степени 𝜃 стало предметом. И для этого нам нужно разделить обе части нашего уравнения на 64. Итак, чтобы сделать это, давайте начнем с расчистки места. У нас есть cos в шестой степени 𝜃 равно следующему выражению. И чтобы оценить это, мы собираемся разделить каждый член в этом выражении на 64.
Сделав это, мы получим два потому что шесть 𝜃 все больше 64 плюс 12 потому что четыре 𝜃 все больше 64 плюс 30 потому что два 𝜃 все больше 64 плюс 20 разделить на 64. Все, что осталось сделать сейчас, это отменить все общие множители два в нашем числителе и знаменателе для всех четырех наших терминов.
Получаем следующее выражение. И это дает нам окончательный ответ. Следовательно, с помощью теоремы де Муавра мы смогли выразить косинус в шестой степени 𝜃 через косинусы целых кратных углов 𝜃. Мы получили потому что в шестой степени 𝜃 равно единице на 32 умножить на шесть 𝜃 плюс три на 16 умножить на четыре 𝜃 плюс 15 на 32 умножить на два 𝜃 плюс пять на 16.
четные-и-нечетные-триггерные-функции-примеры — Google
AlleBilderVideosShoppingMapsNewsBücher
suchoptionen
Косинус и секанс четны; синус, тангенс, косеканс и котангенс нечетны.
6. Окт. 2021
7.4: Другие тригонометрические функции — Math LibreTexts
math.libretexts.org › … › 7: Единичная окружность — функции синуса и косинуса
Hervorgehobene Snippets
Ähn050 Fragen
4 Как определить, является ли функция четной или нечетной Примеры?
Косеканс четный или нечетный?
Что такое нечетная и четная функция на одном примере?
Четные и нечетные триггерные функции — Softschools.
com
www.softschools.com › математика › тригонометрия › четный…
Все функции, включая триггерные, могут быть описаны как четные, нечетные или никакие. Функция нечетна тогда и только тогда, когда f(-x) = — f(x) и симметрична …
Sin(-x) = — sin x: csc (-x) = — csc x
Cos (-x) = cos x: sec (-x) = sec x
Tan (-x) = — tan x: tan (-x) = — cot x
Четные и нечетные тригонометрические функции и тождества — YouTube
www.youtube.com › смотреть
24.06.2017 · … четные и нечетные тригонометрические тождества для вычисления тригонометрических функций синуса, косинуса и тангенса …
Dauer: 10:51
Прислан: 24.06.2017
Что такое четные и нечетные тригонометрические функции — YouTube
www.youtube.com › смотреть
08.11.2012 · Мы будем исследовать такие тождества, как взаимное, частное, пифагорейское, кофункция и даже …
Dauer: 4:05
Прислан: 08.11.2012 Нечетное или ни одно
www.
onlinemathlearning.com › тригонометрические функции-четные-…
Примеры с тригонометрическими функциями: четное, нечетное или ни то, ни другое. В этих уроках мы рассмотрим, как определить, является ли тригонометрическая функция четной, нечетной или …
Как использовать четные и нечетные свойства тригонометрических функций
Study.com › навык › учиться › как использовать четные-нечетные пр…
Научиться использовать четные и нечетные свойства тригонометрических функций функции, а также просмотрите примеры, которые шаг за шагом решают примеры задач, чтобы улучшить свои …
Какие примеры нечетных и четных тригонометрических функций можно привести?
www.quora.com › Какие-примеры-нечетной-четной-тригонометрии…
Когда тригонометрическая функция четна? · Четная функция – это такая функция, что f(-x) = f(x). · Косинус – всегда четная функция, · А поскольку секанс – это …
Тригонометрические четно-нечетные функции | Brilliant Math & Science Wiki
блестящий.