Таблица корней степени 3: Таблица корней | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Содержание

Таблица корней | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Корень – это обратное действие от степени, поэтому у него также имеется своя степень. Квадратный корень является обратным действием от второй степени, которая еще именуется квадратом, так как геометрически берет свое начало в вычислениях площади этой фигуры. Это самый распространенный корень по частоте использования, поэтому в его обозначении степень не пишется, а лишь подразумевается. Следующий по частоте запроса – это кубический корень, корень третьей степени. Третья степень называется кубом, так как ее посредством вычисляется объем куба, соответственно корень третьей степени также становится кубическим. В данном разделе приведены таблицы корней второй и третьей степени, где значение находится в центральных ячейках таблицы. Цифра десятков квадрата или куба записана по вертикали, а цифра единиц – по горизонтали, таким образом, пересечение нужной строки и столбца дает значение корня.

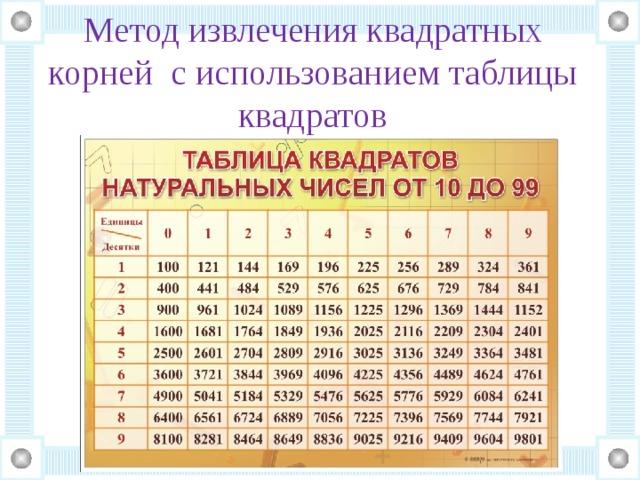
Таблица квадратных корней от 1 до 99

√x	0	1	2	3	4	5	6	7	8	9
0	0	1	1,41421	1,73205	2	2,23607	2,44949	2,64575	2,82843	3
1	3,16228	3,31662	3,4641	3,60555	3,74166	3,87298	4	4,12311	4,24264	4,3589
2	4,47214	4,58258	4,69042	4,79583	4,89898	5	5,09902	5,19615	5,2915	5,38516
3	5,47723	5,56776	5,65685	5,74456	5,83095	5,91608	6	6,08276	6,16441	6,245
4	6,32456	6,40312	6,48074	6,55744	6,63325	6,7082	6,78233	6,85565	6,9282	7
5	7,07107	7,14143	7,2111	7,28011	7,34847	7,4162	7,48331	7,54983	7,61577	7,68115
6	7,74597	7,81025	7,87401	7,93725	8	8,06226	8,12404	8,18535	8,24621	8,30662
7	8,3666	8,42615	8,48528	8,544	8,60233	8,66025	8,7178	8,77496	8,83176	8,88819
8	8,94427	9	9,05539	9,11043	9,16515	9,21954	9,27362	9,32738	9,38083	9,43398
9	9,48683	9,53939	9,59166	9,64365	9,69536	9,74679	9,79796	9,84886	9,89949	9,94987

Таблица кубических корней от 1 до 99

³√x	0	1	2	3	4	5	6	7	8	9
0	0	1	1,25992	1,44225	1,5874	1,70998	1,81712	1,91293	2	2,08008
1	2,15443	2,22398	2,28943	2,35133	2,41014	2,46621	2,51984	2,57128	2,62074	2,6684
2	2,71442	2,75892	2,80204	2,84387	2,8845	2,92402	2,9625	3	3,03659	3,07232
3	3,10723	3,14138	3,1748	3,20753	3,23961	3,27107	3,30193	3,33222	3,36198	3,39121
4	3,41995	3,44822	3,47603	3,5034	3,53035	3,55689	3,58305	3,60883	3,63424	3,65931
5	3,68403	3,70843	3,73251	3,75629	3,77976	3,80295	3,82586	3,8485	3,87088	3,893
6	3,91487	3,9365	3,95789	3,97906	4	4,02073	4,04124	4,06155	4,08166	4,10157
7	4,12129	4,14082	4,16017	4,17934	4,19834	4,21716	4,23582	4,25432	4,27266	4,29084
8	4,30887	4,32675	4,34448	4,36207	4,37952	4,39683	4,414	4,43105	4,44796	4,46475
9	4,4814	4,49794	4,51436	4,53065	4,54684	4,5629	4,57886	4,5947	4,61044	4,62607

Как правильно извлечь корень числа?

Благодаря прочтению этой статьи вы научитесь:

Извлекать корни из разных чисел;
Решать разнообразные задания по этой тематике;
Применять удобные таблицы на практике.

А также пополните свой мозг новыми знаниями, что всегда хорошо и полезно! Приятным бонусом для вас будут задания для отработки материала с ответами, которые вы сможете найти в конце этой статьи. Что значит понятие: «Извлечение корня из числа»?

Определение

Извлечение корня из числа — это нахождение значения корня, т.е. действие, обратное возведению в степень.

Числа b и a равны, ведь при извлечении корня n-ной степени одного из чисел, мы, соответственно, находим и второе.

n — натуральное число, являющиеся степенью корня.
a — подкоренное значение.

Интересно

При помощи разложения функции в ряд можно показать, что сумма всех натуральных чисел равна:

1/12[18]

Когда следует извлекать корень? Если вы видите, что a можно представить в виде n-ной степени какого-либо числа b, то корень a можно извлечь.

Определение

Квадратный корень из числа — это неизвестное число, которое дает это же число при возведении его в квадрат.

Пример извлечения корня:

√25=5×5 — из этого становится ясно, что квадратный корень числа равен 5.

В обратной ситуации, когда нельзя представить корень n-ной степени из числа a, в виде n-ной степени числа b, корень не извлекается или находится лишь приближенное значение этого корня.

Пример:

√6≈√2,44949

Для этого используют различные виды решений, начиная с калькулятора, заканчивая формулами. Калькулятор хоть и посчитает все вместо нас, но не всегда мы можем его применить. Поэтому важно знать другие варианты нахождения приближенного значения корня.

Способы извлечения корня

Для того, чтобы найти значение корня, существуют такие способы извлечения корня, как:

Применение различных таблиц.
Разложение чисел или выражений на простые множители.
Извлечение корней из дробных чисел.
Извлечение отрицательного корня.
Поразрядное нахождение значения корня.

Они основываются на свойствах корней. Далее рассмотрим таблицы, которые могут помочь в процессе извлечения корней.

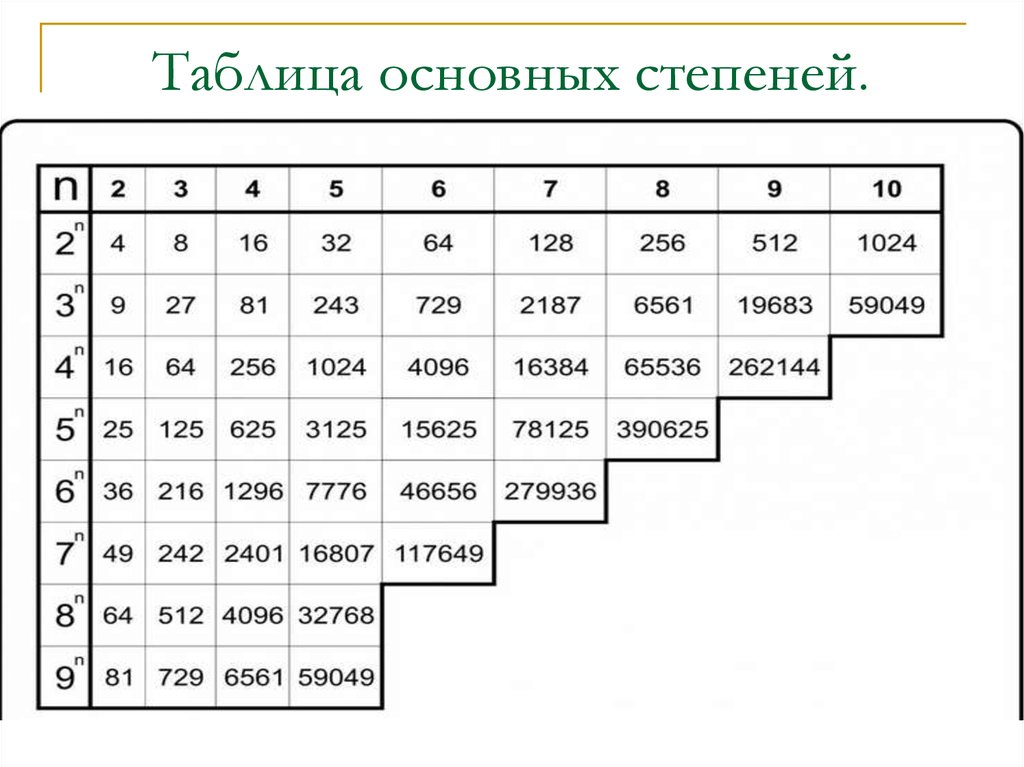
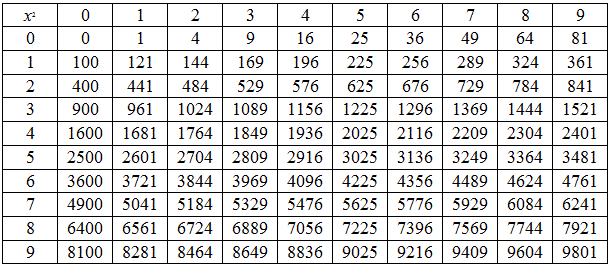
Квадраты натуральных чисел

Основной является таблица квадратов натуральных чисел:

	0	1	2	3	4	5	6	7	8	9
0	0	1	4	9	16	25	36	49	64	81
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Она, пожалуй, самая распространенная среди школьников. Если в какой-то важный момент она вам необходима, но у вас отсутствует к ней доступ, можно воспользоваться несколькими хитростями:

Чтобы быстро возвести в квадрат число, на конце которого 0, можно добавить к нему парочку нулей: 80×80=6400; 30×30=900. Т.е., первые цифры умножаем и дописываем два 0 к этому числу.
Теперь возьмём какое-нибудь число так, чтобы вторая его цифра оканчивалась на 5. Так, например, число 75. Чтобы быстро возвести его в квадрат, прибавьте к первой цифре единицу, из чего получаются цифры 7 и 8.
Умножаем их и приписываем в конец число 25 и получаем конечный результат в виде числа 5625.

Квадратные корни

Вторая таблица — это таблица квадратных корней:

√x	0	1	2	3	4	5	6	7	8	9
0	0	1	1,41421	1,73205	2	2,23607	2,44949	2,64575	2,82843	3
1	3,16228	3,31662	3,4641	3,60555	3,74166	3,87298	4	4,12311	4,24264	4,3589
2	4,47214	4,58258	4,69042	4,79583	4,89898	5	5,09902	5,19615	5,2915	5,38516
3	5,47723	5,56776	5,65685	5,74456	5,83095	5,91608	6	6,08276	6,16441	6,245
4	6,32456	6,40312	6,48074	6,55744	6,63325	6,7082	6,78233	6,85565	6,9282	7
5	7,07107	7,14143	7,2111	7,28011	7,34847	7,4162	7,48331	7,54983	7,61577	7,68115
6	7,74597	7,81025	7,87401	7,93725	8	8,06226	8,12404	8,18535	8,24621	8,30662
7	8,3666	8,42615	8,48528	8,544	8,60233	8,66025	8,7178	8,77496	8,83176	8,88819
8	8,94427	9	9,05539	9,11043	9,16515	9,21954	9,27362	9,32738	9,38083	9,43398
9	9,48683	9,53939	9,59166	9,64365	9,69536	9,74679	9,79796	9,84886	9,89949	9,94987

Числа в кубе

И, конечно же, третья — таблица кубов, при помощи которой осуществляется извлечение кубического корня.

	0	1	2	3	4	5	6	7	8	9
0	0	1	8	27	64	125	216	343	512	729
1	1000	1331	1728	2197	2744	3375	4096	4913	5832	6859
2	8000	9261	10648	12167	13824	15625	17576	19683	21952	24389
3	27000	29791	32768	35937	39304	42875	46656	50653	54872	59319
4	64000	68921	74088	79507	85184	91125	97336	103823	110592	117649
5	125000	132651	140608	148877	157464	166375	175716	185193	195112	205379
6	216000	226981	238328	250047	262144	274625	287496	300763	314432	328509
7	343000	357911	373248	389017	405224	421875	438976	456533	474552	493039
8	512000	531441	551368	571787	592704	614125	636056	658503	681472	704969
9	729000	753571	778688	804357	830584	857375	884736	912673	941192	970299

Эти числа возводятся в третью степень.

Интересно

Название «Куб» приобрелось из-за того, что такая операция проводится для нахождения объема куба. Т.е., для этого нужно возвести длину ребра куба в третью степень.

Такие таблицы достаточно просты в использовании. Слева — десятки, а справа — единицы. С их помощью можно быстро и легко извлечь корень числа от 0 до 99. Это был один из методов извлечения корней, как мне кажется, самый простой после вычислительного средства — калькулятора, но, зачастую, мы не всегда можем им воспользоваться, как говорилось ранее. Так давайте же перейдем к другим интересным и сложным на первый взгляд вариантам решения.

Разложение подкоренного числа на простые множители

Двигаясь от наиболее удобного и быстрого способа к более сложному, давайте разберемся во втором из них — разложение подкоренного числа на простые множители.

Этот метод состоит в том, чтобы представить какое-либо число в виде степени с нужным нам показателем, из чего мы можем получить значение этого корня.

Пример 1:

Возьмём число 196. Для извлечения его квадратного корня, разложим это число на простые множители: √196=2×2×7×7=2²×7²

Теперь делаем следующие действия: 2×7=14.

Ответ: √196=14.

Объяснение:

Множители находятся так: 196 делим на 2, а полученное число 98 мы тоже делим на 2. Делим до тех пор, пока деление станет невозможным. Так, число 49 нельзя поделить пополам, поэтому мы действуем методом подбора. Находим такое число, которое делится. В данном случае — это 7. Два числа, что у нас получились (2 и 7), мы умножаем друг на друга, но уже без степени и получаем число 14, что есть извлечённый корень из числа 196.

Пример 2:

Для того, чтобы лучше понять, как раскладывать на множители, приведем ещё одно число и перейдем к действиям. Деление 441 на 2 невозможно, поэтому подбираем число. Оно делится на 3 два раза. Опять выходит число 49, которое мы делим 2 раза на 7. Из этого следует: √441=3×3×7×7=3²×7²

3×7=21. Значит, ответ: √441=21.

Объяснение:

3 мы умножили на 7, так как это два числа, имеющих 2 степень. Будь у одного из них 4 степень, например: 3⁴×7² — нужно было бы сделать так: 3×3×7. Проще сказать, что мы сокращаем степени ⁴ и ².

Интересно

Подкоренные числа, разложенные на простые множители, могут иметь лишь чётную степень.

Извлечение корней из дробных чисел

Перед тем, как начать вычисления, убедитесь, что дробное число представлено в виде обыкновенной дроби.

Перейдем к свойству корня из частного:

\[\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\]

Далее нужно воспользоваться правилом извлечения корня из дроби, которое гласит: корень из дроби равен от деления корня числителя на корень знаменателя.

Пример 1:

Давайте возьмем любую десятичную дробь и на её примере посмотрим, как нужно извлекать корень.

Так, например, найдем кубический корень из 373,248.

Первый ход — это представление десятичной дроби в виде обыкновенной:

³√373248/³√1000. После этого найдем кубический корень в числе и знаменателе:

³√373248=2×2×2×2×2×2×2×2×2×3×3×3×3×3×3=2⁹×3⁶=72³

Эти действия происходят как с квадратными корнями, но здесь уже мы считаем числа 2 и 3 не по двойке, а тройке, т.е. 2⁹=2×2×2, а 3⁶=3×3. Или же сокращаем ⁹ и ⁶.

Проверим таким образом: из 9 вычитаем тройки до тех пор, пока не придем к 0: 9-3-3-3 – это значит, что двоек у нас будет именно 3. Так и с 3⁶. Если от 6 отнять 3 два раза, то будет 0. Выходит, что троек у нас именно две.

А 1000=10³.

Получается, ³√373248/³√1000=72/10=7,2.

Извлечение отрицательного корня

Существуют вещественные числа, из которых невозможно извлечь корень, т.е. решения нет. А вот из комплексных чисел можно извлекать корень. Для начала узнаем, что это за числа.

Определение

Вещественные (действительные) числа— это рациональные и иррациональные числа, которые можно записать в форме конечной или бесконечной десятичной дроби.

Комплексные числа — это выражение, в котором есть:

вещественные числа a и b;
i — мнимая единица.

Итак, чтобы извлечь корень из отрицательного числа, нужно помнить, что если знаменатель является нечётным, то число под знаком корня может оказаться отрицательным.

Далее, чтобы провести эту операцию с отрицательным числом, перейдем к следующим действиям:

Извлекаем корень из противоположного ему положительного числа.
Ставим перед полученным числом знак минус.

Пример 1:

1. Преобразуем выражение ⁵√-12 640/32 так, чтобы вместо отрицательного числа под корнем оказалось положительное:

⁵√-12 640/32 = -⁵√12 640/32

2. Избавимся от смешанного числа, заменив его обыкновенной дробью:

-⁵√12 640/32= -⁵√1024/32

3. С помощью правила извлечения корней из обыкновенной дроби, начнем извлекать:

-⁵√1024/32 = — ⁵√1024/⁵√32.

4. Теперь нужно вычислить корни в числителе и знаменателе:

— ⁵√1024/⁵√32 = — ⁵√4⁵/⁵√2⁵ = — 4/2 = -2.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Поразрядное нахождение значения корня

Мы разобрали несколько методов, которые вы можете выбрать на своё усмотрение. Однако, есть еще один, который может понадобиться в таких ситуациях, когда нужно знать полное значение корня, а число, находящееся под корнем нельзя представить в виде n-ной степени определенного числа.

Для таких случаев существует алгоритм поразрядного нахождения значения корня, который нужно использовать, чтобы получить нужное количество значений определяемого числа.

Пример 1:

Итак, чтобы в этом разобраться, найдем значение квадратного корня из 7:

1. Находим значение разряда единиц, перебирая значения 0, 1, 2, …, 9, в это же время вычисляя их во 2 степени до нужного значения, которое больше подкоренного числа 7. Значение ряда единиц равняется 2 (потому как 2² < 7, а 2³ > 7).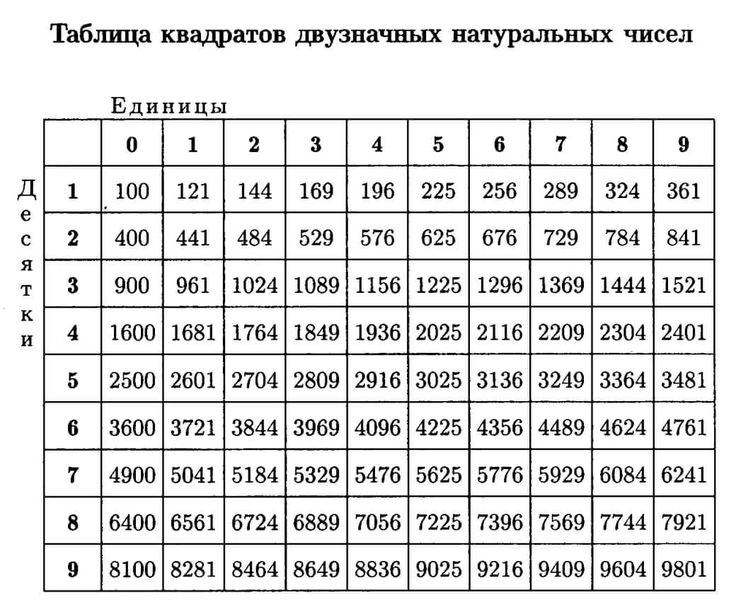

2. Следующий на очереди — разряд десятых. Здесь мы будем возводить в квадрат числа: 2.0, 2.1, 2.2, …, 2.9, сравнивая результат с нужным нам числом 7. Так как 2.6² < 7, а 2.7² > 7, то значение десятых равняется 6.

3. Значение сотых. По аналогии находим приближенное значение к 7.

2.64² = 6,9696 подходит нам, так как 2.65²=7.0225, а это больше 7. Действуя таким же образом, можно и дальше находить значение √7 ≈ 2.64.

Теперь, когда мы разобрались с извлечением корней, перейдем к практике. Специально для вас составлены задания с ответами, чтобы вы попробовали воспользоваться приобретенными знаниями. Решайте без таблиц и калькулятора.

Задания для отработки материала
1 задание
а)√324
б)√900
в)√1369
2 задание
а)³√531,441
б)³√166,375
3 задание
а) ⁵√-14 2471/1024
б) ⁵√-5 1182/3125
4 задание
а)Найдите квадратный корень из 3.
б)Найдите квадратный корень из 5.
в)Найдите квадратный корень из 9.
Ответы с решением
1 задание
а)√324
1)2×2×3×3×3×3=2²×3⁴=√324, а чтобы извлечь, мы умножаем:
2)2×3×3=18. Получается, √324=18.
б)√900
1)2×2×3×3×5×5=2²×3²×5²=√900.
Извлекаем:
2)2×3×5=30. Мы получили √900=30.
в)√1369
1)37×37=37²=√1369.
А здесь мы оставляем 37, так как это единственное число в квадрате. Конечным ответом будет: √1369=37.
2 задание
а)³√531441.
1)3×3×3×3×3×3×3×3×3×3×3×3=3¹²=³√531441.
Разложили на простые множители, а теперь найдем квадратный корень.
2)3¹² это 3×3×3×3, т.к. 3 у нас в 12 степени. Это можно проверить, отняв из 12 столько троек, чтобы вышел 0: 12-3-3-3-3. Так что, 3⁴=81; ³√531441=81.
3)1000=10³.
4)³√531441/³√1000=81/10=8,1.
б)³√166,375.
1) 5×5×5×11×11×11=5³×11³=³√166375.
2)5³×11³=55. Так как числа в кубе – они в степени 1.
3) 1000=10³.
4)³√166375/³√1000=55/10=5,5.
3 задание
а)
1) ⁵√-14 2471/1024 = -⁵√14 2471/1024.
2) -⁵√14 2471/1024= -⁵√16801/1024.
3) -⁵√16801/1024 = — ⁵√16801/⁵√1024.
4) ⁵√16801/⁵√1024 = — ⁵√6⁵/⁵√4⁵ = — 6/4 = — 1,5.
б)
1) ⁵√-5 1182/3125 = -⁵√5 1182/3125.
2) -⁵√5 1182/3125= -⁵√16807/3125.
3) -⁵√16807/3125 = — ⁵√16807/⁵√3125.
4) ⁵√16807/⁵√3125 = — ⁵√7⁵/⁵√5⁵ = — 7/5 = — 1,4.
4 задание
а)√3≈1,73.
б√5≈2,23.
в)√8≈2,82.
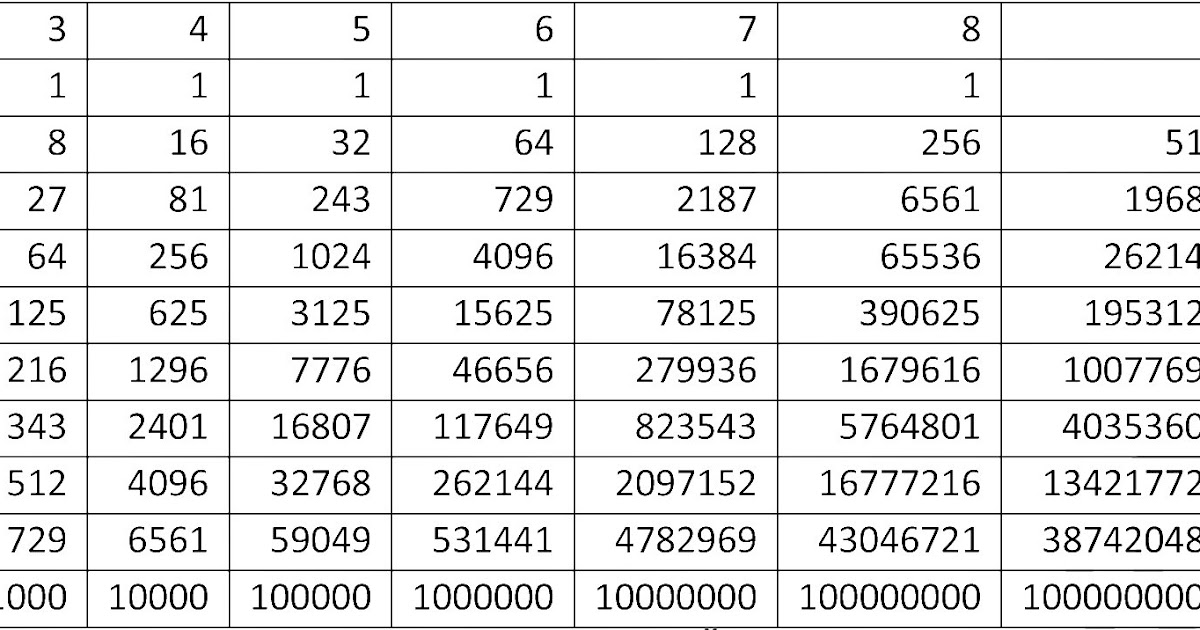
Cube Root Table – Таблица корней идеального куба и таблица кубов от 1 до 50
Математика
Корень идеального куба
Идеальный куб получается в результате трехкратного умножения одного и того же целого числа. Повторение числа 4 раза по три дает 64, а в результате 64 — это совершенный куб. 64 имеет кубический корень из 4. Если число можно разложить на произведение тех же трех чисел, говорят, что это совершенный куб.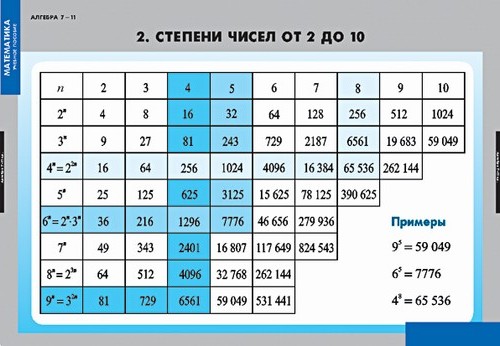
Полный куб — это произведение трех одинаковых чисел. Чтобы увидеть, является ли число (например, n) подходящим кубом, умножьте его в три раза и проверьте, совпадает ли полученное число с «n», если да, то это идеальный куб
Один, восемь, двадцать семь и шестьдесят четыре являются примерами идеальных кубов. Совершенный квадрат — это квадрат, который можно получить, перемножив два числа вместе. Для создания идеальных кубов можно использовать как положительные, так и отрицательные числа. Поскольку это произведение трехкратного умножения -4, -64 является совершенным кубом.
Когда мы говорим, что число возведено в куб, мы имеем в виду, что оно было умножено три раза. Процесс возведения числа в куб зависит от его корня. Например, когда число 5 возводится в куб, мы получаем 55 5, что равно 125. Кубический корень из 5 равен 125. Это потому, что трехкратное умножение числа 5 дает результат 125. Это то же самое, что и квадратный корень. символ с добавлением «3», чтобы указать, что это кубический корень. Кубический корень числа может быть указан в форме экспоненты как (число) 13.
Таблица кубических корней
Таблица кубических корней — это таблица, состоящая из списка чисел и их кубических корней. Прежде чем мы напишем таблицу кубических корней, всем нам очень важно понять, что такое идеальная диаграмма кубических корней и куб числа. Куб любого действительного числа можно определить как то число, которое получается умножением числа само на себя дважды или возведением его в степень до 3. В то же время кубическим корнем любого числа является то число, которое при возведении в степень 3 дает ответ в виде числа, кубический корень которого необходимо определить.
Корневая таблица Perfect Cube
90 030 900 31
1331
90 031
10648
Число Perfect Cube
Корень кубического числа
90 034
1
1
8
2
27
3
64
900 34
4
125
5
216
6
343
7
512
8
729
9
1000
10
11
1728
12
2197
1 3
2744
14
3375
15
4096
16
4913
17
900 34
5832
18
6859
19
800 0
20
9261
21
22
12167
23
13824
9 0034
24
15625
25
Кубический корень числа также может быть экспоненциально представлен как число, возведенное в степень ⅓. Если «x» — любое действительное число, то его кубический корень представлен как (x)⅓ или ∛x. Совершенные кубы — это числа, которые получаются при двукратном умножении натуральных чисел само на себя. Все совершенные кубические числа имеют квадратный корень, равный натуральному числу. Таблица корней совершенного куба первых 25 чисел совершенного куба представлена в таблице ниже.
Хотя очень важно знать кубические корни чисел, также очень важно знать таблицу кубов от 1 до 50 (то есть первые 50 натуральных чисел), чтобы сделать наши математические вычисления простыми и эффективными без калькулятор. Таблица кубиков от 1 до 50 приведена ниже для справки студентов и фасилитаторов.
Таблица кубов от 1 до 50
9003 1
9
900 39 9003 1
24
9 0031
17576
90 039 9003 0 90 031
42875
Натуральное число
Куб числа
1
1
2
900 34
8
3
27
4 900 11
64
5
125
6 90 011
216
7
343
8
512
729
10
1000
11
1331
12
1728
13
2197
14
2744
15
3375 900 11
16
4096
17
9 0010 4913
18
5832
19
6859
20
8000
21
9261
22 9001 1
10648
23
12167
13824
25
15625
26
27
19683
28
21952
29
24389
30
27000
31
29791
32
32768
33
35937
34
39304
35
36
46656
37
50653
38
54872
39
5 9319
40
64000
41
68921
42
74088
43
79507
90 034
44
85184
45
9001 0 46
97336
47
103823
48
9 0010 110592
49
117649
50 90 011
125000
Любой ученик или фасилитатор, увлекающийся математикой, найдет свой собственный способ запомнить список кубических корней от 1 до 100. Хотя в первые дни это может показаться немного сложным, задача запоминания списка кубических корней От 1 до 100 становится все легче благодаря постоянной практике и периодическим повторениям.
Список кубических корней от 1 до 100
Кубический корень
Число
Кубический корень
Число
900 31
Кубический корень
Номер 0010 1.000
26
2,962
51
3,708
76
4.236
2
1.260
27
3.000
52
3,733
77
4,254
9 0039
3
1,442
28
3,037
53
3,756
90 034
78
4. 273
4
1.587
29
3.072
54
3.780
79
4 .291
5
1.710
30
3.107
55
90 031
3.803
80
4.309
6
1,817
31
3.141
56
3.826
81 9001 1
4,327
7
1,913
32
3,175
900 31
57
3,849
82
4,344
8
2. 000
33
3.208
58
3.871 9 0011
83
4,362
9
2.080
34
3.2 40
59
3,893
84
4,380
10
2.154
35
3.271
60
9 0031
3,915
85
4.397
11
2.224
36 90 011
3.302
61
3. 936
86
4.414
12
2,289
37
3,332
9 0010 62
3,958
87
4.431
13
2.351 90 011
38
3.362
63
3.979
88
4.448
14
2.410
39
9 0010 3,391
64
4.000
89
4.465
15
90 034
2.466
40
3. 420
65
4.021
90
4.481
16
2.520
9001 0 41
3,448
66
4.041
91
4.498
90 030
17
2.571
42
3.476
67
4,062
92
4.514
18
2 .621
43
3,503
68
4,082
93
4. 531
19
2. 668
44
3.530
69
4.102
94
4.547
20 9 0011
2,714
45
3,557
70
4,121
95
4,563
21
2,759
46
3,583
71
4.141
96
4.579
9 0039
22
2,802
47
3,609
72
4,160
90 034
97
4. 595
23
2.844
48
3,634
73
4,179
98
4 .610
24
2,884
49
3,659
74
90 031
4.198
99
4.626
25
2,924
50
3.684
75
4.217
100 900 11
4,642
Шаги, чтобы узнать корень из идеального куба
Следуя приведенным ниже шагам, вы можете проверить, является ли число идеальным кубом:
Шаг 1: Начиная с наименьшего простого числа, разложите заданное число на простые множители (2).
Шаг 2: После завершения простой факторизации сгруппируйте вместе все три идентичных множителя.
Шаг 3: Повторите шаг 3 для всех наборов из тех же трех факторов в группе. Приведенное число не является идеальным кубом, если остались какие-либо множители, не вписывающиеся в группу из трех одинаковых множителей. Предоставленное целое число в противном случае является идеальным кубом.
Забавный факт о кубическом корне
Существует метод определения того, являются ли большие целые числа совершенными кубами. Чтобы проверить, найдите сумму цифр числа несколько раз и посмотрите, является ли оно 0, 1, 8 или 9. Если это любое из этих чисел, это может быть идеальный куб, хотя это не всегда так.
Формула идеального куба
Формула идеального куба используется для определения того, является ли число идеальным кубом. Допустим, у нас есть число x, равное yyy. Каждое составное число можно записать как произведение степеней его простых элементов в соответствии с основной теоремой арифметики. Число считается совершенным кубом, если мощность всех простых множителей кратна трем.
От 1 до 50, это список идеальных кубов.
В таблице ниже представлены совершенные кубы целых чисел от 1 до 50. Каждое целое число трижды умножается само на себя, чтобы получить идеальные кубы.
900 31
23
90 031
24 × 24 × 24
9 0030
1
1 × 1 × 1
900 10 1
2
2 × 2 × 2
8
3
3 × 3 × 3
27
4
4 × 4 × 4
64
5
5 × 5 × 5
125
6
6 × 6 × 6
216
7
7 × 7 × 7
343
8
8 × 8 × 8
512 90 011
9
9 × 9 × 9
729
10
10 × 10 × 10
1000
11 900 11
11 × 11 × 11
1331
12
12 × 12 × 12
1728
13 9001 1
13 × 13 × 13
2197
14
14 × 14 × 14
2744
15
15 × 15 × 15
9003 4
3375
16
16 × 16 × 16
4096
17
17 × 17 × 17 90 011
4913
18
18 × 18 × 18
5832
19
19 × 19 × 19
6859 9 0011
20
20 × 20 × 20
8000
21
21 × 21 × 21
9261
90 034
22
22 × 22 × 22
10648
23 × 23 × 23
12167
24
13824
25
25 × 25 × 25
15625
26 900 11
26 × 26 × 26
17576
27
9001 0 27 × 27 × 27
19683
28
28 × 28 × 28
900 34
21952
29
29 × 29 × 29
24389
30
30 × 30 × 30 9 0011
27000
31
31 × 31 × 31
29791
32
32 × 32 × 32
32768
33
33 × 33 × 33
35937
34
34 × 34 × 34
39304
35
35 × 35 × 35
42875
36
36 × 36 × 36
46656
37
90 034
37 × 37 × 37
50653
38
38 × 38 × 38
54872
39
39 × 39 × 39
59319
40
9003 4
40 × 40 × 40
64000
41
41 × 41 × 41
68921
42
42 × 42 × 42
74088
43
43 × 43 × 43
79507
44
44 × 44 × 44
85184
45
45 × 45 × 45
46
46 × 46 × 46
97336
47
47 × 47 × 47
103823
48
48 × 48 × 48
110592
49
49 × 49 × 49
117649
9001 0 50
50 × 50 × 50
125000
Заключение
Вот как мы можем легко вычислить совершенные кубические корни различных чисел.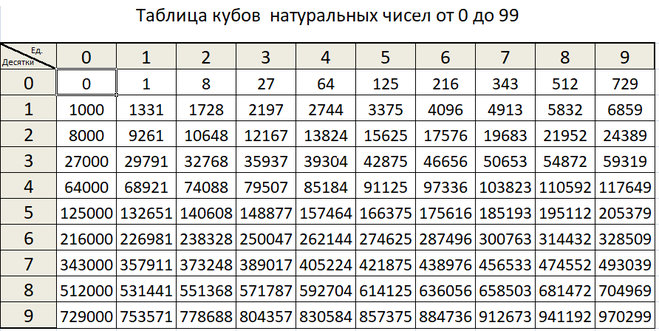 Сосредоточьтесь на концепции идеальных кубических корней и поймите, как они определяются. Следуйте примерам, приведенным в таблицах и диаграммах, чтобы разработать концептуальную основу.
Последняя обновленная дата: 27 апреля 2023 г.
•
Общее представление: 299,1K
•
Просмотр сегодня: 7.67K
Недавно обновленная страница
LCM 3 и 4 и как найти наименьшее общее кратное
Что такое простые проценты? — Пример, формула, решенные примеры и часто задаваемые вопросы
Линейные графики — Определение, решенные примеры и практические задачи
Числа в словах
Доля в процентах
Теорема Коши о среднем значении: введение, история и решенные примеры
НОК из 3 и 4, и Как найти наименьшее общее кратное
Что такое простой процент? — Пример, формула, решенные примеры и часто задаваемые вопросы
Линейные графики — определение, решенные примеры и практические задачи
Числа в словах
Доля в процентах
Теорема Коши о среднем значении: введение, история и решенные примеры
9 2453 Актуальные темы
Использование куба Корневая таблица найдите кубический корень следующего правильного до трех знаков после запятой.
..
Перейти к
Куб и кубические корни. Упражнение 4.1.
Куб и кубические корни. Упражнение 4.2.
Куб и кубические корни. Упражнение 4.3.
Куб и кубические корни. Упражнение 4.4.
Куб и кубические корни. Упражнение 4.5.
Рациональное число
Полномочия
Квадраты и квадратные корни
Куб и кубические корни
Игра с числами
Алгебраические выражения и тождества
Факторизация

Отдел алгебраических выражений
Линейное уравнение с одной переменной
Прямые и обратные варианты
Время и работа
Процент
Скидка на убыток и налог на добавленную стоимость

Сложные проценты
Понимание многоугольников фигур
Понимание фигур Четырехугольники
Понимание фигур Специальные типы четырехугольников
Практическая геометрия
Визуализация фигур
Площадь трапеции и многоугольника
Объем Площадь Прямоугольный Куб
Площадь поверхности и объем правого кругового цилиндра
Классификация и табулирование данных
Классификация и табулирование данных Графическое представление данных в виде гистограмм

Графическое представление данных в виде круговых диаграмм или круговых диаграмм
Вероятность обработки данных
Введение в графики
Главная > РД Шарма Решения Класс 8 Математика > Глава 4. Куб и кубические корни > Куб и кубические корни. Упражнение 4.5. >
Вопрос 3
Вопрос 3 Куб и кубические корни Упражнение 4.5
Используя таблицу корней куба, найдите корень куба следующего (исправьте три десятичных знака):
700
Ответ:
Кубический корень числа — это значение, которое при трехкратном умножении само на себя дает исходное значение.
Таблица кубических корней — это таблица, содержащая список чисел, а также их кубические корни. Давайте воспользуемся этой таблицей и найдем кубический корень:
700 = 70×10
При использовании таблицы кубического корня 700 будет в столбце ∛10x против 70.
Итак, мы получаем,
∛700 = 8,879
∴ ответ 8,879
Похожие вопросы
Используя таблицу кубических корней, найдите кубический корень следующего (исправьте три десятичных знака…
Используя таблицу кубических корней, найдите кубический корень следующего (исправьте три десятичных знака. ..
Используя таблицу кубических корней, найдите кубический корень следующего (исправьте три десятичных знака…
Используя таблицу кубических корней, найдите кубический корень следующего (исправьте три десятичных знака…
Используя таблицу кубических корней, найдите кубический корень следующего (исправьте три десятичных знака…
Используя таблицу кубических корней, найдите кубический корень следующего (исправьте три десятичных знака…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Куб и кубические корни Упражнение 4.
No related posts.