Тангенс равен 0 1: Таблица тангенсов и котангенсов

Содержание

Matematicheskaja regata 10 klassov

10 класс.

Первый тур (10 минут; каждая задача – 6 баллов).
1.1. На координатной плоскости изобразите множество точек, удовлетворяющих неравенству:
1.2. В выпуклом четырехугольнике тангенс одного из углов равен числу m. Могут ли тангенсы каждого из трех остальных углов также равняться m?
1.3. Можно ли поставить в ряд все натуральные числа от 1 до 100 так, чтобы любые два соседних числа отличались или на 2, или в два раза?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. (sinx, siny, sinz) – возрастающая арифметическая прогрессия. Может ли последовательность (cosx, cosy, cosz) также являться арифметической прогрессией?
2.2. Диагонали четырехугольника АВСD пересекаются в точке О, М
и N – середины сторон ВС и AD соответственно. Отрезок MN делит площадь четырехугольника пополам. Найдите отношение ОМ : ОN, если AD = 2BC.
2.3. Число 1047 при делении на A дает остаток 23, а при делении на A + 1 – остаток 7. Найдите A.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Пусть a, b, c, d – действительные числа, удовлетворяющие системе равенств:
Какие значения может принимать выражение ?
3.2. Все грани треугольной пирамиды SABC – остроугольные треугольники. SX и SY – высоты граней ASВ и BSС. Известно, что четырехугольник AXYC – вписанный. Докажите, что прямые AC и BS перпендикулярны.
3.3. Кодовый замок откроется, если в каждой клетке квадрата размером 4×4 набрать число от 1 до 16 (не повторяясь) так, чтобы сумма чисел в каждом квадрате 2×2 была кратна 17.
Можно ли открыть такой замок?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Сто положительных чисел записаны по кругу. Квадрат каждого числа равен сумме двух чисел, стоящих за этим числом по часовой стрелке. Какие числа могут быть записаны?
4.2. Трапеция с основаниями AD и BC описана вокруг окружности, E – точка пересечения ее диагоналей. Докажите, что угол AED – тупой.
4.3. В правильном 21-угольнике 6 вершин покрашены красным цветом, а 7 вершин – синим. Обязательно ли найдутся два равных треугольника, один из которых с красными вершинами, а другой – с синими?
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. Решите уравнение:
5.2. Две окружности пересекаются в точках А и В. Через точку В проведена прямая, пересекающая окружности в точках М и N так, что АВ – биссектриса треугольника МАN. Докажите, что отношение отрезков ВМ и BN равно отношению радиусов окружностей.
5.3. Какие значения может принимать наибольший общий делитель натуральных чисел m и n, если известно, что при увеличении числа m на 6 он увеличивается в девять раз?
Синус, косинус, тангенс, котангенс / Соотношения между сторонами и углами треугольника. Скалярное произведение векторов / Справочник по геометрии 7-9 класс
Главная

Справочники

Справочник по геометрии 7-9 класс

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов

Синус, косинус, тангенс, котангенс

Введем прямоугольную систему координат . В верхней полуплоскости координатной плоскости рассмотрим полуокружность радиуса 1 с центром в начале координат, её называют единичной полуокружностью. Из точки О(0; 0) проведем луч и отметим точку , в которой данный луч пересекает единичную полуокружность. Пусть — угол между лучом и положительной полуосью абсцисс (при совпадении данного луча с положительной полуосью абсцисс будем считать, что = 0⁰):
Пусть 90⁰, тогда из прямоугольного треугольника ЕОМ получаем:
, .
Учитывая, что ОМ
= 1, МЕ = , ОЕ = , получим:
, .                 (1)
То есть синус острого угла равен ординате точки М, а косинус — абсциссе точки М.
Формулы (1) справедливы и в том случае, если угол прямой, тупой и развёрнутый (на рисунке выше АОС, АОF и АОВ). Значит, для любого угла из промежутка 0⁰ 180⁰синусом угла называется ордината точки М, а косинусом угла — абсцисса точки М.
Если — произвольная точка единичной полуокружности, то -1 1 и
0 1, тогда для любого угла из промежутка 0⁰ 180⁰ имеем:
-1 1 и 0 1.
Лучи ОА, ОС и ОВ соответствуют углам, которые равны 0⁰, 90⁰ и 180⁰ соответственно. Точки А, С и В имеют координаты А(1; 0), С(0; 1) и В(-1; 0), поэтому
(2)
Тангенсом угла ( 90⁰) называют отношение , т.

е.
    (3)
Так как 90⁰ = 0, то знаменатель в формуле (3) обращается в нуль, значит, при = 90⁰не определён.
Котангенсом угла (0⁰ 180⁰) называется отношение . Котангенс угла обозначается символом . Таким образом,
.      (4)
Так как 0⁰ = 0 и 180⁰ = 0, то знаменатель в формуле (4) обращается в нуль, значит, при = 0⁰^{и = 180⁰не определён.}
Советуем посмотреть:
Основное тригонометрическое тождество. Формулы приведения.
Формулы для вычисления координат точки
Теорема о площади треугольника
Теорема синусов

Теорема косинусов
Решение треугольников
Измерительные работы
Угол между векторами
Скалярное произведение векторов
Скалярное произведение в координатах
Свойства скалярного произведения векторов
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
Правило встречается в следующих упражнениях:
7 класс
Задание 1016, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1017, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1041, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 7, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Tan 0 градусов – Значение, вывод и уравнения
Синус, косинус и тангенс – это три основные функции тригонометрии, посредством которых формируются тригонометрические тождества, тригонометрические функции и формулы.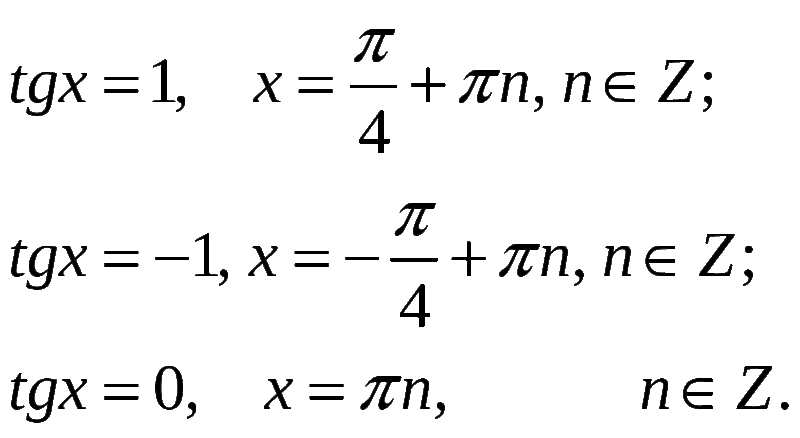 Тангенс определяется как отношение длины противоположной стороны или перпендикуляра прямого угла к углу и длине прилежащей стороны. Функция касательной в тригонометрии используется для вычисления наклона линии между началом координат и точкой, определяющей пересечение гипотенузы и высоты прямоугольного треугольника. В этой статье мы обсудим значения тангенса 0 и как получить значение тангенса 0 градусов.
Чему равно значение Tan 0 градусов?
Значение Tan 0 градусов равно нулю.
Вывод тангенса 0 градусов
Как мы знаем, синус, косинус и тангенс являются тремя основными функциями тригонометрии. Обозначим все три основные функции с помощью прямоугольного треугольника.
(изображение скоро будет загружено)
Что такое синусоидальная функция?
Функция синуса утверждает, что для данного прямоугольного треугольника Sin угла θ определяется как отношение длины противоположной стороны треугольника к его гипотенузе.
Sin θ = противолежащая сторона/гипотенуза.
Что такое функция косинуса?
Функция косинуса утверждает, что для данного прямоугольного треугольника косинус угла θ определяется как отношение длины прилежащей стороны треугольника к его гипотенузе.
Cos θ = Смежная сторона / Гипотенуза.
Что такое касательная функция?
Функция касательной утверждает, что для данного прямоугольного треугольника косинус угла θ определяется как отношение длины противоположной стороны треугольника к углу и прилежащей стороне.
Tan θ = Противоположная сторона / Гипотенуза.
Найти Tan 0°, используя Sin и Cos
Кроме того, значения sin 0° и cos 0° используются для нахождения значения tan 0°, но при условии, что sin 0°, а cos 0 ° должен быть из того же треугольника. Это очень простая концепция тригонометрии, чтобы найти тангенс угла, используя синус и косинус угла.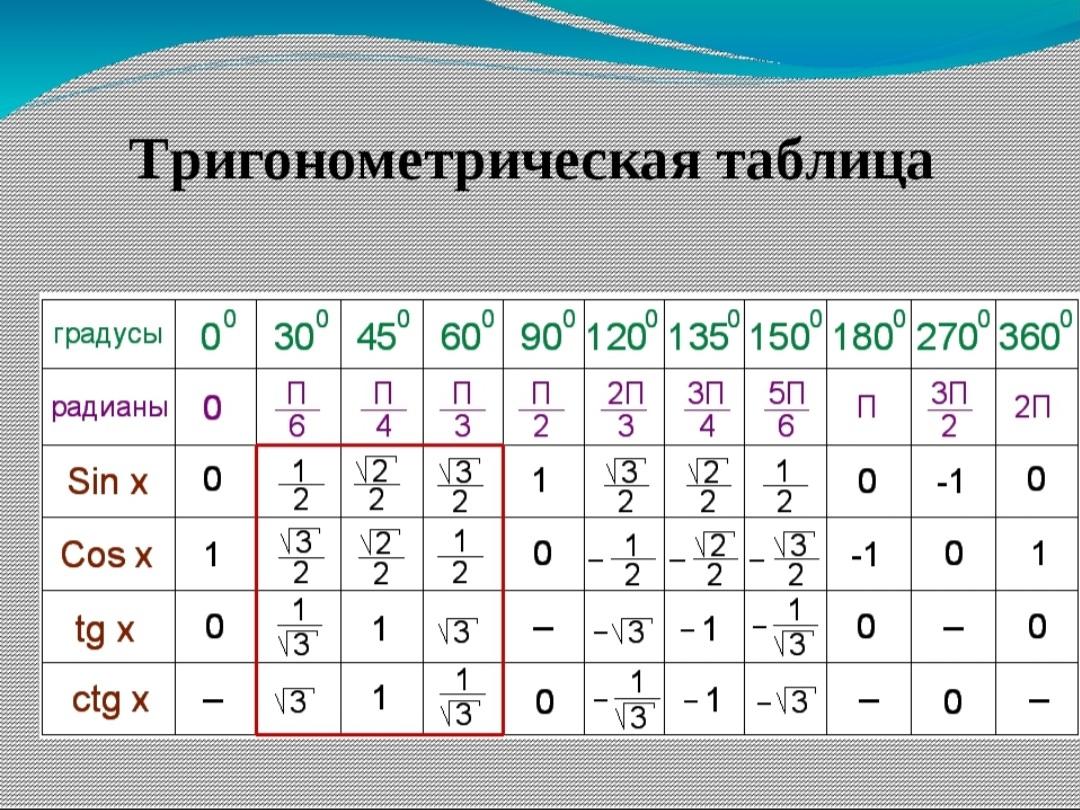 Известно, что отношение синуса и косинуса одного и того же угла дает тангенс этого же угла. Итак, если у нас есть значение sin 0° градусов и cos 0° градусов, то значение tan 0° градусов можно вычислить очень легко.
Соответственно, Tan θ = Sinθ/ Cosθ
Tan 0 градусов в дробях можно выразить как
Tan 0 градусов равно Sin 0° / Cos 0°
Мы знаем, что Sin 0° = 0 и Cos 0° = 1
Следовательно, Tan 0 равен 0/1 или 0.
Отсюда следует, что Tan 0 равен 0.
Тригонометрические уравнения на основе функции тангенса
Различные формулы тангенса могут быть сформулированы с помощью касательная функция в тригонометрии. Основная формула тангенса, которая в основном используется для решения вопросов,
Tan θ = перпендикуляр/основание или Tanθ = Sinθ/Cosθ или Tanθ = 1/Cotθ.
Другие формулы тангенса:
Tan (a+b) равно Tan (a) + Tan (b)/1- Tan (a) Tan (b)
Tan (90 +θ) = Cot θ
Tan (90 — θ) = — Cotθ
Tan (-θ) = Tanθ
Тригонометрическая таблица соотношений различных углов
9008 0
180°
9 0079 90 345
Угол
0°
30°
45°
60°
90°
270°
360°
sin
0
\ [\ frac {1} {2} \]
\ [\ frac {1} {\ sqrt {2} \]
\ [\ frac {\ sqrt {3}}{2}\]
1
0
-1
0
cos
1
\[\frac{\sqrt{3}}{2}\]
\[\frac{ 1}{\sqrt{2}}\]
\[\frac{1}{2}\]
0
-1
900 02 0
1
желтовато-коричневый
0
\[\frac{1}{\sqrt{3}}\]
1
\[\sqrt{3}\]
∞
0
9 0083
∞
1
детская кроватка
∞
\[\sqrt{3}\]
1
\[\frac{1}{\sqrt{2}}\]
9 0002 0
∞
0
∞
csc
∞
2
\[\sqrt{2}\] 9 0003
\[\frac{2}{\sqrt{3}}\]
1
∞
-1
∞
сек
1
\[\frac{2}{\sqrt{3}} \]
\[\sqrt{2}\]
2
∞
-1
∞
1

Вопросы, требующие решения
Оцените следующие вопросы, приведенные ниже-
Вопрос 1) Тан (90- 45)°
Решение: Как мы знаем, Tan (90-θ) = Cot θ
Tan (90 — 45) =Cot 45°
Cot 45° = 1
Итак, соответственно,
Tan (90 — 45)° = 1
Следовательно, значение Tan (90 — 45)° равно 1,
Вопрос 2) Найдите значение Tan 150°
Решение: Tan 150° = Tan (90 + 60)°
Как известно,
Tan (90 + θ) = Cosθ
Tan (90 + 45) ) = Cos 45°
Cos 45° = 1
Соответственно,
Tan (90 + 45)° = 1.
(Изображение будет загружено в ближайшее время)
Tan 0 Значение
Три основные функции тригонометрии являются синус, косинус и тангенс, посредством которых формируются тригонометрические тождества, тригонометрические функции и формулы. Тангенс можно определить как отношение длины противоположной стороны или перпендикуляра прямого угла к углу и длине прилежащей стороны. Функция касательной используется для вычисления наклона линии между началом координат и точкой, определяющей пересечение гипотенузы и высоты прямоугольного треугольника.
Сторона гипотенузы: В прямоугольном треугольнике это сторона, противоположная прямому углу. Гипотенуза — самая длинная сторона любого прямоугольного треугольника, лежащая напротив прямого угла. Сторона, противоположная углу интереса, называется противоположной стороной, а оставшаяся сторона называется смежной стороной, где она образует сторону как прямого угла, так и угла интереса.
Происхождение Тан 0 Степени.
Функция синуса и функция косинуса используются для нахождения значения тангенса 0 градусов, поскольку функция тангенса представляет собой отношение функции синуса и функции косинуса.

Значения градусов тангенса можно найти с помощью функций синуса и косинуса. Зная значение функций синуса, мы сможем найти значения функций cos и tan.
Значения sin 0° и cos 0° используются для нахождения значения tan 0° при условии, что sin 0° и cos 0° принадлежат одному и тому же треугольнику.
Формулы тангенса можно сформулировать с помощью функции тангенса. Основная формула тангенса, которая в основном используется для решения вопросов,
Tan θ = перпендикуляр/основание или Tanθ = Sinθ/Cosθ или Tan Θ = 1/Cosθ.
Другие формулы тангенса:
Tan (a+b) равно Tan (a) + Tan (b)/1- Tan (a) Tan (b)
Tan (90 + θ) = Cot θ
Tan (90 — θ) = — Cotθ
Tan (-θ) = Tanθ.

No related posts.