Определение значения функции: область определения и область значений функций + ПРИМЕРЫ

Области определения и значений • Образавр

Содержание

Область определения

Все значения, которые принимает независимая переменная $x$ (аргумент), называют областью определения функции.

Другими словами, множество всех допустимых значений аргумента $х$ называется областью определения функции. 

Она обозначается как $D(f)$ или $D(y)$.

Рассмотрим, например, функцию $у =\frac{2}{x}$.

Так как на ноль делить нельзя, $x$ не может быть равен $0$.

Область определения можно записать следующим образом:

$D\left(у\right): x ≠ 0$ или $x ≠ 0$.

Рассмотрим функцию $y = 2x$. Переменная $x$ может принимать любые значения, поэтому область определения этой функции будут все числа:

$D\left(у\right) = (-\infin;+\infin)$

Область значений

Все значения зависимой переменной входят в область значений функции.

Другими словами, множество всех значений, которые может принимать зависимая переменная $у$, называют  областью значений функции. 4$. При возведении любого (даже отрицательного) числа в степень с четным показателем мы получим положительное число (или ноль, если основание степени $x = 0$). Следовательно область значения нашей функции можно записать так:

$Е(y): y ≥ 0$

Рассмотрим функцию $y = 5x$. Переменная $y$ может принимать любые значения, также как и $x$. Запишем область значения функции:

$E\left(y\right) = (-\infin;+\infin)$

{"questions":[{"content":"Множество всех допустимых значений аргумента $x$ называется [[fill_choice-1]]
Множество всех значений, которые может принимать зависимая переменная $y$, называют [[fill_choice-3]]","widgets":{"fill_choice-1":{"type":"fill_choice","options":["областью определения функции","областью значений функции"],"answer":0},"fill_choice-3":{"type":"fill_choice","options":["областью определения функции","областью значений функции"],"answer":1}}}]}

5

Оценить урок

Поделиться уроком →

Что можно улучшить?

Изложение материала

Непонятное объяснение

Урок неполный, не хватает информации

Урок перегружен, слишком много информации

Тесты плохого качества

Тестов недостаточно

Тестов слишком много

Тесты слишком легкие

Тесты слишком сложные

Изображения

Изображения плохого качества

Изображений недостаточно

Изображений слишком много

Другое




Войдите, чтобы оценивать уроки

Что нужно исправить?




Спасибо, что помогаете нам стать лучше!

Следующий урок

Способы задания функций.

График функции

Функции — что это, определение и ответ

Функция – это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент второго множества.

СУТЬ ФУНКЦИИ:

Чтобы понять суть функции, можно рассмотреть формулу периметра квадрата. Мы знаем, что периметр квадрата находится так: \(P = 4a\), где a – это сторона квадрата.

Мы можем сами подставить любую длину стороны квадрата, чтобы получить соответствующий ей периметр. Если между двумя какими-либо величинами есть такое соответствие, то между ними существует функция.

Рассмотрим это соответствие на примере квадрата:

Если \(а = 1\), то \(Р = 1 \bullet 4 = 4\)


Если а\(= 2\), то \(Р = 2 \bullet 4 = 8\)

Если \(а = 3\), то \(Р = 3 \bullet 4 = 12\)

и так далее.

Мы говорим, что чтобы получить периметр квадрата, нужно его сторону умножить на 4. Это будет верно для любой стороны квадрата, которую мы сами зададим.

ОПРЕДЕЛЕНИЯ, СВЯЗАННЫЕ С ФУНКЦИЕЙ:

Величина, которую мы подставляем в формулу, называется переменной величиной или аргументом.

Та величина, которая получается в итоге преобразования переменной, называется зависимой величиной или значением функции.

Закон (или принцип) по которому меняется переменная, превращаясь в зависимую, называется функцией.

В нашем примере a – это переменная, P – это зависимая, а действие ( \(\bullet 4\)) – функция.

В общем виде переменную, зависимую и функцию записывают следующим образом:

\(y = f(x)\)

Она означает, что чтобы получить y, нужно преобразовать x по функции f.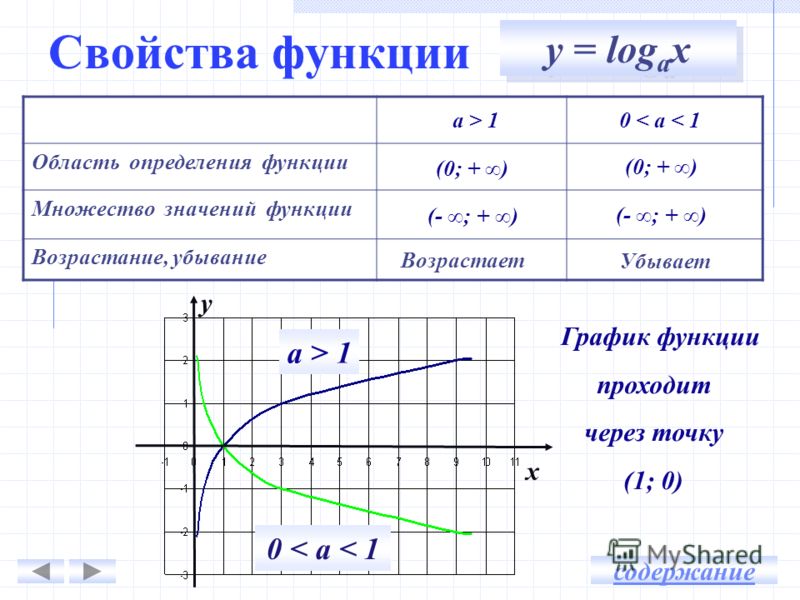 Такую запись можно читать как «\(y\ \)равен \(f\) от\(\ x\)».

При этом не только сама закономерность, по которой меняется \(x\), называется функцией. Для краткости функцией называют всё выражение, в котором есть зависимость. То есть мы можем сказать, что \(Р = 4a\) – это функция, хотя формально это выражение, содержащее аргумент, зависимую и функцию.

Далее, когда мы будем говорить о функции, мы будем иметь в виду целое выражение, подобно формуле площади квадрата, а не только действие преобразования аргумента.

Также каждая функция имеет свою область значений и область определения.

Область определения – это множество чисел, которые могут являться аргументами данной функции.

Область значений – это множество чисел, которые могут являться значением функции.

Например, в случае с периметром квадрата мы можем точно сказать, что сторона квадрата должна быть положительным числом. Потому что длина не может иметь отрицательное значение и не может быть равна 0, ведь в таком случае, квадрата не получится.

А если аргумент функции должен быть положительным, то при умножении положительного числа на 4 получится тоже только положительное число.

Таким образом область значений и областью определений в данном примере являются множества положительных чисел.

СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ:

Описать суть функции можно по-разному. Также можно по-разному описать зависимость, чтобы какую-либо функцию задать.

Рассмотрим различные способы задания одной и той же функции.

1. Словесный способ задания функции.

«У Даши есть яблоки. При этом у её старшего брата Вани всегда на два яблока больше.»

Чтобы словесно задать функцию, нужно описать, как изменяется аргумент. В данном случае в описании ситуации уже словесно задана функция словами «у Вани всегда на два яблока больше, чем у Даши». Эти слова определяют конкретную зависимость количества яблок у Вани от количества яблок у Даши.

2. Табличный способ задания функции.

Посмотрим на таблицу аргументов и зависимых от них величин.

Можем заметить, что каждый y больше своего x на 2. Эта зависимость есть у каждой из пар «аргумент – значение функции».

3. Способ задания функции формулой.

Этот способ мы рассматривали ранее через формулу периметра квадрата. Рассмотрим более общий вид функции, заданной формулой – через \(x\ \)и \(y\):

\(y = x + 2\)

По формуле мы видим, что каждый y на 2 больше, чем соответствующий ему x.

Пример №1

Найдите значение функции:

\(y = \frac{x\ –\ 2}{5}\) при \(x = 2;\ x = 27\).

1. Чем являются значение и аргумент функции мы знаем, это y и x. А вот именно функцией является более сложное действие – «вычесть 2, разделить на 5». Найдем значение этой функции при \(x = 2\):

\(y = f(x) = \frac{x\ –\ 2}{5}\)

\(f(2) = \frac{2\ –\ 2}{5} = \frac{0}{5} = 0\)

Таким образом мы узнали, что аргументу 2 соответствует значение функции 0.

2. Аналогично найдем значение функции при \(x = 27\):

\(f(27) = \frac{27\ –\ 2}{5} = \frac{25}{5} = 5\)

Значит аргументу 27 соответствует значение функции 5.

Ответ: 0; 5.

ГРАФИК ФУНКЦИИ:

Любую функцию можно изобразить на координатной плоскости. Если координатная плоскость состоит из точек, каждая из которой имеет две координаты, то одна координата будет равна аргументу, а вторая координата значению функция, который ей соответствует.

Из этого следует, что точка принадлежит графику некоторой функции, если её координаты равны аргументу и соответствующему ей значению функции.

Пример №2:

Постройте график функции \(y = x + 2.\)

1. Для построения графиков удобнее всего задавать функцию таблицей. Выберем несколько любых аргументов и найдем для них значения функции:

2. У нас есть координаты для четырех точек – А\((–2;\ 0)\), В(\(0;\ 2),\) С\((3;\ 5)\), D\((6;\ 8).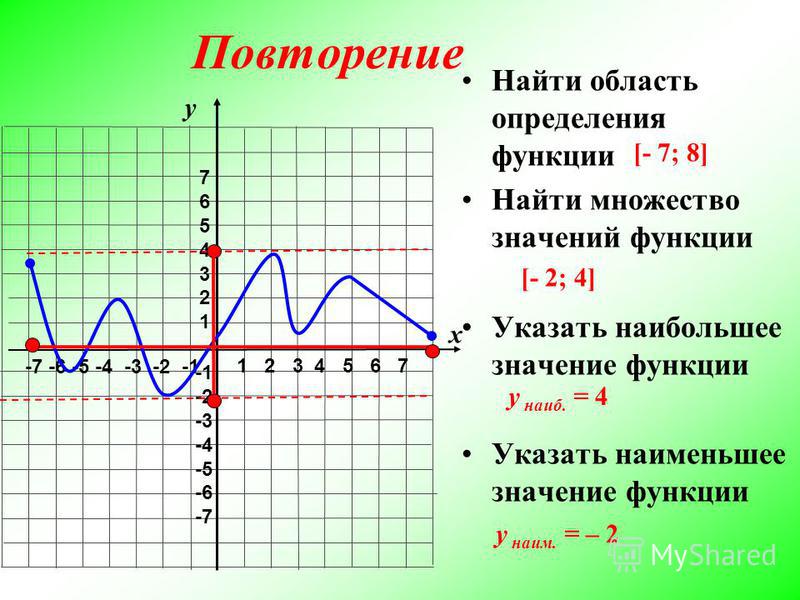 {2}–\ 4.\)

1. Выберем любые аргументы и найдем им соответствующие значения функции. Запишем их в таблице:

2. Построим и соединим на координатной плоскости получившиеся точки:

На данном графике мы видим что одно значение функции может быть у двух аргументов, например точки В\((–2;\ 0)\) и F(\(2;\ 0)\) или С\((–1;\ –3)\) и Е(\(1;\ –3)\) имеют разные аргументы, но одинаковые значения функции. Это не противоречит определению функции.

Для разных аргументов могут совпадать значения функции

Но при этом, НЕ может быть такой ситуации, когда одному аргументу соответствуют несколько значений функций. Так нарушается принцип соответствия и рисунок на координатной плоскости перестает быть графиком функций по определению

Для одного аргумента НЕ может существовать несколько значений функции

Например, вот такой график нельзя назвать графиком функций, потому что одному аргументу соответствует несколько значений:

Пример №4:

Определите без построения графика, принадлежат ли точки А\((2;\ 10)\) и В(\(–3;\ 6)\) графику функций \(y\ = \ 8\ + \ x\)?

1.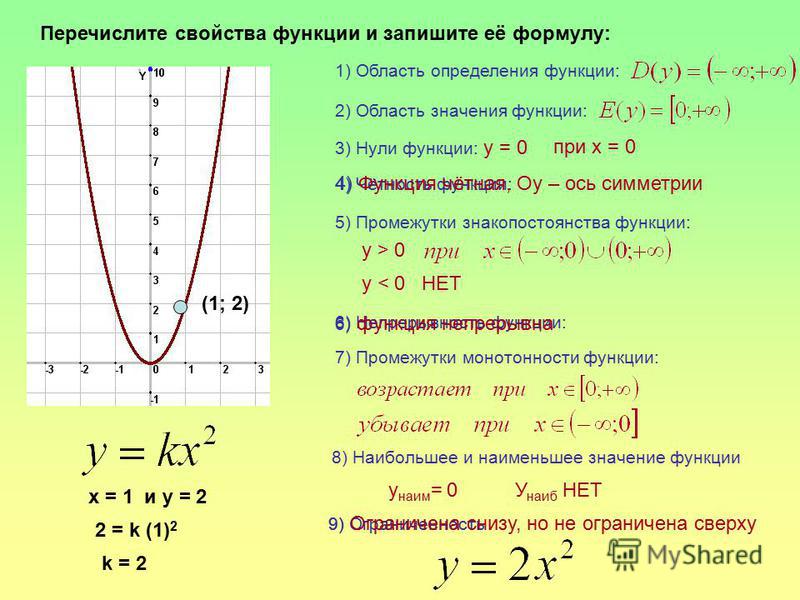 Точка принадлежит графику функций, если её координате x соответствует координата соответствует координата y именно как \(y\ = \ 8\ + \ x.\)

2. Определим принадлежность точки А к графику данной функции. Для этого подставим координату её абсциссы в функцию и найдем соответствующее ей значение:

\({y = 8 + x }{y\left( 2 \right) = 8 + 2 = 10}\)

Мы получили некую точку графика с координатами \((2;\ 10)\). Такие же координаты и у точки А Получается, что точка А\((2;\ 10)\) – это точка графика функции. Значит А принадлежит графику.

3. Аналогично определим принадлежность точки В к графику функции.

\({y = 8 + x }{y(–3) = 8\ –\ 3 = 5}\)

Мы получили точку графика \((–3;\ 5),\) а у точки В координаты \((–3;\ 6)\), значит тока В НЕ принадлежит графику.

Ответ: да; нет.

Функция | Определение, типы, примеры и факты

кубическое уравнение

Просмотреть все СМИ

Ключевые люди:

Поль Пенлеве Карл Вейерштрасс Эмиль Борель Эдвард Чарльз Титчмарш Питер Густав Лежен Дирихле

Похожие темы:

специальная функция корень преемственность Дзета-функция Римана рекурсивная функция

Просмотреть весь связанный контент →

функция , в математике выражение, правило или закон, определяющий связь между одной переменной (независимой переменной) и другой переменной (зависимой переменной). Функции повсеместно используются в математике и необходимы для формулирования физических отношений в естественных науках. Современное определение функции впервые дал в 1837 году немецкий математик Петер Дирихле:

Если переменная y так связано с переменной х , что всякий раз, когда числовое значение присваивается х , существует правило, согласно которому определяется уникальное значение y , тогда y называется функция независимой переменной x .

Это отношение обычно изображается как y = f ( x ) — что называется « f из x » — и y и 9 0026 x связаны так, что на каждые x , есть уникальное значение y . То есть f ( x ) не может иметь более одного значения для одного и того же x . Говоря языком теории множеств, функция связывает элемент x с элементом f ( x ) в другом наборе.

Набор значений x называется доменом функции, а набор значений f ( x ), порожденных значениями в домене, называется диапазоном функции. В дополнение к f ( x ), другие сокращенные символы, такие как g ( x ) и P ( x ), часто используются для представления функций независимой переменной x , особенно когда характер функция неизвестна или не определена.

Общие функции

Многие широко используемые математические формулы являются выражениями известных функций. Например, формула площади круга: A = π r ² дает зависимую переменную A (площадь) как функцию независимой переменной r (радиус). Функции, включающие более двух переменных (называемые многомерными или многомерными функциями), также распространены в математике, как это видно из формулы площади треугольника A = b h /2, которая определяет

A в зависимости от b (основание) и h (высота). В этих примерах физические ограничения заставляют независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями.

Викторина «Британника»

Числа и математика

Формула площади круга является примером полиномиальной функции. Общая форма для таких функций: P ( x ) = a ₀ + a ₁ x + a 90 129 2 х ² +⋯+ а _n x ⁿ , где коэффициенты ( ₀ ,

₁ , ₂ ,…, _n ), x может быть любым действительным числом, и все степени числа x — это счетные числа (1, 2, 3,…). (Когда степени x могут быть любым действительным числом, результат известен как алгебраическая функция. ) Полиномиальные функции изучались с древнейших времен из-за их универсальности — практически любое отношение, включающее действительные числа, может быть точно аппроксимировано с помощью полиномиальная функция. Полиномиальные функции характеризуются наибольшей степенью независимой переменной. Для таких степеней от одного до пяти обычно используются специальные названия: линейная, квадратичная, кубическая, квартическая и квинтическая для высших степеней, равных 1, 2, 3, 4 и 5 соответственно.

Полиномиальные функции могут иметь геометрическое представление с помощью аналитической геометрии. Независимая переменная

x откладывается по оси x (горизонтальная линия), а зависимая переменная y откладывается по оси y (вертикальная линия). Когда график отношения между x и y строится в плоскости x — y , отношение является функцией, если вертикальная линия всегда проходит только через одну точку графической кривой; то есть была бы только одна точка f ( x ) соответствует каждому x , что является определением функции. Затем график функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x ³ − 3 x + 2.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.

Подписаться сейчас

Другим распространенным типом функций, которые изучались с древних времен, являются тригонометрические функции, такие как sin x и cos x , где x — мера угла ( см. рисунок ) . Из-за своего периодического характера тригонометрические функции часто используются для моделирования повторяющегося поведения или «циклов».

Показательная функция представляет собой соотношение вида y = a ^x , с независимой переменной x , расположенной по всей линейке действительных чисел как показатель степени положительного числа a . Вероятно, наиболее важной из экспоненциальных функций является y = e ^x

, иногда пишут y = exp ( x ), в которой e (2,718 2818…) является основой природного система логарифмов (ln). По определению x — это логарифм, и, таким образом, существует логарифмическая функция, обратная экспоненциальной функции. В частности, если y = e ^x , тогда x = ln y . Неалгебраические функции, такие как экспоненциальные и тригонометрические функции, также известны как трансцендентные функции.

Сложные функции

Практические приложения функций, переменными которых являются комплексные числа, не так просто проиллюстрировать, но тем не менее они очень обширны. Они встречаются, например, в электротехнике и аэродинамике. Если комплексная переменная представлена ​​в виде z = x + i y , где i — мнимая единица (квадратный корень из −1), а x и y — действительные переменные (900 26 см.

2$ в $\R$. Возможно, вы сталкивались с функциями в более абстрактных условиях, таких как хорошо; это наша цель. В нескольких последних разделах главы мы использовать функции для изучения некоторых интересных тем теории множеств.

С помощью функции из множества $A$ в множество $B$ мы означает назначение или правило $f$ такое, что для каждого $a\in A$ существует единственный $b\in B$ такой, что $f(a)=b$. Множество $A$ называется областью $f$, а множество $B$ называется кодовым доменом . Мы говорим, что две функции $f$ и $g$ равны , если они имеют один и тот же домен и одинаковые codomain, и если для каждого $a$ в домене $f(a)=g(a)$.

(В интересах полного раскрытия пакостей следует упомянуть что последний абзац вообще не определение! Проблема в том, что слова «назначение» и «правило» являются синонимами «функции». Эту проблему можно «решить», определив функции с точки зрения множеств, но у нас нет удовлетворительного определения из «набора». На данный момент все необходимо интуитивное понимание концепции и способа показывает, что две функции равны.)

Мы часто пишем $f\colon A\to B$, чтобы указать, что $f$ является функцией от $A$ до $B$. Иногда слово «карта» или «отображение» используется вместо «функция». Если $f\colon A\to B$ и $f(a)=b$, мы говорим, что $b$ является образом $a$ при $f$ , а $a$ является прообразом $b$ до $f$ . Когда функция ясна исходя из контекста, фразу «менее $f$» можно опустить.

Пример 4.1.1. Вы знакомы со многими функциями $f\colon \R\to \R$: Полиномиальные функции, тригонометрические функции, экспоненциальные функции, и так далее. Часто вы имели дело с функциями с кодоменом $\R$ доменом которого является некоторое подмножество $\R$. Например, $f(x)=\sqrt x$ имеет домен $[0,\infty)$ и $f(x)=1/x$ имеет домен $\{x\in \R : x\ne 0\}$. Легко видеть, что подмножество плоскости есть граф функция $f\colon \R\to \R$ тогда и только тогда, когда каждая вертикальная линия пересекает его ровно в одной точке. Если эта точка $(a,b)$, то $f(a)=b$. $\квадрат$

Пример 4.1.2. Функции на конечных множествах можно определить, перечислив все задания. Если $A=\{1,2,3,4\}$ и $B=\{r,s,t,u,v\}$, то «$f(1)= t,f(2)= s,f(3)= u,f(4)= t$» определяет функцию от $A$ до $B$. Задание можно выполнить вполне произвольно, без обращения к какой-либо конкретной формуле. $\квадрат$

Пример 4.1.3 Следующие функции не являются функциями из $A=\{1,2,3,4,5\}$ в $B=\{r,s,t,u\}$: $$ \matrix{f(1)= t & \quad & g(1)=u\cr f(2)= s & \quad & g(2)=r\cr f(3)= r & \quad & g(4)=s\cr f(3)= u & \quad & g(5)=t\cr f(4)= u & \quad & \cr f(5)= r & \quad & \cr} $$ Проблема в том, что $f$ отображает $3$ в два значения, а $g$ не отображает $3$. к любым значениям. При перечислении назначений функции элементы домена должны встречаться ровно один раз. (Элементы codomain может появляться более одного раза или не появляться вовсе. В пример 4.1.2, элемент $t$ домена кода имеет два прообраза, а $r$ и $v$ не имеют ни одного. мы обсудим это ситуация подробно описана в следующих разделах. ) $\square$

Пример 4.1.4. Если $A$ и $B$ непустые множества и $b_0$ — фиксированный элемент $B$, мы можем определить константу функцию $f\colon A\to B$ по формуле $f(a)=b_0$ для всех $a\in $. Постоянных функций от $A$ до $B$ столько, сколько элементы $B$. $\квадрат$

Пример 4.1.5. Для множества $A$ определим тождество функцию $i_A\colon A\to A$ по правилу $i_A(a)=a$ для все $a\in A$. Другими словами, функция тождества отображает все элемент на себя. Хотя это кажется довольно тривиальной концепцией, это полезно и важно. Функции тождества ведут себя почти так же, так, как 0 делает по отношению к сложению или 1 по отношению к умножение. $\квадрат$

Пример 4.1.6. Если $A\subseteq B$, определить функцию включения $f\colon A\to B$ на $f(a)=a$ для каждого $a\in A$. Это очень похоже на $i_A$; единственный разница в кодовом домене. $\квадрат$

Определение 4.1.7. Если $f\colon A\to B$ и $g\colon B\to C$ — функции, определим $g\circ f\colon A\to C$ по правилу $(g\circ f)(a)=g(f(a))$ для всех $а\в А$. Это называется композиция из две функции. Заметьте, что $f$ — это первая функция, которая применяется к элементу $a$, хотя он указан справа. Этот нарушение обычного правила слева направо иногда вызывает путаница. $\квадрат$ 9+\cup\{0\}\to \R$ определяется выражением $(g\circ f)(x)=\sin\sqrt x$. Обратите внимание, что $(f\circ g)(x)=\sqrt{\sin x}$ имеет смысл только для таких $x$, что $\sin x\ge 0$. В общем, $f\circ g$ и $g\circ f$ не обязательно равны, и (поскольку в этом случае) их не обязательно определять в одних и тех же точках. $\квадрат$

Пример 4.1.9 Если $A=\{1,2,3,4\}$, $B=\{r,s,t,u\}$, $C=\{\$,\%,\#,\&\ }$ и $$ \matrix{ f(1) & = u &\quad g(r)&= \%\cr f(2) & = r &\quad g(s)&= \#\cr f(3) & = s &\quad g(t)&= \$\cr f(4) & = u &\quad g(u)&= \$\cr } $$ затем $$ \eqalign{ (g\circ f)(1) & = \$ \cr (g\circ f)(2) & = \% \cr (g\circ f)(3) & = \# \cr (g\circ f)(4) & = \$ \cr} $$ $\квадрат$

Пример 4. 1.10. Если $A\subseteq B$, $f\colon A\to B$ является функцией включения (пример 4.1.6) и $g\colon B\to C$ — функция, то $g\circ f\colon A\to C$ называется ограничением от $g$ до $A$ и обычно записывается $г\верт_А$. Для всех $a\in A$ $$ г\верт_А(а)=г(ф(а))=г(а), $$ поэтому $g\vert_A$ — это та же самая функция, что и $g$, но с меньшим домен. $\квадрат$

Следующее простое, но важное наблюдение:

Теорема 4.1.11 Если $f\colon A\to B$, то $f\circ i_A=f=i_B\circ f$.

Доказательство. Все три функции имеют домен $A$ и кодовый домен $B$. Для каждого $a\in A$ $$ (f\circ i_A)(a)=f(i_A(a))=f(a)=i_B(f(a))=(i_B\circ f)(a). $$$\qed$

Аналогичный аргумент показывает, что всякий раз, когда он определен, композиция функций ассоциативна, т. е. $(f\circ g)\circ h=f\circ (g\circ h)$ (см. упражнение 7).

Пример 4.1.1 Решите, определяют ли следующие назначения функции из $A=\{1,2,3,4\}$ в $B=\{r,s,t,u,v\}$. $$ \matrix{f(1)=s &\quad & g(1)= t &\quad & h(1)=v \cr f(2)=t &\quad & g(2)= r &\quad & h(2)=u \cr f(4)=u &\quad & g(3)= s &\quad & h(3)=t \cr &\quad & g(4)= r &\quad & h(2)=s \cr &\quad & &\quad & h(4)=r \cr } $$

Пример 4.

No related posts.