определения в тригонометрии, примеры, формулы
Как найти синус?
Изучение геометрии помогает развивать мышление. Этот предмет обязательно входит в школьную подготовку. В жизнедеятельности знание этого предмета может пригодиться — например, при планировке квартиры.
Из истории
В рамках курса геометрии изучается также тригонометрия, которая исследует тригонометрические функции. В тригонометрии мы изучаем синусы, косинусы, тангенсы и котангенсы угла.
Но на данный момент начнем с самого простого — синуса. Давайте рассмотрим более детально самое первое понятие — синус угла в геометрии. Что такое синус и как его найти?
Понятие «синус угла» и синусоиды
Синус угла — это соотношение значений противоположного катета и гипотенузы прямоугольного треугольника. Это прямая тригонометрическая функция, которая на письме обозначается как «sin (x)», где (х) — угол треугольника.
На графике синус угла обозначается синусоидой со своими особенностями. Синусоида выглядит как непрерывная волнообразная линия, которая лежит в определенных рамках на плоскости координат. Функция нечетная, поэтому симметрична относительно 0 на плоскости координат (выходит из начала отсчета координат).
Синусоида выглядит как непрерывная волнообразная линия, которая лежит в определенных рамках на плоскости координат. Функция нечетная, поэтому симметрична относительно 0 на плоскости координат (выходит из начала отсчета координат).
Область определения этой функции лежит в диапазоне от -1 до +1 на декартовой системе координат. Период функции синус угла составляет 2 Пи. Это означает, что каждые 2 Пи рисунок повторяется, и синусоида проходит полный цикл.
Уравнение синусоиды
- sin х = a / c
- где а — противолежащий к углу треугольника катет
- с — гипотенуза прямоугольного треугольника
Свойства синуса угла
- sin (x) = — sin (x). Эта особенность демонстрирует, что функция симметрична, и если отложить на системе координат в обе стороны значения х и (-х), то ординаты этих точек будут противоположными. Они будут находиться на равном расстоянии друг от друга.
- Еще одной особенностью этой функции является то, что график функции возрастает на отрезке [- П/2 + 2 Пn]; [П/2 + 2Пn], где n — любое целое число.
 Убывание графика синуса угла будет наблюдаться на отрезке: [ П/2 + 2 Пn]; [ 3П/2 + 2Пn].
Убывание графика синуса угла будет наблюдаться на отрезке: [ П/2 + 2 Пn]; [ 3П/2 + 2Пn]. - sin (x) > 0, когда х лежит в диапазоне (2Пn, П + 2Пn)
- (x)
Значения синусов угла определяются по специальным таблицам. Созданы такие таблицы для облегчения процесса подсчета сложных формул и уравнений. Она легка в использовании и содержит значения не только функции sin (x), но также и значения других функций.
Более того, таблица стандартных значений этих функций включена к обязательному изучению на память, как таблица умножения. Особенно это актуально для классов с физико-математическим уклоном. В таблице можно увидеть значения основных используемых в тригонометрии углов: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 и 360 градусов.
Также существует таблица, определяющая значения тригонометрических функций нестандартных углов. Пользуясь разными таблицами, можно без труда вычислить синус, косинус, тангенс и котангенс некоторых углов.
С тригонометрическими функциями составляются уравнения.
Как найти синус угла
Когда стоит задача найти синус угла, а по условию у нас есть только косинус, тангенс, или котангенс угла, мы легко можем вычислить нужное с помощью тригонометрических тождеств.
- sin 2 x + cos 2 x = 1
Исходя из этого уравнения, мы можем найти как синус, так и косинус, в зависимости от того, какое значение неизвестно. У нас получится тригонометрическое уравнение с одним неизвестным:
- sin 2 x = 1 — cos 2 x
- sin x = ± √ 1 — cos 2 x
- ctg 2 x + 1 = 1 / sin 2 x
Из этого уравнения можно найти значение синуса, зная значение котангенса угла. Для упрощения замените sin 2 x = у, и тогда у вас получится простое уравнение. Например, значение котангенса равно 1, тогда:
- 1 + 1 = 1/у
- 2 = 1 / у
- 2у = 1
- у = 1/2
Теперь выполняем обратную замену игрека:
- sin 2 x = ½
- sin x = 1 / √2
Поскольку мы взяли значение котангенса для стандартного угла (45 0), полученные значения можно проверить по таблице .
Если у вас дано значение тангенса, а нужно найти синус, поможет еще одно тригонометрическое тождество:
- tg x * ctg x = 1
Из этого следует, что:
- ctg x = 1 / tg x
Для того чтобы найти синус нестандартного угла, например, 240 0 , необходимо воспользоваться формулами приведения углов. Мы знаем, что π у нас соответствует 180 0 . Таким образом, мы выразим наше равенство с помощью стандартных углов путем разложения.
- 240 0 = 180 0 + 60 0
Нам необходимо найти следующее: sin (180 0 + 60 0). В тригонометрии есть формулы приведения, которые в данном случае пригодятся. Это формула:
- sin (π + х) = — sin (х)
Таким образом, синус угла 240 градусов равен:
- sin (180 0 + 60 0) = — sin (60 0) = — √3/2
В нашем случае, х = 60, а П, соответственно, 180 градусам. Значение (-√3/2) мы нашли по таблице значений функций стандартных углов.
Таким образом можно разложить нестандартные углы, например: 210 = 180 + 30.
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1.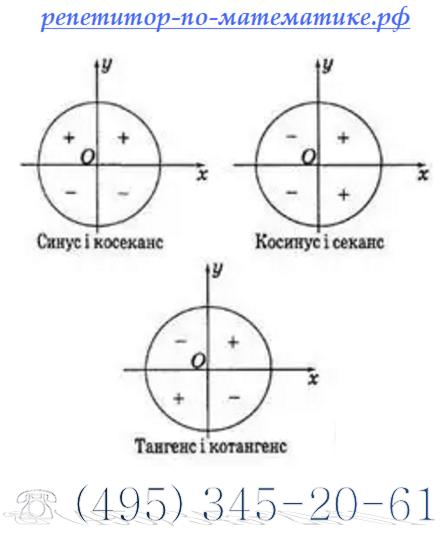 Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.
Инструкция
Первый вариант — классический, с использованием бумаги, транспортира и карандаша (или ручки).По определению синус угла равен противолежащего катета к гипотенузе прямоугольного треугольника. То есть, чтобы вычислить значение, вам надо при помощи транспортира построить прямоугольный треугольник, один из углов которого равен тому, синус которого вас интересует. Затем измерить длину гипотенузы и противолежащего катета и разделить второе на первое с нужной точности.
Затем измерить длину гипотенузы и противолежащего катета и разделить второе на первое с нужной точности.
Второй вариант — школьный. Со школы все помнят «таблицы Брадиса», содержащие тысячи значений тригонометрических от разных углов. Можно поискать как бумажное издание, так и его электронный аналог в формате pdf — они есть в сети. Найдя таблицы, найти значение синуса нужного угла не составит труда.
Третий вариант — оптимальный. Если есть доступ к , то можно воспользоваться стандартным калькулятором ОС Windows. Его следует переключить в расширенный режим. Для этого в разделе «Вид» меню выберите пункт «Инженерный». Вид калькулятора изменится — в нем появятся, в частности, кнопки для вычисления тригонометрических функций.Теперь введите значение угла , синус которого вам требуется вычислить. Можно сделать это как с клавиатуры, так и щелкая курсором мыши нужные клавиши калькулятора. А можно просто и вставить нужное вам значение (CTRL + C и CTRL + V). После этого выберите единицы измерения, в которых должен быть рассчитан — для тригонометрических функций это могут быть радианы, градусы или рады. Делается это выбором одного из трех значений переключателя, расположенного ниже поля ввода вычисляемого значения. Теперь, нажав кнопку с надписью «sin», получите ответ на свой вопрос.
Делается это выбором одного из трех значений переключателя, расположенного ниже поля ввода вычисляемого значения. Теперь, нажав кнопку с надписью «sin», получите ответ на свой вопрос.
Четвертый вариант — самый современный. В эру интернета в сети существуют , предлагающие чуть ли не каждую возникающую проблему. Он-лайн калькуляторы тригонометрических функций с удобным интерфейсом, более продвинутыми функциональными возможностями найти совсем не . Лучшие из них предлагают вычислить не только значения отдельной функции, но и достаточно сложных выражений из нескольких функций.
Функции синус и косинус относятся к области математики, которую называют тригонометрией, поэтому и сами функции называют тригонометрическими. Согласно самому старому из определений они выражают величину острого угла в прямоугольном треугольнике через отношения длин его сторон. Вычисление значений синус а при современном уровне развития электронной техники — довольно простая задача.
Вам понадобится
- Калькулятор Windows.

Инструкция
Используйте для вычисления синус а угла — вычисление тригонометрических функций предусмотрено в большинстве из них. Учитывая наличие калькулятора во многих мобильных телефонах, некоторых наручных и других мобильных гаджетах, не говоря уже о компьютерах, это, пожалуй, доступный способ вычисления синус а. Если вы решите воспользоваться программным калькулятором компьютера, то ссылку на его запуск ищите в главном меню ОС. Если это Windows, нажмите кнопку Win, выберите в меню пункт «Все программы», перейдите в подраздел «Стандартные» и кликните по строчке «Калькулятор». Чтобы открыть в запустившемся приложении доступ к командам вычисления тригонометрических функций нажмите сочетание клавиш Alt + 2.
Если в исходных величина угла, синус которого требуется вычислить, дана в , убедитесь, что рядом с надписью « » в интерфейсе калькулятора
В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.
Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье. Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Навигация по странице.
Связь между синусом и косинусом одного угла
Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида . Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.
Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.
Теперь докажем его.
Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений . Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Тангенс и котангенс через синус и косинус
Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .
Благодаря такой очевидности тождеств и часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
В заключение этого пункта следует отметить, что тождества и имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z — любое .
Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла.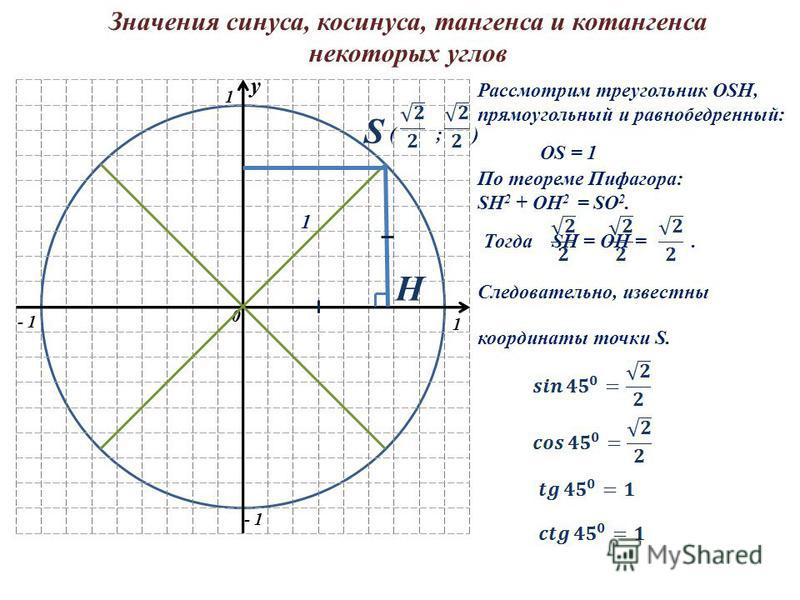 Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.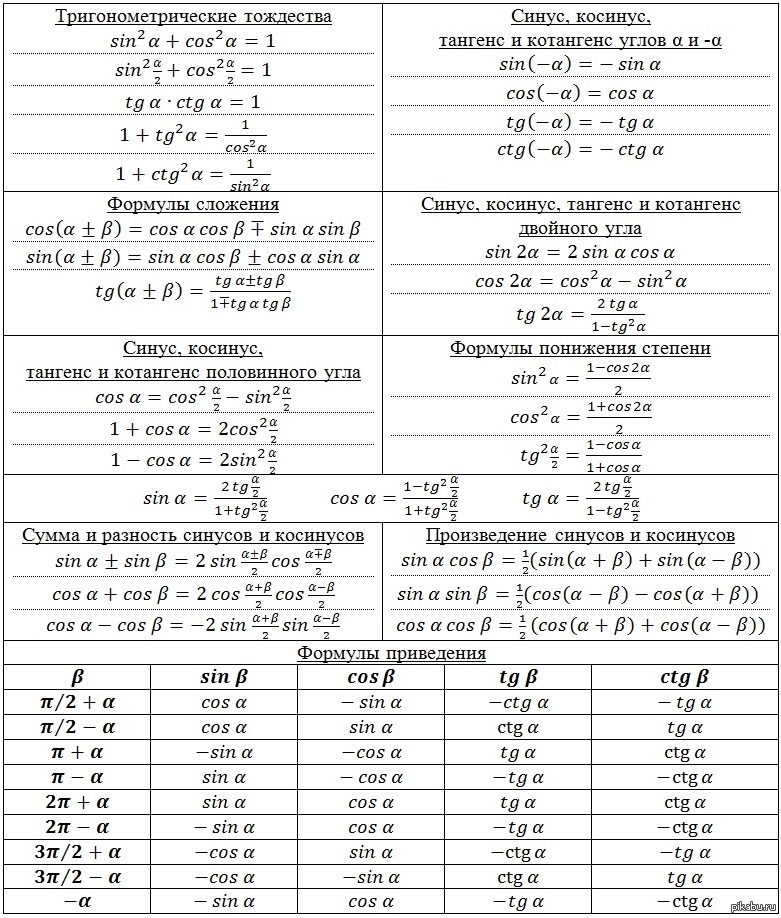
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
|
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ Синус – отношение противолежащего катета к гипотенузе. Косинус – отношение прилежащего катета к гипотенузе. Тангенс – отношение противолежащего катета к прилежащему. Котангенс – отношение прилежащего катета к противолежащему.
Основное тригонометрическое тождество. , . Формулы приведения для 90 и 180 градусов.
Приведение подобных слагаемых. Подобные слагаемые – слагаемые, отличающиеся только коэффициентами, буквенная часть при этом остаётся неизменной (её может не быть). Привести подобные слагаемые: буквенную часть вынести за скобки, а с числовыми коэффициентами произвести соответствующие арифметические действия. Одночлен, многочлен. Действия с ними. Одночлен – это произведение чисел, переменных и их степеней с натуральными показателями. Не являются одночленами: дроби с переменной в знаменателе, степени с отрицательными показателями. Для записи одночлена в стандартном виде необходимо одинаковые переменные записать с помощью степени, далее расположить множители следующим образом: коэффициент, переменные в алфавитном порядке. Степень одночлена – сумма показателей всех переменных. Для умножения одночленов необходимо представить их произведение в стандартном виде. Для возведения одночлена в степень нужно возвести в эту степень каждый множитель. Многочлен – это сумма одночленов. Стандартный вид многочлена – запись, при которой приведены подобные слагаемые и все одночлены записаны в стандартном виде, одночлены более высокой степени расположены левее одночленов более низкой степени. Степень многочлена – наибольшая из степеней одночленов. ! При сложении и вычитании многочленов нужно помнить: если перед скобкой стоит знак минус, то все знаки в скобках меняются на противоположные. Для умножения многочлена на одночлен нужно каждый член многочлена умножить на этот одночлен и произведения сложить, если это возможно. Для умножения многочлена на многочлен нужно каждый член первого многочлена умножить на каждый член второго многочлена и произведения сложить, если это возможно. Формулы сокращённого умножения: квадрат суммы, квадрат разности, разность квадратов. Квадрат суммы: . Квадрат разности: . Разность квадратов: . Куб суммы: . Куб разности: . Разность кубов: . Сумма кубов: . Разложение многочлена на множители: вынесение общего множителя за скобки, группировка, используя формулы сокращённого умножения, комбинирование нескольких методов. 1 способ. Вынесение общего множителя за скобки (найти общий множитель, разделить каждое слагаемое на данный множитель, сумму частных записать в скобках). 2 способ. Группировка (слагаемые, которые имеют общие множители, сгруппировать, взяв каждую группу в скобки, в каждой скобке, если возможно, вынести общий множитель за скобки, снова вынести общий множитель за скобки. 3 способ. С помощью формул сокращённого умножения. 4 способ. Комбинация нескольких методов (в одном примере используются различные из предыдущих методов). Степень: умножение и деление степеней, возведение степени в степень. Отрицательная степень. Умножение степеней с одинаковым основанием: показатели складываются, основание остаётся неизменным. Деление степеней с одинаковым основанием: показатели вычитаются, основание остаётся. Возведение степени в степень: показатели перемножаются, основание остаётся. Отрицательная степень: возвести число, взаимно обратное основанию, в степень противоположную основанию. Например: . Избавление от иррациональности в знаменателе. 1 способ. Если в знаменателе сумма или разность, то умножить числитель и знаменатель на выражение, сопряжённое знаменателю ( с противоположным знаком, если была сумма, то умножаем на разность, если была разность, то умножаем на сумму). 2 способ. Если в знаменателе одночлен, то умножить числитель и знаменатель на корень, который содержится в знаменателе. ⇐ Предыдущая1234Следующая ⇒ |
Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно
Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого — свой тангенс и котангенс. Почему почти? Об этом ниже.
Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов.)
Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов.)
Таблицы бывают разные. Длинные, где можно посмотреть, чему равен, скажем, sin37°6’. Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Для общей эрудиции.)
И зачем тогда этот урок?! — спросите вы.
А вот зачем. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё. На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии.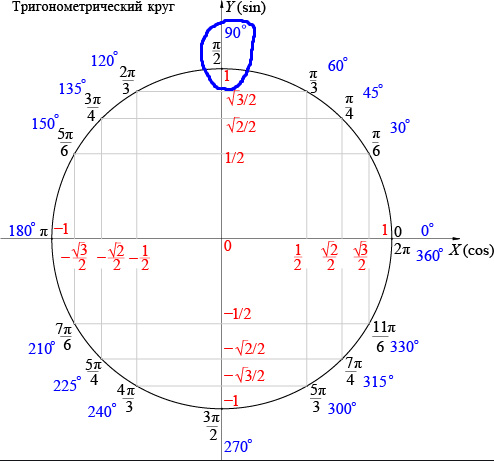 Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…
Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…
Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. И всё. Шесть значений запомнить легче, чем 68, мне кажется…)
Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки- тригонометрического круга.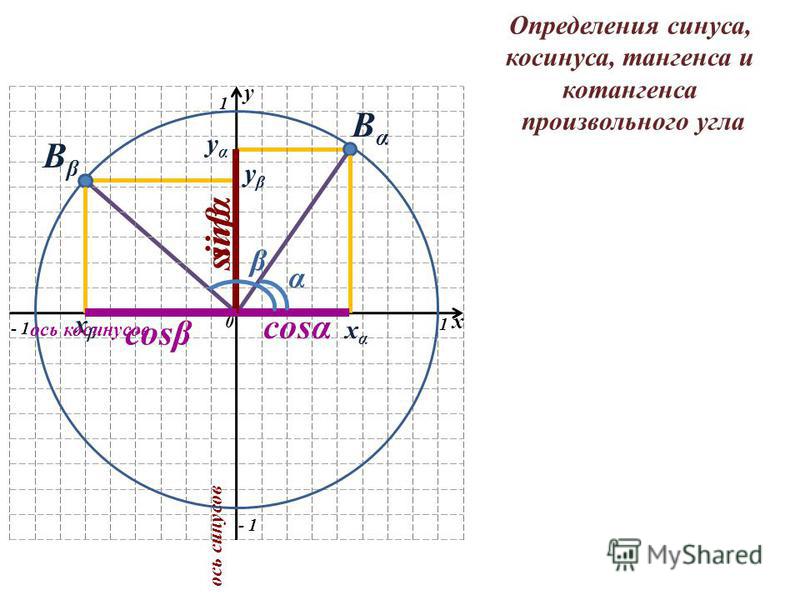 Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу. Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)
Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу. Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)
Итак, начнём. Для начала разобьём все эти особые углы на три группы.
Первая группа углов.
Рассмотрим первую группауглов из семнадцати особых. Это 5 углов: 0°, 90°, 180°, 270°, 360°.
Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов:
| Угол х (в градусах) | |||||
| Угол х (в радианах) | |||||
| sin x | -1 | ||||
| cos x | -1 | ||||
| tg x | не сущ.
| не сущ. | |||
| ctg x | не сущ. | не сущ. | не сущ. |
Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.
Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:
Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ… Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.
Кстати, положение угла в 0 градусов полностью совпадает с положением угла в 360 градусов. Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Угол в 360 градусов я отметил, чтобы замкнуть круг.
Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают…)
Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.
В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.
Для этого на круге нарисуем произвольный угол х. В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. Вот так:
А теперь — внимание! Уменьшим угол х, приблизим подвижную сторону к оси ОХ. Наведите курсор на картинку и всё увидите.
Теперь включаем элементарную логику!.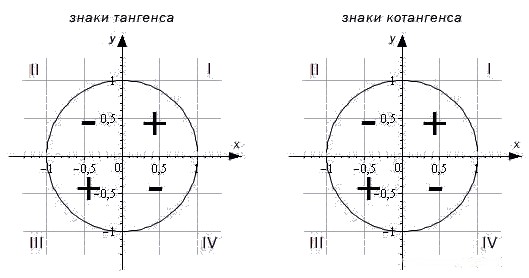 Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!
Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!
Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе быть не может.
Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось. Вот и всё.
Как видите, для этой группы углов ничего заучивать не надо.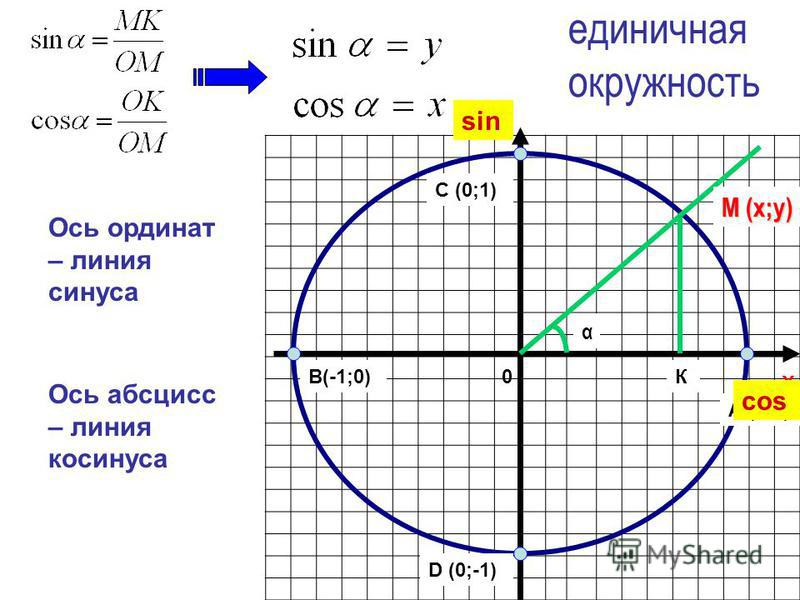 Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса (котангенса) — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге — и нет проблем!
Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество…) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
Но, как раз, с отсчётом углов и случаются проблемы да ошибки… Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)
А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах — покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол
вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 «пи»…) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.
А если угол
Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.
Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.
Итак, с пятью углами из семнадцати — разобрались.
Вторая группа углов.
Следующая группа углов — это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так… Исторически.) Дальше будет видно, чем хороши эти углы.
Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:
| Угол х (в градусах) | |||||
| Угол х (в радианах) | |||||
| sin x | |||||
| cos x | |||||
| tg x | не сущ. | ||||
| ctg x | не сущ. |
Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины. ) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.
) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.
Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов…
Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же. Для углов 20, 50, 80 так бы не получилось…
Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся… Три значения можно выучить, правда?
А дальше опять расходятся… Три значения можно выучить, правда?
С тангенсами — котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.
Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.
Осталось разобраться с последней группой из 9 углов.
Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.
Кошмар, правда?)
А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)
Или углы в радианах? Например, про углы:
и многие другие, вы должны знать всё.
Самое забавное, что знать это всё — невозможно в принципе. Если использовать механическую память.
И очень легко, фактически элементарно — если использовать тригонометрический круг. Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:
Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:
30°, 45°, 60°
А лохматые углы в радианах превратятся в привычные:
Причём в радианах это превращение делается куда проще, чем в градусах. Да-да!
Плюс к тому, умение рисовать углы на круге позволяет элементарно разобраться с последней, третьей группой углов. И тогда, в 99% заданий, таблица синусов и таблица косинусов вам точно не потребуются. Как и таблица тангенсов-котангенсов).
Все тайны последней, третьей группы особенных углов и секреты уверенной работы с ними — в следующем уроке.
Таблица синусов и косинусов.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…» )
Продолжаем осваивать таблицу синусов и косинусов. А именно — привыкаем работать с необходимыми табличными значениями без механической зубрёжки.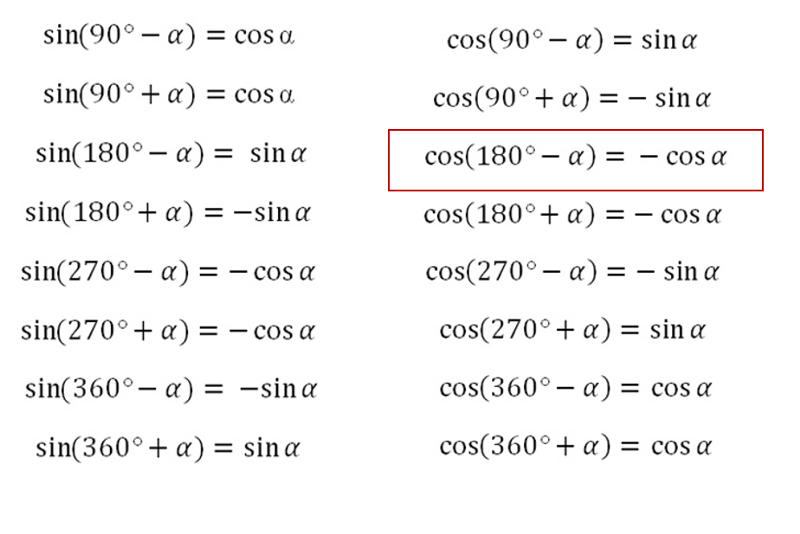 И, разумеется, без бумажек-шпаргалок. Это несложно. Если голову включить. Голова нужна не только шапку носить, да…)
И, разумеется, без бумажек-шпаргалок. Это несложно. Если голову включить. Голова нужна не только шапку носить, да…)
Итак, в предыдущем уроке мы разбили углы, про которые нужно знать всё, на три группы. Первая группа — углы, попадающие точно на оси координат. Вторая группа — всего три угла: 30°, 45°, 60°. Значения таблицы синусов и косинусов для этих трёх углов приходится-таки вызубрить. Аж все три значения!)
Осталась последняя, третья группа углов.
Третья группа углов.
Вот эти девять углов:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°.
Надо железно знать таблицу синусов и косинусов для этих углов. Вот как выглядят эти углы в радианах:
Для пущего устрашения я добавлю, что это углы, которые лежат в пределах всего лишь одного оборота. Т.е в пределах 360°. А надо знать значения таблицы синусов и косинусов и за этими пределами… Скажем, синус 855°, или косинус 21пи/4 вы знать обязаны.
Что, меркнут краски жизни!?)
Спокойствие! Нас спасут житейская смекалка и тригонометрический круг! Я же предупреждал, что с помощью круга все эти несусветные проблемы (и не только эти!) можно решить за пару минут. Слегка скучая.)
В конце предыдущего урока я задавал вопрос: чего особенного в этих девяти углах? Кто сообразил, тот справится. Кто не сообразил, тот прямо сейчас узнает тайну этих углов и тоже справится! Внимайте!
Дело в том, что все эти углы составлены из углов предыдущих двух групп. Например:
120° = 90° + 30°
225° = 180° + 45°
300° = 270° + 30°
Ну, вы поняли…)
Кстати, можно использовать не сумму, а разность, например:
300° = 360° — 60°
135° = 180° — 45°
И так далее.
Другими словами, каждый угол из этой группы есть сумма (разность) одного угла из первой группы (те, что попадают на оси координат) и одного угла из второй группы (30, 45, 60).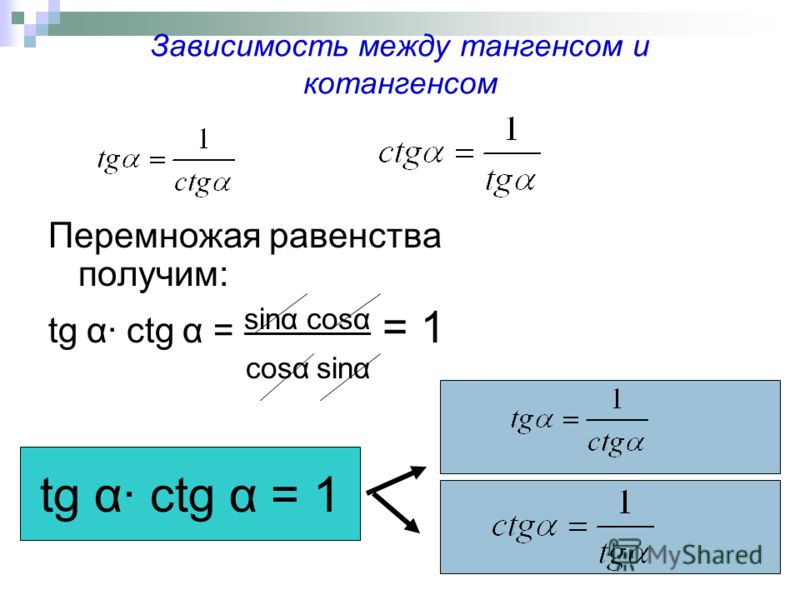 Нет, можно конечно разбить углы на сумму/разность каких попало, но оно нам совсем не надо.) Надо: один угол — из первой группы и один из второй.
Нет, можно конечно разбить углы на сумму/разность каких попало, но оно нам совсем не надо.) Надо: один угол — из первой группы и один из второй.
И как же мы будем использовать этот замечательный факт? Просто складывать-вычитать синусы? Разочарую… Синус суммы углов вовсе не равен сумме синусов каждого угла! Запомните это накрепко! Для суммы есть своя длинная формула. Но такое особое устройство углов позволит нам находить их синусы-косинусы одной левой.) Без таблицы синусов и косинусов.
Здесь нет никакой особой теории. Чистая практика! Поэтому показываю на примерах.
Итак, пусть нам надо найти косинус 150 градусов. Подозреваю, что далеко не каждый сразу и уверенно вспомнит это значение таблицы синусов и косинусов. Ох, не каждый…) А если и вспомнит, сомнения будут грызть. Посему работаем надёжно!
Прежде всего соображаем, из каких особых углов он состоит. Рекомендую в качестве угла из первой группы выбирать 180° или 360° Далее поймёте, почему.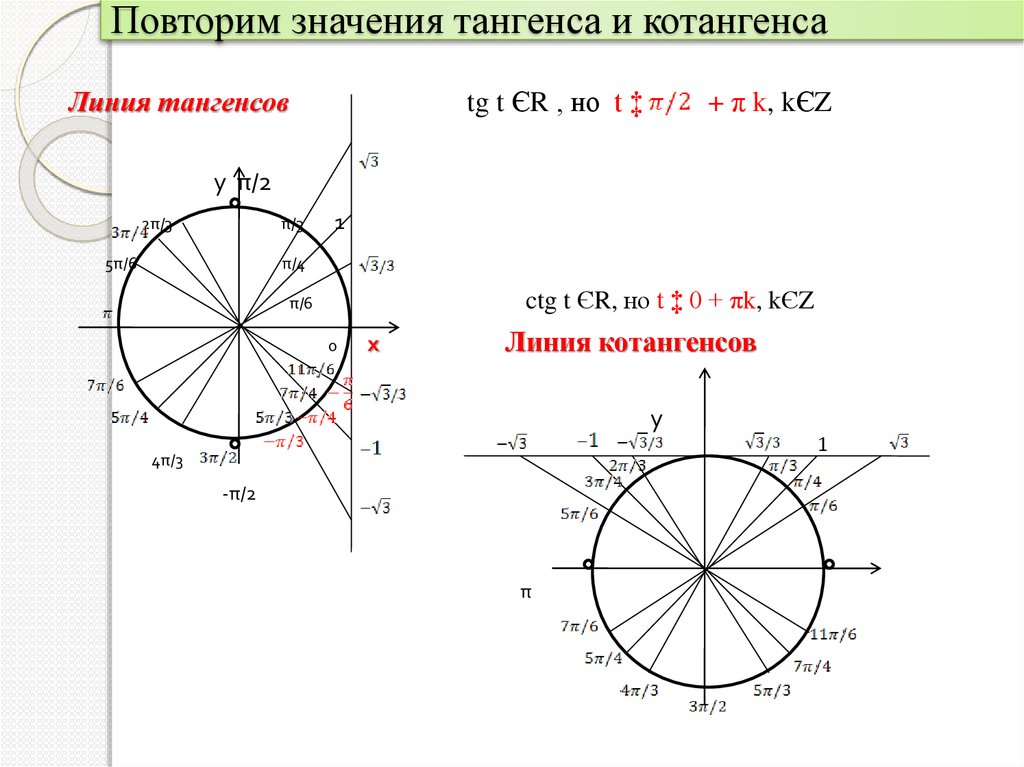 Легко сообразить, что:
Легко сообразить, что:
150° = 180° — 30°
Отлично! Разложился угол классически. Один — из первой группы, другой — из второй. Теперь нарисуем угол 150° на тригонометрическом круге. На глаз нарисуем, примерно. Но рисовать будем, глядя на разложение:
150° = 180° — 30°
Говоря житейским языком, мы крутим подвижную сторону угла (где точка А) на 180° в плюс (по часовой стрелке), затем отматываем угол на 30° обратно!) Надеюсь, вы уже знаете, как отсчитывать углы на тригонометрическом круге? Без этих знаний — никак…
Получаем вот такую картинку:
Зелёным цветом обозначен нужный нам угол в 150° и его косинус. А вот красным цветом я обозначил вспомогательный угол в 30°, который нас и спасёт в этой крутой задаче.) Ведь мы знаем (ну, или должны знать…) косинус 30 градусов из таблицы синусов и косинусов. Правда эти красненькие 30° как бы не совсем правильные 30°, не от той полуоси отсчитаны… .
.
Ну и ладно. Давайте нарисуем правильные 30° на этом же круге. Отсчитанные от положительной полуоси Х. Наводим мышку на рисунок (кликать не надо, а то придётся всё сначала читать)) и видим правильный синий угол в 30° и его косинус.
Ну и…? Как вам кажется, в каком соотношении находятся cos30° и cos150°? Догадаетесь!?
Да! Косинус 150 градусов равен по величине косинусу 30, но имеет отрицательный знак! Треугольнички слева-справа одинаковые, косинусы равны по величине. Вот и всё. Просто мы на тригонометрическом круге просчитали непонятный косинус 150 градусов через известный косинус 30. Не заглядывая в таблицу синусов и косинусов. Так можно делать всегда.
Ответ:
| cos150° | = | -cos30° | = | - |
А если нужен синус 150 градусов? Нет проблем! Опять рисуем круг, угол в 150 градусов (как 180° — 30°). На этот раз отмечаем его синус на оси У.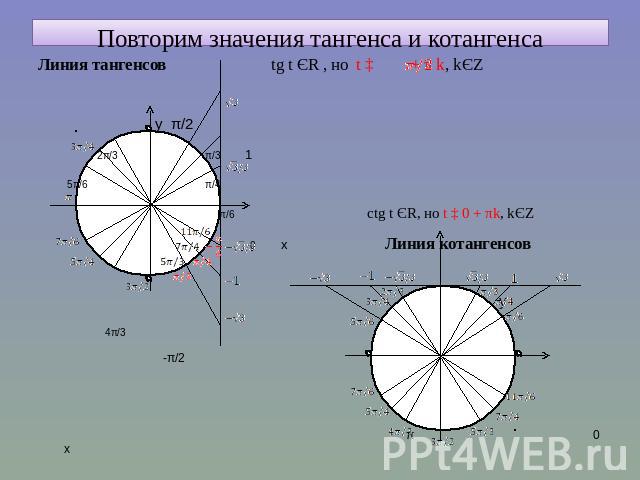 Вот так:
Вот так:
Опять рисуем правильный угол в 30 градусов и отмечаем его синус. Наведите курсор на картинку, чтобы увидеть это сложное построение.) Что мы видим? Мы видим, что синусы углов 150° и 30° равны! Треугольнички-то одинаковые. Пусть даже и углы по 30° находятся вне треугольников. Всё равно, треугольнички — одинаковые.
Ответ:
| sin150° | = | sin30° | = |
Улавливаете суть? Любой угол третьей группы всегда разбивается на сумму/разность угла 180° (или 360°) и угла 30, 45, 60 (какой уж подойдёт). Стало быть, на тригонометрическом круге мы всегда получим вспомогательный угол 30, 45 или 60 градусов. Без разницы, в какой четверти получится этот вспомогательный угол. Достаточно нарисовать правильный угол (в первой четверти), найти одинаковые треугольнички и сравнить по картинке их синусы-косинусы. Тут ошибиться очень трудно!
Тут ошибиться очень трудно!
И не надо зазубривать таблицу синусов и косинусов для этих девяти углов.
Вот и всё. Есть тут, правда одна проблемка. Ленятся люди рисовать круг. Стесняются, что плохо получится, что ли!? Тригонометрический круг — легальная шпаргалка — нужен вам, а не проверяющим! Здесь не требуются линейка, циркуль, транспортир и прочие цветные карандаши. Не черчение, чай…
Так и быть, я личным примером покажу, как выглядит все это рисование в реале!
Пусть мне надо определить cos240°. Без таблицы синусов и косинусов. За пять секунд я соображаю, что:
240° = 180° + 60°
Ещё за десять секунд я рисую мощную картину:
М-да… Ужас какой-то. Ну и что!? Зато я чётко вижу, где располагается мой вспомогательный угол в 60° (третья четверть). Я знаю, что треугольнички, образованные вспомогательным углом в 60° и правильным углом в 60° (в первой четверти) — одинаковые. Пусть даже на картинке они, гм.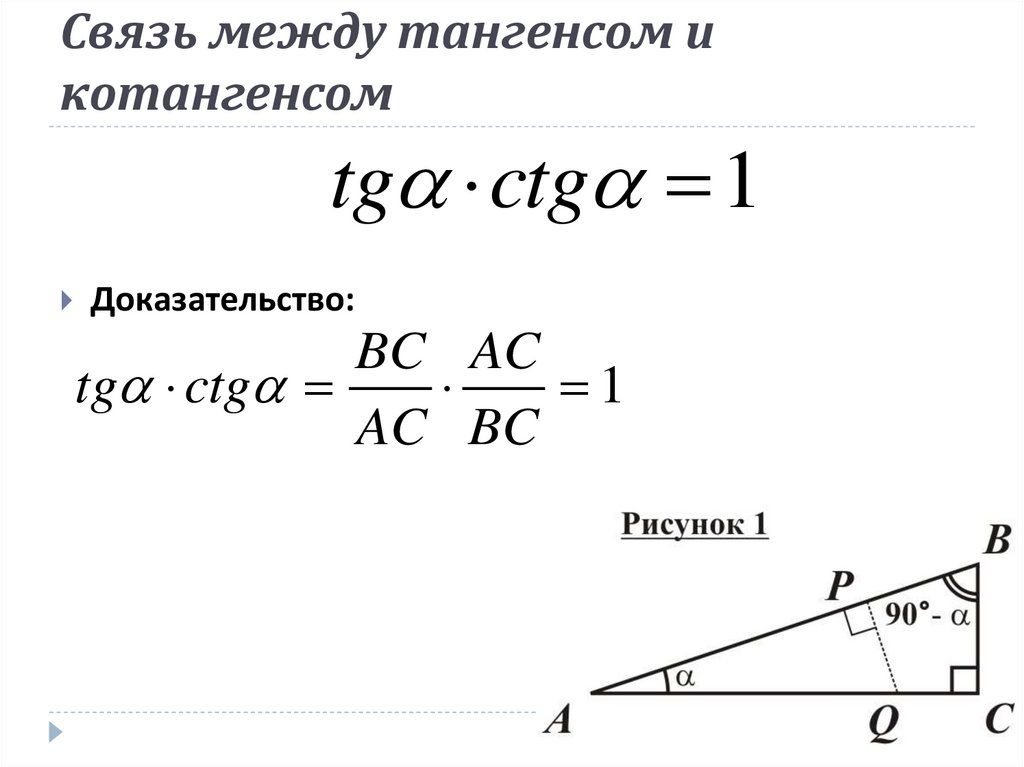 .. не очень равны.) И по этой картинке я стопроцентно понимаю, что косинус 240 градусов равен косинусу 60, но со знаком «минус». Так как cos240° попадает на отрицательную полуось Х. Посему из этой кошмарной картины я надёжно вывожу (за 20 секунд!) правильный ответ. Безо всякой таблицы синусов и косинусов:
.. не очень равны.) И по этой картинке я стопроцентно понимаю, что косинус 240 градусов равен косинусу 60, но со знаком «минус». Так как cos240° попадает на отрицательную полуось Х. Посему из этой кошмарной картины я надёжно вывожу (за 20 секунд!) правильный ответ. Безо всякой таблицы синусов и косинусов:
cos240° = — cos60° = — 1/2
Что мне и надо.)
Тем, кто проникся уважением к тригонометрическому кругу, предлагаю загадку. Как вы думаете, какую функцию и какого положительного угла я искал вот по этому наскальному рисунку?)
Если поняли, вам можно начинать изучать иероглифы.) Ответ будет чуть ниже.
Итак, осталось всего ничего. Разобраться с углами, которые больше360°. Если они приводятся к углам второй группы (30, 45, 60), значения таблицы синусов и косинусов для них тоже знать необходимо. Ну, не совсем знать — таких углов бесконечное множество — но уметь их вычислять.
Здесь всё просто. Опять сплошная практика. Берём пример из начала урока. Пусть нам надо определить sin855°. Понятно, что в этом угле сидит несколько полных оборотов по 360° и ещё какой-то хвостик. Вот и выбросим эти полные обороты. Они никак не сказываются на тригонометрических функциях угла! Только картину путают…
Берём пример из начала урока. Пусть нам надо определить sin855°. Понятно, что в этом угле сидит несколько полных оборотов по 360° и ещё какой-то хвостик. Вот и выбросим эти полные обороты. Они никак не сказываются на тригонометрических функциях угла! Только картину путают…
Еслиу нас на круге есть угол, скажем, в 45°, то прибавьте к нему хоть пять полных оборотов, хоть тридцать пять — положение его не изменится. Не поменяются значения синусов, косинусов и т.д.
Определить количество полных оборотов очень просто. Надо разделить величину угла (в нашем случае — 855°) на 360°. Хоть в уме, хоть уголком. Радует то, что до конца делить не надо! Нам же количество целых оборотов надо знать, а не дробных.
Вот и делим. Получаем два с копейками. Копейки нас не интересуют, их даже и считать не нужно. А два полных оборота — это 2 · 360° = 720°. Считаем хвостик. Отнимаем:
855 — 720 = 135
Хвостик получился 135°. А это классический угол третьей группы! Так как:
135° = 180° — 45°
С этим углом разбираемся, как написано выше. С помощью круга. Вот и все дела. Так нужно поступать всегда. Откинуть от большого значения угла все полные обороты и работать с оставшимся хвостиком. Кстати, если этот хвостик не попадает ни в какую группу (20°, например, или 160°) — значит, где-то ошибка. Или задание — более сложное и рассчитано на какие-то дополнительные преобразования. Синус 20° вы знать не обязаны.
С помощью круга. Вот и все дела. Так нужно поступать всегда. Откинуть от большого значения угла все полные обороты и работать с оставшимся хвостиком. Кстати, если этот хвостик не попадает ни в какую группу (20°, например, или 160°) — значит, где-то ошибка. Или задание — более сложное и рассчитано на какие-то дополнительные преобразования. Синус 20° вы знать не обязаны.
Вернёмся к наскальному рисунку.) Дойти до правильного ответа можно по такой цепочке:
1. Пунктир идёт на ось У. Значит, автора интересует синус угла!
2. Угол в первой четверти отпадает. Это явно угол из таблицы синусов и косинусов, автор его и так знает. Может быть…) Да и зачем тогда отмечен угол в четвёртой четверти!? Значит, автора интересует синус некоего угла из четвёртой четверти!
3. Отмеченные дужками углы, очевидно, должны быть равны… Угол в первой четверти всяко меньше 60°… Да и меньше 45°! Стало быть, это 30 градусов!
4. Угол в четвёртой четверти… Возможны 2 варианта. .. -30° и 330°. Но автора интересует положительный угол… Всё!!! На наскальном рисунке изображена попытка найти sin330°! Возможно, автор даже и определил его.)
.. -30° и 330°. Но автора интересует положительный угол… Всё!!! На наскальном рисунке изображена попытка найти sin330°! Возможно, автор даже и определил его.)
sin330° = -0,5
Пора применить знания на практике. Потренироваться. Намекаю, что таблицу синусов и косинусовможно использовать только для проверки! Тонко так намекаю…) Предупреждаю, что никаких особых формул и тригонометрических преобразований здесь не требуется. Просто определяем значения и подставляем в пример. Чтобы горе от ума не получилось…)
Вычислить:
cos0° + sin90° — cos180° — sin270° =
sin135° · cos315° =
sin240° · cos330° =
cos(-120°) · sin(-330°) =
sin(-2430°) + cos(-1380°) =
Ответы (в беспорядке): 1,5; -0,25; 4; -0,75; 0,5
Получается? Отлично! Не получается? Путаница с отрицательными значениями? Бывает… Ничего страшного. Самое главное — правильно нарисовать (отсчитать) угол на круге. А там уже всё видно. Здесь вам поможет урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах.
Здесь вам поможет урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах.
Самые азы, конечно, но куда без них?)
Усложним задачу. Работаем по-взрослому. С радианами. Именно эта мера угла является основной в солидной математике.
Вычислить:
Ответы (в беспорядке): 0,5; 1,5; -2; -0,5; 0,25.
Что, с радианами сложнее, да? В градусы переводить, потом лишние обороты отбрасывать… Да, хлопотное занятие! Кстати, в этом уроке мы только с градусами работали, если кто заметил…) Это специально.
Только для тех, кто добрался до этих строк!)
Дело в том, что есть очень простой практический приём работы с радианами. Да такой приём, что работа с радианами становится проще, много проще работы с градусами! Поэтому я и не расписывал здесь примеры с радианами и переводом их в градусы. Лишнее это. Гораздо проще и надёжнее работать с радианами напрямую.
Этот практический приём описан в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах.
Подытожим тему. В этом уроке кто хотел, тот научился лихо крутить по кругу углы, откидывать полные обороты и легко определять необходимые значения таблицы синусов и косинусов без этой самой таблицы. Это солидный багаж для контрольных и экзаменов.
Но самое главное в этом уроке — тренировка в работе с тригонометрическим кругом. Определять значения таблицы синусов и косинусов можно и без круга. По формулам приведения, о которых мы ещё поговорим. Но любая формула тригонометрии применима в своей узкой области. А круг помогает во всей тригонометрии. Скажем, тригонометрические неравенства (а это задания уровня С!) решаются на 90% через круг, а оставшиеся 10% — с помощью круга. Круг лишним не бывает!) Освойте его, и тригонометрия будет дружить с вами.
Воспользуйтесь поиском по сайту:
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.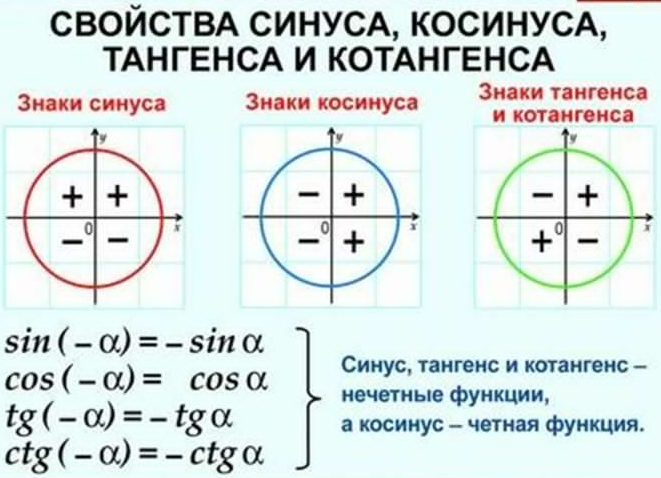 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.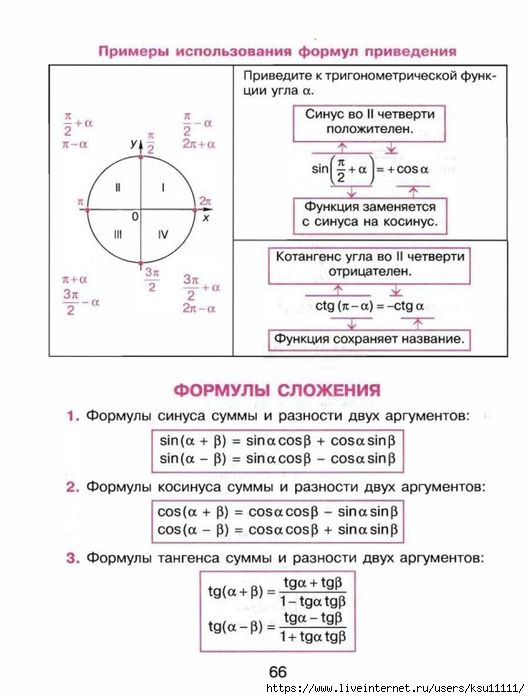 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Котангенс — Формула, График, Область, Диапазон
Котангенс — одна из 6 тригонометрических функций. Обычно его называют «кроваткой». Как и другие тригонометрические отношения, формула котангенса также определяется как отношение сторон прямоугольного треугольника. Формула cot x равна отношению основания и перпендикуляра прямоугольного треугольника. Вот 6 основных тригонометрических функций и их сокращения.
Обычно его называют «кроваткой». Как и другие тригонометрические отношения, формула котангенса также определяется как отношение сторон прямоугольного треугольника. Формула cot x равна отношению основания и перпендикуляра прямоугольного треугольника. Вот 6 основных тригонометрических функций и их сокращения.
| Тригонометрическая функция | Аббревиатура |
|---|---|
| Синусоидальная функция | грех |
| Функция косинуса | потому что |
| Касательная функция | желтовато-коричневый |
| Функция косеканса | КСК |
| Секущая функция | сек |
| Функция котангенса | детская кроватка |
Давайте узнаем больше о котангенсе, изучив его определение, формулу cot x, его область определения, диапазон, график, производную и интеграл. Также мы увидим, каковы значения котангенса на единичной окружности.
Также мы увидим, каковы значения котангенса на единичной окружности.
| 1. | Что такое котангенс? |
| 2. | Формула котангенса |
| 3. | Свойства котангенса |
| 4. | Закон котангенса |
| 5. | Период котангенса |
| 6. | Котангенс единичной окружности |
| 7. | Домен, диапазон и график котангенса |
| 8. | Производная и интеграл от котангенса |
| 9. | Часто задаваемые вопросы о котангенсе |
Что такое котангенс?
Котангенс — одно из основных тригонометрических соотношений. Фактически это одно из обратных тригонометрических соотношений csc, sec и cot. Обычно его обозначают как «кроватка х», где х — угол между основанием и гипотенузой прямоугольного треугольника. Альтернативные названия котангенса — котангенс и котангенс х. Котангенс угла в прямоугольном треугольнике определяется как отношение прилежащей стороны (стороны, прилежащей к углу) к противолежащей стороне (стороны, противолежащей углу).
Альтернативные названия котангенса — котангенс и котангенс х. Котангенс угла в прямоугольном треугольнике определяется как отношение прилежащей стороны (стороны, прилежащей к углу) к противолежащей стороне (стороны, противолежащей углу).
Формула котангенса
Формула котангенса для угла θ: cot θ = (прилежащая сторона) / (противоположная сторона). . Рассмотрим прямоугольный треугольник ABC, образующий прямой угол в точке B. Тогда AB — сторона, примыкающая к A, а BC — сторона, противолежащая A. Тогда котангенс треугольника A (который записывается как детская кроватка A) есть,
детская кроватка A = (прилегающая сторона A) / (противоположная сторона A) = (AB) / (BC).
Например, если AB = 3 и BC = 4, то кроватка A = 3/4.
Свойства котангенса
Мы уже знаем, что кроватка x = (Смежный) / (Противоположный). Помимо этого, существует несколько других формул отношения котангенса, в которых котангенс может быть записан через другие тригонометрические отношения.
Котангенс относительно Cos и Sin
Мы знаем, что sin θ = (Противоположный) / (Гипотенуза) и cos θ = (Смежный) / (Гипотенуза). Если мы разделим cos θ на sin θ , мы получим
(cos θ) / (sin θ) = (Смежный) / (Гипотенуза) × (Гипотенуза) / (Противоположный)
= (Смежный) / (Противоположный)
= кроватка θ
Следовательно, кроватка θ = (cos θ) / (sin θ) — это формула кроватки x с точки зрения cos и sin.
Котангенс через Tan
Мы знаем, что tan θ = (Противоположный)/(Смежный) и cot θ = (Смежный)/(Противоположный). Таким образом, cot и tan обратны друг другу. Таким образом, мы можем написать cot θ = 1/tan θ и tan θ = 1/cot θ. Таким образом, раскладушка с точки зрения загара есть. раскладушка θ = 1/тангенс θ. Существует еще одна формула для записи кроватки в терминах загара: кроватка θ = тангенс (π/2 — θ) (или) тангенс (90° — θ).
Котангенс через косек
Из одного из тождеств Пифагора csc 2 θ — cot 2 θ = 1. Отсюда получаем cot 2 θ = csc 2, Если мы возьмем квадратный корень с обеих сторон, кроватка θ = √(csc 2 θ — 1). Следовательно, детская кроватка в терминах csc равна кроватка θ = √(csc 2 θ — 1)
Отсюда получаем cot 2 θ = csc 2, Если мы возьмем квадратный корень с обеих сторон, кроватка θ = √(csc 2 θ — 1). Следовательно, детская кроватка в терминах csc равна кроватка θ = √(csc 2 θ — 1)
Закон котангенса
Рассмотрим треугольник ABC, где AB = c, BC = a и CA = b. Закон котангенса похож на закон синусов, но включает половинные углы. Закон котангенса гласит: (cot A/2) / (s — a) = (cot B/2) / (s — b) = (cot C/2) / (s — c). Здесь s — полупериметр треугольника. т. е. s = (a + b + c)/2.
Знак котангенса
Отношение котангенса (разумеется, и tan, и cot) положительно только в первой и третьей четвертях. Он отрицателен во втором и четвертом квадрантах. Таким образом,
- раскладушка (π — θ) = — раскладушка θ (2 -й квадрант)
- раскладушка (π + θ) = раскладушка θ (3 -й -й квадрант)
- раскладушка (2π — θ) = — раскладушка θ (4 -й квадрант)
- раскладушка (2π + θ) = раскладушка θ (1 ст квадрант)
г.
Период котангенса
Мы знаем, что все тригонометрические функции являются периодическими функциями. Кроме того, из предыдущего раздела мы знаем, что кроватка (2π + θ) = кроватка θ . Но функция котангенса может иметь меньший период π (поскольку функция котангенса положительна в первом и третьем квадранте, где углы в третьем квадранте равны π + угол в первом квадранте). Таким образом, период котангенса равен π. т. е. кроватка (π + θ) = кроватка θ .
Котангенс отрицательного угла
Котангенс отрицательного угла равен отрицательному значению котангенса положительного угла. т. е. кроватка (-x) = -кроватка x для любого x в области. Отсюда можно сделать вывод, что котангенс является нечетной функцией.
Котангенс единичной окружности
Мы знаем, что каждая точка на единичной окружности дает значения cos и sin соответствующего угла. Чтобы найти котангенс соответствующего угла, мы просто делим соответствующее значение cos на соответствующее значение sin, потому что у нас есть формула cot x, определяемая как cot x = (cos x) / (sin x). Здесь мы можем видеть значения cot θ для некоторых стандартных углов.
Здесь мы можем видеть значения cot θ для некоторых стандартных углов.
Таким же образом мы можем вычислить котангенс всех углов единичной окружности. Вот единичный круг с функцией котангенса.
Домен, диапазон и график котангенса
В этом разделе давайте посмотрим, как мы можем найти область определения и область значений функции котангенса. Кроме того, мы увидим процесс построения графика в своей области.
Область и диапазон котангенса
В предыдущем разделе мы видели, что кроватка не определена при 0° (0π), 180° (1π) и 360° (2π) (другими словами, котангенс не определен везде, где sin x равен нулю, потому что cot x = (cos x)/(sin x)). Мы знаем, что sin x равен нулю для целых чисел, кратных π, поэтому функция котангенса не определена для всех целых чисел, кратных π. Таким образом, кроватка nπ НЕ определена ни для какого целого числа n. Таким образом, областью определения котангенса является множество всех действительных чисел (R), кроме nπ (где n ∈ Z). Опять же, из единичного круга мы можем видеть, что функция котангенса может давать все действительные числа, и, следовательно, ее областью значений является множество всех действительных чисел (R). Таким образом,
Опять же, из единичного круга мы можем видеть, что функция котангенса может давать все действительные числа, и, следовательно, ее областью значений является множество всех действительных чисел (R). Таким образом,
- Областью определения котангенса является множество действительных чисел, кроме всех целых чисел, кратных π
- Областью котангенса является множество всех действительных чисел
т. е. cot x : R — {nπ / n ∈ Z} → R
График котангенса
Поскольку функция котангенса НЕ определена для целых чисел, кратных π, на графике есть вертикальные асимптоты для всех кратных π котангенса. Кроме того, из единичного круга (в одном из предыдущих разделов) мы можем видеть, что котангенс равен 0 во всех нечетных кратных π/2. Кроме того, из единичного круга мы можем видеть, что в интервале, скажем (0, π), значения кроватки уменьшаются по мере увеличения углов. Следовательно, ctg — убывающая функция. Таким образом, график функции котангенса выглядит так.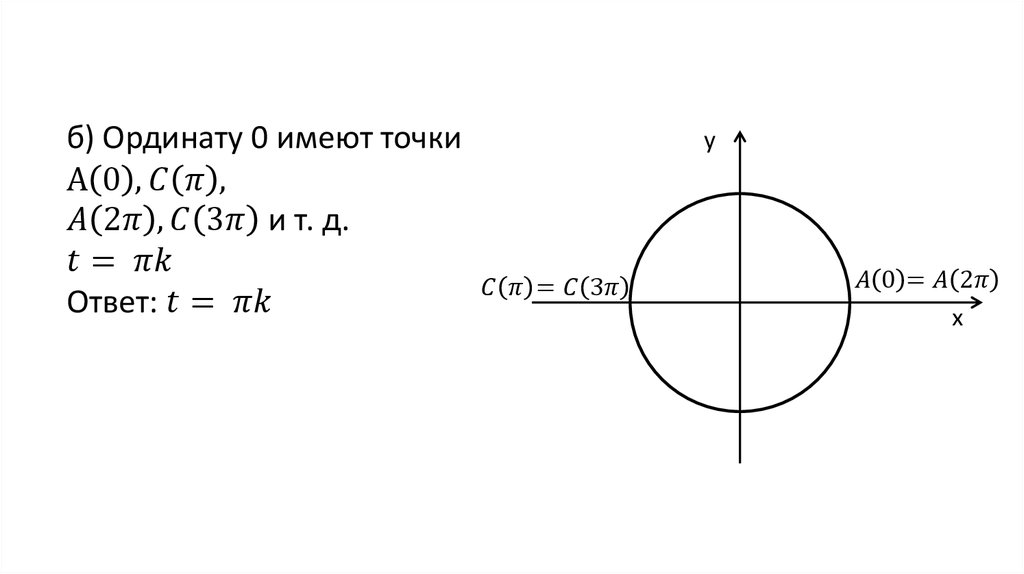
Производная и интеграл от котангенса
Чтобы найти производную и интеграл котангенса, мы используем формулу тождественного котангенса cot x = (cos x) / (sin x). Давайте посмотрим, как.
Производная котангенса
Пусть y = cot x = (cos x) / (sin x). Тогда по правилу частных
y’ = [sin x d/dx(cos x) — cos x d/dx(sin x)] / (sin x) 2
= [sin x (- sin x) — cos x (cos x)] / sin 2 x
= [-sin 2 x — cos 2 x] / sin 2 x
= — [sin 2 x + cos 2 x] / sin 2 x
= — 1/sin 2 x — [Используя тригонометрическое тождество sin 2 x + cos 2 x = 1]
= -csc 2 x — [Поскольку sin x = 1/csc x и csc x = 1/sin x]
Таким образом, производная от cot x равна -csc 2 x.
Интеграл от котангенса
∫ cot x = ∫ (cos x) / (sin x) dx
Вычислим этот интеграл методом подстановки. Для этого пусть sin x = u. Тогда cos x dx = du.
Для этого пусть sin x = u. Тогда cos x dx = du.
Тогда, используя приведенный выше интеграл, получим
∫ (1/u) du = ln |u| + C, где C — постоянная интегрирования.
Замените здесь u = sin x,
∫ cot x dx = ln |sin x| + C
Таким образом, интеграл от cot x равен ln |sin x| + C.
Важные моменты по котангенсу:
- Cot x Формула: cot x = (cos x) / (sin x) г.
- Некоторые важные формулы котангенса:
детская кроватка x = (cos x)/(sin x)
детская кроватка х = 1/загар х
детская кроватка (-x) = — детская кроватка x
детская кроватка θ = √(csc 2 θ — 1) - Домен cot x равен R — {nπ}, а его диапазон равен R.
- Функция котангенса имеет вертикальные асимптоты при всех кратных π.
Темы по теме:
- Детская кроватка — Формула загара
- Тригонометрия
- Тригонометрический калькулятор
- Калькулятор арккотангенса
- Детская кроватка 53 градуса
- Детская кроватка 18 градусов
- Детская кроватка 1 градус
Часто задаваемые вопросы о котангенсе
Что такое котангенс в тригонометрии?
Котангенс является одним из тригонометрических отношений и определяется как cot x = (прилежащая сторона)/(противоположная сторона) для любого угла x между основанием и гипотенузой в прямоугольном треугольнике.
Что такое формулы котангенса?
Вот некоторые важные формулы кроватки x:.
- детская кроватка x = (смежный)/(напротив)
- раскладушка x = (cos x)/(sin x)
- детская кроватка х = 1/загар х
- кроватка (π/2 — x) = tan x
- детская кроватка (π + x) = детская кроватка x
- детская кроватка (2π + x) = детская кроватка x
- детская кроватка (-x) = — детская кроватка x
- раскладушка θ = √csc²θ — 1
Является ли котангенс обратным тангенсу?
Нет, обратным тангенсом является арктангенс. Пишется как загар -1 . Но (tan x) -1 = 1/tan x = кроватка x. (tan x) -1 и tan -1 x НЕ совпадают.
Что такое область определения и диапазон котангенса?
Область определения котангенса равна R — {nπ, где n — целое число}, а диапазон значений котангенса равен R. Здесь R — множество всех действительных чисел.
Что является противоположностью формулы котангенса?
Мы не используем терминологию противоположности котангенса.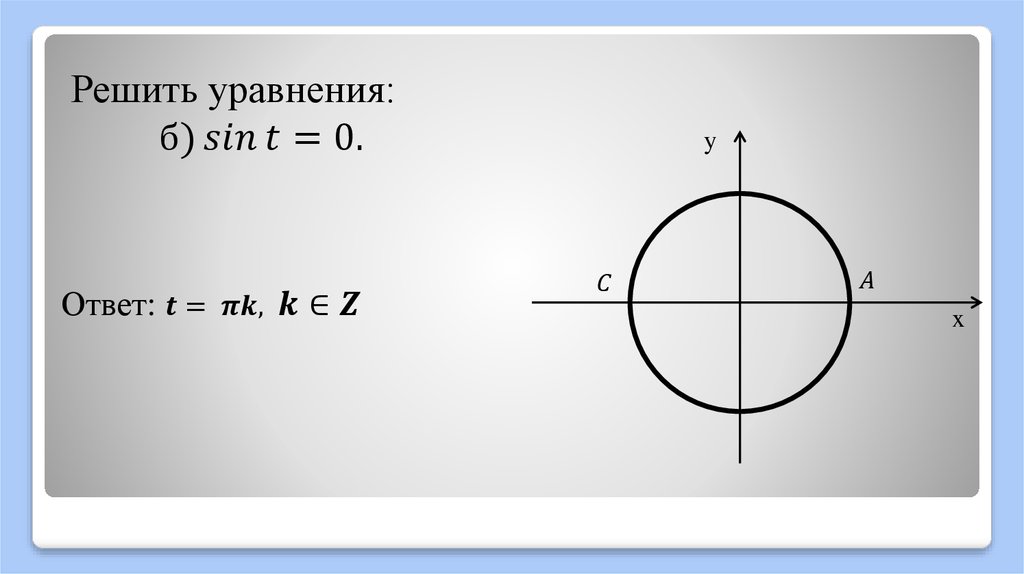

 Убывание графика синуса угла будет наблюдаться на отрезке: [ П/2 + 2 Пn]; [ 3П/2 + 2Пn].
Убывание графика синуса угла будет наблюдаться на отрезке: [ П/2 + 2 Пn]; [ 3П/2 + 2Пn].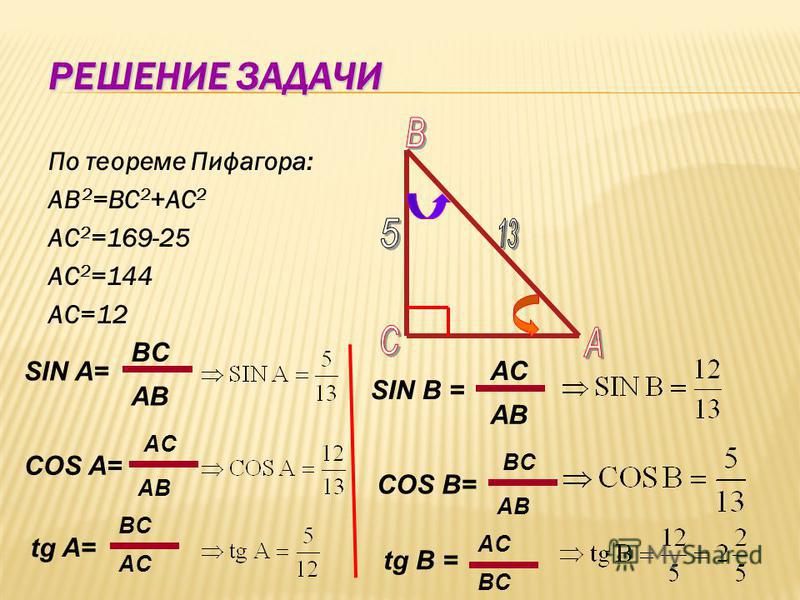
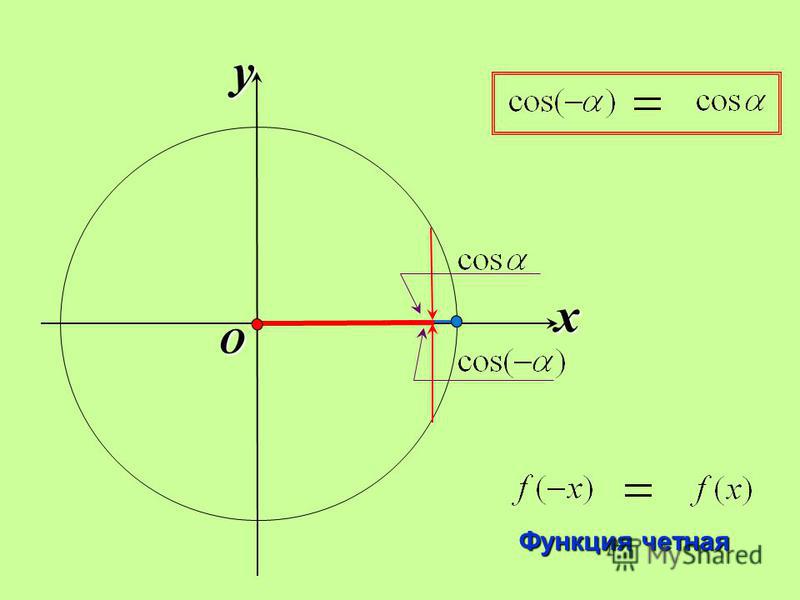


 Выполняется по распределительному закону: ac+bc+dc=c(a+b+d).
Выполняется по распределительному закону: ac+bc+dc=c(a+b+d).