Тела вращения: Тела и поверхности вращения — урок. Геометрия, 9 класс.

Тела вращения — Умскул Учебник

Математика

12.5.2022

1022

Поделитесь статьей в социальных сетях:

На этой странице вы узнаете

• Как с помощью прямоугольника и скульптурного станка создать цилиндр?
• Причем тут тор и почему он без Локи?

Математика такая интересная наука, что голова идет кругом. А если я скажу, что в этом случае голова образует новую фигуру? Как это возможно — узнаем в статье.

Тела вращения

Мы прекрасно знаем, что такое вращение. Балерина, офисный стул, барабан стиральной машинки, планета Земля вращаются вокруг своей оси, как и много-много других примеров. 

Проведем эксперимент. 

Как с помощью прямоугольника и скульптурного станка создать цилиндр? Вырежем из бумаги прямоугольник и зафиксируем его на скульптурном станке.  Скульптурный станок встречался нам во многих фильмах: обычно на нем лепят посуду и другие предметы из глины. Но главное, что нам нужно в станке, это его вращающаяся столешница. Раскрутим наш прямоугольник с очень-очень высокой скоростью.  Теперь прямоугольник будет казаться не плоской бумагой, а объемным цилиндром, в основании которого лежит  круг с радиусом, равным длине этого прямоугольника.

Похожий оптический эффект можно заметить, если посмотреть на двигатель самолета или винт вертолета: в статичном положении мы видим лопасти, а при работе они превращаются в круги. 

Таким же образом образуются любые тела вращения совершенно различных форм.

Наш эксперимент описывает тела вращения. 

Тело вращения — тело в пространстве, которое возникает при вращении какой-то фигуры вокруг определенной оси. 

Вращать можно любую фигуру и вокруг любой оси, тогда у нас будут получаться разные тела. 

Поверхность и ось вращения

На примере выше мы видим вазу. Она состоит только из “оболочки” и полая внутри. В математике существует название и для этой оболочки. Называется она поверхностью вращения. 

Поверхность вращения — граница тела вращения. 

Иными словами, поверхность вращения является внешней оболочкой тела вращения и ограничивает его в пространстве. Как кожа у человека. 

Ось, вокруг которой мы вращаем фигуру, называется осью вращения. 

Ось вращения может по-разному располагаться относительно фигуры. 

• Ось совпадает с одной из ее сторон. 

Выше мы уже рассмотрели пример цилиндра и вазы. В их случае ось вращения лежит на одной из сторон фигуры, которую мы вращаем. 

• Ось лежит внутри фигуры. 

Например, ось может проходить через центр фигуры. Попробуем прокрутить  овал вокруг его горизонтальной оси, проходящей через центр.

Мы получим эллипсоид. Эта фигура очень похожа на мяч для американского футбола.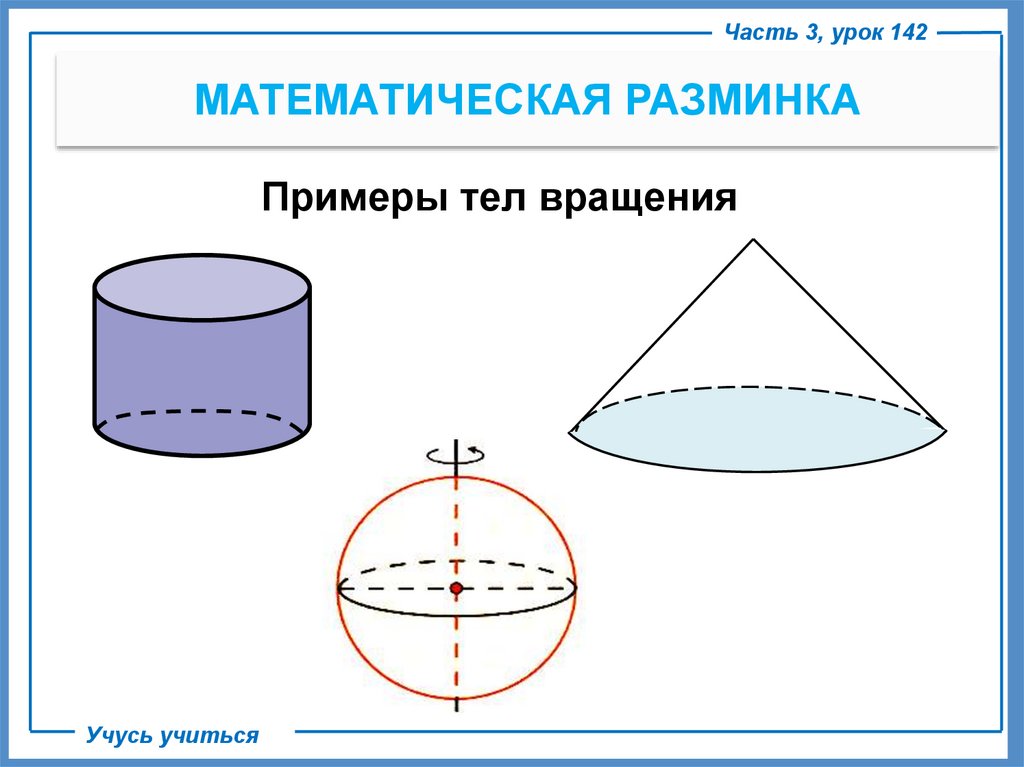

• Ось лежит вне фигуры. 

Например, если мы будем вращать круг относительно оси, лежащей за его пределами, то получим “кольцо”.

Такая фигура в математике называется тором. 

Причем тут тор и почему он без Локи? Разумеется, когда в математике упоминается тор, имеет в виду не скандинавский бог.  Тор — тело вращения, которое получается при вращении круга вокруг оси, лежащей за его пределами.

Среди тел вращения в математике наиболее часто встречаются цилиндр, конус, шар, эллипсоид и тор. Подробнее про некоторые из них можно прочесть в статьях «Цилиндр», «Конус», «Шар». 

Фактчек

• Тело вращения — тело в пространстве, которое возникает при вращении какой-то фигуры вокруг определенной оси. 
• Поверхность вращения — граница тела вращения. Ось вращения — ось, вокруг которой мы вращаем фигуру.  
• Ось, вокруг которой вращается фигура, может совпадать с одной из ее сторон, лежать внутри фигуры или за ее пределами. В каждом из этих случаев получаются различные тела вращения.
• В математике среди тел вращения наиболее часто встречаются цилиндр, конус, шар, эллипсоид и тор. 

Проверь себя

Задание 1. 
Что такое поверхность вращения?

1. Все тело вращения.
2. Граница тела вращения.
3. Ось вращения.
4. Основания тела вращения. 

Задание 2.
Что такое ось вращения?

1. Ось, вокруг которой вращается фигура, в результате чего получается тело вращения.
2. Центральная ось любой фигуры.
3. Ось, пересекающая плоскость фигуры перпендикулярно ей.
4. Любая прямая, расположенная любым способом в пространстве относительно фигуры. 

Задание 3. 
Из каких фигур можно получить тело вращения?

1. Только квадрат, прямоугольник и трапеция.
2. Только круг или овал.
3. Только параллелограмм.
4. Из любой.

Задание 4. 
Где может лежать ось вращения?

1. Принадлежать стороне фигуры.
2. Лежать “внутри” фигуры.
3. Лежать за пределами фигуры.
4. Все вышеперечисленное. 

Ответ: 1. – 2 2. – 1 3. – 4 4. – 4

Математика Тела вращения

Поделитесь статьей в социальных сетях:

Понравилась статья? Оцени:

Читайте также:

3.2. Тела вращения

3.2. Тела вращения

Прямые круговые конус и цилиндр, а также шар являются представителями класса тел вращения.

Телом вращения называется тело, полученное в результате вращения некоторой фигуры (обычно плоской) вокруг прямой. Эта прямая называется осью вращения.

Конус (прямой круговой) представляет собой тело, полученное в результате вращения прямоугольного треугольника вокруг одного из его катетов (точнее вокруг прямой, содержащей катет).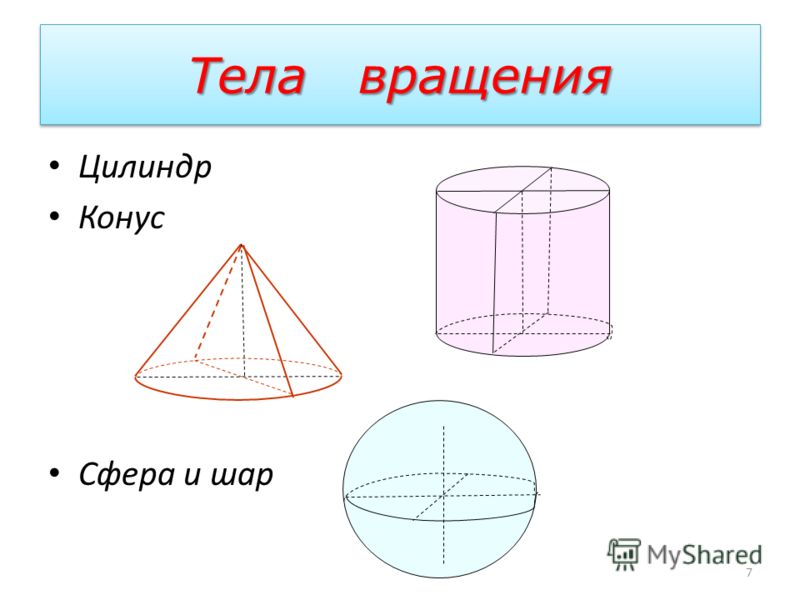 При этом указанный катет неподвижен и называется осью конуса. Так, при вращении прямоугольного треугольника SOA с прямым углом при вершине O вокруг катета SO получается конус с осью SO, где S — вершина конуса, O — центр основания, OA — радиус основания (рис. 67).

Рис. 67

Рис. 68

Цилиндр (прямой круговой) — это тело вращения, получающееся в результате вращения прямоугольника вокруг одной из его сторон (точнее говоря, вокруг прямой, содержащей сторону). При этом указанная сторона образует ось цилиндра. На рисунке 68 изображён цилиндр с осью O1O2, полученный в результате вращения прямоугольника ABO1O2 вокруг прямой O1O2; O1 и O2 — центры оснований цилиндра.

При пересечении конуса, цилиндра или любого тела вращения плоскостью, содержащей ось вращения, получается осевое сечение. Осевое сечение конуса — равнобедренный треугольник, осевое сечение цилиндра — прямоугольник. Все осевые сечения одного тела вращения равны между собой.

Шар как тело вращения может быть получен при вращении круга (или полукруга) вокруг диаметра. Очень важное характеристическое свойство шара даёт следующая теорема.

Теорема 3.1 (о сечениях шара)

Любое сечение шара плоскостью есть круг. (Сечением сферы соответственно является окружность.) При этом если R — радиус шара, d — расстояние от центра шара до плоскости сечения, то радиус сечения равен .

Доказательство. Пусть O — центр шара, O ʹ — проекция центра шара на плоскость сечения, OO ʹ = d, A — некоторая точка, принадлежащая сфере и плоскости сечения (рис. 69). Треугольник OO ʹA  прямоугольный,  ∠ OO ʹA = 90°. Следовательно,

Рис. 69

Отсюда следует, что точка A принадлежит окружности с центром в O ʹ и радиусом r, лежащей в плоскости сечения, ведь такая окружность есть множество точек плоскости, удалённых от O ʹ на расстояние r. Нетрудно проверить, что любая точка этой окружности лежит на данной сфере. ▼

Радиус сечения шара будет наибольшим, когда плоскость проходит через центр шара. Сечение шара плоскостью, проходящей через центр шара, так и называется большим кругом шара, а окружность, его ограничивающая, большой окружностью.

Теорема 3.2* (кратчайший путь по сфере)

Кратчайшим путём по сфере, соединяющим две её точки A и B, является меньшая из двух дуг AB большой окружности, проходящей через A и B.

Рис. 70

Доказательство. Возьмём на меньшей дуге AB произвольную точку M и докажем, что кратчайший путь, соединяющий точки A и B, должен пройти через M (рис. 70). Пусть O — центр сферы. Проведём через M две плоскости, перпендикулярные соответственно OA и OB. Эти плоскости пересекают сферу по двум окружностям w и u, которые имеют единственную общую точку M (это точка касания сферы с прямой, по которой пересекаются плоскости, содержащие w и u). Рассмотрим любой путь из A в B, не проходящий через M. Пусть этот путь пересекает окружность w в точке K, а окружность u — в точке P . Легко видеть, что существует путь, соединяющий точки A и M, такой же длины, что и путь, соединяющий точки A и K. В этом можно убедиться, повернув окружность w вокруг OA так, чтобы точка K перешла в точку M. Аналогично, существует путь, соединяющий точки B и M, такой же длины, что и путь, соединяющий точки B и P .

Отсюда следует, что кратчайший путь, соединяющий A и B, на самом деле должен проходить через M. Теорема доказана, поскольку M — произвольная точка меньшей дуги AB. ▼

Это свойство окружностей позволяет называть их прямыми на сфере. По аналогии с плоскостью можно говорить о треугольниках, многоугольниках, окружностях и т. п. на сфере. Их изучением занимается сферическая геометрия.

Задачи, задания, вопросы

1(в). Высота конуса равна h, а длина образующей l. Найдите радиус основания и площадь осевого сечения конуса.

2.Определите вид тела, получающегося в результате вращения квадрата вокруг его диагонали.

3(в). Найдите угол в осевом сечении конуса (вершина угла совпадает с вершиной конуса), если образующая конуса в два раза больше его высоты.

4(в). Найдите площадь сечения шара радиуса 3 плоскостью, удалённой от его центра на расстояние 2.

5. Осевым сечением конуса является равнобедренный прямоугольный треугольник с гипотенузой 2. Через вершину конуса проведено сечение, образующее угол a с плоскостью основания. Найдите площадь этого сечения.

6.Из круга вырезан сектор, равный четверти круга. Из этого сектора и из оставшейся части круга изготовлены боковые поверхности двух конусов. Найдите отношение высот этих конусов.

7.Сфера радиуса 2 пересечена плоскостью, удалённой от центра на расстояние 1. Найдите длину кратчайшего пути по поверхности сферы между двумя наиболее удалёнными точками сечения.

8.Найдите площадь осевого сечения тела, получающегося при вращении правильного треугольника со стороной a вокруг прямой, проходящей через его центр параллельно одной из сторон.

9(п). Радиус основания цилиндра равен r  . Плоскость пересекает боковую поверхность цилиндра, не пересекает его оснований и образует угол a с плоскостью основания. Найдите площадь сечения цилиндра этой плоскостью.

10(п). Квадрат со стороной a вращается вокруг прямой l, параллельной его плоскости. Расстояние от l до плоскости квадрата равно h, причём проекция l на плоскость квадрата проходит через середины его противоположных сторон. Опишите тело вращения. Найдите площадь осевого сечения.

11(т). Правильная четырёхугольная пирамида вращается вокруг прямой, проходящей через её вершину параллельно одной из сторон основания. Найдите площадь осевого сечения получившегося тела, если сторона основания пирамиды равна a, а высота h.

12(т). На плоскости изображена окружность и две точки A и B1, причём точка A лежит внутри окружности. Известно, что окружность является окружностью основания некоторого конуса, точка A лежит на основании этого конуса, а точка B1 есть проекция точки B, лежащей в плоскости, проходящей через вершину конуса параллельно его основанию. Постройте проекцию (изображение) точки, в которой отрезок AB пересекает боковую поверхность конуса.

13(т). Через вершину конуса (прямого кругового) проведено сечение наибольшей площади. Оказалось, что площадь этого сечения в два раза больше площади осевого сечения конуса. Найдите угол при вершине осевого сечения конуса (угол между образующими).

14(т). Высота цилиндра равна h, радиус основания r . Найдите наибольшее значение площади проекции этого цилиндра на плоскость.

Статья о теле+революции из The Free Dictionary

Тело+революции | Статья о body+of+revolution от The Free Dictionary

Тело+революции | Статья о теле+революции от The Free Dictionary

---

Слово, не найденное в Словаре и Энциклопедии.

Пожалуйста, попробуйте слова отдельно:

тело из революция

Некоторые статьи, соответствующие вашему запросу:

• БОР-ФДТД
• Камера тела
• Совет революционного командования

• Демократический централизм
• Телесный оборот
• Революционный совет

• I-DBOR
• John B. McClelland
• Словацкий национальный совет

• Экватор Солнца
• Подход Аткинса к питанию
• Grand Orient de France

• Датчик скорости
• сфероид
• Учредительное собрание России

Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.

Полный браузер ?

• ▲
• масса тела
• Цепь веса тела
• Постоянная разгрузка веса тела
• Упражнения с собственным весом
• Депрессия набора массы тела
• Потеря веса тела
• Масса тела сельскохозяйственных животных
• коэффициент массы тела
• Вес тела, умноженный на длину кости
• Масса тела человека
• Беговая дорожка с поддержкой веса тела
• отношение массы тела к площади поверхности
• отношение массы тела к площади поверхности
• отношение массы тела к площади поверхности
• отношение массы тела к площади поверхности
• отношение массы тела к площади поверхности
• отношение массы тела к площади поверхности
• Завиток корпуса
• Целительная группа Body Wisdom
• Пожелания тела

• Тело без органов
• Миры тела
• Идентификационный передатчик для ношения на теле
• Поклонение телу
• обертывание тела
• обертывание тела
• обертывание тела
• обертывания
• обертывания
• корпус, поставить бодрость в
• кузов+революции
• Тело человека
• Тело, Разум, Душа
• корпус, регулировка температуры
• корпус, регулировка температуры
• корпус, регулировка температуры
• Боди-арт
• Сумка для тела
• Сумка для тела
• Телесное удовольствие, смех, вовлеченность, удовлетворение и секс
• кузов-панель

• обшивка кузова
• обшивка кузова
• борта кузова
• Самодельное взрывное устройство, переносимое на теле
• кузов
• Бодибилдинг
• Бодибилдинг
• Бодибилдинг
• по центру тела
• Кузовоцентрированный куб
• объемно-центрированная решетка
• Массив с центрированием по телу
• Квадрат по центру тела
• Тетрагональный корпус с центрированием
• Объемно-центрированный кубический
• по центру тела
• Кузов с центрированием на корпусе
• проверка кузова
• проверка кузова
• проверка кузова
• ▼

Сайт: Следовать:

Делиться:

Открыть / Закрыть

 

определение body+of+revolution по The Free Dictionary

Body+of+revolution — определение body+of+revolution по The Free Dictionary

Тело+революции — определение тела+революции в The Free Dictionary

---

Слово, не найденное в Словаре и Энциклопедии.