АНГЛИЙСКИЙ SAT-ПАСПОРТ К ПРОДВИНУТОЙ МАТЕМАТИКЕ-Множественный выбор
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Обновлено: 27-06-2022
Текстовое решение
Ответ
Правильный ответ B
Ответить
Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.
Стенограмма
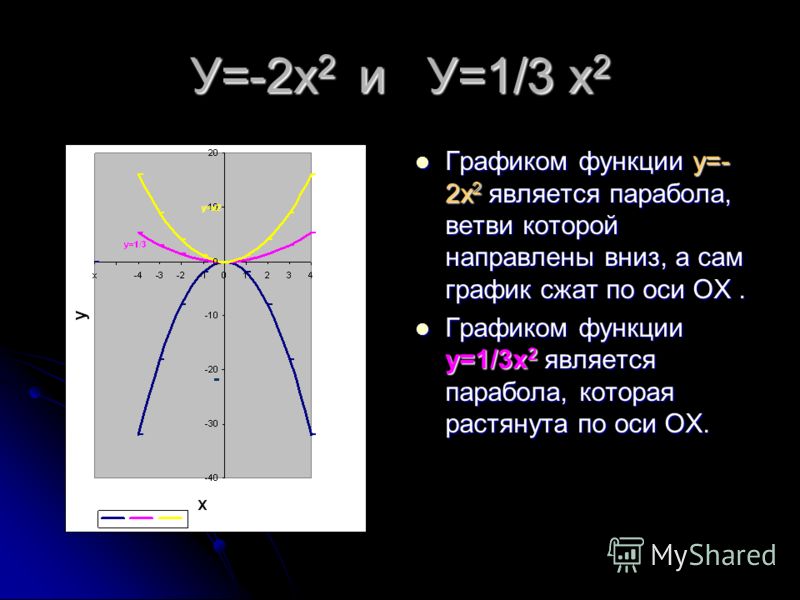
вопрос почему равен 2 х квадрат — 12 х + 11 график уравнения выше это парабола в плоскости ху каково расстояние между вершиной параболы и 31 теперь какова вершина парабола, которая считается параболой, что-то вроде этого, тогда середина параболы — это вершина параболы, это вихрь, поэтому мы можем рассматривать эвакуацию как 2 x квадрат — 12 x + 11.
эти два термина, которые будут квадратом оси — 6 X + 11, теперь, выполнив метод квадрата, завершат квадрат enix, который представляет собой плюс минус b квадрат
равно a квадрат + b квадрат + — 2 AV теперь вы можете видеть, что здесь, если они сделали эту часть это x квадрат — 6 x по сравнению с этой вещью мы можем получить x равно a подобно a и к AV, аналогичный 2 ГБ, подобен 66 и снова равен X, поэтому x b равен 66, то есть P равен 3, поэтому наше уравнение будет таким, поскольку a b равно минус 6 x, поэтому уравнение будет Y равно 2 и 2 x квадрат — 6 X + b квадрат, который равен 9, теперь мы должны вычесть также класс 11
органический 1 к 2 в x минус 3 весь квадрат минус 9+ 11, то есть 2 в х минус 3 весь квадрат минус 18 + 11 снова равно 2 в х минус 3 весь квадрат минус 7 получит 7 место, поэтому Y + 7 равно 2 и 2 х минус 3 вся теперь вершина будет 3 — 7 хорошо подходит с этой поставкой эта часть эксперт равна нулю тогда мы получим х равно 3 тогда когда мы поставим часть Y то есть Y + 7 = 20 тогда почему мы получим 5 равно минус 7, и мы должны найти расстояние между вихрем, равным 35 — 7, и
, точка три прежняя, поэтому формула расстояния говорит, что расстояние между X1 Y1 2 x 2 степени 2 равно под корнем x 1 — x на весь квадрат + на 1 минус b весь квадрат Mall под корнем, поэтому наше расстояние будет 3 — 3 весь квадрат + — 7 — 1 весь квадрат под корнем 3 минус 3 это будет ноль это -8 весь квадрат а под корнем это квадратный корень, поэтому расстояние будет так, что правильный вариант здесь B
Похожие видео
Нарисована парабола с фокусом в (3,4) и вершиной в фокусе параболы y2−12x−4y+4=0.
Уравнение параболы:
118619984
График y+3=(x−4)2−6 представляет собой параболу в плоскости xy. Каковы точки пересечения x параболы?
167970366
График приведенного выше уравнения представляет собой параболу в плоскости xy. Если k>0, каково минимальное значение y, выраженное через k?
167970406
Если уравнением параболы в плоскости xy является f(x)=−(x+2)2−1 , каковы координаты вершины параболы, определяемой как g(x)=f(x−2 )?
167970944
Уравнение параболы в плоскости xy: y=2×2−12x+7. Каково расстояние между вершиной параболы и точкой (3,4)?
167971071
Координата вершины параболы в плоскости xy равна (−4,k). Если число точек пересечения у параболы равно 12 и парабола проходит через точку (−3,7), каково значение k?
167971163
y=−(x−3)2+a
В приведенном выше уравнении a является константой. График уравнения в плоскости xy представляет собой параболу. Что из следующего верно относительно параболы?
174306712
Вершина параболы в плоскости xy выше (0, c).
Что из следующего верно для параболы с уравнением y=−a(x−b)2+c ?
181167019
В плоскости xy парабола с уравнением y=(x−11)2 пересекает прямую с уравнением y = 25 в двух точках, A и B. Какова длина ¯¯¯¯¯¯ АБ?
181168307
Если вершина параболы y=3×2−12x+9 равна (a b), то парабола с вершиной (b a) равна (являются):
(A)y=x2+6x+11(B)y =x2−7x+3
(C)y=−2×2−12x−16(D)y=−2×2+16x−13
205067267
Если вершина параболы y=3×2−12x+9 равна (a b ), тогда парабола с вершиной (b a) равна (являются):
(A)y=x2+6x+11(B)y=x2−7x+3
(C)y=−2×2−12x−16(D) y=−2×2+16x−13205067267
205067321
Если вершина параболы y=3×2−12x+9 равна (a b), то парабола с вершиной (ba) равна (are):
(A)y=x2+6x+11(B)y=x2−7x+3
(C)y=−2×2−12x−16(D)y=−2×2+16x−13
205970728
вершина параболы y=3×2−12x+9 равна (a b), тогда парабола с вершиной (ba) равна (являются):
(A)y=x2+6x+11(B)y=x2−7x+3
(C)y=−2×2−12x−16(D)y=−2×2+16x−13
205970738
График g(x)=(3x−9)(x−1) представляет собой параболу в xy-плоскость.
Если вершина этой параболы имеет координаты (h, k), каково значение h−k?
217887494
Нарисована парабола с фокусом в (3,4) и вершиной в фокусе параболы y2−12x−4y+4=0. Уравнение параболы 92-16x-29=0 Tiger Algebra Solver
Пошаговое решение :
Шаг 1 :
Уравнение в конце шага 1 :
((0 - 2x 2 ) - 16x) - 0
Шаг 2:
Шаг 3:
Вытягивание, как Условия:
3.1 Вытягивание, как факторы:
-2x 2 — 16x — 29 = -1 • (2x 2 + 16x + 29)
Попытка факторинга путем разделения среднего члена
3.2 Факторизация 2x 2 + 16x + 29
Первый член равен 2x 2 , его коэффициент равен 2 .
Средний член равен +16x, его коэффициент равен 16 .
Последний член, «константа», равен +29
Шаг-1: умножьте коэффициент первого члена на константу 2 • 29 = 58
Шаг-2: найдите два множителя 58, сумма которых равна коэффициенту среднего срока, который составляет 16 .
| -58 | + | -1 | = | -59 | ||
| -29 | + | -2 | = | -31 | ||
| -2 | + | -29 | = | -31 | ||
| -1 | + | -58 | = | -59 | ||
| 1 | + | 58 | = | 59 | ||
| 2 | + | 29 | = | 31 | ||
| 29 | + | 2 | = | 31 | ||
| 58 | + | 1 | = | 59 | ||
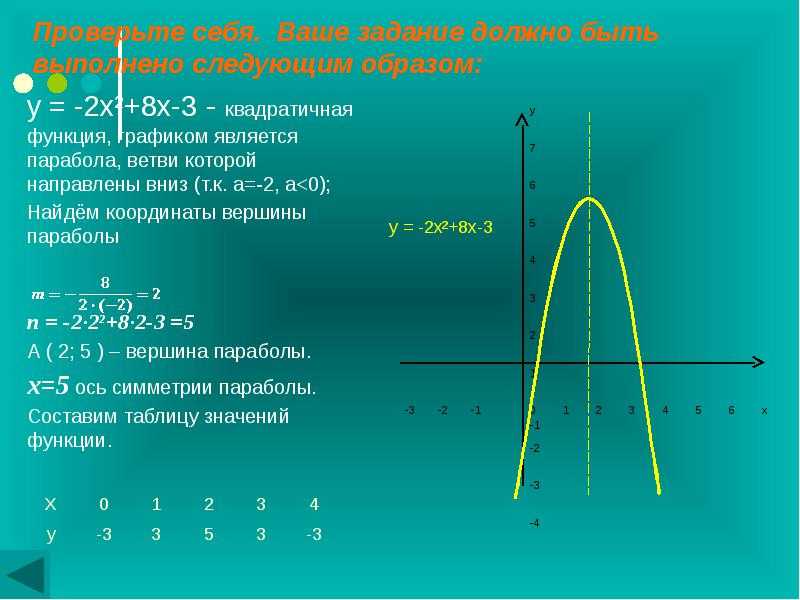Мы знаем это еще до того, как начертили "у", потому что коэффициент первого члена, -2 , отрицательный (меньше нуля).
000
Поскольку 