Часть I, II. 2020 год
При ознакомлении с демонстрационным вариантом контрольных измерительных материалов 2020 г. следует иметь в виду, что задания, включённые в демонстрационный вариант, не отражают всех вопросов содержания, которые будут проверяться с помощью вариантов КИМ в 2020 г. Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене 2020 г., приведён в кодификаторе элементов содержания и требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена 2020 г. по физике.
Назначение демонстрационного варианта заключается в том, чтобы дать возможность любому участнику ЕГЭ и широкой общественности составить представление о структуре будущих КИМ, количестве и форме заданий, об уровне их сложности. Приведённые критерии оценки выполнения заданий с развёрнутым ответом, включённые в этот вариант, дают представление о требованиях к полноте и правильности записи развёрнутого ответа.
Эти сведения позволят выпускникам выработать стратегию подготовки и сдачи ЕГЭ.
Инструкция по заполнению бланков ЕГЭ.
1. На рисзию приведён график зависимости проекции их скорости тела от времени t. Определите путь, пройденный телом в интервале времени от 15 до 19 с.
Ответ: м 2. Ящик массой 10 кг равномерно движется по прямой по горизонтальной
поверхности под действием постоянной горизонтальной силы тяги
величиной 25 Н. Каков коэффициент трения между ящиком и поверхностью?
3. Автомобиль с выключенным двигателем сняли со стояночного тормоза, и он покатился под уклон, составляющий угол 30° с горизонтом. В начале горизонтального участка дороги, который следует за спуском, его скорость составляет 10 м/с. Какое расстояние автомобиль проезжает по склону? Трением пренебречь.
Ответ: м
4. Груз массой 0,16 кг, подвешенный на пружине, совершает свободные
вертикальные гармонические колебания. Груз какой массой нужно подвесить
вместо первого груза, чтобы частота свободных колебаний уменьшилась
в 2 раза?
Груз массой 0,16 кг, подвешенный на пружине, совершает свободные
вертикальные гармонические колебания. Груз какой массой нужно подвесить
вместо первого груза, чтобы частота свободных колебаний уменьшилась
в 2 раза?
5. Два одинаковых бруска толщиной 5 см и массой 1 кг
каждый, связанные друг с другом, плавают в воде так, что
уровень воды приходится на границу между ними
(см. рисунок). Из приведённого ниже списка выберите два
правильных утверждения.
1)
Если воду заменить на подсолнечное масло, то глубина погружения
брусков уменьшится.
2)
Если на верхний брусок поставить гирю массой 1,5 кг, то бруски не
утонут.
3)
Если в стопку добавить ещё три таких же бруска, то глубина её
погружения увеличится на 15 см.

5) Плотность материала, из которого изготовлены бруски, равна 500 кг/м3. Ответы №№:
6. В первой серии опытов брусок с грузом перемещали при помощи нити
равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии
опытов точно так же перемещали этот брусок, но сняв с него груз. Как
изменились при переходе от первой серии опытов ко второй модуль работы
силы трения при перемещении бруска на одинаковые расстояния
и коэффициент трения между бруском и плоскостью?
1) увеличится
2) уменьшится
3) не изменится
Запишите выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
7. На рисунке показан график зависимости координаты x
тела, движущегося вдоль оси Ох, от времени t
(парабола). Графики А и Б представляют собой
зависимости физических величин, характеризующих
движение этого тела, от времени t.
Графики А и Б представляют собой
зависимости физических величин, характеризующих
движение этого тела, от времени t.
Установите соответствие между графиками и
физическими величинами, зависимости которых от
времени эти графики могут представлять.
К каждой позиции первого столбца подберите соответствующую позицию
из второго столбца и запишите в таблицу выбранные цифры под
соответствующими буквами.
| ГРАФИКИ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| 1)
модуль импульса тела 2) проекция перемещения тела на ось Ох 3) кинетическая энергия тела 4) проекция ускорения тела на ось Ох |
8. В сосуде неизменного объёма находится идеальный газ. Во сколько раз
нужно уменьшить количество вещества газа в сосуде, чтобы после
увеличения абсолютной температуры газа в 2 раза его давление стало вдвое
меньше начального?
Во сколько раз
нужно уменьшить количество вещества газа в сосуде, чтобы после
увеличения абсолютной температуры газа в 2 раза его давление стало вдвое
меньше начального?
9. На рисунке показано, как менялось давление газа
в зависимости от его объёма при переходе из состояния 1
в состояние 2, а затем в состояние 3. Каково отношение
работ газа
A 12/A23 в этих двух процессах?
10. В котелок насыпали кусочки олова и поставили на электрическую плитку. В минуту плитка передаёт олову в среднем количество теплоты, равное 500 Дж. График изменения температуры олова с течением времени показан на рисунке. Какое количество теплоты потребовалось для плавления олова, доведённого до температуры плавления?
Ответ: Дж 11. В сосуде под поршнем находятся только пары
аммиака. Поршень медленно и равномерно опускают,
уменьшая объём сосуда. Температура в сосуде
поддерживается постоянной. На рисунке показан
график изменения со временем t концентрации n
молекул паров аммиака внутри сосуда. Из
приведённого ниже списка выберите два правильных утверждения
относительно описанного процесса
В сосуде под поршнем находятся только пары
аммиака. Поршень медленно и равномерно опускают,
уменьшая объём сосуда. Температура в сосуде
поддерживается постоянной. На рисунке показан
график изменения со временем t концентрации n
молекул паров аммиака внутри сосуда. Из
приведённого ниже списка выберите два правильных утверждения
относительно описанного процесса
1) На участке 2 плотность паров аммиака уменьшалась.
2) На участке 1 плотность паров аммиака уменьшалась.
3) На участке 2 давление паров аммиака увеличивалось.
4) На участке 1 пар аммиака ненасыщенный, а на участке 2 насыщенный.
5) На участке 1 давление паров аммиака увеличивалось..
Ответы №№:
12. Температуру нагревателя тепловой машины Карно повысили, оставив
температуру холодильника прежней. Количество теплоты, отданное газом
холодильнику за цикл, не изменилось. Как изменились при этом КПД
тепловой машины и работа газа за цикл?
Как изменились при этом КПД
тепловой машины и работа газа за цикл?
Для каждой величины определите соответствующий характер
изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
13. Электрическая цепь, состоящая из трёх прямолинейных
проводников (2–3, 3–4, 4–1) и источника постоянного
тока, находится в однородном магнитном поле, у
которого вектор магнитной индукции В→направлен к
наблюдателю (см. рисунок). Куда направлена
относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от
наблюдателя) вызванная этим полем сила Ампера, действующая на
проводник 4–1? Ответ запишите словом (словами).
14. На плавком предохранителе сети напряжением 380 В указано: «10 А».
Ответ: Вт
15. В колебательном контуре (см. рисунок) индуктивность
катушки L = 6 мГн. Какой должна быть индуктивность Lx
второй катушки, чтобы при переводе ключа К из
положения 1 в положение 2 период собственных
электромагнитных колебаний в контуре увеличился
в √6 раза?
16. На уединённой неподвижной проводящей сфере радиусом R находится положительный заряд Q. Сфера находится в вакууме. Напряжённость электростатического поля сферы в точке A равна 36 В/м. Все расстояния указаны на рисунке. Выберите два верных утверждения, описывающих данную ситуацию.
1)
Потенциал электростатического поля в точке C выше, чем в точке D:
φC > φD.
2)
Напряжённость электростатического поля в точке C EC = 36 В/м.
3)
Напряжённость электростатического поля в точке B EB = 576 В/м.
4)
Потенциал электростатического поля в точках B и C одинаков: φB = φC.
5)
Потенциал электростатического поля в точках F и D одинаков: φF = φD.
17. Протоны в однородном магнитном поле между полюсами магнита движутся
по окружностям радиусом R под действием силы Лоренца. После замены
магнита по окружностям тем же радиусом между полюсами стали двигаться
α-частицы, обладающие такой же кинетической энергией, как и протоны. Как
изменились индукция магнитного поля и скорость движения α-частиц по
сравнению со скоростью протонов?
1) увеличится
2) уменьшится
3) не изменится
Запишите выбранные цифры для каждой физической величины.
 Цифры в ответе могут повторяться.
Цифры в ответе могут повторяться.Индукция магнитного поля. Скорость α-частиц:
18. Спираль лампочки расположена вблизи главной оптической оси тонкой
рассеивающей линзы с фокусным расстоянием, равным по модулю F,
перпендикулярно этой оси. Расстояние а от линзы до спирали меньше F.
Затем рассеивающую линзу заменили на собирающую с фокусным
расстоянием F. Установите соответствие между видом линзы,
использовавшейся в опыте, и свойствами даваемого ею изображения.
К каждой позиции первого столбца подберите соответствующую позицию
из второго столбца и запишите в таблицу выбранные цифры под
соответствующими буквами.
| ВИД ЛИНЗЫ |
СВОЙСТВА ИЗОБРАЖЕНИЯ |
| А)
линза собирающая Б) линза рассеивающая |
1)
действительное, перевёрнутое,
увеличенное 2) действительное, перевёрнутое, уменьшенное 3) мнимое, прямое, уменьшенное 4) мнимое, прямое, увеличенное |
19. Сколько протонов и сколько нейтронов содержится в ядре
11950Sn?
Сколько протонов и сколько нейтронов содержится в ядре
11950Sn?
20. Модуль импульса фотона красного света в 2 раза меньше модуля импульса
фотона фиолетового света. Найдите отношение длины волны фотона
фиолетового цвета к длине волны фотона красного цвета.
21. Установите соответствие между видами радиоактивного распада и
уравнениями, описывающими этот процесс.
К каждой позиции первого столбца подберите соответствующую позицию из второго
столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| ВИДЫ РАСПАДА | УРАВНЕНИЯ |
| А)
электронный бета-распад Б)
альфа-распад |
АБ:
22. С помощью барометра проводились измерения атмосферного давления.
Верхняя шкала барометра проградуирована в килопаскалях, а нижняя
шкала – в миллиметрах ртутного столба (см. рисунок). Погрешность
измерений давления равна цене деления шкалы барометра. Чему равно
атмосферное давление в килопаскалях по результатам этих измерений?
С помощью барометра проводились измерения атмосферного давления.
Верхняя шкала барометра проградуирована в килопаскалях, а нижняя
шкала – в миллиметрах ртутного столба (см. рисунок). Погрешность
измерений давления равна цене деления шкалы барометра. Чему равно
атмосферное давление в килопаскалях по результатам этих измерений?
23. Необходимо экспериментально изучить зависимость заряда, накопленного конденсатором, от сопротивления резистора. Какие две схемы следует использовать для проведения такого исследования? Запишите в ответе номера выбранных схем.
24. Рассмотрите таблицу, содержащую характеристики планет Солнечной
системы.
Выберите два утверждения, которые соответствуют элементам, обозначенным цифрами 1-5.
| Название планеты |
Диаметр в районе экватора, км |
Период обращения вокруг Солнца |
Период вращения вокруг оси |
Вторая космическая скорость, км/с |
| Меркурий |
4878 | 87,97 суток | 58 суток 15 часов 30 минут |
4,25 |
| Венера |
12 104 | 224,7 суток | 243 суток 0 часов 27 минут |
10,36 |
| Земля |
12 756 | 365,3 суток | 23 часа 56 минут |
11,18 |
| Марс |
6794 | 687 суток | 24 часа 37 минут |
5,02 |
| Юпитер | 142 800 | 11 лет 315 суток |
9 часов 53,8 минут |
59,54 |
| Сатурн | 120 660 | 29 лет 168 суток |
10 часов 38 минут |
35,49 |
| Уран | 51 118 | 84 года 5 суток |
17 часов 12 минут |
21,29 |
| Нептун | 49 528 | 164 года 290 суток |
16 часов 4 минуты |
23,71 |
1)
Первая космическая скорость для спутника Венеры составляет примерно
7,33 км/с.
2)
За один юпитерианский год на Венере проходит 19 венерианских лет.
3)
Ускорение свободного падения на Нептуне примерно равно 23,71 м/с2.
4)
Объём Юпитера почти в 3 раза больше объёма Урана.
5)
Юпитер движется по орбите почти в 3 раза медленнее, чем Сатурн.
Часть II. (Внимание! Решения II части могут содержать нелепости!)
25. В начале процесса температура куска свинца массой 1 кг была равна 47 °С.
Температура плавления свинца равна 327 °С. Какое количество теплоты
передали куску свинца, если расплавилась часть свинца, равная 400 г?
Тепловыми потерями пренебречь.
26. На металлическую пластинку падает монохроматический свет с длиной
волны λ = 400 нм. «Красная граница» фотоэффекта для металла пластинки
λкр = 600 нм. Чему равно отношение максимальной кинетической энергии
фотоэлектронов к работе выхода для этого металла?
Чему равно отношение максимальной кинетической энергии
фотоэлектронов к работе выхода для этого металла?
27. На тонкую собирающую линзу от удаленного
источника падает пучок параллелжых тучей
(см.рисунок). Как изленится положение
изображения источника, создаваемого линзой,
если между линзой и ее фокусом поставить
плоскопараллельную стеклянную пластинку
с показателем преломления n (на рисунке
положение пластинки отмечено пунктиром)?
Ответ поясните, указав, какие физические
закономерности Вы использовали. Сделайте рисунок, поясняющий ход лучей до и после установки плоскопараллельной
стеклянной пластинки.
1) изображение сместится выше от главной оптической оси
2) изображение сместится ниже
3) положение изображения не изменится
28. Два груза подвешены на достаточно длинной невесомой
нерастяжимой нити, перекинутой через идеальный блок
(см. рнсунок). Грузы удерживали неподвижно, а затем осторожно
отпустили, после чего они начали двигаться равноускоренно.
Через t = 1 с после начала движения скорость правого груза
(массой m = 1 кг) была направлена вертикально вверх и равна
4м/с. Определите силу натяжения нити. Трением пренебречь.
Два груза подвешены на достаточно длинной невесомой
нерастяжимой нити, перекинутой через идеальный блок
(см. рнсунок). Грузы удерживали неподвижно, а затем осторожно
отпустили, после чего они начали двигаться равноускоренно.
Через t = 1 с после начала движения скорость правого груза
(массой m = 1 кг) была направлена вертикально вверх и равна
4м/с. Определите силу натяжения нити. Трением пренебречь.
29. Гладкий цилиндр лежит между двумя плоскостями, одна из
которых вертикальна, а линия их пересечения горизонтальна
(см. рисунок). Сила давления цилиндра на вергикальную
стенку равна 10 Н и в n =3 раза меньше, чем сила давления на
цилиндр со стороны другой плоскости. Определите массу
цилиндра. Сделайте рисунок, на котором укажите силы,
действующие на цилиндр.
30. В вертикальном цилиндре, зарытом лёгким поршнем, находится ацетон
(С3Н60) при температуре кипения t = 56° С. В результате сообщения ацетону
некоторого количества теплоты часть его превращается в пар, который при
изобарном расширении совершает работу, поднимая поршень. Удельная
теплота парообразовния ацетона L = 524·103 Дж/кг, а его молярная масса
М = 58·10-3 кг/моль. Какая часть подводимого к ацетону количества теплоты
превращается в работу? Объёмом жидкого ацетона и трением между
поршнем и цилиндром пренебречь.
В вертикальном цилиндре, зарытом лёгким поршнем, находится ацетон
(С3Н60) при температуре кипения t = 56° С. В результате сообщения ацетону
некоторого количества теплоты часть его превращается в пар, который при
изобарном расширении совершает работу, поднимая поршень. Удельная
теплота парообразовния ацетона L = 524·103 Дж/кг, а его молярная масса
М = 58·10-3 кг/моль. Какая часть подводимого к ацетону количества теплоты
превращается в работу? Объёмом жидкого ацетона и трением между
поршнем и цилиндром пренебречь.
31. К аикумутгсдгору с ЭДС = 50 В к внутренним
сопротивлением r = 4 Ом подключили лампу
сопротивлением Rл = 10 Ом и резистор
сопротивлением R =15 0м, а также конденсатор
ёмкостью С= 100 мкФ (см. рисунок). Спустя
длительный промежуток времени ключ К
размыкают. Какое количество теплоты выделится
после этого на резисторе?
Какое количество теплоты выделится
после этого на резисторе?
32. В электрической цепи, показанной на
рисунке, ключ К длительное время замкнут,
ε = 6 В, г = 2 Ом, L = 1 мГн. В момент t = 0
ключ К размыкают. В момент, когда в ходе
еозникших в контуре элекпромагнитных
колебаний напряжение на конденсаторе
равно ЭДС источника, сила тока в коньуре I = 2,4 А. Нвйдите ёмкость конденсагора. С. Сопротивлением проводов
и активным сопротивпением катушки индуктвкостн пренебречь.
Решение: q = cm t
КОЛИЧЕСТВО ТЕПЛОТЫ.
УДЕЛЬНАЯ ТЕПЛОЕМКОСТЬ.
Начальный уровень
1. Что потребует большего количества
теплоты для нагревания на 1°С:
стакан
воды или бидон воды?
Ответ: Q = cm(t 2 -t 1)
масса бидона воды
больше,
поэтому потребуется больше
количества теплоты для нагревания
2. Что потребует большего количества
теплоты для нагревания на 1°С:
Что потребует большего количества
теплоты для нагревания на 1°С:
100 г
воды или 100 г меди?
Ответ: Q = cm(t 2 -t 1)
Удельная теплоемкость
у воды выше (4200,
400),
поэтому потребуется больше количества
теплоты для нагревания воды
3. Какое вещество имеет наименьшую удельную теплоемкость?
Ответ: воздух (?)
4. Какое вещество имеет наибольшую удельную теплоемкость?
Ответ: вода (?)
5. Какое количество теплоты необходимо для нагревания железа массой 1 г на 1°С?
Ответ: Q = cm(t 2 -t 1)
Q
= 460 .
0,001 .
1 = 0,46 Дж
6. Чтобы повысить температуру на 1°С олова массой 1 кг, требуется 230 Дж. Какова удельная теплоемкость олова?
7.
Алюминиевая деталь массой 1 кг остывает
на 1°С. Какое количество теплоты выделится
при остывании детали?
Ответ: Q = cm(t 2 -t 1)
Q
= 920 .
1 .
1 = 920 Дж
8. Чугунную деталь массой 1 кг нагрели на 1°С. На сколько увеличилась при этом внутренняя энергия детали?
Ответ: Q = cm(t 2 -t 1)
ΔU=Q
= 540 . 1 .
1 = 540
Дж
1 .
1 = 540
Дж
Средний уровень
1. Каким количеством теплоты можно нагреть 0,3 кг воды от 12°С до 20°С?
m=0,3
кг
t 1 =12°С
t 2 =20°С
с=4200
Q=?
Q = cm(t 2 -t 1)
Q = 4200 . 0,3 . (20-12) = 10080 Дж
2. Какую массу воды можно нагреть на 10°С 1 кДж теплоты?
t 2 -t 1 =10°С
Q
=1 кДж 1000Дж
с=4200
m
=?
Q = cm(t 2 -t 1)
3. На сколько градусов остыл
кипяток в питьевом баке емкостью 27 л,
если он отдал окружающей среде 1500
кДж теплоты?
V= 27 л
0,027м 3
Q
=1500 кДж 1500000Дж
с=4200
ρ=1000
Q = cm(t 2 -t 1)
4. Чтобы нагреть 110 г алюминия на
90°С, требуется 9,1 кДж.
Вычислите
удельную теплоемкость алюминия.
m=110г 0,11кг
t 2
-t 1 =90°С
Q=9,1
кДж 9100Дж
5. Какое количество теплоты
необходимо для нагревания латунной
гири массой 200 г
от 20 до 28°С?
m=200г 0,2кг
Q = cm(t 2 -t 1)
Q = 400 . 0,2 . (28-20) =
640 Дж
0,2 . (28-20) =
640 Дж
6. Какова масса железной детали, если на ее нагревание от 20°С до 200 °С пошло
20,7 кДж теплоты?
t 2 =200°С
Q
=20,7 кДж 20700000Дж
Q = cm(t 2 -t 1)
7. На сколько градусов повысилась температура 4 л воды, если она получила количество теплоты, равное 168 кДж?
V= 4 л
0,004м 3
Q
=168 кДж 168000Дж
с=4200
ρ=1000
Q = cm(t 2 -t 1)
8. Слиток серебра массой 120 г при остывании от 66°С до 16°С передал окружающей среде 1,5 кДж теплоты. Как велика удельная теплоемкость серебра?
m=120г 0,12кг
Q=1,5 кДж 1500Дж
Достаточный уровень
1. а) Почему в пустынях днем жарко, а ночью температура падает ниже 0°С?
б) Чтобы охладить выточенную из меди деталь, имеющую температуру 100°С, ее погрузили в 420 г воды с температурой 15°С. Определите массу детали, если известно, что в процессе теплообмена вода нагрелась до 18°С.
2. а) По куску свинца и куску стали той же
массы ударили молотком одинаковое
число раз. Какой кусок нагрелся больше? б) Стальную деталь массой 300 г нагрели до
высокой температуры, а затем погрузили
для закалки в 3 кг машинного масла,
имеющего температуру 10°С. Определить
начальную температуру детали, если
температура при установившемся тепловом
равновесии была 30°С.
а) По куску свинца и куску стали той же
массы ударили молотком одинаковое
число раз. Какой кусок нагрелся больше? б) Стальную деталь массой 300 г нагрели до
высокой температуры, а затем погрузили
для закалки в 3 кг машинного масла,
имеющего температуру 10°С. Определить
начальную температуру детали, если
температура при установившемся тепловом
равновесии была 30°С.
3. а) Почему железные печи скорее нагревают
комнату, чем кирпичные, но не так долго
остаются теплыми? б) В алюминиевый калориметр массой 140 г
налили 250 г воды при температуре 15°С.
После того как брусок из свинца массой
100 г, нагретый до 100°С, поместили в
калориметр с водой, там установилась
температура 16°С. Составить уравнение
теплового баланса и определить удельную
теплоемкость свинца.
4. а) Почему реки и озера нагреваются
солнечными лучами медленнее, чем суша?
б) Мальчик наполнил
стакан, емкость которого 200 см 3 ,
кипятком на три четверти и дополнил
стакан холодной водой. Определите,
какая установилась температура воды,
если температура холодной воды равна
20°С.
Определите,
какая установилась температура воды,
если температура холодной воды равна
20°С.
5. а) Медной и стальной гирькам одинаковой массы передали равные количества теплоты. У какой гирьки температура изменится сильнее? б) Стальное изделие закалялось нагреванием до температуры 800°С с последующим опусканием в масло массой 2 кг, взятое при температуре 10°С. При этом масло нагрелось до температуры 40°С. Найти массу стального изделия, если при переносе в масло изделие охладилось на 20°С. Удельная теплоемкость масла 2100 Дж/(кг °С).
6. а) Что эффективнее использовать в качестве грелки — 2 кг воды или 2 кг песка при той же температуре? б) Для приготовления ванны вместимостью 200 л смешали холодную воду при температуре 10°С с горячей при температуре 60°С. Какие объемы той и другой воды надо взять, чтобы установилась температура 40°С?
7. а) На что расходуется больше энергии: на
нагревание воды или алюминиевой
кастрюли, если их массы одинаковы? б) Вода массой 150 г, налитая в латунный
калориметр массой 200 г, имеет температуру
12°С.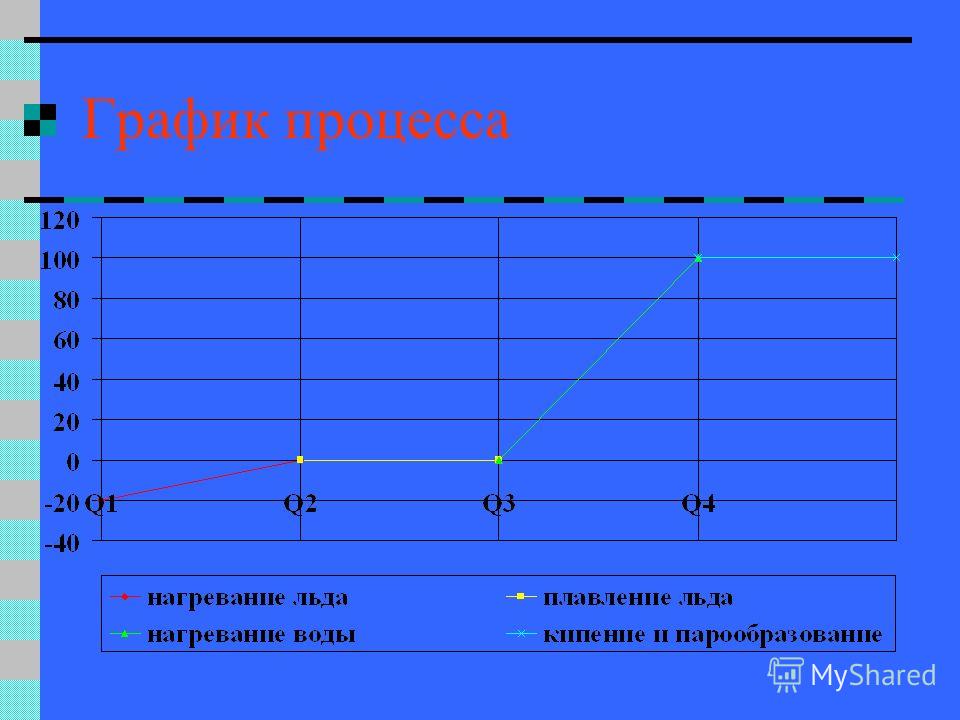 Найти температуру, которая
установится в калориметре, если в воду
опустить железную гирю массой 0,5 кг,
нагретую до 100°С.
Найти температуру, которая
установится в калориметре, если в воду
опустить железную гирю массой 0,5 кг,
нагретую до 100°С.
8. а) В каком случае горячая вода в стакане охладится больше: если в него опустить серебряную или алюминиевую ложку той же массы? Ответ обосновать. б) Смешали 39 л воды при 20°С и 21 л воды при 60°С. Определить температуру смеси.
Высокий уровень
1. Смешали 6 кг воды при 42°С, 4 кг воды при 72°С и 20 кг воды при 18°С. Определить температуру смеси.
2. В алюминиевый сосуд массой 45 г налили 150 г воды при температуре 20°С. В сосуд опустили цилиндр массой 200 г, температура которого 95°С, при этом температура воды повысилась до 30°С. Определить удельную теплоемкость вещества, из которого изготовлен цилиндр.
3. В 200 г воды при 20°С помещают 300 г железа при 10°С и 400 г меди при 25°С. Найти установившуюся температуру.
4. В латунный калориметр массой
128 г, содержащий 240 г воды при температуре
8,5°С, опущен металлический цилиндр
массой 146 г, нагретый до 100°С. В результате
теплообмена установилась температура
10°С. Определить удельную теплоемкость
металла цилиндра.
В результате
теплообмена установилась температура
10°С. Определить удельную теплоемкость
металла цилиндра.
5. Латунный сосуд массой 200 г содержит 400 г анилина при температуре 10°С. В сосуд долили 400 г анилина, нагретого до температуры 31°С. Найти удельную теплоемкость анилина, если в сосуде установилась температура 20°С.
6. В каком отношении надо взять объемы свинца и олова, чтобы их теплоемкости были одинаковы?
7. В железном калориметре массой 100 г находится 500 г воды при температуре 15°С. В калориметр бросают свинец и алюминий общей массой 150 г и температурой 100°С. В результате температура воды поднимается до 17°С. Определить массы свинца и алюминия.
8. После опускания в воду, имеющую температуру 10°С, тела, нагретого до 100°С, через некоторое время установилась общая температура 40°С. Какой станет температура воды, если, не вынимая первого тела, в нее опустить еще одно такое же тело, нагретое до 100°С?
1. Почему разбросанные угли костра гаснут скоро, а сложенные в кучу долго сохраняются в раскалённом виде?
2. При полном сгорании 500г топлива выделилось 22 МДж теплоты. Что это за топливо? (44 МДж/кг)
При полном сгорании 500г топлива выделилось 22 МДж теплоты. Что это за топливо? (44 МДж/кг)
3. На сколько градусов нагреются 3 кг воды, если вся теплота, выделившаяся при полном сгорании 10 г спирта, пошла на её нагревание? (21,4 0)
4. Сколько спирта надо сжечь, чтобы изменить температуру воды массой 2 кг от 14 0 до 50 0 , если вся теплота, выделенная спиртом, пойдёт на нагревание воды? (11 г)
5. Сколько дров необходимо сжечь для того, чтобы нагреть 50 л воды в железном котле массой 10 кг от 15 0 до 65 0 ? Потерями тепла пренебречь. (1,1 кг)
6. Сколько воды можно нагреть от 10 0 до 60 0 ,сжигая 40 кг каменного угля, если КПД нагревателя 40%?
7. Сколько воды можно нагреть кипятильником от 10 0 до кипения, сжигая 600г берёзовых дров, если для нагревания воды пошло 25% теплоты, выделившейся при сжигании дров? (4 кг)
8. В ущелье с высоты 250 м падает камень. Вследствие трения о воздух и удара о землю камень нагревается на 1,5 градуса. Определите удельную теплоёмкость камня, считая, что лишь 50% энергии камня пошло на его нагревание. (817 Дж/кг* 0 С)
(817 Дж/кг* 0 С)
9. Смешали 6 кг воды при 42 0 , 4 кг при 72 0 и 20 кг при 18 0 . Определите температуру смеси. (30 0 С)
10. В алюминиевый сосуд массой 45 г налили 150 г воды при температуре 20 0 С. В сосуд опустили цилиндр массой 200г, температура которого 95 0 С, при этом температура воды повысилась до 30 0 С. Определите удельную теплоёмкость вещества, из которого изготовлен цилиндр. (516 Дж/кг* 0 С)
11. В 1813 году на одном из притоков уральской реки «Исети», где разрабатывались бедные золотоносные кварцевые жилы, малолетняя девчушка Катя Богданова нашла большой самородок платины и принесла его приказчику.Какова масса платинового самородка, найденного на Урале в 1904 г., если для его нагревания на 20 °С потребовалось бы 23 056 Дж энергии? Удельная теплоемкость платины 0,14 кДж/(кг? К).
Ответ: 8,395 кг.
12. Россия, год 1842, 8 октября. На прииске Царево-Александровский близ города Миасс, что на Южном Урале, найден самородок золота весом 36 кг 16 г. Ныне «Большой треугольник» — так назвали уникальный экземпляр — можно увидеть в Алмазном фонде Московского Кремля. Он считается самым крупным, из сохранившихся в мире. На сколько градусов он нагреется, если получит 18 720 Дж тепла? Удельная теплоемкость золота 0,13 кДж/(кг К).
Ныне «Большой треугольник» — так назвали уникальный экземпляр — можно увидеть в Алмазном фонде Московского Кремля. Он считается самым крупным, из сохранившихся в мире. На сколько градусов он нагреется, если получит 18 720 Дж тепла? Удельная теплоемкость золота 0,13 кДж/(кг К).
Ответ: на 4 °С.
13. Самородок «Заячьи Уши» имеет массу 3 344,3 г. Каков объем данного самородка?
14. Самый большой в мире самородок золота был найден в Австралии в 1872г на руднике Хилл-Энд. Самородок имел форму плитки длиной 144 см, шириной — 66 см и толщиной 10 см. Самородок был назван «Плита Холтермана». Чему равна масса самородка?
15. В 1992 г. в Хакасии был найден серебряный самородок массой 30 кг. Какова удельная теплоемкость серебра, если при охлаждении самородка от 80 до 10 °С выделилось 294 кДж энергии?
Ответ: 0,14 кДж/(кг К).
16. В 1986 году в Бразилии найден крупнейший кристалл топаза. Его масса — 8 тонн, размеры 2?1,4?3 м. Чему равна плотность топаза?
17. На сколько изменяется внутренняя энергия Царь-пушки массой 40 т при максимальном зарегистрированном в Москве перепаде температуры от + 36 °С до — 42,2 °С? Удельная теплоемкость металла 0,45 кДж/(кг К).
На сколько изменяется внутренняя энергия Царь-пушки массой 40 т при максимальном зарегистрированном в Москве перепаде температуры от + 36 °С до — 42,2 °С? Удельная теплоемкость металла 0,45 кДж/(кг К).
Ответ: на 1420 МДж.
18. До какой температуры раскаляется почва в Узбекистане, если внутренняя энергия каждого кубометра изменяется при этом на 93,744 МДж? Начальная температура почвы 17 °С, плотность грунта 1800 кг/м3, его удельная теплоемкость 0,84 кДж/(кг К).
Ответ: 79 °С.
19. Самая высокая температура почвы в Туркмении достигает 77 °С. Какова начальная температура куриного яйца-гиганта массой 420 г, зарегистрированного в 1977 г. в Киргизии, если оно получило при засыпании горячим песком 40 кДж энергии? Удельная теплоемкость содержимого яйца 2 кДж/(кг К).
Ответ: 27 °С.
20. В 1879 г. на Урале нашли монолит малахита массой 1054 кг. На сколько изменилась его внутренняя энергия, если при перевозке температура возросла на 20 °С?
Ответ: на 25,3 МДж.
21. В Калининградском музее янтаря хранится уникальная находка массой 2480 г. На сколько изменилась внутренняя энергия этого куска при переносе его в музей, если температура воды в Балтийском море 10 °С, а в музее 20 °С? Удельная теплоемкость янтаря 2 кДж/(кг К).
Ответ: на 85,6 кДж.
22. Какова масса куска янтаря, хранящегося в Паланге, если при изменении температуры от 5 до 18 °С его энергия увеличилась на 93,6 кДж?
Ответ: 3600 г.
23. Самый крупный топаз массой 117 кг был найден на Украине в 1965 г. Как изменится его внутренняя энергия при зимней транспортировке из Москвы в Париж, если средние температуры в этих городах составляют соответственно -10 °С и +3,5 °С? Удельная теплоемкость камня 0,84 кДж/(кг К).
Ответ: увеличится на 1,33 МДж.
24. Какова температура воды в самом горячем озере на Камчатке, если для приготовления ванны объемом 200 л температурой 40 °С в нее влили 40 л воды при 10 °С?
Ответ: 50 °С.
25. Какова летняя температура воды в самом холодном Восточно-Сибирском море, если для получения 10 м3 воды при температуре 20 °С в нее надо добавить 2 л кипятка?
Ответ: 0 °С.
26. В 1968 г. в Благовещенске выпал крупный град, причем при температуре 0 °С масса одной градины составляла 400-600 г. Сколько спирта надо сжечь, чтобы получить из нею воду при 20 °С? Потерями пренебречь. Удельная теплота сгорания спирта 27 МДж/кг.
Ответ: 6,1-9,2 г.
27. В 1965 г. в Кисловодске выпал град, который покрыл почву слоем толщиной 75 см. На сколько изменилась внутренняя энергия каждого квадратного метра при его таянии? Насыпная плотность вещества 800 кг/м3.
Ответ: 198 МДж.
28. В 1843 г. на Урале был найден самородок платины массой 9636 г.
Какова температура плавления платины, если для его переплавки израсходовали 3466 кДж тепла? Удельная теплоемкость платины 140 Дж/(кг* К), удельная теплота плавления 113 кДж/кг, начальная температура 10 °С
Ответ: 1770 °С.
29. Русский мастер Чохов в XVII в. отлил колокол массой 35 т. Какое количество теплоты потребовалось для приготовления расплава, если начальная температура металла была 20 °С? Удельная теплоемкость сплава 0,4 кДж/(кг К), температура плавления 1100 °С, удельная теплота плавления 213 Дж/г.
Ответ: 2260 МДж.
30. В Алмазном фонде Кремля хранится золотой самородок «Лошадиная голова». Какова масса самородка, если для его полного расплавления потребовалось бы 938 кДж тепла?
Ответ: 14 кг.
31. Золотой самородок «Верблюд» имеет массу 9,3 кг и температуру 15 °С. Какова температура плавления золота, если для переплавки потребовалось бы 1892 кДж тепла?
Ответ: 1064 °С.
32. При раскопках в Алуште в 1990 г. нашли 17 слитков серебра общей массой 3,5 кг при температуре 5 °С. Какова удельная теплота плавления серебра, если для переплавки потребовалось 254 г газа удельной теплотой сгорания 45 МДж/кг? Потерями пренебречь.
Ответ: 87 кДж/кг.
33. Какова самая низкая температура, зарегистрированная на арктической станции «Восток», если 200 мл воды температурой 15 °С, вынесенные из помещения и оставленные на ночь, выделили 105 714 Дж энергии?
Ответ: -89,2 °С.
34. Какая самая низкая температура воздуха в районе реки Индигирки была зарегистрирована, если для получения воды при 18 °С из куска льда объемом 0,5 м3 потребовалось сжечь 6 кг дизельного топлива, удельная теплота сгорания которого 42,7 МДж/кг?
Ответ: -78 °С.
35. Самовар, изготовленный в Туле в 1922 г., имел емкость 250 л. За сколько времени он закипал при ежеминутном сгорании 600 г дров? Начальная температура воды 10 °С, КПД 40 %, удельная теплота сгорания дров 10 МДж/кг.
Ответ: за 40 мин.
36. Какую емкость имел новый тульский самовар-рекордсмен, если при КПД 50 % он закипал за 20 мин и потреблял ежеминутно 460 г древесного угля, удельная теплота сгорания которого 35 МДж/кг? Начальная температура воды 15 °С.
Ответ: 450 л.
37. Сколько древесного угля нужно сжечь, чтобы вскипятить воду в 50 литровом Суксунском самоваре, если начальная температура воды равна 20°С? Удельная теплота сгорания древесного угля 35 МДж/кг?
Ответ: 0,48кг
38. Самый экономичный тепловой двигатель 1840 г. потреблял 0,77 кг угля при мощности 735 Вт. Каков КПД установки? Удельная теплота сгорания угля 29 Мдж/кг.
Ответ: 12 %.
39. Самый большой американский бойлер при мощности 1330 МВт дает 4 232 000 кг пара в час. Каков КПД установки, если туда поступает вода при 20 °С?
Ответ: 50%.
40. Самый мощный дизельный двигатель в Швейцарии имеет мощность 41 920 кВт. Сколько топлива в час он потребляет при работе, если его КПД 35 %? Удельная теплота сгорания топлива 42 МДж/кг.
Ответ: 10,3 т.
41. Дизельный двигатель автомобиля КамАЗ-5350 «Мустанг» имеет мощность 191,36 кВт. Сколько топлива в час он потребляет при работе, если его КПД 35 %? Удельная теплота сгорания топлива 42 МДж/кг.
Ответ: 46,86 кг
42. Самая крупная нефтеналивная цистерна имеет емкость 1,5 млн баррелей (1 баррель = 158,988 л). Сколько тепла выделяется при полном сгорании нефти? Удельная теплота сгорания нефти 43 МДж/кг, плотность 0,8 т/м3.
Ответ: 1015 Дж.
· Создаем собственную электронную страничку.
Начальный уровень
1. Что потребует большего количества теплоты для нагревания на 1°С: стакан воды или бидон воды?
2. Что потребует большего количества теплоты для нагревания на 1°С: 100 г воды или 100 г меди?
3. Какое вещество имеет наименьшую удельную теплоемкость?
4. Какое вещество имеет наибольшую удельную теплоемкость?
5. Какое количество теплоты необходимо для нагревания железа массой 1 г на 1°С?
6. Чтобы повысить температуру на 1°С олова массой 1 кг, требуется 230 Дж. Какова удельная теплоемкость олова?
7. Алюминиевая деталь массой 1 кг остывает на 1°С. Какое количество теплоты выделится при остывании детали?
8. Чугунную деталь массой 1 кг нагрели на 1°С. На сколько увеличилась при этом внутренняя энергия детали?
Чугунную деталь массой 1 кг нагрели на 1°С. На сколько увеличилась при этом внутренняя энергия детали?
Средний уровень
1. Каким количеством теплоты можно нагреть 0,3 кг воды от 12°С до 20°С?
2. Какую массу воды можно нагреть на 10°С 1 кДж теплоты?
3. На сколько градусов остыл кипяток в питьевом баке емкостью 27 л, если он отдал окружающей среде 1500 кДж теплоты?
4. Чтобы нагреть 110 г алюминия на 90°С, требуется 9,1 кДж. Вычислите удельную теплоемкость алюминия.
5. Какое количество теплоты необходимо для нагревания латунной гири массой 200 г от 20 до 28°С?
6. Какова масса железной детали, если на ее нагревание от 20°С до 200°С пошло 20,7 кДж теплоты?
7. На сколько градусов повысилась температура 4 л воды, если она получила количество теплоты, равное 168 кДж?
8. Слиток серебра массой 120 г при остывании от 66°С до 16°С передал окружающей среде 1,5 кДж теплоты. Как велика удельная теплоемкость серебра?
Достаточный уровень
1. а) Почему в пустынях днем жарко, а ночью температура падает ниже 0°С? б) Чтобы охладить выточенную из меди деталь, имеющую температуру 100°С, ее погрузили в 420 г воды с температурой 15°С. Определите массу детали, если известно, что в процессе теплообмена вода нагрелась до 18°С.
а) Почему в пустынях днем жарко, а ночью температура падает ниже 0°С? б) Чтобы охладить выточенную из меди деталь, имеющую температуру 100°С, ее погрузили в 420 г воды с температурой 15°С. Определите массу детали, если известно, что в процессе теплообмена вода нагрелась до 18°С.
2. а) По куску свинца и куску стали той же массы ударили молотком одинаковое число раз. Какой кусок нагрелся больше?
б) Стальную деталь массой 300 г нагрели до высокой температуры, а затем погрузили для закалки в 3 кг машинного масла, имеющего температуру 10°С. Определить начальную температуру детали, если температура при установившемся тепловом равновесии была 30°С.
3. а) Почему железные печи скорее нагревают комнату, чем кирпичные, но не так долго остаются теплыми? б) В алюминиевый калориметр массой 140 г налили 250 г воды при температуре 15°С. После того как брусок из свинца массой 100 г, нагретый до 100°С, поместили в калориметр с водой, там установилась температура 16°С. Составить уравнение теплового баланса и определить удельную теплоемкость свинца.
4. а) Почему реки и озера нагреваются солнечными лучами медленнее, чем суша? б) Мальчик наполнил стакан, емкость которого 200 см 3 , кипятком на три четверти и дополнил стакан холодной водой. Определите, какая установилась температура воды, если температура холодной воды равна 20°С.
5. а) Медной и стальной гирькам одинаковой массы передали равные количества теплоты. У какой гирьки температура изменится сильнее? б) Стальное изделие закалялось нагреванием до температуры 800°С с последующим опусканием в масло массой 2 кг, взятое при температуре 10°С. При этом масло нагрелось до температуры 40°С. Найти массу стального изделия, если при переносе в масло изделие охладилось на 20°С. Удельная теплоемкость масла 2100Дж/(кгּ°С).
6. а) Что эффективнее использовать в качестве грелки — 2 кг воды или 2 кг песка при той же температуре? б) Для приготовления ванны вместимостью 200 л смешали холодную воду при температуре 10°С с горячей при температуре 60°С. Какие объемы той и другой воды надо взять, чтобы установилась температура 40°С?
7. а) На что расходуется больше энергии: на нагревание воды или алюминиевой кастрюли, если их массы одинаковы? б) Вода массой 150 г, налитая в латунный калориметр массой 200 г, имеет температуру 12°С. Найти температуру, которая установится в калориметре, если в воду опустить железную гирю массой 0,5 кг, нагретую до 100°С.
а) На что расходуется больше энергии: на нагревание воды или алюминиевой кастрюли, если их массы одинаковы? б) Вода массой 150 г, налитая в латунный калориметр массой 200 г, имеет температуру 12°С. Найти температуру, которая установится в калориметре, если в воду опустить железную гирю массой 0,5 кг, нагретую до 100°С.
8. а) В каком случае горячая вода в стакане охладится больше: если в него опустить серебряную или алюминиевую ложку той же массы? Ответ обосновать. б) Смешали 39 л воды при 20°С и 21 л воды при 60°С. Определить температуру смеси.
Высокий уровень
1. Смешали 6 кг воды при 42°С, 4 кг воды при 72°С и 20 кг воды при 18°С. Определить температуру смеси.
2. В алюминиевый сосуд массой 45 г налили 150 г воды при температуре 20°С. В сосуд опустили цилиндр массой 200 г, температура которого 95°С, при этом температура воды повысилась до 30°С. Определить удельную теплоемкость вещества, из которого изготовлен цилиндр.
3. В 200 г воды при 20°С помещают 300 г железа при 10°С и 400 г меди при 25°С. Найти установившуюся температуру.
Найти установившуюся температуру.
4. В латунный калориметр массой 128 г, содержащий 240 г воды при температуре 8,5°С, опущен металлический цилиндр массой 146г, нагретый до 100°С. В результате теплообмена установилась температура 10°С. Определить удельную теплоемкость металла цилиндра.
2 часть — курсовая — 1. Аргону сообщили количество теплоты, равное 30 кДж, и он изобарно расширился. При этом объём газа увеличился на 0,6 каково давление газа Масса газа постоянна
Скачать 32.69 Kb.
|
С этим файлом связано 1 файл(ов). Среди них: реферат 2.docx. Показать все связанные файлы Подборка по базе: 1_1_ Максимальное количество специальностей и направлений(1).doc, Бостан количество педагогов до 36 лет 08.09..docx, 1_Термодинамика. Количество теплоты.pdf, Учимся решать задачи 8 класс Решение задач по теме_ «Моль. Колич, проверочная количество вещества.docx, В любой современной стране имеется достаточно большое количество, практическая количество ппд.docx, карточки количество.pdf, термодинамические расчеты количество теплоты срс.docx, задание 11 количество теплоты и 1 з тд ЕГЭ.pdf 25 задание 1. Аргону сообщили количество теплоты, равное 30 кДж, и он изобарно расширился. При этом объём газа увеличился на 0,6 м3. Каково давление газа? Масса газа постоянна. 2.Аргону сообщили количество теплоты, равное 50 кДж, и он изобарно расширился, сохраняя своё давление равным 100 кПа. 3. При изохорном нагревании идеального газа на 300 К его давление удвоилось. Какова была первоначальная абсолютная температура газа? Количество вещества газа постоянно. 4.При изобарном нагревании идеального газа на 400 К его объём увеличился втрое. Определите конечную абсолютную температуру газа. Количество вещества газа постоянно. 5. При изобарном расширении неона его объём увеличился на 0,4 м3, при этом газ совершил работу 6 кДж. На сколько увеличилась внутренняя энергия газа? 6. В схеме, изображённой на рисунке, идеальный вольтметр показывает напряжение U = 2 В. Внутреннее сопротивление источника тока г = 1 Ом, а сопротивления резисторов: R1 = 2 Ом и R2 — 2 Ом. Какова ЭДС источника? 7. В схеме, изображённой на рисунке, ЭДС источника ℰ = 9 В, внутреннее сопротивление источника тока r = 1 Ом, а сопротивления резисторов: R2=2 Ом и R2 = 2 Ом. Каковы показания идеального вольтметра?
8. 9. Тепловая машина с максимально возможным КПД имеет в качестве нагревателя резервуар с водой, а в качестве холодильника — сосуд со льдом при О °C. При совершении машиной работы 1 МДж растаяло 12,1 кг льда. Определите температуру воды в резервуаре. Ответ округлите до целых. 10. В калориметр с водой при температуре О °C опущена трубка. По трубке в воду впускают водяной пар при температуре 100 °C. В некоторый момент масса воды перестаёт увеличиваться, хотя пар по-прежнему пропускают. Определите первоначальную массу воды в калориметре, если масса сконденсировавшегося пара 126 г. Тепловыми потерями пренебречь. 11. В начале процесса температура куска свинца массой 1 кг равнялась 37 °C. 28 задание 1. Начальная скорость движения тела равна 5 м/с. Сколько потребуется времени, чтобы увеличить его скорость в 3 раза при равноускоренном движении по прямой в одном направлении на пути в 20 м? 2. Начальная скорость движения тела равна 4 м/с. На сколько метров переместилось тело за 3 с равноускоренного движения по прямой в одном направлении, если за это время его скорость увеличилась в 4 раза? 3. Какой путь пройдёт тело за 2 с, двигаясь по прямой в одном направлении, если его скорость за это время уменьшается в 3 раза? Модуль ускорения тела равен 5 м/с2. 4. За какое время тело, двигаясь по прямой в одном направлении, пройдёт путь 30 м, если его скорость за это время уменьшается в 4 раза? Модуль ускорения тела равен 4 м/с2. 5. Брусок массой m = 2 кг движется поступательно по горизонтальной плоскости под действием постоянной силы, направленной под углом а = 30° к горизонту (см. 6. Снаряд, летящий со скоростью 100 м/с, разрывается на два осколка. Первый осколок летит под углом 90° к первоначальному направлению, а второй — под углом 60°. Какова масса снаряда до разрыва, если второй осколок массой 1 кг имеет скорость 400 м/с? 7. Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы F приложенной к грузуМ1 — 2 кг (см. рисунок). Нить обрывается при значении силы натяжения нити 4 Н, при этом модуль силы F равен 12 Н. Чему равна масса второго груза М2? 8. Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы F приложенной к грузу М1 (см. рисунок). Нить обрывается при значении силы натяжения нити 4 Н, при этом модуль силы F равен 10 Н. |
Тренировочные задачи по физике для 8 класса
Тренировочные задачи по физике для 8 класса.
Автор-составитель: учитель физики Трещина Екатерина Игоревна,
г. Таганрог, МОБУ СОШ № 24
Предлагаю вашему вниманию подборку задач для подготовки к ОГЭ по физике. Задачи можно использовать для подготовки к контрольным и зачетным работам, для индивидуальной работы с учениками. Варианты контрольной и зачетной работ (на выбор) представлены после подборки задач.
Теплопередача и работа
Задачи
Часть А
1. Какое количество теплоты потребуется для нагревания стального бруска массой 0,5 кг от 10⁰ до 40 °С?
2. Какое количество теплоты получила вода массой 200 г при нагревании от 10⁰С до 30 °С?
3. Какое количество теплоты необходимо для нагревания железного утюга массой 2 кг от 20⁰С до 320 °С?
4. Какое количество теплоты потребуется для нагревания на 10⁰С
олова массой 500 г?
Какое количество теплоты потребуется для нагревания на 10⁰С
олова массой 500 г?
5. Какое количество теплоты потребуется для увеличения температуры латуни массой 0,2 т на 1 °С?
6. Кирпичная печь массой 1 т остывает от 20⁰С до 10 °С. Какое количество теплоты при этом выделяется?
7. Чугунная болванка массой 32 кг остывает от 1115⁰С до 15 °С. Какое количество теплоты при этом выделяется?
8. Какое количество теплоты выделится при охлаждении 100 г олова, взятого при температуре 82°С, на 50°С ?
9. Какое количество теплоты выделила вода массой 100 г при остывании от 45⁰С до 25 °С?
10. После обработки алюминиевой детали на станке температура ее понизилась от 420⁰С до 20 °С. На сколько при этом уменьшилась внутренняя энергия детали, если ее масса 0,5 кг?
11. Какое количество теплоты отдаст кирпичная печь массой 0,35 т, остывая с изменением температуры на 50 °С?
12. На сколько уменьшится внутренняя энергия латунной гири массой 200 г, если ее охладить на 10 °С?
13.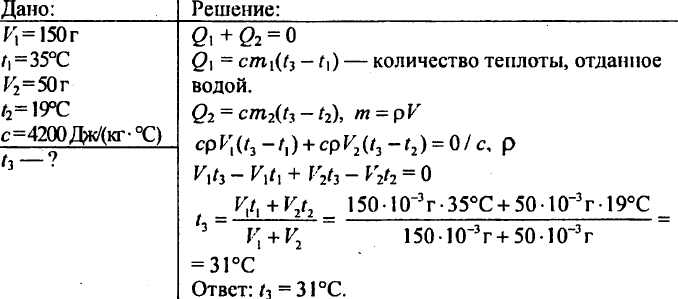 Для нагревания вещества массой 10 кг на 10 °С потребовалось 420 кДж энергии.
Какое вещество нагрели?
Для нагревания вещества массой 10 кг на 10 °С потребовалось 420 кДж энергии.
Какое вещество нагрели?
14. Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей количество теплоты 2,1 кДж. Чему равна удельная теплоемкость камня?
15. Для нагревания 100 г металла от 20⁰С до 40 °С потребовалось 260 Дж энергии. Что это за металл? (Определить удельную теплоемкость.)
16. При охлаждении жидкости массой 210 кг от 25⁰С до 15 °С выделилось 4,41 МДж теплоты. Что это за жидкость?
17. Стальное сверло при работе получило 5 кДж энергии и нагрелось от 15 до 115 °С. Какова масса этого сверла?
18. Мальчик вычислил, что при нагревании воды от 15°С до кипения внутренняя энергия ее увеличится на 178,5 кДж. Какова масса нагреваемой воды?
19.
Стальной молоток был нагрет для закалки до температуры 720 °С, затем быстро
охлажден до температуры 10°С. При этом он отдал окружающей среде 298,2 кДж
энергии. Найти массу молотка.
20. Кирпичная печь, остыв на 50°С, отдала комнате 15400 кДж энергии. Какова масса этой печи?
21. Какую массу воды можно нагреть от 15⁰С до 45 °С, затратив для этого 1260 кДж энергии?
22. Какое количество воды можно нагреть от 10⁰С до 60 °С, затратив для этого 210 кДж энергии?
23. На сколько нужно повысить температуру куска свинца массой 100 г, чтобы внутренняя энергия его увеличилась на 280 Дж?
24. При охлаждении куска олова массой 20 г. внутренняя энергия его уменьшилась на 1 кДж. На сколько изменилась температура олова?
25. На сколько градусов нагреется цинковая деталь массой 40 г, если ей сообщить 760 Дж энергии?
26. Какое количество теплоты выделяется при полном сгорании 2,5 кг природного газа?
27. Какое количество теплоты выделяется при полном сгорании бензина массой 5 кг?
28. Какое количество теплоты выделяется при полном сгорании 1,5 т каменного угля?
29. Сколько энергии выделится при полном сгорании древесного угля массой 15 кг?
Сколько энергии выделится при полном сгорании древесного угля массой 15 кг?
30. Какое количество теплоты выделится при полном сгорании пороха массой 25 г?
31. Какое количество теплоты выделится при полном сгорании 50 кг сухих березовых дров?
32. Двигатель мопеда на пути 10 км расходует бензин массой 100 г. Какое количество теплоты выделяется при полном сгорании бензина?
33. Какое количество теплоты выделяется при полном сгорании 1,3 кг антрацита?
34. Сколько надо сжечь каменного угля, чтобы при этом выделилось 270 МДж теплоты?
35. Сколько надо сжечь дизельного топлива, чтобы при этом в36. Какую массу торфа надо сжечь для обогревания комнаты, если при сгорании топлива в печи должно выделяться не менее 224 МДж энергии?
37. Какую массу бензина надо сжечь, чтобы получить 230 МДж энергии?
38. Сколько керосина сожгли, если при этом выделилось 55,2 МДж энергии?
39. Чему равна масса сосновых дров, если при полном их сгорании получено 127,4 МДж теплоты?
40. Сколько древесного угля использовали для получения тепла, если получено было
1,27 МДж теплоты?
Сколько древесного угля использовали для получения тепла, если получено было
1,27 МДж теплоты?
41. На сколько уменьшилось количество спирта в спиртовке, если при его горении выделилось количество теплоты 243 кДж?
42. При полном сгорании кокса массой 10 кг выделяется 29 МДж энергии. Чему равна удельная теплота сгорания кокса?
43. При полном сгорании 3 кг топлива выделилось 11,4 МДж энергии. Какое топливо сожгли?
44. При полном сгорании 2 кг жидкости выделилось 92 МДж энергии. Какую жидкость сожгли?
45. При полном сжигании жидкого топлива массой 15 г получено 405 кДж энергии. Какую жидкость использовали как топливо?
46. При полном сгорании 0,5 кг топлива выделилось 7 МДж энергии. Найти удельную теплоту сгорания этого топлива.
47. При сжигании газа выделилось 132 МДж энергии. Чему равна удельная теплота сгорания газа, если его масса равна З кг?
48.
При сжигании 300 г каменного угля выделяется 9 МДж тепла. Найти его удельную
теплоту сгорания.
Найти его удельную
теплоту сгорания.
49. Найти удельную теплоту сгорания сосновых дров, если при сжигании 3 кг этих дров выделилось 39 МДж энергии.
50. Для обращения воды в пар при температуре кипения необходимо количество теплоты 65 МДж. Хватит ли для этого 6 кг сухих березовых дров?
Часть В
51. Какое количество теплоты потребуется для нагревания на 15°С воды объемом 0,5 л?
52. Какое количество теплоты получает при нагревании серебро объемом 2 см3 от 10⁰С до 60 ⁰С?
53. Какое количество теплоты необходимо для нагревания стали объемом 0,5 м3 от 10⁰С до 110 °С?
54. Какое количество теплоты получил нагретый от 10⁰С до 20 °С воздух комнаты, объем которой 60 м3?
55. Какое количество теплоты отдаст стакан кипятка, объемом 250 мл, остывая до температуры 15 °С?
56. Какое количество теплоты отдаст кирпичная печь, сложенная из 500 кирпичей, при
остывании от 70⁰С до 20 °С? Масса одного
кирпича равна 4 кг.
57. В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 5⁰С до 25 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке?
58. При изменении температуры куска металла массой 0,08 кг от 20⁰С до 30 °С внутренняя энергия его увеличилась на 320 Дж. Что это заметалл? Найти его объем.
59. Найти объем металлического бруска массой 351 г, если при изменении его температуры от 20 до 24 °С его внутренняя энергия увеличивается на 1326,78 Дж.
60. Как уменьшилась температура кипятка в питьевом баке объемом 27 л, если он отдал окружающей среде 1500 кДж теплоты?
61. На сколько изменится температура воды в стакане, если ей сообщить количество теплоты, равное 109 Дж? Вместимость стакана принять равной 200 см3?
62. При охлаждении куска олова массой 100 г до температуры 32 °С выделилось 5 кДж
энергии. Найти температуру олова до охлаждения.
63. При охлаждении медного паяльника до 20°С выделилось 30,4 кДж энергии. До какой температуры был нагрет паяльник, если его масса 200 г?
64. До какой температуры остынут 5 л кипятка, взятого при температуре 100 °С, отдав в окружающее пространство 1680 кДж энергии?
65. Термос объемом 3 л заполнили кипятком. Через 20 часов температура воды в нем понизилась до 80 °С. На сколько изменилась внутренняя энергия воды?
66. Сколько теплоты выделится при полном сгорании сухихберезовых дров объемом 5 м³?
67. Сколько теплоты выделится при полном сгорании нефти объемом 250 л?
68. В каком случае выделится большее количество теплоты: при полном сгорании древесного угля массой 3 кг или при полном сгорании сухих дров массой 9 кг?
69. На сколько больше теплоты выделится при полном сгорании бензина массой 1,5 кг, чем при сгорании сухих березовых дров той же массы?
70. Во сколько раз больше выделится теплоты при полном сгорании водорода массой 2 кг, чем при полном сгорании сухих березовых дров той же массы?
71. В печи сгорели сухие сосновые дрова объемом 0,02 м3 и торф массой 2 кг. Сколько
теплоты выделилось в печи?
В печи сгорели сухие сосновые дрова объемом 0,02 м3 и торф массой 2 кг. Сколько
теплоты выделилось в печи?
72. Смешали бензин объемом 1,5 л и спирт объемом 0,5 л. Какое количество теплоты выделится при полном сгорании этого топлива?
73. К зиме заготовили сухие березовые дрова объемом 3 м3 и каменный уголь массой 1,5 т. Сколько теплоты выделится в печи при полном сгорании в ней заготовленного топлива?
74. Сколько каменного угля нужно сжечь, чтобы получить столько же энергии, сколько ее выделяется при полном сгорании бензина объемом 6 м3?
75. Какую массу каменного угля нужно сжечь, чтобы получить такое же количество теплоты .которое выделяется при сгорании керосина массой 20 т?
Часть С
76. Какое количество теплоты получила вода при нагревании от 15⁰С до 25 °С в бассейне, длина которого 100 м, ширина 6 м и глубина 20 дм?
77. Какое количество теплоты потребуется для того, чтобы в латунной бочке массой 12 кг нагреть воду объемом 9,5 л от температуры 20⁰С до 100⁰С
78. Алюминиевая фляга массой 12 кг вмещает 36 л молока. Какое количество теплоты
потребуется для нагревания молока во фляге от0 до 60 °С ?
Алюминиевая фляга массой 12 кг вмещает 36 л молока. Какое количество теплоты
потребуется для нагревания молока во фляге от0 до 60 °С ?
79. В железный душевой бак, масса которого 65 кг, налили холодной воды из колодца, объемом 200 л. В результате нагревания солнечным излучением температура воды повысилась от 4⁰С до 29 °С. Какое количество теплоты получили бак и вода?
80. Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения?
81. На сколько изменится температура куска меди массой 500 г, если ему сообщить такое же количество теплоты, которое пойдет на нагревание воды массой 200 г от 10 ⁰С до 60 °С?
82. До какой температуры нагрелась во время работы стальная фреза массой 1 кг, если после погружения ее в сосуд с водой, масса которой 1 кг, температура воды повысилась от 10⁰С до 30 °С?
83.
Двигатель мощностью 75 Вт в течение 5 мин вращает лопасти винта внутри
калориметра, в котором находится вода объемом 5 л. Вследствие трения о воду
лопастей винта вода нагрелась. Считая, что вся энергия пошла на нагревание
воды, определить, как изменилась ее температура?
Вследствие трения о воду
лопастей винта вода нагрелась. Считая, что вся энергия пошла на нагревание
воды, определить, как изменилась ее температура?
84. При работе машины внутренняя энергия одной из алюминиевых деталей массой 2 кг повысилась на столько, на сколько увеличивается внутренняя энергия воды массой 800 г. При нагревании ее от 0⁰С до 100°С. На сколько повысилась температура детали?
85. Как изменится температура воды массой 3 кг, если вся теплота, выделившаяся при полном сгорании спирта объемом 12,5 мм3, пошла на ее нагревание?
86. На сколько изменится температура воды объемом 100 л, если считать, что вся теплота, выделяемая при сжигании древесного угля массой 0,5 кг, пойдет на нагревание воды?
87. На сколько изменится температура воды, масса которой 22 кг, если ей передать всю энергию, выделившуюся при полном сгорании 10 г природного газа?
88. В ванну налили 40 л холодной воды температурой 6 °С. Затем долили горячую воду
температурой 96 °С. Температура воды после этого стала равной 36 °С. Найти массу
долитой воды. Нагреванием ванны и окружающей среды пренебречь.
Температура воды после этого стала равной 36 °С. Найти массу
долитой воды. Нагреванием ванны и окружающей среды пренебречь.
89. Мальчик налил в ведро 3 л воды, температура которой равна 10 °С. Сколько кипятка нужно долить в ведро, чтобы температура воды в нем стала равной 50 °С?
90. В воду объемом 1 л опустили кусок олова, нагретый до температуры 188 °С. Температура воды при этом увеличилась от 10⁰С до 20 °С. Чему равна масса куска олова?
91. В кувшин с водой, масса которой 100 г, а температура 20°С, влили воду при температуре 100 °С, после чего температура воды в кувшине стала равной 75 °С. Определить массу горячей воды. Потери энергии на нагревание кувшина не учитывать.
92. Сколько воды, взятой при температуре 10 «С, можно нагреть до 50 °С, сжигая керосин массой 15 г, считая, что вся выделяемая при горении керосина энергии идет на нагревание воды?
93. Сколько спирта надо сжечь, чтобы изменить температуру воды объемом 2 дм3 от 14⁰С до 50 °С, если вся теплота, выделенная спиртом, пойдет на нагревание воды?
94. Когда в бак с водой добавили еще 3 л воды при 100 °С и перемешали всю воду, то
температура воды в баке стала равна 35°С. Найти начальный объем воды в баке.
Когда в бак с водой добавили еще 3 л воды при 100 °С и перемешали всю воду, то
температура воды в баке стала равна 35°С. Найти начальный объем воды в баке.
95. В сосуд с водой, масса которой 150 г, а температура 16°С, добавили воду массой 50 г при температуре 80 °С. Определить температуру смеси.
96. В кастрюле с холодной водой, масса которой 3 кг, а температура 10°С, влили 2 кг кипятку. Какая установится температура воды? Нагреванием сосуда пренебречь.
97. На нагревание кирпича массой 4 кг на 63°С затрачено такое же количество теплоты, как и для нагревания воды той же массы на 13,2 °С. Определить удельную теплоемкость кирпича.
98. Металлическое тело массой 30 г нагрели в кипящей воде. После этого его перенесли в воду, масса которой 73,5 г и температура 20°С, налитую в калориметр. Вода от этого нагрелась до 23 °С. Из какого металла сделано тело?
99.
В стакан, содержащий 230 г кипятка, опустили ложку массой 150 г, имеющую
температуру 20 °С. Температура воды понизилась от этого до 97°С. Верно ли, что
эта ложка алюминиевая?
Температура воды понизилась от этого до 97°С. Верно ли, что
эта ложка алюминиевая?
100. Твердое тело массой 80 г опустили в кипяток. Затем его перенесли в калориметр, куда была налита вода массой 166,5 г при температуре 20 °С. Температура воды повысилась до 24°С. Найти удельную теплоемкость твердого тела. если выделилось 427 МДж теплоты?
Контрольная работа.
Вариант1
1. Кирпичная печь массой 1 т остывает от 20⁰С до 10 °С. Какое количество теплоты при этом выделяется?
2. Для нагревания вещества массой 10 кг на 10 °С потребовалось 420 кДж энергии. Какое вещество нагрели?
3. При охлаждении куска олова массой 100 г до температуры 32 °С выделилось 5 кДж энергии. Найти температуру олова до охлаждения.
4. Сколько спирта надо сжечь, чтобы изменить температуру воды объемом 2 дм3 от 14⁰С до 50 °С, если вся теплота, выделенная спиртом, пойдет на нагревание воды?
Вариант2
1. Какое количество теплоты получила вода
массой 200 г при нагревании от 10⁰С
до 30 °С?
Какое количество теплоты получила вода
массой 200 г при нагревании от 10⁰С
до 30 °С?
2. После обработки алюминиевой детали на станке температура ее понизилась от 420⁰С до 20 °С. На сколько при этом уменьшилась внутренняя энергия детали, если ее масса 0,5 кг?
3. До какой температуры остынут 5 л кипятка, взятого при температуре 100 °С, отдав в окружающее пространство 1680 кДж энергии?
4. В сосуд с водой, масса которой 150 г, а температура 16°С, добавили воду массой 50 г при температуре 80 °С. Определить температуру смеси.
Вариант3
1. Какое количество теплоты выделится при охлаждении 100 г олова, взятого при температуре 82°С, на 50°С ?
2. При охлаждении жидкости массой 210 кг от 25⁰С до 15 °С выделилось 4,41 МДж теплоты. Что это за жидкость?
3. Смешали бензин объемом 1,5 л и спирт объемом 0,5 л. Какое количество теплоты выделится при полном сгорании этого топлива?
4.
В воду объемом 1 л опустили кусок олова,
нагретый до температуры 188 °С. Температура воды при этом увеличилась от 10⁰С
до 20 °С. Чему равна масса куска олова?
Температура воды при этом увеличилась от 10⁰С
до 20 °С. Чему равна масса куска олова?
Зачет по теме
Вариант 1
1.Каким способом – совершением работы или теплопередачей – изменилась внутренняя энергия детали при ее нагревании в печи перед закалкой?
1) совершением работы 2) теплопередачей 3) совершением работы и теплопередачей
2. Удельная теплоемкость вещества показывает
1) какое количество теплоты необходимо передать телу для изменения его температуры на 1 градус
2) какое количество теплоты необходимо передать 1 кг вещества для изменения его температуры на 100 градусов
3) какое количество теплоты необходимо передать телу массой 1кг для изменения его температуры на 1 градус
3. Что потребует большего количества теплоты для нагревания на 10 С: 100 г воды или 100 г меди?
1) 100 г воды 2) 100 г меди 3) потребуется одинаковое количество теплоты
4. В каком случае кастрюля с горячей водой остынет быстрее, если ее поставить на
лед или если лед на крышку кастрюли положить сверху? Ответ пояснить
В каком случае кастрюля с горячей водой остынет быстрее, если ее поставить на
лед или если лед на крышку кастрюли положить сверху? Ответ пояснить
5. Чтобы нагреть 110 г алюминия на 90 0С требуется количество теплоты, равное 9,1 кДж. Вычислите удельную теплоемкость алюминия.
6. Смешали 39 л воды при температуре 20 0С и 21 л воды при температуре 60 0С. Определите температуру смеси.
Вариант 2
1. Каким способом изменялась внутренняя энергия детали при сверлении в ней отверстия
1) совершением работы 2) теплопередачей 3) совершением работы и теплопередачей
2. Количество теплоты зависит от
1) массы тела и его температуры
2) от рода вещества, из которого изготовлено тело и массы тела
3) от массы тела, начальной и конечной температур тела, рода вещества
3. Как называется величина, показывающая , какое количество теплоты необходимо для нагревания 1 кг железа на 10 С?
1) внутренняя энергия 2) количество теплоты 3) удельная теплоемкость вещества
4. Когда парусным судам легче заходить в гавань – днем или вечером? Ответ пояснить
Когда парусным судам легче заходить в гавань – днем или вечером? Ответ пояснить
5. Какова масса железной детали, если на ее нагревание от 20 0С до 200 0С потребовалось 20,7 кДж теплоты?
6. Вода массой 150 г имеет температуру 10 0С. Найти температуру воды после того, как в нее опустили железную деталь массой 0,5 кг, имеющую температуру 100 0С.
Вариант 3
1. Каким способом изменялась внутренняя энергия воды при ее нагревании в чайнике
1) совершением работы 2) теплопередачей 3) совершением работы и теплопередачей
2. Чугунную деталь массой 1 кг нагрели на 1 0С. На сколько при этом увеличилась ее внутренняя энергия?
1) на 540 Дж 2) на 540 Дж/ кг 0С 3) на 1 Дж
3. По куску свинца и куску стали одинаковой массы ударили молотком одинаковое число раз. Какой кусок нагрелся больше?
1) из стали 2) из свинца 3) невозможно определить
4.
В каком случае лед, внесенный в теплую комнату растает быстрее: если его просто
положить на стол , или, если сверху прикрыть шерстяным платком. Ответ пояснить
Ответ пояснить
5. На сколько градусов повысилась температура 4 кг воды, если она получила количество теплоты, равное 168 кДж?
6. Мальчик наполнил стакан кипятком, налив его 150 г, а затем добавил 50 г воды с температурой 20 0С. Определите температуру, которая установилась в стакане.
Литература
1) Р.А. Рахматуллин. Текстовые расчетные задачи, 8 кл. — Оренбург, 1997 – 59 с
2) Лукашева Е.В. Типовые тестовые задания. Физика. Изд-во «Экзамен», 2016 -126с
Готовимся к ГИА 25.03.2016
Задания 10. Тепловые явления
1. Задание 10 № 36. Сколько литров воды при 83 °С нужно добавить к 4 л воды при 20 °С, чтобы получить воду температурой 65 °С? Теплообменом с окружающей средой пренебречь.
1) 10 л 2) 1,6 л 3) 4 л 4) 6,25 л
2. Задание 10 № 63. Какое количество теплоты выделится при конденсации 2 кг пара, взятого при температуре кипения, и последующего охлаждения воды до 40 °С при нормальном атмосферном давлении?
1) 504 кДж 2) 4600 кДж 3) 4936 кДж 4) 5104 кДж
3. Задание 10 № 90. Три литра воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
Задание 10 № 90. Три литра воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
1) 1 кг 2) 3 кг 3) 4 кг 4) 6 кг
4. Задание 10 № 117. В воду, взятую при температуре 20 °С, добавили 1 л воды при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса холодной воды? Теплообменом с окружающей средой пренебречь.
1) 1 кг 2) 2 кг 3) 3 кг 4) 5 кг
5. Задание 10 № 144. Какое количество теплоты необходимо, чтобы нагреть 1 л воды от 20 °С до 100 °С? Вода нагревается в алюминиевой кастрюле массой 200 г. Тепловыми потерями пренебречь.
1) 14,72 кДж 2) 336 кДж 3) 350,72 кДж 4) 483,2 кДж
6. Задание 10 № 171. Сколько спирта надо сжечь, чтобы нагреть воду массой 2 кг на 29 °С? Считать, что вся энергия, выделенная при сгорании спирта, идёт на нагревание воды.
Задание 10 № 171. Сколько спирта надо сжечь, чтобы нагреть воду массой 2 кг на 29 °С? Считать, что вся энергия, выделенная при сгорании спирта, идёт на нагревание воды.
1) 4,2 г 2) 8,4 г 3) 4,2 кг 4) 8,4 кг
7. Задание 10 № 198. Сколько керосина надо сжечь, чтобы нагреть 3 кг воды на 46 °С? Считать, что вся энергия, выделенная при сгорании керосина, идёт на нагревание воды.
1) 12,6 г 2) 8,4 г 3) 4,6 г 4) 4,2 г
8. Задание 10 № 225. Какое количество теплоты необходимо для плавления куска свинца массой 2 кг, взятого при температуре 27 °С?
1) 50 кДж 2) 78 кДж 3) 89 кДж 4) 128 кДж
9. Задание 10 № 252. В стакан, содержащий лед при температуре −5 °С, налили воду, имеющую температуру 40 °С. Каково отношение массы воды к массе льда, если весь лед растаял и в стакане установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь.
Каково отношение массы воды к массе льда, если весь лед растаял и в стакане установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь.
1) 2,02 2) 1,86 3) 0,5 4) 0,06
10. Задание 10 № 279. По результатам нагревания кристаллического вещества массой 5 кг построен график зависимости температуры этого вещества от количества подводимого тепла.
Считая, что потерями энергии можно пренебречь, определите, какое количество теплоты потребовалось для нагревания 1 кг этого вещества в жидком состоянии на 1 °С?
1) 750 Дж 2) 1200 Дж 3) 2000 Дж 4) 150000 Дж
11. Задание 10 № 306. В сосуд налили 1 кг воды при температуре 90 °С. Чему равна масса воды, взятой при 30 °С, которую нужно налить в сосуд, чтобы в нём установилась температура воды, равная 50 °С? Потерями энергии на нагревание сосуда и окружающего воздуха пренебречь.
1) 1 кг 2) 1,8 кг 3) 2 кг 4) 3 кг
12. Задание 10 № 333. Какое количество теплоты выделится при кристаллизации воды массой 1 кг, взятой при температуре 10 °С?
1) 42 кДж 2) 330 кДж 3) 351 кДж 4) 372 кДж
13. Задание 10 № 360. Литровую кастрюлю, полностью заполненную водой, из комнаты вынесли на мороз. Зависимость температуры воды от времени представлена на рисунке. Какое количество теплоты выделилось при кристаллизации и охлаждении льда?
Примечание.
Удельную теплоту плавления льда считать равной
1) 414 кДж 2) 372 кДж 3) 246 кДж 4) 42 кДж
14. Задание 10 № 414. При охлаждении стальной детали массой 100 г до температуры 32 С° выделилось 5 кДж энергии. Температура стали до охлаждения составляла
Температура стали до охлаждения составляла
1) 168 °С 2) 132 °С 3) 100 °С 4) 68 °С
15. Задание 10 № 468. При нагревании куска металла массой 200 г от 20 °С до 60 °С его внутренняя энергия увеличилась на 2400 Дж. Удельная теплоёмкость металла составляет
1) 600 Дж/(кг·°С) 2) 300 Дж/(кг·°С) 3) 200 Дж/(кг·°С) 4)120 Дж/(кг·°С)
16. Задание 10 № 495. Какое количество теплоты потребуется, чтобы в алюминиевом чайнике массой 700 г вскипятить 2 кг воды? Первоначально чайник с водой имели температуру 20 °С.
Примечание.
Удельную теплоёмкость алюминия считать равной
1) 51,52 кДж 2) 336 кДж 3) 672 кДж 4) 723,52 кДж
17. Задание 10 № 522. Какой объём воды можно нагреть от 20 °С до кипения, сообщив ей 1,68 МДж теплоты?
Какой объём воды можно нагреть от 20 °С до кипения, сообщив ей 1,68 МДж теплоты?
1) 4 л 2) 5 л 3) 20 л 4) 50 л
18. Задание 10 № 549. Как изменится внутренняя энергия превращения 500 г льда, взятого при температуре 0 °С, в воду, имеющую температуру 20 °С? Потерями энергии на нагревание окружающего воздуха пренебречь.
1) уменьшится на 42 кДж 2) увеличится на 42 кДж
3) уменьшится на 207 кДж 4) увеличится на 207 кДж
19. Задание 10 № 576. На рисунке представлен график зависимости температуры от полученного количества теплоты для вещества массой 1 кг. Первоначально вещество находилось в твёрдом состоянии. Определите удельную теплоёмкость вещества в твёрдом состоянии.
1) 217 Дж/(кг·°С) 2) 250 Дж/(кг·°С) 3) 478 Дж/(кг·°С) 4) 550 Дж/(кг·°С)
20. Задание 10 № 603. Килограммовый кусок льда внесли с мороза в тёплое помещение. Зависимость температуры льда от времени представлена на рисунке. Какое количество теплоты было получено в интервале времени от 50 мин до 60 мин?
Задание 10 № 603. Килограммовый кусок льда внесли с мороза в тёплое помещение. Зависимость температуры льда от времени представлена на рисунке. Какое количество теплоты было получено в интервале времени от 50 мин до 60 мин?
1) 84 кДж 2) 42 кДж 3) 126 кДж 4) 330 кДж
21. Задание 10 № 630. На диаграмме для двух веществ приведены значения количества теплоты, необходимого для нагревания 1 кг вещества на 10 °С и для плавления 100 г вещества, нагретого до температуры плавления. Сравните удельную теплоту плавления (λ1 и λ2) двух веществ.
1) 2) 3) 4)
22. Задание 10 № 657. На рисунке представлен график зависимости температуры от времени для процесса нагревания слитка свинца массой 1 кг. Какое количество теплоты получил свинец за 10 мин нагревания?
Какое количество теплоты получил свинец за 10 мин нагревания?
Примечание.
Удельную теплоёмкость свинца считать равной
1) 26 кДж 2) 29,51 кДж 3) 39 кДж 4) 42,51 кДж
23. Задание 10 № 684. На рисунке представлен график зависимости температуры от полученного количества теплоты для вещества массой 2 кг. Первоначально вещество находилось в твёрдом состоянии. Определите удельную теплоту плавления вещества.
1) 25 кДж/кг 2) 50 кДж/кг 3) 64 кДж/кг 4) 128 кДж/кг
24. Задание 10 № 711. На рисунке представлен график зависимости температуры t от времени τ для куска льда массой 480 г, помещённого при температуре −20°С в калориметр. В тот же калориметр помещён нагреватель. Найдите, какую мощность развивал нагреватель при плавлении льда, считая эту мощность в течение всего процесса постоянной. Теплоёмкостью калориметра и нагревателя можно пренебречь.
Найдите, какую мощность развивал нагреватель при плавлении льда, считая эту мощность в течение всего процесса постоянной. Теплоёмкостью калориметра и нагревателя можно пренебречь.
1) 330 Вт 2) 330 кВт 3) 336 Вт 4) 19,8 кВт
25. Задание 10 № 738. Тонкостенный сосуд содержит смесь льда и воды, находящуюся при температуре 0 °С. Масса льда 350 г, а масса воды 550 г. Сосуд начинают нагревать на горелке мощностью 1,5 кВт. Сколько времени понадобится, чтобы довести содержимое сосуда до кипения? Потерями теплоты и удельной теплоёмкостью сосуда, а также испарением воды можно пренебречь.
1) ≈5,5 мин 2) 7,5 мин 3) 4,2 мин 4) 154 с
26. Задание 10 № 792. В тепловой машине потери энергии составляют от энергии, выделяющейся при сгорании топлива. КПД этой тепловой машины равен
КПД этой тепловой машины равен
1) 2) 3) 4)
27. Задание 10 № 819. КПД тепловой машины равен . Какая часть энергии, выделяющейся при сгорании топлива, не используется в этой тепловой машине для совершения полезной работы?
1) 2) 3) 4)
28. Задание 10 № 846. Двигатель трактора совершил полезную работу 23 МДж, израсходовав при этом 2 кг бензина. Найдите КПД двигателя трактора.
1) 10% 2) 25% 3) 50% 4) 100%
29. Задание 10 № 873. Теплоизолированный сосуд содержит смесь льда и воды, находящуюся при температуре 0 °С. Масса льда 40 г, а масса воды 600 г. В сосуд впускают водяной пар при температуре +100 °С. Найдите массу впущенного пара, если известно, что окончательная температура, установившаяся в сосуде, равна +20 ° С.
1) ≈0,4 г 2) ≈25,4 г 3) ≈41 г 4) ≈100 г
30. Задание 10 № 910. При нагревании и последующем плавлении кристаллического вещества массой 100 г измеряли его температуру и количество теплоты, сообщённое веществу. Данные измерений представлены в виде таблицы. Последнее измерение соответствует окончанию процесса плавления. Считая, что потерями энергии можно пренебречь, определите удельную теплоту плавления вещества.
1) 2) 3) 4)
31. Задание 10 № 971. В стакан массой 100 г, долго стоявший на столе в комнате, налили 200 г воды при комнатной температуре +20 °С и опустили в неё кипятильник мощностью 300 Вт. Через 4 минуты работы кипятильника вода в стакане закипела. Пренебрегая потерями теплоты в окружающую среду, найдите удельную теплоёмкость материала стакана.
1) 15 000 Дж/(кг · °С) 2) 8150 Дж/(кг · °С) 3) 600 Дж/(кг · °С) 4) –8150 Дж/(кг · °С)
32. Задание 10 № 998. В стакан массой 100 г, долго стоявший на улице, налили 200 г воды из лужи при температуре +10 °С и опустили в неё кипятильник. Через 5 минут работы кипятильника вода в стакане закипела. Пренебрегая потерями теплоты в окружающую среду, найдите мощность кипятильника. Удельная теплоёмкость материала стакана равна 600 Дж/(кг · °С).
1) 24 Вт 2) 270 Вт 3) 1 кВт 4) 24,12 кВт
33. Задание 10 № 1061. Пластилиновый шар упал без начальной скорости с высоты 5 м на каменный пол. Считая, что вся кинетическая энергия шара, приобретённая им за время свободного падения, превратилась во внутреннюю энергию пластилина, найдите, на сколько градусов нагрелся шар. Удельная теплоёмкость пластилина 2,5 кДж/(кг · °С).
Удельная теплоёмкость пластилина 2,5 кДж/(кг · °С).
1) 0,02 °С 2) 0,2 °С 3) 2,5 °С 4) 25 °С
34. Задание 10 № 1088. Свинцовый шар упал без начальной скорости с некоторой высоты на стальную плиту, в результате чего нагрелся на 0,3 °С. Считая, что вся кинетическая энергия шара, приобретённая им за время свободного падения, превратилась во внутреннюю энергию свинца, найдите, с какой высоты упал шар. Удельная теплоёмкость свинца 130 Дж/(кг · °С).
1) 0,1 м 2) 3,33 м 3) 3,9 м 4) 10 м
35. Задание 10 № 1145. Автомобиль УАЗ израсходовал 30 кг бензина за 2 ч. езды. Чему равна мощность двигателя автомобиля, если его КПД составляет 30%? (Удельная теплота сгорания бензина 4,6·107Дж/кг).
1) 57,5 кВт 2) 575 кВт 3) 1500 кВт 4) 6900 кВт
36. Задание 10 № 1172. Найдите массу бензина, израсходованную автомобилем УАЗ за 3 ч. езды, если мощность его двигателя равна 57,5 кВт, а его КПД 30%? (Удельная теплота сгорания бензина 4,6·107Дж/кг).
Задание 10 № 1172. Найдите массу бензина, израсходованную автомобилем УАЗ за 3 ч. езды, если мощность его двигателя равна 57,5 кВт, а его КПД 30%? (Удельная теплота сгорания бензина 4,6·107Дж/кг).
1) 0,045 кг 2) 13,5 кг 3) 45 кг 4) 72 кг
37. Задание 10 № 1199. В тонкостенный сосуд налили воду массой 1 кг, поставили его на электрическую плитку и начали нагревать. На рисунке представлен график зависимости температуры воды t°от времениτ. Найдите мощность плитки. Потерями теплоты и теплоёмкостью сосуда пренебречь.
1) 100 Вт 2) 700 Вт 3) 1 кВт 4) 30 кВт
38. Задание 10 № 1226. В тонкостенный сосуд налили воду, поставили его на электрическую плитку мощностью 800 Вт и начали нагревать. На рисунке представлен график зависимости температуры воды t от времени τ. Найдите массу налитой в сосуд воды. Потерями теплоты и теплоёмкостью сосуда пренебречь.
Найдите массу налитой в сосуд воды. Потерями теплоты и теплоёмкостью сосуда пренебречь.
1) 0,03 кг 2) 0,5 кг 3) 2 кг 4) 10 кг
39. Задание 10 № 1253. Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С? КПД спиртовки (с учётом потерь теплоты) равен 20%. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
1) 2,2 г 2) 33,6 г 3) 580 г 4) 1,344 г
40. Задание 10 № 1280. Сколько граммов воды можно нагреть на спиртовке на 30 °С, если сжечь в ней 21 грамм спирта? КПД спиртовки (с учётом потерь теплоты) равен 30%. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)).
1) 65 г 2) 990 г 3) 1450 г 4) 16,1 г
41. Задание 10 № 1316. 3 л воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
Задание 10 № 1316. 3 л воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
1) 1 кг 2) 3 кг 3) 4 кг 4) 6 кг
42. Задание 10 № 1380. Д ва однородных кубика привели в тепловой контакт друг с другом (см. рисунок). Первый кубик изготовлен из цинка, длина его ребра 2 см, а начальная температура t1= 1 °C. Второй кубик изготовлен из меди, длина его ребра 3 см, а начальная температура t2 = 74,2 °C. Пренебрегая теплообменом кубиков с окружающей средой, найдите температуру кубиков после установления теплового равновесия.
1) ≈ 20 °C 2) ≈ 44 °C 3) ≈ 60 °C 4) ≈ 71 °C
Примечание.
Плотности цинка и меди соответственно:
Удельные теплоёмкости цинка и меди соответственно:
43. Задание 10 № 1407. Два однородных кубика привели в тепловой контакт друг с другом (см. рисунок). Первый кубик изготовлен из меди, длина его ребра 3 см, а начальная температура t1 = 2 °C. Второй кубик изготовлен из алюминия, длина его ребра 4 см, а начальная температура t2 = 74 °C. Пренебрегая теплообменом кубиков с окружающей средой, найдите температуру кубиков после установления теплового равновесия.
1) ≈ 12 °C 2) ≈ 47 °C 3) ≈ 60 °C 4) ≈ 71 °C
Примечание.
Плотности алюминия и меди соответственно:
Удельные теплоёмкости алюминия и меди соответственно:
44. Задание 10 № 1456. Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре –10°С? Потерями энергии на нагревание окружающего воздуха пренебречь.
Задание 10 № 1456. Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре –10°С? Потерями энергии на нагревание окружающего воздуха пренебречь.
1) 10500 кДж 2) 175500 Дж 3) 165000 Дж 4) 10500 Дж
45. Задание 10 № 1511. Как изменится внутренняя энергия 500 г воды, взятой при 20°С, при её превращении в лёд при температуре 0 °С?
1) уменьшится на 42 кДж | 2) увеличится на 42 кДж |
3) уменьшится на 207 кДж | 4) увеличится на 207 кДж |
46. Задание 10 № 1538. Какое количество теплоты выделится при остывании и дальнейшей кристаллизации воды массой 10 кг, взятой при температуре 10 °С?
1) 420 кДж | 2) 3300 кДж | 3) 3510 кДж | 4) 3720 кДж |
47. Задание 10 № 1571. Двигатель трактора совершил полезную работу 23 МДж, израсходовав при этом 2 кг бензина. Найдите КПД двигателя трактора.
Задание 10 № 1571. Двигатель трактора совершил полезную работу 23 МДж, израсходовав при этом 2 кг бензина. Найдите КПД двигателя трактора.
1) 10% 2) 25% 3) 50% 4) 100%
48. Задание 10 № 1598. Какое количество теплоты выделится при кристаллизации 2 кг расплавленного олова, взятого при температуре кристаллизации, и последующем его охлаждении до 32°С?
1) 210 кДж 2) 156 кДж 3) 92 кДж 4) 14,72 кДж
49. Задание 10 № 1625. В сосуд с водой положили кусок льда. Каково отношение массы льда к массе воды, если весь лёд растаял и в сосуде установилась температура 0°С? Теплообменом с окружающим воздухом пренебречь. Начальные температуры воды и льда определите из графика зависимости температуры t от времени τ для воды и льда в процессе теплообмена.
1) 2,4 2) 1,42 3) 0,42 4) 0,3
50. Задание 10 № 1652. В сосуд с водой положили кусок льда. Каково отношение массы воды к массе льда, если весь лёд растаял и в сосуде установилась температура 0°С? Теплообменом с окружающим воздухом пренебречь. Начальную температуру воды и льда определите из графика зависимости t от времени τ для воды и льда в процессе теплообмена.
1) 2,38 2) 1,42 3) 0,42 4) 0,3
51. Задание 10 № 1689. 3 л воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
Задачи по физике. 9 класс
Соответствие формул и величин
1. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) удельная теплоёмкость вещества
Б) количество теплоты, необходимое для нагревания твёрдого вещества
| 1) 2) 3) 4) |
Ответ:
2. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) количество теплоты, необходимое для нагревания твёрдого вещества
Б) удельная теплота парообразования | 1) 2) 3) 4) |
Ответ:
3. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) удельная теплота плавления
Б) удельная теплоёмкость вещества | 1) 2) 3) 4) |
4. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) удельная теплоёмкость вещества
Б) удельная теплота сгорания топлива | 1) 2) 3) 4) |
5.
Два проводника, имеющие одинаковые сопротивления R1 = R2 = r, соединены параллельно. Установите соответствие между физическими величинами и формулами, по которым рассчитываются соответствующие величины. I1 и I2 — силы тока, U1 и U2 — напряжения на этих сопротивлениях.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) напряжение на участке цепи
Б) сила тока в общей цепи | 1) 2) 3) 4) |
Ответ:
6.
Два проводника, имеющие одинаковые сопротивления R1 = R2 = r, соединены параллельно. Установите соответствие между физическими величинами и формулами, по которым рассчитываются соответствующие величины. I1 и I2 — силы тока, U1 и U2 — напряжения на этих сопротивлениях.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) сила тока в общей цепи
Б) общее сопротивление участка цепи | 1) 2) 3) 4) |
7.
Два проводника, имеющие одинаковые сопротивления R1 = R2= r, включены последовательно. Установите соответствие между физическими величинами и формулами, по которым рассчитываются соответствующие величины при последовательном соединении проводников. I1 и I2 — силы тока, U1 и U2 — напряжения на этих сопротивлениях.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) напряжение на участке цепи
Б) сила тока в общей цепи | 1) 2) 3) 4) |
Ответ:
8.
Два проводника, имеющие одинаковые сопротивления R1 = R2= r, включены последовательно. Установите соответствие между физическими величинами и формулами, по которым рассчитываются соответствующие величины при последовательном соединении проводников. I1 и I2 — силы тока, U1 и U2 — напряжения на этих сопротивлениях.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) сила тока в общей цепи
Б) общее сопротивление участка цепи | 1) 2) 3) 4) |
Ответ:
9. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются.
Установите соответствие между физическими величинами и формулами, по которым эти величины определяются.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) работа тока
Б) сила тока | 1) 2) 3) 4) |
10. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) сила тока
Б) мощность тока | 1) 2) 3) 4) |
Ответ
11.
Сплошной кубик с ребром а полностью погружён в цилиндрический сосуд с жидкостью плотностью ρж так, как показано на рисунке. Рядом с сосудом установлена вертикальная линейка, позволяющая определить положение кубика в сосуде. Используя рисунок, установите соответствие между физическими величинами и формулами, по которым их можно рассчитать: к каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) давление жидкости на нижнюю грань кубика
Б) сила давления жидкости на верхнюю грань кубика | 1) 2) 3) 4) |
12.
Сплошной кубик с ребром а полностью погружён в цилиндрический сосуд с жидкостью плотностью ρ так, как показано на рисунке. Рядом с сосудом установлена вертикальная линейка, позволяющая определить положение кубика в сосуде. Используя рисунок, установите соответствие между физическими величинами и формулами, по которым их можно рассчитать: к каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) сила давления жидкости на верхнюю грань кубика
Б) сила Архимеда, действующая на кубик | 1) 2) 3) 4) |
Ответ:
13. Брусок массой покоится на плоскости, наклонённой под углом к горизонту. Коэффициент трения между бруском и плоскостью равен . Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
Брусок массой покоится на плоскости, наклонённой под углом к горизонту. Коэффициент трения между бруском и плоскостью равен . Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| ФОРМУЛЫ |
А) модуль силы нормальной реакции плоскости Б) модуль силы трения |
| 1) 2) 3) 4) |
Ответ:
14. Брусок массой покоится на плоскости, наклонённой под углом к горизонту. Коэффициент трения между бруском и плоскостью равен . Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| ФОРМУЛЫ |
А) модуль силы трения Б) модуль силы тяжести |
| 1) 2) 3) 4) |
Ответ
15. Брусок массой скользит по плоскости, наклонённой под углом к горизонту. Коэффициент трения между бруском и плоскостью равен . Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| ФОРМУЛЫ |
А) модуль силы трения Б) модуль силы тяжести |
| 1) 2) 3) 4) |
Ответ
16. Брусок массой скользит по плоскости, наклонённой под углом к горизонту. Коэффициент трения между бруском и плоскостью равен . Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
Коэффициент трения между бруском и плоскостью равен . Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| ФОРМУЛЫ |
А) модуль силы нормальной реакции плоскости Б) модуль силы трения |
| 1) 2) 3) 4) |
Ответ:
17. Установите соответствие между формулами для расчёта физических величин и названиями этих величин. В формулах использованы обозначения: m — масса тела; υ — скорость тела. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФОРМУЛЫ |
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
А) Б) |
| 1) работа силы 2) кинетическая энергия тела 3) давление твёрдого тела 4) модуль импульса тела |
Ответ:
18. Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| ФОРМУЛЫ |
А) сила электрического тока Б) электрическое напряжение |
| 1) 2) 3) 4) |
19. Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
| ФОРМУЛЫ |
А) электрическое напряжение Б) мощность электрического тока |
| 1) 2) 3) 4) |
20. Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами.
Установите соответствие между физическими величинами и формулами, по которым они определяются. Запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
А) мощность тока Б) электрическое сопротивление | 1) 2) 3) 4) |
21. Установите соответствие между формулами для расчёта физических величин и названиями этих величин. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФОРМУЛЫ |
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
А) Б) |
| 1) удельная теплота парообразования 2) количество теплоты, необходимое для нагревания твёрдого вещества 3) удельная теплота плавления 4) удельная теплоёмкость вещества |
Ответ:
22. Установите соответствие между формулами для расчёта физических величин и названиями этих величин. В формулах использованы обозначения: R — радиус окружности; T — период обращения. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Установите соответствие между формулами для расчёта физических величин и названиями этих величин. В формулах использованы обозначения: R — радиус окружности; T — период обращения. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФОРМУЛЫ |
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
А) Б) |
| 1) число оборотов за единицу времени 2) угловая скорость 3) линейная скорость 4) частота вращения |
Ответ:
23. Установите соответствие между формулами для расчёта физических величин и названиями этих величин. В формулах использованы обозначения: — единица времени; N — число оборотов. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФОРМУЛЫ |
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
А) Б) |
| 1) частота вращения 2) угловая скорость 3) период вращения 4) скорость вращения |
Ответ:
24. Установите соответствие между формулами для расчёта физических величин и названиями этих величин. В формулах использованы обозначения: m — масса грузика; k — жесткость пружины, l — длина нити, g — модуль свободного падения. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Установите соответствие между формулами для расчёта физических величин и названиями этих величин. В формулах использованы обозначения: m — масса грузика; k — жесткость пружины, l — длина нити, g — модуль свободного падения. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФОРМУЛЫ |
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
А) Б) |
| 1) период свободных гармонических колебаний математического маятника 2) циклическая частота свободных гармонических колебаний математического маятника 3) период свободных гармонических колебаний пружинного маятника 4) частота колебаний свободных гармонических колебаний пружинного маятника |
25. Установите соответствие между формулами для расчёта физических величин и названиями этих величин. В формулах использованы обозначения: — плотность; h — высота столба жидкости, V — объем тела, g — ускорение свободного падения. К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФОРМУЛЫ |
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
А) Б) |
| 1) плотность тела 2) гидростатическое давление жидкости 3) силы Архимеда 4) плотность молекул в некотором объеме |
Тепловые явления Часть 1
1. Внутренняя энергия тела зависит
1) только от температуры этого тела
2) только от массы этого тела
3) только от агрегатного состояния вещества
4) от температуры, массы тела и агрегатного состояния вещества
2. Примером явления, в котором механическая энергия превращается во внутреннюю, может служить
1) кипение воды на газовой конфорке
2) свечение нити накала электрической лампочки
3) нагревание металлической проволоки в пламени костра
4) затухание колебаний нитяного маятника в воздухе
3. При охлаждении столбика спирта в термометре
При охлаждении столбика спирта в термометре
1) увеличивается среднее расстояние между молекулами спирта
2) уменьшается объём каждой молекулы спирта
3) увеличивается объём каждой молекулы спирта
4) уменьшается среднее расстояние между молекулами спирта
4. При нагревании столбика спирта в термометре
1) уменьшается среднее расстояние между молекулами спирта
2) увеличивается среднее расстояние между молекулами спирта
3) увеличивается объём молекул спирта
4) уменьшается объём молекул спирта
5. Выберите из предложенных пар веществ ту, в которой скорость диффузии при одинаковой температуре будет наименьшая.
1) раствор медного купороса и вода
2) крупинка перманганата калия (марганцовки) и вода
3) пары эфира и воздух
4) свинцовая и медная пластины
6. При нагревании газа в герметично закрытом сосуде постоянного объёма
1) увеличивается среднее расстояние между молекулами
2) уменьшается средний модуль скорости движения молекул
3) уменьшается среднее расстояние между молекулами
4) увеличивается средний модуль скорости движения молекул
7. При охлаждении газа в герметично закрытом сосуде постоянного объёма
При охлаждении газа в герметично закрытом сосуде постоянного объёма
1) уменьшается среднее расстояние между молекулами
2) увеличивается среднее расстояние между молекулами
3) уменьшается средний модуль скорости движения молекул
4) увеличивается средний модуль скорости движения молекул
8. Какой(-ие) из видов теплопередачи осуществляется(-ются) без переноса вещества?
1) излучение и теплопроводность
2) излучение и конвекция
3) только теплопроводность
4) только конвекция
9. После того как пар, имеющий температуру 120 °С, впустили в воду при комнатной температуре, внутренняя энергия
1) и пара, и воды уменьшилась
2) и пара, и воды увеличилась
3) пара уменьшилась, а воды увеличилась
4) пара увеличилась, а воды уменьшилась
10. Какой вид теплопередачи происходит без переноса вещества?
А. Конвекция.
Б. Теплопроводность.
Правильным является ответ
1) и А, и Б
2) ни А, ни Б
3) только А
4) только Б
11. В отсутствии теплопередачи объем газа увеличился. При этом
В отсутствии теплопередачи объем газа увеличился. При этом
1) температура газа уменьшилась, а внутренняя энергия не изменилась
2) температура газа не изменилась, а внутренняя энергия увеличилась
3) температура и внутренняя энергия газа уменьшились
4) температура и внутренняя энергия газа увеличились
12. В каком агрегатном состоянии находится вещество, если оно имеет собственные форму и объем?
1) только в твердом
2) только в жидком
3) только в газообразном
4) в твердом или в жидком
13. При охлаждении газа в замкнутом сосуде
1) увеличивается средний модуль скорости движения молекул
2) уменьшается средний модуль скорости движения молекул
3) увеличивается среднее расстояние между молекулами
4) уменьшается среднее расстояние между молекулами
14. На рисунке представлен график зависимости температуры вещества t от полученного количества теплоты Q в процессе нагревания. Первоначально вещество находилось в твёрдом состоянии. Какому агрегатному состоянию соответствует точка А на графике?
Какому агрегатному состоянию соответствует точка А на графике?
1) твёрдому состоянию
2) жидкому состоянию
3) газообразному состоянию
4) частично твёрдому, частично жидкому состоянию
15. Четыре ложки изготовлены из разных материалов: алюминия, дерева, пластмассы и стекла. Наибольшей теплопроводностью обладает ложка, изготовленная из
1) алюминия
2) дерева
3) пластмассы
4) стекла
16. Выберите из предложенных пар веществ ту, в которой скорость диффузии при одинаковой температуре будет наибольшая.
1) раствор медного купороса и вода
2) крупинка перманганата калия (марганцовки) и вода
3) пары эфира и воздух
4) свинцовая и медная пластины
17. При охлаждении газа в замкнутом сосуде
1) увеличивается средний модуль скорости движения молекул
2) уменьшается средний модуль скорости движения молекул
3) увеличивается среднее расстояние между молекулами
4) уменьшается среднее расстояние между молекулами
18. На рисунке приведён график зависимости температуры воды от времени. Какой(-ие) из участков графика относится(-ятся) к процессу охлаждения воды?
На рисунке приведён график зависимости температуры воды от времени. Какой(-ие) из участков графика относится(-ятся) к процессу охлаждения воды?
1) только ЕЖ
2) только ГД
3) ГД и ЕЖ
4) ГД, ДЕ и ЕЖ
19. Какой вид теплопередачи происходит без переноса вещества?
А. Излучение.
Б. Конвекция.
Правильным является ответ
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
20. Вещество в газообразном состоянии
1) имеет собственную форму и собственный объём
2) имеет собственный объём, но не имеет собственной формы
3) не имеет ни собственной формы, ни собственного объёма
4) имеет собственную форму, но не имеет собственного объёма
21. При охлаждении столбика спирта в термометре
1) уменьшается объём молекул спирта
2) увеличивается объём молекул спирта
3) уменьшается среднее расстояние между молекулами спирта
4) увеличивается среднее расстояние между молекулами спирта
22. После того как горячую деталь опустят в холодную воду, внутренняя энергия
После того как горячую деталь опустят в холодную воду, внутренняя энергия
1) и детали, и воды будет увеличиваться
2) и детали, и воды будет уменьшаться
3) детали будет уменьшаться, а воды — увеличиваться
4) детали будет увеличиваться, а воды — уменьшаться
23. Турист разжёг костёр на привале в безветренную погоду. Находясь на некотором расстоянии от костра, турист ощущает тепло. Каким способом в основном происходит процесс передачи теплоты от костра к туристу?
1) путём теплопроводности
2) путём конвекции
3) путём излучения
4) путём теплопроводности и конвекции
24. Какие изменения энергии происходят в куске льда при его таянии?
1) увеличивается кинетическая энергия куска льда
2) уменьшается внутренняя энергия куска льда
3) увеличивается внутренняя энергия куска льда
4) увеличивается внутренняя энергия воды, из которой состоит кусок льда
25. На рисунке изображён график зависимости температуры t двух килограммов некоторой жидкости от сообщаемого ей количества теплоты Q.
Чему равна удельная теплоёмкость этой жидкости?
1) 1600 Дж/(кг · °С)
2) 3200 Дж/(кг · °С)
3) 1562,5 Дж/(кг · °С)
4) 800 Дж/(кг · °С)
26. На рисунке изображён график зависимости температуры t четырёх килограммов некоторой жидкости от сообщаемого ей количества теплоты Q.
Чему равна удельная теплоёмкость этой жидкости?
1) 1600 Дж/(кг · °С)
2) 3200 Дж/(кг · °С)
3) 1562,5 Дж/(кг · °С)
4) 800 Дж/(кг · °С)
27. Лёд начали нагревать, в результате чего он перешёл в жидкое состояние. Молекулы воды в жидком состоянии
1) находятся в среднем ближе друг к другу, чем в твёрдом состоянии
2) находятся в среднем на тех же расстояниях друг от друга, что и в твёрдом состоянии
3) находятся в среднем дальше друг от друга, чем в твёрдом состоянии
4) могут находиться как ближе друг к другу, так и дальше друг от друга, по сравнению с твёрдым состоянием
28. Алюминиевую и стальную ложки одинаковой массы, находящиеся при комнатной температуре, опустили в большой бак с кипятком. После установления теплового равновесия количество теплоты, полученное стальной ложкой от воды,
После установления теплового равновесия количество теплоты, полученное стальной ложкой от воды,
1) меньше количества теплоты, полученного алюминиевой ложкой
2) больше количества теплоты, полученного алюминиевой ложкой
3) равно количеству теплоты, полученному алюминиевой ложкой
4) может быть как больше, так и меньше количества теплоты, полученного алюминиевой ложкой
29. Открытый сосуд заполнен водой. На каком рисунке правильно изображено направление конвекционных потоков при приведённой схеме нагревания?
1) 2) 3) 4)
30. В одинаковые сосуды с равными массами воды при одинаковой температуре погрузили латунный и свинцовый шары с равными массами и одинаковыми температурами, более высокими, чем температура воды. Известно, что после установления теплового равновесия температура воды в сосуде с латунным шаром повысилась больше, чем в сосуде со свинцовым шаром. У какого металла — латуни или свинца — удельная теплоёмкость больше? Какой из шаров передал воде и сосуду большее количество теплоты?
1) удельная теплоёмкость латуни больше, латунный шар передал воде и сосуду большее количество теплоты
2) удельная теплоёмкость латуни больше, латунный шар передал воде и сосуду меньшее количество теплоты
3) удельная теплоёмкость свинца больше, свинцовый шар передал воде и сосуду большее количество теплоты
4) удельная теплоёмкость свинца больше, свинцовый шар передал воде и сосуду меньшее количество теплоты
31. В одинаковые сосуды с равными массами воды при одинаковой температуре погрузили медный и никелевый шары с равными массами и одинаковыми температурами, более высокими, чем температура воды. Известно, что после установления теплового равновесия температура воды в сосуде с никелевым шаром повысилась больше, чем в сосуде с медным шаром. У какого металла — меди или никеля — удельная теплоёмкость больше? Какой из шаров передал воде и сосуду большее количество теплоты?
В одинаковые сосуды с равными массами воды при одинаковой температуре погрузили медный и никелевый шары с равными массами и одинаковыми температурами, более высокими, чем температура воды. Известно, что после установления теплового равновесия температура воды в сосуде с никелевым шаром повысилась больше, чем в сосуде с медным шаром. У какого металла — меди или никеля — удельная теплоёмкость больше? Какой из шаров передал воде и сосуду большее количество теплоты?
1) удельная теплоёмкость меди больше, медный шар передал воде и сосуду большее количество теплоты
2) удельная теплоёмкость меди больше, медный шар передал воде и сосуду меньшее количество теплоты
3) удельная теплоёмкость никеля больше, никелевый шар передал воде и сосуду большее количество теплоты
4) удельная теплоёмкость никеля больше, никелевый шар передал воде и сосуду меньшее количество теплоты
32. Два одинаковых термометра поместили в футляры, сделанные из одинакового материала и имеющие одинаковые размеры. Один из футляров снаружи был выкрашен белой краской, второй — чёрной краской. Оба футляра выставили под прямые солнечные лучи. Термометр, находящийся в белом футляре, покажет
Два одинаковых термометра поместили в футляры, сделанные из одинакового материала и имеющие одинаковые размеры. Один из футляров снаружи был выкрашен белой краской, второй — чёрной краской. Оба футляра выставили под прямые солнечные лучи. Термометр, находящийся в белом футляре, покажет
1) более высокую температуру, чем термометр в чёрном футляре
2) такую же температуру, как и термометр в чёрном футляре
3) более низкую температуру, чем термометр в чёрном футляре
4) температуру воздуха снаружи, а термометр, находящийся в чёрном футляре, покажет температуру воздуха внутри футляра
33. Две коробочки одинаковых размеров сделаны из разных материалов: первая — из пористого материала (пенопласта), а вторая — из плотного материла (жести). В каждую из коробочек поместили по одинаковому термометру, показывающему комнатную температуру, после чего обе коробочки вынесли на улицу на сильный мороз. Через несколько минут пребывания коробочек на улице проверили показания обоих термометров. Температура, которую будет показывать термометр из первой коробочки,
Через несколько минут пребывания коробочек на улице проверили показания обоих термометров. Температура, которую будет показывать термометр из первой коробочки,
1) выше температуры, которую будет показывать термометр из второй коробочки
2) такая же, какую будет показывать термометр из второй коробочки
3) ниже температуры, которую будет показывать термометр из второй коробочки
4) равна комнатной температуре, а температура, которую будет показывать термометр из второй коробочки, равна температуре воздуха на улице
34. Колбу с воздухом, закрытую пробкой и находящуюся длительное время в комнате при температуре +20 °С, целиком погрузили в большую ванну с водой. Температура воды в ванне была равна 0 °С. В результате установления теплового равновесия внутренняя энергия воздуха в колбе
1) увеличится
2) не изменится
3) уменьшится
4) станет равной нулю
35. Колбу с воздухом, закрытую пробкой и находящуюся длительное время в комнате при температуре +20 °С, целиком погрузили в большую ванну с водой. Температура воды в ванне была равна +50 °С. В результате установления теплового равновесия внутренняя энергия воздуха в колбе
Колбу с воздухом, закрытую пробкой и находящуюся длительное время в комнате при температуре +20 °С, целиком погрузили в большую ванну с водой. Температура воды в ванне была равна +50 °С. В результате установления теплового равновесия внутренняя энергия воздуха в колбе
1) увеличится
2) не изменится
3) уменьшится
4) станет равной нулю
36. Стакан воды нагрели от 20 °С до 50 °С. При этом
1) увеличилась внутренняя энергия воды
2) увеличилась кинетическая энергия воды
3) увеличилась потенциальная энергия воды
4) энергия воды не изменилась
37. При резком сжатии воздуха его внутренняя энергия
1) уменьшается
2) увеличивается
3) не изменяется
4) может как увеличиваться, так и уменьшаться — в зависимости от быстроты сжатия
38. Из холодильника вынули закрытую крышкой кастрюлю с водой, имеющую температуру +5 °С. Чтобы подогреть воду, кастрюлю с водой можно:
Чтобы подогреть воду, кастрюлю с водой можно:
А. поставить на газовую горелку; Б. освещать сверху мощной электрической лампой.
В каких из вышеперечисленных случаев вода в кастрюле нагревается в основном путём конвекции?
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
39. Из холодильника вынули закрытую крышкой кастрюлю с водой, имеющую температуру +5 °С. Чтобы подогреть воду, кастрюлю с водой можно:
А. поставить на газовую горелку;
Б. освещать сверху мощной электрической лампой.
В каких из вышеперечисленных случаев вода в кастрюле нагревается в основном путём излучения?
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
40. При охлаждении столбика спирта в термометре
1) увеличивается среднее расстояние между молекулами спирта
2) уменьшается объём каждой молекулы спирта
3) увеличивается объём каждой молекулы спирта
4) уменьшается среднее расстояние между молекулами спирта
41.
На горлышко стеклянной бутылки натянули пустой воздушный шарик, после чего поместили бутылку в тазик с горячей водой. Шарик надулся (см. рисунок). Почему это произошло?
1) Оболочка шарика нагрелась от бутылки посредством теплопроводности и расширилась.
2) При нагревании бутылки воздух в ней также нагрелся, расширился, проник в шарик и надул его.
3) В шарик проникли пары горячей воды, которые расширились и надули его.
4) Давление атмосферного воздуха над тазиком с горячей водой уменьшилось, и это вызвало раздувание шарика.
42.
В стеклянную бутылку налили горячую воду. Через несколько минут эту воду вылили, а на горлышко бутылки натянули пустой воздушный шарик, после чего поместили бутылку под струю холодной воды. Шарик втянулся внутрь бутылки (см. рисунок). Почему это произошло?
1) При охлаждении бутылки холодной водой над ней повысилось атмосферное давление.
2) Оболочка шарика охладилась от бутылки посредством теплопроводности и сжалась.
3) Тёплый воздух, который вначале был в бутылке, при охлаждении сжался, его давление упало, и наружное атмосферное давление протолкнуло воздушный шарик в бутылку.
4) При охлаждении нагретых стенок бутылки они электризуются и притягивают к себе воздушный шарик.
43. В таблице приведены значения коэффициента, который характеризует скорость процесса теплопроводности вещества для некоторых строительных материалов.
Строительный материал | Коэффициент теплопроводности (условные единицы) |
Газобетон | 0,12 |
Железобетон | 1,69 |
Силикатный кирпич | 0,70 |
Дерево | 0,09 |
В условиях холодной зимы наименьшего дополнительного утепления при равной толщине стен требует дом из
1) силикатного кирпича
2) газобетона
3) железобетона
4) дерева
44. Один стакан с водой стоит на столе в комнате, а другой стакан с водой такой же массы и такой же температуры находится на полке, висящей на высоте 80 см относительно стола. Внутренняя энергия воды в стакане на столе
Один стакан с водой стоит на столе в комнате, а другой стакан с водой такой же массы и такой же температуры находится на полке, висящей на высоте 80 см относительно стола. Внутренняя энергия воды в стакане на столе
1) равна нулю
2) меньше внутренней энергии воды на полке
3) больше внутренней энергии воды на полке
4) равна внутренней энергии воды на полке
45.
На рисунке изображён график зависимости давления p от объёма V при переходе газа в отсутствие теплопередачи из состояния 1 в состояние 2. При указанном процессе внутренняя энергия газа
1) не изменяется
2) может увеличиться или уменьшиться
3) обязательно уменьшается
4) обязательно увеличивается
46.
На рисунке изображён график зависимости давления p от объёма V при переходе газа в отсутствие теплопередачи из состояния 1 в состояние 2. При указанном процессе внутренняя энергия газа
1) не изменяется
2) может увеличиться или уменьшиться
3) обязательно уменьшается
4) обязательно увеличивается
47. Утром жаркого дня ветер дует с суши на море. Это объясняется тем, что
Утром жаркого дня ветер дует с суши на море. Это объясняется тем, что
1) удельная теплоемкость воды больше, чем удельная теплоемкость суши
2) удельная теплоемкость воды меньше, чем удельная теплоемкость суши
3) теплопроводность воды больше, чем теплопроводность суши
4) теплопроводность воды меньше, чем теплопроводность суши
48. Мальчик поднес снизу руку к «подошве» нагретого утюга, не касаясь ее, и ощутил идущий от утюга жар. Каким способом, в основном, происходит процесс передачи теплоты от утюга к руке
1) путем теплопроводности
2) путем конвекции
3) путем излучения
4) путем теплопроводности и конвекции
49. В сосуд аккуратно налили, не перемешивая, медный купорос и воду. Сначала сосуд поместили в холодильник, а затем переставили в тёплую комнату. Что произойдёт со скоростью диффузии?
1) увеличится
2) уменьшится
3) не изменится
4) ответ зависит от атмосферного давления
50. Температуру жидкостей, в которых происходит диффузия, повысили. Как изменилась при этом скорость диффузии?
Температуру жидкостей, в которых происходит диффузия, повысили. Как изменилась при этом скорость диффузии?
1) не изменилась
2) увеличилась
3) уменьшилась
4) ответ зависит от плотности жидкостей
Тепловые явления. Часть 2
1. В процессе кипения жидкости, предварительно нагретой до температуры кипения, сообщаемая ей энергия идёт
1) на увеличение средней скорости движения молекул
2) на увеличение средней скорости движения молекул и на преодоление сил взаимодействия между молекулами
3) на преодоление сил взаимодействия между молекулами без увеличения средней скорости их движения
4) на увеличение средней скорости движения молекул и на увеличение сил взаимодействия между молекулами
2. Открытый сосуд с водой находится в лаборатории, в которой поддерживается определённая температура и влажность воздуха. Скорость испарения будет равна скорости конденсации воды в сосуде
1) только при условии, что температура в лаборатории больше 25 °С
2) только при условии, что влажность воздуха в лаборатории равна 100%
3) только при условии, что температура в лаборатории меньше 25 °С, а влажность воздуха меньше 100%
4) при любой температуре и влажности в лаборатории
3. Удельная теплоёмкость стали равна 500 Дж/кг·°С. Что это означает?
Удельная теплоёмкость стали равна 500 Дж/кг·°С. Что это означает?
1) для нагревания 1 кг стали на 1 °С необходимо затратить энергию 500 Дж
2) для нагревания 500 кг стали на 1 °С необходимо затратить энергию 1 Дж
3) для нагревания 1 кг стали на 500 °С необходимо затратить энергию 1 Дж
4) для нагревания 500 кг стали на 1 °С необходимо затратить энергию 500 Дж
4. Удельная теплоёмкость стали равна 500 Дж/кг·°С. Что это означает?
1) при охлаждении 1 кг стали на 1 °С выделяется энергия 500 Дж
2) при охлаждении 500 кг стали на 1 °С выделяется энергия 1 Дж
3) при охлаждении 1 кг стали на 500 °С выделяется энергия 1 Дж
4) при охлаждении 500 кг стали на 1 °С выделяется энергия 500 Дж
5.
На рисунке представлен график зависимости температуры от времени для процесса нагревания воды при нормальном атмосферном давлении. Первоначально вода находилась в твёрдом состоянии.
Какое из утверждений является неверным?
1) Участок DE соответствует процессу кипения воды.
2) Точка С соответствует жидкому состоянию воды.
3) В процессе АВ внутренняя энергия льда не изменяется.
4) В процессе ВС внутренняя энергия системы лёд-вода увеличивается.
6. КПД тепловой машины равен 30%. Это означает, что при выделении энергии Q при сгорании топлива, на совершение полезной работы затрачивается энергия, равная
1) 1,3Q 2) 0,7Q 3) 0,4Q 4) 0,3Q
7.
На рисунке приведён график зависимости температуры t воды от времени τ при нормальном атмосферном давлении. Какое из утверждений является неверным?
1) Участок АБ соответствует процессу нагревания воды.
2) В процессе, соответствующем участку ЕЖ, внутренняя энергия воды уменьшается.
3) Точка Е соответствует твёрдому состоянию воды.
4) В процессе, соответствующем участку БВ, внутренняя энергия системы вода — пар увеличивается.
8.
На рисунке представлен график зависимости температуры от времени для процесса нагревания слитка свинца массой 1 кг. Какое количество теплоты получил свинец за 10 мин нагревания?
Какое количество теплоты получил свинец за 10 мин нагревания?
Примечание.
Удельную теплоёмкость свинца считать равной
1) 1300 Дж
2) 26000 Дж
3) 29510 Дж
4) 78000 Дж
9.
На рисунке приведен график зависимости температуры воды от времени. Начальная температура воды 50 °С. В каком состоянии находится вода в момент времени τ1?
1) только в газообразном
2) только в жидком
3) часть воды — в жидком состоянии и часть воды — в газообразном
4) часть воды — в жидком состоянии и часть воды — в кристаллическом
10. На диаграмме для двух веществ приведены значения количества теплоты, необходимого для нагревания 1 кг вещества на 10 °С и для плавления 100 г вещества, нагретого до температуры плавления. Сравните удельные теплоемкости c двух веществ.
1)
2)
3)
4)
11.
На диаграмме для двух веществ одинаковой массы приведены значения количества теплоты, необходимого для их нагревания на одно и то же число градусов. Сравните удельную теплоемкость c1 и c2 этих веществ.
Сравните удельную теплоемкость c1 и c2 этих веществ.
1)
2)
3)
4)
12.
На рисунке приведен график зависимости температуры спирта от времени при его охлаждении и последующем нагревании. Первоначально спирт находился в газообразном состоянии. Какой участок графика соответствует процессу конденсации спирта?
1) АВ 2) ВС 3) CD 4) DE
13. При опускании в стакан с горячей водой деревянной и алюминиевой ложек
1) алюминиевая ложка нагревается быстрее, так как плотность алюминия больше
2) алюминиевая ложка нагревается быстрее, так как теплопроводность алюминия выше
3) деревянная ложка нагревается быстрее, так как плотность дерева меньше
4) деревянная ложка нагревается быстрее, так как теплопроводность дерева ниже
14. Два шара одинаковой массы, изготовленные соответственно из меди и алюминия, были нагреты на 50 °С. При этом на нагревание медного шара потребовалось
1) больше энергии, так как плотность меди больше
2) больше энергии, так как удельная теплоёмкость меди больше
3) меньше энергии, так как плотность меди меньше
4) меньше энергии, так как удельная теплоёмкость меди меньше
15. Два шара одинакового объёма, изготовленные соответственно из цинка и меди, были нагреты на 50 °С. При этом на нагревание медного шара потребовалось
Два шара одинакового объёма, изготовленные соответственно из цинка и меди, были нагреты на 50 °С. При этом на нагревание медного шара потребовалось
1) больше энергии, так как масса медного шара больше
2) больше энергии, так как удельная теплоёмкость меди больше
3) меньше энергии, так как масса медного шара меньше
4) меньше энергии, так как удельная теплоёмкость меди меньше
16. Удельная теплота плавления стали равна 78 кДж/кг. Это означает, что
1) для плавления 1 кг стали при температуре её плавления потребуется 78 кДж энергии
2) для плавления 78 кг стали при температуре её плавления потребуется 1 кДж энергии
3) для плавления 1 кг стали при комнатной температуре потребуется 78 кДж энергии
4) для плавления 78 кг стали при комнатной температуре потребуется 1 кДж энергии
17. Какие из утверждений верны?
А. Диффузию нельзя наблюдать в твёрдых телах.
Б. Скорость диффузии не зависит от температуры вещества.
1) только А
2) только Б
3) оба утверждения верны
4) оба утверждения неверны
18. Мяч массой m бросают вертикально вверх со скоростью v с поверхности земли. Внутренняя энергия мяча зависит
1) только от массы мяча
2) только от скорости бросания
3) от массы мяча и скорости бросания
4) от массы и температуры мяча
19. Мяч массой m поднят на высоту h относительно поверхности земли. Внутренняя энергия мяча зависит
1) только от массы мяча
2) только от высоты подъёма
3) от массы мяча и высоты подъёма
4) от массы и температуры мяча
20. Удельная теплоёмкость свинца равна 130 Дж/(кг·°С). Это означает, что
1) при охлаждении 1 кг свинца на 130 °С выделяется 1 Дж энергии
2) при охлаждении 1 кг свинца на 1 °С выделяется 130 Дж энергии
3) при охлаждении 130 кг свинца на 1 °С выделяется 1 Дж энергии
4) при охлаждении 130 кг свинца на 130 °С выделяется 1 Дж энергии
21. Один стакан с водой стоит на столе в тёплом помещении, другой с водой такой же массы — в холодильнике. Внутренняя энергия воды в стакане, стоящем в холодильнике,
Один стакан с водой стоит на столе в тёплом помещении, другой с водой такой же массы — в холодильнике. Внутренняя энергия воды в стакане, стоящем в холодильнике,
1) равна внутренней энергии воды в стакане, стоящем на столе
2) больше внутренней энергии воды в стакане, стоящем на столе
3) меньше внутренней энергии воды в стакане, стоящем на столе
4) равна нулю
22. Примером броуновского движения является
1) беспорядочное движение цветочной пыльцы в капельке воды
2) беспорядочное движение мошек под фонарём
3) растворение твёрдых веществ в жидкостях
4) проникновение питательных веществ из почвы в корни растений
23. На рисунке представлены графики зависимости температуры t от времени τ для трёх твёрдых тел одинаковой массы: из алюминия, из меди и из свинца. Тела нагревают на одинаковых горелках. Определите, какой график соответствует нагреванию тела из алюминия, какой — из меди, а какой — из свинца.
1) 1 — медь, 2 — алюминий, 3 — свинец
2) 1 — алюминий, 2 — свинец, 3 — медь
3) 1 — медь, 2 — свинец, 3 — алюминий
4) 1 — алюминий, 2 — медь, 3 — свинец
24.
На рисунке представлены графики нагревания и плавления двух твёрдых веществ — «1» и «2» — одинаковой массы, взятых при одинаковой начальной температуре. Образцы нагреваются на одинаковых горелках. Сравните удельные теплоёмкости этих двух веществ и температуры их плавления
1) У вещества «1» больше удельная теплоёмкость и температура плавления, чем у вещества «2».
2) У вещества «1» меньше удельная теплоёмкость, но выше температура плавления, чем у вещества «2».
3) У вещества «1» больше удельная теплоёмкость, но ниже температура плавления, чем у вещества «2».
4) У вещества «1» такая же удельная теплоёмкость, как у вещества «2», но выше температура плавления.
25. Три цилиндра одинаковых высоты и радиуса, сделанные из алюминия, цинка и меди, нагрели до одинаковой температуры и поставили торцами на горизонтальную поверхность льда, имеющую температуру 0 °С. Когда установилось тепловое равновесие, цилиндры проплавили во льду цилиндрические углубления. Считая, что вся теплота, отводимая от цилиндров при их остывании, передавалась льду, определите, под каким из цилиндров углубление получилось больше.
Считая, что вся теплота, отводимая от цилиндров при их остывании, передавалась льду, определите, под каким из цилиндров углубление получилось больше.
1) под цинковым
2) под алюминиевым
3) под медным
4) под всеми тремя цилиндрами углубления получились одинаковыми
26. Три цилиндра одинаковых высоты и радиуса, сделанные из алюминия, цинка и меди, нагрели до одинаковой температуры и поставили торцами на горизонтальную поверхность льда, имеющую температуру 0 °С. Когда установилось тепловое равновесие, цилиндры проплавили во льду цилиндрические углубления. Считая, что вся теплота, отводимая от цилиндров при их остывании, передавалась льду, определите, под каким из цилиндров углубление получилось меньше.
1) под цинковым
2) под алюминиевым
3) под медным
4) под всеми тремя цилиндрами углубления получились одинаковыми
27.
На рисунке представлены графики нагревания и плавления двух твёрдых веществ одинаковой массы — 1 и 2. Вещества нагреваются на одинаковых горелках при одинаковых условиях. Определите по графикам, у какого вещества — 1 или 2 — выше температура плавления и удельная теплота плавления
Вещества нагреваются на одинаковых горелках при одинаковых условиях. Определите по графикам, у какого вещества — 1 или 2 — выше температура плавления и удельная теплота плавления
1) у вещества 1 выше и температура плавления, и удельная теплота плавления
2) у вещества 1 выше температура плавления, а у вещества 2 выше удельная теплота плавления
3) у вещества 2 выше температура плавления, а у вещества 1 выше удельная теплота плавления
4) у вещества 2 выше и температура плавления, и удельная теплота плавления
28.
На рисунке представлены графики нагревания трёх образцов (А, Б и В), состоящих из одного и того же твёрдого вещества. Масса образца А в четыре раза больше массы образца Б, а масса образца Б в два раза меньше массы образца В. Образцы нагреваются на одинаковых горелках. Определите, какой из графиков соответствует образцу А, какой — образцу Б, а какой — образцу В.
1) график 1 — А, график 2 — Б, график 3 — В
2) график 1 — А, график 2 — В, график 3 — Б
3) график 1 — В, график 2 — Б, график 3 — А
4) график 1 — Б, график 2 — В, график 3 — А
29. Для определения удельной теплоты сгорания топлива необходимо знать
Для определения удельной теплоты сгорания топлива необходимо знать
1) энергию, выделившуюся при полном сгорании топлива, его объём и начальную температуру
2) энергию, выделившуюся при полном сгорании топлива, и его массу
3) энергию, выделившуюся при полном сгорании топлива, и его плотность
4) удельную теплоёмкость вещества, его массу, начальную и конечную температуры
30. Какое(-ие) из нижеприведённых утверждений являе(-ю)тся правильным(-и)?
А. Вещество состоит из мельчайших частиц — атомов или молекул, и доказательством этому служит явление теплопроводности.
Б. Вещество состоит из мельчайших частиц — атомов или молекул, и одним из аргументов в пользу этого служит явление диффузии.
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
31. Какое(-ие) из нижеприведённых утверждений являе(-ю)тся правильным(-и)?
А. Молекулы или атомы в веществе находятся в непрерывном тепловом движении, и одним из аргументов в пользу этого служит явление диффузии.
Б. Молекулы или атомы в веществе находятся в непрерывном тепловом движении, и доказательством этому служит явление конвекции.
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
32.
Из трёх разных холодильников принесли три твёрдых тела (пронумеруем их 1, 2 и 3) одинаковой массы и начали нагревать их на одинаковых горелках. На рисунке приведена зависимость температуры t этих трёх тел от времени τ при передаче им теплоты от горелок (получаемая телами от горелок мощность постоянна). Удельные теплоёмкости c материалов, из которых изготовлены тела, соотносятся как
1) с1 > с2 > с3
2) с1 < с2 < с3
3) с2 > с1 > с3
4) с1 = с2 = с3
33.
Одинаковую жидкость разлили в три сосуда, причём в первый сосуд налили жидкость массой m, во второй сосуд — массой 2m, а в третий сосуд — массой 3m, после чего начали нагревать каждый сосуд на отдельной горелке. Все горелки одинаковые, выделяемая ими теплота полностью передаётся жидкостям. На рисунке показана зависимость температуры t жидкостей в трёх сосудах от времени τ при передаче им теплоты от горелок (мощность горелок постоянна). Укажите, какой график соответствует сосуду с жидкостью массой m, какой — сосуду с жидкостью массой 2m, какой — сосуду с жидкостью с массой 3m. Теплоёмкостью сосудов можно пренебречь.
Все горелки одинаковые, выделяемая ими теплота полностью передаётся жидкостям. На рисунке показана зависимость температуры t жидкостей в трёх сосудах от времени τ при передаче им теплоты от горелок (мощность горелок постоянна). Укажите, какой график соответствует сосуду с жидкостью массой m, какой — сосуду с жидкостью массой 2m, какой — сосуду с жидкостью с массой 3m. Теплоёмкостью сосудов можно пренебречь.
1) 1 — 3m, 2 — 2m, 3 — m
2) 1 — 3m, 2 — m, 3 — 2m
3) 1 — 2m, 2 — m, 3 — 3m
4) 1 — m, 2 — 2m, 3 — 3m
34.
На рисунке приведена зависимость температуры T некоторого вещества массой m от времени t. Вещество в единицу времени получает постоянное количество теплоты. В момент времени t = 0 вещество находилось в твёрдом состоянии. В течение какого интервала времени происходило плавление этого вещества?
1) от 0 до t1
2) от t1 до t2
3) от t2 до t3
4) от t3 до t4
35.
На рисунке приведена зависимость температуры T некоторого вещества массой m от времени t. Вещество в единицу времени получает постоянное количество теплоты. В момент времени t = 0 вещество находилось в твёрдом состоянии. В течение какого интервала времени происходило нагревание этого вещества в жидком состоянии?
1) от 0 до t1
2) от t1 до t2
3) от t2 до t3
4) от t3 до t4
36.
В алюминиевой кастрюле, поставленной на электрическую плитку, нагревается вода. На рисунке представлены графики зависимости количества полученной теплоты Q от времени t для кастрюли (график 1) и для воды (график 2). Потери теплоты в окружающую среду пренебрежимо малы. Масса воды
1) больше массы кастрюли
2) меньше массы кастрюли
3) равна массе кастрюли
4) может быть как больше, так и меньше массы кастрюли
37.
В стальной кастрюле, поставленной на электрическую плитку, нагревается вода. На рисунке представлены графики зависимости количества полученной теплоты Q от времени t для кастрюли (график 1) и для воды (график 2). Потери теплоты в окружающую среду пренебрежимо малы. Масса кастрюли
На рисунке представлены графики зависимости количества полученной теплоты Q от времени t для кастрюли (график 1) и для воды (график 2). Потери теплоты в окружающую среду пренебрежимо малы. Масса кастрюли
1) больше массы воды
2) меньше массы воды
3) равна массе воды
4) может быть как больше, так и меньше массы воды
38.
На рисунке представлены графики 1, 2 и 3 зависимостей температуры t трёх медных образцов от количества сообщённой им теплоты Q. Известно, что массы образцов равны 100 г, 200 г, 300 г, соответственно. Укажите, какая масса образца соответствует каждому графику.
1) 1 — 300 г 2 — 200 г 3 — 100 г
2) 1 — 100 г 2 — 200 г 3 — 300 г
3) 1 — 200 г 2 — 100 г 3 — 300 г
4) 1 — 100 г 2 — 300 г 3 — 200 г
39.
На рисунке представлены графики 1, 2 и 3 зависимостей температуры t трёх алюминиевых образцов от количества сообщённой им теплоты Q. Известно, что массы образцов равны 10 г, 20 г, 30 г, соответственно. Укажите, какая масса образца соответствует каждому графику.
Известно, что массы образцов равны 10 г, 20 г, 30 г, соответственно. Укажите, какая масса образца соответствует каждому графику.
1) 1 — 10 г 2 — 20 г 3 — 30 г
2) 1 — 30 г 2 — 20 г 3 — 10 г
3) 1 — 20 г 2 — 30 г 3 — 10 г
4) 1 — 10 г 2 — 30 г 3 — 20 г
40. Испарение и кипение — два процесса перехода вещества из одного агрегатного состояния в другое. Общей характеристикой этих процессов является то, что они
А. представляют собой процесс перехода вещества из жидкого состояния в газообразное.
Б. происходят при определённой температуре.
Правильным(-и) является(-ются) утверждение(-я)
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
41. Ведущий телепрограммы, рассказывающий о погоде, сообщил, что в настоящее время относительная влажность воздуха составляет 50%. Это означает, что
1) Концентрация водяных паров, содержащихся в воздухе, в 2 раза меньше максимально возможной при данной температуре.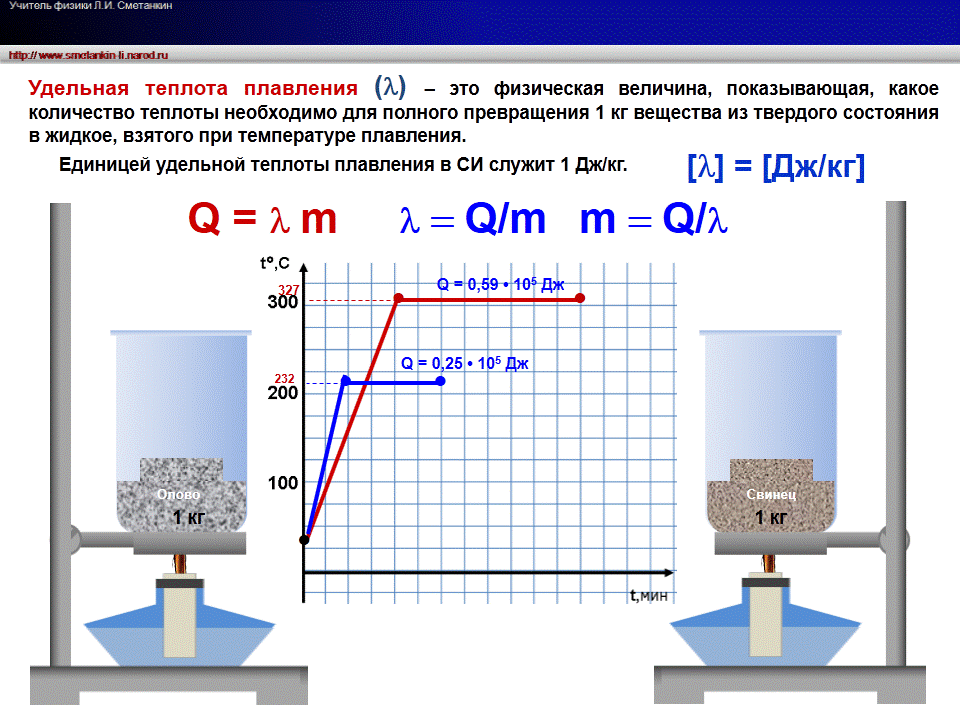
2) Концентрация водяных паров, содержащихся в воздухе, в 2 раза больше максимально возможной при данной температуре.
3) 50% объёма воздуха занимает водяной пар.
4) Число молекул воды равняется числу молекул других газов, содержащихся в воздухе.
42. Ведущий телепрограммы, рассказывающий о погоде, сообщил, что в настоящее время относительная влажность воздуха составляет 25%. Это означает, что
1) Концентрация водяных паров, содержащихся в воздухе, в 4 раза меньше максимально возможной при данной температуре.
2) Концентрация водяных паров, содержащихся в воздухе, в 4 раза больше максимально возможной при данной температуре.
3) 25% объёма воздуха занимает водяной пар.
4) Число молекул воды в 3 раза меньше числа молекул других газов, содержащихся в воздухе.
43.
На рисунке представлен график зависимости температуры от полученного количества теплоты для образцов равной массы из двух разных веществ. Первоначально каждое из веществ находилось в твёрдом состоянии. Сравните значения удельной теплоёмкости с этих веществ в твёрдом и жидком состоянии.
Первоначально каждое из веществ находилось в твёрдом состоянии. Сравните значения удельной теплоёмкости с этих веществ в твёрдом и жидком состоянии.
1) В твёрдом состоянии с1 < с2; в жидком состоянии с1 > с2
2) В твёрдом состоянии с1 > с2; в жидком состоянии с1 < с2
3) В твёрдом состоянии с1 > с2; в жидком состоянии с1 > с2
4) В твёрдом состоянии с1 < с2; в жидком состоянии с1 < с2
44. Испарение и кипение — два процесса перехода вещества из одного агрегатного состояния в другое. Различие между ними заключается в том, что
А. Кипение происходит при определённой температуре, а испарение — при любой температуре.
Б. Испарение происходит с поверхности жидкости, а кипение — во всём объёме жидкости.
Правильным(-и) является(-ются) утверждение(-я)
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
45.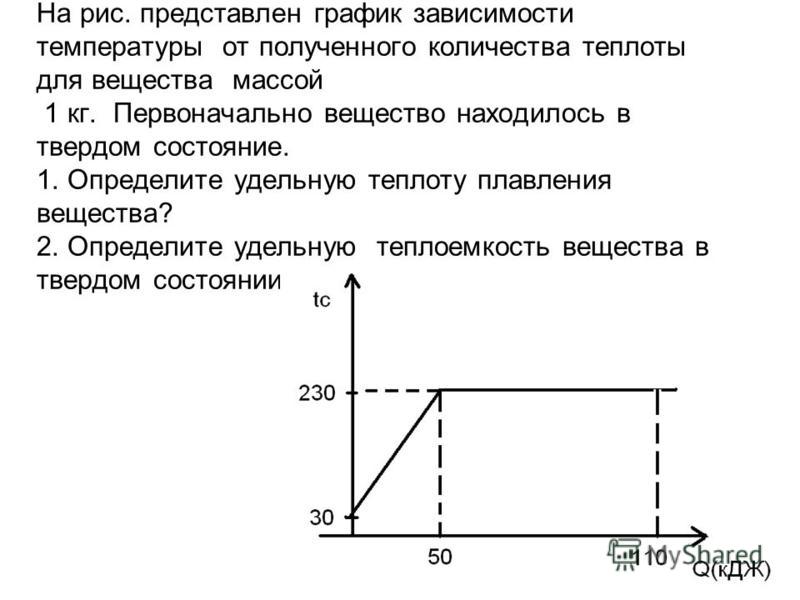 Удельная теплота парообразования спирта 9,0·105 Дж/кг. Это означает, что
Удельная теплота парообразования спирта 9,0·105 Дж/кг. Это означает, что
1) в процессе образования 9,0·105 кг паров из жидкого спирта, взятого при температуре кипения, выделяется количество теплоты 1 Дж
2) для образования 9,0·105 кг паров из жидкого спирта, взятого при температуре кипения, необходимо количество теплоты 1 Дж
3) в процессе образования 1 кг паров из жидкого спирта, взятого при температуре кипения, выделяется количество теплоты 9,0·105 Дж
4) для образования 1 кг паров из жидкого спирта, взятого при температуре кипения, необходимо количество теплоты 9,0·105 Дж
46. Удельная теплоёмкость серебра равна 250 Дж/(кг·°С). Это означает, что
1) при температуре 0°С 1 кг серебра выделяет количество теплоты, равное 250 Дж
2) для нагревания 1 кг серебра на 1°С необходимо количество теплоты, равное 250 Дж
3) при сообщении куску серебра массой 250 кг количества теплоты, равного 250 Дж, его температура повышается на 1°С
4) для нагревания 1 кг серебра на 250°С затрачивается количество теплоты, равное 1 Дж
47. КПД тепловой машины равен 25%. Это означает, что при выделении энергии Q при сгорании топлива на совершение полезной работы не используется энергия, равная
КПД тепловой машины равен 25%. Это означает, что при выделении энергии Q при сгорании топлива на совершение полезной работы не используется энергия, равная
1) 0,75Q 2) 0,6Q 3) 0,4Q 4) 0,25Q
48.
Воду, цинк и алюминий равной массы нагрели в одинаковых условиях на одинаковых горелках. Какой из графиков соответствует изменению температуры цинка?
1) 1 2) 2 3) 3 4) однозначного ответа быть не может
49.
На рисунке изображён график зависимости температуры t вещества от времени τ в процессе непрерывного отвода теплоты. Первоначально вещество находилось в газообразном состоянии. Какой процесс соответствует отрезку CD?
1) охлаждение пара
2) конденсация
3) охлаждение жидкости
4) нагревание жидкости
50.
На рисунке приведён график зависимости температуры t спирта от времени τ при нагревании. Первоначально спирт находился в жидком состоянии. Какая точка графика соответствует началу процесса кипения спирта?
Первоначально спирт находился в жидком состоянии. Какая точка графика соответствует началу процесса кипения спирта?
1) А 2) В 3) С 4) D
51.
В открытый сосуд, заполненный водой, в области А (см. рисунок) поместили крупинки марганцовки (перманганата калия). В каком(-их) направлении(-ях) преимущественно будет происходить окрашивание воды от крупинок марганцовки, если начать нагревание сосуда с водой так, как показано на рисунке?
1) 1 2) 2 3) 3 4) во всех направлениях одинаково
52. Одно из положений молекулярно-кинетической теории строения вещества заключается в том, что «частицы вещества (молекулы, атомы, ионы) находятся в непрерывном хаотическом движении». Что означают слова «непрерывное движение»?
1) Частицы всё время движутся в определённом направлении.
2) Движение частиц вещества не подчиняется никаким законам.
3) Частицы все вместе движутся то в одном, то в другом направлении.
4) Движение молекул никогда не прекращается.
Вычислительная задача. Динамика и кинематика
1. К динамометру прикрепили цилиндр, как показано на рисунке 1. Затем цилиндр полностью погрузили в воду (рисунок 2).
Определите объём цилиндра. Ответ запишите в см3.
2. Шар 1 последовательно взвешивают на рычажных весах с шаром 2 и шаром 3 (рис. а и б). Для объёмов шаров справедливо соотношение V2 = V3 > V1.
Какой шар имеет минимальную плотность? Запишите в ответе цифру, которой обозначен шар.
3.
Сплошной кубик, имеющий плотность ρк и длину ребра a, опустили в жидкость с плотностью ρж = 998 кг/м3 (см. рисунок). Найдите давление, оказываемое жидкостью на верхнюю грань кубика, если h2 = 0,1 м.
4. Площадь большего поршня гидравлического пресса S2 в 4 раза больше площади малого поршня S1. (см. рисунок). Сила F1, действующая на малый поршень, равна 20 Н.
Найдите силу F2.
5. Одно из колен U-образного манометра соединили с сосудом, наполненным газом (см. рисунок). В качестве жидкости в манометре используется ртуть. Чему равно давление газа в сосуде, если атмосферное давление составляет 760 мм рт. ст.? Ответ дайте в мм рт. ст.
рисунок). В качестве жидкости в манометре используется ртуть. Чему равно давление газа в сосуде, если атмосферное давление составляет 760 мм рт. ст.? Ответ дайте в мм рт. ст.
6.
В сосуд с водой плотностью ρ = 998 кг/м3 опущена вертикальная стеклянная пробирка, целиком заполненная водой (см. рисунок). Высота h2 равна 0,3 м. Найдите давление, оказываемое водой на дно сосуда в точке А. (Ускорение свободного падения примите равным 10 м/с2.)
7.
Шар 1 последовательно взвешивают на рычажных весах с шаром 2 и шаром 3 (рис. а и б). Для объёмов шаров справедливо соотношение V1 = V3 < V2.
Какой шар имеет максимальную плотность? Запишите в ответе цифру, которой обозначен шар.
8. В сообщающиеся сосуды поверх воды налиты четыре различные жидкости, не смешивающиеся с водой (см. рисунок). Уровень воды в сосудах остался одинаковым.
Какая жидкость имеет наименьшую плотность?
9.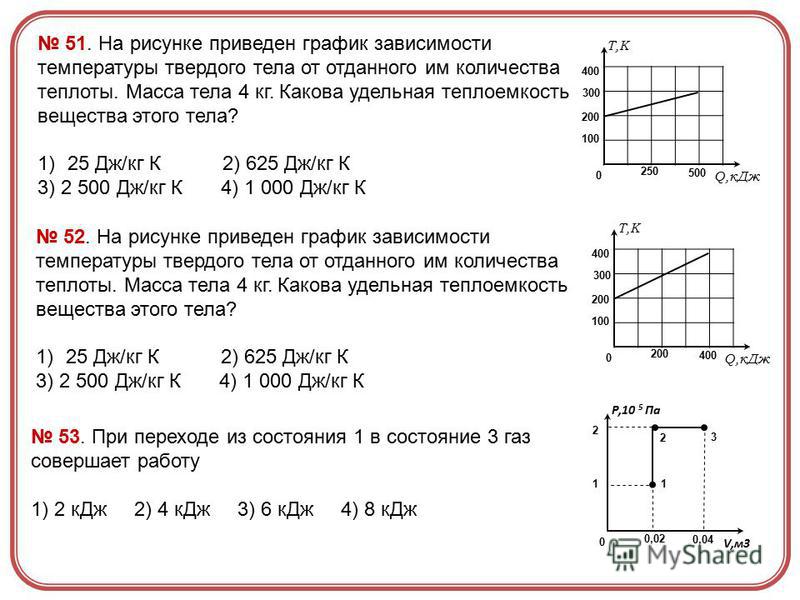
Сосновый брусок в форме прямоугольного параллелепипеда, имеющего размеры a = 30 см, b = 20 см и c = 10 см, начинают осторожно опускать в ванну с водой (как показано на рисунке). Чему будет равна глубина погружения бруска в воду при плавании? Ответ дайте в см. (Плотность сосны )
10.
Сосновый брусок в форме прямоугольного параллелепипеда, имеющего размеры a = 30 см, b = 40 см и c = 30 см, начинают осторожно опускать в ванну с водой (как показано на рисунке). Чему будет равна глубина погружения бруска в воду при плавании? Ответ дайте в см. (Плотность сосны равна 400 кг/м3.)
11. Чему равен объем рыбы, плавающей в морской воде, если на нее действует выталкивающая сила 10,3 Н? Ответ дайте в м3 без указания единиц измерения. Плотность морской воды равна 1030 кг/м3.
12. Шар 1 последовательно взвешивают на рычажных весах с шаром 2 и шаром 3 (рис. а и б). Для объёмов шаров справедливо соотношение V1 = V3 < V2.
Какой шар имеет минимальную среднюю плотность? Запишите в ответе цифру, которой обозначен шар.
13. Цилиндр 1 поочерёдно взвешивают с цилиндром 2 такого же объёма, а затем с цилиндром 3, имеющим меньший объём (см. рисунок).
Какой цилиндр имеет максимальную среднюю плотность? Запишите в ответе цифру, которой обозначен цилиндр.
14. В сосуд с водой плотностью ρ = 998 кг/м3 опущена вертикальная стеклянная пробирка, целиком заполненная водой (см. рисунок). Высота h2 равна 0,05 м. Найдите давление, оказываемое водой на дно сосуда в точке А.
15. Площадь большего поршня гидравлического пресса S2 в 4 раза больше площади малого поршня S1. (см. рисунок). Сила F1, действующая на малый поршень, равна 5 Н.
Найдите силу F2.
16. Одна и та же горизонтальная сила F действует вначале на тело 1 массой 0,5 кг, а затем на тело 2 массой 3 кг. Оба тела до начала действия силы покоились на гладком горизонтальном столе.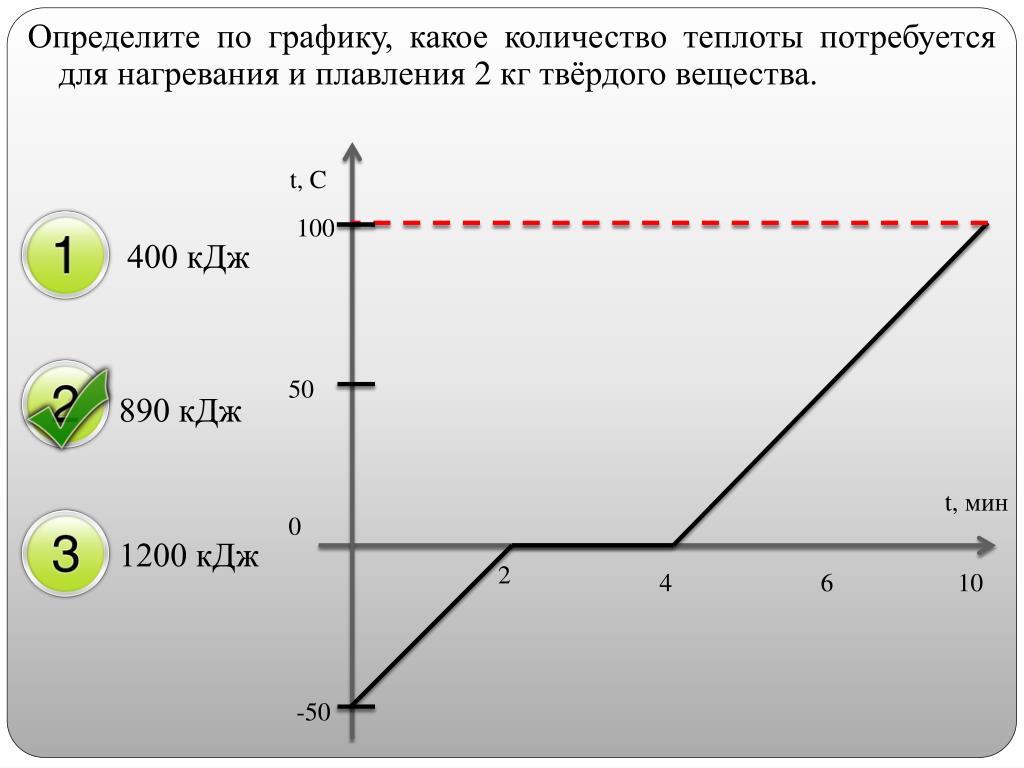 С каким по модулю ускорением будет двигаться тело 2 под действием силы F, если тело 1 движется с ускорением, модуль которого равен 1,8 м/с2?
С каким по модулю ускорением будет двигаться тело 2 под действием силы F, если тело 1 движется с ускорением, модуль которого равен 1,8 м/с2?
17. Деревянную коробку массой 10 кг равномерно и прямолинейно тянут по горизонтальной деревянной доске с помощью горизонтальной пружины жёсткостью 200 Н/м. Удлинение пружины 0,2 м. Чему равен коэффициент трения коробки по доске?
18. Чему равно ускорение груза массой 500 кг, который опускают с помощью троса, если сила натяжения троса 4000 Н? Сопротивлением воздуха пренебречь. Ответ запишите в м/с2.
19. Мальчик стоит на напольных весах в лифте. Лифт начинает движение вверх с ускорением 1 м/с2. Что покажут весы в этот момент времени, если в покоящемся лифте они показывали 40 кг? Ответ запишите в кг.
20. Работа силы тяги автомобиля, прошедшего равномерно 4 км пути, составила 8 МДж. Определите силу трения. Ответ запишите в Н.
21. Из колодца медленно выкачали с помощью насоса 0,5 м3 воды. Совершённая при этом работа равна 30 000 Дж. Чему равна глубина колодца? Ответ запишите в метрах.
Из колодца медленно выкачали с помощью насоса 0,5 м3 воды. Совершённая при этом работа равна 30 000 Дж. Чему равна глубина колодца? Ответ запишите в метрах.
22. Бетонную плиту объёмом 0,5 м3 равномерно подняли на некоторую высоту. Чему равна высота, на которую подняли плиту, если совершённая при этом работа равна 23 кДж? Ответ запишите в метрах
Примечание. Плотность бетона равна 2300 кг/м3.
23. Под действием силы 40 Н груз массой 4 кг перемещается вверх по наклонной плоскости. Коэффициент полезного действия наклонной плоскости — 50%. Чему равна длина наклонной плоскости, если её высота — 1 м? Ответ запишите в метрах.
24.
Два бруска массами m1 = 1 кг и m2 = 3 кг, связанные лёгкой нерастяжимой нитью, находятся на гладкой горизонтальной плоскости (см. рисунок). К ним приложены силы F1 = 2 Н и F2 = 10 Н. Найдите модуль ускорения системы этих тел. Ответ запишите в м/c2.
25.
Через неподвижный лёгкий блок перекинута невесомая нерастяжимая нить, к концам которой подвешены два груза массами m1 = 1 кг и m2 = 3 кг (см. рисунок).Пренебрегая трением, найдите силу натяжения нити при движении грузов. Ответ запишите в Н.
рисунок).Пренебрегая трением, найдите силу натяжения нити при движении грузов. Ответ запишите в Н.
Вычислительная задача. Теплота
1. 3 л воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
2. На рисунке представлен график зависимости температуры t твёрдого тела от полученного им количества теплоты Q. Масса тела 2 кг. Чему равна удельная теплоёмкость вещества этого тела? Ответ запишите в Дж/(кг · °С).
3. На рисунке изображён график зависимости температуры t двух килограммов некоторой жидкости от сообщаемого ей количества теплоты Q.
Чему равна удельная теплоёмкость этой жидкости? В ответ запишите число без указания единиц измерения.
4. На рисунке изображён график зависимости температуры t четырёх килограммов некоторой жидкости от сообщаемого ей количества теплоты Q.
Чему равна удельная теплоёмкость этой жидкости? В ответ запишите число без указания единиц измерения.
5.
На рисунке представлен график зависимости температуры от времени для процесса нагревания слитка свинца массой 1 кг. Какое количество теплоты получил свинец за 10 мин нагревания? Ответ дайте в кДж. (Удельная теплоёмкость свинца — )
6.
На рисунке представлен график зависимости температуры от времени для процесса нагревания слитка свинца массой 1 кг. Какое количество теплоты получил свинец за 15 мин нагревания? Ответ дайте в кДж. (Удельная теплоёмкость свинца — 130 Дж/(кг·°С).)
7. Сколько литров воды при 83 °С нужно добавить к 4 л воды при 20 °С, чтобы получить воду температурой 65 °С? Теплообменом с окружающей средой пренебречь.
8.Какое количество теплоты выделится при конденсации 2 кг пара, взятого при температуре кипения, и последующего охлаждения воды до 40 °С при нормальном атмосферном давлении? Ответ выразите в кДж.
9. Три литра воды, взятой при температуре 20 °С, смешали с водой при температуре 100 °С. Температура смеси оказалась равной 40 °С. Чему равна масса горячей воды? Теплообменом с окружающей средой пренебречь.
10. Какое количество теплоты необходимо, чтобы нагреть 1 л воды от 20 °С до 100 °С? Вода нагревается в алюминиевой кастрюле массой 200 г. Тепловыми потерями пренебречь. (Удельная теплоёмкость алюминия — 920 Дж/(кг·°С), воды — 4200 Дж/(кг·°С).) Ответ дайте в кДж.
11. Сколько спирта надо сжечь, чтобы нагреть воду массой 2 кг на 29 °С? Считать, что вся энергия, выделенная при сгорании спирта, идёт на нагревание воды. (Удельная теплота сгорания спирта 2,9·107Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С)). Ответ дайте в граммах.
12. Какое количество теплоты необходимо для плавления куска свинца массой 2 кг, взятого при температуре 27 °С? (Удельная теплоёмкость свинца — 130 Дж/(кг·°С), удельная теплота плавления свинца — 25 кДж/кг.) Ответ дайте в кДж.
13. В стакан, содержащий лед при температуре −5 °С, налили воду, имеющую температуру 40 °С. Каково отношение массы воды к массе льда, если весь лед растаял и в стакане установилась температура 0 °С? Теплообменом с окружающим воздухом пренебречь. (Удельная теплоёмкость воды — 4,2 кДж/(кг·°С), льда — 2,1 кДж/(кг·°С), удельная теплота плавления льда — 330 кДж/кг.) Ответ дайте с точностью до сотых.
14. По результатам нагревания кристаллического вещества массой 5 кг построен график зависимости температуры этого вещества от количества подводимого тепла.
Считая, что потерями энергии можно пренебречь, определите, какое количество теплоты потребовалось для нагревания 1 кг этого вещества в жидком состоянии на 1 °С?
15. Какое количество теплоты выделится при кристаллизации воды массой 1 кг, взятой при температуре 10 °С? Ответ дайте в кДж. (Удельная теплоёмкость воды — 4,2 кДж/(кг·°С), удельная теплота плавления льда — 330 кДж/кг.)
16. Литровую кастрюлю, полностью заполненную водой, из комнаты вынесли на мороз. Зависимость температуры воды от времени представлена на рисунке. Какое количество теплоты выделилось при кристаллизации и охлаждении льда? Ответ дайте в кДж. (Удельная теплота плавления льда — 330 кДж/кг.)
Зависимость температуры воды от времени представлена на рисунке. Какое количество теплоты выделилось при кристаллизации и охлаждении льда? Ответ дайте в кДж. (Удельная теплота плавления льда — 330 кДж/кг.)
17. Какое количество теплоты потребуется, чтобы в алюминиевом чайнике массой 700 г вскипятить 2 кг воды? Первоначально чайник с водой имели температуру 20 °С. Ответ дайте в кДж. (Удельную теплоёмкость алюминия считать равной )
18. При нагревании куска металла массой 200 г от 20 °С до 60 °С его внутренняя энергия увеличилась на 2400 Дж. Какова удельная теплоёмкость металла? Ответ запишите в Дж/(кг·°С).
19. На рисунке представлен график зависимости температуры от полученного количества теплоты для вещества массой 1 кг. Первоначально вещество находилось в твёрдом состоянии. Определите удельную теплоёмкость вещества в твёрдом состоянии. Ответ запишите в Дж/(кг·°С).
20. На рисунке представлен график зависимости температуры от полученного количества теплоты для вещества массой 2 кг. Первоначально вещество находилось в твёрдом состоянии. Определите удельную теплоту плавления вещества. Ответ запишите в кДж/кг.
Первоначально вещество находилось в твёрдом состоянии. Определите удельную теплоту плавления вещества. Ответ запишите в кДж/кг.
21. В тепловой машине потери энергии составляют от энергии, выделяющейся при сгорании топлива. Чему равен КПД этой тепловой машины? Ответ запишите в виде десятичной дроби.
22. В тепловой машине потери энергии составляют от энергии, выделяющейся при сгорании топлива. Чему равен КПД этой тепловой машины?
23. Двигатель трактора совершил полезную работу 23 МДж, израсходовав при этом 2 кг бензина. Найдите КПД двигателя трактора (удельную теплоту сгорания бензина принять равной 46 МДж/кг). Ответ дайте в %.
24. Пластилиновый шар упал без начальной скорости с высоты 5 м на каменный пол. Считая, что вся кинетическая энергия шара, приобретённая им за время свободного падения, превратилась во внутреннюю энергию пластилина, найдите, на сколько градусов нагрелся шар. Удельная теплоёмкость пластилина 2,5 кДж/(кг · °С). Ответ запишите в °С.
Ответ запишите в °С.
25.
В тонкостенный сосуд налили воду массой 1 кг, поставили его на электрическую плитку и начали нагревать. На рисунке представлен график зависимости температуры воды t от времени τ. Найдите мощность плитки. Потерями теплоты и теплоёмкостью сосуда пренебречь. Ответ запишите в Вт.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/414615-zadachi-po-fizike-9-klass
Калькулятор удельной теплоемкости
Этот калькулятор удельной теплоемкости представляет собой инструмент, который определяет теплоемкость нагретого или охлажденного образца. Удельная теплоемкость – это количество тепловой энергии, которое необходимо передать образцу массой 1 кг, чтобы повысить его температуру на 1 К . Читайте дальше, чтобы узнать, как правильно применить формулу теплоемкости, чтобы получить достоверный результат.
💡 Этот калькулятор работает по-разному, поэтому вы также можете использовать его, например, для расчета количества тепла, необходимого для изменения температуры (если вы знаете удельную теплоемкость). Если вам нужно достичь изменения температуры в определенное время, используйте наш калькулятор мощности для нагрева, чтобы узнать требуемую мощность. Чтобы найти удельную теплоемкость из сложного эксперимента, калориметрический калькулятор может значительно ускорить расчеты.
Если вам нужно достичь изменения температуры в определенное время, используйте наш калькулятор мощности для нагрева, чтобы узнать требуемую мощность. Чтобы найти удельную теплоемкость из сложного эксперимента, калориметрический калькулятор может значительно ускорить расчеты.
Предпочитаете смотреть , а не читать? Узнайте все, что вам нужно, за 90 секунд с помощью этого видео , которое мы сделали для вас :
Как рассчитать удельную теплоемкость
- Определите, хотите ли вы нагреть образец (придать ему тепловую энергию) или охладить его ( отнять часть тепловой энергии).
- Введите количество подаваемой энергии в виде положительного значения. Если вы хотите охладить образец, введите вычитаемую энергию как отрицательное значение. Например, предположим, что мы хотим уменьшить тепловую энергию образца на 63 000 Дж.
 Тогда
Тогда Ом = -63 000 Дж. - Определите разницу температур между начальным и конечным состоянием образца и введите ее в калькулятор теплоемкости. Если образец охладить, то разница будет отрицательной, а если подогреть – положительной. Допустим, мы хотим охладить образец на 3 градуса. Тогда
ΔT = -3 K. Вы также можете перейти в расширенный режим , чтобы ввести начальное и конечное значения температуры вручную. - Определите массу образца. Будем считать
м = 5 кг. - Рассчитайте удельную теплоемкость как
c = Q / (mΔT). В нашем примере она будет равнас = -63 000 Дж/(5 кг * -3 К) = 4 200 Дж/(кг·К). Это типичная теплоемкость воды.
Если у вас возникли проблемы с единицами измерения, не стесняйтесь использовать наши калькуляторы преобразования температуры или веса.
Формула теплоемкости
Формула удельной теплоемкости выглядит так:
c = Q / (mΔT) Q — количество подведенного или отведенного тепла (в джоулях), m — масса образца, ΔT — разница между начальной и конечной температурами. Теплоемкость измеряется в Дж/(кг·К).
Теплоемкость измеряется в Дж/(кг·К).
Типовые значения удельной теплоемкости
Вам не нужно использовать калькулятор теплоемкости для большинства распространенных веществ. Значения удельной теплоемкости для некоторых из наиболее популярных из них перечислены ниже.
- лед:
2 100 Дж/(кг·K) - вода:
4 200 Дж/(кг·K) - водяной пар:
2000 Дж/(кг·K) - базальт:
840 Дж/(кг·K) - гранит:
790 Дж/(кг·К) - алюминий:
890 Дж/(кг·К) - железо:
450 Дж/(кг·K) - медь:
380 Дж/(кг·K) - свинец:
130 Дж/(кг·К)
Имея эту информацию, вы также можете рассчитать, сколько энергии вам нужно передать образцу, чтобы повысить или понизить его температуру. Например, вы можете проверить, сколько тепла вам нужно, чтобы довести до кипения кастрюлю с водой, чтобы приготовить макароны.
Хотите знать, что на самом деле означает результат? Воспользуйтесь нашим калькулятором потенциальной энергии, чтобы проверить, насколько высоко вы поднимете образец с таким количеством энергии. Или проверьте, как быстро может двигаться образец, с помощью этого калькулятора кинетической энергии.
Часто задаваемые вопросы
Как рассчитать удельную теплоемкость?
- Найдите начальную и конечную температуру, а также массу образца и подведенную энергию.
- Вычтите из конечной и начальной температуры, чтобы получить изменение температуры (ΔT).
- Умножьте изменения температуры на массу образца.
- Разделите подведенное тепло/энергию на продукт.
- Формула
C = Q / (ΔT ⨉ m).
Что такое удельная теплоемкость при постоянном объеме?
Удельная теплоемкость – это количество тепла или энергии, необходимое для изменения одной единицы массы вещества постоянного объема на 1 °C . Формула:
Формула: Cv = Q / (ΔT ⨉ m) .
Какова формула удельной теплоемкости?
Формула удельной теплоемкости C вещества с массой m : C = Q /(m ⨉ ΔT) . Где Q — добавленная энергия, а ΔT — изменение температуры. Удельная теплоемкость при различных процессах, таких как постоянный объем, Cv и постоянное давление, Cp , связаны друг с другом отношением удельных теплоемкостей, ɣ= Cp/Cv , или газовая постоянная R = Cp-Cv .
В каких единицах измеряется удельная теплоемкость?
Удельная теплоемкость измеряется в Дж/кг К или Дж/кг С , так как это количество тепла или энергии, необходимое в процессе постоянного объема для изменения температуры вещества единицы массы на 1°С или 1° К.
Каково значение удельной теплоемкости воды?
Удельная теплоемкость воды равна 4179 Дж/кг K , количество теплоты, необходимое для повышения температуры 1 г воды на 1 кельвин.
Какие британские единицы измерения удельной теплоемкости?
Удельная теплоемкость измеряется в БТЕ/фунт °F в имперских единицах и в Дж/кг·К в единицах СИ.
Каково значение удельной теплоемкости меди?
Удельная теплоемкость меди 385 Дж/кг K . Вы можете использовать это значение для оценки энергии, необходимой для нагревания 100 г меди на 5 °C, т. е. Q = m x Cp x ΔT = 0,1 * 385 * 5 = 192,5 Дж.
Каково значение удельной теплоемкости меди? алюминий?
Удельная теплоемкость алюминия 897 Дж/кг K . Это значение почти в 2,3 раза превышает удельную теплоемкость меди. Вы можете использовать это значение для оценки энергии, необходимой для нагрева 500 г алюминия на 5 °C, т. е. Q = m x Cp x ΔT = 0,5 * 897 * 5 = 2242,5 Дж.
The Physics Classroom Tutorial
На На предыдущей странице мы узнали, что теплота делает с объектом, когда она приобретается или выделяется. Притоки или потери тепла приводят к изменениям температуры, изменениям состояния или производительности труда. Тепло – это передача энергии. Когда объект получает или теряет, в этом объекте будут происходить соответствующие энергетические изменения. Изменение температуры связано с изменением средней кинетической энергии частиц внутри объекта. Изменение состояния связано с изменением внутренней потенциальной энергии, которой обладает объект. И когда работа выполнена, происходит общая передача энергии объекту, над которым выполняется работа. В этой части Урока 2 мы исследуем вопрос Как можно измерить количество теплоты, полученное или выделенное объектом?
Тепло – это передача энергии. Когда объект получает или теряет, в этом объекте будут происходить соответствующие энергетические изменения. Изменение температуры связано с изменением средней кинетической энергии частиц внутри объекта. Изменение состояния связано с изменением внутренней потенциальной энергии, которой обладает объект. И когда работа выполнена, происходит общая передача энергии объекту, над которым выполняется работа. В этой части Урока 2 мы исследуем вопрос Как можно измерить количество теплоты, полученное или выделенное объектом?
Удельная теплоемкость
Предположим, что несколько объектов, состоящих из разных материалов, нагреваются одинаковым образом. Будут ли объекты нагреваться с одинаковой скоростью? Ответ: скорее всего нет. Различные материалы будут нагреваться с разной скоростью, потому что каждый материал имеет свою удельную теплоемкость. Под удельной теплоемкостью понимается количество теплоты, необходимое для того, чтобы заставить единицу массы (скажем, грамм или килограмм) изменить свою температуру на 1°C. Удельная теплоемкость различных материалов часто приводится в учебниках. Стандартными метрическими единицами являются Джоули/килограмм/Кельвин (Дж/кг/К). Чаще используются единицы измерения Дж/г/°C. Используйте виджет ниже для просмотра удельной теплоемкости различных материалов. Просто введите название вещества (алюминий, железо, медь, вода, метанол, дерево и т. д.) и нажмите кнопку «Отправить»; результаты будут отображаться в отдельном окне.
Удельная теплоемкость различных материалов часто приводится в учебниках. Стандартными метрическими единицами являются Джоули/килограмм/Кельвин (Дж/кг/К). Чаще используются единицы измерения Дж/г/°C. Используйте виджет ниже для просмотра удельной теплоемкости различных материалов. Просто введите название вещества (алюминий, железо, медь, вода, метанол, дерево и т. д.) и нажмите кнопку «Отправить»; результаты будут отображаться в отдельном окне.
Удельная теплоемкость твердого алюминия (0,904 Дж/г/°C) отличается от удельной теплоемкости твердого железа (0,449 Дж/г/°C). Это означает, что для повышения температуры данной массы алюминия на 1°С потребуется больше тепла, чем для повышения температуры той же массы железа на 1°С. Фактически, для повышения температуры образца алюминия на заданное количество потребовалось бы примерно в два раза больше тепла, чем для того же изменения температуры того же количества железа. Это связано с тем, что удельная теплоемкость алюминия почти в два раза выше, чем у железа.
Теплоемкость указана на основе на грамм или на килограмм . Иногда значение указывается из расчета на моль , и в этом случае оно называется молярной теплоемкостью. Тот факт, что они перечислены на основе 90 197 на количество 90 198, указывает на то, что количество тепла, необходимое для повышения температуры вещества, зависит от количества вещества. Всякий человек, который кипятил на плите кастрюлю с водой, несомненно, знает эту истину. Вода кипит при 100°С на уровне моря и при несколько более низких температурах на возвышенностях. Чтобы довести кастрюлю с водой до кипения, ее температуру нужно сначала поднять до 100°C. Это изменение температуры достигается за счет поглощения тепла от горелки печи. Нетрудно заметить, что для доведения до кипения полной кастрюли воды требуется значительно больше времени, чем для доведения до кипения половины воды. Это связано с тем, что полная кастрюля с водой должна поглощать больше тепла, чтобы привести к такому же изменению температуры.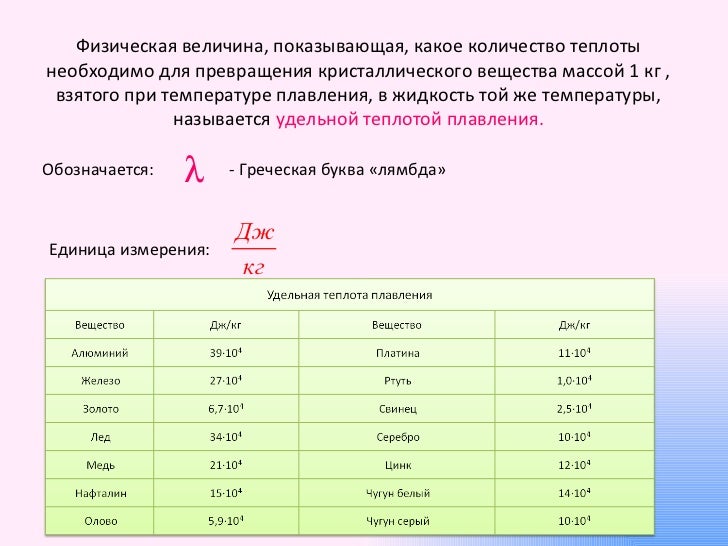 На самом деле, требуется вдвое больше тепла, чтобы вызвать такое же изменение температуры в удвоенной массе воды.
На самом деле, требуется вдвое больше тепла, чтобы вызвать такое же изменение температуры в удвоенной массе воды.
Удельная теплоемкость также указана на основе на K или на °C . Тот факт, что удельная теплоемкость указана в пересчете на 90 197 на градус 90 198, указывает на то, что количество теплоты, необходимое для нагревания данной массы вещества до определенной температуры, зависит от изменения температуры, необходимого для достижения этой конечной температуры. Другими словами, важна не конечная температура, а общее изменение температуры. Для изменения температуры воды с 20°С до 100°С (изменение на 80°С) требуется больше тепла, чем для повышения температуры того же количества воды с 60°С до 100°С (изменение на 40°С). °С). Фактически, для изменения температуры данной массы воды на 80°С требуется в два раза больше тепла, чем для изменения на 40°С. Человек, который хочет быстрее довести воду до кипения на плите, должен начать с теплой водопроводной воды, а не с холодной.
Это обсуждение удельной теплоемкости заслуживает одного последнего комментария. Термин « удельная теплоемкость » является чем-то вроде неправильного употребления . Термин подразумевает, что вещества могут иметь способность содержать вещь, называемую теплотой. Как обсуждалось ранее, тепло не является чем-то, что содержится в объекте. Тепло — это то, что передается объекту или от него. Объекты содержат энергию в различных формах. Когда эта энергия передается другим объектам с другой температурой, мы называем переданную энергию как тепло или тепловая энергия . Хотя это вряд ли приживется, более подходящим термином будет удельная энергетическая емкость.
Удельная теплоемкость позволяет математически связать количество тепловой энергии, полученной (или потерянной) образцом любого вещества, с массой образца и результирующим изменением температуры. Связь между этими четырьмя величинами часто выражается следующим уравнением.
Связь между этими четырьмя величинами часто выражается следующим уравнением.
Q = m•C•ΔT
где Q — количество тепла, переданного объекту или от него, m — масса объекта, C — удельная теплоемкость материала, из которого состоит объект, ΔT – результирующее изменение температуры объекта. Как и во всех ситуациях в науке, значение 90 197 дельта 90 198 (∆) для любой величины рассчитывается путем вычитания начального значения величины из конечного значения величины. В этом случае ΔT равно T final — Т начальный . При использовании приведенного выше уравнения значение Q может оказаться как положительным, так и отрицательным. Как всегда, положительный и отрицательный результат расчета имеет физическое значение. Положительное значение Q указывает на то, что объект получил тепловую энергию из своего окружения; это будет соответствовать повышению температуры и положительному значению ΔT. Отрицательное значение Q указывает на то, что объект выделяет тепловую энергию в окружающую среду; это будет соответствовать снижению температуры и отрицательному значению ΔT.
Знание любых трех из этих четырех величин позволяет вычислить четвертую величину. Распространенной задачей на многих уроках физики является решение задач, связанных с соотношениями между этими четырьмя величинами. В качестве примеров рассмотрим две задачи ниже. Решение каждой проблемы разработано для вас. Дополнительную практику можно найти в разделе «Проверьте свое понимание» внизу страницы.
Пример проблемы 1 |
Как и любая задача в физике, решение начинается с определения известных величин и соотнесения их с символами, используемыми в соответствующем уравнении. В этой задаче мы знаем следующее:
м = 450 г
С = 4,18 Дж/г/°С
T исходная = 15°C
Т окончательная = 85°С
Мы хотим определить значение Q — количество теплоты. Для этого воспользуемся уравнением Q = m•C•ΔT. m и C известны; ΔT можно определить по начальной и конечной температурам.
Для этого воспользуемся уравнением Q = m•C•ΔT. m и C известны; ΔT можно определить по начальной и конечной температурам.
T = T окончательная — T начальная = 85°C — 15°C = 70°C
Зная три из четырех величин соответствующего уравнения, мы можем подставить и решить Q.
Q = м•C•ΔT = (450 г)•(4,18 Дж/г/°C)•(70°C)
Q = 131670 Дж
Q = 1,3×10 5 Дж = 130 кДж (округлено до двух значащих цифр)
Пример задачи 2 |
По сравнению с предыдущей задачей, это гораздо более сложная задача. На самом деле эта проблема как две проблемы в одной. В основе стратегии решения проблем лежит признание того, что количество тепла, потерянного водой (Q вода ), равно количеству тепла, полученному металлом (Q металл ). Поскольку значения m, C и ΔT воды известны, можно рассчитать Q воды . Этот вопрос 9Значение 0256 для воды равно значению Q для металла . Как только значение Q металла станет известно, его можно использовать вместе со значением m и ΔT металла для расчета Q металла . Использование этой стратегии приводит к следующему решению:
Часть 1: Определение потерь тепла с водой
Дано:
м = 50,0 г
С = 4,18 Дж/г/°С
T исходная = 88,6°C
Т окончательная = 87,1°С
ΔT = -1,5°C (T окончательная — T исходная )
Решить для воды Q :
Q вода = m•C•ΔT = (50,0 г)•(4,18 Дж/г/°C)•(-1,5°C)
Q вода = -313,5 Дж (не округлено)
(Знак — означает, что вода теряет тепло)
Часть 2: Определение стоимости C металл
Дано:
Q металл = 313,5 Дж (используйте знак +, так как металл нагревается)
m = 12,9 г
T исходная = 26,5°C
Т окончательная = 87,1°С
ΔT = (T окончательный — T начальный )
Решение для C Металл :
Пересталка Q Металл = M Металл • C Металл • ΔT Металл , чтобы получить C METLE = Q MEALL , чтобы получить C METLE = Q . металл )
металл )
C металл = Q металл / (m металл • ΔT металл ) = (313,5 Дж)/[(12,9 г)•(60,6°C)]
C металл = 0,40103 Дж/г/°C
C металл = 0,40 Дж/г/°C (округлено до двух значащих цифр)
Теплота и изменения состояния
Приведенное выше обсуждение и соответствующее уравнение (Q = m•C•∆T) связывают тепло, полученное или потерянное объектом, с результирующими изменениями температуры этого объекта. Как мы узнали, иногда тепло приобретается или теряется, но температура не изменяется. Это тот случай, когда вещество претерпевает изменение состояния. Итак, теперь мы должны исследовать математику, связанную с изменениями состояния и количеством теплоты.
Чтобы начать обсуждение, давайте рассмотрим различные изменения состояния, которые можно наблюдать для образца материи. В приведенной ниже таблице перечислены несколько изменений состояния и указаны имена, обычно связанные с каждым процессом.
Процесс | Изменение состояния |
Плавление | Из твердого в жидкое |
Замораживание | Из жидкого в твердое |
Испарение | Жидкость в газ |
Конденсат | Газ в жидкость |
Сублимация | Твердое тело в газ |
Депонирование | Из газа в твердое тело |
В случае плавления, кипения и сублимации к образцу вещества необходимо добавить энергию, чтобы вызвать изменение состояния. Такие изменения состояния называются эндотермическими. Замерзание, конденсация и осаждение экзотермичны; энергия высвобождается образцом материи, когда происходят эти изменения состояния. Таким образом, можно заметить, что образец льда (твердая вода) тает, когда его помещают на горелку или рядом с ней. Тепло передается от горелки к образцу льда; лед получает энергию, вызывая изменение состояния. Но сколько энергии потребуется, чтобы вызвать такое изменение состояния? Существует ли математическая формула, которая могла бы помочь в определении ответа на этот вопрос? Наверняка есть.
Такие изменения состояния называются эндотермическими. Замерзание, конденсация и осаждение экзотермичны; энергия высвобождается образцом материи, когда происходят эти изменения состояния. Таким образом, можно заметить, что образец льда (твердая вода) тает, когда его помещают на горелку или рядом с ней. Тепло передается от горелки к образцу льда; лед получает энергию, вызывая изменение состояния. Но сколько энергии потребуется, чтобы вызвать такое изменение состояния? Существует ли математическая формула, которая могла бы помочь в определении ответа на этот вопрос? Наверняка есть.
Количество энергии, необходимое для изменения состояния образца материи, зависит от трех факторов. Это зависит от того, что представляет собой вещество, от того, насколько вещество претерпевает изменение состояния и от того, какое изменение состояния происходит. Например, для плавления льда (твердой воды) требуется разное количество энергии по сравнению с плавлением железа. И для таяния льда (твердой воды) требуется разное количество энергии, чем для испарения того же количества жидкой воды. И, наконец, для плавления 10,0 граммов льда требуется разное количество энергии, чем для плавления 100,0 граммов льда. Вещество, процесс и количество вещества — это три переменные, влияющие на количество энергии, необходимое для того, чтобы вызвать конкретное изменение состояния. Используйте виджет ниже, чтобы исследовать влияние вещества и процесса на изменение энергии. (Обратите внимание, что теплота плавления — это изменение энергии, связанное с переходом из твердого состояния в жидкое.)
И, наконец, для плавления 10,0 граммов льда требуется разное количество энергии, чем для плавления 100,0 граммов льда. Вещество, процесс и количество вещества — это три переменные, влияющие на количество энергии, необходимое для того, чтобы вызвать конкретное изменение состояния. Используйте виджет ниже, чтобы исследовать влияние вещества и процесса на изменение энергии. (Обратите внимание, что теплота плавления — это изменение энергии, связанное с переходом из твердого состояния в жидкое.)
Значения удельной теплоты плавления и удельной теплоты парообразования приводятся на основе на количество . Например, удельная теплота плавления воды равна 333 Дж/г. Чтобы растопить 1 г льда, требуется 333 Дж энергии. Чтобы растопить 10,0 г льда, требуется в 10 раз больше энергии — 3330 Дж. Рассуждения таким образом приводят к следующим формулам, связывающим количество теплоты с массой вещества и теплотой плавления и парообразования.
Для плавления и замораживания: Q = m•ΔH сплавление
Для испарения и конденсации: Q = m•ΔH испарение
где Q представляет собой количество энергии, полученной или высвобожденной в процессе, m представляет собой массу образца, ΔH плавления представляет собой удельную теплоту плавления (в расчете на грамм) и ΔH парообразования представляет собой удельную теплоту плавления испарения (в пересчете на грамм). Подобно обсуждению Q = m•C•ΔT, значения Q могут быть как положительными, так и отрицательными. Значения Q положительны для процесса плавления и парообразования; это согласуется с тем фактом, что образец вещества должен получить энергию, чтобы расплавиться или испариться. Значения Q отрицательны для процессов замерзания и конденсации; это согласуется с тем фактом, что образец вещества должен терять энергию, чтобы замерзнуть или сконденсироваться.
Подобно обсуждению Q = m•C•ΔT, значения Q могут быть как положительными, так и отрицательными. Значения Q положительны для процесса плавления и парообразования; это согласуется с тем фактом, что образец вещества должен получить энергию, чтобы расплавиться или испариться. Значения Q отрицательны для процессов замерзания и конденсации; это согласуется с тем фактом, что образец вещества должен терять энергию, чтобы замерзнуть или сконденсироваться.
В качестве иллюстрации того, как можно использовать эти уравнения, рассмотрим следующие два примера задач.
Пример задачи 3 |
Уравнение, связывающее массу (48,2 г), теплоту плавления (333 Дж/г) и количество энергии (Q), имеет вид Q = m•ΔH слияние . Подстановка известных значений в уравнение приводит к ответу.
Подстановка известных значений в уравнение приводит к ответу.
Q = м•ΔH плавление = (48,2 г)•(333 Дж/г)
Q = 16050,6 Дж
Q = 1,61 x 10 4 Дж = 16,1 кДж (округлено до трех значащих цифр)
Пример Задача 3 включает в себя довольно простой расчет типа «подключи и пыхни». Теперь мы попробуем решить примерную проблему 4, которая потребует значительно более глубокого анализа.
Пример задачи 4 |
В этой задаче лед тает, а жидкая вода остывает. Энергия передается от жидкости к твердому телу. Чтобы растопить твердый лед, необходимо передать 333 Дж энергии на каждый грамм льда. Эта передача энергии от жидкой воды льду охлаждает жидкость. Но жидкость может охлаждаться только до 0°C — точки замерзания воды. При этой температуре жидкость начнет застывать (замерзать) и лед полностью не растает.
Эта передача энергии от жидкой воды льду охлаждает жидкость. Но жидкость может охлаждаться только до 0°C — точки замерзания воды. При этой температуре жидкость начнет застывать (замерзать) и лед полностью не растает.
О льде и жидкой воде известно следующее:
Информация о льде:
м = 50,0 г
ΔH сплав = 333 Дж/г
Информация о жидкой воде:
С = 4,18 Дж/г/°С
T исходная = 26,5°C
Т окончательная = 0,0°С
ΔT = -26,5°C (T окончательная — T исходная )
Энергия, полученная льдом, равна энергии, потерянной водой.
Q лед = -Q жидкая вода
Знак — указывает на то, что один объект получает энергию, а другой объект теряет энергию. Мы можем вычислить левую часть приведенного выше уравнения следующим образом:
Q лед = m•ΔH сплав = (50,0 г)•(333 Дж/г)
Q лед = 16650 Дж
Теперь мы можем положить правую часть уравнения равной m•C•ΔT и начать подставлять известные значения C и ΔT, чтобы найти массу жидкой воды. Решение:
Решение:
16650 J = -Q жидкая вода
16650 Дж = -m жидкая вода •C жидкая вода •ΔT жидкая вода
16650 Дж = -м жидкая вода •(4,18 Дж/г/°C)•(-26,5°C)
16650 Дж = -м жидкая вода •(-110,77 Дж/°C)
m жидкая вода = -(16650 Дж)/(-110,77 Дж/°C)
м жидкая вода = 150,311 г
м жидкая вода = 1,50×10 2 г (округлить до трех значащих цифр)
Новый взгляд на кривые нагрева и охлаждения
На предыдущей странице урока 2 обсуждалась кривая нагрева воды. Кривая нагревания показывала, как температура воды повышалась с течением времени при нагревании образца воды в твердом состоянии (т. е. льда). Мы узнали, что добавление тепла к образцу воды может вызвать либо изменение температуры, либо изменение состояния. При температуре плавления воды добавление тепла вызывает переход воды из твердого состояния в жидкое состояние. А при температуре кипения воды добавление тепла вызывает переход воды из жидкого состояния в газообразное. Эти изменения состояния происходили без каких-либо изменений температуры. Однако добавление тепла к образцу воды, которая не находится при температуре фазового перехода, приведет к изменению температуры.
А при температуре кипения воды добавление тепла вызывает переход воды из жидкого состояния в газообразное. Эти изменения состояния происходили без каких-либо изменений температуры. Однако добавление тепла к образцу воды, которая не находится при температуре фазового перехода, приведет к изменению температуры.
Теперь мы можем подойти к теме кривых отопления на более количественной основе. На приведенной ниже диаграмме представлена кривая нагрева воды. На линиях графика имеется пять помеченных участков.
Три диагональных участка представляют изменения температуры образца воды в твердом состоянии (участок 1), жидком состоянии (участок 3) и газообразном состоянии (участок 5). Два горизонтальных участка отображают изменения состояния воды. В секции 2 происходит таяние пробы воды; твердое тело переходит в жидкое. В секции 4 образец воды подвергается кипячению; жидкость переходит в газ. Количество теплоты, переданной воде в секциях 1, 3 и 5, связано с массой образца и изменением температуры по формуле Q = m•C•ΔT. А количество теплоты, переданной воде в секциях 2 и 4, связано с массой образца и теплотой плавления и парообразования формулами Q = m•ΔH плавление (участок 2) и Q = m•ΔH испарение (участок 4). Итак, теперь мы попытаемся рассчитать количество теплоты, необходимое для перевода 50,0 граммов воды из твердого состояния при -20,0°С в газообразное состояние при 120,0°С. Для расчета потребуется пять шагов — по одному шагу на каждый участок приведенного выше графика. Поскольку удельная теплоемкость вещества зависит от температуры, в наших расчетах мы будем использовать следующие значения удельной теплоемкости:
А количество теплоты, переданной воде в секциях 2 и 4, связано с массой образца и теплотой плавления и парообразования формулами Q = m•ΔH плавление (участок 2) и Q = m•ΔH испарение (участок 4). Итак, теперь мы попытаемся рассчитать количество теплоты, необходимое для перевода 50,0 граммов воды из твердого состояния при -20,0°С в газообразное состояние при 120,0°С. Для расчета потребуется пять шагов — по одному шагу на каждый участок приведенного выше графика. Поскольку удельная теплоемкость вещества зависит от температуры, в наших расчетах мы будем использовать следующие значения удельной теплоемкости:
Твердая вода: C=2,00 Дж/г/°C
Жидкая вода: C = 4,18 Дж/г/°C 90 199 Газообразная вода: C = 2,01 Дж/г/°C
Наконец, мы будем использовать ранее опубликованные значения ΔH плавления (333 Дж/г) и ΔH испарения (2,23 кДж/г).
Раздел 1 : Изменение температуры твердой воды (льда) с -20,0°C до 0,0°C.
Использование Q 1 = m•C•ΔT
, где m = 50,0 г, C = 2,00 Дж/г/°C, T исходный = -200°C и T окончательная = 0,0°C
Q 1 = m•C•ΔT = (50,0 г)•(2,00 Дж/г/°C)•(0,0°C — -20,0°C)
Q 1 = 2,00 x 10 3 Дж = 2,00 кДж
Раздел 2 : Таяние льда при 0,0°C.
Использование Q 2 = m•ΔH сплавление
, где m = 50,0 г и ΔH сплава = 333 Дж/г
Q 2 = m•ΔH сплав = (50,0 г)•(333 Дж/г)
Q 2 = 1,665 x 10 4 Дж = 16,65 кДж
Q 2 = 16,7 кДж (округлено до 3 значащих цифр)
Раздел 3 : Изменение температуры жидкой воды с 0,0°C до 100,0°C.
Использование Q 3 = m•C•ΔT
, где m = 50,0 г, C = 4,18 Дж/г/°C, T начальная = 0,0°C и T конечная = 100,0°C
Q 3 = m•C•ΔT = (50,0 г)•(4,18 Дж/г/°C)•(100,0°C — 0,0°C)
Q 3 = 2,09 x 10 4 Дж = 20,9 кДж
Раздел 4 : Кипячение воды при 100,0°C.
Использование Q 4 = m•ΔH испарение
, где m = 50,0 г и ΔH испарения = 2,23 кДж/г
Q 4 = м•ΔH испарение = (50,0 г)•(2,23 кДж/г)
Q 4 = 111,5 кДж
Q 4 = 112 кДж (округлено до 3 значащих цифр)
Раздел 5 : Изменение температуры жидкой воды со 100,0°C до 120,0°C.
Использование Q 5 = m•C•ΔT
, где m = 50,0 г, C = 2,01 Дж/г/°C, T начальная = 100,0°C и T конечная = 120,0°C
Q 5 = m•C•ΔT = (50,0 г)•(2,01 Дж/г/°C)•(120,0°C — 100,0°C)
Q 5 = 2,01 x 10 3 Дж = 2,01 кДж
Общее количество тепла, необходимое для превращения твердой воды (льда) при -20°C в газообразную воду при 120°C, представляет собой сумму значений Q для каждого участка графика. то есть
Q всего = Q 1 + Q 2 + Q 3 + Q 4 + Q 5
Суммирование этих пяти цифр числа Q приводит к правильному значащему числу Q и округлению значение 154 кДж как ответ на исходный вопрос.
В приведенном выше примере есть несколько особенностей решения, над которыми стоит задуматься:
- Во-первых: длинная задача была разделена на части, каждая из которых представляет одну из пяти секций графа. Поскольку вычислялось пять значений Q, они были помечены как Q 1 , Q 2 и т. д. Этот уровень организации требуется в такой многошаговой задаче, как эта.
- Секунда: внимание было уделено знаку +/- на ΔT. Изменение температуры (или любой величины) всегда рассчитывается как конечное значение величины минус начальное значение этой величины.
- Третье: Внимание уделялось юнитам на протяжении всей проблемы. Единицы Q будут либо в джоулях, либо в килоджоулях, в зависимости от того, какие величины умножаются. Пренебрежение вниманием к единицам измерения является распространенной причиной сбоев в подобных задачах.
- Четвертое: внимание уделялось значащим цифрам на протяжении всей задачи. Хотя это никогда не должно становиться основным акцентом любой проблемы в физике, это, безусловно, деталь, на которую стоит обратить внимание.

Здесь, на этой странице, мы узнали, как рассчитать количество тепла, задействованного в любом процессе нагрева/охлаждения и в любом процессе изменения состояния. Это понимание будет иметь решающее значение, когда мы перейдем к следующей странице урока 2 по теме калориметрии. Калориметрия — это наука, связанная с определением изменений энергии системы путем измерения теплообмена с окружающей средой.
Проверьте свое понимание
1. Вода обладает необычно высокой удельной теплоемкостью. Какое из следующих утверждений логически следует из этого факта?
а. По сравнению с другими веществами горячая вода вызывает сильные ожоги, потому что она хорошо проводит тепло.
б. По сравнению с другими веществами вода при нагревании быстро нагревается до высоких температур.
в. По сравнению с другими веществами, пробе воды требуется значительное количество тепла, чтобы изменить ее температуру на небольшое количество.
2. Объясните, почему большие водоемы, такие как озеро Мичиган, могут быть довольно холодными в начале июля, несмотря на то, что температура наружного воздуха около или выше 90°F (32°C).
3. В таблице ниже описывается термический процесс для различных объектов (обозначены красным жирным шрифтом). Для каждого описания укажите, получает или теряет тепло объект, является ли процесс эндотермическим или экзотермическим, и является ли Q для указанного объекта положительным или отрицательным значением.
| Процесс | Получение или потеря тепла? | Эндо- или экзотермический? | В: + или -? | |
а. | Кубик льда кладут в стакан с лимонадом комнатной температуры, чтобы охладить напиток. | |||
б. | Стакан холодного лимонада стоит на столе для пикника под жарким полуденным солнцем и нагревается до 32°F. | |||
в. | Горелки на электроплите выключаются и постепенно остывают до комнатной температуры. | |||
д. | Учитель достает из термоса большой кусок сухого льда и кладет его в воду. Сухой лед возгоняется, образуя газообразный углекислый газ. | |||
эл. | Водяной пар в увлажненном воздухе попадает на окно и превращается в каплю росы (капли жидкой воды). |
4. Образец металлического цинка весом 11,98 г помещают в баню с горячей водой и нагревают до 78,4°C. Затем его удаляют и помещают в чашку из пенопласта, содержащую 50,0 мл воды комнатной температуры (T=27,0°C, плотность = 1,00 г/мл). Вода прогревается до температуры 28,1°C. Определить удельную теплоемкость цинка.
Вода прогревается до температуры 28,1°C. Определить удельную теплоемкость цинка.
5. Джейк берет из шкафа банку газировки и наливает ее в чашку со льдом. Определить количество теплоты, отдаваемое газировкой комнатной температуры при ее плавлении 61,9.г льда (ΔH сплав = 333 Дж/г).
6. Теплота возгонки (ΔH сублимация ) сухого льда (твердая двуокись углерода) составляет 570 Дж/г. Определите количество теплоты, необходимое для превращения 5,0-фунтового мешка сухого льда в газообразный диоксид углерода. (Дано: 1,00 кг = 2,20 фунта)
7. Определите количество тепла, необходимое для повышения температуры образца твердого пара-дихлорбензола массой 3,82 грамма с 24°C до его жидкого состояния при 75°C. Пара-дихлорбензол имеет температуру плавления 54°C, теплоту плавления 124 Дж/г и удельную теплоемкость 1,01 Дж/г/°C (твердое состояние) и 1,19Дж/г/°C (жидкое состояние).
Следующий раздел:
ChemTeam: как определить удельную теплоемкость: задача 1
ChemTeam: Как определить удельную теплоемкость: задача 1–10Как определить удельную теплоемкость вещества
Задачи №1–10
Перейти к учебнику по удельной теплоемкости
Вернуться в меню термохимии
Задача №1: Предположим, что кусок железа массой 21,5 г при температуре 100,0 °C брошен в изолированный сосуд с водой. Масса воды 132,0 г, ее температура перед добавлением железа 20,0 °С. Какой будет конечная температура системы? Удельная теплоемкость железа 0,449.кДж/кг К.
Масса воды 132,0 г, ее температура перед добавлением железа 20,0 °С. Какой будет конечная температура системы? Удельная теплоемкость железа 0,449.кДж/кг К.
Решение:
1) С
q потеряно, металл = q получено, вода
пишем
(масса) (Δt) (C p, металл ) = (масса) (Δt) (C p, вода )
2) Замена:
(21,5) (100 — х) (0,449) = (132,0) (х — 20) (4,184)
Некоторые пояснения:
а) 100 − x – Δt для металла; она начинается при 100,0 °C и падает до неизвестного конечного значения.
б) x − 20 – Δt для воды; она начинается при 20,0 °C и поднимается до какого-то неизвестного конечного значения.
c) Поскольку и металл, и вода имеют одно и то же конечное значение, нам нужно использовать только одно неизвестное для двух выражений Δt.
3) Немного алгебры:
(2150 − 21,5x) (0,449) = (132x − 2640) (4,184)965,35 — 9,6535х = 552,288х — 11045,76
561,9415x = 12011,11
На 3 знака инжира ответ равен 21,4 °C.
Проблема №2: Образец неизвестного металла массой 12,48 г, нагретый до 99,0 °С, затем погружали в 50,0 мл воды с температурой 25,0 °С. Температура воды поднялась до 28,1°С. Предполагая отсутствие потерь энергии в окружающую среду:
1. Сколько джоулей энергии поглотила вода?
2. Сколько джоулей энергии потерял металл?
3. Какова теплоемкость металла?
4. Что такое удельная теплоемкость металла?
Решение:
1) q = (50,0 г) (3,1 °C) (4,184 Дж г¯ 1 °С¯ 1 ) = 648,52 Дж2) 648,52 Дж
3) 648,52 Дж / 70,9 °С = 9,147 Дж/°С
4) 9,147 Дж/°C разделить на 12,48 г = 0,733 Дж г¯ 1 °C¯ 1
Комментарий №1: в этом вопросе не используется формулировка q потерянных = q приобретенных других вопросов. Это потому, что вопрос разбит на четыре части. Обратите внимание, что части (1) и (2) эквивалентны q потерянных = q приобретенных и что (4) является обычным ответом, который ищут в задачах этого типа.
Комментарий №2: (3) — шаг, ненужный для решения (4). Именно там вы заметите разницу между теплоемкостью и удельной теплоемкостью.
Задача №3: Блок неизвестного металла массой 43,2 г при температуре 89,0 °C был брошен в изотермический сосуд, содержащий 43,00 г льда и 26,00 г воды при 0 °C. После того, как система достигла равновесия, было определено, что 9,15 г льда растаяли. Чему равна удельная теплоемкость металла? (Теплота плавления льда = 334,166 Дж г¯ 1 .)
Решение:
Комментарий: этот вариант обычных подозреваемых (подробно описанных выше) НЕ включает изменение температуры воды, только металла. Скорее, часть льда тает, и вся система лед-вода остается при нуле по Цельсию. Очень интересно!
1) Определить теплоту, полученную таявшим льдом:
9,15 г умножить на 334,166 Дж г¯ 1 = 3057,62 Дж
2) Подставьте и решите удельную теплоемкость:
q = (масса) (Δt) (C р, металл )3057,62 Дж = (43,2 г) (89,0 °С) (х)
x = 0,795 Дж г¯ 1 °C¯ 1
Задача № 4: Блок металла весом 35,0 г при температуре 80,0 °C добавляют к смеси 100,0 г воды и 15,0 г льда в изолированном контейнере. Весь лед растаял, и температура в контейнере поднялась до 10,0 °С. Чему равна удельная теплоемкость металла?
Весь лед растаял, и температура в контейнере поднялась до 10,0 °С. Чему равна удельная теплоемкость металла?
Решение:
1) Определить теплоту, необходимую для растапливания льда:
q = (15,0 г) (334,166 Дж g¯ 1 ) = 5012,49 ДжОбратите внимание, что 100 г воды еще не упоминаются.
2) Определить количество тепла, необходимое для нагревания 115 г воды от 0 до 10,0 °С:
q = (115 г) (10,0 °C) (4,184 Дж g¯ 1 °C¯ 1 ) = 4811,6 ДжОбратите внимание на растаявшие 15 г льда. Также обратите внимание, что температура воды была нулевой °C. Мы знаем это по наличию льда.
3) Определите удельную теплоемкость металла:
(5012,49 Дж + 4811,6 Дж) = (35,0 г) (70,0 °С) (х)x = 4,01 Дж г¯ 1 °C¯ 1
Задача № 5: Образец элемента весом 500,0 г при температуре 153,0 °C падает в смесь льда и воды. 109,5 г льда растаяли и осталась смесь лед-вода. Чему равна удельная теплоемкость металла в Дж/г-°С? Учитывая молярную теплоемкость металла 26,31 Дж/моль°C, каковы атомный вес и идентичность металла?
109,5 г льда растаяли и осталась смесь лед-вода. Чему равна удельная теплоемкость металла в Дж/г-°С? Учитывая молярную теплоемкость металла 26,31 Дж/моль°C, каковы атомный вес и идентичность металла?
Решение:
1) Определить энергию, необходимую для растапливания льда:
(6,02 кДж/моль) (109,5 г / 18,015 г/моль) = 36,5912 кДж
2) Определить удельную теплоемкость:
36591,2 Дж = (500,0 г) (153,0 °С) (х)х = 0,4783 Дж/г-°C
Примечание: мы знаем, что изменение температуры составляет 153,0 °C, потому что в воде все еще есть лед. Это означает, что смесь льда и воды оставалась при нуле по Цельсию, когда растаяли 109,5 г льда.
3) Определить атомную массу элемента:
(0,4783 Дж/г °С) (x) = 26,31 Дж/моль °Сх = 55,0 г/моль
Элемент марганец.
Задача № 6: Образец неизвестного металла весом 12,48 г нагревают до 99,0 °C, а затем погружают в 50,0 мл воды с температурой 25,0 °C. Температура воды поднялась до 28,1°C.
Температура воды поднялась до 28,1°C.
а) Сколько джоулей энергии поглотила вода?
б) Сколько джоулей энергии потерял металл?
(в) Какова теплоемкость металла?
(г) Какова удельная теплоемкость металла?
Определения теплоемкости и удельной теплоемкости можно найти здесь.
1) Решение (а):
q = (50,0 г) (3,1 °C) (4,181 Дж г¯ 1 °C¯ 1 ) = 648,52 Дж
Я использовал 50,0 г, потому что плотность воды составляет 1,00 г/мл, а у меня было 50,0 мл воды.
2) Решение (б):
q = 648,52 Дж
Мы предполагаем, что все тепло, поглощенное водой, было потеряно металлом. Предполагается отсутствие потерь тепловой энергии наружу при передаче.
3) Решение (с):
648,52 Дж / 74,0 °C = 8,76 Дж/°C (или 8,76 Дж/К)
4) Решение (г):
(50,0 г) (3,1 °C) (4,181 Дж г¯ 1 °C¯ 1 ) = (12,48 г) (74,0 °C) (x)Найдите х.
Задача № 7: Какова удельная теплоемкость металла, если прибавление 90,0 г металла при 17,7 °С к 210,0 г меди (s = 0,385 Дж/г-°С) при 153,7 °С дает смеси, достигающей теплового равновесия при 129,1 °С?
Решение:
Комментарий: обратите внимание, что два металла добавляются друг к другу. Представьте себе ситуацию, когда каждый образец состоит из пыли или очень мелких гранул. Затем два сухих образца быстро перемешивают.(90,0 г) (111,4 °C) (x) = (210,0 г) (24,6 °C) (0,385 Дж/г-°C)
х = 0,198 Дж/г-°C
Задача № 8: Блок неизвестного металла массой 31,0 грамм при температуре 88,0 °C был брошен в изолированную колбу, содержащую примерно 30,0 граммов льда и 20,0 граммов воды при 0,0 °C. После того, как система достигла постоянной температуры, было определено, что 12,1 грамма льда растаяли. Чему равна удельная теплоемкость металла? Теплота плавления льда равна 334,166 Дж/г.
Решение:
12,0 г умножить на 334,166 Дж/г = 4009,992 Дж4009,992 Дж = (31,0 г) (88,0 °С) (х)
х = 1,47 Дж/г °С
Комментарий: тот факт, что лед остался в воде, когда температура достигла равновесия, означает, что смесь воды и льда оставалась при нуле по Цельсию. Это означает, что металл перешел от 88,0 ° C к 0 ° C для Δt 88,0 ° C.
Задача №9: Образец метанола массой 25,95 г при температуре 35,60 °C добавляют к образцу этанола массой 38,65 г при температуре 24,70 °C в калориметре постоянного давления. Если конечная температура объединенных жидкостей 28,65 °С, а теплоемкость калориметра 19.3 Дж/Кл, определите удельную теплоемкость метанола.
Решение:
тепло, теряемое метанолом, идет на (1) нагрев этанола и (2) нагрев калориметра(25,95 г) (6,95 °C) (x) = (38,65 г) (3,95 °C) (2,44 Дж г -1 °C -1 ) + (3,95 °C) (19,3 Дж/C)
x = 2,49 Дж г -1 °C -1
Задача №10: Учащийся нагревает 130-граммовый кусок неизвестного сероватого металла до темп. из 99,2 °С. она помещает металл в чашку из пенопласта, содержащую 55,7 г воды при температуре 23,0 °C. Горячий металл нагревает воду в чашке до 31,4 °C.
из 99,2 °С. она помещает металл в чашку из пенопласта, содержащую 55,7 г воды при температуре 23,0 °C. Горячий металл нагревает воду в чашке до 31,4 °C.
а) Рассчитайте удельную теплоемкость металла.
б) Каков атомный вес?
c) Определите металл.
Решение:
q = (55,7 г) (8,4 °C) (4,184 Дж г¯ 1 °C¯ 1 = 1957,61 Дж1957,61 Дж = (130 г) (67,8 °С) (х)
шп вт. = 0,222 Дж г¯ 1 °C¯ 1
Используйте закон Дюлонга–Пти:
М = 3Р/сп. хт
M = (3) (8,31446 Дж моль¯ 1 K¯ 1 ) / 0,222 Дж г¯ 1 K¯ 1
M = 112 г/моль
Кадмий
Обратите внимание на сдвиг от °C к K. Это разрешено, потому что «размер» одного °C равен «размеру» одного K.
Перейти к руководству по удельной теплоемкости
Вернуться в меню термохимии
14.2 Изменение температуры и теплоемкость – College Physics: OpenStax
Глава 14 Тепло и методы теплопередачи
Резюме
- Наблюдайте за теплопередачей и изменением температуры и массы.

- Рассчитать конечную температуру после теплопередачи между двумя объектами.
Одним из основных эффектов теплопередачи является изменение температуры: нагревание повышает температуру, а охлаждение снижает ее. Мы предполагаем, что фазового перехода нет и что над системой или системой не совершается никакой работы. Опыты показывают, что передаваемое тепло зависит от трех факторов — изменения температуры, массы системы, вещества и фазы вещества.
Рисунок 1. Теплота, передаваемая для изменения температуры, зависит от величины изменения температуры, массы системы, а также вовлеченного вещества и фазы. а) Количество переданного тепла прямо пропорционально изменению температуры. Чтобы удвоить изменение температуры массы m , нужно удвоить теплоту. б) Количество переданного тепла также прямо пропорционально массе. Чтобы вызвать эквивалентное изменение температуры в удвоенной массе, нужно добавить в два раза больше тепла. в) Количество переданного тепла зависит от вещества и его фазы. Если требуется сумма Q тепла, чтобы вызвать изменение температуры Δ T в заданной массе меди, потребуется в 10,8 раз больше тепла, чтобы вызвать эквивалентное изменение температуры в той же массе воды при условии отсутствия фазового перехода в любом веществе.
в) Количество переданного тепла зависит от вещества и его фазы. Если требуется сумма Q тепла, чтобы вызвать изменение температуры Δ T в заданной массе меди, потребуется в 10,8 раз больше тепла, чтобы вызвать эквивалентное изменение температуры в той же массе воды при условии отсутствия фазового перехода в любом веществе. Зависимость от изменения температуры и массы легко понять. Благодаря тому, что (средняя) кинетическая энергия атома или молекулы пропорциональна абсолютной температуре, внутренняя энергия системы пропорциональна абсолютной температуре и числу атомов или молекул. Благодаря тому, что переданное тепло равно изменению внутренней энергии, теплота пропорциональна массе вещества и изменению температуры. Переносимое тепло также зависит от вещества, так что, например, теплота, необходимая для повышения температуры, для спирта меньше, чем для воды. Для одного и того же вещества передаваемая теплота также зависит от фазы (газовая, жидкая или твердая). { \circ}\textbf{C)}}.[/latex]Напоминаем, что изменение температуры[latex]\boldsymbol{(\Delta{T})}[/latex]одинаково в единицах кельвина и градусах Цельсия. Если теплоотдачу измерять в килокалориях, то 9{\circ}\textbf{C)}}.[/латекс]
{ \circ}\textbf{C)}}.[/latex]Напоминаем, что изменение температуры[latex]\boldsymbol{(\Delta{T})}[/latex]одинаково в единицах кельвина и градусах Цельсия. Если теплоотдачу измерять в килокалориях, то 9{\circ}\textbf{C)}}.[/латекс]
Значения удельной теплоемкости обычно нужно искать в таблицах, потому что нет простого способа их рассчитать. В общем случае удельная теплоемкость также зависит от температуры. В таблице 1 приведены репрезентативные значения удельной теплоемкости для различных веществ. За исключением газов, зависимость теплоемкости большинства веществ от температуры и объема слабая. Из этой таблицы мы видим, что удельная теплоемкость воды в пять раз больше, чем у стекла, и в десять раз больше, чем у железа, а это значит, что требуется в пять раз больше теплоты, чтобы поднять температуру воды на ту же величину, что и для стекла, и в десять раз больше, чем для стекла. много тепла, чтобы поднять температуру воды, как для железа. На самом деле вода имеет одну из самых больших удельных теплоемкостей среди всех материалов, что важно для поддержания жизни на Земле. 9{\circ}\textbf{C}}.[/latex](a) Сколько тепла требуется? Какой процент тепла используется для повышения температуры (b) кастрюли и (c) воды?
9{\circ}\textbf{C}}.[/latex](a) Сколько тепла требуется? Какой процент тепла используется для повышения температуры (b) кастрюли и (c) воды?
Стратегия
Посуда и вода всегда имеют одинаковую температуру. Когда вы ставите кастрюлю на плиту, температура воды и сковороды увеличивается на одинаковую величину. Воспользуемся уравнением теплообмена при заданном изменении температуры и массы воды и алюминия. Удельные теплоемкости воды и алюминия приведены в табл. 1. 94\textbf{J}=27.0\textbf{кДж}}.[/latex]
[латекс]\boldsymbol{Q_{\textbf{Всего}}=Q_{\textbf{W}}+Q_{\textbf{Al}}=62,8\textbf{кДж}+ 27,0\textbf{кДж}=89,8\ textbf{кДж}}.[/латекс]
Таким образом, количество тепла, идущего на нагрев сковороды, равно
[латекс]\boldsymbol{\frac{27,0\textbf{кДж}}{89,8\textbf{кДж}}}[/latex][латекс]\boldsymbol {\times100\%=30,1\%},[/латекс]
, а количество, идущее на нагрев воды, равно
[латекс]\boldsymbol{\frac{62,8\textbf{кДж}}{89,8\textbf{кДж}}}[/latex][латекс]\boldsymbol{\times100 \%=69,9\%}. [/latex]
[/latex]
Обсуждение
В этом примере тепло, переданное контейнеру, составляет значительную долю от общего количества переданного тепла. Хотя масса кастрюли в два раза больше массы воды, удельная теплоемкость воды более чем в четыре раза больше, чем у алюминия. Следовательно, для достижения заданного изменения температуры воды требуется чуть более чем в два раза больше тепла по сравнению с алюминиевой кастрюлей.
Рисунок 2. Дымящиеся тормоза на этом грузовике являются видимым свидетельством механического эквивалента тепла.Пример 2: Расчет увеличения температуры по работе, проделанной над веществом: Перегрев тормозов грузовика при движении под уклон тормозной материал. Это преобразование предотвращает преобразование потенциальной энергии гравитации в кинетическую энергию грузовика. Проблема заключается в том, что масса грузовика велика по сравнению с массой тормозного материала, поглощающего энергию, и повышение температуры может происходить слишком быстро, чтобы достаточное количество тепла передавалось от тормозов в окружающую среду.
 9{\circ}\textbf{C}}[/latex], если материал удерживает 10% энергии от 10 000-килограммового грузовика, спускающегося с высоты 75,0 м (при вертикальном перемещении) с постоянной скоростью.
9{\circ}\textbf{C}}[/latex], если материал удерживает 10% энергии от 10 000-килограммового грузовика, спускающегося с высоты 75,0 м (при вертикальном перемещении) с постоянной скоростью.Стратегия
Если тормоза не задействованы, гравитационная потенциальная энергия преобразуется в кинетическую энергию. При торможении потенциальная энергия гравитации преобразуется во внутреннюю энергию тормозного материала. Сначала мы вычисляем гравитационную потенциальную энергию[латекс]\boldsymbol{(Mgh)}[/латекс], которую весь грузовик теряет при спуске, а затем находим повышение температуры только в тормозном материале. 9{\circ}\textbf{C}}.[/латекс]
Обсуждение
Эта температура близка к температуре кипения воды. Если бы грузовик какое-то время ехал, то непосредственно перед спуском температура тормозов, вероятно, была бы выше температуры окружающей среды. Повышение температуры при спуске, вероятно, повысит температуру тормозного материала выше точки кипения воды, поэтому этот метод нецелесообразен. Однако та же идея лежит в основе новейшей гибридной технологии автомобилей, где механическая энергия (потенциальная энергия гравитации) преобразуется тормозами в электрическую энергию (аккумулятор).
Однако та же идея лежит в основе новейшей гибридной технологии автомобилей, где механическая энергия (потенциальная энергия гравитации) преобразуется тормозами в электрическую энергию (аккумулятор).
| Вещества | Удельная теплоемкость ( c ) | |
|---|---|---|
| Твердые вещества | Дж/кг⋅ºC | ккал/кг⋅ºC 2 |
| Алюминий | 900 | 0,215 |
| Асбест | 800 | 0,19 |
| Бетон, гранит (средний) | 840 | 0,20 |
| Медь | 387 | 0,0924 |
| Стекло | 840 | 0,20 |
| Золото | 129 | 0,0308 |
| Тело человека (в среднем при 37 °C) | 3500 | 0,83 |
| Лед (средний, от -50°C до 0°C) | 2090 | 0,50 |
| Железо, сталь | 452 | 0,108 |
| Свинец | 128 | 0,0305 |
| Серебро | 235 | 0,0562 |
| Дерево | 1700 | 0,4 |
| Жидкости | ||
| Бензол | 1740 | 0,415 |
| Этанол | 2450 | 0,586 |
| Глицерин | 2410 | 0,576 |
| Меркурий | 139 | 0,0333 |
| Вода (15,0 °C) | 4186 | 1. 000 000 |
| Газы 3 | ||
| Воздух (сухой) | 721 (1015) | 0,172 (0,242) |
| Аммиак | 1670 (2190) | 0,399 (0,523) |
| Углекислый газ | 638 (833) | 0,152 (0,199) |
| Азот | 739 (1040) | 0,177 (0,248) |
| Кислород | 651 (913) | 0,156 (0,218) |
| Пар (100°C) | 1520 (2020) | 0,363 (0,482) |
| Таблица 1. Удельная теплоемкость 1 Различных веществ | ||
Обратите внимание, что Пример 2 является иллюстрацией механического эквивалента тепла. В качестве альтернативы, повышение температуры может быть произведено с помощью паяльной лампы вместо механического. 9{\circ}\textbf{C}}.[/latex]Предположим, что кастрюля находится на изолированной подушке и что незначительное количество воды выкипает. При какой температуре вода и кастрюля через короткое время достигают теплового равновесия?
При какой температуре вода и кастрюля через короткое время достигают теплового равновесия?
Стратегия
Кастрюля размещена на изолирующей подушке, чтобы обеспечить небольшой теплообмен с окружающей средой. Первоначально кастрюля и вода не находятся в тепловом равновесии: кастрюля имеет более высокую температуру, чем вода. Затем теплопередача восстанавливает тепловое равновесие, когда вода и кастрюля соприкасаются. Поскольку теплопередача между кастрюлей и водой происходит быстро, масса испаряемой воды пренебрежимо мала, а величина тепла, теряемого кастрюлей, равна теплу, приобретаемому водой. Обмен теплом прекращается, как только достигается тепловое равновесие между чашей и водой. Теплообмен можно записать как[латекс]\жирныйсимвол{|Q_{\textbf{горячий}}|=Q_{\textbf{холодный}}}.[/латекс] 9{\circ}\textbf{C})}.[/латекс]
 {\circ}\textbf{C}).} \end{массив}[/latex] 9{\circ}\textbf{C}}?[/latex]Причина в том, что вода имеет большую удельную теплоемкость, чем большинство обычных веществ, и, таким образом, подвергается небольшому изменению температуры при заданной теплопередаче. Большому водоему, такому как озеро, требуется большое количество тепла, чтобы заметно повысить его температуру. Это объясняет, почему температура озера остается относительно постоянной в течение дня даже при больших изменениях температуры воздуха. Однако температура воды меняется в течение более длительного времени (например, с лета на зиму).
{\circ}\textbf{C}).} \end{массив}[/latex] 9{\circ}\textbf{C}}?[/latex]Причина в том, что вода имеет большую удельную теплоемкость, чем большинство обычных веществ, и, таким образом, подвергается небольшому изменению температуры при заданной теплопередаче. Большому водоему, такому как озеро, требуется большое количество тепла, чтобы заметно повысить его температуру. Это объясняет, почему температура озера остается относительно постоянной в течение дня даже при больших изменениях температуры воздуха. Однако температура воды меняется в течение более длительного времени (например, с лета на зиму).ДОМАШНИЙ ЭКСПЕРИМЕНТ: ИЗМЕНЕНИЕ ТЕМПЕРАТУРЫ ЗЕМЛИ И ВОДЫ
Что нагревается быстрее, земля или вода?
Для изучения различий в теплоемкости:
- Поместите равные массы сухого песка (или почвы) и воды одинаковой температуры в два небольших сосуда. (Средняя плотность почвы или песка примерно в 1,6 раза выше плотности воды, поэтому вы можете получить примерно равные массы, используя [латекс]\boldsymbol{50\%}[/латекс]больше воды по объему.
 )
) - Нагревайте оба (используя духовку или тепловую лампу) в течение одинакового времени.
- Запишите конечную температуру двух масс.
- Теперь доведите обе банки до одинаковой температуры, нагревая их в течение более длительного периода времени.
- Снимите банки с источника тепла и измеряйте их температуру каждые 5 минут в течение примерно 30 минут.
Какой образец остывает быстрее? Эта деятельность воспроизводит явления, ответственные за наземные и морские бризы.
- Перенос тепла[латекс]\boldsymbol{Q}[/латекс], приводящий к изменению[латекс]\жирныйсимвол{\Delta{T}}[/латекс]температуры тела массой[латекс] \boldsymbol{m}[/latex]является[латекс]\boldsymbol{Q=mc\Delta{T}},[/latex]где[латекс]\boldsymbol{c}[/latex]является удельной теплоемкостью материала . Это соотношение также можно рассматривать как определение удельной теплоемкости. 9{\circ}\textbf{C}},[/latex], если не указано иное, и при среднем давлении 1,00 атм. В скобках указаны значения [латекс]\жирный символ{c_{\textbf{p}}}[/латекс]при постоянном давлении 1,00 атм.

- удельная теплоемкость
- количество теплоты, необходимое для изменения температуры 1,00 кг вещества на 1,00 ºC
- Проверить теплопередачу.
- Рассчитать конечную температуру по теплопередаче.
- Определите известные величины.
 Масса льда м льда = 3 × 6,0 г = 0,018 кг, а масса соды м соды = 0,25 кг.
Масса льда м льда = 3 × 6,0 г = 0,018 кг, а масса соды м соды = 0,25 кг. - Рассчитайте члены в числителе: м сода c Вт (20ºC)=(0,25 кг)(4186 Дж/кг ⋅ ºC)(20ºC) = 20 930 Дж и 9{\ circ} \ text {C} \\ [/ латекс]
- Изучите ситуацию, чтобы определить, есть ли изменение температуры или фазы. Осуществляется ли передача тепла в систему или из нее? Если наличие или отсутствие фазового перехода неочевидно, можно сначала решить задачу, как если бы фазовых переходов не было, и изучить полученное изменение температуры. Если этого достаточно, чтобы преодолеть точку кипения или плавления, вам следует вернуться назад и решить задачу поэтапно — изменение температуры, изменение фазы, последующее изменение температуры и так далее.

- Определите и перечислите все объекты, изменяющие температуру и фазу.
- Точно определите, что нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
- Составьте список того, что дано или что может быть выведено из поставленной задачи (укажите известное).
- Решите соответствующее уравнение для определяемой величины (неизвестной). При изменении температуры переданное тепло зависит от удельной теплоемкости (см. Таблицу 1 в разделе «Изменение температуры и теплоемкость»), тогда как при фазовом переходе переданное тепло зависит от скрытой теплоты. См. Таблицу 1.
- Подставьте известные числа вместе с их единицами измерения в соответствующее уравнение и получите численное решение с единицами измерения. Вам нужно будет сделать это пошагово, если процесс состоит из более чем одной стадии (например, изменение температуры с последующим изменением фазы).
- Проверьте ответ, чтобы убедиться, что он разумен: Имеет ли он смысл? Например, убедитесь, что изменение температуры не вызывает фазового перехода, который вы не учли.

- Большинство веществ могут существовать в твердой, жидкой и газообразной формах, которые называются «фазами».
- Фазовые превращения происходят при фиксированных температурах для данного вещества при данном давлении, и эти температуры называются точками кипения и замерзания (или плавления).
- Во время фазовых переходов поглощаемое или выделяемое тепло определяется по формуле: Q = мл , где L – коэффициент скрытой теплоты.

- Теплопередача может вызывать температурные и фазовые изменения. Что еще может вызвать эти изменения?
- Каким образом скрытая теплота плавления воды помогает замедлить снижение температуры воздуха, возможно, предотвращая падение температуры значительно ниже ºC вблизи больших водоемов?
- Какова температура льда сразу после того, как он образовался замерзшей водой?
- Что произойдет, если поместить лед ºC в воду ºC в изолированном контейнере? Растает ли часть льда, замерзнет ли больше воды или не произойдет ни того, ни другого?
- Какое влияние оказывает конденсация на стакане ледяной воды на скорость таяния льда? Конденсация ускорит процесс плавления или замедлит его?
- В очень влажном климате, где есть многочисленные водоемы, например, во Флориде, температура редко поднимается выше 35ºC (95ºF). Однако в пустынях температура может подняться намного выше. Объясните, как испарение воды помогает ограничить высокие температуры во влажном климате.

- Зимой в Сан-Франциско часто бывает теплее, чем в соседнем Сакраменто, находящемся в 150 км от побережья. Летом в Сакраменто почти всегда жарче. Объясните, как водоемы, окружающие Сан-Франциско, смягчают экстремальные температуры.
- Накрытие крышки на кипящую кастрюлю значительно снижает теплопередачу, необходимую для поддержания кипения. Объяснить, почему.
- Сублимированные продукты были обезвожены в вакууме. Во время процесса пища замерзает и должна быть нагрета, чтобы облегчить обезвоживание. Объясните, как вакуум ускоряет обезвоживание и почему продукты в результате замерзают.
- Когда неподвижный воздух охлаждается за счет излучения в ночное время, температура обычно не падает ниже точки росы. Объяснить, почему.
- На демонстрации в классе физики инструктор надувает воздушный шар ртом, а затем охлаждает его жидким азотом. В холодном состоянии сморщенный шар содержит небольшое количество светло-голубой жидкости, а также несколько кристаллов, похожих на снег.
 При нагревании жидкость закипает, часть кристаллов возгоняется, часть кристаллов задерживается на некоторое время, а затем превращается в жидкость. Определите синюю жидкость и два твердых тела в холодном шаре. Обоснуйте свои идентификации, используя данные из таблицы 1.
При нагревании жидкость закипает, часть кристаллов возгоняется, часть кристаллов задерживается на некоторое время, а затем превращается в жидкость. Определите синюю жидкость и два твердых тела в холодном шаре. Обоснуйте свои идентификации, используя данные из таблицы 1. - Какая теплопередача (в килокалориях) требуется, чтобы оттаять упаковку замороженных овощей массой 0,450 кг при исходной температуре 0ºC, если их теплота плавления такая же, как у воды?
- Пакет со льдом при температуре 0ºC намного эффективнее поглощает энергию, чем пакет, содержащий такое же количество воды при температуре 0ºC. (a) Какая теплопередача необходима для повышения температуры 0,800 кг воды с 0ºC до 30,0ºC? (b) Какая теплопередача требуется, чтобы сначала растопить 0,800 кг льда с температурой 0ºC, а затем повысить его температуру? (c) Объясните, как ваш ответ подтверждает утверждение о том, что лед более эффективен.
- (a) Какая теплопередача требуется, чтобы поднять температуру алюминиевого горшка весом 0,750 кг, содержащего 2,50 кг воды, с 30,0°C до точки кипения, а затем выкипятить 0,750 кг воды? (b) Сколько времени это займет, если скорость теплопередачи составляет 500 Вт 1 Вт = 1 Дж/сек (1 Вт = 1 Дж/сек)?
- Образование конденсата на стакане ледяной воды приводит к тому, что лед тает быстрее, чем в противном случае.
 Если на стакане воды и 200 г льда образуется 8,00 г конденсата, сколько граммов льда при этом растает? Предположим, что другой передачи тепла не происходит.
Если на стакане воды и 200 г льда образуется 8,00 г конденсата, сколько граммов льда при этом растает? Предположим, что другой передачи тепла не происходит. - В поездке вы замечаете, что мешка со льдом весом 3,50 кг хватает в холодильнике в среднем на один день. Какова средняя мощность в ваттах, поступающая в лед, если он начинается при 0ºC и полностью тает до 0ºC воды ровно за один день 1 ватт = 1 джоуль/сек (1 Вт = 1 Дж/сек)?
- В один сухой солнечный день температура в бассейне поднялась бы на 1,50ºC, если бы не испарение. Какая часть воды должна испариться, чтобы унести достаточно энергии, чтобы поддерживать постоянную температуру?
- (a) Какая теплопередача необходима для повышения температуры куска льда массой 0,200 кг с −20,0°C до 130°C, включая энергию, необходимую для фазовых переходов? (b) Сколько времени требуется для каждой стадии при постоянной скорости теплопередачи 20,0 кДж/с? (c) Постройте график зависимости температуры от времени для этого процесса.

- В 1986 году от шельфового ледника Росса в Антарктиде откололся гигантский айсберг. Это был примерно прямоугольник длиной 160 км, шириной 40,0 км и толщиной 250 м. а) Какова масса этого айсберга, если плотность льда равна 917 кг/м 3 ? (б) Сколько теплоты (в джоулях) необходимо для его плавления? (c) Сколько лет потребуется только солнечному свету, чтобы растопить лед такой толщины, если лед поглощает в среднем 100 Вт/м 2 , 12,00 ч в день?
- Сколько граммов кофе должно испариться из 350 г кофе в 100-граммовой стеклянной чашке, чтобы охладить кофе с 95,0°С до 45,0°С? Вы можете предположить, что кофе имеет те же термические свойства, что и вода, и что средняя теплота парообразования составляет 2340 кДж/кг (560 кал/г). (Вы можете пренебречь изменением массы кофе по мере его охлаждения, что даст вам ответ, который немного больше правильного.)
- (a) Трудно потушить пожар на танкере с сырой нефтью, потому что каждый литр сырой нефти выделяет 2,80 × 10 7 Дж энергии при сгорании.
 Чтобы проиллюстрировать эту трудность, подсчитайте количество литров воды, которое необходимо затратить, чтобы поглотить энергию, выделяющуюся при сжигании 1,00 л сырой нефти, если температура воды повышается с 20,0 °С до 100 °С, она закипает, а образующийся пар подняли до 300ºC. (b) Обсудите дополнительные сложности, вызванные тем фактом, что сырая нефть имеет меньшую плотность, чем вода.
Чтобы проиллюстрировать эту трудность, подсчитайте количество литров воды, которое необходимо затратить, чтобы поглотить энергию, выделяющуюся при сжигании 1,00 л сырой нефти, если температура воды повышается с 20,0 °С до 100 °С, она закипает, а образующийся пар подняли до 300ºC. (b) Обсудите дополнительные сложности, вызванные тем фактом, что сырая нефть имеет меньшую плотность, чем вода. - Энергия, высвобождаемая при конденсации во время грозы, может быть очень большой. Рассчитайте энергию, выделившуюся в атмосферу при небольшой грозе радиусом 1 км, предполагая, что 1,0 см дождя выпадает равномерно на этой территории.
- Чтобы предотвратить повреждение от мороза, на фруктовое дерево распыляют 4,00 кг воды с температурой 0ºC. (а) Сколько тепла происходит при замерзании воды? (b) Насколько уменьшится температура 200-килограммового дерева, если это количество тепла будет передано от дерева? Примем удельную теплоемкость равной 3,35 кДж/кг · ºC и предположим, что фазового перехода не происходит.

- Алюминиевая миска весом 0,250 кг, вмещающая 0,800 кг супа при температуре 25,0°C, помещается в морозильную камеру. Какова будет конечная температура, если от миски и супа будет передано 377 кДж энергии, если предположить, что тепловые свойства супа такие же, как у воды?
- Кубик льда весом 0,0500 кг при температуре -30,0°C помещают в 0,400 кг воды при температуре 35,0°C в хорошо изолированном контейнере. Какая конечная температура?
- Если вы выльете 0,0100 кг воды с температурой 20,0 ºC на кусок льда массой 1,20 кг (который изначально имеет температуру -15,0 ºC), какова будет конечная температура? Вы можете предположить, что вода остывает так быстро, что влияние окружающей среды можно пренебречь.
- Коренные жители иногда готовят пищу в водонепроницаемых корзинах, помещая горячие камни в воду, чтобы довести ее до кипения. Какую массу камня с температурой 500°С нужно поместить в 4,00 кг воды с температурой 15,0°С, чтобы довести ее температуру до 100°С, если 0,0250 кг воды выделится в виде пара из начального шипения? Вы можете пренебречь влиянием окружающей среды и принять среднюю удельную теплоемкость горных пород за удельную теплоемкость гранита.

- Какой была бы конечная температура кастрюли и воды в расчете конечной температуры при передаче тепла между двумя телами: заливка холодной воды в горячую кастрюлю, если бы 0,260 кг воды было помещено в кастрюлю и 0,0100 кг воды немедленно испарилось , оставив остаток доходить до общей температуры со сковородой?
- В некоторых странах жидкий азот используется на молоковозах вместо механических холодильников. Для 3-часовой доставки требуется 200 л жидкого азота плотностью 808 кг/м 3 . (a) Рассчитайте теплопередачу, необходимую для испарения этого количества жидкого азота и повышения его температуры до 3,00ºC. (Используйте c p и предположите, что оно постоянно во всем диапазоне температур.) Это значение представляет собой степень охлаждения подачи жидкого азота. (б) Какова эта скорость теплопередачи в киловатт-часах? (c) Сравните степень охлаждения, полученную при плавлении идентичной массы льда при температуре 0ºC, с охлаждающей способностью при испарении жидкого азота.

- Некоторые любители оружия изготавливают свои собственные пули, которые включают плавление и отливку свинцовых пуль. Какая теплопередача необходима, чтобы поднять температуру и расплавить 0,500 кг свинца, начиная с 25,0°С?
- Значения приведены при нормальных температурах плавления и кипения при стандартном атмосферном давлении (1 атм). ↵
- При 37,0ºC (температура тела) теплота парообразования Lv для воды составляет 2430 кДж/кг или 580 ккал/кг ↵
- При 37,0ºC (температура тела) теплота парообразования Lv для воды составляет 2430 кДж/ кг или 580 ккал/кг ↵
- Ответьте на следующие вопросы по термохимии.

- Мармеладный мишка массой 0,88 г сжигается в бомбовом калориметре. Температура начиналась с 21,5°С и стабилизировалась на уровне 24,2°С. Изготовитель бомбового калориметра определил теплоемкость калориметра равной 11,4 кДж/°С. Рассчитайте теплоту сгорания одного грамма мармеладного мишки.
- Ответ
- ΔE = C v ΔT = (11,4 кДж/°C)(24,2-21,5°C) = (11,4 кДж/°C)(2,7°C) = 30,78 кДж (30,78 кДж)/(0,88 г) = 34,98 кДж/г
- При сжигании 100 г образца метана СН 4 в бомбовом калориметре температура изменяется с 21 °С до 31 °С и выделяется 2200 Дж тепла. Какова удельная теплоемкость метана?
- Ответ
- ΔE = C v ΔT ⇒ C v = ΔE/ΔT = (2200 Дж)/(10 °C) = 220 Дж/°C Удельная теплоемкость = C v /г = (220 Дж/°С)/(100 г) = 2,20 Дж/г-°С
- Температура блока меди массой 0,85 кг оказалась равной 21 °C. Медь поместили на солнце и подняли температуру до 28 °C. Примите удельную теплоемкость меди равной 0,385 Дж/г-°С и определите количество теплоты, поглощенное куском меди.

- Ответ
- ΔH = C p ΔT = (850 г)(0,385 Дж/г-°C)(7 °C) = 2291 Дж = 2,3 кДж
- Кусок твердого калия массой 0,258 г помещают в воду внутри калориметра кофейной чашки, что приводит к бурной реакции. Предположим, что общий объем полученного раствора составляет 100 мл. Температура раствора изменяется от 22°C до 25,1°C за счет реакции. Какое количество теплоты выделяется в этой реакции на 1 грамм калия? Предположим, что плотность раствора после реакции равна плотности воды и что теплоемкость раствора и реакционного сосуда обусловлена только водой, имеющей удельную теплоемкость 4,184 Дж/г-°С.
- Ответ
- ΔH = C p ΔT = (100 г) (4,184 Дж/г-°C) (3,1 °C) = 1297 Дж (1297 Дж)/(0,258 г) = 5027 Дж/г .
- Образец натрия массой 22,99 г реагирует с 1,0 л воды в калориметре постоянного давления следующим образом: температура воды колеблется от 20°C до 65°C. Предположим, что объем раствора остается равным 1,0 л, но плотность изменяется до 1,02 г/мл, а удельная теплоемкость изменяется до 4,00 Дж/г-°С.
 Сколько тепла выделяется на каждый моль H 2 (г) произведено?
Сколько тепла выделяется на каждый моль H 2 (г) произведено?- Ответ
- ΔH = C p ΔT = (1000 мл)(1,02 г/мл)(4,00 Дж/г-°C)(45°C) = 183600 Дж = 183,6 кДж
(183,6 кДж)/(0,5 моль H 2 (г)) = 367,2 кДж на моль H 2 (г) .( 22,99 г Na(s) ) ( 1 моль Na 22,99 г Na(s) ) ( 1 моль H 2 (г) 2 моль Na ) = 0,5 моль H 2 (г) 
- ΔH = C p ΔT = (1000 мл)(1,02 г/мл)(4,00 Дж/г-°C)(45°C) = 183600 Дж = 183,6 кДж
- Блок никеля массой 1,5 кг при температуре 100 °С помещают в 500 мл воды с температурой 21 °С. Чему равна конечная температура, если предположить, что удельная теплоемкость никеля равна 0,44 Дж/г-°С, а удельная теплоемкость воды равна 4,184 Дж/г-°С. Подсказка: общее количество потерянного тепла равно общему полученному теплу!
- Ответ
- Общее количество тепла, потерянного Ni = (1500 г Ni) (0,44 Дж/г-°C) (100 °C — T f )
Общее количество тепла, полученное H 2 O = (500 мл)(1 г/1 мл)(4,184 Дж/г-°C)(T ф — 21 °С)
Установите два выражения равными друг другу и найдите T f = 40 °C .
———————
Обратите внимание, что для расчета общего количества тепла, потерянного никелем, конечная температура была вычтена из начальной температуры, чтобы получить положительное число.
Другой способ взглянуть на это — записать выражения для ΔH никеля и ΔH воды, а затем сделать ΔH никеля отрицательным значением ΔH воды.
 Это потому, что Ni выделяет тепло, а вода поглощает такое же количество тепла.
Это потому, что Ni выделяет тепло, а вода поглощает такое же количество тепла.ΔH вода = (500 мл)(1 г/1 мл)(4,184 Дж/г-°C)(T f — 21 °C)
ΔH Ni = (1500 г Ni)(0,44 Дж/г-°C)(T f — 100°C)
ΔH вода = -ΔH Ni дает те же выражения, что и выше.
- Общее количество тепла, потерянного Ni = (1500 г Ni) (0,44 Дж/г-°C) (100 °C — T f )
Общее количество тепла, полученное H 2 O = (500 мл)(1 г/1 мл)(4,184 Дж/г-°C)(T ф — 21 °С)
Установите два выражения равными друг другу и найдите T f = 40 °C .
- Какая химическая реакция соответствует ΔH o f для каждого из следующих веществ?
- HClO
- ½H 2 (г) + ½Cl 2 (г) + ½O 2 (г) → HClO
- С 2 Н 5 ОХ
- 2C(т) + 3H 2 (г) + ½O 2 (г) → C 2 H 5 OH
- КМНО 4
- K(s) + Mn(s) + 2O 2 → KMnO 4
- Ответ
- Ответ
- Ответ
- Используйте Приложение C для расчета ΔH° для каждой из следующих реакций?
- 4FeO(т) + O 2 (г) → 2Fe 2 O 3 (т)
- ΔH rxn = (2 моль)(-822,16 кДж/моль) — (4 моль)(-297,9 кДж/моль) = -452,72 кДж
- H 2 SO 4 (л) + 2NaCl(т) → 2HCl(г) + Na 2 SO 4 (т)
- (-1387,1 кДж) + (2)(-92,30 кДж) — (-814,0 кДж) — (2)(-410,9 кДж) = 64,1 кДж
- 4ХНО 3 (г) + 2H 2 O(г) → 2N 2 H 4 (г) + 7O 2 (г)
- (2)(95,4 кДж) + 0 — 4(-134,63 кДж) — (2)(-241,82 кДж) = 1212 кДж
- C 2 H 5 OH(ж) + O 2 (г) → H 2 O(ж) + CO 2 (г)
- (-285,83 кДж) + (-393,5 кДж) — (-277,7 кДж) — 0 = -401,63 кДж
- Ответ
- Ответ
- Ответ
- Ответ
- Рассчитайте ΔH для
O 3 (г) + 2NO 2 (г) → N 2 O 5 (г) + O 2 (г)
Учитывая следующие уравнения:O 3 (г) + NO 2 (г) → NO 3 (г) + O 2 (г) ΔH = 10,1 кДж
N 2 O 5 (г) → NO 3 (г) + NO 2 (г) ΔH = 48,3 кДж
- Ответ
- Переключите второе уравнение и прибавьте к первому.

O 3 (г) + NO 2 (г) → NO 3 (г) + O 2 (г) ΔH = 10,1 кДж
NO 3 (г) + NO 2 (г) → N 2 O 5 (г)) ΔH = -48,3 кДж
Объединение уравнений дает:
O 3 (г) + 2NO 2 (г) → N 2 O 5 (г) + O 2 (г) ΔH = -38,2 кДж
- Переключите второе уравнение и прибавьте к первому.
- Рассчитайте ΔH для
4K 2 O(s) + 3O 2 (g) → 3K 2 O 2 (s) + 2KO 2 (s)
Учитывая следующие уравнения:K 2 O(т) + ½O 2 (г) → K 2 O 2 (т) ΔH = -132,6 кДж
4KO 2 (т) → 2K 2 O(т) + 3O 2 (г) ΔH = 411,6 кДж
2КО 2 (т) → К 2 О 2 (т) + О 2 (ж) ΔH = 73,2 кДж
- Ответ
- Умножьте первое уравнение на 2, поменяйте местами второе уравнение, добавьте их к последнему уравнению.

2K 2 O(т) + O 2 (г) → 2K 2 O 2 (т) ΔH = -265,2 кДж
2K 2 O(т) + 3O 2 (г) → 4KO 2 (т) ΔH = -411,6 кДж
2КО 2 (с) → К 2 О 2 (с) + О 2 (г) ΔH = 73,2 кДж
Объединение уравнений дает:
4К 2 О(т) + 3О 2 (ж) → 3К 2 О 2 (т) + 2КО 2 (т)
ΔH = -265,2 кДж — 411,6 кДж + 73,2 кДж = -603,6 кДж
- Умножьте первое уравнение на 2, поменяйте местами второе уравнение, добавьте их к последнему уравнению.
- При полном сгорании одного моля твердого нафталина C 10 H 8 выделяется 4981 кДж теплоты. Предположим, что образуется H 2 O(г), а для CO 2 , ΔH o f = -393,5 кДж/моль. Что такое ΔH o f для нафталина?
- Ответ
C 10 H 8 (т) + 12O 2 (г) → 10CO 2 (г) + 4H 2 O(г) ∆H = -4981 кДж
ΔH RXN = 4ΔH O F, H 2 O + 10ΔH O F, CO 2 — ΔH O 2 — ΔH O 2 .

Глоссарий
Фазовый переход и скрытая теплота
Цели обучения
К концу этого раздела вы сможете:
До сих пор мы обсуждали изменение температуры в результате теплопередачи. Никакого изменения температуры в результате теплопередачи не происходит, если лед тает и становится жидкой водой (т. е. во время фазового перехода). Например, рассмотрим воду, капающую с тающих сосулек на нагретую солнцем крышу. И наоборот, вода замерзает в лотке для льда, охлаждаемом более низкой температурой окружающей среды.
Рис. 1. Тепло от воздуха передается льду, вызывая его таяние. (кредит: Майк Брэнд)
Энергия требуется для плавления твердого тела, потому что когезионные связи между молекулами в твердом теле должны быть разрушены, так что в жидкости молекулы могут двигаться с сопоставимыми кинетическими энергиями; таким образом, нет повышения температуры. Точно так же энергия необходима для испарения жидкости, потому что молекулы в жидкости взаимодействуют друг с другом через силы притяжения. Изменение температуры не происходит до тех пор, пока не завершится фазовый переход. Температура чашки содовой, изначально равная 0ºC, остается такой же, пока весь лед не растает. И наоборот, при замерзании и конденсации выделяется энергия, обычно в виде тепловой энергии. Работа совершается силами сцепления, когда молекулы сближаются. Соответствующая энергия должна быть выделена (рассеяна), чтобы позволить им оставаться вместе. Рисунок 2.
Точно так же энергия необходима для испарения жидкости, потому что молекулы в жидкости взаимодействуют друг с другом через силы притяжения. Изменение температуры не происходит до тех пор, пока не завершится фазовый переход. Температура чашки содовой, изначально равная 0ºC, остается такой же, пока весь лед не растает. И наоборот, при замерзании и конденсации выделяется энергия, обычно в виде тепловой энергии. Работа совершается силами сцепления, когда молекулы сближаются. Соответствующая энергия должна быть выделена (рассеяна), чтобы позволить им оставаться вместе. Рисунок 2.
Энергия фазового перехода зависит от двух основных факторов: количества и силы связей или силовых пар. Количество связей пропорционально количеству молекул и, следовательно, массе образца. Сила сил зависит от типа молекул. Теплота Q , необходимая для превращения фазы образца массой м , равна
Q = мл f (плавление/замерзание,
Q 8). 0197 mL v (испарение/конденсация),
0197 mL v (испарение/конденсация),
, где скрытая теплота плавления, L f , и скрытая теплота парообразования, L v , являются материальными константами, которые определяются экспериментально. См. (табл. 1).
Рис. 2. (а) Энергия требуется для частичного преодоления сил притяжения между молекулами в твердом теле с образованием жидкости. Та же самая энергия должна быть удалена, чтобы произошло замораживание. (b) Молекулы разделяют большие расстояния при переходе из жидкости в пар, и для преодоления молекулярного притяжения требуется значительная энергия. Такая же энергия должна быть удалена, чтобы произошла конденсация. Изменение температуры не происходит до тех пор, пока не завершится фазовый переход.
Скрытая теплота измеряется в Дж/кг. Как L f , так и L v зависят от вещества, особенно от силы его молекулярных сил, как отмечалось ранее. L f и L v вместе называются коэффициентами скрытой теплоты . Они латентные , или скрытые, потому что при фазовых переходах энергия входит или выходит из системы, не вызывая изменения температуры в системе; так что, по сути, энергия скрыта. В таблице 1 перечислены репрезентативные значения 9.0197 L f и L v вместе с температурами плавления и кипения.
Они латентные , или скрытые, потому что при фазовых переходах энергия входит или выходит из системы, не вызывая изменения температуры в системе; так что, по сути, энергия скрыта. В таблице 1 перечислены репрезентативные значения 9.0197 L f и L v вместе с температурами плавления и кипения.
Таблица показывает, что в фазовые переходы затрачивается значительное количество энергии. Посмотрим, например, сколько энергии нужно, чтобы растопить килограмм льда при 0ºC, чтобы произвести килограмм воды при 0 ° C. Используя уравнение изменения температуры и значение для воды из табл. 1 , мы находим, что Q = мл f = (1,0 кг) (334 кДж/кг) = 334 кДж – это энергия, необходимая для плавления килограмма льда. Это много энергии, так как она представляет такое же количество энергии, которое необходимо для повышения температуры 1 кг жидкой воды с 0ºC до 79.0,8ºС. Еще больше энергии требуется для испарения воды; для превращения 1 кг жидкой воды при нормальной температуре кипения (100ºC при атмосферном давлении) в пар (водяной пар) потребуется 2256 кДж. Этот пример показывает, что энергия фазового перехода огромна по сравнению с энергией, связанной с изменением температуры без фазового перехода.
Этот пример показывает, что энергия фазового перехода огромна по сравнению с энергией, связанной с изменением температуры без фазового перехода.
| Таблица 1. Теплоты плавления и парообразования [1] | ||||||
|---|---|---|---|---|---|---|
| Л ф | Л v | |||||
| Вещество | Температура плавления (ºC) | кДж/кг | ккал/кг | Температура кипения (°С) | кДж/кг | ккал/кг |
| Гелий | −269,7 | 5,23 | 1,25 | −268,9 | 20,9 | 4,99 |
| Водород | −259,3 | 58,6 | 14,0 | −252,9 | 452 | 108 |
| Азот | −210,0 | 25,5 | 6,09 | −195,8 | 201 | 48,0 |
| Кислород | −218,8 | 13,8 | 3,30 | −183,0 | 213 | 50,9 |
| Этанол | −114 | 104 | 24,9 | 78,3 | 854 | 204 |
| Аммиак | −75 | 108 | −33,4 | 1370 | 327 | |
| Меркурий | −38,9 | 11,8 | 2,82 | 357 | 272 | 65,0 |
| Вода | 0,00 | 334 | 79,8 | 100,0 | 2256 [2] | 539 [3] |
| Сера | 119 | 38,1 | 9. 10 10 | 444,6 | 326 | 77,9 |
| Свинец | 327 | 24,5 | 5,85 | 1750 | 871 | 208 |
| Сурьма | 631 | 165 | 39,4 | 1440 | 561 | 134 |
| Алюминий | 660 | 380 | 90 | 2450 | 11400 | 2720 |
| Серебро | 961 | 88,3 | 21.1 | 2193 | 2336 | 558 |
| Золото | 1063 | 64,5 | 15,4 | 2660 | 1578 | 377 |
| Медь | 1083 | 134 | 32,0 | 2595 | 5069 | 1211 |
| Уран | 1133 | 84 | 20 | 3900 | 1900 | 454 |
| Вольфрам | 3410 | 184 | 44 | 5900 | 4810 | 1150 |
Фазовые превращения могут иметь огромный стабилизирующий эффект даже при температурах, не близких к точкам плавления и кипения, поскольку испарение и конденсация (превращение газа в жидкое состояние) происходят даже при температурах ниже точки кипения. Возьмем, к примеру, тот факт, что температура воздуха во влажном климате редко превышает 35,0ºC, потому что большая часть теплопередачи идет на испарение воды в воздух. Точно так же температура во влажную погоду редко опускается ниже точки росы, потому что при конденсации водяного пара выделяется огромное количество тепла.
Возьмем, к примеру, тот факт, что температура воздуха во влажном климате редко превышает 35,0ºC, потому что большая часть теплопередачи идет на испарение воды в воздух. Точно так же температура во влажную погоду редко опускается ниже точки росы, потому что при конденсации водяного пара выделяется огромное количество тепла.
Мы более точно изучили эффекты фазового перехода, рассмотрев добавление тепла к образцу льда при температуре -20ºC (рис. 3). Температура льда растет линейно, поглощая тепло с постоянной скоростью 0,50 кал/г⋅ºC, пока не достигнет 0ºC. При такой температуре лед начинает таять до тех пор, пока весь лед не растает, поглощая 79,8 кал/г тепла. Температура остается постоянной на уровне 0ºC во время этого фазового перехода. Как только весь лед растаял, температура жидкой воды повышается, поглощая тепло с новой постоянной скоростью 1,00 кал/г⋅ºC. При 100ºC вода начинает кипеть и температура снова остается постоянной, пока вода поглощает 539кал/г тепла во время этого фазового перехода. Когда вся жидкость превратилась в пар, температура снова повышается, поглощая тепло со скоростью 0,482 кал/г⋅ºC.
Когда вся жидкость превратилась в пар, температура снова повышается, поглощая тепло со скоростью 0,482 кал/г⋅ºC.
Рис. 3. График зависимости температуры от добавленной энергии. Система сконструирована таким образом, что пар не испаряется, пока лед нагревается до жидкой воды, и чтобы при испарении пар оставался в системе. Длинные отрезки постоянных значений температуры при 0ºC и 100ºC отражают большую скрытую теплоту плавления и испарения соответственно.
Вода может испаряться при температуре ниже точки кипения. Энергии требуется больше, чем при температуре кипения, потому что кинетическая энергия молекул воды при температуре ниже 100ºC меньше, чем при 100ºC, следовательно, меньше энергии доступно от случайных тепловых движений. Возьмем, к примеру, тот факт, что при температуре тела пот с кожи требует подводимой теплоты 2428 кДж/кг, что примерно на 10% больше, чем скрытая теплота парообразования при 100°С. Это тепло исходит от кожи и, таким образом, обеспечивает эффективный механизм охлаждения в жаркую погоду. Высокая влажность препятствует испарению, поэтому температура тела может подняться, и на лбу останется неиспарившийся пот.
Высокая влажность препятствует испарению, поэтому температура тела может подняться, и на лбу останется неиспарившийся пот.
Пример 1. Расчет конечной температуры по фазовому переходу: охлаждение содовой с помощью кубиков льда
Три кубика льда используются для охлаждения содовой до 20ºC массой м содовой = 0,25 кг. Лед имеет температуру 0ºC, и каждый кубик льда имеет массу 6,0 г. Предположим, что сода хранится в контейнере из пенопласта, так что потерями тепла можно пренебречь. Предположим, что сода имеет такую же теплоемкость, как вода. Найдите конечную температуру, когда весь лед растает.
Стратегия
Кубики льда имеют температуру таяния 0ºC. Тепло передается от газировки льду для плавления. Плавление льда происходит в два этапа: сначала происходит фазовый переход и твердое тело (лед) переходит в жидкую воду при температуре плавления, затем температура этой воды повышается. Плавление дает воду при температуре 0ºC, поэтому от соды к этой воде передается больше тепла, пока система вода + сода не достигнет теплового равновесия, Q лед = − Q сода .
The heat transferred to the ice is
Q ice = m ice L f + m ice c W ( T f −0ºC).
Теплота, выделяемая содой, равна Q соды = m соды c W ( T f −20ºC). Since no heat is lost, Q ice = − Q soda , so that
m ice L f + m ice c W ( T f −0ºC) = – m сода c W ( T f −20ºC).
Приведите все термины, связанные с T 9{\ circ} \ text {C} \ right) -m _ {\ text {ice}} L _ {\ text {f}}} {\ left (m _ {\ text {газировка}} + m _ {\ text {лед} }\right)c_{\text{W}}}\\[/latex]
Решение
Обсуждение
Этот пример иллюстрирует огромные энергии, связанные с изменением фазы. Масса льда составляет около 7 процентов от массы воды, но приводит к заметному изменению температуры соды. Хотя мы предположили, что лед был при температуре замерзания, это неверно: типичная температура -6ºC. Однако эта поправка дает конечную температуру, практически идентичную найденному нами результату. Можете ли вы объяснить, почему?
Рисунок 4. Конденсат на стакане чая со льдом. (кредит: Дженни Даунинг)
Мы видели, что испарение требует передачи тепла жидкости из окружающей среды, так что окружающая среда высвобождает энергию. Конденсация – это обратный процесс, повышающий температуру окружающей среды. Это увеличение может показаться удивительным, поскольку мы связываем конденсацию с холодными предметами — например, со стеклом на рисунке. Однако энергия должна быть удалена от конденсирующихся молекул, чтобы заставить пар сконденсироваться. Энергия точно такая же, как требуется для осуществления фазового перехода в другом направлении, от жидкости к пару, поэтому ее можно рассчитать из Q = мл v .
Это увеличение может показаться удивительным, поскольку мы связываем конденсацию с холодными предметами — например, со стеклом на рисунке. Однако энергия должна быть удалена от конденсирующихся молекул, чтобы заставить пар сконденсироваться. Энергия точно такая же, как требуется для осуществления фазового перехода в другом направлении, от жидкости к пару, поэтому ее можно рассчитать из Q = мл v .
Конденсат образуется на рисунке 4, потому что температура окружающего воздуха снижается ниже точки росы. Воздух не может содержать столько воды, сколько при комнатной температуре, поэтому вода конденсируется. Энергия высвобождается, когда вода конденсируется, ускоряя таяние льда в стакане.
Реальное применение
Энергия также высвобождается при замерзании жидкости. Это явление используется садоводами во Флориде для защиты апельсинов, когда температура близка к точке замерзания (0ºC). Садоводы распыляют воду на растения в садах, чтобы вода замерзала и тепло отдавалось растущим на деревьях апельсинам. Это предотвращает падение температуры внутри апельсина ниже точки замерзания, что может привести к повреждению плода.
Это предотвращает падение температуры внутри апельсина ниже точки замерзания, что может привести к повреждению плода.
Рисунок 14.11. Лед на этих деревьях выделял большое количество энергии при замерзании, помогая предотвратить падение температуры деревьев ниже 0ºC. Вода намеренно распыляется на сады, чтобы предотвратить сильные морозы. (кредит: Герман Хаммер)
Сублимация — это переход из твердого состояния в парообразное. Возможно, вы замечали, что снег может раствориться в воздухе без следа жидкой воды или исчезновение кубиков льда в морозильной камере. Верно и обратное: иней может образовываться на очень холодных окнах, не проходя стадию жидкости. Популярным эффектом является создание «дыма» из сухого льда, представляющего собой твердый углекислый газ. Сублимация происходит потому, что равновесное давление паров твердых тел не равно нулю. В некоторых освежителях воздуха используется сублимация твердого вещества для введения аромата в помещение. Шарики от моли являются слегка токсичным примером фенола (органического соединения), который возгоняется, в то время как некоторые твердые вещества, такие как четырехокись осмия, настолько токсичны, что их необходимо хранить в герметичных контейнерах, чтобы предотвратить воздействие на человека их сублимационных паров.
Рис. 5. Прямые переходы между твердым телом и паром распространены, иногда полезны и даже красивы. (а) Сухой лед сублимируется непосредственно в углекислый газ. Видимый пар состоит из капель воды. (кредит: Уинделл Оскей) (b) Фрост образует узоры на очень холодном окне, пример твердого тела, образованного непосредственно из пара. (кредит: Лиз Уэст)
Все фазовые переходы связаны с выделением тепла. В случае прямых переходов твердое тело-пар необходимая энергия определяется уравнением Q = мл s , где л s – это теплота сублимации , которая представляет собой энергию, необходимую для превращения 1,00 кг вещества из твердой фазы в паровую фазу. L s аналогичен L f и L v , и его значение зависит от вещества. Сублимация требует затрат энергии, поэтому сухой лед является эффективным хладагентом, в то время как обратный процесс (т. е. замораживание) высвобождает энергию. Количество энергии, необходимое для сублимации, того же порядка, что и для других фазовых переходов.
Количество энергии, необходимое для сублимации, того же порядка, что и для других фазовых переходов.
Материал, представленный в этом и предыдущем разделах, позволяет нам рассчитать любое количество эффектов, связанных с температурой и фазовым переходом. В каждом случае необходимо определить, какие температурные и фазовые изменения имеют место, а затем применить соответствующее уравнение. Имейте в виду, что теплообмен и работа могут вызывать как температурные, так и фазовые изменения.
Стратегии решения проблем с эффектами теплопередачи
Проверьте свое понимание
Почему снег остается на горных склонах даже при дневных температурах выше нуля?
Раствор
Снег образуется из кристаллов льда и, таким образом, является твердой фазой воды. Поскольку для фазовых переходов необходимо огромное количество тепла, для накопления этого тепла из воздуха требуется определенное время, даже если температура воздуха выше 0ºC. Чем теплее воздух, тем быстрее происходит этот теплообмен и тем быстрее тает снег.
Резюме раздела
Концептуальные вопросы
Задачи и упражнения
Глоссарий
теплота сублимации: энергия, необходимая для превращения вещества из твердой фазы в паровую
коэффициент скрытой теплоты: физическая постоянная, равная количеству тепла, переданному на вещества при изменении фазы вещества
сублимация: переход из твердой фазы в паровую
Избранные решения задач и упражнений
1. 35,9 ккал
3. (а) 591 ккал; (б) 4,94 × 10 3 s
5. 13,5 Вт
7. (а) 148 ккал; (б) 0,418 с, 3,34 с, 4,19 с, 22,6 с, 0,456 с
9, 33,0 г
10, (а) 9,67 л; (b) Сырая нефть менее плотна, чем вода, поэтому она плавает поверх воды, тем самым подвергая себя воздействию кислорода воздуха, который она использует для сжигания. Кроме того, если вода находится под маслом, она менее эффективно поглощает тепло, выделяемое маслом.
Кроме того, если вода находится под маслом, она менее эффективно поглощает тепло, выделяемое маслом.
12. (а) 319 ккал; (б) 2,00ºC
14. 20,6ºC
16. 4,38 кг
18. (a) 1,57 × 10 4 ккал; (б) 18,3 кВт⋅ч; (c) 1,29 × 10 4 ккал
Химия I Домашнее задание 3
Химия I Домашнее задание 3Страница домашнего задания по химии I, материал для экзамена 3
Страница домашнего задания без видимых ответов
На этой странице есть все необходимые домашние задания по материалу третьего экзамена первого семестра по общей химии.
Учебником, связанным с этим домашним заданием, является ХИМИЯ Центральная наука Брауна, ЛеМэя и др. Последним изданием, которое я требовал от студентов, было издание 12 9.0308 th edition (Chemistry The Central Science, 12th ed. by Brown, LeMay, Bursten, Murphy and Woodward), но для этого курса подойдет любое издание этого текста.
Примечание: вы ожидаете, что дойдет до конца задач вашего учебника, найдет похожие вопросы и решит эти задачи. Это всего лишь обязательный список задач для целей викторины. Вы также должны изучить упражнения в главах. Упражнения представляют собой отработанные примеры вопросов в конце главы. В учебном пособии также проработаны примеры.
Это голые вопросы. Вопросы из учебника будут содержать дополнительную информацию, которая может оказаться полезной и свяжет задачи с приложениями в реальной жизни, многие из которых относятся к биологии.

 docx
docx На сколько увеличился объём газа? Масса газа постоянна.
На сколько увеличился объём газа? Масса газа постоянна.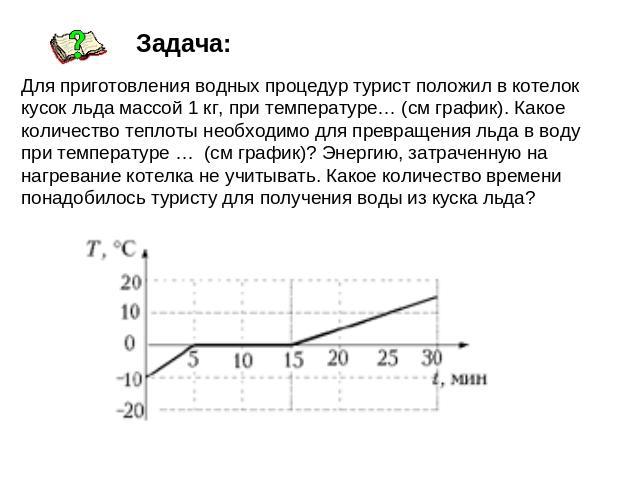 В стакан калориметра, содержащий воду массой т, опустили кусок льда массой 56 г, имевший температуру 0 °C. Начальная температура калориметра и воды 45 °C. В момент времени, когда наступило тепловое равновесие, температура воды и калориметра стала равной 5 °C. Чему равна масса т? Теплоёмкостью калориметра пренебречь.
В стакан калориметра, содержащий воду массой т, опустили кусок льда массой 56 г, имевший температуру 0 °C. Начальная температура калориметра и воды 45 °C. В момент времени, когда наступило тепловое равновесие, температура воды и калориметра стала равной 5 °C. Чему равна масса т? Теплоёмкостью калориметра пренебречь. Ему передали количество теплоты, равное 47,7 кДж. Температура плавления свинца 327 °C. Какова масса расплавившейся части свинца? Тепловыми потерями пренебречь.
Ему передали количество теплоты, равное 47,7 кДж. Температура плавления свинца 327 °C. Какова масса расплавившейся части свинца? Тепловыми потерями пренебречь. рисунок). Коэффициент трения между бруском и плоскостью ц = 0,2. Модуль силы трения, действующей на брусок, FTp =2,8 Н. Чему равен модуль силы F?
рисунок). Коэффициент трения между бруском и плоскостью ц = 0,2. Модуль силы трения, действующей на брусок, FTp =2,8 Н. Чему равен модуль силы F? Чему равна масса первого груза М1 если масса второго М2 = 2 кг.
Чему равна масса первого груза М1 если масса второго М2 = 2 кг.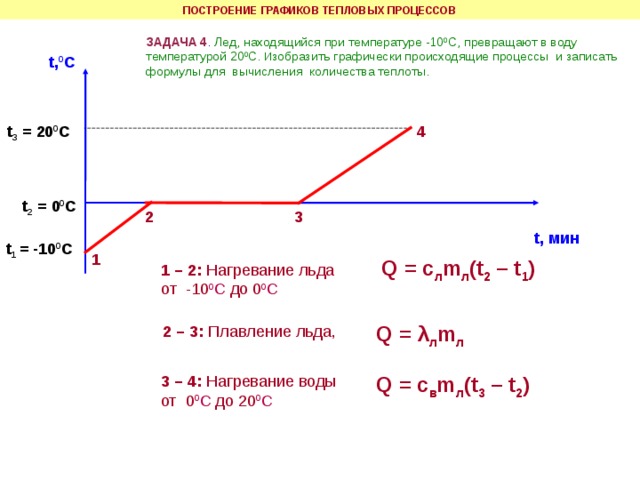 Тогда
Тогда  Удельная теплоемкость воды составляет 4,18 Дж/г/°С.
Удельная теплоемкость воды составляет 4,18 Дж/г/°С.




 )
)