 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Функция корень из х. Ее свойства и график
Похожие презентации:
Функция у х, её свойства и график
Функция у=n квадратный корень из х, их свойства и графики
Функция у=√х, её свойства и график
Свойства и график функции у = sin x
Функции и их свойства
Функция у=kx², её свойства и график
Функция у=кх², её свойства и график
Логарифмическая функция, ее свойства и график
Функция у=х в степени n , график и свойства
Функции. Их свойства и графики
Функция
у х,
её свойства и график.
Решить уравнения:
a )2 x 8 10;
1
б)
x 9 6;
3
в) x x 2
1)Вычислите:
11
1
0,36 ; 1 ;0,2 400 ; 81;
25
3
0,49 0,09 ; 2 1; 5 12 .
3
2)Решите уравнение:
x 4; x 4
2
x 1; x 1
2
2
2
Решите уравнение
1
x 5
3
1
x 52
3
1
x 25
3
x 75
Ответ : 75
Решите уравнение:
а )( x 3)( x 1) 0
б )( x 2)( x 1) 0
Вычислите, укажите правильный
ответ
64
36
63
7
1,2
2
3
16
14
8
5
12
10
3,2
Вычислите, укажите правильный
ответ
169 16
63
7
1,2
2
3
16
150
8
5
12
10
3,2
Какое целое число заключено между
45 и
54
63
7
1,2
2
180
16
150
8
5
12
10
3,2
Что больше?
π; 5 ;3,2
63
100
1,2
2
180
16
150
8
5
12
10
3,2
Найти наибольшее значение
функции
y= x на отрезке [1;25]
63
100
1,2
2
180
16
150
8
5
12
10
270
Решить уравнение:
x =4
63
100
1,2
2
180
16
8
260
12
10
270
Найти наибольший корень
уравнения:
x 4
2
63
100
1,2
2
180
280
150
8
260
12
10
270
Вычислите, укажите правильный
ответ
49
81
63
100
1,2
290
180
280
150
8
260
12
10
270
Вычислите, укажите правильный
ответ
81 1
300
100
1,2
290
180
280
150
8
260
12
10
270
Вычислите, укажите правильный
ответ
11
1
25
300
100
1,2
290
180
280
150
8
260
12
310
270
Найти сторону квадрата, если его
площадь равна
64 см
2
300
100
320
290
180
280
150
8
260
12
310
270
Найти периметр квадрата, если его
площадь равна
2
см
9
300
100
320
290
180
280
150
330
260
12
310
270
18.
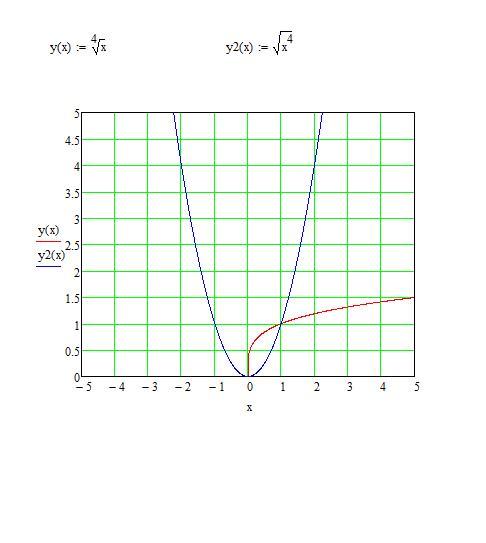 Арифметический квадратный корень АРИФМЕТИЧЕСКИЙ
Арифметический квадратный корень АРИФМЕТИЧЕСКИЙвыражение
-3 49
уравнение
x 8
функция
?
у х
х≥0
Х
0
У
0
1 2,25 4 6,25 9
1 1,5 2 2,5 3
у
3
2
1
0 1 2 3 4 5 6 7 8 9
х
Свойства функции
1.Область
1. D ( у ) 0 ;
определения
у
2.
2.Область
значений
3. у=0, если х= 0 4
у>0, если
3
у=√х:
E ( у ) 0;
х 0;
1
х
4. Функция
-1 0 1 2 3 4 5 6 7 8 9 10 11
возрастает
при х 0 ;
ограничена снизу, но не
5. Функция
Ограниченность
ограничена сверху.
6. унаим.= 0
Непрерывна.
7. Непрерывность
7.
унаиб.= НЕТ
у х
х≥0
Х
0
У
0
1 2,25 4 6,25 9
-1 -1,5 -2 -2,5 -3
у
х
-1
-2
-3
-4
0 1 2 3 4 5 6 7 8 9 10 11
Свойства функции
1.Область
1. D ( у ) 0 ;
определения
2.
2.Область
значений
3. у=0, если х= 0
E ( у ) ;0
у<0, если
х 0;
4.
 Функция
Функцияубывает
при х 0 ;
-1
-2
-3
-4
у=-√х:
у
х
0 1 2 3 4 5 6 7 8 9 10 11
ограничена сверху, и не
5. Функция
Ограниченность
ограничена снизу.
6. унаим.= НЕТ
Непрерывна.
7. Непрерывность
7.
унаиб.= 0
Постройте график
функции:
у
y х 3 4
система
координат:
х= 3
у= 4
-2 -1
2. Привязываем к
ней график функции
х
y х 3 4
7
6
5
4
3
2
1
1.Вспомогательная
y
х=3
-1
-2
у=4
х
01 2 3 4 5 6 7 8 9
Х
0
1
У
0
1
4
2
Найдите наименьшее и наибольшее значения
у х
функции
на отрезке от 0 до 4.
у
4
3
2
1
у х
х
-1 0 1 2 3 4 5 6 7 8 9 10 11
Унаим.=0
Унаиб.=2
Найдите наименьшее и наибольшее значения
функции у х 2 на отрезке от 3 до 11.
у
х=2
3
у х 2
1
х
-1 0 1 2 3 4 5 6 7 8 9 10 11
Унаим.=1
Унаиб.
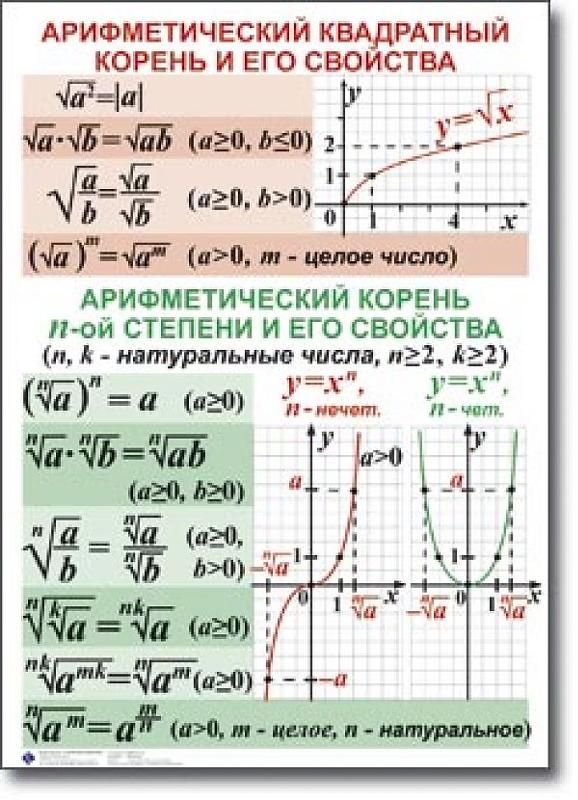 =3
=3Решить графически уравнение:
√х=х-6
1
4
3
2
Построим в одной системе
координат графики функций:
у=√х
у=х-6
Х 0 6
У -6 0
2
3
у х
1
-1
-2
-3
-4
-5
-6
Х 0 1 4 9
У 0 1 2 3
у
х
0 1 2 3 4 5 6 7 8 9
у=х-6
Найдём абсциссы точек
пересечения графиков
ОТВЕТ:
9
Решить графически систему уравнений:
у
9
8
7
Построим в одной системе
1 координат графики функций: 6
5
у=(х-3)²
4
В.С.К. х=3, у=0
3
у=х²
2
Х 0 ±1 ±2±3
1
у=(х-3)²
у=√х-3
У 0 1 4 9
у=√х-3
В.С.К. х=3, у=0
0
4
Х
1
у=√х
У 0 1 2
-1
х=3
у=(х-3)²
у=√х-3
(4;1)
у=0
01 2 3 4 5 6 7 8 9 х
(3;0)
Найдём координаты точек
пересечения графиков
2
3 ОТВЕТ
(3;0) , (4;1)
English Русский Правила
3-8
Нули и кратность | Колледж Алгебра
Результаты обучения
- Определение нулей полиномиальных функций с четной и нечетной кратностью.
 {3}[/латекс].
{3}[/латекс].Обратите внимание на рисунок ниже, что поведение функции на каждом из отрезков x отличается.
Поведение графика на точке пересечения с х можно определить, исследуя кратность нуля.
Отрезок x [латекс]х=-3[/латекс] является решением уравнения [латекс]\влево(х+3\вправо)=0[/латекс]. Граф проходит непосредственно через точку пересечения x в точке [latex]x=-3[/latex]. Фактор является линейным (имеет степень 1), поэтому поведение вблизи точки пересечения похоже на поведение линии; он проходит прямо через перехват. Мы называем это одиночным нулем, потому что ноль соответствует одному фактору функции. 9{2}=\left(x — 2\right)\left(x — 2\right)[/latex]
Множитель повторяется, то есть множитель [латекс]\left(x — 2\right) [/latex] появляется дважды. Количество раз, когда данный множитель появляется в факторизованной форме уравнения многочлена, называется кратностью . Нуль, связанный с этим множителем, [латекс]х=2[/латекс], имеет кратность 2, потому что множитель [латекс]\левый(х — 2\правый)[/латекс] встречается дважды.
 { 3}[/латекс]. Мы называем это тройным нулем или нулем с кратностью 3,9.1819
{ 3}[/латекс]. Мы называем это тройным нулем или нулем с кратностью 3,9.1819Для нулей с четными кратностями графики касаются или касаются оси x при этих значениях x. Для нулей с нечетной кратностью графики пересекают или пересекают ось x при этих значениях x. На приведенных ниже графиках приведены примеры графиков полиномиальных функций с кратностью 1, 2 и 3. но для каждой увеличивающейся четной степени график будет казаться более плоским по мере приближения и выхода из 9{p}[/latex], поведение вблизи точки пересечения x h определяется степенью p . Мы говорим, что [latex]x=h[/latex] является нулем кратности p .
График полиномиальной функции будет касаться оси x нулями с четными кратностями. График будет пересекать ось x по нулям с нечетной кратностью.
Сумма кратностей является степенью полиномиальной функции.
Как: Имея график полиномиальной функции степени [latex]n[/latex], определите нули и их кратности.

- Если график пересекает ось x и кажется почти линейным на пересечении, это один ноль.
- Если график касается оси x и отскакивает от оси, это нуль с четной кратностью.
- Если график пересекает ось x в нуле, это ноль с нечетной кратностью.
- Сумма кратностей равна степени п .
Пример: определение нулей и их кратностей
Используйте график функции степени 6 для определения нулей функции и их возможных кратностей.
Показать решение
Попробуйте
Используйте график функции степени 5, чтобы определить нули функции и их кратности.
Показать решение
Определение конечного поведения
Как мы уже узнали, поведение графа 9{n — 1}+…+{a}_{1}x+{a}_{0}[/latex]
в конечном счете либо вырастет, либо упадет, как x неограниченно увеличивается, и будет либо расти, либо падать, как x неограниченно уменьшается.
 {п}[/латекс], является четной степенной функцией, поскольку x увеличивается или уменьшается без ограничений, [латекс]f\left(x\right)[/латекс] увеличивается без ограничений. Когда ведущий член представляет собой нечетную степенную функцию, поскольку x убывает неограниченно, [латекс]f\left(x\right)[/латекс] также неограниченно уменьшается; поскольку x увеличивается без ограничений, [латекс]f\left(x\right)[/латекс] также увеличивается без ограничений. Если ведущий член отрицательный, он изменит направление конечного поведения. В таблице ниже представлены все четыре случая.
{п}[/латекс], является четной степенной функцией, поскольку x увеличивается или уменьшается без ограничений, [латекс]f\left(x\right)[/латекс] увеличивается без ограничений. Когда ведущий член представляет собой нечетную степенную функцию, поскольку x убывает неограниченно, [латекс]f\left(x\right)[/латекс] также неограниченно уменьшается; поскольку x увеличивается без ограничений, [латекс]f\left(x\right)[/латекс] также увеличивается без ограничений. Если ведущий член отрицательный, он изменит направление конечного поведения. В таблице ниже представлены все четыре случая.Четная степень Нечетная степень Попробуйте
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Функция извлечения квадратного корня — график, домен, диапазон, примеры
Функция извлечения квадратного корня включает символ квадратного корня √ (который читается как «квадратный корень из»).
 Квадратный корень числа «x» — это число «y», такое, что y 2 = х. т. е. если y 2 = x ⇒ y = √x. т. е. если «x» — это квадрат «y», то «y» — это квадратный корень из «x». Некоторые примеры:
Квадратный корень числа «x» — это число «y», такое, что y 2 = х. т. е. если y 2 = x ⇒ y = √x. т. е. если «x» — это квадрат «y», то «y» — это квадратный корень из «x». Некоторые примеры:- 2 2 = 4 ⇒ √4 = 2
- 4 2 = 16 ⇒ √16 = 4
Мы знаем, что квадратный корень из числа может быть как положительным, так и отрицательным. т. е. √ 4 = ± 2. Но при определении функции квадратного корня мы ограничиваем ее диапазон множеством всех положительных действительных чисел (иначе она вообще не станет функцией), и, следовательно, в случае функции квадратного корня результат всегда положительный. . Давайте воспользуемся всеми этими фактами, чтобы понять функцию квадратного корня.
1. Что такое функция извлечения квадратного корня? 2. Домен и диапазон функции квадратного корня 3. 
График квадратного корня 4. График любой функции квадратного корня 5. Свойства функции квадратного корня 6. Часто задаваемые вопросы о функции извлечения квадратного корня Что такое функция извлечения квадратного корня?
Функция квадратного корня в основном имеет вид f(x) = √x. т. е. родительская функция квадратного корня есть f(x) = √x. Это обратная функция квадрата g(x) = x 2 , поскольку квадрат и квадратный корень являются обратными операциями друг друга. Поскольку функция квадратного корня увеличивается (поскольку значения f (x) увеличиваются с увеличением значений x) и поскольку она является взаимно однозначной, это биекция и, следовательно, она имеет обратную. Графики функции квадратного корня f(x) = √x и обратной функции g(x) = x 2 над областью [0, ∞) и диапазоном [0, ∞) симметричны относительно прямой y = x, как показано на рисунке ниже.

f(x) = √x является исходной функцией квадратного корня, но когда к ней применяются преобразования, она может выглядеть как f(x) = a√(b(x — h)) + k, где a , b, h и k — такие числа, что
- ‘a’ — вертикальное расширение
- ‘b’ — горизонтальное расширение
- ‘h’ — это горизонтальный перевод
- ‘k’ — вертикальный перевод
Домен и диапазон функции квадратного корня
Квадратный корень из отрицательного числа НЕ является действительным числом. т. е. функция квадратного корня не может принимать отрицательные числа в качестве входных данных. т. е.
- Область определения функции извлечения квадратного корня f(x) = √x — это множество всех неотрицательных действительных чисел. т. е. область определения функции квадратного корня равна [0, ∞). Обратите внимание, что он также включает 0 в домене.
В общем случае квадратный корень из числа может быть как положительным, так и отрицательным.
 т. е. √25 = 5 или -5 как 5 2 = 25 и (-5) 2 = 25. Но диапазон функции квадратного корня (т. е. ее значения y) ограничен только положительными числами, потому что в противном случае он не пройдет тест вертикальной линии и не будет функцией, если вход имеет два выхода. Таким образом,
т. е. √25 = 5 или -5 как 5 2 = 25 и (-5) 2 = 25. Но диапазон функции квадратного корня (т. е. ее значения y) ограничен только положительными числами, потому что в противном случае он не пройдет тест вертикальной линии и не будет функцией, если вход имеет два выхода. Таким образом,- Область значений функции квадратного корня f(x) = √x совпадает с ее областью определения [0, ∞). Обратите внимание, что он также включает 0 в диапазоне. г.
График квадратного корня
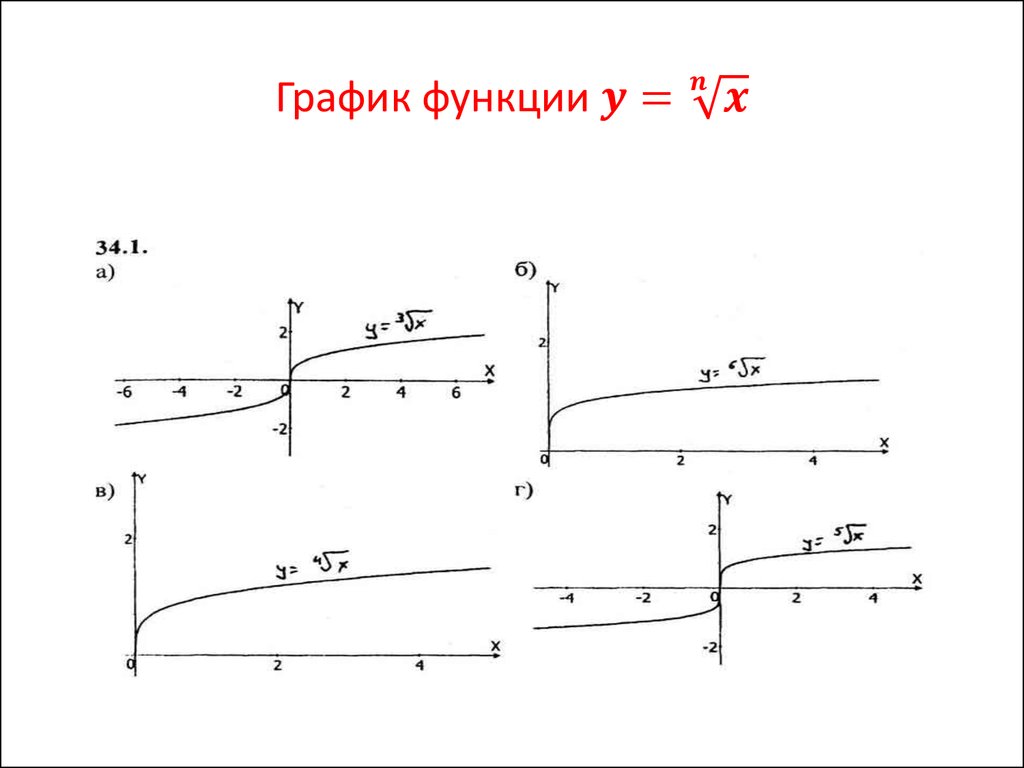
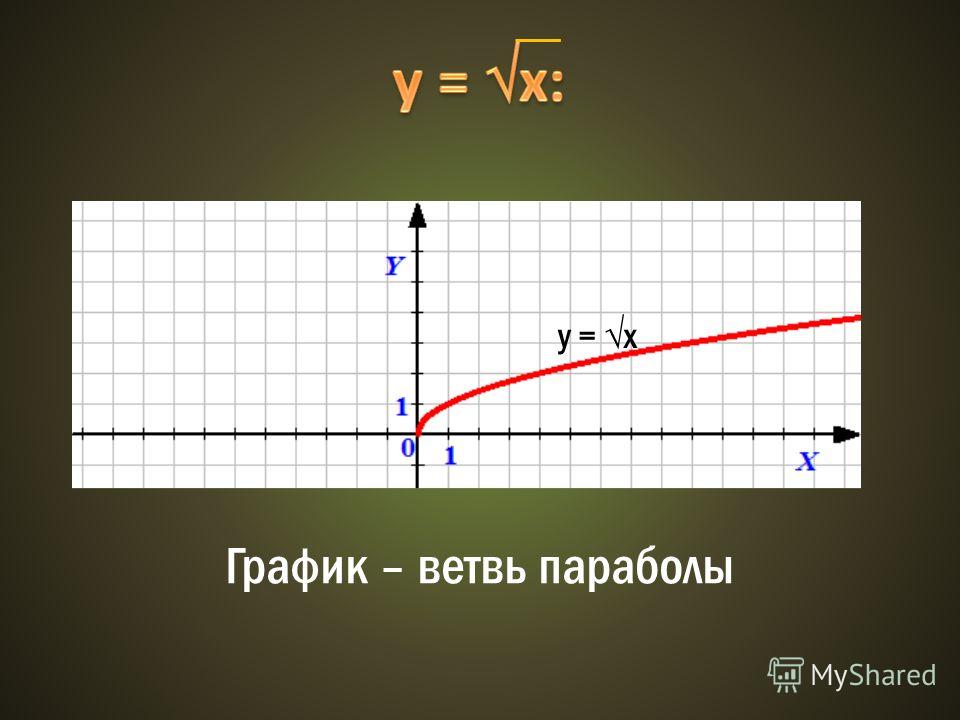
Мы уже видели, как выглядит граф квадратного корня. Но теперь мы увидим, как построить график квадратного корня из x. Мы уже видели, что область определения и область значений исходной функции квадратного корня f(x) = √x — это множество всех неотрицательных действительных чисел. Таким образом, график квадратного корня функции f(x) = √x лежит только в первом квадранте. Мы можем нарисовать его график, построив таблицу значений с некоторыми случайными значениями x (из области [0, ∞), а затем вычислив соответствующие значения y, подставив каждое x в y = √x.
 Затем мы можем получить несколько точек, которые мы нанесем на координатную плоскость, и соединим их все кривой.
Затем мы можем получить несколько точек, которые мы нанесем на координатную плоскость, и соединим их все кривой.х г 0 √0 = 0 1 √1 = 1 4 √4 = 2 Обратите внимание, что когда к графику применяются некоторые преобразования, сам график может не лежать в первом квадранте.
График любой функции квадратного корня
г.Мы видели, как построить график родительской функции квадратного корня f(x) = √x. Вот шаги, которые полезны при построении графика любой функции квадратного корня, имеющей форму f (x) = a √ (b (x — h)) + k в целом.
- Шаг 1: Определите область определения функции, установив «выражение внутри квадратного корня» больше или равное 0 и найдя x.
- Шаг 2: Диапазон любой функции квадратного корня всегда равен y ≥ k, где k — вертикальный сдвиг функции f(x) = a√(b(x — h)) + k.
 г.
г. - Шаг 3: Построить таблицу значений с двумя столбцами x и y, взять несколько случайных чисел для x (только из домена), начиная с первого значения домена, подставить их в заданную функцию и найти соответствующие значения у.
- Шаг 4: Нанесите все точки на плоскость и соедините их кривой, а также продлите кривую в том же направлении.
Примечание: Вычисление точек пересечения по осям x и y также может помочь в построении графика функции квадратного корня.
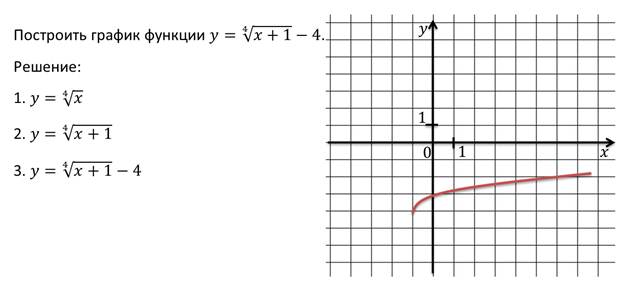
Пример: Постройте график функции квадратного корня f(x) = √(x — 2) + 3.
Решение:
Чтобы найти ее область определения, x — 2 ≥ 0 ⇒ x ≥ 2.
Его вертикальный сдвиг равен 3, и, следовательно, его диапазон равен y ≥ 3.
Теперь мы построим таблицу с некоторыми значениями, большими 2 (поскольку домен x ≥ 2). Выберите некоторые значения для x так, чтобы √(x — 2) был правильным квадратом, чтобы упростить вычисление.

х г 2 √(2 — 2) + 3 = 0 + 3 = 3 3 √(3 — 2) + 3 = 1 + 3 = 4 6 √(6 — 2) + 3 = 2 + 3 = 5 11 √(11 — 2) + 3 = 3 + 3 = 6 Теперь постройте эти точки и соедините их кривой.
Мы также можем построить график функции квадратного корня, применив преобразования к родительскому графику квадратного корня f(x) = √x.
Свойства функции квадратного корня
Вот важные моменты/свойства, которые следует отметить в отношении функции квадратного корня f(x) = √x.
- Его домен [0, ∞).
- Его диапазон равен [0, ∞).
- Не имеет относительных максимумов, но имеет минимум в точке (0, 0).
- Функция квадратного корня не имеет асимптот.
- Это возрастающая функция во всей области определения [0, ∞).

- Функция квадратного корня f(x) = √x имеет критическую точку в точке (0, 0) и не имеет точек перегиба.
Часто задаваемые вопросы о функции извлечения квадратного корня
Что такое родительская функция извлечения квадратного корня?
Родительская функция квадратного корня имеет вид f(x) = √x. Эту функцию можно транслировать/расширять/отражать и приводить к виду f(x) = a√(b(x — h)) + k.
Что такое формула функции квадратного корня?
Формула для функции квадратного корня: f(x) = √x. Это означает, что вывод каждого входного значения равен квадратному корню из входного значения. Например, f(25) = √25 = 5. Обратите внимание, что все входы и выходы функции квадратного корня всегда неотрицательны.
Что такое производная функции квадратного корня?
Производная функции квадратного корня f(x) = √x вычисляется по степенному правилу дифференцирования d(x n )/dx = nx n-1 .
 По этому правилу d(√x)/dx = d(x 1/2 )/dx = (1/2) x (1/2) — 1 = (1/2) x -1/ 2 = 1/(2√x). Таким образом, производная от √x равна 1/(2√x).
По этому правилу d(√x)/dx = d(x 1/2 )/dx = (1/2) x (1/2) — 1 = (1/2) x -1/ 2 = 1/(2√x). Таким образом, производная от √x равна 1/(2√x).Как построить график квадратного корня из x?
Чтобы построить график квадратного корня из x, просто заметьте, что все его входы и выходы неотрицательны и, следовательно, его график лежит в первом квадранте. Далее, чтобы получить четкую форму графика, вычислите на нем несколько точек, взяв несколько случайных чисел за x и вычислив для них соответствующие значения y.
Что такое область функции квадратного корня?
Функция квадратного корня не может быть вычислена для отрицательных входных данных. Попробуйте ввести √(-2) в калькуляторе, он показывает ошибку. Таким образом, функция квадратного корня f(x) = √x принимает только неотрицательные значения и, следовательно, ее областью определения является множество всех неотрицательных действительных чисел, [0, ∞). В дальнейшем, если функция похожа на f (x) = a√ (b (x — h)) + k, то ее область определения равна x ≥ h.

В чем разница между графом кубического корня и графом квадратного корня?
Граф кубического корня может принимать любое действительное число в качестве входных данных и выдавать любое действительное число в качестве выходного. Но функция квадратного корня принимает и производит только неотрицательные действительные числа.
Каковы асимптоты функции квадратного корня?
Не существует горизонтальной или вертикальной линии, которая могла бы разорвать график функции квадратного корня, и, следовательно, он не имеет вертикальных/горизонтальных асимптот.
Что такое интеграл функции квадратного корня?
Интеграл функции извлечения квадратного корня √x можно найти с помощью степенного правила интегрирования ∫x n dx = x n+1 /(n + 1) + C.. Используя это, ∫√x dx = ∫x 1/2 dx = x (1/2 + 1) /( 1/2 + 1) + C = x 3/2 /(3/2) + C = (2/3) x 3/2 + C.
Полиномиальные графы: нули и их кратности
Конец Поведение «Изгибание» «Удары» Графика
Purplemath
Вещественные (то есть некомплексные) нули полинома соответствуют x -перехватам графика этого полинома.
 Таким образом, мы можем найти информацию о количестве действительных нулей полинома, взглянув на график, и, наоборот, мы можем сказать, сколько раз график будет касаться или пересекать x -ось, глядя на нули многочлена (или на факторизованную форму многочлена).
Таким образом, мы можем найти информацию о количестве действительных нулей полинома, взглянув на график, и, наоборот, мы можем сказать, сколько раз график будет касаться или пересекать x -ось, глядя на нули многочлена (или на факторизованную форму многочлена).Ноль имеет «кратность», которая относится к числу раз, которое связанный с ним множитель встречается в многочлене. Например, квадратичный ( x + 3)( x — 2) имеет нули x = -3 и x = 2, каждый из которых встречается один раз. Многочлен одиннадцатой степени ( x + 3) 4 ( x — 2) 7 имеет те же нули, что и квадратичный, но в этом случае 9Решение 1817 x = −3 имеет кратность 4, поскольку множитель ( x + 3) встречается четыре раза (то есть множитель возводится в четвертую степень), а решение x = 2 имеет кратность 7, поскольку множитель ( x — 2) встречается семь раз.
Содержимое продолжается ниже
MathHelp.
 com
comНули функции (и, да, «нули» — правильный способ написания множественного числа от «ноль») — это решения линейных множителей, которые они мне дали. . Решение каждого фактора дает мне:
x + 5 = 0 ⇒ x = −5
x + 2 = 0 ⇒ x = −2
x − 1 = 0 ⇒ x = 1
х — 5 = 0 ⇒ х = 5
Кратность каждого нуля — это количество раз, когда встречается соответствующий ему множитель. Другими словами, множественности — это мощности. (Для множителя x — 5 понятная степень равна 1.) Тогда мой ответ:
x = -5 с кратностью 3·
x = −2 с кратностью 4
x = 1 с кратностью 2
x = 5 с кратностью 1 (то есть любые нули, встречающиеся дважды, четыре раза, шесть раз и т. д.) являются квадратами, поэтому они не меняют знак. Квадраты всегда положительны. Это означает, что точка пересечения x , соответствующая нулю четной кратности, не может пересечь x , потому что ноль не может заставить график изменить знак с положительного (выше оси x ) на отрицательный (ниже оси x ) или наоборот.
Практический результат заключается в том, что нуль четной кратности заставляет график едва касаться оси x , а затем поворачивает его обратно в исходное положение. Вы можете увидеть это на следующих графиках:
y = ( x + 6)( x — 7)
x = -6 один раз
x = 7 Однаждыy = ( x + 6) ( x — 7) 2
x = –6 3
x = –6 3
x = –6
x = −6
x = −6
x = −6
x = −6
x . = ( x + 6) 2 ( x — 7)
x = -6 дважды
x = 7 один раз17 x = 7 Once
17 x = 7 один раз
x = 7 один раз x = 7 ( х — 7) 2х = -6 дважды
x = 7 дваждыВсе четыре графика имеют одни и те же нули, при x = −6 и при x = 7, но кратность нуля определяет, пересекает ли график ось x при этом ноль или если вместо этого он вернется туда, откуда пришел.
 Если ноль имел кратность 1, график пересекал ось x в нуле; если ноль имел кратность 2, график просто «поцеловал» ось x , прежде чем вернуться в исходное положение.
Если ноль имел кратность 1, график пересекал ось x в нуле; если ноль имел кратность 2, график просто «поцеловал» ось x , прежде чем вернуться в исходное положение.Любой ноль, соответствующий множитель которого встречается парами (то есть два раза, или четыре раза, или шесть раз и т. д.), будет «отскакивать» от x — ось и вернуть как было. Любой ноль, соответствующий множитель которого встречается нечетное количество раз (то есть один раз, или три раза, или пять раз и т. д.), пересечет ось x . Полиномиальные нули с четной и нечетной кратностью будут всегда вести себя таким образом.
На графике видно, что нули x = -15, x = -10, x = -5, x = 18 x 17, 918 = 0, 918 = 0, 918 х 91 818 = 15, так как график касается или пересекает ось 91 817 x 91 818 в этих точках. (По крайней мере, я предполагаю, что график пересекается именно в этих точках, поскольку упражнение не дает мне точных значений.
 Когда я делаю предположения по картинке, мне приходится делать определенные предположения.)
Когда я делаю предположения по картинке, мне приходится делать определенные предположения.)Поскольку график просто касается x = -10 и x = 10, то эти нули должны встречаться четное количество раз. Остальные нули должны встречаться нечетное количество раз. Нули нечетной кратности могут встречаться только один раз, а могут встречаться три, пять и более раз каждый; по графику не скажешь. (По крайней мере, нельзя сказать , но — мы узнаем об этом подробнее на следующей странице.) А нули четной кратности могут встречаться четыре, шесть и более раз каждый; Я не могу сказать, глядя.
Но если я суммирую минимальную кратность каждого, я должен получить степень, потому что в противном случае эта задача потребует больше информации, чем я могу дать. У меня есть четыре нуля нечетной кратности ( x = −15, x = −5, x = 0 и x = 15) и два нуля четной кратности ( x = 15).1817 x = –10 и x = 10).
 Суммируя их минимальные кратности, я получаю:
Суммируя их минимальные кратности, я получаю:1 + 2 + 1 + 1 + 2 + 1 = 8
… что является степенью многочлена. Таким образом, минимальные кратности являются правильными кратностями, и мой ответ таков:
x = -15 с кратностью 1,
x = -10 с кратностью 2,
x = -5 с кратностью 1,
x = 0 с кратностью 1,
x = 10 с кратностью 2 и
x = 15 с кратностью 1Мне удалось вычислить кратности нулей частично из того факта, что кратности будут в сумме равняться степени многочлена, или на два меньше, или на четыре меньше и т. д. в зависимости от того, сколько комплексных нулей может быть. Но проблемы кратности обычно не затрагивают комплекснозначные корни. Так что, если вас попросят угадать кратности по графику, как показано выше, вы, вероятно, можете с уверенностью предположить, что все корни являются действительными числами.
URL: https://www.purplemath.com/modules/polyends2.
 htm
htmСтраница 1Страница 3Страница 4Страница 5
Объяснение урока: область определения и диапазон радикальной функции
В этом объяснении мы узнаем как найти область определения и диапазон радикальной функции либо по ее графику, либо по определяющему правилу.
В частности, мы сосредоточимся на области и диапазоне функций, включающих квадратные и кубические корни.
Начнем с определения области определения и области значений функции.
Теорема: область определения и область значений функции
Область определения функции 𝑓(𝑥) — это множество всех возможных значений 𝑥, таких, что выражение 𝑓(𝑥) определено.
Диапазон функции 𝑓(𝑥) — это множество всех возможных значений, которые может принимать выражение 𝑓(𝑥), когда 𝑥 — любое число из области определения функции.
Например, рассмотрим функцию 𝑓(𝑥)=√𝑥. Если существует действительное число 𝑦, удовлетворяющее 𝑦=√𝑥, должно быть так, что 𝑥=𝑦. Мы знаем, что квадрат любого действительного числа не является отрицательным; таким образом, 𝑥 должно быть неотрицательным.
 Это говорит нам о том, что область определения функции квадратного корня равна 𝑥≥0, что выражается в интервальной записи как [0,∞[.
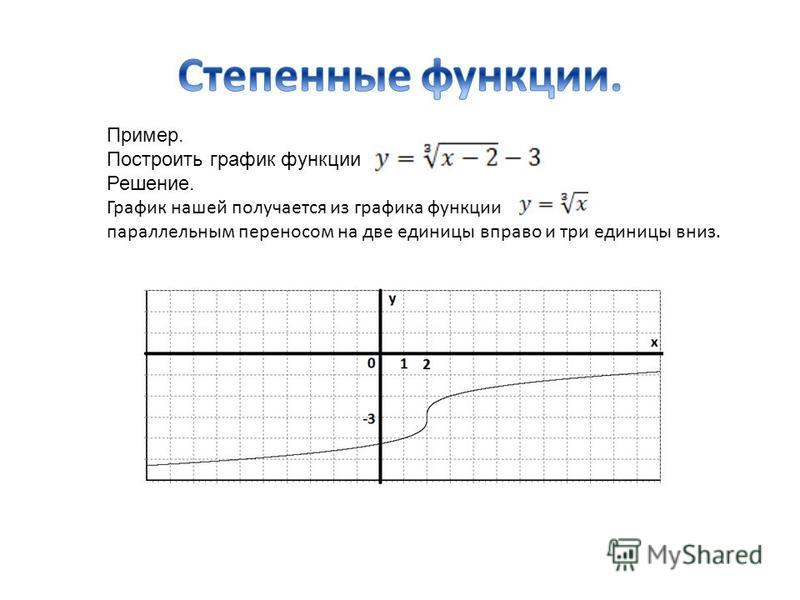
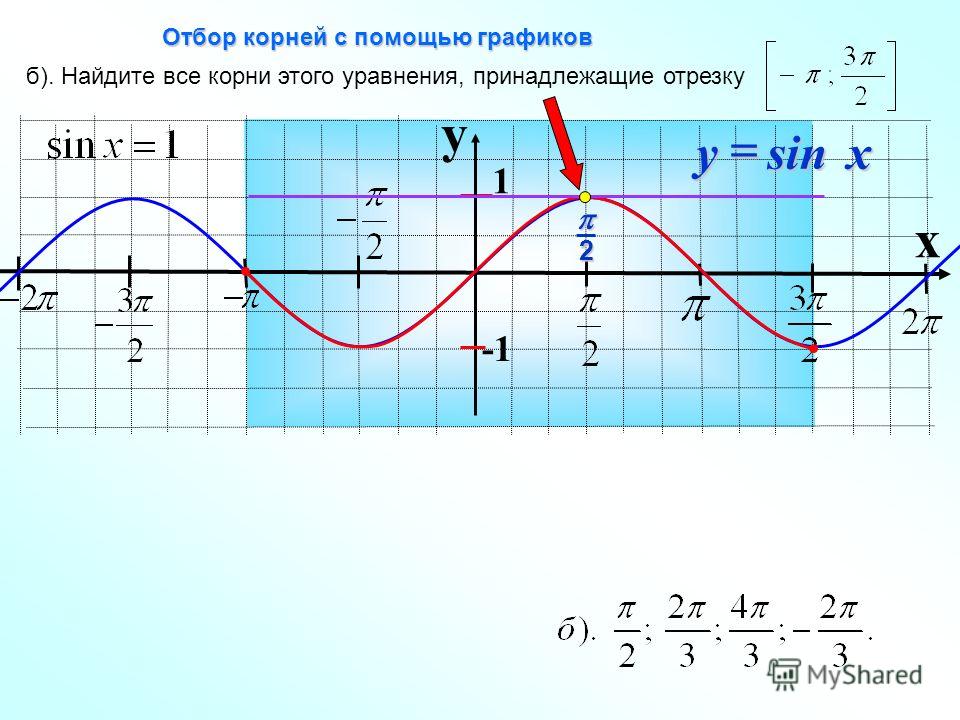
Это говорит нам о том, что область определения функции квадратного корня равна 𝑥≥0, что выражается в интервальной записи как [0,∞[.График функции извлечения квадратного корня показан ниже.
На рисунке выше функция квадратного корня изображена на интервале [0,2]. Хотя график функции кажется более плоским при больших значениях 𝑥, он продолжает неограниченно увеличиваться. Мы можем наблюдать этот эффект, построив график функции квадратного корня на большем интервале [0,1000].
Мы видим, что 𝑦-значение графика продолжает увеличиваться для больших значений 𝑥. Фактически, для любого большого положительного числа 𝑦 мы знаем, что √𝑦=𝑦. Также мы знаем, что √0=0. Следовательно, диапазон функции квадратного корня равен [0,∞[.
Теорема: Область определения и область значений функции квадратного корня
Область определения и область значений функции квадратного корня 𝑓(𝑥)=√𝑥 равна [0,∞[.
В более общем смысле область определения функции составного квадратного корня √𝑔(𝑥) можно определить, найдя значения 𝑥, удовлетворяющие 𝑔(𝑥)≥0.

Рассмотрим несколько примеров, в которых мы идентифицируем область определения и диапазон функций, включающих квадратный корень.
Пример 1. Нахождение области определения корневых функций
Рассмотрим функцию 𝑓(𝑥)=√−𝑥.
- Найдите домен 𝑓(𝑥).
- Найдите диапазон 𝑓(𝑥).
Ответ
Часть 1
Напомним, что квадратный корень не может принимать в качестве аргумента отрицательное число. Следовательно, область определения данной функции находится путем установки выражения внутри квадратного корня больше или равного нулю. Другими словами, −𝑥≥0.
Это приводит к 𝑥≤0, что равно ]−∞,0] в интервальной записи.
Область определения 𝑓(𝑥) равна ]−∞,0].
Часть 2
Диапазон функции — это набор всех возможных значений функции. Мы знаем, что диапазон функции квадратного корня √𝑥 равен [0,∞[. Другими словами, для любого числа 𝑦 в интервале [0,∞[ можно найти некоторое число 𝑥, удовлетворяющее 𝑦=√𝑥.
 Это означает, что число −𝑥 удовлетворяет
𝑓(−𝑥)=√−(−𝑥)=√𝑥=𝑦.
Это означает, что число −𝑥 удовлетворяет
𝑓(−𝑥)=√−(−𝑥)=√𝑥=𝑦.Следовательно, любое число в интервале [0,∞[ является возможным значением функции 𝑓(𝑥)=√−𝑥.
Диапазон 𝑓(𝑥) равен [0,∞[.
Рассмотрим еще один пример получения области определения функции составного квадратного корня.
Пример 2. Нахождение области определения корневых функций
Найдите область определения функции 𝑓(𝑥)=√7𝑥−7.
Ответ
Напомним, что областью определения функции √𝑔(𝑥) называется множество 𝑥-значений, удовлетворяющих 𝑔(𝑥)≥0.
В этом примере 𝑔(𝑥)=7𝑥−7. Следовательно, областью определения этой функции является множество 𝑥-значений таких, что 7𝑥−7≥0.
Изменение этого неравенства приводит к 𝑥≥1, что записывается как [1,∞[ в интервальной записи.
Область определения 𝑓(𝑥)=√7𝑥−7 равна [1,∞[.
В следующем примере мы определим правильный график составной функции квадратного корня, учитывая ее область определения и область значений.
Пример 3.
 Определение графика радикальной функции
Определение графика радикальной функцииЧто из следующего является графиком 𝑓(𝑥)=√1−2𝑥?
Ответ
Давайте используем домен и диапазон 𝑓(𝑥)=√1−2𝑥 для идентификации графа. Мы знаем, что область определения √𝑔(𝑥) — это множество 𝑥-значений, удовлетворяющих 𝑔(𝑥)≥0.
В этом примере 𝑔(𝑥)=1−2𝑥. Следовательно, областью определения этой функции является множество 𝑥-значений таких, что 1−2𝑥≥0.
Изменение этого неравенства приводит к 𝑥≤12, что в интервальной записи записывается как −∞,12. Следовательно, область определения 𝑓(𝑥) равна −∞,12.
Напомним, что диапазон функции извлечения квадратного корня √𝑥 равен [0,∞[. Мы заметили, что 𝑓(𝑥)=√𝑔(𝑥), где 𝑔(𝑥)=1−2𝑥. Поскольку диапазон 𝑔(𝑥)=1−2𝑥 — это все действительные числа, √𝑔(𝑥) должен иметь тот же диапазон, что и √𝑥. Это приводит к диапазону 𝑓(𝑥), который равен [0,∞[.
Определим, какой из графиков представляет функцию, область определения которой равна −∞,12, а область значений равна [0,∞[.
 На каждом заданном графике область определения функции, соответствующей графику, является частью горизонтальной оси, на которой существует график. Кроме того, диапазон функции — это часть вертикальной оси, на которой существует график. Мы получаем область определения и диапазон каждой функции, используя ее график.
На каждом заданном графике область определения функции, соответствующей графику, является частью горизонтальной оси, на которой существует график. Кроме того, диапазон функции — это часть вертикальной оси, на которой существует график. Мы получаем область определения и диапазон каждой функции, используя ее график.- Домен: 12,∞, диапазон: [0,∞[
- Домен: −∞,12, диапазон: ]−∞,0[
- Домен: ]−∞,∞[ диапазон: ]−∞,∞[
- Домен: −∞,12, диапазон: [0,∞[
- Домен: −12,∞, диапазон: [0,∞[
Следовательно, единственно возможный соответствие для 𝑓(𝑥)=√1−2𝑥 равно D.
Мы могли бы вспомнить, что при работе с рациональными функциями мы должны быть осторожны, чтобы ограничить область определения, чтобы гарантировать, что функция в знаменателе выражения не может быть равна нулю . Покажем, как найти область определения функции, являющейся отношением двух составных функций квадратного корня.
Пример 4. Нахождение области определения рациональных функций
Определите область определения функции 𝑓(𝑥)=√𝑥+7√𝑥−5.

Ответ
В данной функции мы наблюдаем два типа ограничений на домен.
- Квадратный корень: есть два выражения √𝑥+7 и √𝑥−5. Напомним, что функция квадратного корня не может принимать отрицательное число.
- Знаменатель: это выражение √𝑥−5. Напомним, что знаменатель дроби не может быть равен нулю.
Начнем с рассмотрения ограничений, накладываемых квадратными корнями. Чтобы √𝑥+7 было корректно определено, нам нужно 𝑥+7≥0. Это приводит к 𝑥≥−7, что является интервалом [−7,∞[.
Чтобы √𝑥−5 было корректно определено, нам нужно 𝑥−5≥0, что приводит к 𝑥≥5 или [5,∞[.
Наконец, рассмотрим знаменатель. Поскольку знаменатель не может быть равен нулю, нужно исключить случай, когда √𝑥−5=0. Возведение в квадрат обеих частей этого уравнения дает 𝑥−5=0, что приводит к 𝑥=5. Следовательно, нам нужно наложить 𝑥≠5.
Областью определения этой функции является множество 𝑥-значений, удовлетворяющих всем трем условиям: [−7,∞[[5,∞[𝑥≠5.
Чтобы увидеть, как взаимодействуют эти три ограничения, проведем числовую линию с этими ограничениями.

На приведенной выше диаграмме фиолетовое выделение представляет интервал [−7,∞[ зеленое выделение представляет интервал [5,∞[ а красный крестик представляет ограничение 𝑥≠5. Мы можем нарисовать интервал, который одновременно удовлетворяет пересечению этих ограничений.
Следовательно, область определения 𝑓(𝑥) равна ]5,∞[.
Пример 5. Нахождение области определения рациональных функций
Найдите область определения 𝑓(𝑥)=√𝑥−1√9−𝑥−√𝑥−3.
Ответ
В данной функции мы наблюдаем два типа ограничений на домен.
- Квадратный корень: есть три выражения √𝑥−1, √9−𝑥 и √𝑥−3. Напомним, что функция квадратного корня не может принимать отрицательное число.
- Знаменатель: это выражение √9−𝑥−√𝑥−3. Напомним, что знаменатель дроби не может быть равен нулю.
Начнем с рассмотрения ограничений, накладываемых квадратными корнями. Чтобы √𝑥−1 было корректно определено, нам нужно 𝑥−1≥0. Это приводит к 𝑥≥1, что является интервалом [1,∞[.

Аналогично выражения √9−𝑥 и √𝑥−3 приводят к интервалам ]−∞,9] и [3,∞[ соответственно.
Далее рассмотрим знаменатель. Поскольку знаменатель не может быть равен нулю, нужно исключить случай, когда √9−𝑥−√𝑥−3=0.
Мы можем добавить √𝑥−3 к обеим частям этого уравнения, чтобы получить √9−𝑥=√𝑥−3.
Возведение обеих сторон в квадрат приводит к 9−𝑥=𝑥−312=2𝑥𝑥=6.
Следовательно, нам нужно наложить 𝑥≠6.
Мы обнаружили четыре доменных ограничения для 𝑓(𝑥): [1,∞[]−∞,9],[3,∞[𝑥≠6.
Давайте проведем числовую линию, чтобы представить, как взаимодействуют эти ограничения.
На приведенной выше диаграмме фиолетовое выделение представляет интервал [1,∞[ зеленое выделение представляет интервал ]−∞,9], синее выделение представляет [3,∞[ а красный X представляет ограничение 𝑥 ≠6. Мы можем нарисовать множество, удовлетворяющее всем четырем ограничениям одновременно.
Следовательно, область определения 𝑓(𝑥) равна [3,9]−{6}.
В предыдущих примерах мы рассматриваем область определения и диапазон функций квадратного корня с линейными выражениями, 𝑎𝑥+𝑏.
 В следующем примере мы найдем домен и диапазон функции составного квадратного корня, где выражение внутри квадратного корня включает функцию абсолютного значения.
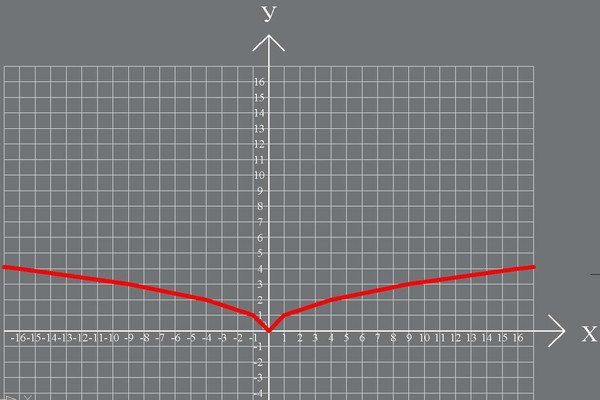
В следующем примере мы найдем домен и диапазон функции составного квадратного корня, где выражение внутри квадратного корня включает функцию абсолютного значения.Пример 6. Нахождение области рациональных функций
Рассмотрим функцию 𝑓(𝑥)=√4−|𝑥−5|.
- Найдите домен 𝑓(𝑥).
- Найдите диапазон 𝑓(𝑥).
Ответ
Часть 1
Найдем область определения заданной функции. Мы знаем, что область определения √𝑔(𝑥) — это множество 𝑥-значений, удовлетворяющих 𝑔(𝑥)≥0.
В функции 𝑓(𝑥) выражение 4−|𝑥−5| находится под квадратным корнем. Следовательно, нам нужно найти такие значения 𝑥, что 4−|𝑥−5|≥0.
Чтобы решить неравенство с абсолютным значением, мы начинаем с выделения абсолютного значения на одной стороне неравенства. Добавление |𝑥−5| к обеим частям неравенства, получаем 4≥|𝑥−5|.
Мы можем рассмотреть это в двух отдельных ситуациях. Сначала рассмотрим случай, когда 𝑥−5 неотрицательно. Поскольку абсолютное значение не изменяет неотрицательное число, неравенство такое же, как 4≥𝑥−5.

Во-вторых, рассмотрим случай, когда 𝑥−5 отрицательно. Поскольку абсолютное значение убирает отрицательный знак, 𝑥−5 должно быть не менее −4, чтобы удовлетворить неравенству 4≥|𝑥−5|. Другими словами, 𝑥−5≥−4. Вместе, 4≥|𝑥−5| такой же как −4≤𝑥−5≤4.
Добавление 5 к неравенству приводит к 1≤𝑥≤9.
Область определения 𝑓(𝑥) равна [1,9].
Часть 2
Найдем диапазон 𝑓(𝑥). Диапазон функции — это множество всех возможных значений функции. Мы можем получить диапазон функции, рассмотрев максимальное и минимальное возможные значения функции. Поскольку любое значение функции 𝑓(𝑥) является квадратным корнем числа, мы знаем, что оно не может быть отрицательным. Таким образом, 0 будет наименьшим возможным значением функции, если это возможно. Для этого нужно, чтобы выражение под квадратным корнем было равно нулю. Это ведет к 4=|𝑥−5|.
Это возможно, когда 𝑥=1 или 𝑥=9. Это означает, что наименьшее возможное значение 𝑓(𝑥) равно 0.
Чтобы найти максимально возможное значение 𝑓(𝑥), заметим, что |𝑥−5| является неотрицательным числом.
 Поскольку выражение внутри квадратного корня равно 4−|𝑥−5|, функция будет иметь наибольшее значение, когда |𝑥−5|=0, что происходит, когда 𝑥=5. В этом случае значение функции равно √4=2. Итак, максимальное возможное значение 𝑓(𝑥) равно 2.
Поскольку выражение внутри квадратного корня равно 4−|𝑥−5|, функция будет иметь наибольшее значение, когда |𝑥−5|=0, что происходит, когда 𝑥=5. В этом случае значение функции равно √4=2. Итак, максимальное возможное значение 𝑓(𝑥) равно 2.Чтобы окончательно заключить, что диапазон этой функции равен [0,2], нам нужно знать, что возможны все значения от 0 до 2. Если 𝑦 — любое значение от 0 до 2, найдем число 𝑥 такое, что 𝑓(𝑥)=𝑦. У нас есть 𝑦=√4−|𝑥−5|.
Возводя в квадрат обе части уравнения, 𝑦=4−|𝑥−5|.
Преобразуя уравнение, |𝑥−5|=4−𝑦.
Как и раньше, мы можем разделить это уравнение на два случая в зависимости от знака 𝑥−5. Но так как нам просто нужно найти одно возможное значение 𝑥, давайте просто возьмем 𝑥−5>0. В этом случае мы имеем 𝑥−5=4−𝑦, что приводит к 𝑥=9−𝑦. Проверим, если 𝑓9−𝑦=𝑦. Подставляя 𝑥=9−𝑦 в функцию 𝑓(𝑥), получаем 𝑓9−𝑦=√4−|(9−𝑦)−5|=√4−|4−𝑦|.
Поскольку 0≤𝑦≤2, мы знаем, что 4−𝑦>0, поэтому мы можем игнорировать абсолютное значение в ||4−𝑦||.
 Продолжая сверху:
=√4−(4−𝑦)=√4−4+𝑦=√𝑦.
Продолжая сверху:
=√4−(4−𝑦)=√4−4+𝑦=√𝑦.Поскольку 𝑦>0, √𝑦=𝑦. Следовательно, мы показали, что для любого 0≤𝑦≤2 имеем 𝑥=9−𝑦, удовлетворяющее 𝑓(𝑥)=𝑦.
Диапазон 𝑓(𝑥) равен [0,2].
Мы рассмотрели множество примеров области определения и диапазона функций, включающих квадратный корень. В отличие от квадратного корня, функция кубического корня не накладывает никаких ограничений на домен или диапазон. Ниже приведен график функции кубического корня √𝑥.
В отличие от функции квадратного корня, мы отмечаем, что функция распространяется на левую и правую стороны оси 𝑦, что указывает на то, что кубический корень может принимать любые действительные числа. Мы также отмечаем, что 𝑦-значения стремятся к положительной или отрицательной бесконечности, когда мы движемся влево или вправо. Это указывает на то, что областью действия функции кубического корня являются все действительные числа.
Теорема: Область определения и область значений функции кубического корня
Область определения и область значений функции кубического корня, 𝑓(𝑥)=√𝑥, являются действительными числами.
 Это обозначается как ]−∞,∞[ или ℝ.
Это обозначается как ]−∞,∞[ или ℝ.В следующем примере мы определим область определения функции кубического корня, где выражение под кубическим корнем является линейным, 𝑎𝑥+𝑏.
Пример 7. Нахождение области определения функции кубического корня
Определите область определения функции 𝑓(𝑥)=√4𝑥+3.
Ответ
Напомним, что область определения и область значений функции кубического корня √𝑥 равны ]−∞,∞[. Другими словами, функция кубического корня не накладывает никаких ограничений на предметную область. Поскольку выражение 4𝑥+3 под кубическим корнем не имеет ограничений по домену, нет никаких ограничений на возможные 𝑥-значения для этой функции.
Следовательно, областью определения 𝑓(𝑥)=√4𝑥+3 являются все действительные числа, ℝ.
В нашем последнем примере мы найдем область определения и область значений функции, включающей квадратный и кубический корни.
Пример 8. Нахождение области рациональных функций
Рассмотрим функцию 𝑓(𝑥)=125−√2𝑥+3.

- Найдите домен 𝑓(𝑥).
- Найдите диапазон 𝑓(𝑥).
Ответ
Часть 1
Найдем область определения 𝑓(𝑥). Напомним ограничения области для квадратного и кубического корней.
- Функция квадратного корня √𝑥 имеет область определения [0,∞[.
- Функция кубического корня √𝑥 не имеет доменных ограничений. Область определения функции кубического корня — все действительные числа, или ℝ.
Поскольку кубический корень не накладывает никаких ограничений на домен, нам нужно только рассмотреть ограничение из выражения квадратного корня √2𝑥+3. Сделав выражение 2𝑥+3 неотрицательным, 2𝑥+3≥0.
Изменение этого неравенства приводит к 𝑥≥−1,5.
Область определения 𝑓(𝑥) равна [−1,5,∞[.
Часть 2
Найдем диапазон 𝑓(𝑥). Сначала рассмотрим выражение √2𝑥+3. Напомним, что диапазон функции квадратного корня √𝑥 равен [0,∞[. Обратите внимание, что √2𝑥+3 можно записать как √2𝑥+3=𝑔(2𝑥+3),𝑔(𝑥)=√𝑥.
 где
где𝑔(𝑥). Таким образом, диапазон √2𝑥+3 равен [0,∞[. Это говорит нам о том, что выражение √2𝑥+3 будет выводить неотрицательные значения. Тогда возможные значения для 𝑓(𝑥)=125−√2𝑥+3 можно записать как √125−𝑎,𝑎≥0, для некоторых
Наибольшее возможное значение этого происходит, когда 𝑎=0, что дает нам √125=5. Поскольку наибольшее значение функции равно 5, и мы знаем, что функция кубического корня √𝑥 стремится к −∞ слева от оси 𝑦, мы хотели бы заключить, что диапазон функции равен ]−∞,5] . Тщательно обоснуем этот вывод.
Если 𝑦 — некоторое число, удовлетворяющее 𝑦≤5, нам нужно показать, что 𝑦=√125−𝑎𝑎≥0,для некоторых
Мы можем возвести обе части уравнения в кубическую степень, чтобы получить 𝑦=125−𝑎.
Преобразование этого уравнения приводит к 𝑎=125−𝑦.
Поскольку 𝑦≤5, имеем 𝑦≤125, что означает 𝑎≥0. Это говорит нам о том, что 𝑦 является возможным значением функции, пока 𝑦≤5.
Диапазон 𝑓(𝑥) равен ]−∞,5].
Давайте закончим повторением нескольких важных понятий из этого объяснения.


 {3}[/латекс].
{3}[/латекс].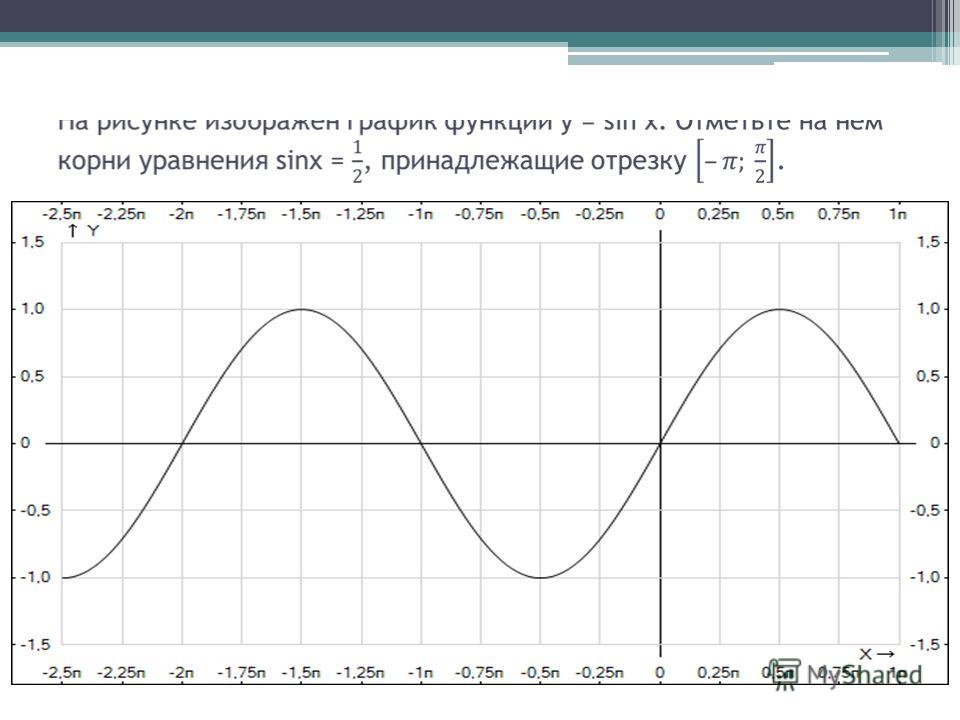 { 3}[/латекс]. Мы называем это тройным нулем или нулем с кратностью 3,9.1819
{ 3}[/латекс]. Мы называем это тройным нулем или нулем с кратностью 3,9.1819
 {п}[/латекс], является четной степенной функцией, поскольку x увеличивается или уменьшается без ограничений, [латекс]f\left(x\right)[/латекс] увеличивается без ограничений. Когда ведущий член представляет собой нечетную степенную функцию, поскольку x убывает неограниченно, [латекс]f\left(x\right)[/латекс] также неограниченно уменьшается; поскольку x увеличивается без ограничений, [латекс]f\left(x\right)[/латекс] также увеличивается без ограничений. Если ведущий член отрицательный, он изменит направление конечного поведения. В таблице ниже представлены все четыре случая.
{п}[/латекс], является четной степенной функцией, поскольку x увеличивается или уменьшается без ограничений, [латекс]f\left(x\right)[/латекс] увеличивается без ограничений. Когда ведущий член представляет собой нечетную степенную функцию, поскольку x убывает неограниченно, [латекс]f\left(x\right)[/латекс] также неограниченно уменьшается; поскольку x увеличивается без ограничений, [латекс]f\left(x\right)[/латекс] также увеличивается без ограничений. Если ведущий член отрицательный, он изменит направление конечного поведения. В таблице ниже представлены все четыре случая. Квадратный корень числа «x» — это число «y», такое, что y 2 = х. т. е. если y 2 = x ⇒ y = √x. т. е. если «x» — это квадрат «y», то «y» — это квадратный корень из «x». Некоторые примеры:
Квадратный корень числа «x» — это число «y», такое, что y 2 = х. т. е. если y 2 = x ⇒ y = √x. т. е. если «x» — это квадрат «y», то «y» — это квадратный корень из «x». Некоторые примеры:
 т. е. √25 = 5 или -5 как 5 2 = 25 и (-5) 2 = 25. Но диапазон функции квадратного корня (т. е. ее значения y) ограничен только положительными числами, потому что в противном случае он не пройдет тест вертикальной линии и не будет функцией, если вход имеет два выхода. Таким образом,
т. е. √25 = 5 или -5 как 5 2 = 25 и (-5) 2 = 25. Но диапазон функции квадратного корня (т. е. ее значения y) ограничен только положительными числами, потому что в противном случае он не пройдет тест вертикальной линии и не будет функцией, если вход имеет два выхода. Таким образом, Затем мы можем получить несколько точек, которые мы нанесем на координатную плоскость, и соединим их все кривой.
Затем мы можем получить несколько точек, которые мы нанесем на координатную плоскость, и соединим их все кривой.

 По этому правилу d(√x)/dx = d(x 1/2 )/dx = (1/2) x (1/2) — 1 = (1/2) x -1/ 2 = 1/(2√x). Таким образом, производная от √x равна 1/(2√x).
По этому правилу d(√x)/dx = d(x 1/2 )/dx = (1/2) x (1/2) — 1 = (1/2) x -1/ 2 = 1/(2√x). Таким образом, производная от √x равна 1/(2√x).
 Таким образом, мы можем найти информацию о количестве действительных нулей полинома, взглянув на график, и, наоборот, мы можем сказать, сколько раз график будет касаться или пересекать x -ось, глядя на нули многочлена (или на факторизованную форму многочлена).
Таким образом, мы можем найти информацию о количестве действительных нулей полинома, взглянув на график, и, наоборот, мы можем сказать, сколько раз график будет касаться или пересекать x -ось, глядя на нули многочлена (или на факторизованную форму многочлена). com
com
 Если ноль имел кратность 1, график пересекал ось x в нуле; если ноль имел кратность 2, график просто «поцеловал» ось x , прежде чем вернуться в исходное положение.
Если ноль имел кратность 1, график пересекал ось x в нуле; если ноль имел кратность 2, график просто «поцеловал» ось x , прежде чем вернуться в исходное положение. Когда я делаю предположения по картинке, мне приходится делать определенные предположения.)
Когда я делаю предположения по картинке, мне приходится делать определенные предположения.) Суммируя их минимальные кратности, я получаю:
Суммируя их минимальные кратности, я получаю: htm
htm Это говорит нам о том, что область определения функции квадратного корня равна 𝑥≥0, что выражается в интервальной записи как [0,∞[.
Это говорит нам о том, что область определения функции квадратного корня равна 𝑥≥0, что выражается в интервальной записи как [0,∞[.
 Это означает, что число −𝑥 удовлетворяет
𝑓(−𝑥)=√−(−𝑥)=√𝑥=𝑦.
Это означает, что число −𝑥 удовлетворяет
𝑓(−𝑥)=√−(−𝑥)=√𝑥=𝑦. Определение графика радикальной функции
Определение графика радикальной функции На каждом заданном графике область определения функции, соответствующей графику, является частью горизонтальной оси, на которой существует график. Кроме того, диапазон функции — это часть вертикальной оси, на которой существует график. Мы получаем область определения и диапазон каждой функции, используя ее график.
На каждом заданном графике область определения функции, соответствующей графику, является частью горизонтальной оси, на которой существует график. Кроме того, диапазон функции — это часть вертикальной оси, на которой существует график. Мы получаем область определения и диапазон каждой функции, используя ее график.

 В следующем примере мы найдем домен и диапазон функции составного квадратного корня, где выражение внутри квадратного корня включает функцию абсолютного значения.
В следующем примере мы найдем домен и диапазон функции составного квадратного корня, где выражение внутри квадратного корня включает функцию абсолютного значения.
 Поскольку выражение внутри квадратного корня равно 4−|𝑥−5|, функция будет иметь наибольшее значение, когда |𝑥−5|=0, что происходит, когда 𝑥=5. В этом случае значение функции равно √4=2. Итак, максимальное возможное значение 𝑓(𝑥) равно 2.
Поскольку выражение внутри квадратного корня равно 4−|𝑥−5|, функция будет иметь наибольшее значение, когда |𝑥−5|=0, что происходит, когда 𝑥=5. В этом случае значение функции равно √4=2. Итак, максимальное возможное значение 𝑓(𝑥) равно 2.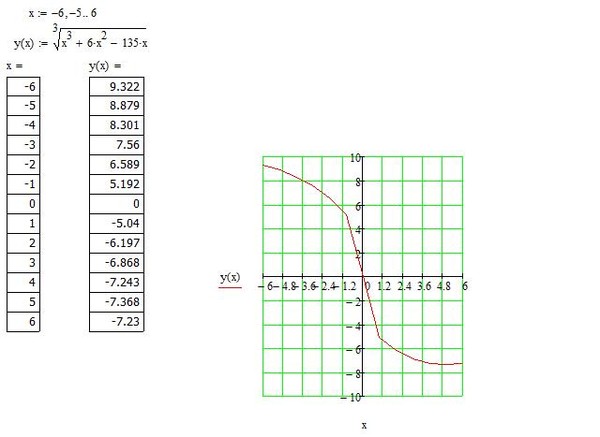 Продолжая сверху:
=√4−(4−𝑦)=√4−4+𝑦=√𝑦.
Продолжая сверху:
=√4−(4−𝑦)=√4−4+𝑦=√𝑦.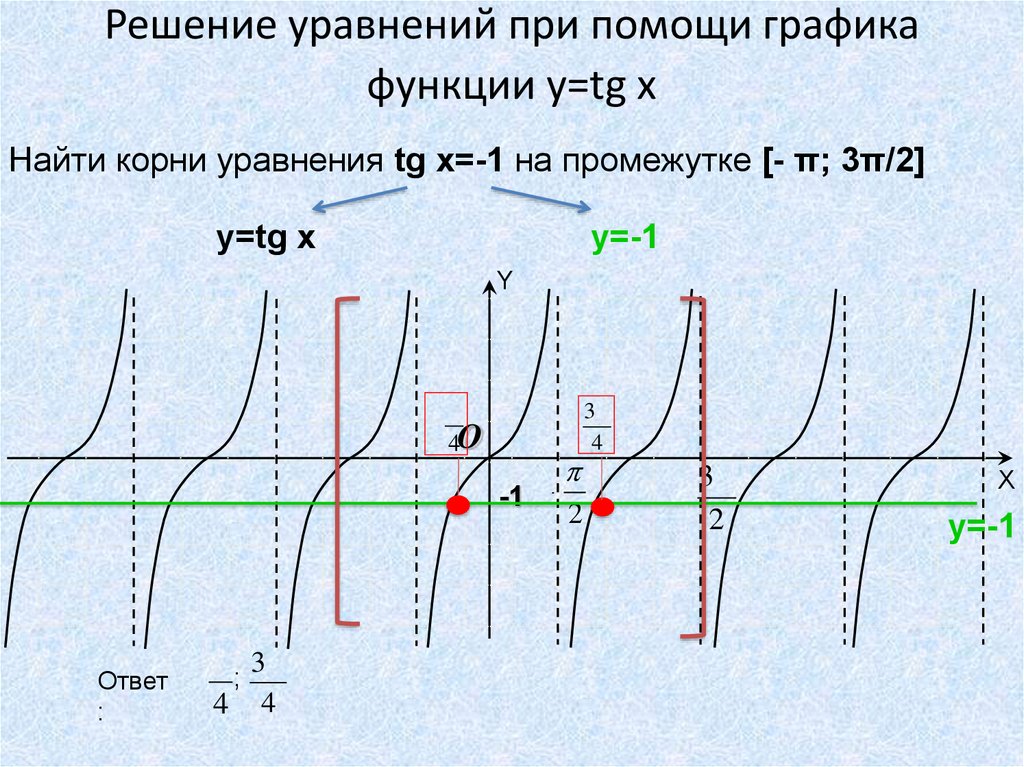 Это обозначается как ]−∞,∞[ или ℝ.
Это обозначается как ]−∞,∞[ или ℝ.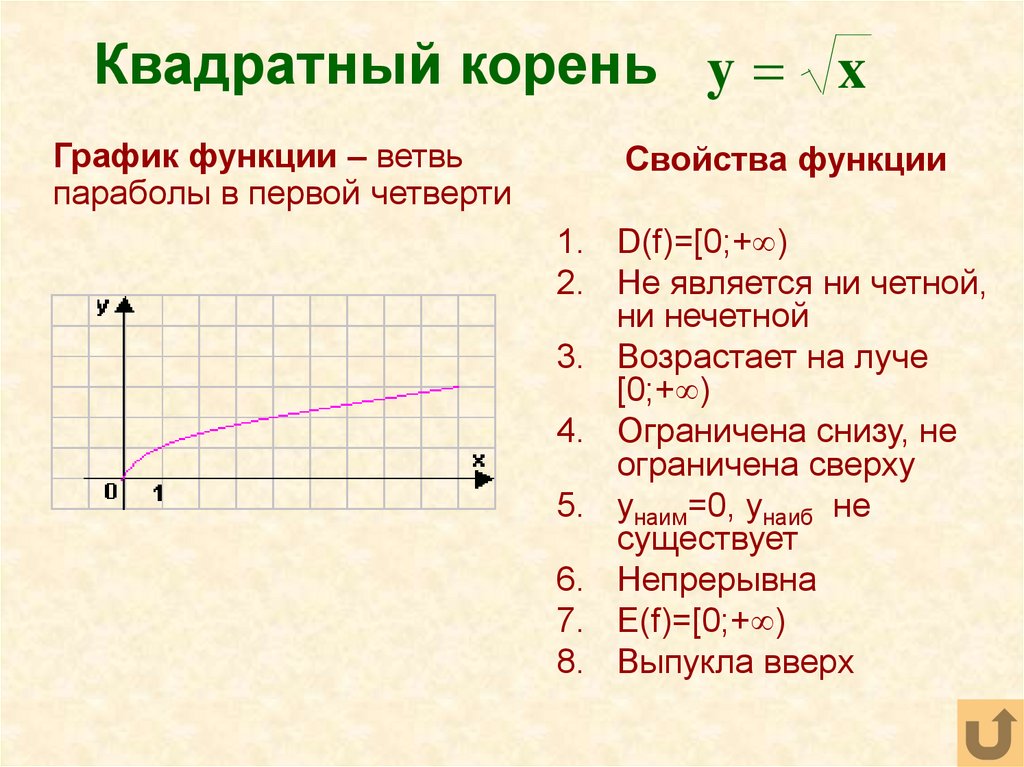
 где
где